Services on Demand
article
Indicators
Share
Avaliação Psicológica
Print version ISSN 1677-0471On-line version ISSN 2175-3431
Aval. psicol. vol.7 no.3 Porto Alegre Dec. 2008
ARTIGOS
Índices educacionais associados à proficiência em língua portuguesa: um estudo multinível
Educational indices associated with proficiency in portuguese: a multilevel regression study
Jacob Arie Laros*; João Luiz Marciano**
Universidade de Brasília
RESUMO
A identificação de variáveis que influenciam a proficiência em Língua Portuguesa é essencial para a elaboração de intervenções que visam melhorar o desempenho acadêmico dos alunos. Para tanto, os dados de 33.962 alunos da 3ª série de 1.661 escolas de Ensino Médio que fizeram o teste de Língua Portuguesa aplicado pelo SAEB em 2001 foram analisados utilizando análise multinível. Os resultados mostram que, depois do controle das variáveis relacionadas com a composição e seletividade da escola, o efeito escola está variando entre as regiões brasileiras de 0,10 para o Sul a 0,13 para o Norte. Estes valores indicam que mesmo depois da inserção das variáveis de controle, o conjunto de fatores escolares pode explicar entre 10% e 13% da variabilidade total do desempenho em português. As análises permitiram a identificação de três variáveis no nível da escola e dez variáveis no nível do aluno associados ao desempenho em Língua Portuguesa.
Palavras-chave: Avaliação educacional, Provas de desempenho, SAEB, Análise de regressão.
ABSTRACT
The identification of variables that affect proficiency in Portuguese Language is essential for the elaboration of interventions that seek to improve student achievement in Brazil. To achieve this goal, we analyzed the data of 33,962 third grade students of 1,661 secondary schools who took the Portuguese Language test of the National Basic Education System of Evaluation of Basic Education (SAEB) in 2001 using multilevel analysis. The results of this study showed that, after controlling the effect of variables related to the composition and selectivity of the schools, the intraclass correlation varied among the Brazilian regions between 0.10 for the South and 0.13 for the North. These figures indicate that even after the insertion of the control variables, school factors can explain between 10% and 13% of the total variability in Portuguese performance. Three variables on school level and ten variables on student level were identified as affecting proficiency in Portuguese Language.
Keywords: Educational evaluation, Proficiency test, SAEB, Regression analysis.
Introdução
No Brasil, a partir da última década, a técnica de modelos hierárquicos lineares começou a ser utilizada numa freqüência maior para interpretar e analisar os dados de avaliação educacional em larga escala. Como exemplos, podem-se citar o Sistema Nacional de Avaliação da Educação Básica (SAEB), a Prova Brasil, o Exame Nacional do Ensino Médio (ENEM), o Exame Nacional de Desempenho de Estudantes (ENADE), o Sistema de Avaliação de Rendimento Escolar do Estado do São Paulo (SARESP) e Programa de Avaliação da Educação Básica (PROEB) do Estado de Minas Gerais. Todas estas avaliações educacionais em larga escala têm em comum o objetivo geral de identificar e contextualizar os resultados dos alunos para melhorar a qualidade da educação brasileira (Albernaz, Ferreira & Franco, 2002; Fletcher, 1998).
A técnica de modelos hierárquicos lineares precisa ser utilizada sempre que os dados que queremos analisar têm uma estrutura hierárquica, ou seja, quando os dados são coletados de indivíduos que são aninhados em grupos ou contextos, uma situação bastante comum na pesquisa educacional. O que estimulou o uso crescente da referida técnica foi a maior disponibilidade de pacotes estatísticos no mercado, como HLM (Hierarchical Linear Models; Bryk e Raudenbush & Congdon, 1996) e MLwiN (Rashbash, Prosser & Goldstein, 1991). Outros nomes utilizados para modelos hierárquicos lineares são: modelos de regressão multinível, modelos lineares de coeficientes randômicos, modelos lineares mistos e análise de regressão multinível. O termo linear indica que os modelos hierárquicos lineares são associados aos modelos lineares bem conhecidos, como regressão tradicional e análise de variância (ANOVA). O termo randômico significa que o coeficiente de regressão nos modelos multinível não precisa ser igual para todas as unidades do nível macro. Para reconhecer explicitamente o contexto de grupo das observações, os modelos hierárquicos levam em conta a correlação intra-classe (i.c.c. - intraclass correlation), produzindo erros padrão de coeficientes que levam em conta o chamado efeito de delineamento. O efeito de delineamento é a quantidade de viés nos erros padrão por causa de observações dependentes (Hox & Maas, 2005). Kish (1965) define o efeito de delineamento como a razão entre a variância efetiva da amostra e a variância observada. Um exemplo apontado por Hox (2002) indica que uma amostra de 200 alunos agrupados em 10 classes, com uma correlação intra-classe igual a 0,10, corrigida pelo efeito de delineamento, equivale a uma amostra real de 69 alunos. Assim, o tamanho factual da amostra de 200 é reduzido para um tamanho efetivo de apenas 69, ou seja, uma diminuição de 66%.
Um dos primeiros estudos no Brasil utilizando a análise de regressão multinível na área de avaliação educacional foi o de Fletcher (1998). Fletcher analisou a base de dados da prova de Matemática do Sistema Nacional de Avaliação da Educação Básica (SAEB) de 1995, administrada aos alunos da 8a série do Ensino Fundamental. O SAEB avalia, desde 1993, a cada dois anos, alunos ao final de cada ciclo, no ensino fundamental (4a e 8a séries) e no ensino médio (3a série). O autor alerta para a necessidade de ajustar os resultados médios das provas do SAEB pelas diferenças na composição social do alunado das escolas. Para identificar as características das escolas que são associadas com um bom desempenho escolar é necessário levar em conta o ambiente familiar do aluno e o nível sócio-econômico da comunidade em torno da escola.
Fletcher (1998) relata uma correlação i.c.c. bruta de 0,31 e uma i.c.c. corrigida pelo nível sócio-econômico de 0,14. A i.c.c. corrigida, também chamada de i.c.c. residual ou i.c.c. condicional, representa, neste caso, o grau de dependência entre as observações em escolas do mesmo nível sócio-econômico. Mesmo depois de condicionar pelo nível sócio-econômico médio da escola, resta variância significativa entre as escolas para identificar fatores no nível macro que são associadas ao desempenho escolar. O autor observou que 63,1% da variância entre as escolas no desempenho em Matemática se atribuem à seletividade de ordem socioeconômica das escolas e somente 0,8% da variância no nível micro é explicada pelo nível sócio-econômico do aluno. Fletcher (1998) chega à conclusão de que a associação entre o desempenho em Matemática e os fatores socioeconômicos é muito mais forte no nível da escola do que no nível de alunos individuais. Portanto, para prever o desempenho médio da escola o conhecimento do nível socio-econômico médio dos alunos é extremamente importante. As análises de Fletcher (1998) apontam para efeitos positivos da proporção na escola de alunos do sexo masculino e de cor branca sobre o desempenho em Matemática. O autor observou que um ponto fraco do seu modelo final de regressão multinível é a capacidade de explicar a variância no nível individual dentro de escolas: apenas 6,5% da variabilidade no nível do aluno foram explicados versus 71,6% da variabilidade no nível da escola. O autor sugere que os questionários contextuais do SAEB deveriam ser examinados para aprimorar seu potencial de explicar as diferenças no desempenho individual dentro das escolas.
Ferrão e Fernandes (2003) utilizaram a técnica de modelos hierárquicos lineares para analisar os dados coletados no SAEB de 1997, abrangendo 3.739 alunos da 4a série do Ensino Fundamental da região Sudeste (estados de Minas Gerais, Espírito Santo, Rio de Janeiro e São Paulo), aos quais foi aplicado o teste de Matemática. Os pesquisadores utilizaram um modelo de regressão multinível de três níveis hierárquicos (aluno, turma e escola). A i.c.c. bruta neste estudo foi de 0,37 indicando que 37% da variância total podem ser atribuídas aos níveis de escola e turma juntas e 57% ao nível do aluno. Neste estudo não foi possível calcular a i.c.c. corrigida pelo NSE, porque como variável de controle foi utilizada a escolaridade do pai e não o NSE da família. Depois do controle do nível da educação do pai, os autores verificaram que variáveis referentes à infra-estrutura e aos equipamentos escolares são preditores de um bom desempenho dos alunos. Ferrão e Fernandes (2003) assinalam que, quando se objetiva pesquisar sobre o desempenho escolar, o nível socioeconômico familiar e o conhecimento prévio do aluno devem ser primeiramente considerados. O modelo final deste estudo explicou 99,1% da variância do nível da escola, 39,5% do nível da turma e 5,5% do nível do aluno. Os autores chegam à conclusão de que as características associadas a professores reduzem a variabilidade entre escolas em 24% e entre turmas em 26%.
Albernaz, Ferreira e Franco (2002) analisaram os dados das provas de Ciência, Geografia, História, Português e Matemática aplicadas na 8a série do SAEB, aplicadas em 1999, utilizando análise de regressão multinível. Como variáveis de controle foram inseridas o nível socioeconômico, a repetência escolar e o gênero dos alunos. Os autores relataram uma i.c.c. bruta de 0,28 e uma i.c.c. residual de 0,08; isto indica que mesmo após a entrada das variáveis de controle ainda 8% da variância total presente nas provas do SAEB podem ser atribuídos à variabilidade entre escolas. Os resultados deste estudo indicaram um desempenho superior dos alunos de sexo masculino em Matemática, Geografia e Ciências e um desempenho melhor das alunas em Português. Depois da entrada das variáveis de controle, os autores ainda encontraram uma diferença média nas provas de alunos brancos e negros de 7,5 pontos na escala do SAEB. Os autores observaram que o NSE médio da escola é associado ao rendimento escolar do aluno. Mesmo depois de controlar pelo NSE médio da escola, o NSE do aluno individual tem um efeito positivo no seu desempenho escolar. Mas este efeito positivo do NSE individual não é igual em todas as escolas. Quanto mais alto o NSE médio da escola, menor o efeito do NSE individual do aluno. Os autores concluíram que as escolas com alunos mais ricos tendem a compensar melhor pelas desvantagens educacionais de alunos oriundos de famílias mais pobres do que escolas com alunos mais pobres. No modelo final deste estudo, pelo menos 5,6% da variância no nível micro e 80,4% da variância do nível macro foram explicados.
Soares e Alves (2003) pesquisaram as desigualdades raciais no sistema brasileiro de educação básica utilizando a análise de regressão multinível. Os autores analisaram a base de dados referente à prova de Matemática da 8a série do ensino fundamental do SAEB 2001. A base de dados tinha as respostas de 50.300 alunos de 4.056 escolas. No nível micro, foram incluídas como variáveis de controle o nível socioeconômico do aluno e o atraso escolar e no nível macro o nível socioeconômico médio, o atraso escolar médio e a rede escolar. O atraso escolar foi incluído como um indicador da proficiência prévia do aluno. Por proficiência em língua portuguesa, entende-se o domínio pelo aluno dos conceitos e conhecimentos relacionados com leitura em língua portuguesa compatíveis com sua série escolar, avaliada pelos testes (Barbosa & Fernandes, 2001). No modelo básico, no qual os efeitos das variáveis de controle foram retirados, a diferença entre o desempenho de alunos brancos e negros na prova de Matemática foi de 10 pontos na escala do SAEB. Antes da entrada das variáveis de controle a diferença entre o desempenho de alunos brancos e negros na prova foi de quase 28 pontos.
Soares e Alves (2003) relatam que a qualificação e o salário dos docentes têm efeito na diferença de desempenho entre alunos brancos e negros no sentido de aumentar o hiato no desempenho escolar desses grupos. Quanto melhor a qualificação e quanto mais alto o salário do docente, tanto maior a diferença entre alunos brancos e negros. Entre fatores escolares foi observada a mesma tendência. Escolas mais bem equipadas e com diretores mais envolvidos estão associadas com um aumento da média do desempenho escolar em Matemática, mas aumentam também as diferenças raciais. Os resultados deste estudo mostram que a melhoria das condições de ensino pode contribuir para elevar a média do desempenho escolar, mas ao mesmo tempo pode aumentar as diferenças entre alunos brancos e negros. Aparentemente, os alunos negros não usufruem as melhorias da escola tanto quanto os alunos brancos (Soares & Alves, 2003). Na pesquisa de destes autores não havia informação sobre quanta variância foi explicada no nível do aluno e no nível da escola.
Um estudo mais recente que objetivou identificar as características associadas com o desempenho acadêmico (Jesus & Laros, 2004) analisou os dados de 49.075 alunos da 8ª série de Ensino Fundamental que fizeram a prova de Língua Portuguesa do SAEB-2001. Como técnica de análise de dados foi utilizada a regressão multinível. Os autores relataram uma correlação intra-classe (i.c.c.) bruta de 0,35. Como variáveis de controle no primeiro nível (o nível de alunos) entraram na modelagem o status socioeconômico da família do aluno, a escolaridade do pai e a etnia do aluno. Como variáveis de controle do segundo nível foram incluídas as mesmas variáveis do nível do aluno - com a diferença de que foram agregadas para o nível da escola. Assim, o status socioeconômico médio dos alunos, a escolaridade média dos pais e a percentagem de alunos não-brancos ou não-asiáticos na escola entraram como variáveis de controle no nível de escola. O índice que representa o nível socioeconômico (NSE) do aluno foi obtido por meio de análise de componentes principais (ACP) e foi composto de 13 itens do questionário contextual aplicado junto com a prova de português. Os itens são principalmente relacionados aos bens na residência dos alunos como, por exemplo, a quantidade de automóveis, computadores, televisões, rádios etc. O índice da escala de NSE mostrou um coeficiente de fidedignidade de 0,86. As outras variáveis de controle (escolaridade do pai e etnia do aluno) foram baseadas em uma única questão do questionário contextual.
Depois do controle das variáveis acima mencionadas, a i.c.c. corrigida apresentou um valor de 0,10; isso significa que mesmo após o controle das diferenças socioeconômicas entre o alunado das diversas escolas, 10% da variância total presente na prova de Língua Portuguesa devem-se à variabilidade entre escolas. Como Soares (2004) argumentou, é de suma importância relatar a correlação intra-classe corrigida pelo nível socioeconômico (NSE) do alunado, porque a i.c.c. bruta leva a atribuir às escolas um efeito que não é delas, mas da família, devido ao seu capital econômico e cultural. Escolas que recrutam alunos com um nível socioeconômico e cultural alto obterão resultados melhores nas provas do SAEB do que escolas que recrutam um alunado com um nível socioeconômico e cultural baixo. O valor da i.c.c. corrigida de 0,10 encontrado neste estudo está dentro do esperado, levando-se em consideração os resultados de uma revisão de Ferrão e Fernandes (2003) de investigações empíricas no Brasil sobre a i.c.c. em relação às provas de Matemática do SAEB nos anos 1995-2001. Os autores relataram valores da i.c.c. corrigida variando de 0,08 a 0,17 para as cinco regiões do Brasil.
Uma primeira conclusão do estudo de Jesus e Laros (2004) tem relação com o grande impacto do nível socioeconômico sobre o desempenho na prova de português: 79% da variância entre as escolas devem-se às variáveis relacionadas à composição socioeconômica das escolas. Este resultado é consistente com os valores achados por outros estudos multinível realizados com os dados das provas do SAEB (Barbosa & Fernandes, 2001; Soares, 2004; Soares, Cesar & Mambrini, 2001; Soares & Alves, 2003). É importante ressaltar que depois de controlar a influência do nível socioeconômico médio dos alunos da escola, o impacto do NSE individual do aluno sobre o desempenho em português é pequeno e tem sinal negativo. Depois de controlar o efeito do NSE médio da escola, o conhecimento do NSE individual do aluno ajuda muito pouco a prever o seu desempenho em português e alunos com NSE individual mais baixo têm um desempenho melhor. Este achado está em concordância com os resultados do estudo de Albernaz, Ferreira e Franco (2002).
Após o controle das variáveis relacionadas com a seletividade e composição escolar, a análise de regressão multinível permitiu a identificação de sete variáveis do nível da escola e quatro variáveis do nível do aluno. No nível micro - o nível dos alunos - as seguintes variáveis mostraram um efeito significativo no desempenho em Língua Portuguesa: (1) o grau de regularidade da trajetória escolar (sem atraso escolar); (2) a freqüência com que o aluno faz o dever de casa; (3) o grau em que o aluno pode se dedicar integralmente às atividades da escola e (4) quanto o aluno recebe apoio dos pais. É importante notar que a última variável mostrou uma relação negativa com o desempenho na prova de português. O sinal negativo não pode ser interpretado de tal forma que a ajuda dos pais causa o pior desempenho do aluno, pelo contrário: um desempenho fraco em português leva a mais ajuda e cobrança da parte dos pais. Aparentemente, quanto mais fraco o desempenho do aluno em Língua Portuguesa mais ajuda ele vai receber dos seus pais.
No nível macro, o nível das escolas, foram encontrados os seguintes índices com impacto positivo no desempenho em português: (1) a freqüência com que os professores passam e corrigem a lição de casa; (2) o grau de manutenção e utilização de recursos tecno-pedagógicos da escola; (3) a percentagem de alunos na turma cujos pais apóiam, incentivam e conversam com eles sobre assuntos diversos; (4) a percentagem de alunos na turma que só estudam e não têm vínculo trabalhista; (5) quanto os professores são comprometidos com a aprendizagem dos alunos; (6) quanto os professores têm altas expectativas em relação ao desempenho dos alunos, e (7) o estado de conservação das instalações físicas na escola. O modelo final neste estudo conseguiu explicar pelo menos 6,9% da variância no nível micro e 84,9% da variância do nível macro.
Andrade e Laros (2007) analisaram as características de alunos e escolas associadas ao desempenho escolar de 72.379 alunos de 3a série de Ensino Médio que fizeram a prova de Matemática ou a prova de Língua Portuguesa do SAEB em 2001. Neste estudo de regressão multinível, os autores acharam uma correlação intra-classe (i.c.c.) bruta de 0,46 e uma i.c.c. corrigida de 0,17, indicando que 17% da variância no desempenho escolar podem ser atribuídos ao nível de escola e o restante da variância (83%) ao nível dos alunos.
Como variáveis de controle no primeiro nível (o nível de alunos) foram incluídas o NSE da família do aluno, o gênero do aluno e a etnia do aluno. Como variáveis de controle do segundo nível (o nível de escola) foram incluídas o NSE médio dos alunos, a percentagem de meninos e a percentagem de alunos não-brancos ou não-asiáticos. O índice que representa o NSE do aluno foi construído através de ACP e foi composto por 16 itens do questionário contextual aplicado junto com as provas de Matemática e Língua Portuguesa. A escala de NSE neste estudo mostrou um coeficiente de fidedignidade de 0,87.
O efeito da composição socioeconômica e da seletividade da escola sobre o desempenho acadêmico médio entre as escolas encontrado neste estudo foi muito forte: 76% da variância entre as escolas podem ser atribuídos a estas variáveis. Depois da entrada no modelo das variáveis de controle, sete índices foram encontrados associados com o desempenho escolar no nível do aluno e dez índices no nível da escola. No nível do aluno, os seguintes índices mostraram um efeito positivo no desempenho escolar: (1) o grau de regularidade da trajetória escolar; (2) quanto o aluno se compara positivamente com os colegas da turma em relação ao seu desempenho escolar; (3) a falta de cobrança dos pais para fazer lição de casa; (4) quanto o aluno gosta de estudar Língua Portuguesa ou Matemática; (5) a quantidade de recursos culturais na família do aluno; (6) a freqüência com que o aluno faz o dever de casa e (7) o grau em que o aluno pode se dedicar exclusivamente às atividades da escola. Destas variáveis, a terceira merece destaque, pois pode parecer que quanto menos os pais cobram do aluno fazer o dever de casa, tanto melhor seu desempenho em português: como no estudo de Jesus e Laros (2004) parece que um desempenho fraco do aluno causa cobrança dos pais e não o contrário.
No nível da escola, os seguintes índices mostraram uma relação positiva com o desempenho escolar: (1) nível médio de recursos culturais na família dos alunos; (2) proporção dos alunos com uma trajetória escolar regular; (3) falta de cobrança dos pais quanto à lição de casa; (4) proporção dos alunos com dedicação exclusiva nas atividades escolares; (5) clima disciplinar na escola; (6) trabalho colaborativo entre os membros da equipe escolar; (7) manutenção e utilização de recursos tecno-pedagógicos; (8) quantidade de alunos na turma que fazem a lição de casa e (9) grau de experiência do professor. É importante observar que exceto pelas variáveis (6), (7) e (9) os valores foram obtidos por agregação. No modelo final neste estudo foram explicadas pelo menos 14,0% da variância no nível micro e 84,9% da variância do nível macro.
Um estudo de regressão multinível com intuito de identificar os fatores associados ao desempenho na prova de Matemática do SAEB-2001 (Laros, Marciano & Andrade, submetido) revelou que 77% da variabilidade no desempenho médio das escolas em Matemática podem ser atribuídos às variáveis relacionadas com a composição socioeconômica do alunado da escola. Foi encontrada uma i.c.c. bruta de 0,43. Depois do controle das variáveis relacionadas com a composição socioeconômica e cultural do alunado da escola, a i.c.c. residual diminuiu para o valor de 0,15 indicando que após o controle ainda 15% da variância total presente na prova de Matemática podem ser atribuídos à variabilidade entre escolas.
Depois de incluir as variáveis de controle, os seguintes índices no nível do aluno mostraram uma relação positiva com o desempenho em Matemática: (1) o grau de regularidade da trajetória escolar; (2) se o aluno é do sexo masculino; (3) quanto o aluno gosta de estudar Matemática; (4) o grau em que o aluno se compara positivamente com os colegas em relação ao seu desempenho em Matemática; (5) a falta de cobrança dos pais para fazer lição de casa; (6) a ausência de repetência do ano e (7) a freqüência com que o aluno faz o dever de casa. No nível da escola, os seguintes índices mostraram um efeito no desempenho em Matemática, sendo que o sinal dos dois primeiros efeitos é negativo e dos três últimos é positivo: (1) repetência agregada; (2) a quantidade de faltas agregada; (3) recursos culturais agregados; (4) trabalho colaborativo na escola e (5) clima disciplinar na escola. No modelo final de Laros, Marciano e Andrade foram explicadas pelo menos 19,8% do nível micro e 85,0% da variância do nível macro.
Em um estudo de Soares (2005) empregou-se uma análise de regressão multinível de três níveis hierárquicos para analisar quais fatores são associados ao desempenho dos alunos de 4ª série do ensino fundamental na prova de Língua Portuguesa de 2002 do Programa de Avaliação da Educação Básica (PROEB) do Estado de Minas Gerais. Neste estudo as informações de 2.438 escolas, 6.286 turmas e 161.904 alunos foram analisadas. Diferentemente do SAEB, todos os alunos da quarta e oitava série do ensino fundamental e da terceira série do ensino médio da rede estadual fazem o teste do PROEB. É importante ressaltar que foi possível utilizar o modelo de três níveis porque somente as escolas com quatro ou mais turmas de 4a série foram analisadas neste estudo. Soares (2005) utilizou na construção de modelos hierárquicos a estratégia bottom-up, isto é, parte-se do modelo nulo e vai-se incluindo as variáveis do primeiro nível (nível dos alunos), segundo nível (nível das turmas) e terceiro nível (nível das escolas). Por fim, as interações entre variáveis de diferentes níveis entram no modelo. Neste estudo a i.c.c. bruta tomou o valor de 0,43, indicando que 43% da variância total podem ser atribuídas aos níveis de escola e turma juntas e 57% ao nível do aluno.
Depois de controlar a influência de nível socioeconômico, atraso escolar, gênero do aluno e etnia do aluno, três variáveis do nível do aluno entraram: (1) se a família do aluno recebe bolsa escola; (2) o número de anos do aluno na pré-escola e (3) a taxa de estudos por parte do aluno. É interessante notar que o efeito da bolsa escola é negativo: alunos que possuem bolsa escola tendem a apresentar uma proficiência bem inferior aos que não possuem. Este resultado não deve ser interpretado erradamente no sentido de que a bolsa escola causa um desempenho fraco em Língua Portuguesa. O efeito negativo está associado à baixa condição social desse tipo de aluno, ou seja, alguns aspectos não foram controlados com a entrada das variáveis de controle do modelo. Aparentemente, o nível de conhecimento de Língua Portuguesa dos alunos que entraram na escola com uma bolsa família é menor do que o de outros alunos com um NSE similar. No nível da turma as seguintes variáveis mostraram um efeito sobre o desempenho em português: (1) se o professor passa dever de casa; (2) o grau de exigência do professor; (3) a motivação média da turma dos alunos; (4) o grau de dedicação e disponibilidade do professor e, por fim, (5) a quantidade de faltas do professor na sala de aula. No nível da escola as seguintes variáveis mostraram um efeito significativo, e relevante, sobre o desempenho em português: (1) a percentagem na escola de professores que participam de formação continuada; (2) a quantidade de equipamentos de informática na escola e (3) a idade média dos professores na escola. Quanto à influência da última variável é importante observar que quanto mais velhos os professores da escola tanto menor o desempenho em português dos alunos. O modelo final deste estudo explicou pelo menos 75,7% da variância do nível da escola, 69,1% do nível da turma e 7,5% do nível do aluno.
As pesquisas na área de avaliação educacional em larga escala realizadas no Brasil entre 1998 e 2007 com análise multinível, acima relatadas, mostram valores altamente diferenciados da i.c.c. incondicional (sem controle pelo NSE), variando de 0,28 (Albernaz, Ferreira & Franco, 2002) a 0,46 (Andrade & Laros, 2007). Os valores da i.c.c. condicional (após controle pelo NSE) mostram menos variabilidade: eles variam entre 0,08 (Albernaz, Ferreira & Franco, 2002) e 0,17 (Andrade & Laros, 2007). Estes valores estão em concordância com os valores relatados por Ferrão e Fernandes (2003) e compatíveis com os valores relatados nos trabalhos internacionais (conforme afirmado por Soares, 2004).
Conforme frisa Soares (2004), o que interessa relatar não é tanto a i.c.c. incondicional (também chamada de i.c.c. bruta), mas a i.c.c. condicional, representando a percentagem da variância total que o conjunto de fatores escolares pode explicar, após a retirada da influência das variáveis socioeconômicas sobre o desempenho dos alunos. Em concordância com Soares (2004), podemos afirmar que os valores da i.c.c. condicional dos estudos revisados são suficientemente grandes para o reconhecimento da existência de variação entre as escolas, de forma que a escola freqüentada faz diferença na vida do aluno. Ou seja, é possível melhorar o desempenho dos alunos através de mudanças na estrutura escolar.
Os estudos citados acima têm em comum uma quantidade baixa de variância explicada no nível do aluno: entre 5,5% (Ferrão & Fernandes, 2003) e 19,8% (Laros, Marciano & Andrade, submetido). Isso ocorre, entre outras coisas, em decorrência da falta de dados sobre características individuais dos alunos antes de entrar na escola como, por exemplo, a habilidade cognitiva, o desempenho acadêmico prévio e certas características de personalidade como motivação e persistência (Soares, Ribeiro & Castro, 2001; Teddlie & Reynolds, 2000). Ou seja, o que falta para poder explicar uma parte considerável da variância no nível micro são medidas fidedignas das habilidades cognitivas, do nível do conhecimento acadêmico e dos fatores da personalidade dos alunos antes do início da trajetória escolar.
A variância explicada do nível da escola nos estudos revisados, entretanto, é alta: situa-se entre 75,7% (Soares, 2005) e 99,1% (Ferrão & Fernandes, 2003). Na verdade, estes valores são tão elevados porque o modelo de referência utilizado para calcular esses valores foi o modelo vazio. O que produziria um retrato muito mais fiel da realidade seria utilizar o modelo básico e não o modelo vazio como ponto de referência para calcular os valores da variância explicada. O modelo básico é o modelo no qual o impacto do NSE é controlado simultaneamente nos dois níveis de agregação. Tomando o modelo básico como modelo de referência, a variância explicada do nível da escola dos estudos revisados fica bem menor: varia nos estudos brasileiros revisados entre 23,1% (Fletcher, 1998) e 36,7% (Andrade & Laros, 2007). Os valores da variância explicada do nível do aluno não mudam tanto tomando o modelo básico como referência: situam-se entre 6,5% (Fletcher, 1998) e 18,1% (Laros, Marciano & Andrade, submetido). Deve-se registrar que calcular a variância explicada com o uso de análise de regressão multinível é um assunto bastante complicado. Depois da entrada de variáveis com efeitos aleatórios, ou seja, com efeitos que podem variar entre as escolas, praticamente não é mais possível calcular quanta variância foi explicada. Por esta razão, precisa-se calcular a variância explicada antes da entrada das variáveis com efeitos aleatórios (Snijders & Bosker, 1994; 1999). Uma conseqüência disso é que na presença de variáveis aleatórias podemos somente fazer afirmações sobre o limite inferior da variância explicada. Ou seja, nestes casos, precisamos sempre utilizar uma restrição tipo pelo menos nas nossas afirmações sobre a variância explicada no modelo final.
Os estudos acima revisados mostram que no Brasil o volume de estudos que usam análise de regressão multinível para detectar os fatores que têm impacto no desempenho escolar dos alunos está aumentando. O uso da análise de regressão multinível, comparado às técnicas convencionais de análise de regressão, ajuda a identificar com um grau mais alto de confiança os fatores que realmente são associados com um bom desempenho escolar. A identificação de tais fatores é de suma importância para a elaboração de políticas públicas que possam melhorar a qualidade da educação brasileira (Soares, Cesar e Mambrini, 2001). Entretanto, é bom lembrar, como afirmam Soares e Alves (2003), que os fatores identificados são relacionados e que qualquer intervenção em fatores sociais, escolares ou familiares impacta não só a proficiência do aluno, mas também os outros fatores explicativos.
O objetivo prioritário do presente trabalho é identificar o impacto de características de alunos e escolas sobre a proficiência em português de alunos da 3a série do Ensino Médio no Brasil. Um segundo objetivo é verificar se existem diferenças no impacto das características de alunos e escolas sobre a proficiência em português entre as cinco regiões do Brasil.
Para atingir esses objetivos, foram considerados os alunos avaliados pelo Sistema Nacional de Avaliação da Educação Básica (SAEB) da 3ª série do Ensino Médio do ano de 2001. O SAEB foi implantado pelo Instituto Nacional de Estudos e Pesquisas Educacionais Anísio Teixeira (INEP), a partir de 1990. O objetivo do SAEB é fornecer informações sobre o Ensino Fundamental e Médio brasileiro, com o intuito de contribuir para a melhoria da qualidade da educação brasileira e para a universalização do acesso à escola (INEP, 2001).
Método
Participantes
A população de referência do SAEB 2001 correspondeu a todos os alunos matriculados, em 2001, na 4ª ou 8ª séries do Ensino Fundamental ou 3ª série do Ensino Médio, com exceção dos alunos das escolas federais, rurais ou de turmas multisseriadas. Somente para a 4ª série, foram mantidos os alunos das escolas rurais dos estados do Nordeste, Minas Gerais e Mato Grosso do Sul.
Para o presente trabalho, foram analisados os dados de 33.962 alunos da terceira série do ensino médio, distribuídos em 1.661 escolas brasileiras pesquisadas no SAEB/2001. Para mais informações sobre a amostra do SAEB 2001, ver Andrade, Silva e Bussab (2001) e Riether e Rauter (2002).
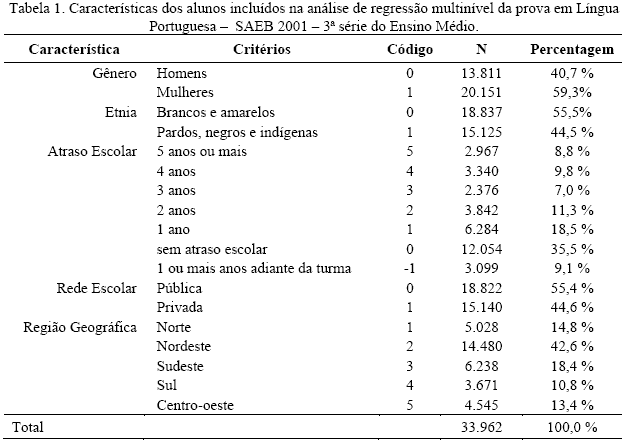
A Tabela 1 mostra as características dos alunos incluídos na regressão multinível da prova de Língua Portuguesa do exame do SAEB/2001. Observa-se que 59,3% dos alunos analisados pertencem ao gênero feminino, sendo os 40,7% restantes do gênero masculino, em uma relação de aproximadamente 3 mulheres para 2 homens. Quanto à etnia dos alunos, procedeu-se à codificação das etnias branca e amarela com o código 0, representando 55,5% da amostra, e as etnias parda, negra e indígena com o código 1, representado os demais 44,5%.
Quanto ao atraso escolar, ou seja, a diferença entre a idade atual e a idade ideal (indicada pela série em que o aluno está matriculado), os valores foram codificados de modo a indicar as categorias descritas na Tabela 1. O valor modal desta variável apresenta-se na categoria sem atraso escolar, representando 35,5% da amostra.
Os respondentes foram categorizados, ainda, quanto à rede de ensino que freqüentam no momento da prova: 55,4% da amostra são alunos da rede pública, sendo os demais 44,6% da rede privada. Por fim, quanto à região geográfica, o Nordeste apresentou a maior contribuição à amostra, com 42,6% dos alunos, seguido pelo Sudeste, com 18,4%, o Norte com 14,8%, o Centro-Oeste com 13,4% e o Sul com 10,8% dos alunos da amostra.
Instrumentos
O desempenho dos estudantes em Língua Portuguesa foi aferido por meio de um teste cognitivo, composto por questões objetivas envolvendo os seguintes tópicos: procedimento de leitura, implicações do suporte, do gênero e/ou do enunciador na compreensão do texto; relação entre textos; coerência e coesão no processamento do texto; relações entre recursos expressivos e efeito de sentido; e variação lingüística. Além disso, foram aplicados questionários contextuais dos alunos, professores, diretores e escolas. Esses questionários visam captar a origem social dos alunos e as condições em que eles estudam. O leitor interessado pode obter maiores detalhes em INEP (2001).
Análise de dados
Com o intuito de estimar os parâmetros de grupos populacionais específicos, a população de referência foi dividida em estratos segundo variáveis de interesse: série, unidade da federação, dependência administrativa (estadual, municipal ou particular) e localização (capital ou interior). Estatisticamente, a amostra analisada dispõe-se em uma distribuição complexa, ou seja, com probabilidades desiguais de inclusão dos elementos, além de estratificada mediante diferentes critérios, como se viu acima. Em tais casos, Pfeffermann, Skinner, Holmes, Goldstein e Rasbash (1998) recomendam enfaticamente a utilização de pesos amostrais, uma vez que, sem o uso de tais mensurações, as estimativas pontuais dos parâmetros, a variância e os erros-padrão podem não ser corretos. Sem o uso de pesos amostrais, apresenta-se uma tendência a subestimar os valores do erro-padrão, o que pode, por sua vez, levar à aceitação de efeitos espúrios, os quais não se verificariam se os pesos fossem aplicados. No presente estudo, todas as estimativas foram realizadas com a aplicação de pesos amostrais.
Com o uso dos pesos brutos, o tamanho da amostra torna-se igual à soma desses pesos, que corresponde ao tamanho da população. Segundo Brogan (1998), esse valor alto impossibilita a realização adequada de testes nos pacotes estatísticos padrão, que sempre tendem a ser significativos. Por isso, seguindo a recomendação da autora, o peso original das escolas foi multiplicado pela fração amostral (n/N, onde n é o tamanho da amostra e N é o tamanho da população). O novo peso amostral, chamado peso normalizado, foi utilizado em todos os procedimentos de análise dos dados. A soma dos pesos amostrais adotados resultou, então, no tamanho da amostra (e não mais da população), respeitando-se, desta forma, a proporção de participação de cada escola nos dados.
Para a análise de regressão multinível utilizou-se o programa MLwiN em sua versão 2.02, desenvolvido por Rasbash, Steele, Browne e Prosser (2005). Inicialmente foi rodado o modelo nulo ou vazio que, segundo a literatura (Ferrão & Fernandes, 2003; Kreft & De Leeuw, 1998; Snijders & Bosker, 1999), serve como base para comparação com os modelos subseqüentes. Em seguida, conforme sugere Fletcher (1998), pretendeu-se controlar as características relacionadas ao nível socioeconômico do aluno e da escola, bem como as características de composição escolar e familiar (escolaridade da mãe e etnia do aluno), a fim de verificar quais eram as outras fontes de variação entre as escolas passíveis de intervenção. Posteriormente, atentando para os procedimentos propostos por Hox (2002), foram incluídas as variáveis explicativas do nível micro com efeito fixo. O passo seguinte foi incluir as variáveis explicativas do nível macro. Em seguida, foi avaliado se alguns dos coeficientes de inclinação das variáveis explicativas do nível micro possuíam componente de variância significativo entre as escolas. Em outras palavras, foi verificado se as variáveis tinham efeito diferenciado entre as escolas. Por fim, foram testadas possíveis interações das variáveis entre os níveis (efeito cross-level).
O SAEB possui como indicadores esperados para os escores os valores descritos na Tabela 2. A escala de avaliação foi construída de modo tal a permitir a comparação entre os valores obtidos por alunos de diferentes séries. Espera-se o aumento no escore médio, no caso de língua portuguesa, de setenta e cinco pontos da segunda série para a quarta, e aumentos equivalentes ao término de cada ciclo - do final da quarta série para o final da oitava e do final desta para o final do nível secundário. Deve-se levar esta escala em consideração, ao observarem-se os resultados obtidos e analisados neste trabalho.

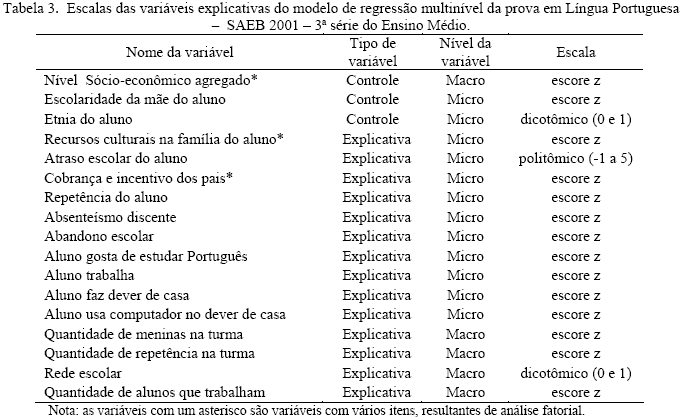
As variáveis explicativas analisadas nos modelos construídos compreendem itens simples obtidos a partir dos questionários respondidos pelos alunos, itens compostos calculados a partir de análise de componentes principais e valores obtidos por agregação, ou seja, valores originalmente obtidos no nível micro que foram agrupados para obter valores médios do nível da escola. A Tabela 3 descreve as diferentes variáveis inseridas nos modelos construídos. Nota-se que quase todas as variáveis explicativas foram transformadas para os respectivos escores-z, a fim de permitir comparações. Cumpre observar que a variável Rede escolar foi inserida durante o processo de modelagem, mas foi descartada em etapas posteriores por não mais se mostrar com um efeito significativo.
As seguintes variáveis são medidas multi-item (multi-item measures) baseadas na análise de componentes principais:
a) Nível sócio-econômico (NSE): composta por 16 itens (alfa = 0,87, carga fatorial média = 0,59). Alguns exemplos de itens da medida NSE são (todas relacionadas à residência do respondente): número de televisões; quantidade de automóveis; número de computadores; número de banheiros; quantidade de quartos na residência e número de empregados domésticos.
b) Recursos culturais: composta por 12 itens (alfa = 0,75, carga fatorial média = 0,51). Alguns exemplos de itens desta variável composta são: o aluno tem acesso à internet em casa; o número de livros disponíveis em casa; na residência do aluno há revistas de informação em geral; o aluno fez ou faz curso de língua estrangeira extracurriculares; a casa do aluno possui dicionário; a casa do aluno possui enciclopédia; o aluno tem acesso a um jornal diário, e o aluno fez ou faz aulas extracurriculares de música, dança ou teatro.
c) Cobrança e incentivo dos pais: composta por 4 itens (alfa = 0,72, carga fatorial média = 0,69) - o grau em que os pais cobram a lição de casa do filho; em que os pais incentivam que o filho tire boas notas na escola; em que os pais procuram fazer com que o filho não se atrase para a escola e em que os pais ajudam o filho a fazer a lição de casa.
Resultados e discussão
Seguindo os passos de modelagem multinível propostos por Hox (2002), inicialmente foi estimado o modelo vazio, ou seja, o modelo sem variáveis explicativas. Vale salientar que o modelo vazio serve como base para a estimação da variância explicada versus a variância não explicada em comparação aos modelos condicionais estimados a posteriori. Ainda, a estimação do modelo vazio é necessária para o cálculo do coeficiente de correlação intra-classe (i.c.c.), o que é calculado dividindo a variância do nível macro sobre a variância total e que portanto pode variar de 0 a 1. Quando seu valor é nulo ou se aproxima de zero, isso significa que as escolas são homogêneas entre si e que o desempenho escolar do aluno é independente da escola que freqüenta (Ferrão & Fernandes, 2003), e a análise multinível não precisa ser aplicada. Por outro lado, ignorar uma correlação intra-classe não trivial (substancialmente diferente de zero), e analisar os dados no nível dos estudantes resulta em testes estatísticos de significância lenientes demais, aumentando assim a ocorrência de falsos positivos, ou em outras palavras, aumentando a quantidade de erros do tipo I (Hox, 2002; Kreft & De Leeuw, 1998). O resultado encontrado nos nossos dados sugere que, a princípio, 33% da variância do desempenho escolar dos alunos estão associados à variabilidade entre as escolas, o que torna necessário o uso de modelos de regressão multinível (ver Tabela 4).
Merece destaque na Tabela 4 o valor do intercepto (264,90), que representa o valor médio da proficiência em Língua Portuguesa dos alunos da 3ª série do Ensino Médio. Neste estudo, a proficiência está expressa na escala do SAEB, calibrada no desempenho em Língua Portuguesa da 8a série em 1997 com um escore médio de 250 e desvio-padrão de 50, e cuja escala assume valores entre 100 e 500. O valor de desempenho médio esperado no teste de Língua Portuguesa para o final da 3ª série do Ensino Médio é 325 (Soares & Alves, 2003). Conclui-se que o desempenho dos alunos da 3ª série é consideravelmente menor que o esperado, estando, na verdade, mais próximo do valor esperado para os alunos ao final da 8ª série do nível fundamental (ver Tabela 2).
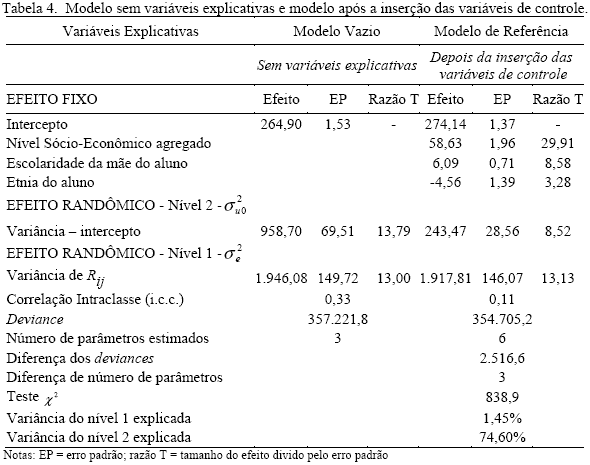
Ainda, a inspeção da Tabela 4 revela que a estimativa do deviance (-2 log verossimilhança, ou -2 log likelihood) para o modelo vazio é igual a 357.221,8. Este valor tem pouco significado em si, mas é utilizado como referência para comparação com os modelos posteriores. O deviance reflete a falta de ajuste entre os dados e o modelo. Como regra para sua interpretação, deve-se comparar a magnitude das diferenças entre o seu valor e aquele encontrado no modelo seguinte (Snijders & Bosker, 1999). Se a diferença dos deviances for significativa, o modelo com o menor deviance é considerado melhor ajustado aos dados (Kreft & De Leeuw, 1998).
Em seguida, foram inseridas as variáveis de seletividade e composição escolar, a saber: nível socioeconômico da escola, escolaridade da mãe e etnia do aluno (modelo de referência). Os resultados também podem ser observados na Tabela 4. Foi calculado quanto de variância que as variáveis relacionadas à seletividade e composição escolar são capazes de explicar, em relação à variância total dos níveis micro e macro. Os resultados sugerem que 74,6% da variância do desempenho médio no teste de Língua Portuguesa entre as escolas devem-se a diferenças na composição socioeconômica de seus alunos, o que indica um efeito muito grande de seleção e composição dos alunos nas escolas. Como assinala Soares (2004), controlar estatisticamente o efeito dessas variáveis é absolutamente necessário, caso contrário se atribuiria às escolas um efeito que não é delas, e sim do capital econômico e cultural das famílias dos alunos.
Ainda na Tabela 4 vários resultados merecem destaque. É verificado que, mesmo controlando os efeitos de seletividade e de composição escolar, a variância do intercepto continua relativamente alta (243,47) e estatisticamente significativa. A variabilidade do intercepto indica a existência de diferenças notáveis no desempenho médio em Língua Portuguesa das escolas. Ou seja, existem diferenças no desempenho médio em Língua Portuguesa das escolas em torno da média nacional. O intercepto, depois do controle para as variáveis de seletividade e composição escolar pode ser interpretado como a eficácia escolar. Antes do controle para estas variáveis o intercepto reflete por uma parte considerável o nível socio-econômico do alunado da escola. Podemos então interpretar a variância relativamente alta do intercepto do modelo de referência como um indicador da existência de diferenças substanciais na eficácia escolar no ensino da Língua Portuguesa.
Pode-se verificar também na Tabela 4 que a correlação intra-classe diminui para 0,11 depois da inserção das variáveis de controle dos efeitos de seletividade e composição escolar. Ou seja, depois deste controle, 11% da variância do desempenho em Língua Portuguesa podem ser atribuídos às escolas. Este valor é compatível com o valor da correlação intra-classe de outros estudos elaborados com os bancos de dados do SAEB, depois de efetuado o mesmo tipo de controle (Albernaz, Ferreira & Franco, 2002; Fletcher, 1998; Ferrão & Fernandes, 2003; Ferrão & Fernandes, 2003; Jesus & Laros, 2004; Soares, 2004).
Deve-se lembrar que, nos modelos multinível, a significância dos coeficientes de regressão é verificada por meio da divisão do parâmetro estimado pelo erro padrão. Esta divisão resulta num escore z: qualquer escore z maior que 1,96 indica que a estatística estimada é significativa no nível de 5%.
A Tabela 4 revela, também, que o efeito do nível socioeconômico da escola (variável agregada) é muito forte (58,63) e estatisticamente significativo. A variável escolaridade da mãe tem um efeito positivo sobre o desempenho dos alunos em Língua Portuguesa mesmo depois da inserção da variável nível socioeconômico da escola. Isso também é verificado em relação à variável etnia do aluno, indicando que estudantes de etnia branca e amarela têm um desempenho melhor que estudantes das demais etnias mesmo depois de controlar a influência do nível socioeconômico da escola e a escolaridade da mãe. Este resultado está em consonância com os achados por Soares e Alves (2003). Segundo aqueles autores, a diferença de desempenho entre alunos brancos e negros, especificamente, não encontra explicação somente nas condições socioeconômica e cultural. Aparentemente, os alunos negros não usufruem das oportunidades da escola da mesma maneira que os alunos brancos e amarelos.
Outro resultado importante obtido da Tabela 4 é o ajuste do modelo aos dados. O valor do deviance do modelo de referência diminuiu 2.516,6 pontos em comparação com o deviance do modelo vazio, sendo estimados três parâmetros a mais no modelo de referência. Deste modo, o valor do teste 2 resultou em 838,9. Este valor é obtido pelo quociente da diferença entre os deviances dos dois modelos e a diferença entre o número de parâmetros estimados. Este quociente deve ser maior que 1,96 (aproximadamente 2) para possuir um nível de significância de 5%. Uma vez que 838,9 é consideravelmente maior que 1,96 o modelo de referência é muito mais ajustado que o anterior, com um índice de significância de cerca de 1%.
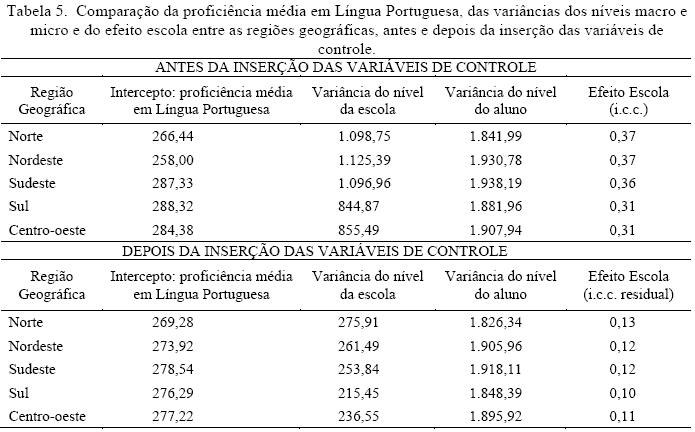
Estabeleceu-se, ainda, uma comparação entre as diferentes regiões geográficas do país. A Tabela 5 mostra os valores obtidos após a construção de modelos diferenciados por localização geográfica, antes e depois da inserção das variáveis de seletividade e composição escolar. Observa-se, no primeiro caso, que entre 31% (Sul e Centro-Oeste) e 37% (Norte e Nordeste) da variância entre as escolas podem ser explicados pelos modelos construídos. No segundo caso, após a inserção das variáveis de seletividade e composição escolar, estes índices variam entre 10% (Sul) e 13% (Norte). Estes resultados estão em consonância com os resultados de Barbosa, Fernandes, Beltrão, Santos e Suárez (2001) que acharam índices da i.c.c. depois de controlar pelo nível econômico dos alunos variando entre cerca de 8% para o Sul e 17% para o Nordeste.
Merece destaque na Tabela 5 a diferença observada entre os valores de intercepto para as regiões, antes e depois da inserção das variáveis de controle. Após a inserção, a amplitude entre os valores de intercepto se reduz. Ou seja, depois de controlar para as variáveis de seletividade e composição escolar a eficácia escolar média das cinco regiões do Brasil ficou menos desigual, com valores ao redor de 277 para o Sul, Sudeste e o Centro-oeste e valores ao redor de 270 para o Norte e o Nordeste. Obviamente, estes valores representam a eficácia escolar muito melhor do que os valores antes de controlar para as variáveis de seletividade e composição escolar. O maior diferencial na Tabela 5, entretanto, é observado na variância do nível da escola: os valores são grandemente reduzidos após a inserção das variáveis de controle, conseqüentemente reduzindo o efeito escola para cerca de um terço do valor antes observado. De acordo com outros estudos multinível de fatores associados ao desempenho escolar (Albernaz, Ferreira & Franco, 2002; Andrade & Laros, 2007; Jesus & Laros, 2004; Soares, 2004), uma vez controlados os efeitos da seletividade e composição das escolas, ainda existe variância que pode ser explicada tanto pelos efeitos do nível macro quanto do nível micro.
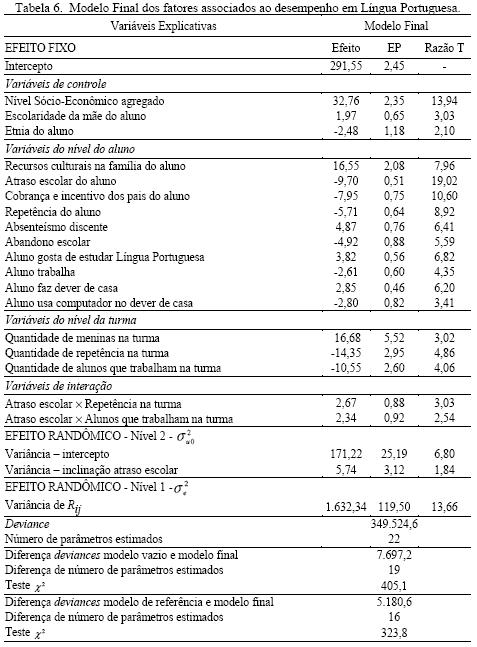
No processo de desenvolver o modelo final da regressão multinível foram estimados, primeiramente, os efeitos do nível micro, devido ao maior número de observações. As seguintes variáveis deste nível foram incluídas no modelo: recursos culturais na família do aluno, atraso escolar, cobrança e incentivo dos pais, repetência, absenteísmo discente, abandono escolar, aluno gosta de estudar Língua Portuguesa, aluno trabalha, aluno faz dever de casa, e, por fim, aluno usa computador no dever de casa. Em seguida, foram incluídas no modelo as variáveis explicativas referentes ao nível da escola. As três variáveis referentes ao nível macro foram mensuradas no nível do aluno e agregadas para o nível da escola, a saber: quantidade de meninas na turma, a quantidade de repetência na turma e a quantidade de alunos que trabalham na turma. Depois a inclusão das variáveis do nível macro verificou-se se houve um efeito randômico dos coeficientes de inclinação das variáveis do nível micro que já haviam entrado no modelo. Em outras palavras, procurou-se verificar se essas variáveis se comportam diferentemente entre as escolas. As variáveis que não apresentaram coeficiente de regressão com efeito randômico foram estimadas novamente com os coeficientes de regressão fixos. O último passo considerado foi o de verificar efeitos de interação entre os níveis (efeito cross-level). Uma interação entre níveis na modelagem multinível refere-se ao efeito conjunto de uma variável de nível micro com uma variável de nível macro. Os resultados do modelo final podem ser observados na Tabela 6.
Como pode ser observada na Tabela 6, todos os coeficientes de regressão das variáveis incluídas do nível do aluno foram estatisticamente significativos (razão t > 2). A variável do nível micro que mais afeta o desempenho escolar dos alunos é Recursos culturais na família do aluno, seguida de Atraso escolar. Verifica-se que a cada aumento de uma unidade na escala de escore padrão de Recursos culturais, o desempenho médio dos alunos aumenta em 16,55 pontos (com erro padrão de 2,08). Com cada aumento de um ano de Atraso escolar o desempenho médio dos alunos piora em 9,70 pontos (com erro padrão de 0,51). Um dos efeitos do nível micro que merecem destaque é o efeito negativo da variável relacionada com a cobrança e incentivo dos pais do aluno. Com um efeito negativo pode parecer que quanto menos os pais cobram do aluno fazer o dever de casa, tanto melhor seu desempenho em português, mas é ao contrário: parece que um desempenho fraco do aluno causa cobrança dos pais. Este achado está em concordância com os resultados relatados por Jesus e Laros (2004), Andrade e Laros (2007) e Laros, Marciano & Andrade (submetido). Outro resultado que merece destaque é o efeito negativo da variável relacionada ao uso de computador do aluno no dever da casa: esse resultado corrobora os resultados da pesquisa do Dwyer, Wainer, Dutra e Covic (2007). Os pesquisadores analisaram os dados dos 287.719 alunos que participaram do SAEB 2001 e constataram que o uso intensivo do computador está diretamente ligado à queda das notas dos alunos. A constatação foi válida para todas as séries analisadas (4a e 8a séries do ensino fundamental e 3o ano do ensino médio), tanto para alunos ricos quanto para pobres.
A Tabela 6 mostra ainda que a variável do nível macro que mais afeta no desempenho escolar dos estudantes é a variável Quantidade de meninas na turma. Os resultados indicam que com cada aumento de uma unidade na escala de escore padrão de Quantidade de meninas na turma, o desempenho médio dos alunos aumenta em 16,68 pontos (com erro padrão de 5,52). As demais variáveis do nível macro têm um sinal negativo. O que chama atenção na inspeção da Tabela 6 é que os erros padrão dos coeficientes de regressão do nível macro são substancialmente maiores do que os do nível micro. Isso possivelmente ocorre devido ao número menor de observações no nível macro.
A análise do deviance sugere que o modelo final é muito mais adequado que o modelo vazio e que o modelo de referência. O teste de 2 mostra um valor de 405,1 em comparação com o modelo vazio e um valor de 323,8 em comparação com o modelo de referência. Isso significa que o modelo final se mostou o modelo mais adequado.
Seguindo as recomendações de Snijders e Bosker (1999) os pressupostos de normalidade e heterogeneidade para a análise multinível foram verificados por meio da análise dos resíduos padronizados do modelo final. Se os pressupostos não são satisfeitos os procedimentos para estimar os coeficientes de regressão podem não ser válidos. Os resíduos padronizados do modelo final foram inspecionados com base em dois gráficos: um com os escores preditos e outro com os escores normais. Ambos mostravam a normalidade da distribuição da variável dependente.
O modelo final está representado esquematicamente na Figura 1. As variáveis do nível do aluno são colocadas abaixo da linha tracejada e as variáveis do nível da escola acima desta linha (ver Figura 1).
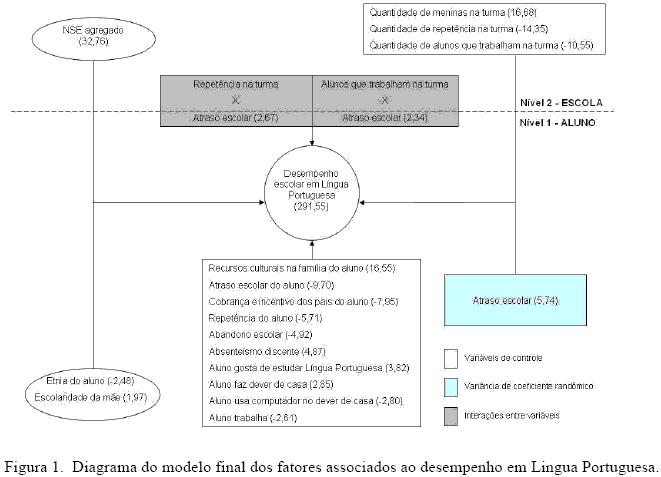
Pode ser observado que o modelo final é composto por 19 variáveis: uma dependente e 18 independentes. As 18 variáveis independentes podem ser classificadas da seguinte maneira: três variáveis de controle, dez variáveis do nível micro, três variáveis do nível macro e duas variáveis de interação entre os níveis. Deve-se ressaltar que nem todas as variáveis independentes são baseadas em um único item dos questionários. O valor da variável dependente no modelo final (291,55) é o valor médio dos alunos da 3ª série na escala do SAEB se todas as variáveis independentes assumirem o valor zero. Merece destaque na Figura 1 que a variável Atraso escolar é a única variável que tem um coeficiente de regressão que não é igual para todas as escolas: existe variância de 5,74 ao redor do valor médio de -9,70.
Considerações finais
O objetivo central do presente estudo foi ampliar o conhecimento sobre fatores associados ao desempenho em Língua Portuguesa. Utilizou-se a técnica de regressão multinível que simultaneamente leva em conta múltiplos níveis hierárquicos presentes nos dados. De acordo com as recomendações de Soares e Andrade (2006), o efeito do nível socioeconômico (NSE) dos alunos e da escola foi controlado na análise de dados. Os autores acima referidos assinalam que no Brasil não se deve estudar a realidade educacional sem considerar o NSE dos alunos e das escolas. Entre as variáveis de controle, a maior contribuição no modelo final foi da variável nível socioeconômico da escola: para cada aumento de um desvio-padrão desta variável, há um aumento de 32,8 pontos (cerca de 2/3 de desvio-padrão) na escala de proficiência do SAEB. Como afirmam Soares e Alves (2003) é um verdadeiro constrangimento o fato de que, no Brasil, o nível socioeconômico tem uma influência tão grande na aprendizagem do aluno.
O valor do intercepto de 264,9 encontrado antes da inserção das variáveis de controle, que pode ser interpretado como a média nacional na prova de português dos alunos da 3a série do ensino médio, deixa bem claro que os alunos não estão aprendendo o suficiente em relação à Língua Portuguesa nas escolas, uma vez que o nível esperado para esta série é de 325. Em relação ao desempenho em português dos alunos brasileiros, Oliveira e Araujo (2005) confirmam estes resultados. Os pesquisadores relatam que 56% dos estudantes brasileiros que participaram do PISA-2000 (Project of International Student Assessment) demonstraram que, ao final da etapa elementar de escolarização, conseguem, no máximo, compreender textos simples, não tendo se beneficiado suficientemente das oportunidades educacionais e não tendo adquirido os conhecimentos e habilidades esperadas para esta etapa de escolarização.
A comparação do intercepto das cinco regiões do Brasil antes da inserção das variáveis de controle evidencia valores entre 258,0 para o Nordeste e 288,3 para o Sul; depois de inserir as variáveis de controle os interceptos assumam valores entre 269,3 para o Norte e 278,5 para o Sudeste. Pode ser concluído que a desigualdade entre regiões em relação ao desempenho médio das escolas em Língua Portuguesa é fortemente relacionada com o nível socioeconômico dos alunos e das escolas.
Depois da inserção de variáveis de controle nos modelos, obteve-se uma i.c.c. residual variando entre 0,10 (região Sul) e 0,13 (região Norte), indicando que entre 10% e 13% da variância observada devem-se a diferenças entre escolas. Isso implica que mesmo depois de controlar o NSE do nível micro e macro existem potencialidades para as políticas públicas educacionais de melhorar o desempenho em Língua Portuguesa dos alunos brasileiros da 3a série do ensino médio.
Das variáveis relacionadas ao nível do aluno, verificou-se que as que mais afetam o desempenho em português são: Recursos culturais na família do aluno e Atraso escolar. A cada aumento de um desvio-padrão de Recursos culturais na família do aluno o desempenho médio dos alunos aumentou em 16,6 pontos na escala do SAEB. Um aumento de um ano de Atraso escolar significa uma diminuição de 9,7 pontos.
Chama a atenção o fato de que as variáveis Cobrança e incentivo dos pais do aluno e Aluno usa computador no dever de casa mostram um efeito negativo no desempenho escolar dos alunos. Em relação à primeira variável é importante assinalar que outros estudos dos dados do SAEB usando regressão multinível também relataram um efeito negativo (Andrade & Laros, 2007, Jesus & Laros 2004; Laros, Marciano & Andrade, submetido). Aparentemente, um desempenho escolar fraco do aluno leva a mais ajuda e cobrança da parte dos pais e não ao contrário. Em relação à segunda variável podemos informar que a pesquisa de Dwyer, Wainer, Dutra e Covic (2007) corrobora os resultados do presente estudo. Os pesquisadores analisaram os dados dos 287.719 alunos que participaram do SAEB 2001 e constataram que o uso intensivo do computador está diretamente ligado à queda das notas dos alunos. A constatação foi válida para todas as séries analisadas (4a e 8a séries do ensino fundamental e 3o ano do ensino médio), tanto para alunos ricos quanto para pobres.
Verificou-se que das variáveis do nível da escola, as que mais afetam o desempenho em português são: Quantidade de meninas na turma e Quantidade de repetência na turma. Deve-se observar que a primeira variável tem um efeito positivo, enquanto a segunda tem efeito negativo. Não se deve perder de vista que a técnica de análise multinível em si não permite conclusões sobre a causalidade da relação entre variáveis. Portanto, não podemos concluir que a repetência causa um desempenho fraco em português: a hipótese de que um desempenho fraco em português causa repetência escolar parece mais razoável. Esta hipótese está de acordo com a afirmação de Oliveira e Araujo (2005) de que a repetência escolar não é a causa de um mau desempenho em português, mas é efeito de uma educação que se estendeu consideravelmente para quase toda a população brasileira sem uma correlata preocupação com a extensão de parâmetros de qualidade a serem atingidos pelas escolas e pelo sistema de ensino.
Como afirmam Soares e Alves (2003) os fatores que determinam o desempenho cognitivo do aluno pertencem a três grandes categorias: a estrutura escolar, a família e características do próprio aluno. O presente estudo identificou fatores de todas as três categorias, sendo que os fatores com mais impacto no desempenho em Língua Portuguesa de cada categoria são: Quantidade de meninas na turma (estrutura escolar), Recursos culturais na família do aluno (família) e Atraso escolar (características do aluno). Esperamos que os fatores identificados por este estudo possam contribuir na melhoria da qualidade do ensino em Língua Portuguesa na educação básica do Brasil.
Referências
Albernaz, A., Ferreira, F. H. G. & Franco, C. (2002). Qualidade e eqüidade na educação fundamental brasileira. Rio de Janeiro: PUC-Rio. [ Links ]
Andrade, D. F., Silva, P. L. N. & Bussab, W. O. (2001). Plano amostral para o SAEB 2001. Relatório Técnico, INEP. [ Links ]
Andrade, J. M. de & Laros, J. A. (2007). Fatores associados as desempenho escolar: estudo multinível com dados do SAEB/2001. Psicologia: Teoria e Pesquisa, 23(1), 33-42. [ Links ]
Barbosa, M. E. F. & Fernandes, C. (2001). A escola faz diferença? Uma investigação dos efeitos da esco la na proficiência em matemática dos alunos da 4a série. Em C. Franco (Org.), Avaliação, ciclos e promoção na educação (pp. 155-172). Porto Alegre: ArtMed. [ Links ]
Barbosa, M. E. F., Fernandes, C., Beltrão, K. Santos, D. & Suárez, M. (2001). Modelos multiníveis aplicados a dados de proficiência escolar: uma comparação entre as regiões brasileiras (relatório técnico da Fundação Getulio Vargas). Disponível em http://epge.fgv.br/portal/arquivo/1059.pdf. Acessado em 12 de outubro de 2007. [ Links ]
Brogan, D. J. (1998). Software for sample survey data: misuse of standard packages. Em: Encyclopedia of Biostatistics (pp. 4167-4174). New York: John Wiley. [ Links ]
Bryk, A. S., Raudenbush, S. W. & Congdon, R. (1996). Hierarchical linear and nonlinear modeling with the HLM/2L and HLM/3L programs. Chicago: Scientific Software International. [ Links ]
Dwyer, T., Wainer, J., Dutra, R. S. & Covic, A. (2007). Desvendando mitos: os computadores e o desempenho no sistema escolar. Educação e Sociedade, 28, 1303-1328. [ Links ]
Ferrão, M. E. & Fernandes, C. (2003). O efeito-escola e a mudança - dá para mudar? Evidencias da investigação brasileira. Revista Eletrônica Ibero-americana sobre Qualidade, Eficácia e Mudança em Educação (REICE), 1(1), 1-13. [ Links ]
Fletcher, P. R. (1998). À procura do ensino eficaz. Ministério da Educação e Cultura, Departamento da Avaliação da Educação Básica, Rio de Janeiro. [ Links ]
Hox, J. J. (2002). Multilevel analysis: techniques and applications. Mahwah, NJ: Lawrence Erlbaum Associates. [ Links ]
Hox, J. J. & Maas, C. J. M. (2005). Multilevel analysis. Em K. Kempf-Leonard (Org.), Encyclopedia of Social Measurement, Volume 2 (pp. 785-793). San Diego, CA: Academic Press. [ Links ]
Instituto Nacional de Estudos e Pesquisas educacionais Anisio Teixeira - INEP (2001). O quadro de referência para a construção dos questionários contextuais do SAEB 2001. Brasília: Ministério da Educação. [ Links ]
Jesus, G. R. de & Laros, J. A. (2004). Eficácia escolar: regressão multinível com dados de avaliação em larga escala. Avaliação Psicológica, 3(2), 21-31. [ Links ]
Kish, L. (1965). Survey sampling. New York, Wiley. [ Links ]
Kreft, I.G.G. & Leeuw, J. de (1998). Introducing multilevel modeling. Newbury Park, CA: Sage Publications. [ Links ]
Laros, J. A., Marciano, J. L. P. & Andrade, J. M. de (submetido). O impacto de variáveis dos níveis micro e macro sobre o desempenho no teste de Matemática do SAEB/2001. Educação e Pesquisa. [ Links ]
Oliveira, R. P. de & Araujo, G. D. de (2005). Qualidade de ensino: uma nova dimensão da luta pelo direito à educação. Revista Brasileira de Educação, 28, 5-23. [ Links ]
Pfeffermann, D., Skinner, C. J., Holmes, D. J., Goldstein, H. & Rasbash, J. (1998). Weighting for unequal selection probabilities in multilevel models. Journal of the Royal Statistical Society, 60, 23-40. [ Links ]
Rasbash, J., Prosser, R. & Goldstein, H. (1991). A user´s guide to MlwiN. Multilevel Models Project., Institute of Education, University of London [ Links ]
Rasbash, J., Steele, F, Browne, W., & Prosser, B. (2005). A user's guide to MLwiN Version 2.0. London: Centre for Multilevel Modeling, Institute of Education. [ Links ]
Riether, M. M. & Rauter, R. (2002). A metodologia de amostragem do SAEB. Revista Brasileira de Estudos Pedagógicos, 81, 143-153. [ Links ]
Soares, J. F. (2004). O efeito escola no desempenho cognitivo de seus alunos. REICE -Revista Electrónica Iberoamericana sobre Calidad, Eficácia e Cambio em Educación, 2(2), 83-104. [ Links ]
Soares, J. F. & Alves, M. T. G. (2003). Desigualdades raciais no sistema brasileiro de educação básica. Educação e Pesquisa, 29(1), 147-165. [ Links ]
Soares, J. F. & Andrade, R. J., de (2006). Nível socioeconômico, qualidade e eqüidade das escolas de Belo Horizonte. Ensaio: Avaliação e Políticas Públicas em Educação, 14 (50), 107-126. [ Links ]
Soares, J. F., Cesar, C. C. & Mambrini, J. (2001). Determinantes de desempenho dos alunos do ensino básico brasileiro: evidências do SAEB de 1997. Em C. Franco (Org.), Avaliação, ciclos e promoção na educação. (pp.121-154). Porto Alegre: Artmed. [ Links ]
Soares, J. F., Ribeiro, L. M. & Castro M. C. (2001). Valor agregado de instituições de ensino superior em Minas Gerais para os cursos de Direito, Administração e Engenharia Civil. Dados, 44(2), 1-28. [ Links ]
Soares, T. M. (2005). Modelo de três níveis hierárquicos para a proficiência dos alunos de 4a série de língua portuguesa do SIMAVE/PROEB-2002. Revista Brasileira de Educação, 29, 73-87. [ Links ]
Snijders, T. A. B. & Bosker, R. J. (1994). Modeled variance in two-level models Sociological Methods & Research, 22(3), 343-363. [ Links ]
Snijders, T. A. B. & Bosker, R. J. (1999). Multilevel analysis: an introduction to basic and advanced multilevel modeling. Newbury Park, CA: Sage Publications. [ Links ]
Teddlie, C. T. & Reynolds, D. (2000). The international handbook of school effectiveness research. London: Falmer Press. [ Links ]
 Endereço para correspondência
Endereço para correspondência
E-mails: jalaros@unb.br
Recebido em Abril de 2008
Reformulado em Setembro de 2008
Aceito em Novembro de 2008
Sobre os autores:
* Jacob Arie Laros: É PhD em Personality and Educational Psychology pela University of Groningen - Holanda (1991), e, ainda Pós-Doutor (2002) em Educational Psychology pela mesma universidade. Professor adjunto III no Instituto de Psicologia da Universidade de Brasília (UnB) e no curso de pós-gradução em Psicologia Social, do Trabalho e das Organizações (PSTO).
** João Luiz Marciano: é bacharel em Ciência da Computação pela Universidade de Brasília (1994), mestrado em Ciência da Computação pela Universidade de Brasília (1997) e doutorado em Ciências da Informação pela Universidade de Brasília (2006). Atualmente é analista de informática legislativa - Câmara dos Deputados.
Com agradecimentos ao Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq).