ARTIGOS

 

AlphaCI: un programa de cálculo de intervalos de confianza para el coeficiente alfa de Cronbach

 

AlphaCI: a computer program for computing confidence intervals around Cronbach's alfa coefficient

 

 

Rubén Ledesma^{* 1}

Universidad Nacional de Mar del Plata. Faculdad de Psicología. Grupo de Investigación en Psicología Cognitiva y Educacional

 

 

---

RESUMEN

El coeficiente alfa de Cronbach es el modo más habitual de estimar la fiabilidad de pruebas basadas en Teoría Clásica de los Test. En dicha estimación, los investigadores usualmente omiten informar intervalos de confianza para el coeficiente, un aspecto no solo recomendado por los especialistas, sino también requerido explícitamente en las normas editoriales de algunas revistas especializadas. Esta situación puede atribuirse a que los métodos de estimación de intervalos de confianza son poco conocidos, además de no estar disponibles al usuario en los programas estadísticos más populares. Así, en este trabajo se presenta un programa desarrollado dentro del sistema estadístico ViSta que permite calcular intervalos de confianza basados en el enfoque clásico y mediante la técnica bootstrap. Se espera promover la inclusión de intervalos de confianza para medidas de fiabilidad, facilitando el acceso a las herramientas necesarias para su aplicación. El programa es gratuito y puede obtenerse enviando un mail de solicitud al autor del trabajo.

Palabras clave: Alfa de Cronbach, Intervalos de confianza, Programa informático.

---

ABSTRACT

Cronbach's alpha coefficient is the most popular way of estimating reliability in measurement scales based on Classic Test Theory. When estimating it, researchers usually omit to report confidence intervals of this coefficient, as it is not only recommended by experts, but also required by some journal's guidelines. This situation is because the different methods of estimating confidence intervals are not well-known by researchers, as well as they are not being available among the most popular statistical packages. Therefore, this paper describes a computer program integrated into the ViSta statistical system, which allows computing confidence intervals based on the classical approach and using bootstrap technique. It is hoped that this work promotes the inclusion of confidence intervals of reliability measures, by increasing the availability of the required computer tools. The program is free and it can be obtained by sending an e-mail to the author.

Keywords: Cronbach's alpha, Confidence intervals, Computer program.

---

 

 

El análisis de la fiabilidad de los instrumentos psicológicos es un aspecto clave en Psicometría básica y aplicada; por este medio, se obtiene información sobre el grado en que los instrumentos son relativamente libres de error medida (Muñiz, 1996). Esta propiedad de las medidas psicológicas, su fiabilidad, resulta fundamental tanto en la investigación como en la práctica profesional, siempre que se utilicen instrumentos psicométricos para indagar variables o constructos psicológicos en individuos o grupos. Por esta razón, se han desarrollado diferentes enfoques y métodos que permiten estimar la fiabilidad y el error de medida asociados a una medición dada. En este sentido, una propuesta pionera y aún vigente, fue iniciada por Spearman (1904) en base a lo que se conoce como Modelo Lineal Clásico, fundamento de la Teoría Clásica de los Test (TCT), formalizada posteriormente por Novic (1966) y expuesta sistemáticamente en Lord y Novick (1968).

Dentro de la TCT, los diseños más conocidos para estimar fiabilidad de medidas son Formas Paralelas, Test-retest y Consistencia interna. El método de Formas Paralelas implica un análisis de la relación entre dos mediciones basadas en formas paralelas de un mismo instrumento. El método del Test-retest analiza la relación entre dos mediciones realizadas en diferentes momentos temporales, lo que proporciona una medida de la estabilidad temporal de las medidas. Por último, el método de Consistencia interna analiza la relación entre las diferentes partes de un mismo instrumento, generalmente ítems o reactivos.

Si bien cada uno de estos métodos tienen ventajas y desventajas comparativas, en la práctica el método de Consistencia interna es el camino más habitual para estimar fiabilidad, debido a su simplicidad y economía, pues requiere solo un instrumento y una administración de la prueba. De hecho, el coeficiente alfa de Cronbach (Cronbach, 1943, 1946, 1947, 1951), utilizado como vía de estimación en el caso de diseños de Consistencia interna, es la forma más popular y extendida de estimación entre los investigadores. Originalmente, la importancia del trabajo de Cronbach puede atribuirse al avance realizado en relación a los enfoques existentes en el momento, ya que el coeficiente alfa extendía el método de división por mitades (Spearman, 1910; Brown, 1910) y el método de Kuder y Richardson (1937) para datos binarios. En la actualidad, su popularidad práctica puede atribuirse también a su sencillez de cálculo y al hecho de estar disponible como opción de análisis en los programas estadísticos más conocidos, como SPSS o Statistica.

Mencionada la existencia de métodos y enfoques alternativos, resulta evidente que la fiabilidad de las pruebas psicológicas, tal como se evalúa en la práctica, no se refiere a una propiedad absoluta de los instrumentos, sino a una estimación obtenida mediante algún procedimiento específico y sujeta a diferentes fuentes posibles de error. Los investigadores y especialistas en psicometría suelen insistir en este aspecto, enfatizando tanto su implicancias científicas como praxiológicas. Sin embargo, este reconocimiento teórico no se corresponde exactamente con lo que sucede en la práctica. Tal como es recogido en algunos estudios empíricos de la literatura (Vacha-Haase, Kogan, & Thompson, 2000; Vacha-Haase, Ness, Nilsson, & Reetz, 1999, Whittington, 1998), los investigadores suelen incurrir en errores tales como dar por supuesto valores de fiabilidad informados en estudios previos, como si esta fuese una propiedad estable, incluso a través de muestras que no son en ningún modo equiparables.

En tal sentido, otro aspecto destacable es que solo excepcionalmente los investigadores informan intervalos de confianza (IC) para las medidas de fiabilidad, lo cual sería oportuno siempre que se trata de una estimación estadística. Por regla, este punto es omitido sistemáticamente, aun entre los investigadores expertos en la materia. Esta situación ha llevado a algunas revistas especializadas a elaborara y publicar guías editoriales específicas solicitando a los autores el uso de métodos de estimación de IC para medidas de fiabilidad. Tal es el caso de la revista Educational and Psychological Measurement (Fan & Thompson, 2001), que ha publicado recomendaciones de este tipo inspiradas en los lineamientos de la Task Force on Statistical Inference de la APA (Wilkinson & APA Task Force on Statistical Inference, 1999). Estas recomendaciones editoriales buscan promover en los lectores la idea de que todas las estimaciones estadísticas, incluyendo la fiabilidad, están afectadas por error muestral y que los test no poseen una fiabilidad absoluta o invariante a través de las muestras.

No obstante, aún cuando el investigador reconozca y acepte la necesidad de calcular IC para sus estimaciones de fiabilidad, en la práctica se encontrará con la dificultad añadida de que estos métodos de cálculo no están directamente disponibles al usuario en los programas más populares, como SPSS, Statistica o SAS. Estos sistemas, si bien incorporan varias alternativas de estimación de fiabilidad, no proporcionan métodos de estimación de IC.

En este contexto, nos hemos interesado en desarrollar y dar a conocer el presente programa informático denominado Alpha-CI, que permite calcular IC para el caso más extendido del coeficiente alfa de Cronbach. Como se sabe, alfa estima el límite inferior del coeficiente de fiabilidad en función de dos componentes del test: el número de ítems (o longitud de la prueba) y la proporción de varianza total de la prueba debida a la covarianza entre sus partes (ítems). Ello significa que la fiabilidad del test depende de sus longitud y de la covarianza entre sus ítems. Alfa se expresa como:

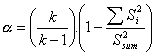
Donde k es el número de ítems de la prueba, es la varianza de los ítems (desde 1...i) y es la varianza de la prueba total. Como hemos mencionado, este coeficiente es la forma más habitual de estimación de fiabilidad cuando se aplica el método de Consistencia interna en pruebas basadas en TCT.

El programa que presentamos se integra a un sistema estadístico mayor denominado ViSta "The Visual Statistics System" (Young, 2003), y permite calcular IC para el coeficiente alfa de Cronbach desde el modelo clásico y desde el enfoque bootstrap (Efron & Tibshirani, 1993). En el primer caso, el cálculo de IC se basa en las populares investigaciones de Kristof (1963) y Feldt (Feldt, 1965, 1980; Feldt, Woodruff & Salih, 1987), quienes asumiendo ítems paralelos y distribuciones normales obtuvieron la distribución muestral exacta del coeficiente. En el segundo caso, el método bootstrap proporciona una alternativa no paramétrica de estimación que puede utilizarse cuando existe incertidumbre con respecto al cumplimiento de los supuestos del enfoque clásico. Recientemente, Yuan, Guarnaccia y Bert (2003) compararon la adecuación de ambos métodos como medio para obtener IC para el coeficiente alfa para el caso, muy habitual en Psicología, de ítems en formato Likert. Su estudio indica que la teoría basada en el modelo normal muestra un sesgo sistemático en la descripción del comportamiento muestral del coeficiente para este caso, y recomiendan el método bootstrap ya que toma automáticamente en consideración la distribución y el tamaño muestral de los propios datos empíricos. En términos más generales, también discuten la adecuación de este método para el caso de alfa cuando la distribución subyacente de los datos es desconocida.

El hecho de que el enfoque bootstrap tome en cuenta la distribución y el tamaño muestral de los datos se debe a que, en realidad, es un método de "aproximación empírica" al problema de la distribución muestral de un estadístico. En oposición a los métodos analíticos clásicos, que se basan en asumir supuestos teóricos, el método bootsrap deriva las distribuciones de un estimador estadístico empíricamente, utilizando información tomada de los propios datos que serán utilizados para realizar la estimación estadística. De esta forma, el enfoque bootstrap permite eludir las limitaciones del enfoque estadístico clásico que se derivan principalmente de asumir supuestos que en muchas ocasiones prácticas resultan poco realistas (Fan, 2003). Además de poder ser utilizado como método no paramétrico de inferencia, puede aplicarse como técnica de réplica interna para analizar descriptivamente la estabilidad y replicabilidad de los resultados de un estudio particular (Thompson, 1993). Este uso se puede dar cuando el interés del investigador, en lugar realizar una inferencia, es evaluar cuan estable son los resultados obtenidos a través de muestras repetidas.

Hay que mencionar que el desarrollo de este enfoque ha sido posible gracias a las capacidades de cómputo de las computadoras personales de la actualidad. Este aspecto es clave, ya que la técnica bootstrap - como las técnicas Monte Carlo y Jackknife - es un "método de cómputo intensivo", que aprovecha el poder y la velocidad de las PCs para realizar simulaciones de procesos aleatorios. En tal sentido, cabe destacar que el software de apoyo para la aplicación de estos métodos aún se encuentra en estado incipiente, es poco conocido y puede presentar dificultades para el investigador sin demasiada experticia en métodos cuantitativos. Al respecto, es de destacar la contribución del trabajo de Fan (2003), quien proporciona una excelente revisión de recursos informáticos disponibles para aplicaciones bootstrap en Psicología. Una revisión más general, incluyendo otros métodos intensivos de cómputo y una discusión sobre las potencialidades aplicaciones en Psicología, puede encontrarse también en Yu (2003).

En términos computacionales, la técnica bootstrap opera según los siguientes pasos generales: a) se obtiene una muestra con reemplazo de los datos empíricos; b) se calcula el estadístico en cuestión para la muestra obtenida en a; c) se repiten los pasos a y b un gran número de veces, y d) se obtiene la distribución bootstrap del estadístico, la cual se utiliza con propósitos inferenciales en lugar de las distribuciones teóricas utilizadas en el enfoque clásico. En este punto, pueden obtenerse IC basados en el resultado de la simulación.

En nuestro caso, el programa proporciona resultados basados en dos métodos de cálculo de IC apropiados para el caso del coeficiente alfa, estos son, el método de los percentiles y el método Bca (Bias corrected and accelerated) (Yuan & col., 2003). El primer método consiste, simplemente, en calcular los percentiles inferior y superior correspondientes a un determinado nivel de confianza, cuyo valor por defecto es 95%. El segundo método, desarrollado por Efron y Tibshirani (1993), proporciona una alternativa superior al método de los percentiles cuando la distribución bootstrap obtenida es asimétrica, lo cual es frecuente para el caso del coeficiente alfa. El interesado en profundizar el enfoque bootsrap y las diferentes opciones para calcular IC puede consultar Efron y Tibshirani (1993). Remitimos al lector al trabajo de Yuan y col. (2003) para una profundización del método bootstrap aplicado al coeficiente alfa de Cronbach.

Finalmente, esperamos que la presente herramienta contribuya a promover la inclusión de IC como parte de las estimaciones de fiabilidad en el trabajo de investigación. De este modo, se busca lograr una mayor correspondencia entre teoría y práctica en psicometría aplicada.

 

Descripción del programa

Generalidades
El programa Alpha-CI ha sido desarrollado en lenguaje XlispStat (Tierney, 1990) para funcionar integrado al sistema estadístico ViSta, un software académico gratuito, abierto y extensible creado por Forrest W. Young en el L. L. Thurstone Psychometric Laboratory de la Universidad de Carolina del Norte en Chapel Hill. ViSta es un entorno interesante para desarrollar procesos de análisis psicométrico, ya que incluye varias opciones de análisis para ítems, métodos de análisis factorial y técnicas de escalamiento, entre otros métodos específicos. Además, se trata de un programa multiusuario - puede ser utilizado por analistas principiantes y avanzados - y multiplataforma, existiendo versiones para Mac, Windows y Unix.

El módulo que aquí presentamos funciona integrado como plug-in de análisis a ViSta 6.4, es decir se instala completa y automáticamente en el menú del programa con la etiqueta Alpha-CI, y puede ser utilizado en conjunción con el resto de las opciones de análisis del sistema. Los datos para el análisis pueden ser creados directamente en ViSta o importados en formato texto delimitado por espacios, luego de lo cual puede aplicarse el análisis. El programa lee matrices de datos donde las filas son sujetos y las columnas ítems, estructura de datos que ViSta denomina "multivariados".

Opciones de análisis
Cuando se selecciona el ítem correspondiente al método en el menú de análisis de ViSta, se presenta un cuadro de diálogo con opciones para que el usuario pueda determinar el nivel de confianza para la estimación, cuyo valor por defecto es 95%, y el número de muestras para la simulación bootstrap, fijado inicialmente en 300 réplicas. La Figura 1 muestra el cuadro de diálogo para modificar estas opciones de análisis y ofrece una imagen parcial del entorno ViSta.

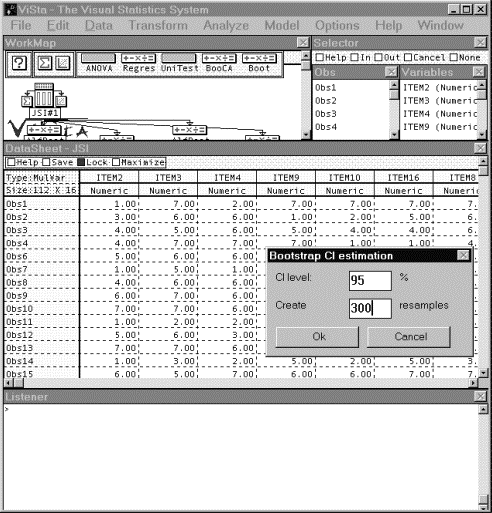
Figura 1 - Imagen parcial de ViSta y opciones de análisis para el cálculo de IC para el coeficiente alfa

Como hemos mencionado, el método bootstrap es una técnica de remuestreo de los datos empíricos, con lo cual el tiempo requerido para la ejecución del análisis depende de la cantidad de sujetos (observaciones), ítems (variables) y muestras requeridas en la simulación. Por ejemplo, en una PC de 950 mhz, para el caso de 10 variables, 200 sujetos y 200 réplicas, el análisis puede consumir aproximadamente 10 segundos, luego de lo cual ViSta estará en condiciones de mostrar los resultados del análisis en formato texto y/o gráfico.

Salida numérica del análisis
Finalizada la fase de cómputo, puede obtenerse un informe numérico del resultado y gráficos especializados para visualizar el proceso bootstrap. El siguiente es un ejemplo de salida en formato texto habiendo aplicado el programa a datos provenientes de un cuestionario unidimensional sobre Satisfacción Laboral compuesto por 16 ítems en formato Likert (Terrony, 2002):

La primera parte de la salida incluye datos generales sobre la aplicación, nombre del archivo de datos utilizado y valores seleccionados por el usuario en las opciones de análisis (Number of resamples: 300; y CI-level: 95%). A continuación se informa el valor observado del coeficiente alfa para la muestra (Cronbach's Alpha: .888) y el IC para dicho coeficiente utilizando el método clásico (Confidence Interval for Alpha: .855, .916).

La segunda parte informa los resultados bootstrap, incluyendo alfa estimado (BootAlpha: .886), sesgo (Bias: -0.002), error estándar (SE: 0.017) e intervalos de confianza basados en percentiles (0.8435, 0.9161) y en el método BCa (0.8413, 0.9150).

Salida gráfica del análisis
Además de la salida numérica, el programa permite generar gráficos especializados para visualizar y analizar en detalle diferentes aspectos del proceso bootstrap. Los gráficos se presentan simultáneamente en la misma pantalla utilizando el método de gráficos extendidos (Young, Valero Mora, Faldowsky & Bann, 2000) tal como se muestra en la Figura 2. En dicha figura se observan los tres gráficos que componen la visualización, un histograma con la distribución bootstrap, un gráfico de probabilidad normal de la misma distribución y un gráfico de estabilidad del proceso.

La primera ventana a la izquierda muestra un histograma con la distribución bootstrap para el coeficiente alfa obtenido desde los datos de origen, es decir basada en muestras con reemplazos de los propios datos empíricos. Puede observarse que la distribución es asimétrica, sesgada negativamente. La ventana central, muestra un gráfico de Probabilidad Normal que permite evaluar más apropiadamente la normalidad de la distribución empírica. La línea recta representa el modelo de la distribución normal y la línea quebrada la distribución empírica. Alejamientos sistemáticos de la línea recta indican alejamientos del modelo normal. Nuevamente, el gráfico refleja que la distribución está levemente sesgada en sentido negativo. Por último, la tercera ventana muestra un gráfico de estabilidad, que presenta la evolución de la estimación bootstrap (media de la distribución) a través de las muestras acumuladas. Este gráfico permite inspeccionar la estabilidad de la estimación final, y decidir si es necesario utilizar un número mayor de muestras en la simulación. En nuestro ejemplo, se observa que él número seleccionado (300 muestras) parece suficiente, ya que la estimación final se ha estabilizado en torno a un valor que prácticamente no presenta fluctuaciones. El valor final es el alfa estimado mediante la técnica bootstrap.

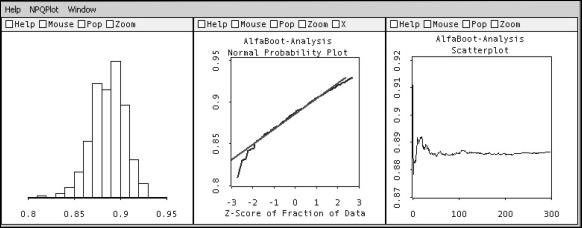
Figura 2 - Salida gráfica del programa para visualizar los resultados del proceso bootstrap

Entendemos que estos gráficos, considerados en conjunto, pueden resultar de utilidad para el analista experto y para aquellos docentes que quieran introducir a sus estudiantes en la metodología bootstrap. En este sentido, los gráficos brindan un apoyo visual de gran utilidad para una comprensión intuitiva de tales métodos y para un análisis detallado de sus resultados.

Disponibilidad del programa
El programa puede obtenerse de forma completamente gratuita enviando un mensaje de solicitud a la dirección electrónica del autor. Para su utilización, el usuario interesado debe instalar previamente WinViSta versión 6.4 (solo disponible en idioma inglés) que puede obtener desde la siguiente dirección URL: http://forrest.psych.unc.edu/research/index.html.

 

Discusión

El análisis de fiabilidad es una cuestión clave para el desarrollo, validación y uso de instrumentos psicológicos. En este análisis, dado el alcance y naturaleza de los enfoques utilizados, el cálculo de IC para las medidas estadísticas que se utilizan en la estimación de fiabilidad resulta un aspecto crítico. No obstante, aún cuando los expertos y las normas editoriales de algunas revistas especializadas han realizado recomendaciones específicas al respecto, en la práctica el cálculo de IC para medidas de fiabilidad es algo poco extendido.

Esta situación puede atribuirse, en parte, a que los métodos de cálculo son poco conocidos y, además, al hecho de no encontrarse disponibles en los paquetes estadísticos más conocidos, como SPSS, Statistica o SAS. En este contexto, nos hemos propuesto contribuir a la difusión de esta metodología y facilitar el acceso a las tecnologías informáticas necesarias para su aplicación. En particular, hemos presentado un programa denominado Alpha-CI que permite calcular IC para el caso del coeficiente alfa de Cronbach, la forma más extendida de estimación de fiabilidad basada en el método de Consistencia interna dentro de la TCT.

El programa calcula IC para el coeficiente alfa utilizando el enfoque clásico y el método bootstrap. La técnica bootstrap sustituye las derivaciones teóricas del enfoque clásico por esfuerzo computacional, ya que estima la distribución muestral del estadístico mediante el remustreo de los propios datos empíricos. Por este medio se pueden calcular IC sin asumir supuestos sobre la distribución subyacente de los datos. El enfoque también puede utilizarse descriptivamente para evaluar la estabilidad del coeficiente a través de réplicas internas de los propios datos.

El software es sencillo de utilizar, se integra a un programa estadístico de carácter gratuito y proporciona informes numéricos y gráficos especializados para visualizar el resultado del proceso bootstrap. Se espera que esta herramienta informática contribuya a promover la inclusión de IC como parte de las estimaciones de fiabilidad, logrando una mayor correspondencia entre teoría psicométrica y prácticas de investigación en los distintos ámbitos de la Psicología. Asimismo, se espera contribuir a una mayor difusión y uso de la metodología bootstrap aplicada al análisis de datos en Psicología.

 

Referencias

Brown, W. (1910). Some experimental results in the correlation of mental abilities. British Journal of Psychology, 3, 296-322.        [ Links ]

Cronbach, L. J. (1943). On estimates of test reliability. The Journal of Educational Psychology, 34, 485-494.        [ Links ]

Cronbach, L. J. (1946). A case study of the split-half reliability coefficient. The Journal of Educational Psychology, 37, 473-480.        [ Links ]

Cronbach, L. J. (1947). Test "reliability": Its meaning and determination. Psychometrika, 12, 1-16.        [ Links ]

Cronbach, L. J. (1951). Coefficient alpha and the internal structure of tests. Psychometrika, 16, 297-334.        [ Links ]

Efron, B. & Tibshirani, R. J. (1993). An introduction to the bootstrap. New York: Chapman & Hall.        [ Links ]

Fan, X. (2003). Using commonly available software for bootstrapping in both substantive and measurement analyses. Educational and Psychological Measurement, 63, 24-50.        [ Links ]

Fan, X. & Thompson, B. (2001). Confidence intervals about score reliability coefficients, please: an EPM guidelines editorial. Educational and Psychological Measurement, 61, 517-531.        [ Links ]

Feldt, L. S. (1965). The approximate sampling distribution of Kuder-Richardson coefficient twenty. Psychometrika, 30, 357-370.        [ Links ]

Feldt, L. S. (1980). A test of the hypothesis that Cronbach's alpha reliability coefficient is the same for two tests administered to the same sample. Psychometrika, 45, 99-105.        [ Links ]

Feldt, L. S., Woodruff, D. J. & Salih, F. A. (1987). Statistical inference for coefficient alpha. Applied Psychological Measurement, 11, 93-103.        [ Links ]

Kristof, W. (1963). The statistical theory of stepped-up reliability coefficients when a test has been divided into several equivalent parts. Psychometrika, 28, 221-238.        [ Links ]

Kuder, G. F. & Richardson, M. W. (1937). The theory of the estimation of test reliability. Psychometrika, 2, 151-160.        [ Links ]

Lord, F. M. & Novick, M. R. (1968). Statistical theories of mental test scores. Reading, MA: Addison-Wesley.        [ Links ]

Muñiz, J. (Org.). (1996). Psicometría. Madrid: Editorial Universitas.        [ Links ]

Novick, M. R. (1966). The axioms and principal results of classical test theory. Journal of Mathematical Psychology, 3, 1-18.        [ Links ]

Spearman, C. (1904). The proof and measurement of association between two things. American Journal of Psychology, 15, 72-101.        [ Links ]

Spearman, C. (1910). Correlation calculated from faulty data. British Journal of Psychology, 3, 271-295.        [ Links ]

Terroni, N. (2002). El nivel de satisfacción de los trabajadores de una institución de salud pública. Su relación con el ausentismo y la salud psicofísica. Tesis de Maestría en Psicología Social, Facultad de Psicología de la UNMdP, Mar del Plata.         [ Links ]

Thompson, B. (1993). The use of statistical significance tests in research: Bootstrap and other alternatives. Journal of Experimental Education, 61, 361-377.        [ Links ]

Tierney, L. (1990). Lisp-Stat an object-oriented environment for statistical computing and dynamic graphics. NY: John Wiley & Sons.        [ Links ]

Vacha-Haase, T., Kogan, L. R. & Thompson, B. (2000). Sample compositions and variabilities in published studies versus those in test manuals:Validity of score reliability inductions. Educational and Psychological Measurement, 60, 509-522.        [ Links ]

Vacha-Haase, T., Ness, C., Nilsson, J. & Reetz, D. (1999). Practices regarding reporting of reliability coefficients: A review of three journals. Journal of Experimental Education, 67, 335-341.        [ Links ]

Whittington, D. (1998). How well do researchers report their measures? An evaluation of measurement in published educational research. Educational and Psychological Measurement, 58, 21-37.        [ Links ]

Wilkinson, L. & APA Task Force on Statistical Inference (1999). Statistical methods in psychology journals: Guidelines and explanations. American Psychologist, 54, 594-604. Disponible: http://www.apa.org/journals/ amp/amp548594.html]        [ Links ]

Young, F., Valero Mora, P., Faldowsky, R. A., & Bann, C. (2000). Spreadplots. The Visual Statistic project, Report Number 2000-4. L. L. Thurstone Psychometric Lab, University of North Carolina at Chapel Hill, May 2000.        [ Links ]

Young, F. W. (2003). ViSta "The Visual Statistics System". [programa informático] [en línea] Disponible: URL: http://forrest.psych.unc.edu/research/index.html        [ Links ]

> Yu, Ch. H. (2003). Resampling methods: concepts, applications, and justification. Practical Assessment, Research & Evaluation, 8, 19. Disponible: http://PAREonline.net/getvn.asp?v=8&n=19        [ Links ]

Yuan, K-H, Guarnaccia, Ch. & Bert, H. (2003). A study of the distribution of sample coefficient alpha with the hopkins symptom checklist: bootstrap versus asymptotics. Educational and Psychological Measurement, 63, 5-23.        [ Links ]

 

 

Recebido em março de 2004
Reformulado em maio de 2004
Aprovado em junho de 2004
Este trabajo ha sido financiado con el apoyo de una Beca Posdoctoral del CONICET (Argentina).

 

 

¹ Endereço para correspondência: Funes 3.250, Cuerpo V - Nivel III - Mar del Plata (7600)-Bs. As. - Argentina. E-mail: rledesma@mdp.edu.ar
^* doutor, professor e membro do Grupo de Investigación en Psicología Cognitiva y Educacional da Facultad de Psicología de la Universidad Nacional de Mar del Plata e bolsista de pós-doutorado pelo Consejo Nacional de Investigaciones Científicas y Tecnológicas, Argentina.