ARTIGOS ORIGINAIS

 

A lógica e a teoria de Jean Piaget: a implicação significante

 

Logic and Piaget's theory: the significant implication

 

 

Leonidas Hegenberg

Professor titular - colaborador do Instituto de Psicologia da USP

 

 

---

RESUMO

O termo "implicação" tem como referente principal o que se poderia denominar "situação dedutiva", isto é, cabe afirma "P₁, P₂, ...., P_n implicam C" sempre que C, seja conclusão deduzível das premissas Pi (com i variando de 1 a n). A implicação, nesse caso (e em casos de inferências similares) admite a leitura com o condicional "Se, então". Não raro, o condicional é usado para ler o composto 'p q', do cálculo proposiocional, construído com o juntor filônico, assim chamado em homenagem a Filon, de Megara, o que provoca certas dificuldades, particularmente se ele sugere ter havido dedução. A par disso, o condicional "Se, então" ocupa um posto de relevo nas explicações (inclusive as causais). Identificando os vários empregos de "Se, então, caracteriza-se o significado apropriado de 'implicação significante' (termo introduzido por Piaget) e se mostra de que modo permite superar a dicotomia operações-causalidade.

Descritores: Lógica. Jean Piaget. Implicação significante

---

ABSTRACT

"Implication" has, as a very important referent, some deductive situation. In other word, we may say that "P1, P₂, ..., P_n imply C" whenever C is a conclusion that follows from the premisses Pi (i = 1, 2, ...,n). Implication, in such cases (and in similar inferential situations), admits reading with the help of "If .... then.,.". Very often, the same locution is used to read the expression "p 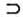q", constructed with the horseshoe of prepositional calculus (the "philonical juntor", as we may call it, homage to Philon, of Megara). It's not unusual to associate this horseshoe with some type of dedution — a serious mistake, if it is used as a simple operator from the calculus. Besides, the "If,.., then..." has a relevant role in explanations (including causal ones). Identifying the various forms of use of the expression "If..., then..." we come to an appropriate characterization of the meaning to give to the term 'significant implication', as it was considered by Jean Piaget. At the same time, sugestion is made as for the way of understanding the "operations-causality" dichotomy.

Index terms: Logic. Jean Piaget. Significant implicatiom.

---

 

 

PRIMEIRA PARTE

1. Preâmbulo

O termo 'implicação' é de uso relativamente com um. Todavia, seu referentes nem sempre são explicitados de maneira satisfatória e, não raro, seus significados chegam a entrar em conflito. Com naturalidade, dizemos

x + 3 = 9 implica x = 6

Com a mesma naturalidade, afirmamos que uma dada causa implica certo efeito; e admitimos que a inscrição em um torneio esportivo implique aceitação das regras que norteiem sua realização.

Estudiosos de lógica não contribuíram para afastar ambiguidades que cercam o uso do termo 'implicação'. Ao contrário, falando em implicações "materiais", "formais", "escritas" ou "relevantes", acabaram criando novas dificuldades para quem apreciaria empregar o termo de modo correto.

O objetivo deste ensaio é, justamente, o de afastar algumas incongruências que cercam o uso do termo ' implicação' para tentar, em seguida, determinar o melhor referente de 'implicação significante', introduzida por Piaget, uma noção que se presta para lançar luz sobre um problema importante, o das relações entre casualidade e operações.

2. Piaget e a implicação significante

Piaget, como sabe, discutiu amplamente a implicação. Em 1967, no livro Biologie et connaissance (p. 63) há uma clara ligação entre implicação e causa:

... la conscience constitue un système de significations dont les deux notions centrales sont la dèsignation et l' "implication" entre significations: par example 2 n' est pas la cause de 4, mais sa signification "implique" que 2+2 = 4 ...

Alguns anos mais tarde (ef. Réussir et comprendre, p. 240), Piaget introduz o termo 'implicação significante', afirmando

... le caractère le plus général des étals conscients, ... est d'exprimer des significations et de les relier par un mode de conexion que nous appellerons faute de mieux l'implication signifiante.

Cerca de três meses antes de sua morte (ocorrida em 16 de setembro de 1980), Piaget pronunciava, no Centre International d'Épistémologie Génétique, sua última conferencia, que a profa. Zelia Ramozzi-Chiarottino leve a fortuna de ouvir e gravar. De novo, a implicação significante ganhava destaque: tema estudado no ano acadêmico 1979-1980 e, talvez, a retomar no período seguinte.

Como se percebe, a implicação significante preocupava nosso filósofo e, aos seus olhos, devia parecer fecunda. No que estava certo.

3. Implicação (e argumentação)

O vocábulo 'implicação' admite um referente principal.

Falemos dele.

Quando uma dada conclusão C é afirmada com base em certas premissas (explicitamente mencionadas ou, muitas vezes, apenas tacitamente admitidas), há o que se denomina uma inferência. A par disso, a coleção das premissas, devidamente explicitadas, e a conclusão formam o que se chama argumento.

Usualmente, um argumento é apresentado com o objetivo de dar credibilidade a uma conclusão. As premissas são arroladas para que essa credibilidade se apresente.

Nos casos mais favoráveis, a inferência é dedutiva. Quer dizer: regras de inferência (admitidas e legítimas) autorizam passar das premissas para a conclusão. Por conseguinte, aceitas as premissas, a conclusão também se imporá.

Existindo uma dedução que permita obter C a partir das premissas P₁ P₂,..., P_n, escreve-se

P₁, P₂,..., Pⁿ 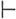C

o que se lê "As premissas acarretam C" ou C" é consequência lógica das premissas". Outra leitura adequada seria, ainda,

As premissas implicam a conclusão.

Quando formulamos argumentos, é natural dizer

Se P₁, P₂,. ...Pⁿ, então C

de modo que o condicional adquire posto de destaque, na condição de recurso lingüístico para expressar a implicação.

Na língua de todo dia, contudo, o condicional "Se, então" é utilizado com certa sem-cerimônia, de modo que

Se P₁, P₂,..., Pn, então C

pode associar-se a situações em que C não seja estritamente deduzível das premissas — mas tão somente uma consequência plausível dessas premissas.

Lembrando que o condicional "Se então" pode aludir a uma inferência não-dedutiva, fica fácil perceber porque a palavra 'implicação" tembém teve seu significado ampliado para abranger inferências não-dedutivas.

A rigor, para evitar malentendidos, uma tal ampliação de significado não deveria ser autorizada: há implicação quando há dedução.

4. Implicação (como juntor proposicional)

Para complicar um pouco mais a situação, lembremos que o condicional tem outra função: no cálculo proposocional, "Se, então" é um juntor que permite formar uma proposição

Se p, então q

a partir de duas proposições dadas (não obrigatoriamente distintas — ou seja, permitindo" Se p, então p").

Recapitulemos.

Nos estudos de lógica bivalente clássica, aceita-se a existência de proposições p, q, r, etc.; admite-se que cada proposição tem um e um só de dois valores-verdade (o valor V, de verdadeira; ou o valor F, de falsa); e se estipula, ainda, que certos operadores podem "atuar" sobre proposições para formar compostos (proposições moleculares) cujo valor-verdade dependa exclusivamente dos valores-verdade dos componentes.

Exemplificativamente, um dos operadores corresponde à negação e permite formar o composto "não p", representado por

~P

cujo valor é o contrário do valor de p.

Dadas duas proposições, p, q,, outros operadores (agora convenientemente chamados juntores) adquirem destaque. Um deles, p. ex., corresponde à conjunção e permite formar o composto "p e q", representado por

p & q

Esse composto toma o valor V quando val (p) = val (q) = V (e toma valor F nos demais casos). Concretamente, a proposição

Hoje é terça e chove

será verdadeira apenas se hoje for terça e se estiver chovendo.

Em homenagem a Filon, de Megara, que viveu aproximadamente em 300 a. C, daremos o nome de juntor filônico a um especial juntor que forma composto representado por

p 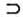q

que só toma valor F quando val (p) = V e val (q) = F (e toma valor V nos demais casos).

Adotando a prática usual, diremos que p é o antecedente e q o consequente do composto p 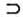q. Concretamente, são verdadeiras as três seguintes proposições

(É dia ) 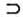(está claro)
(A lua voa) 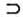(a lua existe)
(A lua voa) 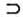(a lua tem asas)

e é falsa esta outra

(É dia) 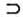(é noite).

Por um desses estranhos golpes do destino, o composto

p 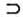q

recebeu a leitura

Se p, então q

e, pior do que isso,

p implica q

Assim, o que seria uma proposição "neutra"

p ferradura q

passou a ser encarado como condicional da inferência, insinuando que o consequente q teria sido obtido por inferência, com base na (pseudo) premissa p!

É natural que a proposição "neutra"

(A lua tem asas) 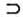(a lua voa)

possa ser vista como verdadeira. Dificilmente, porém, uma pessoa deixará de reagir com desagrado diante de

Se a lua tem asas, então a lua voa

E mais dificilmente ainda, admitirá que

A lua tem asas implica a lua voa

seja uma verdade, por ter antecedente falso...

A maioria dos leitores de livros de lógica se espanta e se aborrece com exemplos desse gênero. Piaget mesmo, em seu "Essai sur la necessité" (1977), não esconde seu desagrado e considera

"Si le vinaigre est acide, alors certains personnages portent la barbe"

como uma "implication paradoxale".

Os que assim reagem estão certos, naturalmente, pois os próprios estudiosos de lógica permitem que se instale a confusão entre dois itens diversos

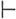da dedução (ou inferência)
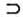do juntor filônico

e agravam essa confusão admitindo, nos dois casos, a leitura "Se, então" ou, o que ainda é pior, autorizando, nos dois casos, o emprego da palavra 'implicação'.

Não custa notar, p, ex., que GRIZE & MATALON (1962), no artigo "Introduction a une étude expérimentale et formelle du raisonnement naturel" utilizam os símbolos lógicos 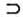(do condicional) e 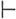(da dedução), sem deixar clara a distinção que entre eles deveria ser estabelecida. Além disso, os autores também usam o termo 'implicação' para o condicional e para a dedução.

5. Implicação (num condicional explicativo)

Deve ter ficado claro, nas seções anteriores, de que modo a expressão "Se .... então..." se associou à dedução ("Se tais ou quais premissas, então esta conclusão") e também a uma proposição composta, formada com duas proposições dadas ("Se p, então q").

Veremos, agora, de que modo o mesmo "Se..., então.,." aparece como elemento indispensável nas explicações, especialmente as causais. Veremos, também, em que medida o condicional, para tornar aceitável, deve estar imerso em um "sistema" - seja uma teoria bem formulada, seja um conjunto de crenças não muito bem delineadas.

A discussão seguinte está assentada no que disse TOULMIN (1958). De acordo com Toulmin, há uma "fôrma" a que se acomodam variados tipos de explicação, inclusive a causal.

Em lermos genéricos, dispomos de certos dados (D) e, em função deles, justificamos a ocorrência de um evento (E). A fim de que E possa apresentar-se como decorrência dos dados D, algum nexo deve existir entre eles. Esse nexo é o condicional.

Se D, então E

formulado com as respectivas descrições dos dados e do evento. Esse condicional atua como garantia (G) da existência de nexo entre D e E.

A credibilidade que associamos ao condicional está, porém, associada (1) à presença (ou não) de condições restritivas (R), capazes de impedir o surgimento de E, ainda quando presentes os dados D ; e (2) à existência (ou não) de um corpo de conhecimentos prévios, ou seja, de um "suporte" (S), capaz de atuar como "fiador" do condicional "Se D, então E".

De modo esquemático,

 

 

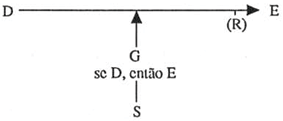
Quando uma explicação atinge esse genero de coesão, de modo que o condiciona] "Se D, então E" esteja colocado em um suporte aceitável (sendo negligenciáveis os possíveis fatores restritivos), é comum afirmar

Dados de tipo D implicam E

ou mesmo

D é a causa de E.

Em outras palavras, o diagrama permite dizer

dados de tipo D conduzem a E pois se D, então E,
a menos que prevaleçam as restrições R. A relação
entre D e E está assegurada pelo suporte S.

Tudo isso se abrevia no condicional

Se D, então E

ficando o resto subentendido; às vezes, se expressa de modo mais categórico em

Dados de tipo D implicam E

ou mesmo em

D é causa de E.

Ao dizer que D implica E, tem-se em conta uma forma de interferência (talvez dedutiva), apoiada no suporte S. Quanto mais "coeso" esse S, tanto mais confiável o condicional "Se D, então E" e, pois, mais aceitável a explicação da ocorrência de E, face aos dados D.

O "quadro" resume o que foi dito até agora, relativamente ao condicional e à implicação.

 

 

SEGUNDA PARTE

É tempo de voltar à implicação significante de Piaget.

Para compreender o que nosso pensador pretendeu dizer, usaremos alguns exemplos concretos.

Comecemos com

x -4 = 6 implica x= 10.

Existe uma teoria (a aritmética) perfeitamente estabelecida, cujos teoremas, postos ao Lido do antecedente "x - 4 = 6", permitem deduzir que x = 10. Em termos gerais, chamando A os axiomas da aritmética, estamos nesta situação:

A & (x - 4 = 6) 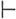x = 10

Em vista de um famoso resultado (denominado teorema da dedução, demonstrado por A. Tarski em 1930 e, de modo independente, na mesma época, por J. Herbrand) é possível concluir, em seguida, que

A 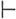[(x - 4 = 6)...(x = 10)]

Quer dizer: o condicional, com o juntor filônico, é deduzível dos axiomas da aritmética.

Generalizemos a situação agora descrita.

Dispomos de uma teoria θ perfeitamente estabelecida, com seus axiomas e teoremas. Admitamos ter conseguido efetuar a seguinte dedução

θ & p 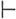q

Assim sendo, usamos o teorema de Tarski para assegurar que

θ 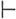(p...q)

Invejando os estudiosos de lógica, inventores de variados tipos de implicação, inventarei minha própria implicação: direi que p 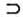q é uma implicação teoremática (pois surge como teorema de uma teoria). Prossigamos. Consideremos

Se é dia, então há luz.

Esse condicional poderia ser denominado diodórico, em homenagem a Diodoro (falecido em 307 a. C, contemporâneo de Filon, também de Megara). Diodoro estudou os condicionais conexos, entendendo que o uso de "Se, então" deveria limitar-se ao caso de impossibilidade de se dar o antecedente e não se dar o conseqüente; "não é possível ter (é dia e não há luz)".

Com os recursos da lógica modal, lembrando que o losango é símbolo empregado para a possibilidade, o condicional diodórico "Se p, então q" significaria

~◊ (p & ~ q)

ou seja: não possível (p e não q).

Apenas para estabelecer certos contrastes, consideremos, a seguir, os condicionais

Se Patrícia não tomar aspirina,
continuará com dor de cabeça

e

Se 2 + 2 = 7, então a lua é cúbica.

Não nos deteremos neste último condicional. Já deve ter ficado claro que se trata de proposição composta com o juntor filônico

(2 + 2 = 7) 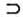(a lua é cúbica)

e que, por sinal, deve ser vista como verdadeira, por motivos estritamente formais — e não por motivos que tenham algo a ver com o assunto mencionado.

Salientemos, aliás, que o vocábulo "implicação" não pode nem deve ser usado nesse caso e em casos análogos.

Acresce que nem sequer chegamos a imaginar um sistema q (uma teoria), ligado ao real, em que um condicional desse tipo pudesse comparecer. Esse é, muito bem balizado, o "condicional louco" dos lógicos. (Apenas, para defender um pouquinho os lógicos, lembremos que é um "condicional louco", não uma implicação"!.E sublinhemos que, a rigor, nem condicional chega a ser; é um composto com o juntor filônico).

No outro exemplo, admitimos a possibilidade de uma explicação do gênero "Se D, então E", isto é, dados de certo tipo dão margem a uma espécie de conseqüência. Não há um sistema (uma teoria) estabelecido(a) com o(a)qual obter

(Pat não toma aspirina) 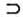(Pat continua com dor de cabeça)

Entretanto, o condicional, embora sujeito a restrições R de considerável peso, não parece "flutuar no espaço", sem apoio de algum suporte S.

Mary Henle (1962), em seu artigo "On the relation between logic and thinking" acentua as diferenças que há entre um raciocínio formal e um raciocínio prático. Ali, as informações admitidas são apenas as que hajam sido explicitamente apresentadas; aqui, uma ampla gama de informações disponíveis poderá ser utilizada. Em geral, os pressupostos de que nos servimos, nos diálogos corriqueiros, não constituem um sistema com as características de uma teoria formal. Todavia, são suficientes para uma espécie de "caminhada dedutiva" capaz de dar suporte a um condicional.

Nossa confiança no suporte pode ser "grande", como no caso "Se é dia, há luz" (onde S envolve a astronomia, a mecânica celeste, etc.) ou "pequena", como no caso de "Se for de avião chegarei mais depressa" pois pode haver mau tempo, greve de aeroviários, etc).

De qualquer forma, a fim de que um condicional, sobretudo ao traduzir o juntor filônico, não desperte desconfianças, há de ser plausível a correspondente conjunção.

Em outras palavras, p 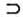q (lido como condicional, "Se p, então q") é tanto mais aceitável quanto mais habituados estejamos com a correspondente função p & q.

Exemplificando, "Se é domingo, há missa" tem boa parte de sua aceitabilidade presa ao fato de já termos vivido (ou ouvido falar da) situação "É domingo e há missa".

Um condicional "quase louco"do tipo "Se for à livraria, comerei empadas" só começará a tornar-se aceitável se pudermos revelar que há um (pseudo) sistema, ou seja, a circunstância de a livraria estar ao lado de uma rotisseria, tornando plausível a conjunção "vou à livraria e como empadas".

Estamos preparados para concluir.

Recapitularemos algumas afirmações feitas por Piaget. Em 1949, no segundo volume da Introduccion à l'epistemologie génétique, ele registrou

La pensée physique prolonge ainsi directement la pensée mathématique dans son effort d'assimilation de l'eperience aux opérations du sujet,... mais... elle n'est jamais... rèductible aux coordinations... de l'action.

Em 1963, no primeiro volume do Traité de Psycologie experimentale, Piaget abre uma seção para lhe dar o título "L'isomorphisme entre la causalité et 1' "implication" "Conclusions". Quatro anos depois, em Biologie et connaissance(p. 63) lemos

le fameux principe de parallèlisme psychophysiologique n'est en réalité qu'un principe d'isomorphisme entre la casualité et l'implication.

Enfim lembremos de um trecho do artigo "La causalité selon E. Meyerson". (1971, p. 197)

... il est d'autant plus aisé ... de discerner à partir de quel point débute la casualité: c'est à partir du moment où un système de lois acquiert un caractère de nécessité en tant que système.

As citações permitem perceber que Piaget procurava caracterizar satisfatoriamente a implicação significante em busca da superação da dicotomia operações/casualidade.

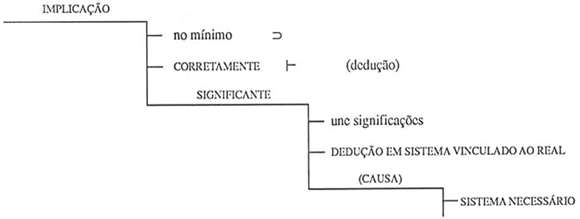
Apoiando-nos no que ficou dito neste ensaio, podemos concluir, antes de mais nada que para haver implicação deve haver dedução.

Mas a implicação em tela é a significante. Quer isso dizer que a dedução se processa (com as técnicas da lógica e da matemática) em um sistema no qual tenha sido possível exprimir significações. Dito de maneira mais direta, a dedução se processa em um sistema vinculado ao real.

Caso o sistema seja necessário, isto é, esteja formado por generalizações e leis necessárias ("não podia ser de outro modo"), a noção de causa ter-se-á apresentado com todo seu "esplendor".

O quadro abaixo, presta-se para deixar explícito o pensamento que norteou estas últimas afirmações.

 

 

REFERÊNCIAS BIBLIOGRÁFICAS

GRIZE, J. E. & MATALON, B. Introduction a une étude experiméntale et formelle du raisonnement naturel. In:_____. Implication, formalization et logique naturelle. Paris, P. U. F,, 1962.        [ Links ]

HENLE, M. On the relation between logic and thinking. Psychological Review, 69( ): - ,1962        [ Links ]

PIAGET, J. Bilogie et connaissance. Paris, Gallimard, 1967        [ Links ]

PIAGET, J. La causalité selon E. Meyerson. In: BUNGE, M. et al. Les théories de la casualité, Paris, P. U. F., 1971.        [ Links ]

PIAGET, J. Essai sur la necéssité. Archives de Psychologie, Paris, 45,1977        [ Links ]

PIAGET, J. Introduction à l'epistémologie génétique, Paris, P. U. F., 1949        [ Links ]

PIAGET, J. Reussir et comprendre. Paris, P. U. F., 1974.        [ Links ]

PIAGET, J. Traité de Psychologie experimentale. Paris, P. U. F., 1963.        [ Links ]

TOULMIN, S. The uses of argument, Cambridge, University Press, 1958.        [ Links ]