ARTICLE

 

Desempenho de alunos do quarto ano em testes de subitização e estimativa e no Teste de Desempenho Escolar (TDE)

 

Fourth grade students' performance on subitizing and estimation tasks, and School Performance Test (TDE)

 

Rendimiento de alumnos del cuarto año en pruebas de subitización y estimativa y Prueba de Rendimiento Escolar (TDE)

 

 

Paulo Sérgio Teixeira do Prado^I; Mariana de Freitas Betetto^II; Ivana Gisel Casali-Robalinho^III; Rogério Crevelenti Fioraneli^IV; Alessandra Campanini Mendes^IV; Júlia Zanetti Rocca^V; Leila Estevão da Silva Cacciacarro Lincoln^VI; Marília Zampieri^VII; João dos Santos Carmo^VIII

^IDepartamento de Psicologia da Educação da Universidade Estadual Paulista Júlio de Mesquita Filho, Marília, SP, Brasil
^IIConsultoria de Psicologia Educacional, Rio Claro, SP, Brasil
^IIICentro Universitário Adventista de São Paulo, Engenheiro Coelho, SP, Brasil
^IVPrograma de Pós-Graduação em Psicologia da Universidade Federal de São Carlos, São Carlos, SP, Brasil
^VUniversidade Federal do Mato Grosso, Rondonópolis, MT, Brasil
^VIVictor Vision Indústria e Comércio de Equipamentos Médicos e Odontológicos, São Carlos, SP, Brasil
^VIICurso de Especialização em Psicologia Clínica Comportamental do Instituto de Terapia por Contingências de Reforçamento, Campinas, SP, Brasil
^VIIIDepartamento de Psicologia da Universidade Federal de São Carlos, São Carlos, SP, Brasil Instituto Nacional de Ciência e Tecnologia sobre Comportamento, Cognição e Ensino, São Carlos, SP, Brasil

Endereço para correspondência

 

 

---

RESUMO

O texto relata uma pesquisa feita com 62 alunos do quarto ano escolar de duas escolas do interior de São Paulo: uma da rede privada e outra pública. O propósito foi o de investigar a relação entre o desempenho daqueles alunos em testes de subitização e estimativa e no Teste de Desempenho Escolar (TDE). Subitização e estimativa numérica aproximada são partes do senso numérico, considerado inato, razão pela qual ele não sofreria influência de fatores ambientais, como o tipo de escola frequentada, ao contrário do que seria de se esperar com relação a habilidades matemáticas adquiridas na escola. Adicionalmente, sendo o senso numérico inato, ele estaria restrito a limites cuja superação é possibilitada por avanços de ordem cultural. Portanto, entre ele e habilidades matemáticas seria de se esperar uma correlação fraca ou ausente. Os resultados do teste de subitização e estimativa replicam, com fidelidade, o padrão de desempenho encontrado na literatura: praticamente nenhum erro com numerosidades de 1 a 4 e queda abrupta de 5 a 10. Comparações por dependência administrativa das escolas, idade e sexo dos participantes, não revelaram diferenças estatisticamente significantes. Quanto aos resultados do subteste de aritmética do TDE, eles indicam um desempenho melhor dos alunos da escola privada, não tendo sido observadas diferenças quanto às outras variáveis. Finalmente, a análise de Correlação (de Pearson) entre os dados dos dois testes apresentou um coeficiente moderado a baixo. Os resultados, pois, confirmam as hipóteses testadas e fornecem evidências adicionais em favor da tese de um senso numérico inato.

Palavras-chave: Senso numérico; Psicologia Matemática; desempenho escolar; aptidão numérica; correlação estatística.

---

ABSTRACT

The paper reports a research conducted with 62 students enrolled in the fourth grade of two schools of different cities of São Paulo state: one private and another public. Its purpose was to investigate the relation between their performance on probes of subitizing and estimation and on the School Performance Test (TDE). Subitizing and approximate numerical estimation are part of number sense, which is considered innate, therefore not subject to influence of environmental factors such as type of school attended, contrary to what would be expected with respect to math skills learned in school. Additionally, once number sense is innate it would be restricted to limits whose overcoming is made possible by cultural advancements. So between it and math skills one would expect a weak or absent correlation. Results of subitizing and estimating test showed the same pattern of performance found in the literature: virtually no errors with numerosities 1 to 4 and an abrupt drop from 5 to 10. Comparisons were performed according to administrative dependence of schools, age and sex of the participants. No statistically significant differences were found. The results of the arithmetic subtest of the TDE indicate a better performance of private school students, with no differences in respect to the other variables. Finally, the analysis of Correlation (by Pearson) between the data from the two tests showed a moderate to low coefficient. Therefore, the results confirm the hypotheses tested and provide additional evidence in favor of the thesis of an innate numerical sense.

Keywords: Number sense; Mathematical Psychology; school performance; numerical aptitude; statistical correlation.

---

RESUMEN

El texto narra una pesquisa con 62 estudiantes de cuarto año de dos escuelas en el interior de Sao Paulo: una privada y otra pública. El propósito era investigar la relación entre su desempeño en pruebas de subitización y estimativa y en la Prueba de Rendimiento Escolar (TDE). Subitización y estimativa numérica aproximada forman el sentido numérico, considerado innato, razón por qué él podría no estar influenciado por factores ambientales tales como el tipo de escuela, contrariamente a lo que uno esperaría en cuanto a habilidades matemáticas adquiridos en la escuela. Además, siendo el sentido numérico innato, él estaría restringido a límites cuya superación es posible por la evolución cultural. Por lo tanto, entre él y habilidades matemáticas esperaría una correlación débil o no correlación. Los resultados de las pruebas de subitizacion y estimativa reproducen, con fidelidad, el estándar de rendimiento encontrado en la literatura: prácticamente ningún error con numerosidades 1-4 y abrupta caída 5-10. Comparaciones por dependencia administrativa de las escuelas, la edad y el sexo de los participantes no reveló diferencias estadísticamente significativas. Los resultados de la subprueba de aritmética de lo TDE indican un mejor rendimiento de los estudiantes de la escuela privada, no habiendo sido observado diferencias en relación con las otras variables. Finalmente, el análisis de Correlación (de Pearson) entre los datos de las dos pruebas mostró un coeficiente de moderado a bajo. Los resultados confirman las hipótesis a prueba y proporcionan evidencia adicional a favor de la tesis de un sentido numérico innato.

Palabras clave: Sentido numérico; Psicología Matemática; rendimiento escolar; aptitud numérica; correlación estadística.

---

 

 

Habilidades matemáticas têm desafiado pesquisadores de diferentes áreas, uma vez que elas envolvem desde capacidades muito simples, como a diferenciação de pequenas quantidades de objetos, até operações com alto grau de formalização e resolução de problemas intrincados. Parte da literatura apresenta dados do que pode ser chamado de protomatemática, ou noções matemáticas iniciais, inferidas a partir da observação do comportamento de várias espécies não-humanas (Hauser & Carey, 2003) e de bebês humanos (Berger, Tzur, & Posner, 2006; Geary, 1994; Starkey & Cooper, 1980; Strauss & Curtis, 1981; Wynn, 1990, 1992b). Essas observações autorizam autores a afirmar que algumas habilidades surgiram antes do aparecimento da nossa espécie, foram filogeneticamente herdadas por nós e constituem a base do desenvolvimento cultural e da aprendizagem individual da matemática (Hauser & Spelke, 2004).

Essa é uma implicação da teoria da evolução, no sentido de que os processos adaptativos não se restringem a aspectos anatômicos e fisiológicos dos organismos, mas incluem o comportamento e a cognição (se é que se trata de coisas distintas). Além de permitir a compreensão de semelhanças e diferenças entre espécies em suas interações com o meio ambiente, ela permite também o avanço para uma compreensão da continuidade entre biologia e cultura (Bussab, 2000; Geary, 1996) e, por conseguinte, a identificação de origens biológicas de várias de nossas conquistas culturais, como parece ser o caso da matemática (Dehaene, Spelke, Pinel, Stanescu, & Tsivkin, 1999; Geary, 1996, 2001; Hauser & Spelke, 2004).

Especificamente, são duas as habilidades que subjazem à aprendizagem ulterior da matemática: subitização e estimativa numérica aproximada. Ambas compõem o senso numérico inato (Dehaene, 1997) e constituem nossa capacidade de processamento numérico não simbólico. A primeira diz respeito ao reconhecimento e à discriminação exatos de numerosidades até três ou quatro, ao passo que a segunda está relacionada com o julgamento aproximado de quantidades iguais ou superiores a cinco. Essas habilidades já foram observadas em animais não-humanos e em bebês. E em experimentos com adultos, os estímulos são apresentados por apenas alguns milésimos de segundo, impedindo o recurso à contagem, de modo que a subitização e a estimativa numérica aproximada são consideradas independentes da linguagem (Dehaene & Cohen, 1994; Dehaene et al., 1999; Trick & Pylyshyn, 1994). A contagem, por sua vez, é um produto de avanços culturais na história da humanidade, que envolve a linguagem e permite o processamento simbólico exato de grandes numerosidades, isto é, de conjuntos com número de elementos igual ou superior a cinco (Gordon, 2004; Pica, Lemer, Izard, & Dehaene, 2004; Prado, 2008, 2010; Wynn, 1992a).

Embora essa temática venha sendo estudada há algumas décadas em vários países, gerando um grande volume de publicações, no Brasil ainda são pouco numerosas as pesquisas sobre ela (Santos, Da Silva, Ribeiro, Dias, et al., 2012; Santos, Silva, Ribeiro, Dellatolas, & von Aster, 2012; Silva & Santos, 2011). Por essa razão, um dos objetivos do trabalho aqui relatado foi replicar procedimentos usados em pesquisas sobre subitização e estimativa numérica aproximada, com uma amostra brasileira. A hipótese subjacente é a de que, se o fenômeno é de natureza biológica, portanto, independente da cultura, espera-se sua reprodução também nessa amostra, com o mesmo padrão de ruptura do desempenho a partir da numerosidade quatro. Também será testada uma hipótese adicional de que, sendo inatas as duas habilidades referidas anteriormente, elas teriam uma correlação fraca ou nenhuma correlação com a aprendizagem da matemática escolar, que é eminentemente cultural, lida com números muito superiores aos subitizáveis e requer seu processamento exato, no plano simbólico.

As hipóteses acima foram testadas por meio de dois estudos, os quais serão relatados na sequência. No Estudo 1 foi utilizado um programa de computador com o objetivo de sondar a subitização e a estimativa numérica aproximada a partir de respostas apresentadas oralmente pelos participantes quando expostos a slides contendo de um a 10 pontos (círculos pretos sólidos). O Estudo 2 consistiu da avaliação do desempenho em matemática dos mesmos participantes. O instrumento utilizado para isso foi Teste de Desempenho Escolar (TDE) (Stein, 1994), particularmente o subteste de aritmética.

 

Estudo 1

Método

Participantes

Participaram do estudo 62 crianças regularmente matriculadas e cursando o quarto ano do Ensino Fundamental de duas escolas do interior do Estado de São Paulo: uma da rede privada do município de São Carlos (n = 30) e outra da rede municipal de Aguaí (n = 32). A idade dos alunos variou entre 8 e 13,9 anos (média = 9,6; DP = 1,2). A amplitude da faixa etária deveu-se à inclusão, na amostra, de alunos que haviam sido retidos em alguma série ou ingressado tardiamente na escola.

Situação e Estímulos Experimentais

Cada participante foi recebido individualmente numa sala disponibilizada pela respectiva escola, com mobiliário adequado e suficiente para acomodar os pesquisadores e os alunos, sendo livre de ruídos ou outras interferências que pudessem prejudicar a condução da sessão experimental.

O procedimento foi executado por meio de um software não comercial, elaborado especialmente para o uso em pesquisas. Os estímulos experimentais consistiram de um conjunto de 30 slides, cada um contendo uma quantidade de um a 10 pontos. Em um terço deles, os pontos foram distribuídos espacialmente de forma canônica, isto é, de acordo com um padrão de linhas e colunas semelhante ao usado no jogo de dominó. Nos outros dois terços, os pontos foram distribuídos aleatoriamente. A área ocupada pelos pontos também foi controlada, de modo que ela fosse sempre a mesma, independentemente do número de pontos. Encontrada a área de um ponto (conjunto unitário), ela foi dividida por dois para definir a área de cada ponto para o conjunto de dois elementos, por três para o conjunto de três elementos e assim por diante.

Procedimento

Inicialmente, foi realizado contato com a direção de cada uma das duas escolas para exposição dos objetivos do estudo e os procedimentos a serem adotados na coleta de dados, a fim de obter o consentimento para a participação dos alunos. Os alunos selecionados foram aqueles que atingiram os critérios de composição da amostra quanto à idade e série escolar, buscando-se balancear o número de participantes por sexo. A seleção da amostra foi aleatória.

Todos os alunos foram informados de que sua participação não era obrigatória e que as atividades não tinham qualquer finalidade avaliativa. Eles também foram informados que a qualquer momento poderiam interromper ou desistir de sua participação, sem qualquer tipo de punição ou constrangimento¹.

Cada participante foi conduzido pelo experimentador até a sala onde seria realizada a sessão experimental. Ali, ele era posicionado frente ao monitor de vídeo do computador e instruído a dizer, em voz alta, o número de pontos que seriam apresentados na tela. Uma vinheta sinalizava a apresentação de cada slide e as respostas orais foram gravadas pelo próprio software, para posterior mensuração da latência (tempo de reação). Cada um de trinta slides foi exposto durante 200 milissegundos e o intervalo entre tentativas foi de dois segundos, durante o qual a tela permanecia em branco. Em dez dos slides foram apresentados conjuntos de 1 a 10 pontos com distribuição canônica. Nos outros vinte, cada conjunto de 1 a 10 pontos, com distribuição espacial aleatória, foi apresentado duas vezes. Portanto, foram 30 tentativas no total. A ordem de apresentação dos slides foi randomizada, tendo sido preparadas quatro sequências distintas, de modo que, em um dia de coleta de dados, o primeiro participante seria exposto à sequência 1, o segundo à sequência 2, e assim por diante até o quarto participante, após o que, voltava-se à sequência 1. A aplicação do teste de subitização e estimativa teve duração de aproximadamente três minutos. Concluída essa parte da sessão experimental, seguia-se a aplicação do Teste de Desempenho Escolar (TDE), a ser descrita mais adiante, no relato do Estudo 2. Finalizada a sessão, a criança era levada de volta à sua sala de aula.

Para análise do desempenho foram considerados: (a) o número total de acertos; (b) os acertos em função da distribuição espacial dos pontos: canônica ou aleatória e; (c) acertos em função da faixa de número de pontos: 1 a 4 (numerosidades subitizáveis) ou 5 a 10 (numerosidades estimáveis). No que diz respeito a respostas incorretas, foi analisada a proximidade relativa da resposta em relação ao número de pontos. Também foram feitas comparações entre alunos: por escola, por sexo e por faixa etária.

Resultados e Discussão

A seguir, são apresentados os dados do teste de subitização e estimativa. A análise leva em conta a frequência de participantes com respostas corretas, a frequência de acertos por valores (subitizáveis e estimáveis), o padrão de disposição espacial dos elementos dos conjuntos e comparações por dependência administrativa da escola, sexo e idade.

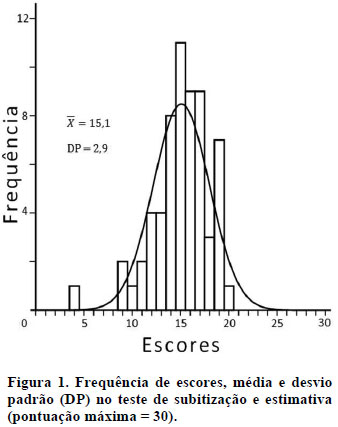
O histograma da Figura 1 apresenta a frequência de participantes por número de acertos dentre os 30 possíveis, correspondes ao total de tentativas. A criança com pior desempenho acertou quatro delas, ao passo que a criança com melhor desempenho acertou 20. A maioria dos alunos concentra-se entre esses extremos, sendo a maior frequência igual a 11 participantes que responderam corretamente em metade (15) das tentativas. A distribuição de frequências se encaixa no padrão estatístico de normalidade, sendo a média de acertos igual 15,1 e o desvio padrão (DP) igual a 2,9.

 

 

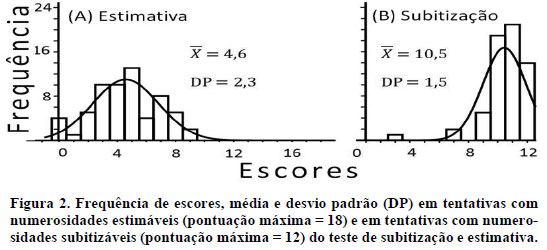
Para os propósitos do presente estudo, é importante que além da análise do padrão geral de desempenho, este seja analisado também, de modo mais específico, em função do número de elementos nos conjuntos, que se subdivide em duas categorias: numerosidades subitizáveis (1 a 4) e numerosidades estimáveis (5 a 10, no presente caso). Parte dos resultados dessa análise é apresentada na Figura 2. Mais especificamente, a Figura 2A apresenta a frequência de participantes que responderam corretamente às numerosidades estimáveis, cujas tentativas foram 18. Por sua vez, a Figura 2B apresenta a frequência de participantes que responderam corretamente às numerosidades subitizáveis, cujas tentativas foram 12. O padrão mesocúrtico e a ligeira assimetria positiva da curva da esquerda (Figura 2A) mostram que os escores mais frequentes estão bem distantes e abaixo da máxima pontuação possível e que seus valores se distanciam da média mais do que o que se observa com relação à subitização (Figura 2B). De fato, o número máximo de acertos foi nove, o qual foi alcançado por um único participante. Conforme se observa Figura na 2A, o escore médio nas tentativas com numerosidades estimáveis foi de 4,6 e o DP = 2,3, ao passo que, em numerosidades subitizáveis a média de acertos sobe para 10,5, havendo menor dispersão dos valores, como indica o DP = 1,5. Diferentemente do gráfico da Figura 2A, o da Figura 2B, apresenta um padrão leptocúrtico com assimetria negativa, demonstrando, comparativamente, uma frequência maior de escores máximos e pouco distanciamento da média.

 

 

O contraste entre a frequência de respostas corretas a numerosidades subitizáveis (de 1 a 4) e estimáveis (de 5 em diante) fica evidente na Figura 3. As curvas nela projetadas representam o número de participantes que responderam corretamente a cada um dos conjuntos de 1 a 10 elementos, estivessem estes distribuídos de forma canônica (uma tentativa cada) ou aleatória (duas tentativas cada). As três curvas se sobrepõem num patamar elevado até a numerosidade 4, refletindo a praticamente ausência de erros. A partir desse valor, contudo, há uma queda abrupta, baixando para menos da metade o número de participantes que responderam corretamente às numerosidades de 5 em diante, especialmente no que diz respeito à distribuição aleatória dos pontos.

 

 

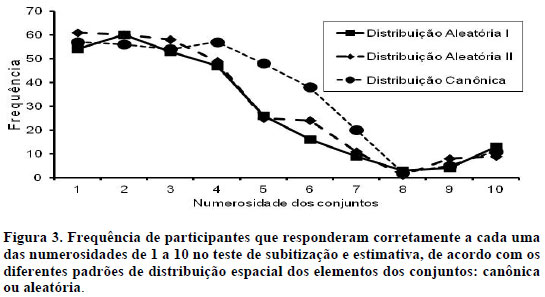
Ainda na Figura 3, a curva representando os pontos com distribuição canônica apresenta uma queda bem mais suave, que vai de 4 a 8. Desse valor em diante, as três curvas voltam a se sobrepor, agora num nível baixo. É clara a influência da variável "distribuição espacial dos elementos" sobre a acurácia das respostas. Como ponderaram Beckwith e Restle (1966), várias décadas atrás, determinados tipos de arranjo visual podem facilitar uma combinação, por parte do participante, de sua capacidade de subitização com sua habilidade de somar (e de multiplicar) para determinar o número de elementos no slide. Levando-se em conta a série em que estudavam os alunos que participaram desta pesquisa, essa é uma hipótese plausível e, ao que parece, é o que reflete a referida curva.

Considerando a influência do padrão de distribuição espacial dos elementos sobre a resposta numérica, levamos a cabo uma tentativa de mensurar sua magnitude. O resultado é apresentado na Figura 4, que resume a análise de erros cometidos em função dessa variável. As colunas representam a diferença média entre o número de pontos dos conjuntos e as respostas dos participantes. No que diz respeito às numerosidades subitizáveis, nota-se uma pequena diferença, cujo valor é 0,5 para mais e para menos, independente da distribuição espacial dos pontos. Com relação às numerosidades estimáveis, observa-se uma diferença de 0,5 para itens com distribuição canônica e maior do que 2,0 para itens com distribuição aleatória. Novamente, os dados indicam que a variável distribuição espacial exerce influência sobre a acurácia das respostas, particularmente as apresentadas a numerosidades estimáveis.

 

 

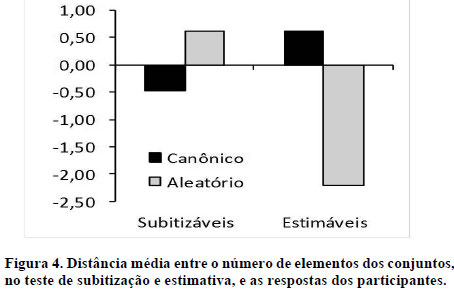
Os dados expostos até aqui replicam, com alto grau de fidelidade, o mesmo padrão de ruptura do desempenho a partir de numerosidades superiores a 4 encontrado na literatura internacional (Geary, 1994; Starkey & Cooper, 1980; Strauss & Curtis, 1981; Trick, & Pylyshyn, 1994; Wynn, 1992b), robustecendo as evidências que têm sido tomadas em apoio à tese de um senso numérico inato (Berger et al., 2006; Dehaene, 1997; Dehaene & Cohen, 1994; Geary, 1994, 1996, 2001; Hauser & Spelke, 2004; Starkey & Cooper, 1980; Strauss & Curtis, 1981; Trick & Pylyshyn, 1994; Wynn, 1992b). Dados comparativos, apresentados a seguir, apontam na mesma direção.

Conduzimos uma série de comparações. Uma delas foi entre os escores dos alunos das escolas pública e privada, a qual revelou um t (60) = 1,5 (p = 0,171), indicando não haver diferenças significativas entre eles, exceto por uma maior variação nos escores dos alunos da escola particular, que foi de 4 a 20, ao passo que os dos participantes da escola pública ficaram entre 11 e 19. Na comparação por sexos (33 meninos e 29 meninas), obteve-se um t = -0,381 (p = 0,703), evidenciando não haver diferenças significativas em função dessa variável. Finalmente, a execução de uma Análise de Variância (ANOVA) para a constatação de eventuais diferenças por faixa etária produziu um F (3, 58) = 1,300; (p = 0,283), revelando que também não houve diferenças de desempenho em função da idade.

O fato de as variáveis: dependência administrativa das escolas, idade e sexo não terem exercido influência no desempenho dos participantes no teste de subitização e estimativa, corrobora resultados de outras pesquisas e são condizentes com os dados da pesquisa aqui relatada, dos quais se disse que contribuem para fortalecer evidências em favor da tese inatista.

O Estudo 2, descrito à continuidade do presente relato, foi realizado com o propósito de trazer à luz a relação entre o senso numérico inato e o repertório matemático das séries iniciais do ensino fundamental.

 

Estudo 2

Diferente das habilidades inatas e não simbólicas que compõem o senso numérico analisadas no Estudo 1, a matemática escolar é um produto histórico-cultural, é eminentemente sim-bólica e lida com valores bem superiores aos dos números subitizáveis, processando-os com exatidão. Em razão dessas características, parece razoável supor que, embora habilidades inatas possam constituir o fundamento biológico da matemática desenvolvida culturalmente, haveria uma correlação fraca ou totalmente ausente entre ambos, senso numérico e comportamento matemático. Esta hipótese foi testada e os resultados são apresentados a seguir.

O Estudo 2 consistiu em investigar o repertório matemático dos participantes, fazendo-o por meio da aplicação do subteste de aritmética do Teste de Desempenho Escolar (TDE) e verificar se havia correlação entre seu desempenho nesse teste e o de subitização e estimativa.

 

Método

Participantes, Situação, Material e Procedimento

Os participantes do Estudo 2 foram os mesmos do Estudo 1 e os dados foram coletados na mesma situação descrita anteriormente, imediatamente em seguida à conclusão do teste de subitização e estimativa. O instrumento utilizado para a coleta de dados foi o Teste de Desempenho Escolar (TDE), elaborado para a avaliação de escolares da primeira à sexta séries, de acordo com a seriação anterior ao atual ensino fundamental de nove anos. Ele é composto por três subtestes: escrita, aritmética e leitura. Em razão do objetivo da pesquisa, foi aplicado apenas o subteste de aritmética, com duração de aproximadamente quinze minutos por aluno. Ele contém 35 problemas que estão organizados em ordem crescente de dificuldade. Os quatro primeiros são de adição e subtração, todos com dois números de um algarismo, seguidos de cinco das mesmas operações, com um a três números de dois algarismos. Na sequência, há um grupo de seis problemas, sendo os dois primeiros de multiplicação e divisão, com dois números de um algarismo e os outros quatro de multiplicação e adição, com dois a três números de até três dígitos. Depois são apresentados cinco problemas de subtração, multiplicação e divisão, todos com dois números de até quatro algarismos. Os cinco problemas seguintes incluem subtração com valores monetários em Reais (R$), com dois números de três a quatro algarismos e duas casas decimais, relativas aos centavos, divisão com dois números de dois a quatro dígitos e operações com frações envolvendo números de um dígito. Nos dois últimos conjuntos, com cinco problemas cada, há operações com frações com números de até dois algarismos, divisão com dividendo maior do que o divisor, potenciação e operações de adição e multiplicação com números de um dígito com sinais diferentes.

A aplicação do teste foi feita individualmente, seguindo-se as instruções contidas no respectivo manual, que, dentre outras recomendações, orienta a explicitar ao estudante que os exercícios destinam-se a alunos de diferentes idades e séries e que, portanto, haverá alguns que ele já estudou e outros que ainda não estudou, encorajando-o a fazer da melhor maneira tudo o que puder. Lembrando que os participantes eram alunos do quarto ano, seguindo essas instruções, eles foram orientados a fazer o máximo de exercícios que pudessem, sendo dispensados de fazer aqueles que lhes parecessem além de suas possibilidades, por serem relativos a conteúdos que ainda não haviam estudado.

Os itens com resposta correta foram contabilizados e compõem o escore bruto (EB) do teste, permitindo a classificação de cada aluno em relação à amostra para a qual o teste foi padronizado: níveis inferior, médio e superior, conforme critérios explicitados adiante.

 

Resultados e Discussão

A pontuação média obtida pelos participantes que compuseram a amostra, como um todo, foi de 17,02 pontos, com DP = 3,52. A Figura 5 representa a frequência de participantes por número de acertos, a qual apresenta distribuição normal, com concentrações maiores na zona intermediária e menores nas extremidades.

 

 

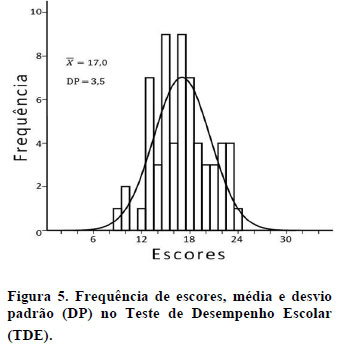
Problemas como os propostos pelo subteste de aritmética do TDE exigem raciocínio lógico e habilidades de cálculo praticadas no e ensinadas pelo meio sociocultural. Sua resolução, portanto, requer habilidades que vão além daquelas herdadas filogeneticamente. O papel do meio ambiente (padrões de reforço e punição na escola e na família, por exemplo) é decisivo para que a aprendizagem individual ocorra e adquira-se o domínio de ferramentas culturais transmitidas socialmente. Em decorrência, algumas diferenças são esperadas. À semelhança das comparações relatadas no Estudo 1, no presente também foi comparado o desempenho dos alunos por dependência administrativa das escolas, sexo e faixa etária.

Comparando a pontuação obtida pelos alunos de cada uma das escolas, encontramos uma diferença estatisticamente significante: t (60) = 2,44 (p = 0,018), com pontuação média mais elevada dos alunos da escola privada (18,1) do que dos da pública (16,0). A pontuação máxima no subteste de aritmética do TDE é 38 e as categorias são assim definidas, de acordo com a pontuação obtida: inferior < 14; médio, de 15 a 17 e superior > 18. A Figura 6 apresenta a frequência de alunos, em termos percentuais, de acordo com os referidos níveis e segundo a escola frequentada. Nas categorias inferior e médio, houve maior porcentagem de participantes da escola pública, ao passo que na categoria superior, o maior percentual de participantes foi da escola particular.

 

 

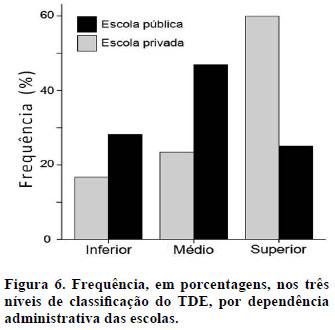
Sendo a amostra relativamente balanceada quanto ao sexo: 33 meninos e 29 meninas, foi possível verificar a influência dessa variável. O teste t (de Student) não revelou diferenças estatisticamente significantes de desempenho no TDE: t (60) = -0,037; (p = 0,971). E apesar de todos os participantes cursarem o quarto ano do ensino fundamental, sua idade variava de oito a 13 anos, razão pela qual analisamos também a possibilidade de influência dessa variável. A ANOVA de um fator não apontou diferenças significativas em função da idade: F (3, 58) = 1,082 (p= 0,364).

Dos dados expostos acima constata-se, portanto, que a única variável a interferir no desempenho dos alunos em aritmética foi a dependência administrativa da escola em que estudavam.

Correlação entre os Dados do Teste de Subitização e Estimativa e os do TDE

O índice de correlação de Pearson entre os escores do teste de subitização e estimativa e os do TDE foi: r = 0,38 (p = 0,01), significando uma força moderada a baixa, como previsto anteriormente. Se a análise levar em conta apenas as tentativas com numerosidades subitizáves do primeiro teste, temos um r = 0,17 (p = 0,10), o que indica ausência de relação entre a subitização e as habilidades matemáticas testadas. Por outro lado, se a análise levar em conta apenas as tentativas com numerosidades estimáveis do primeiro teste, tem-se, coincidentemente, também neste caso, um r = 0,38 (p = 0,01), o que significa uma correlação de força moderada a baixa entre os escores dos dois testes.

A análise da correlação entre duas variáveis sempre deixa margem ao questionamento sobre uma eventual interferência de uma terceira variável, além de não permitir afirmar, de modo inequívoco, uma relação de causalidade entre elas. No presente caso, considerando-se a idade dos participantes e a série escolar que cursavam, é plausível supor a interferência de, pelo menos, duas variáveis: a linguagem e a aprendizagem da própria matemática promovida pela escola. Nesse sentido, esses fatores, isolados ou em combinação poderiam influenciar, em alguma medida, o desempenho no teste de subitização e estimativa, como aventado anteriormente em referência às ponderações de Beckwith e Restle (1966), especialmente no que diz respeito aos conjuntos com distribuição espacial canônica dos itens.

 

Discussão Geral

O presente relato tratou de um experimento conduzido com o duplo intuito de replicar pesquisas feitas em outros países sobre habilidades numéricas consideradas inatas e verificar sua relação com a matemática aprendida no contexto escolar. Foram apresentados dados de dois estudos, sendo que os do primeiro foram coletados por meio de um software que permite o controle do tempo de apresentação dos estímulos - conjuntos de pontos, neste caso - na ordem de milésimos de segundo, em combinação com o controle do intervalo entre tentativas. Esse procedimento praticamente anula a interveniência da linguagem na realização da tarefa, ou seja, reduz a possibilidade de que o número seja determinado por contagem. Ele tem produzido um padrão de desempenho em que numerosidades de 1 a 4 são reconhecidas virtualmente sem erros, observando-se uma queda abrupta na acurácia das respostas a partir desse valor. Numerosidades de 5 em diante são determinadas por aproximação, mas as respostas nunca se distanciam muito do número real. Esses fenômenos da cognição numérica, chamados, respectivamente, de subitização e estimativa numérica aproximada, foram reproduzidos com fidelidade neste experimento, robustecendo o corpo de evidências que sustentam a afirmação de que o senso numérico é inato.

No segundo estudo foram apresentados dados sobre o desempenho dos participantes em matemática, os quais foram obtidos aplicando-se o subteste de aritmética do TDE. Em ambos os estudos, os dados produzidos com a aplicação dos referidos testes foram submetidos a análises cuja finalidade foi a de verificar eventual influência das variáveis: dependência administrativa das escolas, sexo e idade dos participantes. Uma habilidade de origem filogenética, seria de se esperar, estaria isenta de tais interferências, sobretudo, a experiência escolar, ao passo que o desempenho em matemática, ao contrário, não teria tal isenção. De fato, foi exatamente o que os resultados trouxeram à tona. O desempenho dos alunos nas tarefas de subitização e estimativa numérica aproximada revelou-se livre de influências da escola que frequentavam, ao passo que, no que diz respeito às suas habilidades matemáticas, foi observada influência do ambiente escolar.

O senso numérico (subitização e estimativa) é considerado uma herança filogenética subjacente à criação cultural da matemática e à aprendizagem individual dessa disciplina. Sendo ele, no entanto, inato e, em alguma medida, imune a influências ambientais e socioculturais, seria de se supor uma correlação fraca ou ausente entre ele e a matemática que se ensina na escola. Essa hipótese foi testada e os dados obtidos realmente revelaram uma correlação de força moderada a baixa (para evidências adicionais, ver: Santos, Silva, Ribeiro, Dellatolas, et al., 2012; Silva & Santos, 2011). Considerando que os dados que revelaram alguma correlação com os escores do TDE foram os relativos às tentativas com numerosidades estimáveis do teste de subitização e estimativa, é plausível supor que, no caso da nossa amostra, a capacidade de determinar o valor de conjuntos com "grandes" numerosidades seja uma função do conhecimento matemático adquirido. Em favor dessa hipótese pesam o fato de a amostra ter sido composta por alunos do quarto ano escolar, que, portanto, tiveram amplo contato com a disciplina, como também o fato de possuírem um repertório linguístico avançado.

A força e a fraqueza do presente trabalho residem, ambas, no mesmo fato: o de ser ele uma réplica de outras pesquisas. Por conta deste aspecto, ele, necessariamente, não pode ser considerado totalmente original. Não o bstante, a replicabilidade dos fatos científicos é condição fundamental para termos alguma certeza quanto à sua veracidade.

As evidências às quais somam-se as aqui apresentadas incluem dados de pesquisas com bebês pré-linguais, com animais não-humanos, com pacientes de lesão cerebral, de imageamento cerebral, de intervenção experimental por meio estimulação magnética intracraniana e várias outras. Elas têm permitido a forja de uma visão que rompe a dicotomia entre biologia e cultura e declara que uma é continuidade da outra (Geary, 1996, 2001; Hauser & Spelke; 2004; Pica et al., 2004; Prado, 2010). Entende-se que as conquistas culturais da humanidade só são possíveis porque a evolução nos dotou de um cérebro que nos capacita a isso. O processo adaptativo não se restringe, pois, à anatomia e à fisiologia, mas inclui comportamento e cognição. Nesse sentido, o senso numérico teve um papel na adaptação de espécies que nos antecederam. Essa discussão foge ao escopo deste trabalho, mas, ao que tudo indica, ele nos foi legado filogeneticamente e tem sido tomado como o fundamento biológico da criação e desenvolvimento culturais da matemática, bem como de seu aprendizado individual.

Pesquisas neurocientíficas identificaram regiões cerebrais específicas envolvidas no processamento numérico simbólico e não-simbólico (para uma discussão mais profunda e referências adicionais, ver Andrade, Prado, & Carmo, neste número). E há relato de experimento em que a estimulação magnética intracraniana de uma dessas regiões alterou o desempenho dos participantes em tarefas que requerem aquele tipo de processamento (Cappelletti, Barth, Fregni, Spelke, & Pascual-Leone, 2007). A descoberta da especificidade de funções dessas áreas do cérebro conduz à conclusão de que habilidades numéricas e matemáticas são de domínio específico. A propósito, é critério para o diagnóstico de discalculia - transtorno caracterizado por uma dificuldade extrema para a aprendizagem da matemática - que a pessoa possua inteligência geral normal, boas oportunidades educacionais e ausência de qualquer tipo de dano neurológico ou sensorial, havendo testes neuropsicológicos que permitem distinguir dificuldades oriundas de fatores socioambientais e relativamente de fácil superação, daquelas mais persistentes, de origem neurobiológica e que requerem procedimentos especiais para serem sanadas (ver, por exemplo, Santos, Kikuchi, & Ribeiro, 2009; Shaywitz et al., 2004; Silva & Santos, 2009, 2011). A implicação pedagógica decorrente é que aquelas habilidades devem ser objeto de ensino específico e explícito, como ilustrado a seguir.

Pesquisas psicoeducacionais empregando técnicas prospectivas (por exemplo: Aunola, Leskinen, Lerkkanen, & Nurmi, 2004; Koponen, Aunola, Ahonen, & Nurmi, 2007) mostram que habilidades numéricas básicas (como, por exemplo, recitação dos nomes dos numerais em ordem direta e inversa, contagem de objetos, leitura e escrita de numerais, relacionar numeral a quantidade e vice-versa) e cognitivas (como atenção, memória de trabalho e outras) em pré-escolares, permitem prever seu desempenho em matemática em séries futuras, ou seja, crianças com melhor repertório e desenvoltura em tais habilidades tendem a se sair melhor nessa disciplina. O ensino sistemático de habilidades semelhantes em crianças da mesma faixa etária produz resultados compatíveis. Arnold, Fisher, Doctoroff, e Dobbs (2002) relatam que, sob sua supervisão, professores implementaram um programa de seis semanas para o ensino de contagem, reconhecimento e escrita de numerais, correspondência um-a-um, comparação (como maior que, menor que), operações de modificação (como acréscimo ou remoção de elementos de um conjunto), emparelhamento de numerais (ou palavras-número) a quantidades. Após o período de intervenção, o grupo experimental apresentou escores significantemente superiores aos do grupo controle num teste padronizado de habilidades matemáticas.

Resultados como esses que acabamos de resumir são bastante convincentes sobre quão proveitoso é que já desde os anos pré-escolares as crianças apresentem pré-requisitos para a aprendizagem da matemática, ou que eles lhes sejam ensinados, para que essa matéria possa ser aprendida em níveis desejáveis e sem grandes dificuldades em séries mais avançadas, de modo que isso ocorra sem efeitos colaterais emocionais, como a ansiedade matemática, identificada num grande número de estudantes (Carmo & Ferraz, 2012; Carmo & Simionato, 2012; Mendes & Carmo, 2011). Isso, contudo, não basta para assegurar um bom aproveitamento por todos os alunos, senão pela maior parte deles. É necessário monitoramento constante da aprendizagem.

Uma linha crescente de pesquisa no exterior, mas ainda incipiente no Brasil, tem levado pesquisadores a focarem sua atenção em investigações sobre o desenvolvimento de um modelo de intervenção pedagógica denominado "Resposta à Intervenção" ou RTI, da sigla, em inglês para "Response to Intervention". Em linhas gerais, ele consiste em identificar precocemente crianças em risco para transtornos de aprendizagem. Isso requer a aplicação de instrumentos de avaliação que permitam discriminar entre dificuldades eventualmente oriundas de fatores ambientais, daquelas com possíveis causas de natureza ções, a equipe escolar multidisciplinar planeja e implementa ações pedagógicas diferenciadas com tais alunos. A avaliação constante, feita periodicamente, permite acompanhar seu progresso, de maneira que alguns poderão ser retirados do grupo considerado de risco, ao passo que os que permanecem continuam sendo alvo de atenção especial. Iniciativas nessa direção começam a surgir em nosso meio, por exemplo, por Andrade, Andrade, e Capellini, (2014), que se concentraram na leitura. Ao que nos consta, não há iniciativa semelhante no que diz respeito à matemática, havendo, portanto, um amplo campo para investigações.

 

Referências

Andrade, O. V. C. A., Andrade, P. E., & Capellini, S. A. (2014). Caracterização do perfil cognitivo-linguístico de escolares com dificuldades de leitura e escrita. Psicologia: Reflexão e Crítica, 27(2),358-367. doi:10.1590/1678-7153.201427217        [ Links ]

Andrade, P. E., Prado, P. S. T., & Carmo, J. S. (2015). Das representações numéricas inatas à Matemática culturalmente construída. Temas em Psicologia, 23(1),225-242. doi:10.9788/TP2015.1-15        [ Links ]

Arnold, D. H., Fisher, P. H., Doctoroff, G. L., & Dobbs, J. (2002). Accelerating math development in Head Start classrooms. Journal of Educational Psychology, 94(4),762. doi:10.1037/0022-0663.94.4.762        [ Links ]

Aunola, K., Leskinen, E., Lerkkanen, M. K., & Nurmi, J. E. (2004). Developmental dynamics of math performance from preschool to grade 2. Journal of Educational Psychology, 96(4),699. doi: 10.1037/0022-0663.96.4.699        [ Links ]

Beckwith, M., & Restle, F. (1966). Process of enumeration. Psychological Review, 73(5),437-444.         [ Links ]

Berger, A., Tzur, G., & Posner, M. I. (2006). Infant brains detect arithmetic errors. Proceedings of the National Academy of Sciences of the United States of America, 103(33),12649-12653. doi:10.1073/pnas.0605350103        [ Links ]

Bussab, V. S. R. (2000). Fatores hereditários e ambientais no desenvolvimento: A adoção de uma perspectiva interacionista. Psicologia: Reflexão e Crítica, 13(2),233-243. doi: 10.1590/S0102-79722000000200004        [ Links ]

Cappelletti, M., Barth, H., Fregni, F., Spelke, E. S., & Pascual-Leone, A. (2007). rTMS over the intraparietal sulcus disrupts numerosity processing. Experimental Brain Research, 179(4),631-642. doi:10.1007/s00221-006-0820-0        [ Links ]

Carmo, J. S., & Ferraz, A. C. T. (2012). Ansiedade relacionada à matemática e diferenças de gênero: Uma análise da literatura. Psicologia da Educação, 35,53-71.         [ Links ]

Carmo, J. S., & Simionato, A. M. (2012). Reversão de ansiedade em relação à matemática: Alguns dados da literatura. Psicologia em Estudo, 17,317-327. doi:10.1590/S1413-73722012000200015        [ Links ]

Dehaene, S. (1997). The number sense: How the mind creates mathematics. New York: Oxford University Press.         [ Links ]

Dehaene, S., & Cohen, L. (1994). Dissociable mechanisms of subitizing and counting: Neuropsychological evidence from simultanagnosic patients. Journal of Experimental Psychology: Human Perception and Performance, 20,958-975. doi:10.1037/0096-1523.20.5.958        [ Links ]

Dehaene, S., Spelke, E., Pinel, P., Stanescu, R., & Tsivkin, S. (1999). Sources of mathematical thinking: Behavioral and brainimaging evidence. Science, 284,970-974. doi:10.1177/0956797614523297        [ Links ]

Geary, D. C. (1994). Children's mathematical development: Research and practical applications. Washington, DC: American Psychological Association.         [ Links ]

Geary, D. C. (1996). Biology, culture, and cross-national differences in mathematical ability. In R. J. Sternberg & T. Ben-Zeev (Eds.), The nature of mathematical thinking (pp. 145-171). Mahwah, NJ: Lawrence Erlbaum.         [ Links ]

Geary, D. C. (2001). A Darwinian perspective on mathematics and instruction. In T. Loveless (Ed.), The great curriculum debate: How should we teach reading and math? (pp. 85-107). Washington, DC: Brookings Institute.         [ Links ]

Gordon, P. (2004). Numerical cognition without words: Evidence from Amazonia. Science, 306(5695), 496-499. doi:10.1126/science.1094492        [ Links ]

Hauser, M. D., & Carey, S. (2003). Spontaneous representations of small numbers of objects by rhesus macaques: Examinations of content and format. Cognitive Psychology, 47,367-401. doi:10.1016/S0010-0285(03)00050-1        [ Links ]

Hauser, M. D., & Spelke, E. (2004). Evolutionary and developmental foundations of human knowledge. In M. Gazzaniga & N. Logothetis (Eds.), The cognitive neurosciences (3rd ed.). Cambridge, MA: Massachusetts Institute of Technology Press.         [ Links ]

Koponen, T., Aunola, K., Ahonen, T., & Nurmi, J. E. (2007). Cognitive predictors of single-digit and procedural calculation skills and their covariation with reading skill. Journal of Experimental Child Psychology, 97(3),220-241. doi:10.1016/j.jecp.2007.03.001        [ Links ]

Mendes, A. C., & Carmo, J. S. (2011). Estudantes com grau extremo de ansiedade à matemática: Identificação de casos e implicações educacionais. Psicologia da Educação, 33,119-133.         [ Links ]

Pica, P., Lemer, C., Izard, V., & Dehaene, S. (2004). Exact and approximate arithmetic in an Amazonian indigene group. Science, 306,499-503. doi:10.1126/science.1102085        [ Links ]

Prado, P. S. T. (2008). Análise correlacional entre contagem e equiparação de conjuntos. In W. C. M. P. da Silva (Ed.), Sobre comportamento e cognição: Reflexões epistemológicas e conceituais, considerações metodológicas, relatos de pesquisa (Vol. 22, pp. 185-200). Santo André, SP: Esetec.         [ Links ]

Prado, P. S. T. (2010). Números e linguagem. In J. S. Carmo & P. S. T. Prado (Eds.), Relações simbólicas e aprendizagem da matemática (pp. 273-303). Santo André, SP: Esetec.         [ Links ]

Santos, F. H. D., Da Silva, P. A., Ribeiro, F. S., Dias, A. L. R. P., Frigério, M. C., Dellatolas, G., & von Aster, M. (2012). Number processing and calculation in Brazilian children aged 7-12 years. The Spanish Journal of Psychology, 15(2),513-525. doi:10.5209/rev_SJOP.2012.v15.n2.38862        [ Links ]

Santos, F. H., Kikuchi, R. S., & Ribeiro, F. S. (2009). Atualidade em discalculia do desenvolvimento. In J. M. Montiel & F. C. Capovilla (Eds.), Atualização em transtorno de aprendizagem (pp. 37-55). São Paulo, SP: Artes Médicas.         [ Links ]

Santos, F. H., Silva, P. A. D., Ribeiro, F. S., Dellatolas, G., & von Aster, M. (2012). Development of numerical cognition among Brazilian schoolaged children. Journal Internacional de Estudos em Educação Matemática, 5,44-64.         [ Links ]

Shaywitz, B. A., Shaywitz, S. E., Blachman, B. A., Pugh, K. R., Fulbright, R. K., Skudlarski, P., ...Gore, J. C. (2004). Development of left occipitotemporal systems for skilled reading in children after a phonologically-based intervention. Biological Psychiatry, 55(9),926-933. doi:10.1016/j.biopsych.2003.12.019        [ Links ]

Silva, P. A., & Santos, F. H. (2009). Prejuízos específicos em habilidades matemáticas de crianças com transtornos de aprendizagem. In J. M. Montiel & F. C. Capovilla (Eds.), Atualização em transtorno de aprendizagem (pp. 57-71). São Paulo, SP: Artes Médicas.         [ Links ]

Silva, P. A., & Santos, F. H. S. (2011). Discalculia do Desenvolvimento: Avaliação da representação numérica pela ZAREKI-R1. Psicologia: Teoria e Pesquisa, 27(2),169-177. doi:10.1590/S0102-37722011000200003        [ Links ]

Starkey, P., & Cooper, R. (1980). Perception of numbers by human infants. Science, 210(28),1033-1034. doi:10.1126/science.7434014        [ Links ]

Stein, L. M. (1994). TDE - Teste de Desempenho Escolar. São Paulo, SP: Casa do Psicólogo.         [ Links ]

Strauss, M. S., & Curtis, L. E. (1981). Infant perception of numerosity. Child Development, 52,1146-1152.         [ Links ]

Trick, L., & Pylyshyn, Z. W. (1994). Why are small and large numbers enumerated differently? A limited capacity preattentive stage in vision. Psychological Review, 101,80-102. doi:10.1037/0033-295X.101.1.80        [ Links ]

Wynn, K. (1990). Children's understanding of counting. Cognition, 36,155-193. doi:10.1016/0010-0277(90)90003-3        [ Links ]

Wynn, K. (1992a). Children's acquisition of the number words and the counting system. Cognitive Psychology, 24,220-251. doi:10.1016/0010-0285(92)90008-P        [ Links ]

Wynn, K. (1992b). Addition and subtraction in infants. Nature, 358,749-750. doi:10.1038/358749a0        [ Links ]

 

 

Endereço para correspondência:
Paulo Sérgio Teixeira do Prado
Universidade Estadual Paulista Júlio de Mesquita Filho, Departamento de Psicologia da Educação, Faculdade de Filosofia e Ciências, Campus de Marília
Av. Hygino Muzzi Filho, 737, Campus Universitário
Marília, SP, Brasil 17525900
Caixa-postal: 420
Fone: (14) 3402-1300, Ramal: 1371; Fax: (14) 3422-4797
E-mail: pradopst@marilia.unesp.br e carmojs@gmail.com

Recebido: 24/04/2014
1ª revisão: 09/07/2014
2ª revisão: 28/07/2014
Aceite final: 06/08/2014

 

 

1 O projeto que deu origem à pesquisa aqui relatada foi aprovado pelo Comitê de Ética em Pesquisa em Seres Humanos da Universidade Federal de São Carlos (UFSCar), conforme Parecer 106/2012.