ARTICLE

 

Os Princípios Invariantes da noção de medida investigados a partir da perspectiva de sentido numérico

 

The invariant principles of measurement examined in the perspective of number sense

 

Los principios invariantes de la noción de medida investigados a partir de la perspectiva de sentido numérico

 

 

Alina Galvão Spinillo^I; Rosita Marina Ferreira Batista Martins^II

^IDepartamento de Psicologia e da Pós-Graduação em Psicologia Cognitiva da Universidade Federal de Pernambuco, Recife, PE, Brasil Coordenadora do Núcleo de Pesquisa em Psicologia da Educação Matemática, Recife, PE, Brasil
^IISecretaria de Saúde da Prefeitura Municipal de Carpina, Carpina, PE, Brasil

Endereço para correspondência

 

 

---

RESUMO

O presente estudo investiga o conhecimento de crianças sobre medidas a partir da noção de princípios invariantes e sentido numérico. Quarenta crianças (6 a 8 anos) foram solicitadas a fazer julgamentos acerca de situações envolvendo medidas de volume, massa, distância e comprimento. A Tarefa 1 examinou a habilidade de identificar unidades apropriadas para medir diferentes grandezas, e a Tarefa 2 examinou a compreensão acerca das relações inversas entre o tamanho da unidade e o número de unidades necessário para medir uma dada magnitude de um objeto. Os resultados mostraram que as crianças apresentam um sentido sobre medida o qual não se manifesta igualmente em relação a diferentes grandezas. Observou-se, também, que as crianças tinham uma melhor compreensão acerca das relações inversas entre o tamanho da unidade e o número de unidades do que acerca da relação entre unidade e a magnitude do objeto a ser medida.

Palavras-chave: Crianças; medidas; princípios invariantes; sentido numérico.

---

ABSTRACT

This study investigates children's knowledge about measurements based on the idea of invariants principles, and of number sense. Forty children (6 and 8 years old) made judgments about situations involving measurements of volume, mass, distance and length. Task 1 examined the ability to identify the appropriate unit to measure different magnitudes, and Task 2 the understanding of the inverse relation between the size of the unit and the number of units needed to measure a magnitude of an object. Results showed that children have a sense of measurement and that this sense does not manifest itself equally in relation to different magnitudes. Also, children showed a better understanding about the inverse relation between the size of the unit and the number of units than of the relation between unit and the magnitude of the object to be measured.

Keywords: Children; measurement; invariant principles; number sense.

---

RESUMEN

El presente estudio investiga el conocimiento de los niños sobre medidas a partir de la noción de principios invariantes y sentido numérico. A cuarenta niños (6 a 8 años) les fue solicitado hacer juicios sobre situaciones que implicaban medidas de volumen, masa, distancia y longitud. La Tarea 1 examinó la habilidad para identificar unidades apropiadas para medir diferentes magnitudes y la Tarea 2 examinó la comprensión acerca de las relaciones inversas entre el tamaño de la unidad y el número de unidades necesario para medir una determinada magnitud de un objeto. Los resultados muestran que los niños presentan un sentido de medida que no se manifiesta de la misma forma en relación con diferentes magnitudes. También se observó que los niños tenían una mejor comprensión de las relaciones inversas entre el tamaño de la unidad y el número de unidades de que una comprensión de la relación entre unidades y la magnitud del objeto a ser medida.

Palabras clave: Niños; medidas; principios invariantes; sentido numérico.

---

 

 

Medir é atividade matemática que desde muito cedo faz parte das situações do cotidiano das crianças. Qual a altura de meu irmão? Qual a distância entre Recife e Olinda? Quantos copos de suco cabem nesta jarra? Quanto pesa este saco de arroz? Qual a temperatura hoje? Quanto tempo dura o filme? Responder tais perguntas não é tarefa trivial, apesar da precocidade e da familiaridade que as crianças têm com tais situações. Na realidade, medir implica em uma série de conhecimentos por parte de quem mede uma dada grandeza, como por exemplo, comparar, estabelecer padrões, usar unidades apropriadas de medida (convencionais ou não-convencionais), usar diferentes instrumentos etc.

Do ponto de vista matemático, medir refere-se à possibilidade de determinar um valor de uma dada grandeza relativa a um fenômeno, corpo ou substância (Coutinho, 1967). A grandeza, por sua vez, é um atributo de um fenômeno, corpo ou substância que pode ser quantitativamente determinado, podendo ser dividida em grandezas fundamentais e grandezas derivadas. As grandezas fundamentais são aquelas que se definem por si mesmo (comprimento, massa, tempo etc.); enquanto as grandezas derivadas são geradas a partir das fundamentais como é o caso da velocidade que envolve relações entre tempo e distância (C. X. Silva & Lousada, 2001). Historicamente, dois aspectos surgem como fundamentais na ação de medir: a ideia de uma unidade para se realizar uma medição e a noção de que esta unidade deve ser padronizada de modo a ser compartilhada por outras pessoas (Dias, 1998; P. P. A. Silva, 2003).

Do ponto de vista psicológico, medir é uma ação associada à quantificação, envolvendo a conservação de quantidades e a inferência transitiva. De acordo com Piaget e Inhelder (1983), a conservação é o ponto de partida para a quantificação das grandezas como peso, volume, densidade etc. Quantificar uma dada grandeza, por sua vez, requer o uso de instrumentos de medição e de unidades de medida estáveis que sirvam como padrão. Nesta direção, a inferência transitiva surge como operação cognitiva da maior relevância, pois para realizar uma comparação entre duas quantidades é necessário saber que essas só podem ser comparadas através de uma unidade ou instrumento comum.

Além dessas operações lógicas (conservação de quantidades e inferência transitiva), é necessário compreender a unidade de medida como termo de comparação entre grandezas de uma mesma natureza. A compreensão das unidades é considerada como fundamental para o entendimento das medidas, por se tratarem de construtos estabelecidos pela cultura e utilizados para constituir um modelo de referência estável que pode ser utilizado como uma unidade de comparação (Nunes & Bryant, 1997). Outros autores destacam que a ação de medir envolve uma série de princípios como a transferência de uma medida aplicada a outra extensão, a iteração das partes, ou seja, a repetição em toda extensão do objeto tomado como referência para realizar a medição; bem como a compreensão de que o todo é formado por partes, aspecto este que relaciona a noção de medida com a divisão e com a fração (e.g., Piaget, Inhelder, & Szeminska, 1960).

Do ponto de vista educacional, o ensino de medidas assume lugar de destaque nos currículo ao longo dos diferentes segmentos escolares (pré-escola, ensino fundamental e médio), como se observa nos Parâmetros Curriculares Nacionais (PCN) de Matemática (Secretaria de Educação Fundamental, 1997) e nos livros didáticos. A proposta para o ensino de medidas compreende tanto o reconhecimento das diferentes grandezas como também a utilização de instrumentos de medida (convencionais ou não) e a compreensão das relações (inclusive de equivalência) entre diferentes unidades de medida próprias a uma dada grandeza.

Dada sua relevância e complexidade, há muito, este tema tem sido investigado no âmbito da psicologia do desenvolvimento cognitivo, como ilustram as pesquisas pioneiras realizadas pelo grupo de Genebra (e.g., Piaget et al., 1960). Tais pesquisas, de modo geral, investigavam o conhecimento de crianças sobre grandezas de comprimento, distância, área, massa, tempo e volume, explorando medidas em relação à noção de conservação de quantidade. No âmbito da psicologia, essas grandezas assumem o estatuto de noções ou conceitos relativos ao campo das medidas (Hart, 1981; Lovell, 1966).

O comprimento tem sido a grandeza mais investigada. A compreensão da medida de comprimento, observada desde muito cedo, serve de base para a compreensão de outros conceitos como área e volume; bem como para o entendimento da noção de escala, noções essas geralmente investigadas em crianças entre 9 e 11 anos (Bragg & Outhred, 2001, 2004; Kidman, 2001; Kordaki & Potari, 1998; Outhred & Mitchelmore, 2000).

Associado ao comprimento tem-se o conceito de distância. Importante esclarecer a distinção feita por Piaget e cols. (1960) entre comprimento e distância, ambas as grandezas lineares de uma dimensão, sendo a primeira relacionada a uma grandeza relativa a um objeto (sua altura, largura ou profundidade) e a segunda sendo definida como a separação linear entre objetos.

A compreensão acerca das unidades de medida relativas ao comprimento foi investigada por Bragg e Outhred (2001, 2004) em crianças de 6 a 10 anos. Os resultados mostraram que poucas crianças, mesmo aos 10 anos, compreendiam o significado do centímetro em uma régua, visto que antes desta idade, a tendência era considerar o centímetro apenas como uma marca na régua.

Nunes e Bryant (1997) investigaram como crianças inglesas (5 a 7 anos), familiarizadas com dois sistemas de medidas (o imperial e o métrico), lidavam com unidades de tamanhos diferentes (polegadas e centímetros) ao comparar o comprimento de fitas. As situações apresentadas requeriam que as crianças compreendessem que em sendo o número de unidades o mesmo e as unidades de tamanhos diferentes (polegada maior que centímetro), as fitas necessariamente apresentariam comprimentos diferentes, sendo uma maior que a outra. A investigação foi dividida em dois momentos. No primeiro, fitas de tamanhos diferentes tinham seu comprimento medido em centímetros tanto pela criança como pelo examinador. No segundo momento as fitas, de tamanhos diferentes, eram medidas através de unidades diferentes: a criança usava polegadas e o experimentador usava centímetros. Os resultados mostraram um ótimo desempenho no primeiro momento em que a unidade de medida era a mesma, principalmente em crianças de 6 e 7 anos. No segundo momento, em que foram usadas unidades diferentes, o desempenho foi um pouco acima da média; tendo, as crianças de 5 e 6 anos, dificuldades em resolver a tarefa.

De modo geral, as pesquisas mostram que a concepção de medida de comprimento requer a integração de uma diversidade de noções como espaço, número (em termos de iteração) e divisão das unidades; bem como requer a compreensão acerca dos usos de instrumentos e de sistemas de medidas convencionais (régua, fita métrica) e não convencionais (polegadas, palmos) e que a partir dos 7 anos é que as crianças apresentam um nível de compreensão apropriado desses aspectos.

Pesquisas acerca do conceito de distância foram conduzidas por Piaget e cols. (1960) com crianças de 5 a 7 anos. Em um desses estudos eram apresentadas duas árvores de brinquedo com uma distancia de 30 cm entre elas, sendo as crianças perguntadas se as árvores estavam próximas ou distantes uma da outra. Em seguida foram feitas algumas variações, primeiro colocando um anteparo entre as árvores e feita a mesma pergunta, e segundo introduzindo um cubo grande entre as árvores. Observou-se que as crianças antes dos 7 anos compreendiam a distância como um espaço vazio, não considerando o espaço preenchido pelos objetos como fazendo parte da distância entre dois pontos. Só a partir dos 7 anos é que compreendiam que os objetos inseridos não alteravam a distância entre os pontos.

Piaget e cols. (1960) observaram que o conceito de área pressupõe a compreensão de medidas de comprimento, e que por volta dos 7 anos as crianças começam a operar a noção de área em termos lógicos mais que perceptuais. Ainda nesta mesma obra, os autores apresentam estudos conduzidos sobre o conceito de volume cuja compreensão plena parece emergir por volta dos 12 anos, sendo uma aquisição tardia que requer estabelecer relações entre três dimensões distintas e que requer a noção de espaço ocupado por um sólido ou por um líquido. Importante comentar que muitos dos estudos conduzidos por esses autores estavam também associados à ideia de conservação de quantidades, como se observa também em relação ao conceito de massa.

O experimento clássico de Piaget sobre a conservação de massa foi realizado com crianças entre 5 e 7 anos. Admitida a igualdade entre duas bolas de argila, foram apresentadas situações em que uma das bolas tinha sua forma transformada em uma salsicha, partida em vários pedaços, achatada. As crianças foram solicitadas a justificar se após as transformações ocorridas a bola continuava ou não com a mesma quantidade de argila. Observou-se que antes dos 7 anos as crianças voltavam-se para o aspecto perceptual imediato, ou seja, para a forma apresentada, acreditando que por ser mais longa a salsicha teria mais massa. Só a partir dos 7 ou 8 anos é que reconheciam os aspectos lógicos relativos à conservação da massa, admitindo que a quantidade de matéria permanecia a mesma independentemente da forma dada.

A concepção de volume é considerada complexa, pois, diferentemente das grandezas line-ares, ela envolve três dimensões. Piaget e cols. (1960) mostraram a crianças (5 a 9 anos), blocos que representavam uma casa, com base e altura de tamanhos diferentes; sendo solicitado que construíssem blocos semelhantes ao mode-lo. De modo geral, observou-se que entre 5 e 6 anos as crianças tendiam a focalizar em apenas uma dimensão do modelo (ou a base ou a altura), enquanto que por volta dos 7 anos as crianças tendiam a considerar as duas dimensões, embora construíssem blocos mais altos que o modelo. Segundo os autores, a compreensão inicial de volume é de caráter topológico, ou seja, a criança pensa inicialmente no volume como forma e não em termos do espaço ocupado. Assim, esta é uma noção tardia em termos de desenvolvimento.

Com o objetivo de examinar como o uso de diferentes instrumentos de medida influenciava a habilidade de resolver situações-problema envolvendo medições de comprimento e de área, Nunes, Light e Mason (1993) conduziram dois experimentos. No primeiro experimento, duplas de crianças (6 a 8 anos) eram solicitadas a medir e comparar comprimentos usando um cordão, uma régua e uma régua quebrada. Os resultados mostraram que as crianças se beneficiavam de instrumentos que forneciam uma representação numérica da grandeza que estava sendo medida, tendo um melhor desempenho com o instrumento convencional (régua) do que com o não convencional (cordão), sendo isso observado mesmo quando a régua quebrada era utilizada. No segundo experimento, duplas de crianças (8-10 anos) eram solicitadas a medir e comparar áreas pintadas de paredes (representadas por retângulos em uma cartela) usando duas réguas e blocos. O principal resultado foi que as crianças tiveram um desempenho muito limitado ao usar as réguas, enquanto foram bem sucedidas ao usar os blocos. Isso ocorreu porque podiam contar quantos blocos eram necessários para cobrir os retângulos, enquanto o uso das réguas requeria compreender as relações de multiplicação entre altura e largura das paredes. Os dados mostram que para medir o comprimento, a régua mostrou-se mais efetiva para as crianças do que o cordão; enquanto que para medir a área, a régua foi me-nos apropriada que os blocos. Assim, a eficácia de um instrumento depende da grandeza que está sendo medida e que o instrumento usado influencia a habilidade de medir, indicando haver uma relação entre a unidade de medida e a grandeza a ser medida. Outro dado gerado deste estudo é que nem sempre um instrumento ou unidade de medida não convencional é adequado ou melhor do que um o instrumento ou unidade convencional, como muitas vezes se pensa, sobretudo no contexto escolar que tende a privilegiar o uso de unidades não convencionais, acreditando que elas são mais fáceis que as convencionais, devendo, inclusive, serem trabalhadas antes que as convencionais.

Curry, Mitchelmore e Outhred (2006) examinaram em um mesmo estudo a compreensão de crianças de 6 a 10 anos a respeito das grandezas de comprimento, volume e área. Ao invés de focalizarem a atenção na grandeza, como ocorre na maioria das pesquisas, os autores focalizaram os princípios constitutivos da noção de medida. Os princípios investigados foram: (a) a relação entre unidade de medida e a grandeza do objeto a ser medida; (b) a seleção de uma unidade apropriada para medir uma dada grandeza; (c) o uso de uma mesma unidade ao comparar grandeza de mesma natureza em objetos distintos; (d) a relação inversa entre o número de unidades e o tamanho da unidade de medida; e (e) a estrutura da iteração da unidade. A preocupação dos autores era a de tornar comparáveis as diferentes grandezas. Teorizando acerca desses princípios, é possível inseri-los em duas perspectivas teóricas que, pelo que se sabe, não foram, até o momento associadas: a teoria de Vergnaud (1997, 2003) e a noção de sentido numérico (Greeno, 1991; Howder, 1989; Sowder, 1995; Spinillo, 2006).

De acordo com Vergnaud (2003), os invariantes podem ser considerados propriedades ou procedimentos relacionados a um determinado conceito (ver também Franchi, 2008; Magina, Campos, Nunes, & Gitirana, 2001). Segundo nossa análise, os princípios acima indicados são, em última instância, os invariantes do conceito de medida, presentes e requeridos na medição de qualquer grandeza.

Por sua vez, sentido numérico pode ser definido como uma boa intuição sobre números, suas propriedades e suas relações que permite ao indivíduo interagir com recursos da situação, gerando soluções bem sucedidas para realizar as atividades matemáticas do cotidiano (Greeno, 1991; Yang, 2003; Yang & Reys, 2002). Na realidade, sentido numérico pode ser entendido como uma forma de pensar matematicamente, se caracterizando por uma intenção de construir significado para situações numéricas. Segundo nossa análise, os princípios invariantes do conceito de medidas podem ser intuitivamente compreendidos pelas crianças que, a partir de situações do cotidiano, desenvolveram um sentido numérico relativo a grandezas e medidas. Desta forma, a presente pesquisa examina noções sobre medidas em crianças, procurando relacionar essas duas perspectivas teóricas em um estudo empírico, envolvendo diversas grandezas simultaneamente.

Dos cinco princípios anteriormente citados, dois deles são explorados no presente estudo: a relação entre unidade de medida e grandeza do objeto a ser medida e a relação inversa entre o número de unidades e o tamanho da unidade de medida. Importante comentar que a maioria dos estudos sobre este tema utiliza situações em que as crianças são solicitadas a realizar ações de medir, usando algum tipo de instrumento e obtendo um valor preciso. A presente pesquisa, entretanto, investiga este tema a partir de recursos metodológicos próprios da área de estudo sobre sentido numérico, recursos estes que consistem em situações de julgamento em que não é necessário realizar medições.

O conhecimento de crianças sobre o uso apropriado de unidades de medidas é aqui investigado em relação a quatro grandezas: volume, massa, distância e comprimento. A partir da perspectiva de sentido numérico e de princípios invariantes, pergunta-se: Será que o conhecimento intuitivo sobre medidas se manifesta igualmente em relação a diferentes grandezas? A compreensão dos princípios invariantes é algo geral ou relacionado ao tipo de grandeza? Esses princípios apresentam um mesmo nível de complexidade ou um é mais complexo que o outro?

 

Método

Participantes

Quarenta crianças de baixa renda, de ambos os sexos, alunas de escolas públicas da cidade do Recife foram igualmente divididas em dois grupos: Grupo 1 formado por crianças de 6 anos (média: de 6 anos e 5 meses), alunas do 1º ano do ensino fundamental; e Grupo 2 formado por crianças de 8 anos (média: 8 anos e 4 meses), alunas do 3º ano do ensino fundamental.

Material, Procedimento e Planejamento Experimental

O estudo consistiu em duas tarefas de julgamento relativas a situações que envolviam o uso de unidades de medida convencionais e não convencionais. As tarefas foram aplicadas individualmente em duas sessões com tempo livre, com um intervalo de três a cinco dias entre elas. A ordem de apresentação das tarefas variava de maneira que metade das crianças em cada grupo realizava a Tarefa 1 na primeira sessão e a Tarefa 2 na segunda sessão, e a outra metade realizava as tarefas na ordem inversa. Foi utilizado um roteiro com os itens de cada tarefa, gravador áudio digital, lápis e folha de papel para registro da examinadora.

Tarefa 1: Relação entre Unidade de Medida e Grandeza. O objetivo desta tarefa foi examinar se a criança era capaz de compreender a relação entre uma dada unidade de medida e a grandeza a ser medida, percebendo que existem unidades de medidas que são apropriadas para medir uma dada grandeza.

Inicialmente foi dito à criança que ela iria participar de um jogo de adivinhação. Era dito que dois personagens (João e Flávia) gostavam muito de medir as coisas e mediam várias coisas em diferentes situações. A examinadora mostrava, então, uma cartela com o desenho dos personagens.

A tarefa era composta por 20 perguntas apresentadas em duas etapas. Na primeira etapa eram feitas quatro perguntas abertas, uma para cada grandeza, por exemplo: "João mediu uma coisa e disse que essa coisa media 5 litros (3 quilos/12 quilômetros/2 metros). O que você acha que ele mediu?". Justificativas eram solicitadas após cada resposta dada ("Como descobriu?", "Porque pensou assim?"). A ordem de apresentação dessas quatro perguntas foi decidida por sorteio com cada participante

A segunda etapa, com 16 perguntas de múltipla escolha (quatro para cada grandeza) com duas alternativas, por exemplo: "João mediu uma coisa, e disse que essa coisa media 2 quilos. O que você acha que foi esta coisa que ele mediu: a quantidade de suco em uma jarra ou o peso de um pacote de açúcar?". Justificativas eram solicitadas após cada resposta dada. Em metade das perguntas referentes a cada grandeza, a alternativa correta era apresentada como primeira opção de escolha e na outra metade como segunda opção. A ordem de apresentação das perguntas foi definida por sorteio com cada participante com a restrição de que nunca dois itens consecutivos envolvessem grandeza de uma mesma natureza.

Tarefa 2: Relação Inversa entre o Tamanho da Unidade e Número de Unidades Necessário para Medir uma Dada Grandeza. O objetivo desta tarefa foi examinar se a criança era capaz de compreender a relação inversa entre o tamanho da unidade e o número de unidades necessário para medir uma dada grandeza de um objeto.

A tarefa era formada por oito perguntas (duas para cada grandeza). Era dito à criança que dois personagens (João e Flávia) gostavam muito de medir as coisas e mediam várias coisas em diferentes situações. A examinadora mostrava, então, uma cartela com o desenho dos persona-gens. Em seguida eram apresentadas perguntas como aquelas ilustradas na Figura 1 e na Figura 2. Justificativas eram solicitadas após cada resposta dada ("Como descobriu?", "Porque pen-sou assim?").

 

 

 

 

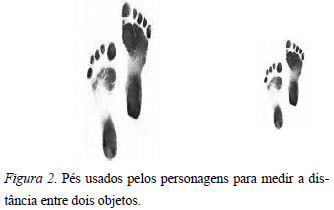
"Flávia mediu o comprimento de uma mesa com palitos de fósforos. João mediu o comprimento desta mesma mesa com palitos de picolé. Quem vai precisar de mais palitos para medir o comprimento da mesa: Flávia ou João?"

Flávia mediu a distância entre a janela e a porta de seu quarto usando seu pé. João mediu esta mesma distância, mas ele usou o seu próprio pé. Quem vai usar mais pés para medir esta mesma distância: João ou Flávia?

A ordem de apresentação dos itens foi definida por sorteio com cada participante, com as seguintes restrições (a) nunca dois itens consecutivos envolviam uma mesma grandeza; (b) como em cada item havia dois personagens (João e Flávia), em metade das perguntas a resposta correta estava associada ao personagem Flávia e a outra metade ao personagem João.

 

Análise dos Dados e Resultados

As respostas em ambas as tarefas foram classificadas em tipos e analisadas por dois juízes independentes cujo percentual de concordância entre eles foi de 84,2% na Tarefa 1; 92,7% na Tarefa 2. Os casos de discordância foram analisados por um terceiro juiz, também independente, cuja classificação foi considerada final. Cada tipo de resposta é descrito a seguir e exemplificado na Tabela 1¹.

Tipo 1: resposta incorreta sem explicações ou acompanhada de explicações vagas, subjetivas ou inapropriadas.

Tipo 2: resposta correta sem explicações ou acompanhada de explicações vagas, subjetivas ou inapropriadas.

Tipo 3: resposta correta acompanhada de explicações apropriadas.

Resultados da Tarefa 1

Como mostra a Tabela 2, e confirmado pelo Teste de U de Mann-Whitney, os grupos se diferenciam apenas em relação à resposta Tipo III (Z= -2,505, p= 0,012) que era mais frequente entre as crianças do Grupo 2 (8 anos: 25,2%) do que entre as do Grupo 1 (6 anos: 12,6%).

Com o objetivo de explorar diferenças entre as respostas no interior de cada grupo foi aplicado o Teste de Friedman que apontou diferenças significativas tanto em relação ao Grupo 1 (X²= 22,279, p= 0,001) como em relação ao Grupo 2 (X²= 16,121, p= 0,001 ). Isso ocorreu porque as respostas das crianças do Grupo 1 (6 anos) se concentravam no Tipo I, enquanto as respostas das crianças do Grupo 2 (8 anos) se concentravam de forma equilibrada entre Tipo I e na Tipo II (Tabela 2).

Além das relações entre tipos de respostas e a idade dos participantes, também se examinou se os tipos de respostas variavam em função da natureza da grandeza em questão (Tabela 3).

Em relação ao Grupo 1 (6 anos), o Teste de Friedman, aplicado a cada tipo de resposta separadamente, detectou haver diferenças significativas entre as grandezas em relação às respostas Tipo I (X²= 10,677, p= 0,030) e Tipo III (X²= 10,774, p= 0,029). Para essas crianças, as respostas Tipo I eram mais frequentes quando a grandeza era a Distância do que em relação às demais grandezas (como identificado pelo Wilcoxon, p < 0,03) e as Tipo III, embora muito raras em todas as grandezas, eram mais frequentes em Massa e Comprimento do que em Volume e Distância (como também identificado pelo Wilcoxon, p< 0,03). Ao que parece, aos 6 anos as crianças apresentam dificuldades em fornecer uma justificativa apropriada em relação a qualquer uma das grandezas investigadas, ainda que possam até acertar a resposta. Essa dificuldade é particularmente acentuada em relação à Distância, tanto em termos de número de erros, que é elevado, como em termos de frequência de respostas Tipo III, que são raras.

Quanto ao Grupo 2 (8 anos), diferenças significativas entre as grandezas foram detectadas em relação às respostas Tipo II (X²= 11,912, p= 0,018) e Tipo III (X²= 11,278, p= 0,024), como revelou o Teste de Friedman. De acordo com o Teste de Wilcoxon, isso ocorreu porque as respostas Tipo II (Z=-2,184, p= 0,029) eram pouco frequentes em relação à Massa (22%) e muito mais frequentes em relação à Distância (47%); enquanto observavase o oposto em relação às respostas Tipo III (Z= -2,635, p= 0,008) que eram pouco frequentes em relação à Distância (19%) e mais frequentes em relação à Massa (34%).

Resultados da Tarefa 2

Como mostra a Tabela 4, e confirmado pelo Teste de U de Mann-Whitney aplicado a cada tipo de resposta separadamente, os grupos não diferiam entre si.

O que se nota é que em cada grupo, havia uma concentração nas respostas Tipo III, como revelado pelo Teste de Friedman (Grupo 1: X²= 15,529, p= 0,001; e Grupo 2: X²= 31,946, p= 0,001). Assim, tanto aos 6 como aos 8 anos, as crianças fornecem respostas corretas acompanhadas de justificativa apropriada que expressa a compreensão acerca da relação inversa entre o tamanho da unidade e o número de unidades necessário para medir uma dada grandeza.

De acordo com o Teste de Friedman, no Grupo 1 (6 anos) foram detectadas diferenças significativas entre as grandezas em relação às respostas Tipo II (X²= 32,938, p= 0,001) e às respostas Tipo III (X²= 41,965, p= 0,001), como ilustrado na Tabela 5. O Teste de Wilcoxon (p< 0,01) mostrou que as respostas Tipo II são mais oferecidas em relação ao Volume (12,5%) e ao Comprimento (15%) do que em relação à Massa (7,5%) e à Distância (7,5%). Por outro lado, altos percentuais de respostas Tipo III são observados em relação ao Volume (67,5%) e à Distância (70%).

No Grupo 2 (8 anos), de acordo com o Teste de Friedman, foram identificadas diferenças significativas entre respostas Tipo I (X²= 11,467, p= 0,022) e Tipo II (X²= 19,300, p= 0,001). O Teste de Wilcoxon indicou que respostas Tipo I (20%) ocorrem mais em relação ao Volume que às demais grandezas (Z= -2,236, p= 0,025); enquanto respostas Tipo II são mais frequentes em relação à Massa (15%) e muito raras em relação à Distância (5%).

Importante comentar que em ambos os grupos foram observados percentuais altos de resposta Tipo III em relação a todas as grandezas investigadas, sobretudo em relação à Distância (Grupo 1: 70%; Grupo 2: 85%).

Para finalizar, a Tabela 6 ilustra o desempenho dos dois grupos nas duas tarefas. De acordo com o Teste U de Mann-Whitney, o desempenho não se altera em função da idade, quer na Tarefa 1, quer na Tarefa 2. Isso indica que a habilidade de identificar a relação entre unidade de medida e grandeza a ser medida (Tarefa 1) e a habilidade de reconhecer a relação inversa entre o tamanho da unidade e a quantidade de unidades necessárias para medir algo (Tarefa 2) são habilidades que estão presentes nas crianças desde os 6 anos e não apresentam uma progressão dos 6 aos 8 anos de idade.

 

Discussão e Conclusões

Partindo da perspectiva de que medidas é um conceito (e como tal envolve um conjunto de invariantes ou propriedades que o definem) e que crianças podem apresentar desde muito cedo noções intuitivas sobre medidas, a presente investigação estabeleceu uma aproximação entre os princípios invariantes de medidas com a perspectiva de sentido numérico.

Os resultados mostraram que desde os 6 anos, as crianças já apresentam certa habilidade em identificar uma unidade apropriada para medir uma dada grandeza, habilidade esta que não se altera de forma expressiva até os 8 anos. Apenas em relação à Distância é que são observadas diferenças entre as idades, uma vez que a relação unidade de medida e grandeza a ser medida mostrou ser difícil para as crianças de 6 anos que apresentavam um alto percentual de respostas incorretas e, além disso, tinham dificuldades em fornecer explicações apropriadas a respeito desta relação quanto a essa grandeza. Uma possível explicação para isso é a pouca familiaridade que as crianças nesta faixa etária têm com a medição de distância e, consequentemente, em relação à unidade de medida a ela associada. Aos 8 anos é provável que a escola, ainda que de forma introdutória, trabalhe noções de distância em sala de aula no ensino fundamental.

Outra diferença entre as idades no que concerne à capacidade de estabelecer relações entre unidade de medida e grandeza refere-se à dificuldade que a criança de 6 anos apresenta quanto a fornecer uma justificativa apropriada em relação às quatro grandezas investigadas. Ainda que possam até acertar a resposta, as crianças de 6 anos raramente são capazes de oferecer explicações apropriadas. Na realidade esta dificuldade também é observada entre as crianças de 8 anos. O que se conclui é que parece haver um conhecimento intuitivo, um sentido numérico em relação a medidas, que habilita a criança a estabelecer uma relação entre unidade e grandeza; porém a capacidade de explicitar esta relação é muito limitada, sobretudo aos 6 anos de idade.

Os dados mostraram ainda, que tanto aos 6 como aos 8 anos, as crianças são capazes de reconhecer a relação inversa entre o tamanho da unidade e o número de unidades necessário para medir uma dada grandeza, sendo isso evidenciado tanto pelo número de respostas corretas como pelas explicações apropriadas oferecidas.

Assim, entre as idades de 6 e 8 anos, as crianças já apresentam um sentido sobre medidas que lhes permite, ainda que de forma intuitiva, compreender que uma dada unidade está associada a uma dada grandeza e que quanto maior a unidade, menor o número de unidades necessário para medir uma dada grandeza (e vice versa). Esses são princípios invariantes constitutivos do conceito de medidas. Esses princípios parecem ter níveis de complexidade distintos, uma vez que as crianças tanto de 6 como de 8 anos demonstraram uma maior compreensão acerca das relações inversas entre o tamanho da unidade e o número de unidades necessário para medir uma dada grandeza do que a respeito da relação unidade e grandeza. Vale comentar que o percentual de acertos relativos à compreensão dessas relações inversas foi bastante alto, mesmo entre as crianças de 6 anos. Este foi um resultado não esperado, dado que compreender relações inversas parece ser um desafio para crianças, como documentado na literatura quanto a outros conceitos matemáticos, como é o caso da divisão (Lautert, Spinillo, & Correa, 2012) e da adição e da subtração (Spinillo, 2011). No entanto, ficou evidenciado que as crianças compreendem esta relação em termos de uma intuição sobre medidas.

Os dados mostram, ainda, que o sentido de medida não se manifesta igualmente em relação a todas as grandezas, pois, enquanto Massa e Comprimento parecem ser mais facilmente compreendidas, a noção de Distância mostrou-se mais difícil para as crianças de 6 e para as de 8 anos. É possível supor que isso se explique pela maior ou menor familiaridade que as crianças têm com essas grandezas em seu cotidiano dentro e fora da escola, como já mencionado.

Do ponto de vista teórico, as relações entre sentido numérico e princípios invariantes podem ser consideradas uma nova abordagem no estudo sobre medidas. Esta nova abordagem abre novas frentes de investigação, como por exemplo, explorar outros princípios invariantes que não foram examinados neste estudo, descobrindo as limitações e as possibilidades do raciocínio infantil frente a cada um deles.

Do ponto de vista metodológico, explorar julgamentos sobre situações envolvendo a ação de medir pode ser um recurso metodológico complementar que pode ser associado a situações em que a criança efetivamente é colocada na situação de medir algo. A combinação desses recursos poderia fornecer informações importantes acerca do conhecimento de crianças sobre medidas.

Do ponto de vista educacional, a associação desses recursos metodológicos poderia ser adaptada para o contexto de sala de aula e transformar-se em um recurso didático com vistas a desenvolver na criança um sentido sobre medidas associado a uma compreensão dos princípios invariantes.

 

Agradecimentos

Ao Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq) que conferiu bolsa de estudos de mestrado para a segunda autora sob orientação da primeira; e a Síntria Lautert, Juliana Gomes e Tatyane Queiroz que contribuíram com discussões a respeito da análise dos dados.

 

Referências

Bragg, P., & Outhred, L. (2001). So that's what a centimetre looks like: Students' understandings of linear units. In Proceedings of the 25^th Annual Conference of the International Group for the Psychology of Mathematics Education (Vol. 1, pp. 377-384). Utrecht, Netherlands: International Group for the Psychology of Mathematics Education.         [ Links ]

Bragg, P., & Outhred, L. (2004). A measure of rulers: The importance of units in a measure. In Proceedings of the 28^th Annual Conference of the International Group for the Psychology of Mathematics Education (Vol. 2, pp. 159-165). Bergen, Norway: International Group for the Psychology of Mathematics Education.         [ Links ]

Coutinho, C. A. (1967). Metrologia atual. Rio de Janeiro, RJ.         [ Links ]

Curry, M., Mitchelmore, M., & Outhred, L. (2006). Development of children's understanding of length, area, and volume measurement principles. In Proceedings of the 30^th Annual Conference of the International Group for the Psychology of Mathematics Education (Vol. 2, pp. 377-384). Prague, Czech Republic: International Group for the Psychology of Mathematics Education.         [ Links ]

Dias, J. L. M. (1998). Medida, normalização e qualidade: Aspectos da história da metrologia no Brasil. Rio de Janeiro, RJ: Ilustrações.         [ Links ]

Franchi, A. (2008). Considerações sobre a teoria dos campos conceituais. In S. D. A. Machado (Ed.), Educação Matemática: Uma (nova) introdução. São Paulo, SP: Editora da Pontifícia Universidade Católica de São Paulo.         [ Links ]

Greeno, J. (1991). Number sense as situaded knowing in a conceptual domain. Journal for Research in Mathematics Education, 22(3),170-218.         [ Links ]

Hart, K. M. (1981). Children's understanding of mathematics 11-16. Oxford, UK: Murray.         [ Links ]

Howder, H. (1989). Teaching number sense. Arithmetic Teacher, 36(6),6-11.         [ Links ]

Kidman, G. C. (2001). Links between intuitive thinking and classroom area tasks. In Proceedings of the 25^th Conference of the International Group for the Psychology of Mathematics Education (Vol. 5, pp. 233-240). Utrecht, Netherlands: International Group for the Psychology of Mathematics Education.         [ Links ]

Kordaki, M., & Potari, D. (1998). Childrens' approaches on area measurement through different contexts. Journal of Mathematical Behavior, 17,303-316. doi:10.1016/S0364-0213(99)80065-2        [ Links ]

Lautert, S. L., Spinillo, A. G., & Correa, J. (2012). Children's difficulties with division: An intervention study. Educational Research, 3(5),447-456.         [ Links ]

Lovell, K. (1966). O desenvolvimento dos conceitos matemáticos e científicos na criança. Porto Alegre, RS: Artes Médicas.         [ Links ]

Magina, S., Campos, T. M. M., Nunes, T., & Gitirana, V. G. (2001). Repensando adição e subtração: Contribuições da teoria dos campos conceituais. São Paulo, SP: Programa de Bolsas para Alunos do Ensino Médio em Escolas Públicas.         [ Links ]

Nunes, T., & Bryant, P. (1997). Crianças fazendo matemática. Porto Alegre, RS: Artes Médicas.         [ Links ]

Nunes, T., Light, P., & Mason, J. (1993). Tools for thought: The measurement of length and area. Learning and Instruction, 3,39-54.         [ Links ]

Outhred, L., & Mitchelmore, M. C. (2000). Young children's intuitive understanding of rectangular area measurement. Journal for Research in Mathematics Education, 31,144-167.         [ Links ]

Piaget, J., & Inhelder, B. (1983). O desenvolvimento das quantidades físicas na criança. Rio de Janeiro, RJ: Zahar.         [ Links ]

Piaget, J., Inhelder, B., & Szeminska, A. (1960). The child's conception of geometry. London: Routledge & Kegan Paul.         [ Links ]

Secretaria de Educação Fundamental. (1997). Parâmetros Curriculares Nacionais: Matemática. Brasília, DF: Autor.         [ Links ]

Silva, C. X., & Lousada, F. M. (2001). Medir é comparar. São Paulo, SP: Ática.         [ Links ]

Silva, P. P. A. (2003). Metrologia nas normas, normas na metrologia (Dissertação de mestrado, Programa de Pós-Graduação em Metrologia, Pontifícia Universidade Católica do Rio de Janeiro, RJ, Brasil). Recuperada em 20 de setembro de 2007, de http://www.maxwell.lambda.ele.puc-rio.br/cgi-bin/PRG_0599.EXE/7362_3.PDF?NrOcoSis=21083;CdLinPrg=pt        [ Links ]

Sowder, J. T. (1995). A compreensão de número na escola de primeiro grau. In L. Meira & A. G. Spinillo (Eds.), Anais da I Semana de Estudos em Psicologia da Educação Matemática (pp. 19-27). Recife, PE: Editora da Universidade Federal de Pernambuco.         [ Links ]

Spinillo, A. G. (2006). O sentido de número e sua importância na Educação Matemática. In M. R. F. de Brito (Ed.), Solução de problemas e a Matemática (pp. 83-111). Campinas, SP: Alínea.         [ Links ]

Spinillo, A. G. (2011). Number sense in children: Understanding number as an operator when adding and subtracting. In Proceedings of the 35^th Conference of the International Group for the Psychology of Mathematics Education (Vol. 2, pp. 201-209). Ankara, Turkey: International Group for the Psychology of Mathematics Education.         [ Links ]

Vergnaud, G. (1997). The nature of mathematical concepts. In T. Nunes & P. Bryant (Eds.), Learning and teaching mathematics: An international perspective (pp. 5-28). Hove, UK: Psychology Press.         [ Links ]

Vergnaud, G. (2003). A gênese dos campos conceituais. In E. P. Grossi (Ed.), Por que ainda há quem há não aprende? A teoria (pp. 21-64). Rio de Janeiro, RJ: Vozes.         [ Links ]

Yang, D.-C. (2003). Teaching and learning number sense: An intervention study of fifth grade students in Taiwan. International Journal of Science and Mathematics Education, 1(1),115-134.         [ Links ]

Yang, D.-C., & Reys, R. E. (2002). Fractional number sense strategies possessed by sixth grade student in Taiwan. Hiroshima Journal of Mathematics Education, 10,53-70.         [ Links ]

 

 

Endereço para correspondência:
Alina Galvão Spinillo
Universidade Federal de Pernambuco, Centro de Filosofia e Ciências Humanas, Programa de Pós-Graduação em Psicologia Cognitiva
Av. Arquitetura, s/n, 8º andar, Cidade Universitária
Recife, PE, Brasil 50740-550
Fone: (81) 2126-8272; Fax: (81) 2126-7330
E-mail: alinaspinillo@hotmail.com

Recebido: 20/09/2012
1ª revisão: 21/05/2014
Aceite final: 31/07/2014

 

 

1 Entre parênteses consta a fala da examinadora.