Artigo Científico

 

Os modelos mentais de alunos em relação a vetores em duas e três dimensões: uma análise da dinâmica da aprendizagem e da inadequação das avaliações tradicionais

 

Mental models of vectors in two and three dimensions: analysis of the learning dynamics and the inadequacy of traditional evaluation

 

 

Niltom Vieira Junior^I; Laurence Duarte Colvara^II

^IInstituto Federal de Educação, Ciência e Tecnologia de Minas Gerais (IFMG), Belo Horizonte, Minas Gerais, Brasil;
^IIUniversidade Estadual Paulista (UNESP), São Paulo, São Paulo, Brasil

 

 

---

Resumo

Este trabalho apresenta uma investigação realizada com alunos de cursos superiores do Instituto Federal de Educação, Ciência e Tecnologia de Minas Gerais (IFMG) - Campus Formiga. Ao se analisar as estratégias de raciocínio e dificuldades conceituais para lidar com vetores no plano e no espaço, identificadas via modelos mentais, verificou-se que nem sempre o sistema de crenças dos professores coincide com o dos alunos. Para isto são apresentadas evidências de que os métodos tradicionais de avaliação, em alguns casos, não mensuram adequadamente o nível conceitual dos estudantes e de que as metodologias de ensino podem também apresentar incompatibilidade de interesses entre alunos e professores. Nesta abordagem foram utilizadas entrevistas semi-estruturadas e análise de mapas conceituais desenvolvidos pelos alunos. Por fim são apresentados os modelos mentais identificados para vetores em duas e três dimensões, com vistas a propiciar intervenções mais bem elaboradas para o ensino deste conteúdo. © Cien. Cogn. 2010; Vol. 15 (2): 055-069.

Palavras-chave: modelos mentais; representação vetorial; ensino de ciências e matemática.

---

Abstract

This work presents an investigation with students from Federal Institute of Minas Gerais (IFMG) - Campus Formiga. After identifying the thinking strategies and the students difficulties to deal with vectors in two and three dimensions, through mental models, it was found that not always the system of beliefs from teachers match with that one from students. Then this paper shows that the traditional methods of evaluation, sometimes, may not mensure the level of students and the teaching methodologies may also be in disagreement with the need of students. Here were used interviews and analysis of conceptual maps developed by the students. So, are present here the mental models of vectors in two and three dimensions, to allow interventions more precise in science teaching. © Cien. Cogn. 2010; Vol. 15 (2): 055-069.

Keywords: mental models; vector representation; science and math education.

---

 

Introdução

Embora nem sempre possam ser caracterizadas por uma determinada corrente filosófica, as teorias da aprendizagem dividem-se principalmente em três abordagens: humanista, comportamentalista e cognitivista (Moreira, 1999).

O humanismo, por exemplo, postula que o primordial nos processos de aquisição de conhecimento é o aprendiz, seus sentimentos, pensamentos e ações; enquanto, o behaviorismo se opõe a esta visão, concentrando-se nos comportamentos do sujeito e responsabilizando fatores externos pela conduta humana. Em outra vertente surge o cognitivismo, cujo foco é o ato ou processo de conhecer. A cognição pode ser definida como o conjunto de processos mentais que envolve atenção, percepção, memória, raciocínio, juízo, imaginação, pensamento e linguagem. Com origem latina, derivada de cognitione, significa a aquisição de um conhecimento por meio da percepção e é segundo Fonseca (2009) a nova tendência pedagógica. É baseado então nas Ciências Cognitivas que este trabalho está fundamentado.

Este campo de estudo tem por origem aspectos interdisciplinares oriundos das diversas bases científicas que o compõe. Esta "nova ciência da mente", assim chamada por Gardner (2003), é produto da convergência de pesquisas em diversas áreas do conhecimento (como psicologia, linguística, neurociência, inteligência artificial, antropologia, filosofia etc.) e uma de suas hipóteses é de que o funcionamento da mente seja mais bem entendido em termos de representações mentais e procedimentos computacionais que atuam sobre tais representações (Moreira, 1997).

Historicamente nota-se que os avanços tecnológicos e a atuação conjunta de estudiosos de diversas áreas influenciaram decisivamente a evolução da ciência e a maneira pela qual a própria psicologia considerava a mente humana. O papel da matemática, engenharia e computação, por exemplo, no que tange aos progressos em sistemas de comunicação e sistemas automatizados fez com que se começasse a considerar códigos ou sistemas de símbolos para representar as informações e características do processamento mental (Gardner, 2003).

Tais representações simbólicas podem ser divididas em dois grandes tipos: as analógicas, do tipo imagem, e as proposicionais, do tipo linguagem. Todavia, há controvérsias sobre a existência de tal distinção, pois alguns teóricos argumentam que imagens (representações analógicas) podem ser também reduzidas a representações proposicionais (Moreira, 1999).

Mantendo sua tendência à própria Ciência Cognitiva que, segundo Gardner (2003: 56), deixou de lado conceitos mais obscuros que aqueles com os quais estava lidando no primeiro estágio de sua evolução, este trabalho optou por utilizar a teoria dos Modelos Mentais de Johnson-Laird (1983) que propõe um terceiro construto representacional, considerando ambas as formas de representação (analógicas e representacionais) e as distinguindo com maior clareza.

Para Johnson-Laird (1983), embora a representação analógica seja condição necessária e, às vezes, suficiente para a existência de um modelo mental, eles (modelos e imagens) se distinguem ao passo que imagens representam aspectos particulares em relação a algo, enquanto um modelo mental pode ser caracterizado como uma representação mais ampla e genérica. Pode-se, por exemplo, possuir um modelo mental de um quadro no aspecto geral, mas, uma imagem remeteria a um quadro em específico.

Quanto à distinção entre modelos e proposições, um experimento realizado por Mani e Johnson-Laird (1982) ilustra a questão. Para um grupo de pessoas foram dadas informações detalhadas quanto à distribuição espacial de objetos, enquanto para outro grupo informações pouco precisas. Os primeiros foram capazes de inferir informações adicionais não incluídas nas descrições originais, mas apresentaram dificuldades em lembrar literalmente das informações recebidas. Os últimos, por sua vez, não inferiram informações espaciais adicionais àquelas recebidas, porém lembravam-se melhor das descrições transmitidas.

Sugere-se que os primeiros haviam construído um modelo mental da informação, enquanto os últimos não formularam um modelo em razão das inúmeras alternativas que as informações imprecisas possibilitariam. Em ambos os grupos os sujeitos representaram mentalmente a distribuição de objetos, entretanto, o primeiro formou um modelo mental e o segundo trabalhou com um conjunto de proposições descritivas.

Para Johnson-Laird (1983), então, as proposições são verbalmente expressáveis e interpretadas como sendo verdadeiras ou falsas em relação a um modelo mental, enquanto as imagens correspondem às vistas (perspectivas) deste modelo (Moreira e Oliveira, 2003). Assim, um modelo mental é um análogo estrutural do mundo, constituído a partir dos seguintes princípios (Moreira, 1999):

• Princípio da computabilidade - modelos mentais são computáveis, a partir de procedimentos específicos, como aqueles executados por uma máquina;
• Princípio da finitude - eles não representam diretamente um domínio infinito;
• Princípio do construtivismo - são construídos, a partir de elementos básicos, para representar um estado de coisas.

Conclui-se, portanto, que os modelos mentais sejam representações de alto nível que facilitam o entendimento da cognição humana mesmo que, em última análise, o processamento seja realizado proposicionalmente por alguma espécie de código, tal como em um computador. Tal fato dispensa discussões polêmicas quanto ao processamento das informações e, na medida em que torna a teoria mais objetiva, a permite ser aplicada nas investigações sobre o ensino de ciências e matemática, já que mantém uma consistente base científica.

Fundado nestes conceitos buscou-se identificar os modelos utilizados por alunos ao lidar com abstrações na sala de aula, como as envolvidas no estudo da geometria analítica. Levanta-se a hipótese de que conhecer as estratégias de raciocínio e as dificuldades conceituais, perante assuntos menos tangíveis, possibilita mediações mais bem elaboradas no ensino. Para esta análise, elaborou-se uma metodologia de pesquisa para o tema "Representação Vetorial no Plano e no Espaço".

 

Metodologia

A definição da metodologia para a investigação dos modelos mentais foi impulsionada por outras experiências, como as apresentadas nos trabalhos de Borges, 1998; Barbosa e Borges, 2006; Vieira Junior e Colvara (2010); e pelo estudo de validade (da estrutura fatorial) desta teoria realizado por Greca e Moreira (1996; 1997). Estes autores, ao utilizar diversas estratégias de investigação, identificaram variáveis (definidas por análise qualitativa) como: conceito, problema, laboratório, mapa conceitual, trabalho em grupo e modelo. Atribuíram, então, escores a cada variável e uma matriz de correlações foi construída. Uma análise fatorial mostrou que todos os itens correspondiam a um único fator, "modelo", e que as variáveis "conceito" (construída a partir das respostas dos alunos à entrevistas) e "mapa conceitual" foram as que apresentaram maior correlação. Deste modo, a investigação aqui exposta baseou-se na realização de uma entrevista semi-estruturada e na construção de mapas conceituais pelos alunos que, em síntese, se constituem de uma representação gráfica do tipo organograma onde todos os conceitos são descritos e conectados conforme suas relações (um exemplo pode ser visto no Anexo A).

Participaram deste estudo vinte e cinco (25) alunos do Instituto Federal de Educação, Ciência e Tecnologia de Minas Gerais (IFMG), Campus Formiga, todos pertencentes às ciências exatas, sendo doze (12) do curso de licenciatura em matemática, sete (7) do curso de tecnologia em gestão financeira e seis (6) do curso de engenharia elétrica. Tal atividade foi desenvolvida com anuência da Secretaria de Ensino desta instituição e dos alunos envolvidos, sendo os mesmos informados a respeito da finalidade do estudo.

As entrevistas individuais foram guiadas por um questionário composto por dezenove (19) perguntas, elaborado a partir de quatro (4) níveis progressivos de dificuldade definidos pelos autores:

• Nível 1 - Identificação de vetores bidimensionais e suas operações de adição e subtração;
• Nível 2 - Identificação de vetores tridimensionais e suas operações de adição e subtração;
• Nível 3 - Representação e visualização de vetores no plano; e
• Nível 4 - Representação e visualização de vetores no espaço.

Esta classificação de níveis foi previamente planejada com base no estudo sobre a evolução dos modelos mentais apresentado por Borges (1999). Em suas pesquisas, ele identificou que a evolução dos modelos observados para um tema específico, tende a percorrer quatro níveis gerais definidos segundo sua ordem de complexidade. Portanto, de modo a antever e facilitar a análise dos resultados esta divisão foi estabelecida.

Considerou-se que para atingir o primeiro nível, o entrevistado precisava conhecer os vetores no R² e efetuar operações algébricas com eles, somando-os ou subtraindo-os. Para o segundo nível, o entrevistado deveria dominar o primeiro nível, conhecer os vetores no R³ e efetuar as operações propostas. Para o terceiro, além de dominar o primeiro e o segundo nível, o entrevistado deveria representar os vetores no plano cartesiano, inclusive aqueles gerados pelas operações propostas anteriormente. Por fim, o quarto nível englobava os três anteriores e exigia que o entrevistado soubesse representar os vetores no espaço definindo, principalmente, as variações em suas coordenadas. Acreditou-se que o quarto nível representaria o "Modelo Científico" para o escopo definido neste trabalho.

As perguntas que guiaram a entrevista, acompanhadas das respostas esperadas para o nível máximo (elaboradas pelos autores), podem ser vistas a seguir.

1. Como podemos representar o Plano Cartesiano?

 

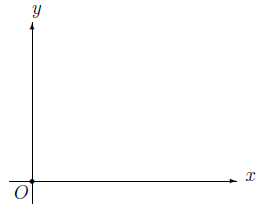
Figura 1 - Plano cartesiano.

 

O ponto O=(0,0) indica a origem dos eixos coordenados, os quais são perpendiculares e representados por x e y, sendo x o eixo das abscissas e y o eixo das ordenadas.

2. Podemos representar um ponto qualquer no plano? Se Sim, como identificamos o ponto P = (x; y)?

 

 

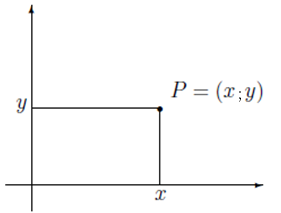
Figura 2 - Um ponto no plano.

 

3. Podemos associar o ponto P = (x; y) a um vetor? Se Sim, como seria?

 

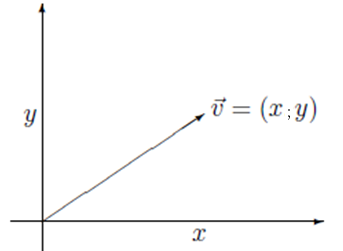
Figura 3 - Um vetor no plano.

 

4. Tomando os vetores v = (a; b) e u = (c; d), como seria a soma dos dois?

(a) v + u = (a + b + c + d)

(b) v + u = (a + b ; c + d)

(c) v + u = (a + c; b + d)

5. Ainda com os vetores anteriores em mãos, como seria a diferença de ? Existe comutatividade?

(a) v - u = (a - b - c - d)

(b) v - u = (a - b; c - d)

(c) v - u = (c - a; d - b)

(d) v - u = (a - c; b - d) - Não existe Comutatividade

6. Como seria a representação geométrica de v = (2; 3) ?

 

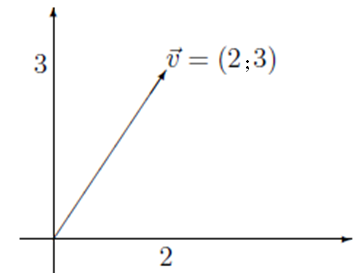
Figura 4 - O vetor v = (2; 3).

 

7. Como seria a representação de u = (3;-1) partindo da extremidade de v = (2; 3)?

 

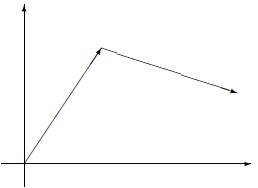
Figura 5 - Os vetores v = (2;3); u = (3; -1).

 

8. Considerando a representação gráfica do item anterior, como seria a representação geométrica do vetor soma de u e v?

 

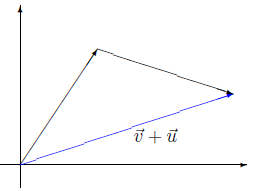
Figura 6 - O vetor soma v + u.

 

9. Como seria a representação dos vetores v e u no mesmo plano, partindo da origem?

 

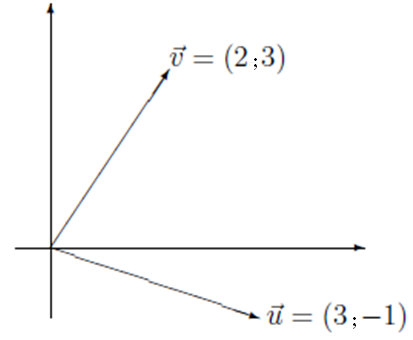
Figura 7 - Os vetores v e u.

 

10. Considerando o gráfico anterior, como seria a representação geométrica do vetor diferença v - u?

 

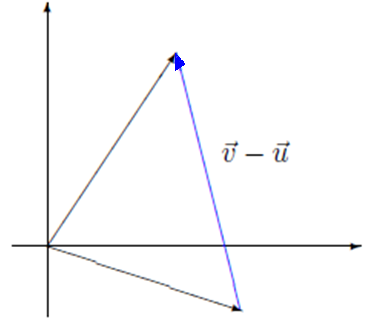
Figura 8 - O vetor diferença v - u.

 

11. Na subtração de vetores, existe diferença entre a representação geométrica dos vetores v - u e u - v? Ou seus gráficos representam a mesma situação?

 

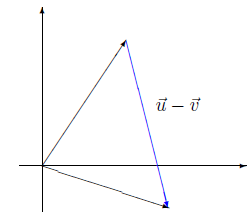
Figura 9 - O vetor u - v.

 

Observando o gráfico da questão 10 que indica a diferença v - u e este gráfico de u - v, conclui-se que representam situações diferentes.

12. Quantas dimensões a figura a seguir representa?

 

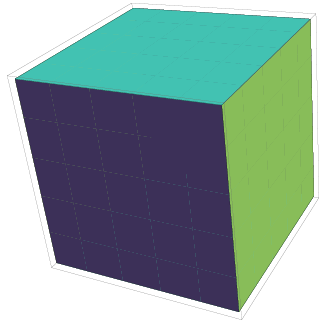
Figura 10 - Representação de um espaço tridimensional.

(a) 2 Dimensões, R³

(b) 3 Dimensões, R²

(c) 3 Dimensões, R³

13. Podemos associar eixos coordenados à figura 10? Como poderia seria? Podemos nomear esse conjunto de eixos?

Sim. Pode-se representar a profundidade, largura e altura por meio dos eixos x, y e z.

14. A partir da visão representada na figura 10, podemos trabalhar com vetores em R³? Se sim, como um vetor poderia ser escrito algebricamente?

(a) v = (x; y + z)

(b) v = (x + y; z)

(c) v = (x; y; z)

15. Podemos somar vetores em R³? Como seria escrita a soma de v = (a; b; c) com u = (x; y; z)?

(a) v + u = (a + b + c; x + y + z)

(b) v + u = (a + b; c + x; y + z)

(c) v + u = (a + x; b + y; c + z)

16. Podemos também subtrair um vetor de outro? Como seria representada a diferença v - u, sendo de v = (a; b; c) e u = (x; y; z)? Existe comutatividade na subtração?

(a) v - u = (a - b; c - x; y - z)

(b) v - u = (x - a; y - b; z - c)

(c) v - u = (a - x; b - y; c - z) - Não existe comutatividade

17. Como podemos representar geometricamente um vetor em R³?

 

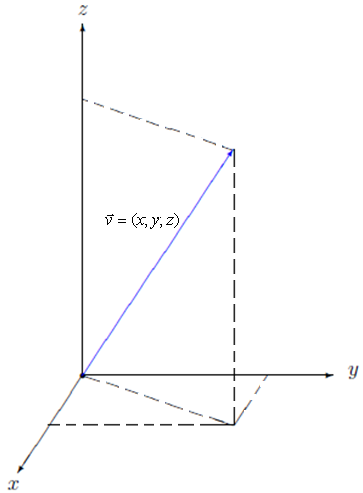
Figura 11 - Representação geométrica de um vetor no espaço.

 

18. Com o auxílio de uma caixa que exemplifica o espaço real(neste momento foi solicitado ao entrevistado que utilizasse o fundo de uma caixa de papelão), como seria a visualização de um vetor no espaço tridimensional?

 

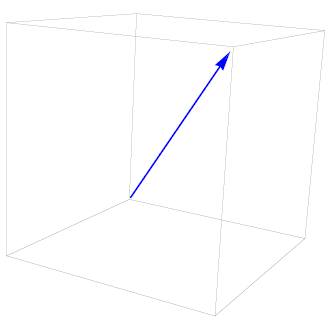
Figura 12 - Um vetor no espaço tridimensional.

 

19. Com a mesma ferramenta do item anterior em mãos e sabendo que um vetor em R³ possui coordenadas x, y e z, o que aconteceria se variasse somente a coordenada x? E se variasse somente y? E se variasse somente z?

Para um x > 0, à medida que ele aumenta, o vetor cresce em módulo e se aproxima do plano xz, mas se o valor de x diminui, o vetor diminui em módulo e se distancia do plano xz. Já para um x < 0, à medida que ele diminui, o vetor aumenta em módulo e se aproxima do plano xz, entretanto, se o valor de x aumenta, o vetor diminui em módulo e se distancia do plano xz. Nas mesmas condições de variação em x, à medida que variamos y, ele aumenta ou diminui em módulo, se aproxima ou se distancia do plano yz. Não diferente de x e y, à medida que variamos z, ele aumenta ou diminui em módulo, se aproxima ou se distancia do plano xy.

Ao término desta etapa foi solicitado que os alunos construíssem um mapa conceitual expressando seu conhecimento sobre o assunto e estabelecendo as conexões convenientes. Ao confrontar os dados das entrevistas, que foram gravadas em áudio para posterior análise a luz da teoria de Johnson-Laird (1983) com os mapas conceituais produzidos pelos participantes (Anexo A), alguns modelos mentais puderam ser identificados.

 

Análise dos resultados

Do público investigado verificou-se que 8% não possuía nenhum modelo mental, demonstrando apenas a capacidade mecanicista de resolução a partir de manipulação numérica. Entretanto, puderam ser observados quatro (4) modelos por meio dos quais os alunos resolviam os problemas. Esses modelos claramente eram estruturados, e puderam ser pelos autores definidos, a partir de conhecimentos algébricos, geométricos ou de ambos.

• Modelo Algébrico - 52% dos alunos identificavam e interagiam com os vetores efetuando as operações corretamente a partir da aplicação de definições e conceitos algébricos. Entretanto, não eram capazes de manipulá-los geometricamente;
• Modelo Geométrico Simples - 16% dos entrevistados representavam os vetores no plano e no espaço, mas não conseguiam representar um mesmo vetor quando da existência de variações como, por exemplo, ao trabalhar com um vetor sendo gerado por outros dois. Apresentavam dificuldades algébricas para manipular as coordenadas;
• Modelo Geométrico Múltiplo - 12% dos participantes representavam múltiplos vetores no plano de maneira eficaz, mesmo aqueles gerados por operações algébricas, manipulando-os adequadamente. No espaço, estes indivíduos eram capazes de representar apenas vetores isolados, faltando-lhes maior domínio das coordenadas no R³;
• Modelo científico - 12% dos entrevistados trabalhavam com os vetores tanto algebricamente quanto geometricamente, identificando, interagindo e representando-os de maneira eficaz. Estes indivíduos eram capazes de relacionar e manipular as coordenadas do vetor no plano e no espaço, reconhecer sua direção e sentido, e visualizar tanto os vetores geradores quanto os vetores gerados em uma única ilustração.

A distribuição das ocorrências pode ser mais bem observada na Figura 13.

 

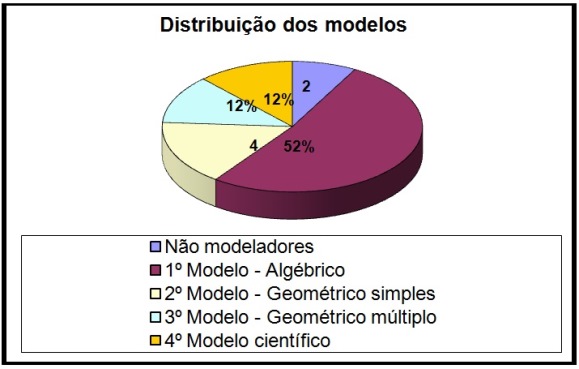
Figura 13 - Distribuição de ocorrências.

 

Embora não fosse regra, havia a expectativa de que os licenciandos em matemática apresentassem os melhores resultados, entretanto 8,33% destes alunos não possuíam modelo mental, a maioria de 58,33% encontrava-se apenas no primeiro modelo, 25% no segundo modelo e os 8,33% restantes no terceiro modelo, não havendo nenhum aluno deste curso classificado no modelo científico. A distribuição detalhada de ocorrências por curso pode ser vista na Figura 14.

 

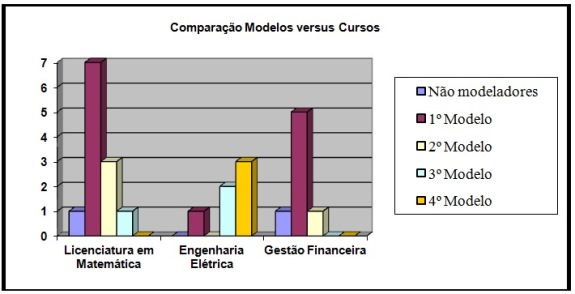
Figura 14 - Distribuição de modelos por curso.

 

Após a análise dos resultados um outro fato chamou a atenção. Se os modelos mentais identificados fossem classificados segundo os níveis previamente estabelecidos para elaboração do questionário, observar-se-ia que a suposição de pré-requisitos e níveis de dificuldade não coincidiria com a realidade dos alunos.

• Nível 1 e Nível 2: os indivíduos classificados no primeiro modelo obtiveram bom desempenho nas questões referentes a estes dois níveis, assim como os indivíduos não-modeladores que o fizeram, porém, de modo mecânico. O que representou 60% dos entrevistados;
• Nível 3: alguns indivíduos possuidores do primeiro modelo e aqueles que apresentaram o segundo modelo obtiveram êxito nas questões consideradas do terceiro nível, perfazendo 28% dos entrevistados;
• Nível 4: os 12% pertencentes ao modelo científico saíram-se bem perante as questões avançadas presentes no último nível.

A definição a respeito da evolução dos modelos mentais proposta por Borges (1999) sugere tendências pelas quais o conhecimento evolui até tornar-se científico e deixa claro, ainda, que diferentes modelos podem ser classificados em um mesmo nível desde que possibilitem, por distintas estratégias, a resolução de um mesmo problema.

Esta pesquisa, entretanto, considerou os prováveis níveis de evolução desde a elaboração das questões tal qual normalmente um professor faz ao elaborar suas provas. Contudo, o conhecimento dos alunos foi, a princípio, subestimado haja vista que o modelo mais elementar (1º modelo) atingiu o segundo e, em alguns casos, o terceiro nível da entrevista. Em contrapartida, outras habilidades foram superestimadas, uma vez que não se previu as dificuldades encontradas ao se manipular um vetor isolado comparadas àquelas para manipular múltiplos vetores.

Deste modo se após a investigação a definição hierárquica das questões, e dos níveis, fosse reconsiderada sua distribuição ficaria assim:

• Nível 1 (alcançado pelos indivíduos do modelo 1): Identificação e operação com vetores em duas e três dimensões;
• Nível 2 (alcançado pelos indivíduos do modelo 2): Representação e visualização de vetores isolados no plano e no espaço;
• Nível 3 (alcançado pelos indivíduos do modelo 3): Representação e visualização de múltiplos vetores no plano;
• Nível 4 (alcançado pelos indivíduos do modelo 4): Representação e visualização de múltiplos vetores no espaço.

Como a entrevista tinha por objetivo investigar as estratégias de raciocínio utilizadas, via modelos mentais, a alteração na ordem dos níveis e consequentemente na ordem em que as questões foram apresentadas não prejudicaram os objetivos do trabalho. Entretanto se o referido questionário (construído com base na experiência dos autores) fosse empregado em uma avaliação, sendo a pontuação distribuída do modo como ele foi idealizado, a medição efetiva do aprendizado seria comprometida.

Neste caso foi constatado que os modelos mentais dos professores podem influenciar os métodos de avaliação utilizados, a distribuição de pontos adotada e o nível de habilidade exigido, fazendo com que a evolução ou o domínio de níveis inferiores sejam vistos com menor importância ou até mesmo desconsiderados durante uma prova.

Este comportamento é justificado segundo o que Norman (1983) identifica como "sistema individual de crenças", que suporta os modelos mentais de cada pessoa conforme seu nível de instrução em determinado assunto.

Por outro lado há de se considerar também o fato de indivíduos não-modeladores apresentarem, em alguns casos, desempenho similar àqueles classificados no primeiro modelo. Portanto, mesmo que a situação anteriormente exposta seja minimizada, corre-se ainda o risco de não se avaliar adequadamente o nível conceitual dos distintos alunos. Baseados nestes fatos e nas particularidades dos modelos mentais identificados estabeleceram-se as conclusões deste trabalho.

 

Conclusões

Este estudo apresenta importantes resultados quanto à dinâmica pela qual o aprendizado ocorre via identificação dos modelos mentais. Verificou-se que o entendimento conceitual dos alunos encontra-se abaixo do esperado, evidenciando que a academia tem apresentado falhas no que concerne às relações de ensino-aprendizagem e promovendo, em alguns casos, apenas a capacidade mecanicista de resolver problemas.

Destaca-se que esta pesquisa foi realizada em uma instituição federal de ensino que, em tese, seleciona melhor seus alunos em função da alta concorrência por vagas. Entretanto, notaram-se raros casos em que os indivíduos apresentavam entendimento conceitual bem estabelecido, múltiplas visões para um mesmo problema e, principalmente, a capacidade de visualizar os sistemas trabalhados.

Aliado a isto demonstrou-se empiricamente que o sistema de crenças dos professores (haja visto o dos autores) pode influenciar o modo pelo qual eles avaliam e, provavelmente, transmitem informações aos seus alunos. Ademais, observou-se também que as avaliações tradicionais muitas vezes não mensuram o aprendizado conceitual, considerando além da situação anterior o fato de não-modeladores terem apresentado o mesmo desempenho, ao menos para os primeiros níveis, que alunos que possuíam modelos mentais elementares. Tal evidência sugere novas tendências avaliativas como, por exemplo, a já adotada no exame nacional do ensino médio em que habilidades cognitivas têm sido levadas em consideração (Gomes, 2005).

Por fim, este trabalho trata de uma tentativa inicial de apresentar alguns problemas relativos ao ensino além de atestar que compreender as estratégias de raciocínio e, consequentemente, as dificuldades conceituais apresentadas pelos alunos possibilita a realização de avaliações e intervenções mais bem elaboradas. Tais características para o estudo específico da representação vetorial, em duas e três dimensões, foram aqui apresentadas. Conclui-se, portanto, que a educação cognitiva merece de fato espaço nos procedimentos escolares, sendo o estudo dos modelos mentais um dos recursos para lidar com estes aspectos na sala de aula de ciências e matemática.

 

Referências bibliográficas

Barbosa, J.P.V. e Borges, A.T. (2006). O entendimento dos estudantes sobre energia no início do ensino médio. Caderno Brasileiro de Ensino de Física, 23, 182-217.         [ Links ]

Borges, A.T. (1998). Modelos mentais de eletromagnetismo. Caderno Catarinense de Ensino de Física, 15(1), 7-31.         [ Links ]

Borges, A.T. (1999). Como evoluem os modelos mentais. Ensaio - Pesquisa em Educação em Ciências: Ensaio, 1 (1), 85-125.

Fonseca, V. (2009). Cognição, neuropsicologia e aprendizagem. Petrópolis: Vozes.         [ Links ]

Gardner, H. (2003). A nova ciência da mente. São Paulo: Editora da Universidade de São Paulo.         [ Links ]

Gomes, C.M.A. (2005). Uma análise das habilidades cognitivas mensuradas pelo exame nacional do ensino médio. 2005. Tese de Doutorado, Faculdade de Educação, Universidade Federal de Minas Gerais, Belo Horizonte, MG.         [ Links ]

Greca, I.M. e Moreira, M.A. (1996). Un estúdio piloto sobre representaciones mentales, imágenes, proposiciones y modelos mentales respecto al concepto de campo electromagnético em alumnos de Física General, estudiantes de postgrado y físicos profesionales. Investigações em Ensino de Ciências, 1 (1), 95-108.         [ Links ]

Greca, I.M. e Moreira, M.A. (1997). The kinds of mental representations - models, propositions, and images - used by college physics students regarding the concept of field. Int. J. Sci. Educ., 19 (6), 711-724.         [ Links ]

Johnson-Laird, P. (1983). Mental models. Cambridge: Harvard University Press.         [ Links ]

Mani, K. e Johnson-Laird, P. (1982). The mental representation of spatial descriptions. Memory Cogn., 10 (2), 181-187.         [ Links ]

Moreira, M.A. (1997). Modelos Mentais. Em: Faculdade de Educação da UFMG (Org.), Anais, I Encontro Sobre Teoria e Pesquisa em Ensino de Ciência. Belo Horizonte: Faculdade de Educação, UFMG.         [ Links ]

Moreira, M.A. (1999). Teorias da aprendizagem. São Paulo: Editora EPU.         [ Links ]

Moreira, M.A. e Oliveira, A.P. (2003). Dificuldade dos alunos na aprendizagem da lei de Ampère, à luz da teoria dos modelos mentais de Johnson-Laird. Revista Brasileira de Ensino de Física, 25 (3), 317-325.         [ Links ]

Norman, D.A. (1983). Some observations on mental models. Em: Gentner, D. e Stevens, A.L. (Ed.). (1983). Mental models. Hillsdale: Lawrence Erlbaum Associates.         [ Links ]

Vieira Junior, N. e Colvara, L.D. Os modelos mentais de frações: como universitários lidam com conceitos fundamentais de matemática? Ciências & Cognição, v. 15 (1), 124-136. Disponível em www.cienciasecognicao.org.         [ Links ]

 

 

Agradecimentos

Os autores agradecem aos alunos Antônio Marcos de Sousa, Kátia Costa, Eduardo Franco e João Paulo Costa, do curso de licenciatura em matemática, pelo apoio na realização das entrevistas e contribuição ao ensino de ciências e matemática.

 

Notas

Niltom Vieira Junior
E-mail para correspondência: niltom@gmail.com.

 

 

ANEXO A

A figura abaixo exemplifica um tipo de mapa conceitual para o tema analisado. Este mapa foi produzido por um dos alunos classificados no modelo científico.

 

Figura 15

Figura 15 - Mapa conceitual criado por um dos alunos.