LA PSICOLOGÍA EN LA TRANSFORMACIÓN EDUCATIVA

 

El razonamiento del espacio y la geometría dinámica: un estudio de caso en la educación media en Río de Janeiro

 

 

George Alves; Adriana Soares; Cabral Lima

Universidade Federal de Rio de Janeiro (UFRJ)(Brasil)

 

 

---

RESUMEN

El tema de la investigación fue el desarrollo del raciocinio espacial a partir del uso de una herramienta computacional dinámica. El problema de la investigación fue verificar si la adopción de una secuencia didáctica adecuada, combinada con la utilización de la geometría dinámica, contribuye para el desarrollo del raciocinio espacial. La hipótesis adoptada por el trabajo fue la de que si la geometría dinámica posibilita que el alumno vea las construcciones geométricas de diferentes puntos de vista debido a la posibilidad de la movimentación de estas figuras y si el principio de Cavalieri permite un abordaje más intuitivo para justificar formulas de volumen, entonces los alumnos tienen una mejor aprehensión de la fórmulas de volumen. Los sujetos eran 70 alumnos de un curso técnico del tueno de la noche, con edades variando entre 17 a 44 años, siendo que 39 de ellos asistieron a las clases auxiliadas por un software de geometría dinámica, mientras que los 31 restantes asistieron clases clásicas de geometría espacial. Los resultados permitieron concluir que el enfoque adoptado facilitó a comprensión de las formulas de los volúmenes de los sólidos geométricos mas utilizados en la enseñanza de secundaria y mostró un mejor desempeño en el teste de raciocinio espacial entre los alumnos que utilizaron la herramienta computacional.

---

 

 

1. Introducción

Algunos trabajos están preocupados con el desarrollo de la capacidad del niño para representar objetos geométricos y percibir, criar y visualizar imágenes. El objetivo del presente estudio es investigar, si la combinación de una secuencia didáctica y la utilización de un software de geometría dinámica contribuyen para una mejor representación mental de conceptos y objetos geométricos por los alumnos.

Partimos de la hipótesis de que la geometría dinámica posibilita que el alumno vea las construcciones geométricas de diferentes puntos de vista y si el Principio de Cavalieri permite un abordaje más intuitivo para justificar las fórmulas de volumen, entonces los estudiantes tienen una mejor comprensión de las mismas y desenvuelven su raciocinio espacial utilizando el computador como herramienta.

Los sujetos materia de este estudio eran alumnos de cursos técnicos del área industrial, sector que exige de sus futuros profesionales una buena capacitación para el raciocinio espacial, entre otras competencias. De allí la preocupación por encontrar caminos y soluciones para el desarrollo de esta habilidad a través del proceso de enseñanza-aprendizaje de la geometría usando un software de geometría dinámica.

 

2. El software Calques 3D

El Calques 3D es un software gratuito de geometría dinámica destinado al aprendizaje de la geometría espacial creado por Nicolas Van Labeke en 1999.

El usuario tiene la posibilidad de ver, observar y comprender el espacio tridimensional, modificando el sistema de referencia espacial, escogiendo la perspectiva y modificando el ponto de vista del observador. Se puede realizar construcciones dinámicas de figuras geométricas, explorar y descubrir las propiedades geométricas de estas figuras, deformándolas a través del "arrastrar" de algunos puntos (Van Labeke, 1998).

La interfase (fig.1) permite un acceso intuitivo y adaptable, así el alumno no necesita tener una preparación especial para utilizarlo y el profesor puede decidir, de acuerdo con la secuencia didáctica preparada por él e cuales funcionalidades deben estar disponibles para el estudiante.

 

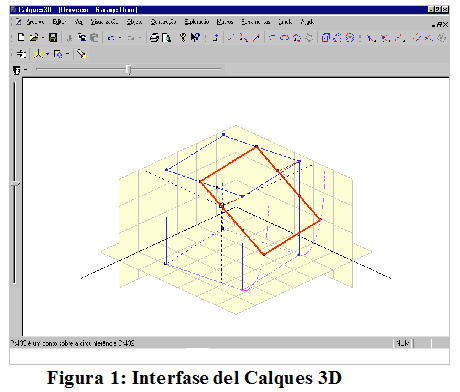
Figura 1: Interfase del Calques 3D

 

3. Metodología

En un software de geometría dinámica, las actividades que estimulan la exploración y el descubrimiento de invariantes son realizadas a través de experiencias visuales. La construcción del conocimiento por los alumnos ocurre a través de investigación, exploración y descubrimiento, usando los diferentes recursos disponibles en estos softwares que sirven de soporte para sus acciones mentales (Alves & Soares,2003).

Según Vergnaud (1985), el concepto de representación es fundamental para analizar la formación de concepciones y competencias, así como para analizar la formación y los procesos de transmisión del conocimiento. El considera esencial la relación del sujeto con el mundo real, pues es partir de allí que este pone a prueba sus representaciones y concepciones.

Los alumnos fueron clasificados en un grupo de control de 31 sujetos y en un grupo experimental de 39 sujetos.

Los instrumentos utilizados para la observación y análisis fueron un cuestionario para caracterización de los grupos, un teste de conocimiento geométrico, las notas de pruebas realizadas con el contenido propuesto y los testes de raciocinio verbal, raciocinio abstracto, raciocinio numérico y raciocinio espacial da Batería de Pruebas de Raciocinio (BPR-5) da Casa del Psicólogo. El último de estos fue aplicado antes y después del trabajo del salón de clases, a fin de verificar si el desempeño de los alumnos había sido modificado con el uso o no del software de geometría dinámica.

El asunto abordado durante las clases fue el cálculo de volúmenes de los sólidos más vistos en la enseñanza media. De acuerdo con Lima (1991), hay tres maneras para el abordaje de este asunto en este nivel de enseñanza: utilizar la presentación clásica de Euclides y Arquímedes, usar el cálculo infinitesimal o utilizar el Principio de Cavalieri. La opción adoptada durante las clases fue el Principio de Cavalieri.

Las secuencias didácticas utilizadas fueron basadas en las propuestas de Dante (1999) y Trotta, Imenes & Jakubovic (1980). Inicialmente se comprueba la fórmula para el cálculo del volumen del paralelepípedo rectángulo, en seguida se parte para la fórmula de un prisma cualquiera, para la del cilindro, la de una pirámide cualquiera, la del cono y, finalmente la de la esfera.

Las clases clásicas también no fueron completamente tradicionales, pues ellas no eran exclusivamente expositivas y, así como las del laboratorio, también fueron basadas en actividades de enseñanza en que el movimiento de las figuras era substituido por diseños estáticos en las hojas impresas.

 

4. Resultados

Para el análisis de los resultados fueron consideradas tres variables: las medias de las pruebas aplicadas durante los bimestres en que las clases fueron realizadas, el desempeño de los alumnos en el teste de conocimiento geométrico y en el teste de raciocinio espacial. Este último teste es el que posibilitó verificar la capacidad de visualización de los alumnos o la capacidad de formar representaciones mentales visuales y manipularlas, transformándolas en nuevas representaciones.

4.1. Media de las pruebas aplicadas

La media obtenida por los sujetos del grupo de control fue de 5,86 y la obtenida por los sujetos del grupo experimental fue de 7,36, aproximadamente 26% superior.

Hubo la necesidad de aplicación del teste t para decidir si la diferencia entre las medias de los dos grupos era apenas resultado de fluctuaciones casuales o si fue significativa. En el cuadro 1, GE indica la media de los sujetos del grupo experimental y GC la media de los sujetos del grupo de control, N indica el número de sujetos usados en la comparación, df = N - 1 es el grado de libertad, t indica la medida de comparación y p es la probabilidad o nivel de significancia, cuyo valor utilizado por la psicología experimental es p < 0,05.

 

Cuadro 1: Resultados del teste t para las medias de las pruebas aplicadas

GE	GC	N	df	t	p
7,36	5,86	31	30	3,322	0,002

 

La hipótesis nula garante que solo hay diferencia significativa entre los grupos si t no fuera lo suficientemente grande, o sea, si la diferencia entre los grupos no fuera grande demás para ser explicada únicamente por las fluctuaciones casuales o por un error experimental.

En este caso recusase a aceptar como razonable que la diferencia real entre las medias de los dos grupos sea cero y se supone que fueron utilizadas todas las garantías experimentales adecuadas en la obtención de estos resultados y consecuentemente los grupos difieren solamente en términos que cada uno sufrió un tratamiento experimental diferente, pues recibieron valores diferentes para la variable independiente. Luego esta fue capaz de influir en las medidas de la variable dependiente y este es justamente el objeto del experimento (MacGuigan, 1976).

Conforme los resultados presentados en el cuadro 1, se puede rechazar la hipótesis nula en el caso de las medias presentadas, ya que t = 3,322 y p = 0,002 < 0,05, mostrando que la diferencia obtenida puede ser atribuida al hecho de los grupos haber sufrido tratamiento experimental diferenciado.

4.2. Teste de conocimiento geométrico

El teste de conocimiento geométrico fue aplicado antes (pre-teste) y después de las clases (pos-teste) realizadas.

En un análisis inicial se percibe una superioridad en el desempeño del grupo experimental sobre el grupo de control. Cuando son analizadas las medias de aciertos en el pre-teste, el grupo de control presenta desempeño de 42,80% pasando para 53,54% en el pos-teste. El crecimiento fue de 25,09%.

En el grupo experimental hubo una media inicial de 43,59% de aciertos en el pre-teste y de aproximadamente 62,90% en el pos-teste, demostrando un a ganancia de 44,30%. Por tanto, superior al del grupo de control.

Cuando el teste t es aplicado para comparar la variación del desempeño de los grupos en el pre y pos-teste, los resultados apuntan para diferencias de desempeño significativas en los dos casos, pues t = 9,909 y p = 0,000 < 0,05 para el grupo experimental y t = 7,835 y p = 0,000 < 0,05 para el grupo de control (cuadro 2). Se observa que los resultados obtenidos por el software SPSS son aproximados hasta la casa de milésimos.

 

Cuadro 2: Resultados del teste t comparando el pre y pos-teste de conocimiento geométrico para el grupo experimental (GE) y grupo de control (GC)

	Pre-teste	Pos-teste	N	df	t	p
GE	43,59%	62,90%	39	38	9,909	0,000
GC	42,81%	53,55%	31	30	7,835	0,000

 

Los resultados del cuadro 3 indican que antes del inicio de la experiencia en el salón de clases no había diferencia significativa entre los grupos, ya que t = 0,141 y p = 0,89 > 0,05. Entretanto, cuando fueron comparadas las medias de las pruebas aplicadas al final de cada etapa del estudio, se puede considerar que hubo significancia en la diferencia entre los grupos, ya que t = 3,063 y p = 0,05. Mismo que el valor no sea menor que 0,05 parece razonable rechazar la hipótesis nula en este caso.

Se observa que las medias obtenidas por los dos grupos no son excelentes, pues no ultrapasaron 65% de aciertos del pos-teste, pero los resultados de los testes de raciocinio de la batería BPR-5 indicaron que la grande mayoría de los sujetos de los dos grupos poseen una capacidad debajo de lo que seria esperado en ese nivel de escolaridad para resolver problemas que requieren el análisis de las informaciones presentadas por la situación, el cruzamiento de las informaciones, la creación de concepciones abstractas y la deducción de respuestas para el problema a partir de estas concepciones.

 

Cuadro 3: Resultados del teste t comparando los grupos experimental y control a partir de las medias de aciertos en el teste de conocimiento geométrico en el pre y pos-teste

	GE	GC	N	df	t	p
Pre-teste	43,22%	42,80%	31	30	0,141	0,89
Pos-teste	63,64%	53,54%	31	30	3,063	0,05

 

Los resultados presentados sobretodo en el cuadro 2 pueden indicar que la utilización de la secuencia utilizando el Princípio de Cavalieri, con o sin el uso del software de geometría dinámica, ya trae ganancias significativas para el desempeño de los alumnos, por eso en el cuadro 3, cuando los dos grupos fueron comparados en el pos-teste, se verifico que el desempeño del grupo experimental fue significativamente mejor que el del grupo de control.

4.3. Teste de raciocinio espacial

El teste de raciocinio espacial fue de grande importancia para la verificación de la hipótesis general establecida en el estudio realizado: la de que la geometría dinámica contribuye para la representación mental de objetos y conceptos geométricos y para el desenvolvimiento del raciocinio espacial de los alumnos.

La primera comparación realizada fue aquella que confronta el desempeño de los dos grupos en el teste de raciocinio espacial, antes y después de la realización de las clases. A través del cuadro 4 es posible verificar que antes de la realización del presente trabajo de campo la hipótesis nula no podría ser descartada, o sea, no había diferencia significativa entre los grupos, pues t = 0,948 e p = 0,351 > 0,05.

Después de las clases, según la aplicación del teste t, la diferencia entre los grupos permaneció no siendo significativa, pues t = 1,734 y p = 0,093 > 0,05. Aun así es posible percibir que el valor del parámetro p presentó una grande mejora aproximándose bastante del valor de corte adoptado por la psicología experimental.

 

Cuadro 4: Resultados del teste comparando el grupo experimental (GE) con el grupo de control (GC) en el teste de raciocinio espacial

	GC	GE	N	df	t	p
Pre-teste	38,99	45,25	31	30	0,948	0,351
Pos-teste	42,19	53,93	31	30	1,734	0,093

 

Cuadro 5: Resultados del teste t comparando el pre y pos-teste de raciocinio espacial en el grupo de control (GC) y en el grupo experimental (GE)

	Pre-teste	Pos-teste	N	df	t	p
GC	38,39	42,19	31	30	1,696	0,100
GE	42,92	51,84	39	38	3,846	0,000

 

Cuando el teste t es aplicado a los resultados obtenidos por los sujetos de los dos grupos, antes y después de las clases ministradas, se observa que el grupo experimental hubo ganancias significativas, ya que t = 3,846 y p = 0,000 < 0,05. La hipótesis nula puede, por tanto, ser descartada en este caso. En tanto, en el grupo de control no es posible considerar que haya habido una ganancia significativa, pues t = 1,696 y p = 0,100 > 0,05 y de este modo, la hipótesis nula no debe ser descartada. Ver el cuadro 5.

 

5. Consideraciones Finales

El estudio aquí presentado y analizado buscó comprender, de que forma el uso del computador, en conjunto con una secuencia didáctica adecuada, podría auxiliar en la mejoría del raciocinio espacial de alumnos de la secundaria de la escuela pública.

Los resultados mostraron que los sujetos que pertenecían al grupo experimental obtuvieron un desempeño significativamente superior con relación a aquellos del grupo de control en el pos-teste de conocimiento geométrico y en la media de las pruebas aplicadas. Por eso, en el pos-teste de raciocinio espacial, esta diferencia no a sido significativa.

Talvez este último hecho se explique porque los resultados verificados en los pre-testes de la batería BPR-5 sugerían que la grande mayoría de los sujetos de los dos grupos poseía una capacidad debajo de lo que seria esperado en este nivel de escolaridad para resolver problemas que requerían el análisis de las informaciones presentadas por la situación, el cruzamiento de las informaciones, la creación de concepciones abstractas y la deducción de respuestas para el problema a partir de estas concepciones.

Además de posibilitar la mejoría del desempeño de los alumnos y de su interés por las clases de geometría, el uso de la geometría dinámica puede traer una importante implicación para el propio currículo de matemáticas tanto de la primaria como de la secundaria, pues as clases con el uso de estos softwares ciertamente exigirán mas tiempo para formalización de los conceptos y mucho planeamiento de las actividades por parte del profesor.

 

6. Referencias

Almeida, L.S.; Primi, R. (2000). Manual Técnico - Bateria de Provas de Raciocínio. São Paulo: Casa do Psicólogo.        [ Links ]

Alves, G.S.; Soares, A.B. (2003). "Geometria Dinâmica: um estudo de seus recursos, potencialidades e limitaciones através do Software Tabulae". In: XXIII Congresso da Sociedade Brasileira de Computación - IX Workshop de Informática na Escola. Campinas: Unicamp. 2003, pp 275-286.        [ Links ]

Dante, L.R. (1999). Matemática - Contexto e Aplicacões, vol. 2, Ática: São Paulo.        [ Links ]

Lima, E.L. (1991). Medida e forma em Geometria: comprimento, área, volume e semelhança, Grafitex - Coleção do Professor de Matemática, Rio de Janeiro.        [ Links ]

Trotta, F., Imenes , L.M.P.& Jakubovic, J. (1980). Matemática Aplicada, vol.3, Editora Moderna, São Paulo.        [ Links ]

Van Labeke, N. (1998). "Calques 3D: a microworld for spatial geometry learning". In: ITS'98 - System Demonstrations, San Antonio (Texas), August 16-19. Disponível em http://www.psyc.nott.ac.uk/staff/nvl/docs/its_sd1998.pdf. Acesso em 08/02/2005.        [ Links ]

Vergnaud, G. (1985). "Conceitos e esquemas numa teoria operatória da representación". Trad. Anna Franchi e Dione Luchesi de Carvalho. In: Psychologie Française, no30-3/4, pp.245-252.        [ Links ]