PsicoUSF
ISSN 1413-8271
ARTIGOS
Teoria de Resposta ao Item na análise de uma prova de estatística em universitários
Item Response Theory to analyze a statistics test in university students
Claudette Maria Medeiros Vendramini1; Anelise Silva Dias2
Universidade São Francisco
RESUMO
Este estudo objetivou aplicar a Teoria de Resposta ao Item na análise das 15 questões de múltipla escolha de uma prova de estatística apresentada na forma de gráficos ou de tabelas estatísticas. Participaram 413 universitários, selecionados por conveniência, de duas instituições da rede particular de ensino superior, predominantemente do curso de Psicologia (91,5%). Os universitários foram 80% do gênero feminino e do período diurno (69,8%), com idades de 16 a 53 anos, média 24,4 e desvio padrão 7,4. A prova é predominantemente unidimensional e os itens são mais bem ajustados ao modelo logístico de três parâmetros. Os índices de discriminação, dificuldade e correlação bisserial apresentam valores aceitáveis. Os resultados mostram as dificuldades apresentadas pelos estudantes com relação aos conceitos matemáticos e estatísticos, dificuldades essas observadas em outras pesquisas desde o ensino fundamental. Sugere-se que esses conceitos sejam tratados mais profundamente no ensino superior.
Palavras-chave: Representação tabular e gráfica, Dificuldades matemáticas, Estudantes de psicologia.
ABSTRACT
This study aimed to use the Item Response Theory to analyze the 15 multiple-choice questions of a statistics test presented in the statistics graphics or tables form. The 414 university students were selected by convenience from two private universities, predominantly psychology students (91.5%). The university students were 80% female and with 16-53 years old, mean 24.4 and standard deviation 7.4. The test has predominantly one dimension and the items can be better fitting to the model of three parameters. The indexes of difficulty, discrimination and bisserial correlation presented acceptable values. The results indicate the difficulties of university students in the mathematic and statistic concepts, that difficulties are observed in the other studies since the elementary education. One suggests making more profound studies of these concepts in higher education.
Keywords: Graphic and tabular presentation, Mathematic difficulties, Psychology students.
Atualmente, os testes estão sofrendo significa-tivas revisões, bem como novos instrumentos estão sendo criados, principalmente na área educacional. Para uma avaliação educacional adequada é necessário veri-ficar qual conhecimento está sendo transmitido durante o curso universitário e como este conhecimento está sendo assimilado pelos alunos. É importante acompanhar o desenvolvimento das habilidades básicas necessárias para o bom desempenho acadêmico dos estudantes, além de avaliar a qualidade do ensino, e criar oportunidades de conscientização sobre as qualidades e fraquezas dos es-tudantes, visando ao planejamento de ações futuras que desenvolvam neles essas habilidades básicas. Observa-se na literatura que os educadores estão cada vez mais conscientes das dificuldades de aprendizagem dos estudantes, inclusive entre alunos universitários. Há uma preocupação crescente com habilidades pouco desen-volvidas de leitura, escrita e aritmética que motiva a busca por testes de competências e habilidades básicas como um meio de certificar a obtenção de uma competência mínima (Anastasi & Urbina, 2000).
De acordo com Smole e Diniz (2001), em qualquer área do conhecimento a leitura deve possibi-litar a compreensão de diferentes linguagens, as pessoas devem aprender progressivamente a utilizar a leitura para buscar informações, e para que enfim possam aprender. A leitura pode ser vista como um processo de comunicação, sua prática gerando reflexão, trazendo um conteúdo novo que pode confirmar e contestar opiniões, provocando conflitos. Quanto maior a compreensão do texto, mais o leitor poderá aprender a partir do que lê. Grande parte das informações necessárias para se viver em sociedade e construir conhecimentos é encontrada na forma escrita, seja ela descritiva, tabular ou gráfica.
A compreensão de um texto envolve alguns processos: interpretação, decodificação, análise, síntese, seleção, antecipação e autocorreção. Entretanto, no que se refere à escrita matemática, as autoras Smole e Diniz (2001) esclarecem que há uma especificidade, uma característica própria que envolve uma combinação de sinais, letras e palavras que se organizam de acordo com regras para expressar idéias. A organização desta escrita aritmética é diferenciada com relação a outros textos como, por exemplo, os livros de leitura, pois exige um processo particular de leitura.
Ainda segundo as autoras, recursos utilizados pela matemática, assim como pela estatística, como os gráficos e tabelas, são uma das maneiras de leitura de matemática que podem ser encontradas facilmente no dia-a-dia das pessoas, em que a leitura e interpretação desses recursos desenvolvem habilidades de questionar, levantar hipóteses, bem como procurar relações entre os dados, habilidades essenciais ao processo de ler qualquer tipo de textos. A dificuldade que alguns alunos apresentam pode ser decorrência da falta de compreensão de um conceito envolvido na escrita da matemática, no problema, ou do uso de termos específicos da matemá-tica que não fazem parte do cotidiano do aluno, e até mesmo palavras que têm significados diferentes, como: diferença, ímpar, média, probabilidade, entre outras.
Também na linguagem escrita da estatística há uma característica própria que envolve sinais, letras, palavras que se organizam de acordo com regras especí-ficas. Assim como para a escrita matemática, a lingua-gem escrita da estatística exige do indivíduo uma leitura diferenciada, que muitas vezes inclui a leitura de tabelas e gráficos estatísticos que resumem grande quantidade de informações. O estudo dessas e de outras variáveis ligadas ao ensino-aprendizagem da estatística ocupa cada vez mais um lugar importante tanto nas instituições de ensino fundamental quanto superior.
A necessidade de assimilar novas informações de um mundo em constante transformação, que muitas vezes são representadas resumidamente em gráficos e tabelas estatísticas, tem levado pesquisadores a explorar a leitura, interpretação e utilização dessas representações. Segundo Vendramini e Brito (2001), os atuais profissio-nais precisam estar capacitados para lidar com grande quantidade de informações, saber processá-las em tempo mínimo, não apenas ter domínio de conheci-mentos específicos, mas ter a capacidade de se adaptar rapidamente a novas situações.
Esta necessidade do mundo atual tem motivado estudos sobre o ensino-aprendizagem da estatística, como a pesquisa de Woehlke e Leitner (1980), os quais explo-raram as diferenças de gênero no desempenho de alunos de graduação e pós-graduação em disciplinas de estatística. As autoras aplicaram um teste de matemática e um de estatística, no início e no final do semestre, além de observar as notas finais nas disciplinas de Estatística, Estatística Básica no nível de mestrado e Estatística Inferencial e Regressão Múltipla Linear, ambas no nível de doutorado. Os resultados revelaram que os alunos do gênero masculino obtiveram notas ligeiramente maiores no pré-teste de matemática que os do gênero feminino, mas o gênero não foi uma variável preditora do desempenho na disciplina e o desempenho no pré-teste de matemática foi uma variável preditora do desempenho na disciplina no nível de mestrado.
Para Garfield (1995) os educadores precisam compreender como os estudantes aprendem, por meio do estudo das teorias de aprendizagem, assim como determinar o que realmente querem que seus alunos aprendam, a fim de modificar seu ensino. Além disso, devem utilizar a avaliação para determinar a eficácia do ensino, ou seja, para verificar se os estudantes estão desenvolvendo a compreensão e a competência em estatística. Segundo Gal e Garfield (1997), a instituição deve proporcionar ao estudante as capacidades de compreender e lidar com incerteza, variabilidade e informação estatística, assim como contribuir ou tomar parte na produção, interpretação e comunicação de dados pertencentes a problemas que eles devem encontrar na sua vida profissional.
A utilização de gráficos e tabelas estatísticas é necessária para a comunicação de dados, e por este motivo deve ser estudada desde a educação infantil. De acordo com Moore (1997), os estudantes deveriam aprender a olhar os dados a partir de gráficos e cálculos simples, procurando padrões gerais e seus desvios, questionando sempre a que os dados se referem nos contextos que eles descrevem.
Um gráfico, uma representação simbólica de dados, geralmente relaciona duas ou mais variáveis num sistema de coordenadas cartesianas (Leinhardt, Zaslavsky & Stein, 1990). É a forma mais efetiva de descrever, ex-plorar e resumir um conjunto de dados, mesmo quando este é grande. Geralmente, os gráficos mostram uma grande quantidade de informações em um pequeno espaço, sendo um importante meio de comunicação escrita de dados quantitativos em artigos científicos, em artigos de interesse geral, ou em relatórios técnicos de universidades ou de outros tipos de instituições. Segundo Cazorla (2002), é um método efetivo de comunicação, uma vez que utilizam mecanismos cognitivos, principal-mente de percepção, sendo uma forma de apresentação mais prazerosa do que formas não pictóricas, como listas de posições e tabelas, entre outras.
Uma outra maneira de sintetizar as informações obtidas na observação de uma ou mais variáveis, para que se tenha uma visão global de seu comportamento e de sua variação, é a representação tabular. Uma tabela estatística resume um conjunto de observações de uma ou mais variáveis (Crespo, 1997), e tem por objetivo a transformação de dados brutos em um conjunto de mensurações dotadas de sentido (Feijoo, 1996).
As tabelas podem conter dados que variam de acordo com o local, a época ou a espécie, sendo expressos por meio de porcentagens, índices, coeficientes ou taxas, de modo a atingir o objetivo principal de forne-cer informações rápidas e seguras a respeito de variáveis em estudo, permitindo inferências mais coerentes e científicas. É fundamental que indivíduos saibam ler, compreender, realizar cálculos matemáticos e inferir so-bre as informações contidas em tabelas e gráficos assim como avaliar o desempenho na realização de provas que contemplem esse tipo de conhecimento.
A avaliação do desempenho de estudantes em provas de leitura e interpretação de gráficos e tabelas, bem como em operações matemáticas básicas (razão, porcentagem, taxa, entre outras) deve ser confiável e válida, para que se possa contribuir com um melhor entendimento desse desempenho e das habilidades acadêmicas em matemática e estatística. A avaliação e interpretação de provas destinadas para esse fim podem ser realizadas por diferentes técnicas de análise de dados, entre elas a Teoria de Resposta ao Item (TRI). Com a utilização dessa técnica é possível representar a relação entre a probabilidade de um aluno responder corretamente a um item e suas habilidades na área de conhecimento que será avaliada (Valle, 2000), que nesta pesquisa refere-se à habilidade de leitura de dados apresentados em gráficos e tabelas estatísticas por uni-versitários. Assim, a relação que se estabelece é sempre expressa de tal modo que quanto maior a habilidade de leitura, maior a probabilidade de acerto no item (Silva, Brito, Cazorla & Vendramini, 2002).
Na área educacional é crescente o interesse pela aplicação de técnicas derivadas da TRI, já que esta metodologia vem sendo utilizada em processos qualitativos da avaliação psicológica e educacional, em instrumentos de medida como as escalas de habilidades, para avaliar e acompanhar o conhecimento adquirido e o desenvolvimento de habilidades básicas dos estudantes (Vendramini, 2002).
Dois são os pressupostos a serem verificados para que os modelos da TRI possam ser utilizados: o critério de unidimensionalidade (os itens devem medir uma única habilidade); e o critério da independência local (as respostas dos itens não devem ser influenciadas pelas respostas fornecidas a outros itens). Os modelos mais utilizados atualmente diferem pelo número de parâ-metros que utilizam para descrever cada item de uma prova ou teste: índice de discriminação do item (a), que indica quanto indivíduos de diferentes habilidades diferem em relação à probabilidade de acertar um item; índice de dificuldade do item (b), medido na mesma escala de habilidade (q), que corresponde à habilidade necessária para uma probabilidade de acerto calculada a partir da probabilidade de acerto ao acaso; e probabilidade de acerto ao acaso (c), que corresponde à probabilidade de indivíduos de baixa habilidade darem uma resposta correta a um item difícil. O modelo teórico mais completo é o de três parâmetros, que possui em sua função o índice de dificuldade, o índice de discriminação e a probabilidade de acerto ao acaso. Já o modelo de dois parâmetros possui em sua função o índice de dificuldade e o de discriminação como variáveis que influenciam a probabilidade do indivíduo de acertar o item. O modelo de um parâmetro possui em sua função apenas o índice de dificuldade.
Nesse sentido, o presente estudo objetivou analisar uma prova de estatística apresentada na forma de gráficos e de tabelas estatísticas pela Teoria de Resposta ao Item, e assim contribuir para o melhor entendimento de habilidades básicas necessárias para o ensino e a aprendizagem de estatística, principalmente em cursos de nível superior que a utilizam como uma ferramenta de análise de dados.
Método
Participantes
Foram sujeitos do presente estudo 413 alunos de graduação de duas universidades particulares, do interior do Estado de São Paulo e do Estado de Minas Gerais, predominantemente do curso de Psicologia (91,5%). A idade dos universitários variou de 16 a 53 anos, com média de 24,4 e desvio padrão de 7,4 anos, a maioria deles pertencente ao gênero feminino (80,0%) e ao período diurno (69,8%).
Instrumento e procedimento
A prova é composta de 15 questões de múltipla escolha sobre conceitos básicos de matemática e estatís-tica, apresentadas na forma de gráficos ou de tabelas estatísticas. As questões envolvem operações matemá-ticas básicas tais como: adição, subtração, multiplicação, divisão, razão, taxa e porcentagem, como nos exemplos a seguir.
As questões de número 1 a 3 referem-se à Figura 1 ou à Tabela 1.


Questão 1: Qual o terceiro personagem preferido divul-gado pela mídia em 2003?
a) Gollum b) Neo c) Nemo d) Bob Esponja e) Wolverine
Questão 2: Qual a porcentagem de pessoas que preferem o personagem Harry Potter?
a) 50,7% b) 25,3% c) 50% d) 51% e) nenhuma das anteriores
Questão 3: Qual a razão de votos entre o 6o e o 9o colocados?
a) 2 para 1 b) 1 para 2 c) 4 para 2 d) 2 para 4 e) ne-nhuma das anteriores
O instrumento foi aplicado coletivamente em sala de aula, para aqueles que aceitaram participar da pesquisa. O aplicador distribuiu aleatoriamente quanti-dades iguais de ambas as formas de apresentação das informações (tabelas ou gráficos estatísticos) após a explicitação dos objetivos da pesquisa e da assinatura do termo de consentimento livre e esclarecido. O tempo médio que os estudantes levaram para responder à prova foi de aproximadamente 40 minutos.
Análise de dados
Para a análise de dados foram consideradas as respostas dos participantes a uma das cinco alternativas de cada questão. Indicadas as respostas corretas, os dados foram transformados em itens do tipo certo/ errado (itens dicotômicos) e analisados com o auxílio de programas computacionais específicos: o programa SPSS TESTFACT, para a análise da dimensionalidade da prova (Wilson, Wood & Gibbons, 1998); o programa RASCAL para análise do ajuste do modelo de um parâmetro de Rasch (Assessment System Corporation, 1995a); e o XCALIBRE para o ajuste dos modelos de dois e três parâmetros pela estimação marginal de máxima verossimilhança (Assessment System Corporation, 1995b).
Resultados e discussão
O desempenho médio dos estudantes na prova não diferiu significativamente quanto à forma de apre-sentação (t [411]=-0,648; p=0,411), entre os gêneros (t [411]=0,894; p=0,372) e entre os turnos dos partici-pantes (t [411]=1,877; p=0,061). Assim, as médias não diferiram significativamente entre estudantes que respon-deram aos testes de gráficos estatísticos, que acertaram em média 9,4 das 15 questões da prova, e os que responderam aos testes de tabelas estatísticas, que acertaram em média 9,5 questões. Os estudantes do gênero masculino acerta-ram em média 9,7 questões e os do feminino, 9,4. Os estudantes do diurno acertaram em média 9,6 questões e os do noturno, 9,1. Esses resultados foram encon-trados também por Vendramini e colaboradores (2005) ao aplicarem a mesma prova de estatística, sob a forma de tabelas e gráficos, em 303 estudantes de 7a e 8a séries do ensino fundamental.
A interpretação da distribuição das respostas dos estudantes em cada questão da prova foi feita inicialmente a partir dos seguintes parâmetros descritivos de cada questão: (1) índice de facilidade - proporção de participantes que responderam ao item corretamente; (2) correlação ponto bisserial entre a resposta correta no item e a pontuação total na prova; e (3) a média do total de acertos dos participantes que acertaram um determinado item.
Os resultados revelaram que a prova apresenta questões fáceis (com índices de facilidade acima de 75% de acertos - questões 1, 2, 4, 6 e 13) e questões difíceis (com índices de facilidade inferiores a 25% de acertos - questões 5 e 15). As questões fáceis são aquelas que não exigem do participante cálculo matemático além da adição ou subtração, e que são obtidas diretamente ao ler os dados apresentados na forma de tabela ou de gráfico. As questões difíceis envolvem conceitos estatís-ticos como freqüência acumulada e média. As correlações ponto bisserial (item-total) revelaram uma tendência de escolha da opção errada pelos partici-pantes que obtiveram os escores mais altos no teste como um todo nas questões 2, 5, 9 e 13.
Observou-se que a prova de estatística aplicada neste estudo apresenta parâmetros descritivos semelhantes aos encontrados para uma prova de raciocínio estatístico, aplicada por Vendramini, Silva e Canale (2004) em 325 universitários de várias áreas de conhecimento. As questões da presente pesquisa foram construídas com o objetivo de melhorar a prova aplicada anteriormente. No estudo das autoras os índices de facilidade variaram de 0,15 a 0,79, enquanto nesta pesquisa variaram de 0,22 a 0,95, e as correlações item-total variaram no primeiro estudo de 0,10 a 0,63 e neste de 0,16 a 0,63. Quanto à facilidade dos itens, a presente pesquisa é mais abrangente, e quanto às correlações, praticamente iguais.
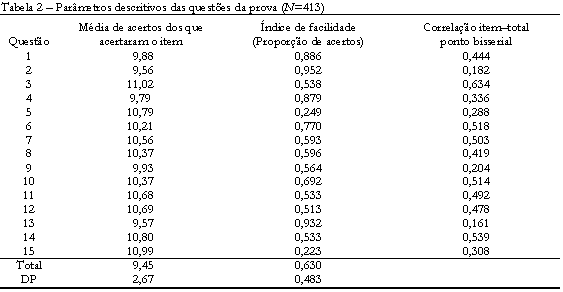
As estatísticas apresentadas na Tabela 2 atendem razoavelmente aos requisitos necessários, pelos instrumentos de medida. A média de acertos na prova (9,45) é superior ao ponto médio da escala (7,5), com desvio padrão igual a 2,67, tendo variado de 9,56 a 11,02 a média de acertos na prova para os participantes que acertaram um determinado item. Os itens foram considerados de dificuldade mediana e consistência interna razoável pela técnica de Kuder-Richardson, que permite verificar a fidedignidade do teste (KR20 = 0,651).
Umas das suposições para se utilizarem modelos unidimensionais da TRI é que a prova possa assumir um fator predominante, isto é, que seja unidimensional. A análise efetuada a partir das respostas dos participantes, em vez da matriz de correlação de dados dicotômicos, é denominada Análise Fatorial com Informação Completa (Full Information Factor Analysis). Esta análise feita pelo programa computacional TESTFACT inclui progressiva-mente fatores que explicam as correlações entre os itens. Quando os itens são completamente independentes, ou quando medem um único fator ou mais de um fator, diferentes padrões de resposta podem ser esperados. A adequação de um modelo unidimensional ou multidi-mensional aos padrões de respostas dos participantes é verificada no programa TESTFACT pelo teste Qui-quadrado, que indica se a inclusão sucessiva de fatores nos modelos tem um efeito significativo.
A análise fatorial com informação completa efetuada para as prova de estatística indicou uma baixa correlação média tetracórica (rtet = 0,19) entre os 105 pares de combinações, dois a dois, das questões. Ao considerar o modelo unidimensional, podem ser explicados 22,2% da variância entre as questões. Incluindo-se um segundo fator, modelo bidimensional, a variância explicada aumenta para 28,3%. A magnitude da diferença entre os padrões de resposta observados e os reproduzidos pelo modelo é estatisticamente significativa quando se acrescenta esse segundo fator (x2 [4]=33,29; p<0,0001), indicando que ele representa uma parte significativa das correlações não explicadas pelo primeiro fator. Ao se considerar um modelo tridimensional, a variância explicada entre as questões aumenta para 36,32%. A magnitude da diferença entre os padrões de resposta observados e os reproduzidos pelos modelos, quando se acrescenta um terceiro fator, não é significativa (x2 [13]=36,36; p=0,002), podendo-se supor que ele não seja necessário. Na Tabela 3 estão apresentadas as cargas fatoriais das questões nos dois fatores considerados para a análise fatorial com informação completa e rotação promax, que estão correlacionados entre si (r =0,352).
Dado que os itens 9 e 13 apresentam carga fatorial baixa (menor que 0,30) nos dois fatores, a análise fatorial com informação completa efetuada para as 13 questões que permaneceram na prova indicou um aumento da correlação média tetracórica (rtet=0,24) entre os 78 pares de combinações, e também da variância explicada para o modelo unidimensional (25,4%), bidi-mensional (32,4%) e tridimensional (38,7%). A magnitude da diferença entre os padrões de resposta observados e os reproduzidos pelo modelo é estatisticamente significativa quando se acrescenta o segundo fator (x2 [12]=34,65; p=0,0005), mas não significativa quando se acrescenta o terceiro fator (x2 [11]=21,00; p=0,033), podendo-se supor que ele não seja necessário. Considerando essas estatísticas e o fato de que os fatores do modelo bidimensional estão correlacionados entre si (r=0,426), será assumido o modelo como predominantemente unidimensional. As cargas fatoriais das questões neste fator estão apresentadas na Tabela 3.

Desta forma, os resultados da análise fatorial com informação completa, efetuada para os dados em questão, indicaram que os itens 2, 5, e 15 apresentaram cargas fatoriais inferiores a 0,30. Por esse motivo esses itens foram excluídos, o que implicou um modelo unidi-mensional com um número menor de itens, maior variância explicada e maior consistência interna dos itens (KR20=0,681). Buscou-se um modelo que melhor se ajustasse aos dados e que apresentasse propriedades (índice de dificuldade, de discriminação e correlação bisserial) dentro de padrões aceitáveis, garantindo parâme-tros invariantes para as questões e para o desempenho na prova como um todo, pois só com um modelo bem ajustado isso é possível, segundo Hambleton, Swaminathan e Rogers (1991).
Na TRI a probabilidade de resposta correta aos itens de um instrumento, ou questões de uma prova, depende da habilidade do sujeito j (qj), cujo valor pode variar de -¥ a + ¥, e dos parâmetros dos itens, valores estimados que melhor explicam as respostas dos sujeitos aos itens. São três os parâmetros dos itens: índice de discriminação (ai), que indica o quanto indivíduos de diferentes habilidades diferem em relação à probabili-dade de acertar um item i (se ai for menor que 0,30, o item é problemático); índice de dificuldade (bi), que se refere à habilidade necessária para uma dada proba-bilidade de acertar o item, calculada a partir da probabi-lidade de acertá-lo por acaso (se bi igual a -3, o item é extremamente fácil; zero, de dificuldade média; e 3, extre-mamente difícil); e probabilidade de acerto ao acaso (ci), ou seja, a probabilidade de um sujeito de baixa habilidade dar uma resposta correta a um item difícil.
Os modelos matemáticos podem ser apresen-tados sob três expressões, dependendo de o modelo ser de um parâmetro (só inclui o índice de dificuldade), de dois parâmetros (inclui os índices de discriminação e de dificuldade) ou de três parâmetros. Esses modelos representam para cada item i a função de probabilidade de um indivíduo j com habilidade qj acertar esse item. O modelo teórico mais completo está apresentado a seguir (Vendramini e cols., 2004). A representação gráfica desse modelo, denominada Curva Característica do Item (CCI), é apresentada posteriormente para os itens da prova de estatística analisada nesta pesquisa.

(1) com i = 1, 2, ... , n e j = 1, 2, ... , m, sendo:
n o número de itens;
m o número de indivíduos;
Xij uma variável dicotômica que assume os valores 1 ou 0, conforme o indivíduo j responda correta ou incorretamente ao item i, respectivamente;
qj o valor que representa a variável latente (aptidão ou habilidade) que permite explicar a resposta do j-ésimo indivíduo aos itens;
P(Xij = 1 | qj) = Pi(q) a probabilidade de um indivíduo j com habilidade qj responder corretamente ao item i;
ci a probabilidade de acerto ao acaso;
bi o índice de dificuldade (ou parâmetro de posição) do item i, medido na mesma escala da habilidade q. Corresponde à habilidade necessária para uma probabilidade de acerto igual a (1 + ci) / 2;
ai o índice de discriminação (ou parâmetro de inclinação) do item i, com valor proporcional à inclinação da CCI no ponto bi;
D um fator de escala constante, igual a 1 ou a 1,7 (quando se deseja que a função logística se aproxime da ogiva normal);
e um número transcendental, base dos logaritmos neperianos, cujo valor é aproximadamente 2,718.
Os seguintes problemas podem ocorrer com os parâmetros dos itens: (1) valor do índice de discri-minação a abaixo do valor crítico 0,30; (2) índice de dificuldade b acima do valor crítico 2,95 ou abaixo de -2,95; (3) probabilidade de acerto casual acima do valor crítico 0,40; (4) erro de chaveamento, isto é, correlação entre uma das opções de resposta incorreta e o escore total mais alta que a correlação entre a resposta correta e o escore total; e (5) resíduos padronizados do ajuste do modelo que excedem o valor crítico 2,0.
Após a constatação de que o modelo logístico de um parâmetro implicava a eliminação de mais três questões da prova, por não atenderem às condições exigidas, decidiu-se analisar os modelos de dois e três parâmetros para não comprometer a representatividade do domínio avaliado. As dez questões se ajustam aos modelos de dois e três parâmetros, não tendo ocorrido nenhum dos problemas citados.
Embora não se tenha observado discrepância significativa dos modelos ajustados (Resíduos>2,0), aquele que apresentou menor resíduo foi o modelo de três parâmetros (Tabela 4). A representação gráfica das curvas características das questões está apresentada na Figura 1, onde se destacam os valores extremos dos índices de discriminação e dificuldade. A questão 4 foi a mais fácil da prova e a questão 12 a mais difícil. A questão 8 a de menor discriminação e maior probabilidade de acerto ao acaso, enquanto a questão 3 a de maior discri-minação e menor probabilidade de acerto ao acaso. Como na pesquisa de Vendramini, Silva e Canale (2004), os itens mais fáceis correspondem a questões obtidas diretamente das informações apresentadas nas tabelas ou nos gráficos, sem envolver qualquer operação matemática comple-mentar e as questões mais difíceis envolvem comparações e cálculo de freqüência acumulada, porcentagem ou média.

Com relação à probabilidade de acerto ao acaso (c), o teste apresenta um valor médio igual a 0,24, um pouco acima do esperado, uma vez que os itens do teste são questões com cinco alternativas cada, podendo-se afirmar matematicamente que a probabilidade de um estudante de baixa habilidade acertar o item é aproximadamente igual a 0,20. Resultados próximos a este foram observados em outras pesquisas de desempenho em estatística que estudaram questões de múltipla escolha com cinco alternativas de resposta (Vendramini, 2002; Vendramini, Silva & Canale, 2004; Chenta, Vendramini & Dias, 2005).

Considerações finais
De acordo com os resultados obtidos, conclui-se que a prova se ajustou ao modelo de três parâmetros para as dez questões que permaneceram na prova, apresentando índice médio de discriminação igual a 0,79, índice médio de dificuldade igual a -0,29, e probabilidade média de acerto ao acaso de 0,24. A prova apresenta também um índice de fidedignidade razoável (KR-20=0,68).
Os resultados mostram as dificuldades apresen-tadas pelos estudantes, na sua maioria de psicologia, com relação aos conceitos matemáticos, dificuldades essas já apresentadas desde o ensino fundamental, como indica a pesquisa de Vendramini e colaboradores (2005), havendo assim, uma necessidade de retomada desses conceitos antes de se desenvolver a habilidade de leitura e compreensão de dados estatísticos.
Para estudantes da área de humanas, e em parti-cular de psicologia, é freqüente a observação de dificul-dades associadas à leitura de dados apresentados em tabelas e gráficos estatísticos, ao cálculo e à interpretação de fre-qüências relativas, razão, proporção, porcentagem, taxa e a conceitos estatísticos tais como média, desvio padrão e coeficientes de correlação. Embora esse conhecimento seja necessário e importante para a interpretação de dados apresentados em pesquisas científicas, os conceitos estatísticos e a superação das dificuldades matemáticas nem sempre são trabalhados no ensino superior.
Alem disso, várias pesquisas têm apontado que os alunos da área de humanas apresentaram atitudes mais negativas em relação à estatística que os alunos de outras áreas. Em pesquisa realizada por Silva, Brito, Cazorla e Vendramini (2002) os cursos de psicologia e comunicação foram os principais responsáveis pelas atitudes mais negativas dos estudantes em relação à estatística.
Na psicologia, vários conceitos estatísticos são necessários para a construção, validação e normatização de testes psicológicos, assim como para a realização de pesquisas científicas que utilizam métodos quantitativos de análise de dados. Sem o domínio de alguns conceitos de estatística muitos resultados de pesquisa podem ficar sem significado, o que dificulta a análise e interpretação de resultados.
Muitas das informações contidas nos manuais de testes psicológicos estão apresentadas na forma de tabelas e gráficos estatísticos e envolvem proporção, porcentagem, percentil, média, desvio padrão, entre outros conceitos matemáticos e estatísticos. Sugere-se, então, que sejam incluídos esses conceitos no nível superior de ensino, para possibilitar que os universitários realizem com-parações entre dados apresentados em tabelas e gráficos estatísticos e que novos estudos incluam a análise de propriedades psicométricas de instrumentos a serem utilizados na avaliação de desempenho em tópicos de estatística.
Referências
Anastasi, A. & Urbina, S. (2000). Testagem psicológica. Porto Alegre: Artmed. [ Links ]
Andrade, D. F. (2001). Comparando desempenhos de grupos de alunos por intermédio da Teoria de Respos-ta ao Item. Estudos em Avaliação Educacional, 23, 31-69. [ Links ]
Andrade, D. F. & Valle, R. C. (1998). Introdução à Teoria de Resposta ao Item: conceitos e aplicações. Estudos em Avaliação Educacional, 18, 13-32. [ Links ]
Andrade, D. F., Tavares, H. R. & Valle, R. C. (2000). Teoria de Resposta ao Item: conceitos e aplicações. São Paulo: ABE. [ Links ]
Assessment System Corporation (1995a). User's manual for the RASCAL-Rasch Analysis Program. 2nd ed. Windows version 3.50e, St. Paul, MN: Author. [ Links ]
Assessment System Corporation (1995b). User's manual for the XCALIBRE-Marginal Maximum-Likelihood IRT Parameter Estimation Program. 2nd ed. Windows 3.x/95/NT version, St. Paul, MN: Author. [ Links ]
Cazorla, I. M. (2002). A relação entre a habilidade vixo-pistórica e o domínio de conceitos estatísticos na leitura de gráficos (Tese de Doutorado). Campinas: Universidade Estadual de Campinas. [ Links ]
Chenta, V. C., Vendramini, C. M. M. & Dias, A. S. (2005). A Teoria de Resposta ao Item na análise de um teste de estatística em alunos do ensino fundamental. Trabalho apresentado no XI Encontro de Iniciação Científica. Itatiba, SP. [ Links ]
Crespo, A. A. (1997). Estatística fácil. São Paulo: Saraiva. [ Links ]
Feijoo, A. M. L. C. (1996). A pesquisa e a estatística na psicologia e na educação. Rio de Janeiro: Bertrand Brasil. [ Links ]
Gal, I. & Garfield, J. (1997). Curricular goals and assessment challenges in Statistics Education. Em I. Gal & J. B. Garfield (Eds.). The assessment challenge in statistics education. International Statistical Institute, Amsterdan: IOS Press. [ Links ]
Garfield, J. (1995). How students learn Statistics. Interna-tional Statistical Review, 63(1), 77-81. [ Links ]
Hambleton, R. K., Swaminathan, H. & Rogers, H. J. (1991). Fundamentals of Item Response Theory. Newbury Park: Sage Publishers. [ Links ]
Leinhardt, G., Zaslavsky, O. & Stein, M. K. (1990). Functions, graphs, and graphing: Task, learning and teaching. Review of Education Research, 60(1), 1-64. [ Links ]
Moore, D. S. (1997). New pedagogy and new content: The case of statistics. International Statistical Review, 65(2), 123-165. [ Links ]
Silva, C. B., Brito, M. R. F., Cazorla, I. M. & Vendramini, C. M. M. (2002). Atitudes em relação à estatística e à matemática. Psico-USF, 7(2), 219-228. [ Links ]
Smole, K. S. & Diniz, M. I. (2001). Ler e aprender matemática. Em K. C. S. Smole & M. I. Diniz. Ler, escrever e resolver problemas: habilidades básicas para aprender matemática (pp. 69-86). São Paulo: Artmed. [ Links ]
Valle, R. C. (2000). Teoria de Resposta ao Item. Estudos em Avaliação Educacional, 21, 7-91. [ Links ]
Vendramini, C. M. M. (2002). Aplicação da Teoria de Resposta ao Item na avaliação educacional. Em R. Primi (Org.). Temas em avaliação psicológica (pp. 116-127). Campinas: Instituto Brasileiro de Avaliação Psicológica. [ Links ]
Vendramini, C. M. M. & Brito, M. R. F. (2001). Relações entre atitude, conceito e utilidade da estatística. Psicologia Escolar Educacional, 5(1), 59-73. [ Links ]
Vendramini, C. M. M., Silva, M. C. & Canalle, M. (2004). Análise de itens de uma prova de raciocínio estatístico. Psicologia em Estudo, 9(3), 331-342. [ Links ]
Vendramini, C. M. M., Chenta, V. C., Dias, A. S., Gattis, S. & Silva, L. S. (2005). Habilidades acadêmicas no ensino fundamental: um estudo com gráficos e tabelas estatísticas. Em Resumos dos trabalhos do I Congresso Latino-Americano da Psicologia. São Paulo: [ Links ] União Latino Americana de Entidades de Psicologia - ULAPSI.
Wilson, D. T., Wood, R., & Gibbons, R. (1998). TESTFACT 2 - test scoring, item statistics, and item factor. Chicago: Scientific Software International. [ Links ]
Woehlke, P. L. & Leitner, D. W. (1980). Gender differences in performance on variables related to achievement in graduate-level educational statistics. Psychological Reports, 47, 1119-1125. [ Links ]
 Endereço para correspondência
Endereço para correspondência
Claudette Maria Medeiros Vendramini
Rua Herculano Pupo Nogueira, 309 - Vila Belém
13256-300 Itatiba-SP
E-mail: cvendramini@uol.com.br
Anelise Silva Dias
E-mail: anelisesd@gmail.com
Recebido em outubro de 2004
Reformulado em novembro de 2005
Aprovado em novembro de 2005
Sobre as autoras:
1 Claudette Maria Medeiros Vendramini é graduada e mestre em Estatística pelo Instituto de Matemática, Estatística e Ciências da Computação da Universidade Estadual de Campinas - UNICAMP, doutora em Educação pela Faculdade de Educação dessa mesma universidade e docente da graduação e do Programa de Pós-Graduação Stricto Sensu em Psicologia da Universidade São Francisco - USF.
2 Anelise Silva Dias é aluna do curso de Psicologia da Universidade São Francisco - USF e bolsista de Iniciação Científica do Programa de Bolsas Auxílio de Iniciação Científica - PROBAIC/USF.
Agradecimentos
Agradecemos ao apoio financeiro da Univer-sidade São Francisco e do CNPq.













