ARTIGO ORIGINAL

 

O que a inteligência prediz: diferenças individuais ou diferenças no desenvolvimento acadêmico?

 

What does the Intelligence Predicts: Individual Differences or Academic Development Differences?

 

¿Lo que la Inteligencia Predice: las Diferencias Individuales o las Diferencias en el Desarrollo Académico?

 

 

Cristiano Mauro Assis Gomes; Hudson Fernandes Golino

Universidade Federal de Minas Gerais, Belo Horizonte – MG – Brasil

Endereço para correspondência

 

 

---

RESUMO

A psicometria tem enfatizado o papel da inteligência na explicação das diferenças individuais do rendimento escolar (DI). Este artigo questiona esse foco e investiga o papel preditivo da inteligência fluida (Gf) sobre as diferenças de desenvolvimento do rendimento escolar (DD). São analisados dados de 684 estudantes do sexto ano do ensino fundamental ao terceiro ano do ensino médio de uma escola particular de Belo Horizonte. As DI foram medidas via equalização das notas anuais em matemática, português, geografia e história. As DD foram mensuradas pelo vertical scaling, em matemática e português (no ensino fundamental) e matemática (no ensino médio). A Gf foi medida pelo conjunto de testes de inteligência fluida (Ctif). Um modelo via modelagem por equação estrutural foi gerado, no qual a Gf explica as DI e DD. O modelo apresentou adequado grau de ajuste aos dados. Os resultados indicam que a Gf explica diretamente apenas as diferenças de desenvolvimento. Implicações são discutidas para o campo psicométrico.

Palavras-chave: diferenças individuais; rendimento escolar; inteligência; avaliação educacional; desenvolvimento.

---

ABSTRACT

The psychometrics has emphasized the role of intelligence in explaining individual differences (ID) in academic performance. The current paper questions this focus and investigates the predictive role of fluid intelligence (Gf) on developmental differences (DD) of school performance (DD). Data from 684 students from 6th to 12nd grades of a Belo Horizonte private school were analyzed. The IDs were measured through the equalization of annual Math, Portuguese, Geography and History grades. The DD were measured through the vertical scaling of Math and Portuguese grades of the elementary school students, and Math grades of the high school students. Gf was measured through the Ctif. A model via structural equation modeling was created, with Gf explaining the IDs and DDs. The model showed adequate data fit. The results indicate that Gf directly explains only the differences in development. Implications for the psychometric field will be discussed.

Keywords: individual differences; academic achievement; intelligence; academic assessment; development.

---

RESUMEN

La psicometría ha centrado en el papel de la inteligencia para explicar las diferencias individuales (DI) en el rendimiento académico. Este artículo cuestiona este enfoque y se investiga el papel predictivo de la inteligencia fluida (Gf) en las diferencias de desarrollo (DD) del rendimiento escolar (DD). Se analizaron datos de 684 estudiantes de sexto grado de primaria hasta el tercer año secundario de una escuela privada en Belo Horizonte. Los DI se midieron a través de la igualación anual de notas en matemáticas, portugués, geografía e historia. El DD se mide por el procedimiento de vertical scaling de matemáticas y portugués de los años primarios, y matemáticas de los años de secundaria. Gf se midió por el Ctif. Se ha generado un modelo a través de modelos de ecuaciones estructurales con Gf a explicar los DIs y los DDs. El modelo mostró un grado adecuado de ajuste a los datos. Los resultados indican que Gf directamente sólo explica las diferencias de desarrollo. Se discuten las implicaciones para el campo psicométrico.

Palabras clave: diferencias individuales; rendimiento escolar; inteligencia; evaluación educativa; desarrollo.

---

 

 

Introdução

Até meados da década de 1990, a psicometria tinha diferentes modelos sobre a inteligência que se contradiziam, seja pela quantidade argumentada de níveis de habilidades cognitivas, seja pelo reconhecimento da presença do fator geral. Concomitante, a década de 1990 foi um marco para unificar o campo. Nesse período, Carroll (1993) publicou uma metanálise de 461 artigos que contemplava todos os trabalhos importantes da psicometria sobre inteligência, desde o início do século XX até meados dos anos de 1980. Métodos robustos de análises fatoriais exploratórias trouxeram consistência a seus resultados, que foram considerados pelo campo como evidências fortes a respeito da arquitetura da inteligência humana. Seu modelo sustenta que a inteligência é formada por um conjunto vasto de habilidades cognitivas. Há habilidades bastante específicas que atuam no processamento cognitivo de comportamentos mais localizados e contextualizados, habilidades que atuam em processamentos cognitivos mais genéricos, apesar de delimitados em termos de conteúdo psicológico, e uma habilidade cognitiva geral. Foram identificadas empiricamente dezenas de habilidades bastante específicas que compuseram o nível um ou estrato um do modelo de Carroll (1993), assim como oito habilidades mais genéricas que perfizeram o nível ou estrato dois, e um fator geral de inteligência, localizado no terceiro nível do seu modelo.

Apresentada como um campo unificado no que diz respeito à inteligência, a psicometria tem se destacado como uma área importante para a investigação do papel preditivo das variáveis psicológicas ante o desempenho escolar. Um largo conjunto de evidências sustenta que as habilidades cognitivas de segundo e terceiro níveis do modelo de Carroll (1993), principalmente o fator geral, explicam em torno de 30% a 60% do desempenho escolar (Colom; Flores-Mendoza, 2007; Deary et al., 2007; Gustafsson; Undheim, 1996; LEMOS et al., 2008; Neisser et al., 1996; Naglieri; Bornstein, 2003; Spinath et al., 2006; WatkinS; LEI; CANIVEZ, 2007). Em função dessas evidências, a inteligência concebida pelo campo psicométrico é vista como um preditor-chave do rendimento escolar, o que leva uma corrente de pesquisadores a considerar até mesmo desnecessária a presença de outras variáveis psicológicas correlatas, na medida em que a inteligência tenderia a incorporar toda a variância das mesmas evidências (Gagné; St. Pére, 2002; Gottfredson, 2002a, 2002b; KUNCEL; HEZLETT; ONES, 2004).

Em síntese, a psicometria tem um papel central e um mérito relevante em apresentar muitas evidências a respeito do valor preditivo da inteligência ante o desempenho dos estudantes. No entanto, a área psicométrica tem priorizado estudos que investigam o papel da inteligência na predição das diferenças individuais do rendimento escolar, gerando uma lacuna de pesquisas sobre o papel da inteligência no desenvolvimento escolar dos alunos. Afinal, a inteligência pode ter um papel importante na predição tanto das diferenças individuais de rendimento escolar quanto nas diferenças de desenvolvimento do rendimento escolar ao longo de vários anos. Para que se possa verificar o papel preditivo da inteligência sobre esses dois aspectos do rendimento escolar, é preciso que ambos sejam analisados conjuntamente. Este artigo tem como objetivo realizar tal análise. Para isso, pretende-se investigar se a inteligência fluida (Gf) – principal representante do fator geral de inteligência, segundo o modelo de Carroll (1993) – tem um papel preditivo em ambas as condições, diferenças individuais e diferenças desenvolvimentais do rendimento acadêmico discente, ou se tem um papel preditivo em apenas um desses aspectos. A questão a ser investigada visa contribuir para a ampliação da investigação a respeito do papel da inteligência concebida pela psicometria sobre o rendimento escolar, ao analisar conjuntamente dois dados distintos: diferenças individuais do rendimento escolar e diferenças no desenvolvimento do rendimento escolar. Até o presente, os estudos sobre a inteligência, de base psicométrica, têm se concentrado exclusivamente no primeiro aspecto.

As seguintes hipóteses delineiam a questão de investigação:

• A Gf apresenta efeitos diretos de relação causal nas diferenças de desenvolvimento acadêmico discente.

• A Gf apresenta efeitos indiretos de relação causal nas diferenças individuais de rendimento acadêmico discente. Ou seja, a relação causal entre Gf e diferenças individuais é mediada pelas diferenças de desenvolvimento.

Apesar de o foco dos estudos que incorporam a inteligência de base psicométrica ser a predição das diferenças individuais do rendimento escolar, é possível realizar a investigação conjunta das diferenças individuais e das diferenças de desenvolvimento do rendimento escolar discente. Estudos longitudinais ou transversais que utilizam testes educacionais padronizados que mensuram habilidades acadêmicas relacionadas a vários anos escolares são capazes de gerar dados e análises sobre o desenvolvimento do rendimento acadêmico de estudantes. Rindermann (2007) expõe uma lista de testes educacionais padronizados que compõem um projeto internacional audacioso de medida do desenvolvimento acadêmico. Esses testes são aplicados em muitos países, como o Programe for International Student Assessment (Pisa) (ORGANISATION FOR ECONOMIC CO-OPERATION AND DEVELOPMENT, 2007), o Progress in International Reading Literacy Study (Pirls) (MULLIS et al., 2007) e o Trends in International Mathematics and Science Study (Timss) (ARORA et al., 2009; MARTI N et al., 1997; MULLIS et al., 1997, 2009; OLSON; MARTI N; MULLIS, 2008). Esses instrumentos permitem a geração de dados a respeito de como os estudantes de anos escolares distintos progridem nos conteúdos escolares, para fornecer informações relevantes não apenas sobre as diferenças individuais entre alunos de um mesmo ano escolar, mas também sobre a diferença de desenvolvimento entre estudantes de anos diferentes.

Além dos testes educacionais padronizados, as notas escolares também têm se tornado um meio possível na geração de dados sobre o desenvolvimento acadêmico discente, por meio de tratamentos metodológicos específicos, como o vertical scaling. O presente estudo utiliza a estratégia do vertical scaling para gerar dados de desenvolvimento do rendimento escolar discente, com base em notas escolares comuns, de modo que verifique as hipóteses elencadas para investigação.

 

Método

Participantes

Fazem parte deste estudo os dados de 684 alunos do sexto ano do ensino fundamental ao terceiro ano do ensino médio de uma instituição particular de Belo Horizonte, Minas Gerais, obtidos em 2008. Os participantes são predominantemente do sexo feminino (52,00%), com idades entre 10 e 18 anos (m = 13,71 e dp = 2,11). A quantidade de participantes por ano escolar é equilibrada, variando entre 13,00% (terceiro ano do ensino médio) e 16,90% (nono ano do ensino fundamental).

Instrumentos

Utilizaram-se os seguintes instrumentos:

• Conjunto de testes de inteligência fluida (Ctif): foram utilizados 27 itens do Ctif, pertencente à bateria de fatores cognitivos de alta-ordem (BaFaCalo). Destes, usaram-se 8 itens do teste de indução, 11 itens do teste de raciocínio lógico e 8 itens do teste de raciocínio geral. O Ctif apresenta evidências de adequada confiabilidade (alfa maior que 0,70) e validade convergente e divergente (GOMES; BORGES, 2009; PARREIRAS; GOMES, 2009). A seguir, descrevem-se esses testes:

a) T este de indução (I): foram selecionados 8 itens com um tempo-limite de 8 minutos. Cada item é formado por cinco grupos de quatro letras. Cada grupo possui quatro letras que mostram o mesmo padrão. O respondente deve identificar o grupo que não apresenta o padrão e marcá-lo com um X.

b) T este de raciocínio lógico (RL): selecionaram-se 11 itens com um tempo restrito de 11 minutos. Cada item é formado por uma conclusão proveniente de duas premissas abstratas. O respondente deve indicar se a conclusão é logicamente corretamente.

c) T este de raciocínio geral (RG): foram selecionados 8 itens com um tempo-limite de 12 minutos. Cada item é formado por uma situação-problema matemática e cinco opções de múltipla escolha.

Uma medida de Gf foi obtida por meio de todos os itens selecionados. A consistência interna dos itens é adequada, com um alfa de 0,75. A análise fatorial confirmatória (AFC) mostra que o modelo unidimensional é adequado para explicar a variância dos itens (χ² = 233,56; df = 134; CFI = 0,90; RMSEA = 0,03). Com exceção dos itens RL1 (0,34), RL4 (0,27), RL5 (0,39), RL9 (-0,05), RL10 (0,23), RL 11 (0,39), RG 1 (0,29), RG7 (0,35), todos os outros tiveram carga factorial maior do que 0,40 no traço latente Gf. As análises foram elaboradas por meio do software Mplus 5.2, apropriado para análises fatoriais de dados dicotômicos. O escore fatorial gerado foi utilizado para a análise de dados das variáveis da questão de estudo.

Coleta de dados

A aplicação do instrumento foi realizada no início de 2008, em 19 turmas de uma escola particular de Belo Horizonte, sendo 13 do ensino fundamental e 6 do ensino médio. A aplicação dos testes foi realizada de forma coletiva, e sempre por psicólogos ou estudantes de psicologia devidamente treinados. Foram tomados todos os cuidados éticos em relação aos participantes, e a pesquisa contou com a aprovação de Comitê de Ética da Universidade Federal de Minas Gerais, n. 456/07.

Tratamento das notas escolares e análise de dados

Para a análise das diferenças individuais da proficiência escolar discente, selecionaram-se as notas anuais em matemática, português, geografia e história. A escolha de notas anuais nessas disciplinas se deveu ao fato de que elas aparecem em todas as séries estudadas, diferentemente de ciências, física, química, biologia, religião, inglês, entre outras.

Com o propósito de verificar as diferenças individuais, as notas foram equalizadas, tendo como referência a escala de uma turma do sexto ano do ensino fundamental. As notas de todas as outras turmas e anos escolares foram transformadas em função da turma de referência. O método de equalização adotado foi o circle-arc method (LIVINGSTON; KIM, 2009), um procedimento eficaz para amostras pequenas, com menos de 50 estudantes por turma, como é o caso da amostra utilizada neste estudo, em que as turmas não ultrapassam esse tamanho. Posteriormente à equalização, as notas foram transformadas em escores Z (média 0 e desvio padrão 1) dentro de cada ano escolar. Para analisar as diferenças de desenvolvimento da proficiência acadêmica discente, as notas de português e matemática do ensino fundamental II (do sexto ao nono ano) e matemática do ensino médio foram tratadas. A escola onde foi feita a coleta de dados tem dois testes educacionais que avaliam desenvolvimento escolar ao longo dos anos escolares. O primeiro teste avalia o conteúdo de matemática e português, entre outras disciplinas, de todo o ensino fundamental II. O segundo avalia o conteúdo de matemática, entre outras áreas, de todo o ensino médio. Os testes educacionais foram aplicados pela escola em boa parte dos alunos de uma das duas unidades da escola (N = 1.156, ensino fundamental II; N = 732, ensino médio). Apesar das diferenças entre as duas unidades escolares, ambas são frequentadas predominantemente por crianças e adolescentes cuja renda varia de média a média alta, e as duas têm um padrão comum de diretrizes e política pedagógica. Nesse sentido, foi creditado que o resultado obtido nos testes educacionais é representativo de todo o conjunto de estudantes das duas unidades.

Pela aplicação dos dois testes educacionais, obtiveram-se as médias e os desvios padrão dos estudantes nas respectivas séries. Por meio desses indicadores, foi possível transformar as notas escolares, de acordo com o procedimento do scaling design (TONG; KOLEN, 2007). As notas anuais de cada aluno foram multiplicadas pelo desvio padrão e somadas à média do seu ano escolar, relativo ao teste educacional. Exemplo: se a nota anual em matemática de um aluno do sexto ano era de 80 pontos, e a média e o desvio padrão referentes ao sexto ano no teste educacional do ensino fundamental II eram de 100 e 15 pontos, respectivamente, então a nota era multiplicada pelo desvio padrão do seu ano escolar (80 x 15 = 1.200) no teste educacional, e o produto era somado à média do seu ano escolar (1.200 + 100 = 1.300) no teste educacional. Desse modo, obtiveram-se os escores de desenvolvimento acadêmico discente, por meio da transformação da nota escolar.

Uma AFC mostra que o modelo bidimensional das diferenças individuais e do desenvolvimento acadêmico é adequado para explicar a variância das notas escolares equalizadas e dos escores de desenvolvimento (χ² = 12,15; df = 6; CFI = 1,00; RMSEA = 0,05). Esse modelo é apresentado na Figura 1.

 

 

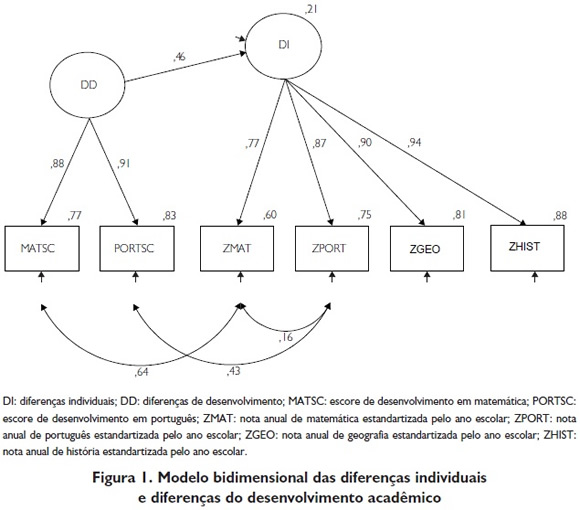
Modelamento por equação estrutural

Para averiguar as hipóteses do estudo, empregou-se o modelamento por equação estrutural (MEE). Desenharam-se dois modelos: um para o ensino fundamental II e outro para o ensino médio. A diferença entre eles refere-se à presença do escore de desenvolvimento acadêmico em português no ensino fundamental II e sua ausência no ensino médio. O modelo 1 (ensino fundamental II) postula que os escores de desenvolvimento acadêmico em matemática e português são explicados pelo traço latente diferenças de desenvolvimento acadêmico (DD). Os escores sobre diferenças individuais em matemática, português, geografia e história são explicados pelo traço latente diferenças individuais do rendimento acadêmico (DI). O escore fatorial em Gf é usado nesse modelo como variável observável exógena que explica ambas as variáveis latentes: DD e DI. Os erros das variáveis observáveis e os erros dos traços latentes compõem o restante das variáveis latentes. O modelo 2 (ensino médio) é idêntico ao modelo 1, exceto pelo fato de que ele tem apenas um escore de desenvolvimento acadêmico e não há uma variável latente de desenvolvimento acadêmico (DD). Em ambos os modelos, a Gf pôde explicar diretamente as diferenças individuais em matemática. As relações não significativas foram eliminadas progressivamente dos modelos, se assim fossem constatadas.

Para verificar a adequação do modelo aos dados, utilizaram-se o índice comparativo de ajuste (comparative fit index – CFI) (BENTLER, 1990) e a estatística raiz quadrática média residual padronizada (root mean square error of approximation – RMSEA). Valores com CFI ≥ 0,90 e RMSEA ≤ 0,08 indicam modelos com bom ajuste aos dados (BYRNE, 2001).

 

Resultados

Os resultados serão apresentados em termos dos modelos 1 e 2. Em todos os modelos, foi realizado um bootstrap de mil casos, visando identificar o intervalo de confiança (90%) das cargas fatoriais e da variância explicada. As relações do modelo 1 são mostradas na Figura 2, assim como as cargas fatoriais, correlações e variâncias explicadas. As regressões entre as variáveis com valores estatisticamente não significativos foram eliminadas.

O modelo 1 tem adequado grau de ajuste aos dados (χ² = 17,13; df = 10; CFI = 1,00; RMSEA = 0,04). O traço latente diferenças individuais do desempenho acadêmico (DI) explica fortemente as notas escolares equalizadas em matemática (ZMAT), português (ZPORT ), geografia (ZGEO) e história (ZHIST). Matemática é explicada por DI em 55,20% de sua variância (49,56% – 61,00%), que prediz 75,00% (70,73% – 79,03%) da variância em português, 81,54% (77,79% – 84,64%) da variância em geografia e 88,17% (84,82% – 91,20%) da variância em história. O traço latente diferenças de desenvolvimento acadêmico (DD) explica fortemente os escores de desenvolvimento. As diferenças de desenvolvimento em matemática (MATSC) são explicadas por DD em 78,32% de sua variância (75,17% – 81,36%). As diferenças de desenvolvimento em português (PORT SC) são explicadas por DD em 83,36% (80,28% – 85,75%) de sua variância.

 

 

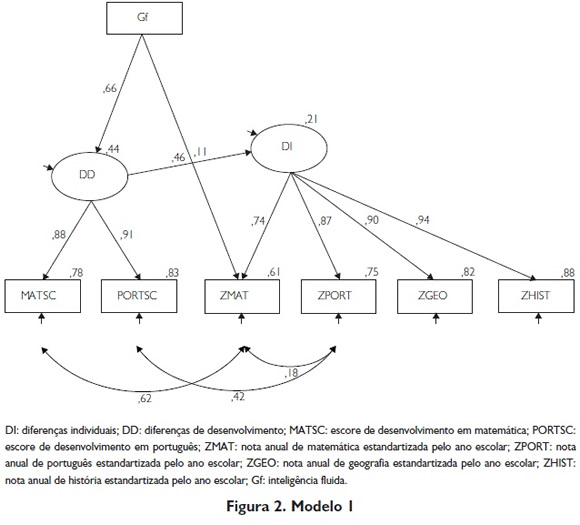
O traço DD explica 20,98% (14,82% – 27,46%) da variância do traço diferenças individuais (DI) do desempenho acadêmico. O traço Gf explica 1,21% (0,37% – 2,56%) da variância das diferenças individuais em matemática. O traço Gf explica 43,82% (37,33% – 50,55%) da variância em DD, mas não tem nenhum efeito direto estatisticamente significativo sobre a variância em DI.

As relações declaradas anteriormente são efeitos diretos, ou seja, explicações diretas de uma variável sobre outra. Além das explicações diretas, Gf e DD apresentam efeitos indiretos, explicando algumas variáveis por meio da mediação de uma variável intermediária. O traço Gf explica indiretamente 9,18% (6,10% – 12,74%) da variância de DI. O traço DD medeia essa relação, indicando o seguinte caminho, da esquerda para a direita: Gf – DD – DI. O traço Gf também explica indiretamente 5,06% (3,31% – 7,24%) da variância das diferenças individuais em matemática, 6,92% (4,49% – 9,86%) da variância em português, 7,51% (4,97% – 10,37%) da variância em geografia e 8,12% (5,43% – 11,22%) da variância em história. O caminho do efeito de Gf sobre as notas equalizadas segue a seguinte direção, da esquerda para a direita: Gf – DD – DI – notas equalizadas. O traço Gf também explica indiretamente os escores de desenvolvimento em matemática e português. O traço Gf explica indiretamente 34,34% (28,84% – 40,32%) da variância das diferenças de desenvolvimento em matemática e 36,48% (30,58% – 42,77%) da variância das diferenças de desenvolvimento em português. O caminho da relação é: Gf – DD – escores de desenvolvimento. O traço DD, por sua vez, explica indiretamente 11,56% (7,90% – 15,60%) da variância das diferenças individuais em matemática, 15,68% (10,89% – 20,98%) da variância em português, 17,06% (11,83% – 22,56%) da variância em geografia e 18,49% (13,03% – 24,11%) da variância em história.

Conforme exposto, o modelo 2 tem apenas o escore de desenvolvimento acadêmico em matemática, e, em função disso, não foi possível identificar um traço latente desse desenvolvimento acadêmico. No entanto, consideramos que o escore das diferenças de desenvolvimento em matemática do modelo 2 pode ser definido como um bom indicador do traço latente DD. No ensino fundamental, a variância das diferenças de desenvolvimento em matemática é explicada entre 75% e 81%. Supondo que essa relação possa estar relativamente presente no ensino médio, utilizamos o escore de desenvolvimento em matemática como possível indicador de DD.

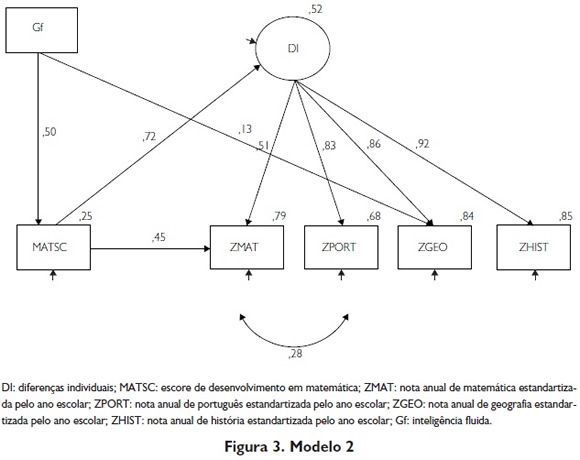
O modelo 2 (Figura 3) tem adequado grau de ajuste aos dados (χ² = 8,80; df = 6; CFI = 1,00; RMSEA = 0,04). O traço latente diferenças individuais do desempenho acadêmico (DI) explica moderadamente as notas escolares equalizadas em matemática (ZMAT) e fortemente em português (ZPORT ), geografia (ZGEO) e história (ZHIST). Matemática é explicada por DI em 26,32% de sua variância (19,62% – 33,41%), português em 68,06% (62,09% – 74,13%) de sua variância, geografia em 73,96% (67,57% – 80,10%) de sua variância e história em 85,01% (80,46% – 88,92%) de sua variância.

Os escores de desenvolvimento acadêmico em matemática (MATSC), como indicador dessas diferenças de desenvolvimento (DD), explicam 52,27% (44,36% – 59,75%) da variância do traço diferenças individuais (DI) do desempenho acadêmico. O traço Gf explica 1,77% (0,66% – 3,39%) da variância das diferenças individuais em geografia, assim como explica 25,20% (18,40% – 33,29%) da variância dos escores das diferenças de desenvolvimento em matemática (MATSC), indicador de DD. O traço Gf não tem nenhum efeito direto estatisticamente significativo sobre a variância em DI.

As relações declaradas anteriormente são efeitos diretos. O traço Gf e o indicador de DD, MATSC, também apresentam efeitos indiretos. O traço Gf explica indiretamente 13,18% (9,06% – 18,23%) da variância de DI, e MATSC medeia essa relação, indicando o seguinte caminho: Gf – MATSC – DI. O traço Gf também explica indiretamente 16,81% (11,90% – 22,66%) da variância das diferenças individuais em matemática, 9,00% (6,00% – 12,89%) da variância em português, 9,73% (6,66% – 13,69%) da variância em geografia e 11,22% (7,67% – 15,60%) da variância em história. O caminho da relação é o seguinte: Gf – MATSC – DI – notas equalizadas. O traço MATSC explica indiretamente, via mediação de DI, 13,76% (9,86% – 18,15%) da variância das diferenças individuais em matemática, 35,64% (28,73% – 41,99%) da variância em português, 38,69% (31,81% – 45,43%) da variância em geografia e 44,49% (37,09% – 50,98%) da variância em história.

 

 

 

Discussão

Ao considerar o tratamento das notas escolares, este estudo incorporou a perspectiva desenvolvimental ao estudo dos preditores do rendimento escolar que utilizam a abordagem de inteligência da psicometria. Foi concebido que os estudantes desenvolvem seu conhecimento na medida em que avançam os anos escolares. Com o propósito de ajustar o conhecimento em função dos anos escolares, adotaram-se conjuntamente a perspectiva desenvolvimental e a perspectiva das diferenças individuais, para incorporar uma análise mais ampla à vertente da tradição psicométrica que estuda os preditores do rendimento escolar.

Considerar a perspectiva das diferenças individuais no estudo do papel preditivo da inteligência sobre o desempenho escolar é importante, pois elas trazem informações sobre a conexão existente entre o desempenho e construtos relacionados. Entretanto, considerar a perspectiva desenvolvimental talvez seja ainda mais importante. A informação sobre o papel da inteligência como preditor do desenvolvimento acadêmico do estudante fornece pistas fundamentais sobre a qualidade das políticas públicas educacionais e, em nível mais localizado e contextual, oferece dicas sobre tarefas e lacunas que precisam ser consideradas por escola, pais, professores e alunos. Integrar as duas perspectivas parece ser a melhor estratégia. A análise conjunta das diferenças individuais e das diferenças de desenvolvimento do desempenho estudantil possibilita uma compreensão sobre como esses dois aspectos se relacionam e são influenciados pela inteligência.

Algumas pistas a respeito dessas relações podem ser obtidas a partir das conclusões deste estudo. A primeira delas mostra que as diferenças individuais de rendimento escolar no ensino médio são mais fortemente afetadas pelas diferenças de desenvolvimento escolar, em comparação ao ensino fundamental II. Esse resultado faz sentido, na medida em que o conhecimento no ensino médio se torna mais especializado e denso, de forma que a história de desenvolvimento do conhecimento e das habilidades escolares passa a se tornar um preditor ainda mais relevante para a performance escolar.

A segunda conclusão obtida por meio dos resultados é a constatação da presença de uma relação inversamente proporcional entre Gf e DD. No ensino fundamental II, Gf prediz em torno de 50% de DD e DD explica cerca de 20% de DI. No ensino médio, Gf explica cerca de 20% de DD e DD explica em torno de 50% de DI. O preditor forte no ensino fundamental II é Gf. No ensino médio, a força preditiva encontra-se em DD. A relação preditiva inversamente proporcional entre Gf e DD (quando uma variável perde força preditiva, a outra variável ganha força preditiva semelhante à perda da primeira) parece indicar que o desenvolvimento acadêmico ocupa no ensino médio parte do efeito preditivo direto de Gf no ensino fundamental II. Essa evidência é favorável à hipótese de que a inteligência é um precursor cronológico do desenvolvimento acadêmico. No entanto, esse é um resultado inicial que necessita ser investigado detalhadamente em estudos futuros.

Uma terceira conclusão permite afirmar que, apesar dos efeitos indiretos de Gf sobre as diferenças individuais, Gf tem um efeito direto tanto no ensino fundamental II quanto no ensino médio apenas no traço de diferenças de desenvolvimento acadêmico. A inteligência atua diretamente sobre as diferenças de desenvolvimento e não nas diferenças individuais acadêmicas. Essa afirmação, no entanto, deve ser tratada com cautela, pois a amostra deste estudo é bastante limitada e circunscrita a uma realidade bastante localizada, ou seja, uma única escola particular da cidade de Belo Horizonte.

Dentre as conclusões apresentadas, possivelmente a última é a mais importante, em função das questões mobilizadas por ela. A Gf tem um efeito proximal sobre o desenvolvimento e não sobre as diferenças individuais. Se isso de fato é replicável e generalizável, então se pode pensar que a inteligência (Gf) tem um papel relevante no impulsionamento direto das diferenças do desenvolvimento escolar dos alunos, mas não nas diferenças individuais por si mesmas. Essa é uma implicação relevante do ponto de vista educacional e social. Se a inteligência tem uma relação importante com o desenvolvimento escolar dos estudantes, e não com as diferenças individuais, isso possibilita novas maneiras de ver o papel da inteligência no progresso acadêmico do alunado. Intervenções para promover o crescimento da inteligência poderão vislumbrar a perspectiva de que a inteligência atua diretamente sobre o desenvolvimento escolar, de modo a focar propostas em médio e longo prazos. Ao mesmo tempo, propostas de intervenção intelectual deverão focar atuações de médio e longo prazos, na medida em que estas têm condições de atuar e alterar o fluxo de desenvolvimento, ao contrário de intervenções de curto prazo. Outra implicação envolve considerar que a inteligência e o desenvolvimento acadêmico, seja este em termos de conhecimentos ou habilidades acadêmicas, se relacionam de maneira importante. Os resultados preliminares deste estudo indicam que a inteligência e o desenvolvimento escolar são interdependentes e um possivelmente tem impacto sobre o outro, apesar de a inteligência poder ser um precursor do desenvolvimento acadêmico. Em outras palavras, ao desenvolverem o conhecimento escolar dos estudantes, muito provavelmente as escolas ajudam a desenvolver a inteligência deles. Nessa visão, as escolas poderão ser compreendidas como ambientes de desenvolvimento da inteligência.

Além dos aspectos práticos e psicoeducacionais, outra implicação desse resultado envolve a necessidade de que os pesquisadores das diferenças individuais com foco nos modelos psicométricos de inteligência passem a considerar, em suas pesquisas e métodos de coleta e análise de dados, as diferenças de desenvolvimento, quando investigarem a proficiência acadêmica. Essa última condição poderá, em médio prazo, promover a integração de duas tradições que, em muitos casos, permanecem ainda relativamente separadas: a psicologia do desenvolvimento e a psicologia das diferenças individuais.

Em suma, defende-se o argumento de que as diferenças individuais presentes em uma variável psicológica dependente podem e devem ser mais bem identificadas por meio do controle das diferenças de desenvolvimento dessa variável. Quando se omite essa necessidade, corre-se o risco de superestimar a força preditiva das variáveis psicológicas sobre as diferenças individuais e subestimar a força preditiva delas sobre as diferenças de desenvolvimento.

Conforme argumentado, as conclusões provenientes deste estudo devem ser consideradas de forma cautelosa, em função da presença de uma amostra limitada e do uso limitado de medidas de inteligência (apenas Gf). Apesar dessa condição, as conclusões também podem ser percebidas como promissoras, pois trazem perspectivas de novos estudos e investigações sobre o papel preditivo da inteligência sobre o desempenho escolar, assim como possíveis implicações psicoeducacionais envolvendo a relação escola e inteligência.

 

Referências

ARORA, A. et al. (Org.). TIMSS advanced 2008 technical report. Chestnut Hill: TIMMS & PIRLS International Study Center, Boston College, 2009.         [ Links ]

BENTLER, P. M. Comparative fit indexes in structural models. Psychological Bulletin, v. 107, n. 2, p. 238-251, 1990.         [ Links ]

BYRNE, B. M. Structural equation modeling with AMOS: basic concepts, applications, and programming. Mahwah: Lawrence Erlbaum Associates, 2001.         [ Links ]

CARROLL, J. B. Human cognitive abilities: a survey of factor analytic studies. New York: Cambridge University Press, 1993.         [ Links ]

COLOM, R.; FLORES-MENDOZA, C. E. Intelligence predicts scholastic achievement irrespective of SES factors: evidence from Brazil. Intelligence, v. 35, n. 3, p. 243-251, 2007.         [ Links ]

DEARY , I. J. et al. Intelligence and educational achievement. Intelligence, v. 35, n. 1, p. 13-21, 2007.         [ Links ]

GAGNÉ, F.; ST. PÉRE, F. When IQ is controlled does motivation still predict achievement? Intelligence, v. 30, n. 1, p. 71-100, 2002.         [ Links ]

GOMES, C. M. A.; BORGES, O. N. Qualidades psicométricas do conjunto de testes de inteligência fluida. Avaliação Psicológica, v. 8, n. 1, p. 17-32, 2009.         [ Links ]

GOTTFREDSON, L. S. g: highly general and highly practical. In: STERNBERG, R. J.; GRIGORENKO, E. L. (Org.). The general factor of intelligence: how general is it? Mahwah: Erlbaum, 2002a. p. 331-380.         [ Links ]

GORENKO, E. L. Where and why g matters: not a mystery. Human Performance, v. 15, p. 25-46, 2002b.         [ Links ]

GUSTAFSSON, J. E.; UNDHEIM, J. O. Individual differences in cognitive functions. In: BERLI NER , D. C.; CALFEE, R. C. (Org.). Handbook of educational psychology. New York: Prentice Hall International, 1996. p. 186-242.         [ Links ]

KUNCEL, N. R.; HEZLETT, S. A.; ONES, D. S. Academic performance, career potential, creativity, and job performance: can one construct predict them all? Journal of Personality and Social Psychology, v. 86, n. 1, p. 148-161, 2004.         [ Links ]

LEMOS, G. et al. Inteligência e rendimento escolar: análise da sua relação ao longo da escolaridade. Revista Portuguesa de Educação, v. 21, n. 1, p. 83-99, 2008.         [ Links ]

LIVINGSTON, S. A.; KIM. S. The circle-arc method for equating in small samples. Journal of Educational Measurement, v. 46, n. 3, p. 330-343, 2009.         [ Links ]

MARTI N, M. O. et al. Science achievement in the primary school years. Chestnut Hill: TIMSS Study Center, 1997.         [ Links ]

MULLIS, I. V. S. et al. Mathematics achievement in the primary school years. Chestnut Hill: TIMSS Study Center, 1997.         [ Links ]

MULLIS, I. V. S. et al. IEA's progress in international reading literacy study in primary school in 40 countries. Chestnut Hill: TIMMS & PIRLS International Study Center, Boston College, 2007.         [ Links ]

MULLIS, I. V. S. et al. TIMMS advanced 2008 international report: findings from IEA's study of achievement in advanced mathematics and physics in the final year of secondary school. Chestnut Hill: TIMMS & PIRLS International Study Center, Boston College, 2009.         [ Links ]

NAGLIERI, J. A.; BORNSTEIN, B. T. Intelligence and achievement: just how correlated are they? Journal of Psychoeducational Assessment, v. 21, p. 244-260, 2003.         [ Links ] NEISSER, U. et al. Intelligence: knowns and unknowns. American Psychologist, v. 51, n. 2, p. 77-101, 1996.         [ Links ]

OLSON, J. F.; MARTI N, M. O.; MULLIS, I. V. S. (Org.). TIMSS 2007 technical report. Chestnut Hill: TIMSS & PIRLS International Study Center, Boston College, 2008.         [ Links ]

ORGANISATION FOR ECONOMIC CO-OPERATION AND DEVELOPMENT. PISA 2006: science competencies for tomorrow's world. Paris: OECD, 2007.         [ Links ]

PARREIRAS, J. S.; GOMES, C. M. A. Metacognição ou metacognições? In: IV CONGRESSO BRASILEIRO DE AVALIAÇÃO PSICOLÓLICA E XIV CONFERÊNCIA INTERNACIONAL DE AVALIAÇÃO PSICOLÓGICA: FORMAS E CONTEXTOS, 2009, Campinas. Anais... Ribeirão Preto: Instituto Brasileiro de Avaliação Psicológica, 2009. p. 360.         [ Links ]

RINDERMANN, H. The g-factor of international cognitive ability comparisons: the homogeneity of results in PISA, TIMSS, PIRLS and IQ-tests across nations. European Journal of Personality, v. 21, n. 5, p. 667-706, 2007.         [ Links ]

SPINATH, B. et al. Predicting school achievement from general cognitive ability, self-perceived ability, and intrinsic value. Intelligence, v. 34, n. 4, p. 363-374, 2006.         [ Links ]

TONG, Y.; KOLEN, M. J. Comparisons of methodologies and results in vertical scaling for educational achievement tests. Applied Measurement in Education, v. 20, n. 2, p. 227-253, 2007.         [ Links ]

WATKINS, M. W.; LEI, P. W.; CANIVEZ, G. L. Psychometric intelligence and achievement: a cross-lagged panel analysis. Intelligence, v. 35, n. 1, p. 59-68, 2007.         [ Links ]

 

 

Endereço para correspondência
Contato
Cristiano Mauro Assis Gomes
e-mail: cristianogomes@ufmg.br

Tramitação
Recebido em novembro de 2010
Aceito em julho de 2011