Psicometria: fundamentos matemáticos da Teoria Clássica dos Testes

 

Psychometrics: mathematical foundations of classical test theory

 

Psicometría: fundamentos matemáticos de la teoría clásica de los tests

 

 

Ricardo Primi

Universidade São Francisco

 

 

---

RESUMO

Este artigo revisita textos clássicos em psicometria e apresenta os fundamentos matemáticos da Teoria Clássica dos Testes. Aborda o modelo matemático da análise fatorial, o modelo linear clássico, a derivação do índice de precisão e dos tipos de cálculo do coeficiente de precisão, o erro padrão da medida, o equacionamento da validade com a análise fatorial e, por último, a análise de itens. O texto interessa àqueles que queiram ampliar seu conhecimento nos conceitos de psicometria, entendendo de onde surgem as principais fórmulas que usamos na prática psicométrica de análise de testes e escalas.

Palavras-chave: teoria clássica dos testes; psicometria; precisão; validade; análise fatorial.

---

ABSTRACT

This paper revisits the classic texts in psychometrics and presents the mathematical foundations of the classical test theory. It discusses the mathematical model of factor analysis, the classical linear model, the derivation of the reliability and types of calculation of the reliability coefficient, the standard error of measurement, the integration of validity with factor analysis and, finally, item analysis procedures. The text concerns those who want to deepen their knowledge in the concepts of psychometrics, understanding the origin of the main formulas that we use when doing psychometric analysis of tests and scales.

Keywords: classical test theory; psychometrics; reliability; validity; factor analysis.

---

RESUMEN

Este artículo repasa los textos clásicos en psicometría y presenta los fundamentos matemáticos de la teoría clásica de los testes. Explica el modelo matemático de análisis factorial, el modelo lineal clásico, la derivación del índice de precisión y los tipos de cálculo del coeficiente de precisión, el error estándar de medición, el ecuacionamento de la validez con el análisis factorial y, por último, el análisis de ítems. El texto es de interés para aquellos que desean ampliar sus conocimientos sobre los conceptos de la psicometría, la comprensión de donde surgen las principales fórmulas que se presentan en la práctica psicométrica de tests y escalas.

Palabras-clave: teoría clásica de los tests; psicometría; precisión; validez; análisis factorial.

---

 

 

Com a popularização do uso de computadores, as análises estatísticas e psicométricas ficaram muito mais acessíveis e fáceis de serem executadas. A formação em pós-graduação tende, compreensivelmente, a focar um conteúdo instrumental sobre como operar os programas e executar as análises. Assim há uma carência de formação mais aprofundada nos fundamentos dos procedimentos psicométricos que são frequentemente usados nas pesquisas. Este artigo pretendeu revisitar trabalhos clássicos da psicometria (Ferguson 1981; Guilford 1954; Gulliksen, 1950; Lord, & Novick, 1974) e resumir os princípios matemáticos da Teoria Clássica dos Testes (TCT). Pretende-se apresentar: o modelo matemático da análise fatorial, o modelo linear clássico, a derivação do índice de precisão e dos tipos de cálculo do coeficiente de precisão, o erro padrão da medida, o equacionamento da validade com a análise fatorial e, por último, a análise de itens. O texto interessa àqueles que queiram aprofundar seu conhecimento nos conceitos de psicometria, entendendo de onde surgem as principais fórmulas que usamos na prática psicométrica de análise de testes e escalas.

Análise fatorial e modelos estruturais da inteligência e personalidade

Como afirma Cattell (1973), nas fases iniciais do desenvolvimento das ciências em geral, observam-se esforços procurando definir a taxonomia ou estrutura de seu fenômeno particular. Assim, a química definiu inicialmente os elementos constituintes da matéria antes de edificar teorias gerais sobre fenômenos complexos. Essa orientação esteve presente nos estudos sobre a inteligência, desenvolvidos pelos psicometristas no século passado. As pesquisas procuravam definir quais seriam as estruturas constituintes da inteligência humana que seriam as causas do comportamento observável.

O objetivo central desses estudos era identificar quais seriam as habilidades latentes básicas, definindo o seu número e estrutura de organização. Para isso, foi utilizada a análise fatorial, que é um método estatístico que busca analisar estruturas em matrizes de covariância ou correlação, redefinindoas em um número menor de variáveis. Segundo Johnson e Wichern (1992), "o propósito essencial da análise fatorial é descrever, se possível, as covariâncias entre variáveis em termos de um número menor de variáveis aleatórias subjacentes, mas inobserváveis, chamadas fatores" (p. 396).

Os psicometristas procuravam mensurar um conjunto amplo de habilidades cognitivas, por exemplo, por meio de uma bateria de testes de inteligência envolvendo conteúdos diversificados. Segue-se então a lógica de que se vários testes estão altamente inter-relacionados, de maneira que se pode então inferir a existência de uma única variável latente, inobservável, que é responsável por estas inter-relações. Analisando os testes inter-relacionados, se chegaria a compreender essa estrutura. Formalmente, supondo que tenham sido observadas p variáveis em uma dada amostra de sujeitos, o modelo fatorial ortogonal diz que:

 

 

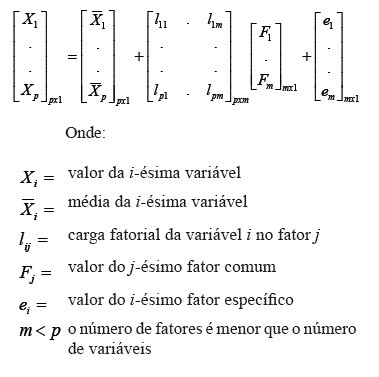
O modelo fatorial ortogonal supõe que: (1) a média dos valores dos fatores comuns e específicos seja zero, (2) a variância dos fatores seja igual a 1 e a covariância entre eles seja zero (portanto que a matriz de covariância entre os fatores seja igual à matriz identidade) e (3) a covariância entre os fatores específicos seja zero, portanto que a matriz de covariância entre os fatores específicos seja igual a uma matriz diagonal. Portanto, para uma variável particular i supõe-se que seu valor possa ser dado pela seguinte equação:

 

 

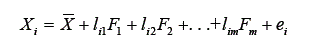
Pode-se notar nessa equação que: (1) o valor da variável observada i está em função de um conjunto m de variáveis latentes (portanto inobserváveis), ou seja, os m fatores comuns (F₁ . . . F_m), e também em função de um componente específico a esta variável (e_i). Assim, os desvios em relação à média, ou seja, a variância da variável _i é explicada pela variação de um conjunto de variáveis comuns, ou seja, associadas também à variância do conjunto mais amplo contendo as p variáveis do qual a variável i faz parte, e também pela variação específica desta variável que não é compartilhada pelas outras p variáveis; (2) a magnitude com que a variação de um determinado fator j está associada à variação na variável i, chamada de carga fatorial, é dada por l_ij; (3) a relação entre os m fatores e a variável i é linear.

Ainda, segundo o modelo fatorial ortogonal, a matriz de variâncias e covariâncias entre as p variáveis poderia ser reescrita da seguinte forma (ver Johnson & Wichern, 1992, para a dedução detalhada dessa equação):

 

 

Nota-se, na equação, que a variância de uma variável i é dada pela soma do quadrado das cargas fatoriais desta variável nos m fatores mais a variância específica. Essa soma dos quadrados das cargas é também chamada de comunalidade e denotada por h₂:

 

 

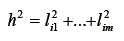
Assim, a variância da variável i pode ser reescrita:

 

 

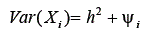
Tal equação aponta que a variância de uma variável i pode ser dividida em duas parcelas. A primeira, a comunalidade, representa a parcela da variância dessa variável associada às variações dos fatores. O termo comunalidade refere-se ao fato de que, sendo os fatores comuns, sua variação está associada também às p-1 variáveis restantes. Portanto, essa parcela da variância de i é potencialmente compartilhada pelas p-1 variáveis restantes (usa-se o termo potencialmente compartilhável, já que não se sabe a carga fatorial das p-1 variáveis restantes). A segunda parcela, no entanto, representa a porção da variância não associada aos m fatores, ou seja, não compartilhada pelas variáveis restantes. Sendo assim, essa variância é específica à variável em análise.

As equações dizem ainda que a covariância entre duas variáveis é igual à soma dos produtos das cargas que estas variáveis têm nos fatores comuns, ou seja, sua covariância é única e exclusivamente dada pelos fatores. Elas também mostram que a covariância entre uma variável e um fator é igual à carga da variável no fator.

Com a análise fatorial, a psicometria procurou explicar a relação entre escores de diferentes testes em função de um número menor de habilidades latentes. Nota-se, portanto, que esse método tentou criar um modelo para explicar as diferenças entre indivíduos nos escores dos testes (portanto os desvios em relação à média, X_i – 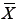dos resultados dos n sujeitos, nas p medidas efetuadas) em função de um conjunto menor de variáveis latentes (F_j). Essas estruturas seriam as habilidades mentais latentes que representariam as causas das diferenças, entre os sujeitos, nos escores dos testes.

Diante do exposto, fica claro que a análise fatorial tornou possível o estudo empírico de variáveis internas não observáveis, diretamente, sejam elas da inteligência ou personalidade e por isto representou um grande avanço para a psicologia. Isso ocorreu porque o pesquisador podia partir de um conjunto de variáveis observáveis e, por meio das inter-relações entre elas, investigar as possíveis dimensões subjacentes que seriam as causas desses comportamentos. Nota-se que esse método é puramente correlacional, não implicando, em nenhum momento, na manipulação experimental. Em uma analogia interessante, Cattell (1975) tornou claro o método da análise fatorial:

O problema que por muitos anos desconcertou os psicólogos era encontrar um método que deslindasse essas influências funcionalmente unitárias na floresta caótica do comportamento humano. Mas como é que numa floresta tropical de fato decide o caçador se as manchas escuras que vê são dois ou três troncos apodrecidos ou um só jacaré? Ele fica à espera de movimento. Se eles se movem juntos - aparecem e desaparecem juntos - ele conclui por uma única estrutura. Da mesma forma como John Stuart Mill observou em sua filosofia da ciência o cientista deveria ter em mira a "variação concomitante" na busca de conceitos unitários (p. 55).

Utilizando esse instrumental estatístico, os psicometristas investigaram a estrutura da inteligência (bem como da personalidade). Surgiram, então, várias teorias postulando estruturas únicas, múltiplas e simultaneamente únicas e múltiplas. Uma revisão desses modelos pode ser encontrada em Sternberg (1981, 1984, 1986) e Almeida (1988).

Precisão e validade

Ao lado da pesquisa sobre as estruturas da personalidade, a psicometria foi também responsável pelo aprimoramento das técnicas de medida na psicologia. Ela foi e continua sendo um ramo específico da psicologia, destinado ao desenvolvimento de técnicas de mensuração de variáveis psicológicas, introduzindo um instrumental estatístico adequado as suas complexidades. Seus fundamentos básicos são parte do que se chamou teoria clássica dos testes.

Os instrumentos de avaliação psicológica podem ser caracterizados por duas propriedades métricas básicas: Precisão e Validade [em inglês: reliability, validity]. Precisão está associada ao erro de medida, isto é, à diferença entre o escore observado de um sujeito em um teste, do valor verdadeiro que ele tem na variável latente. Em razão da complexidade própria às variáveis psicológicas, praticamente nunca a variabilidade em escores observados refletem com exatidão e precisão as diferenças reais na variável latente. Sempre haverá um erro de medida, ou seja, variações que não refletem as diferenças reais. Portanto, uma prática corrente é estimar a precisão de um determinado teste para conseguir estabelecer uma expectativa de quão errônea poderá ser a medida.

Validade, por sua vez, relaciona-se à questão que investiga se o teste está medindo o construto que se propõe medir. Nesse sentido, é de se esperar que a variação nos escores observados em um teste esteja associada, em certo grau, ao construto psicológico que o teste se propõe medir. Os estudos de validade investigam essa expectativa testando empiricamente se o teste está medindo a variável conforme foi planejado.

Sobre as relações entre essas duas propriedades dos testes, sabe-se que uma boa precisão é uma condição necessária, mas não suficiente para que um teste seja válido. Mesmo preciso, um teste pode estar medindo uma variável diferente daquela a que se propôs. Assim, a psicometria estruturou um sistema conceitual básico, o qual denominou modelo linear clássico. Esse sistema será tratado a seguir e resume a exposição feita nos trabalhos de Ferguson (1981), Guilford (1954), Gulliksen (1950), Muñiz (1994) e Pivatto (1992).

O modelo linear clássico: Precisão

O modelo linear clássico postula que um escore observado de um determinado sujeito X_i em um teste pode ser decomposto em duas partes aditivas:

(1) T_i, o escore verdadeiro [em inglês: true score] do sujeito na variável medida pelo teste;

(2) e_i, o escore de erro que ocorre em função da imprecisão das medidas psicológicas.

Assim, o escore observado pode ser definido como:

 

 

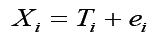
O escore verdadeiro (T_i) pode ser concebido teoricamente de duas maneiras: (a) uma medida da variável em análise, sob condições ideais, usando um instrumento perfeito ou (b) a média de um conjunto de infinitas medidas da mesma variável, no mesmo sujeito, quando estas são independentes, usando um instrumento imperfeito – com erros de medidas. Ferguson (1981) estabelece essa definição como:

 

 

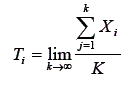
O escore de erro (e_i) pode ser entendido como uma variável aleatória associada a eventuais erros associados às condições particulares de aplicação. Ele assume valores positivos e negativos, fazendo, portanto, com que os escores observados sejam ora maiores e ora menores do que os escores verdadeiros. Assume-se que o erro seja assistemático, aleatório, ou seja, não mostra tendência sistemática de assumir valores positivos ou negativos. Nota-se que o valor do escore verdadeiro é fixo entre diferentes aplicações, enquanto o erro tende a variar.

Ainda seguindo essa lógica, três postulados são explicitados:

(1) Se os erros são assistemáticos, em um conjunto grande de medidas, a média dos erros será igual a zero:

 

 

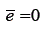
(2) em um grande conjunto de medidas espera-se que não exista correlação entre os escores verdadeiros e os escores de erro, já que é razoável supor que sujeitos com altos escores tenham a mesma tendência a sofrer acréscimos (erro positivo) ou decréscimos em seus escores (erro negativo) e vice versa:

 

 

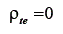
(3) supõe-se que não existirá correlação entre os escores de erro de dois testes diferentes a e b, que meçam a mesma variável, portanto testes paralelos:

 

 

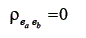
Como decorrência da definição e dos postulados, várias relações podem ser deduzidas. Com relação à média, pode-se dizer que, supondo que se meça uma determinada variável em uma população, a média destes escores observados pode ser escrita como:

 

 

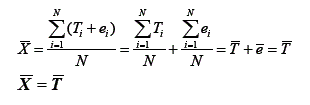
Assim, a média de um conjunto muito grande de escores observados é igual à média dos escores verdadeiros. Entretanto, a variância dos escores observados é dada por:

 

 

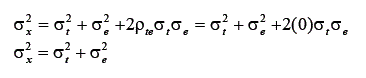
Portanto, como não há correlação entre escore de erro e escore verdadeiro, a variância do escore observado não sofrerá contribuição vinda da covariância entre escore de erro e escore verdadeiro, restringindo-se à variância dos escores verdadeiros mais a variância dos escores dos erros. Uma dedução importante ocorre quando se aplicam esses princípios à equação da covariância entre os escores observados e os escores verdadeiros, tal como é dada a seguir:

 

 

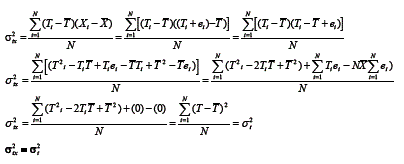
Nota-se, por meio dessa dedução que, como o erro não está correlacionado com o escore verdadeiro, os termos da equação que contém o escore de erro desaparecem. Assim, a covariância entre o escore observado e o escore verdadeiro é igual à variância do escore verdadeiro. Utilizando essas informações no cálculo do coeficiente de correlação, entre o escore observado e o escore verdadeiro, tem-se que:

 

 

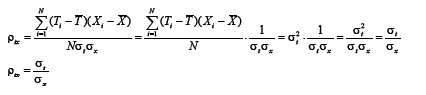
Essa equação diz que a correlação entre o escore verdadeiro e o escore observado é igual a uma proporção entre os desvios do escore verdadeiro e os desvios do escore observado. Essa fórmula refere-se à variação em termos de desvios padrão. Contudo, na literatura, definiu-se o índice de precisão [em inglês: index of reliability - ^ρ_ii] utilizando, em vez do desvio padrão, a variância. Assim, esse é dado por:

 

 

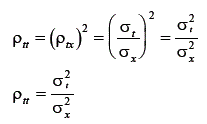
Como a variância do escore observado (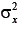) é composta pela variância do escore verdadeiro mais a variância do escore de erro, o índice de precisão
sempre será igual ou maior que a variância do escore verdadeiro (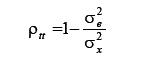). Portanto, esse índice assume valores entre 0 e 1. O seu valor significa qual parcela da variância dos escores observados é variância verdadeira. Quanto menor for o coeficiente, menor será a parcela verdadeira e maior a parcela de erro de medida. Outra forma de se expressar o índice de precisão, por meio de substituições nas fórmulas dadas, é:

 

 

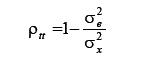
Nessa fórmula, fica evidente que, quanto maior for a proporção do erro na variância total do escore observado, mais próxima de 1 fica a segunda parte da equação e menor o índice de precisão. Conhecendo os valores da variância do escore verdadeiro e do escore observado, pode-se calcular o índice de precisão. Contudo, como o escore verdadeiro não é observável diretamente, sua variância é desconhecida. O método de estimação desse índice decorre do conceito de formas paralelas de um teste. Formas paralelas de um mesmo teste equivalem a medidas idênticas, independentes, de uma mesma variável psicológica. Medidas paralelas têm a mesma média, variância e correlação entre todos os pares possíveis entre as formas (Guilford, 1954). Sendo assim, como demonstra Ferguson (1981), aplicando-se duas formas paralelas a e b de um mesmo teste a uma população, tem-se que:

 

 

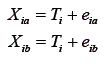
Nota-se que as duas medidas estão em função do mesmo escore verdadeiro e ambas sujeitas a erros. Calculando-se a correlação entre os escores observados, tem-se:

 

 

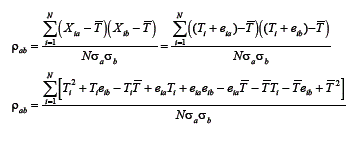
Como os escores de erro são aleatórios e não estão correlacionados entre si e nem com os escores verdadeiros, os termos que contêm escore de erro serão iguais a zero, assim:

 

 

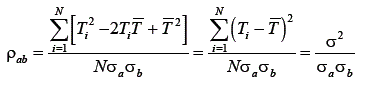
Como os desvios padrões são iguais para as duas formas paralelas σ_a = σ_b = σ_x´ então

 

 

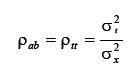
Conclui-se, a partir da dedução exposta, que a correlação entre os escores observados é igual ao índice de precisão. Com base nesse fato, a prática de estimação da precisão de um teste envolve, de alguma forma, correlacionar medidas paralelas. Anastasi (1961) faz uma descrição detalhada dos métodos empregados na estimação do índice de precisão. Basicamente são quatro.

O primeiro método é denominado precisão por formas alternativas e consiste na aplicação simultânea, à mesma amostra, de duas formas paralelas de um teste. A estimação do índice de precisão é dada pela correlação entre os dois escores observados, como ficou evidente na dedução apresentada anteriormente.

O segundo método é denominado precisão teste-reteste e envolve a aplicação do mesmo teste, em uma mesma amostra, duas vezes, supondo que estas duas aplicações sejam independentes, ou seja, a primeira não influencie a segunda. O índice de precisão é dado mais uma vez pela correlação entre os dois conjuntos de escores. Isso se dá porque é evidente que a forma mais paralela possível de um determinado teste é ele mesmo. Podendo-se supor que a primeira aplicação não afete a segunda, têmse duas medidas paralelas do mesmo construto e a dedução apresentada, referente à correlação entre dois escores paralelos, passa a ser válida.

O terceiro método é denominado precisão pelas metades e consiste na aplicação de um único teste a uma única amostra e, posteriormente, na divisão deste teste em duas metades comparáveis, isto é, duas metades semelhantes, ou paralelas. A correlação entre essas duas metades é igual à estimação do índice de precisão. Supõe-se que, estando todos os itens de um teste medindo o mesmo construto psicológico, a divisão deste teste em duas metades comparáveis equivale a obter duas medidas por meio de formas paralelas do mesmo teste e, portanto, passam a ser válidas as deduções para medidas paralelas.

Nesse último caso, da precisão pelas metates, como o coeficiente de precisão é afetado pelo número de itens que compõem o teste, é comum empregar uma fórmula denominada correção de Spearman-Brown para se estimar o coeficiente de precisão caso o teste fosse composto por duas vezes mais itens. Isso é feito porque o coeficiente de correlação é calculado a partir de um teste com a metade do número de itens da forma. A fórmula empregada é (para uma dedução detalhada, da equação a seguir, a partir das equações apresentadas anteriormente, veja Muñiz, 1994 ou Guilford, 1954):

 

 

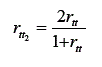
O quarto método é denominado precisão por consistência interna. Esse método se baseia-se na suposição de que cada item representa uma medida paralela do mesmo construto e, portanto, pode-se estimar a precisão de um teste baseando-se na covariância entre os itens. Ou seja, se a correlação entre medidas paralelas é igual ao índice de precisão e cada item do teste é uma medida paralela do construto em análise, então se pode estimar o coeficiente de precisão baseando-se nas intercorrelações entre os itens. Esse coeficiente foi desenvolvido em 1937 por Kuder e Richardson e, portanto, é conhecido como Kuder Richardson - 20:

 

 

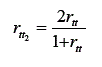
Onde:

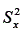é a variância do escore observado x

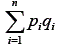representa a soma das variâncias dos n itens

Quando se somam variáveis para se compor um escore - como no caso do escore observado que é composto pela soma da pontuação nos itens - a variância desse novo escore é composta pela soma da variância dessas variáveis (itens) mais a covariância entre elas. Portanto, quando há covariância (ou seja, correlação entre os itens), a variância do escore do teste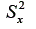será maior do que a soma da variância nos itens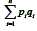Isso fará com que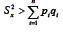resultando um numerador positivo. Quanto maior a variância dos testes em relação a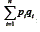mais o resultado da divisão se aproximará de 1. Portanto, nesse caso, r_tt estará também próximo de 1, indicando alta consistência interna. Já, quando as covariâncias forem próximas de zero, a variância dos escores será praticamente igual à soma das variâncias dos itens. Assim, o numerador da segunda divisão será próximo de zero fazendo com que r_ii esteja próximo de zero, indicando, portanto, baixa consistência interna do teste.

Uma medida com importância prática derivada do índice de precisão é o Erro Padrão da Medida (EPM). Como foi colocado anteriormente:

 

 

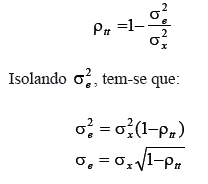
Nessa fórmula, foi isolado o desvio padrão dos escores de erro. Ela diz que, conhecendo o índice de precisão de um teste, a variância (ou desvio padrão) dos escores de erro pode ser calculada.

Considerando-se diferentes medidas, passíveis de erro, de um construto psicológico constante (sejam elas medidas repetidas independentes ou medidas feitas por testes paralelos), o valor do escore verdadeiro (T_i) será constante de medida a medida – para um mesmo sujeito. O escore de erro (e_i), no entanto, irá variar. Portanto, a variação nos escores observados X_i, entre as aplicações, para um mesmo sujeito, será causada pela variação dos escores de erro. Dessa maneira, a variação encontrada em medidas repetidas de um construto psicológico, que tem seu valor constante, é chamada erro padrão da medida. Ela é nada mais do que o desvio padrão dos escores de erro.

A fórmula apresentada coloca o erro padrão da medida em função do índice de precisão. Por meio dela pode-se extrair qual proporção da variância do escore observado será atribuída ao erro. Assume-se que, em repetidas medidas, os escores observados distribuem-se normalmente ao redor do escore verdadeiro com desvio padrão igual ao erro padrão da medida. Essa informação é usada para calcular a expectativa de variação dos escores de um teste (em função de um dado coeficiente de precisão e um dado desvio padrão) quando se repete a mesma medida.

O modelo linear clássico: Validade

A estimação da precisão é um passo relativamente fácil e comumente atingido nos estudos das propriedades psicométricas dos testes. Já a estimação da validade é um assunto bem mais complexo. Uma das formas de se verificar a validade é pela correlação entre os resultados do teste e uma medida externa independente. Essa medida externa deve ser necessariamente uma medida válida da variável latente que o teste se propõe medir (portanto associada ao T_i).

Em termos matemáticos, o problema da validade é tratado por Guilford (1954) por meio de uma junção da teoria da análise fatorial com o modelo clássico linear. Como afirma ele, na página 354:

A teoria clássica divide a variância do escore observado em dois componentes: variância verdadeira e variância de erro. Essencialmente, o novo passo está em supor que a variância verdadeira pode ser ainda decomposta em dois componentes aditivos. Estes componentes são: a variância comum ou comunalidade e mais possivelmente uma variância específica. A variância comum entre os fatores são compartilhadas pelos outros testes assim como a variância verdadeira é compartilhada por duas formas paralelas do mesmo teste. O componente específico, até onde se tem informação, é único a um teste particular. É parte da variância verdadeira e, portanto, compartilhada por duas formas do mesmo teste.

Na análise fatorial, o escore de uma variável qualquer é dado pela equação:

 

 

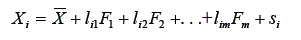
Também no modelo linear clássico, o escore de uma variável qualquer é dado por:

 

 

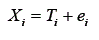
Assumindo que o escore verdadeiro seja determinado por m variáveis latentes, este pode ser decomposto usando o modelo fatorial com m fatores, ou seja,

 

 

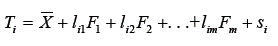
A fórmula do escore observado será reescrita como:

 

 

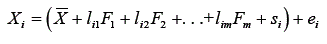
Essas relações trazem uma análise mais detalhada do conceito de escore verdadeiro. Nota-se que o escore verdadeiro é representado por um conjunto de variáveis latentes – construtos psicológicos - e mais um componente específico associado às particularidades do teste. Portanto, Guilford (1954) propõe que aquilo que é medido por um teste seja concebido como algo multifacetado ou multivariado ou como um conjunto de variáveis latentes comuns.

Os escores de um teste expressam as tentativas de se medir um construto psicológico. As medidas externas são mais próximas e válidas desse construto, portanto, com o componente específico e o erro próximos de zero. Simultaneamente, terão carga fatorial alta nos fatores subjacentes que compõem esse construto psicológico. Portanto, ambas variáveis, o teste e a variável externa, se medirem um mesmo construto, terão cargas fatoriais altas nos fatores que compõem o construto. Como foi dito, a correlação ou covariância entre duas variáveis se relacionam às cargas dessas variáveis nos fatores comuns subjacentes a elas. Essa correlação é obtida somando o produto das cargas que as duas variáveis tem nos fatores comuns:

 

 

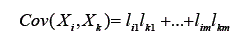
Assim, quanto maiores as cargas que duas variáveis têm em um fator comum maior, será a correlação entre estas variáveis. Isso ocorre porque a análise fatorial extrai e concretiza, nos escores dos fatores, a variância comum. Com base nisso, se um teste e uma variável externa medem um mesmo atributo psicológico, suas cargas fatoriais nas variáveis latentes que compõem este construto serão altas. Embasando-se na fórmula apresentada, pode-se deduzir que a correlação entre o teste e a variável externa será alta, provando assim que, quanto maior a correlação teste e variável externa, mais válido é o teste. Assim sendo, o método de estimação da validade envolve a análise correlacional com medidas externas, buscando-se esclarecer a rede de relações com variáveis externas – rede nomológica (Embretson, 1994).

Análise de itens pela TCT

Para que os critérios de precisão e validade de um teste sejam satisfeitos, inicialmente devese partir para a análise das unidades básicas que compõem o teste, ou seja, os itens. Geralmente, as análises quantitativas incluem a análise da distribuição de respostas nos itens (ou o índice de dificuldade, quando o item é dicotômico), o poder discriminativo, a análise das alternativas, a probabilidade de acerto ao acaso e a validade externa do item (Almeida, 1993).

Supondo que os itens representem respostas dicotômicas como acerto ou erro, e que N sujeitos respondam a n itens, os dados podem ser arranjados na matriz a seguir (Figura 1) onde cada sujeito é representado em uma linha e cada item em uma coluna:

 

 

No corpo da matriz estão representadas as respostas dos sujeitos aos itens. Na coluna marginal direita estão representados os acertos dos sujeitos (X_i), ou seja, a somatória de pontos nos itens. Na linha marginal inferior estão representados os escores dos itens (P_j), ou seja, quantos sujeitos acertaram o item j. Um dos primeiros atributos dos itens é o índice de dificuldade (ID). Ele representa a probabilidade de acerto no item em causa. Portanto, ID = P_j/N. Assim, um ID = 0,87, para um determinado item j indica que 87% das pessoas acertaram o item j.

Considerando, nesse momento, somente o índice de dificuldade, pode-se dizer que um bom item é aquele que possui alta variância, visto que o objetivo do teste é explicitar as variações que existem entre os indivíduos, itens com alta variância irão contribuir para uma maior variância do escore do teste, já que uma das parcelas da variância do escore é a soma da variância dos itens individuais. Isso irá permitir uma maior discriminação dos indivíduos em função dos escores. Um item com ID = 1,00 ou 0,00 não traz informação alguma, pois não permitirá uma separação dos sujeitos já que, em um caso 100% acertam e, no outro, 100% erram.

É sabido que os indivíduos diferem entre si no construto que se deseja avaliar, então um item com variância próxima a zero pode ser considerado como um item inadequado para o teste. Em contrapartida, itens com ID = 0,50 são os que apresentam maior variância já que dividem o grupo de sujeitos pela metade, permitindo a comparação de cada um dos 50 sujeitos que erraram com cada um dos 50 sujeitos que acertaram, ou seja, 50 X 50 = 2500 comparações (em um grupo de 100 sujeitos). Desse modo, são considerados bons itens aqueles que possuem ID's entre 0,30 e 0,70, ou seja perto de 0,50 (Ferguison, 1981). Em termos técnicos, o que se deseja é que a variância dos escores do teste seja máxima. Índices com ID's próximos a 0,50 contribuem aumentando a variância dos escores. Contudo, um segundo fator também contribui para isso: a covariância entre os itens. Quando os itens estão altamente correlacionados, a variância do escore aumenta.

Um exemplo simples pode ajudar a compreender esse fato. Suponha que um teste seja composto por 20 itens com ID's = 0,50, suponha também que todos os itens tenham uma correlação perfeita entre si, ou seja, um indivíduo que acerte o item j acerte também os j-1 itens restantes e inversamente um sujeito que erre o item j erre também os j-1 itens restantes. Como a probabilidade de acerto de qualquer um dos itens é 0,50, e como a correlação entre todos os itens é 1, para qualquer item j, os 50% que acertam este item acertam também todos os j-1 itens restantes, chegando assim ao escore máximo no teste. Já os 50% que erram têm, pelas mesmas razões, o escore 0.

A variância dos escores no teste, definida por S₂ = S(∑ - 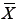)² / N, será máxima, pois 100% dos indivíduos estarão a uma distância máxima da média, ora para cima (50% dos sujeitos com escore máximo), ora para baixo (50% dos sujeitos com escore mínimo), elevando a soma de quadrados. Mais uma vez, supondo que esse teste tenha sido aplicado a 100 sujeitos, os 50 sujeitos com escore máximo poderão ser comparados com cada um dos 50 sujeitos com escore mínimo, portanto 2500 comparações poderiam ser feitas.

Em situações práticas, não serão encontrados testes com esses padrões perfeitos de correlação 1 e ID's = 0,50 como é exemplificado. Pode-se pensar, no entanto, em diferentes graus de covariância entre os itens. Quanto maior a covariância, maior será a variância do escore total. Um método muito frequente de se avaliar quanto um item contribui para a diferenciação dos sujeitos é calcular a correlação entre o item e o escore total no teste. Esse coeficiente é chamado de correlação ponto bisserial (r_pbi) e expressa a correlação entre uma variável categórica dicotômica (acerto ou erro) e uma variável intervalar (o escore no teste que, embora não possa ser considerada uma variável intervalar genuína, para fins práticos é considerada como tal). Ver argumentos de Ferguson (1981) e Lord e Novick (1974).

Esse coeficiente também é chamado de poder discriminativo do item. Esse nome é dado já que uma alta correlação entre o item e o escore indica que o item contribui para aumentar a variância dos escores ajudando a discriminação entre os sujeitos. O cálculo desse coeficiente é dado por:

 

 

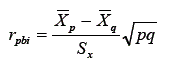
Onde

p representa a probabilidade de acerto ou o ID do item em causa q=1-p

S_x representa o desvio padrão da variável contínua

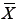_p,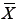_q a média dos sujeitos que acertaram o item e dos que erraram

Em suma, um bom teste deve ser composto por itens com alta variância (ID) e com alta correlação com o escore total (rpbi). Isso faz com que a variância do escore seja alta e possa captar as variações do atributo psicológico que é mensurado.

Como foi visto anteriormente, o método de precisão por consistência interna baseia-se na covariação entre os itens para estimar a precisão. Altas correlações item-total associam-se à alta consistência interna e à alta precisão. A análise dos itens possibilita um olhar mais apurado às características dos itens para que se possa fazer uma seleção daqueles que contribuem, em maior grau, para o teste como um todo no aumento da precisão. Contudo, essa variância capturada deve estar associada à variável latente em análise. Da mesma forma que é julgada a validade de um teste, a validade de um item é dada pela correlação entre o item e um critério externo.

Haveria ainda muitos detalhes a tratar para que se possa analisar todo o conjunto teórico e prático edificado pela psicometria. No entanto, este artigo trata somente dos conceitos básicos referentes à analise fatorial e ao modelo clássico e como as práticas mais comuns de construção de instrumentos de avaliação se relacionam a eles. Atualmente, novas abordagens têm surgido dentro dos modelos da Teoria de Resposta ao Item (Hambleton & Swaminatham, 1985) e deverão ser objeto de reflexão em trabalhos futuros, de forma a enriquecer a discussão sobre as teorias da medida.

 

Referências

Almeida, L. S. (1993). Relatório da disciplina de métodos de observação e investigação Psicológica -1º ano. Braga: Universidade do Minho.         [ Links ]

Almeida, L. S. (1988). Teorias da inteligência. Porto: Edições Jornal de Psicologia.         [ Links ]

Anastasi, A. (1961) Testes Psicológicos. São Paulo: EPU.         [ Links ]

Cattell, R. B. (1973). Personality and mood by questionaire: a handbook of interpretative theory, psychometrics, and pratical procedures. San Francisco: Jossey-Bass Publishers.         [ Links ]

Cattell, R. B. (1975). Análise científica da personalidade. São Paulo: Ibrasa.         [ Links ]

Embretson, S. (1994). Applications of cognitive design systems to test development. Em: C. R. Reynolds (Org.), Cognitive assessment: a multidisciplinary perspective (pp. 107-135). New York: Plenum Press.         [ Links ]

Ferguson, G. A. (1981). Statistical Analysis in Psychology and Education. New York: McGraww-Hill. International Editions - Psychology Series.         [ Links ]

Guilford, J. P. (1954). Psychometric Methods. New York: McGraw-Hill.         [ Links ]

Gulliksen, H. (1950). Theory of mental tests. New York: John Wiley & Sons.         [ Links ]

Hambleton, H. K. & Swaminatham, H. (1985). Item Response Theory: Principles and Applications. Boston: Kluwer.         [ Links ]

Johnson, R. A. & Wichern, D. W. (1992). Applied multivariate statistical analysis. London: Prentice Hall international.         [ Links ]

Lord, F. M. & Novick, N. R. (1974). Statistical Theories of mental test scores. Oxford, England: Addison-Wesley.         [ Links ]

Muñiz, J. (1994). Teoría Clásica de los Tests. Madrid: Ediciones Pirámide.         [ Links ]

Pivatto, M. M. (1992). Modelos para testes com respostas dicotômicas com principal enfoque em teoria de resposta ao item. Dissertação de Mestrado não publicada. Instituto de Matemática Estatística e Ciências da Computação, Universidade Estadual de Campinas, Campinas.         [ Links ]

Sternberg, R. J. (1981). The evolution of theories of intelligence. Intelligence, 5, 209-230.         [ Links ]

Sternberg, R. J. (1984). Toward a triarchic theory of human intelligence. The Behaviour and Brain Sciences, 7, 269-315.         [ Links ]

Sternberg, R. J. (1986). Toward a unified theory of human reasoning. Intelligence, 10, 281-314.         [ Links ]

 

 

Recebido em maio de 2012
Aceito em junho de 2012

 

 

Sobre o autor:

Ricardo Primi: psicólogo pela PUC Campinas, doutor em Psicologia Escolar e do Desenvolvimento Humano pela Universidade de São Paulo. É professor associado do Programa de Pós-Graduação em Psicologia da Universidade São Francisco.

Endereço para correspondência:
R. Dr. José Bonifácio Coutinho Nogueira, 225 - Cond. 4, Town House 8, 13091611 Campinas, São Paulo, Brasil.
E-mail: rprimi@mac.com

Essa pesquisa teve financiamento do CNPq.