ARTIGO ESPECIAL

 

Discalculia del desarrollo (DD)

 

Dyscalculia of development (DD)

 

 

Sandra Torresi

Psicopedagoga; Licenciada en Educación; Doctoranda en Psicología (Universidad de Palermo); Vicepresidente de la Sociedad Iberoamericana de Neuroeducación, Buenos Aires, Argentina

Dirección para correspondência

 

 

---

RESUMEN

Es relativamente reciente el interés por parte del ámbito científico con respecto al estudio de la cognición numérica. En la actualidad, los hallazgos provenientes de la neurociencia cognitiva y la psicología cognitiva se consideran aportes muy significativos para comprender el desarrollo de la competencia numérica y sus dificultades y a partir de esta evidencia científica, reducir la incertidumbre teórica en el diseño de estrategias de intervención psicopedagógicas y pedagógicas.

Palabras clave: Cognición Matemática. Neurociencia Cognitiva. Psicología Cognitiva. Estrategias de Intervención.

---

SUMMARY

The interest of the scientific field with respect to the study of the numerical cognition is relatively recent. Currently, evidence from cognitive neuroscience and cognitive psychology are considered very significant contributions to understand the development of numerical competence and its difficulties and, based on this scientific evidence, to reduce the theoretical uncertainty in the design of psychopedagogical and pedagogical strategies.

Keywords: Mathematical Cognition. Cognitive Neuroscience. Cognitive Psychology. Intervention Strategies.

---

 

 

¿CÓMO SE DESARROLLA LA COMPETENCIA NUMÉRICA?

 

 

El desarrollo del proceso numérico comienza con habilidades innatas que le permiten a un bebé de 6/7 meses detectar cambios en el número de objetos presentados visualmente. Este sentido numérico es una capacidad de adaptación al medio con la que también cuentan otras especies animales¹.

 

 

Cuando se inicia el lenguaje, los niños "nombran" con palabras-número: /uno/ /dos/, /tres/; aprenden a contar en voz alta y manipulan cantidades y números de forma muy simple. Con el inicio de la escolarización, se sistematiza la representación en formato arábigo con una "gramática" particular y diferente de la representación verbal de los números². Este sistema posicional es una forma económica de simbolizar un número con pocos dígitos respecto de la cantidad de palabras que exige el formato verbal.

 

 

Paralelamente, los niños van construyendo una "línea mental numérica"³ fundamental en el desarrollo del pensamiento matemático y el cálculo mental.

 

 

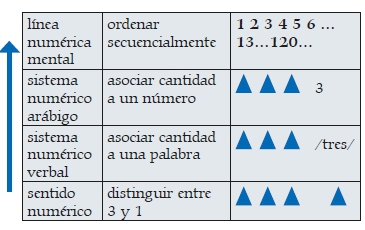
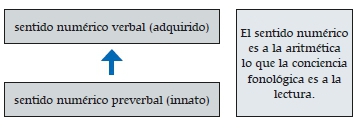
El sentido numérico es esencial para establecer las bases del aprendizaje matemático: las habilidades numéricas innatas se vinculan con los logros posteriores en la matemática simbólica¹.

 

 

¿QUÉ ES LA DISCALCULIA DEL DESARROLLO?

La discalculia del desarrollo (DD) es una dificultad en el aprendizaje de las habilidades aritméticas básicas⁴ que impacta en el nivel de rendimiento escolar y en las actividades de la vida cotidiana⁵. La DD es un trastorno del neurodesarrollo primario y específico… no es secundario a un déficit intelectual o sensorial ni tampoco a la falta de oportunidades educativas o un ambiente familiar adverso.

Es tan frecuente como las otras dificultades de aprendizaje, 3-8% de los estudiantes⁵ pero menos conocida en los ámbitos educativos probablemente porque es reciente el incremento de interés en su estudio por parte de la comunidad científica. La constante percepción de incompetencia lleva a los estudiantes con DD a desarrollar una actitud negativa hacia el conteo y la aritmética que luego evoluciona como ansiedad hacia la matemática o inclusive como fobia, por eso resulta imprescindible detectar e intervenir lo más tempranamente posible.

 

 

Si bien se utilizan indistintamente diferentes expresiones para hacer referencia a la misma dificultad, algunos investigadores reservan el término discalculia del desarrollo (DD) para nombrar al déficit específico de mayor severidad en las habilidades numéricas básicas y dificultades en el aprendizaje matemático (DAM) para las dificultades en matemática que surgen de algún déficit general en capacidades cognitivas (memoria, atención, habilidades visoespaciales).

 

 

La investigación sobre la base neurobiológica de la competencia matemática verifica la existencia de un sistema funcional complejo porque muchas áreas del cerebro sustentan las actividades matemáticas y varios sistemas están encargados de los distintos aspectos del número y la cantidad, sistemas que generalmente funcionan en forma conjunta integrando toda esa información para que tenga sentido como un todo⁶.

Las neuroimágenes de cerebros de niños con DD revelan anomalías estructurales y funcionales en las zonas cerebrales parietales de ambos hemisferios⁷, menor densidad de materia gris⁸ y menor activación en el surco intraparietal durante la ejecución de tareas sobre magnitudes⁹ que afectaría a las representaciones de cantidad.

 

UNA DIFICULTAD MUY HETEROGÉNEA

 

 

La variabilidad de las manifestaciones es muy significativa porque un número importante de niños con discalculia del desarrollo también tienen ADHD o dislexia (comorbilidad). Los perfiles de desempeño varían, por ejemplo, las dificultades ejecutivas se manifiestan en las estrategias y procedimientos matemáticos en el caso de DD asociado a ADHD, por otro lado, las dificultades de tipo verbal en conteo o recuerdo de hechos numéricos básicos surgen al asociarse DD y dislexia¹⁰.

 

¿TODOS LOS ESTUDIANTES CON BAJO DESEMPEÑO TIENEN DD O DAM?

Muchos estudiantes tienen un rendimiento bajo en matemática y no es por causa de una dificultad específica de aprendizaje. Es frecuente la presencia de "vacíos" conceptuales que impiden la construcción progresiva de la red de saberes jerarquizados e interrelacionados que exige la matemática. Como se trata de un problema vinculado a lo pedagógico, las estrategias didácticas sistemáticas, individualizadas e intensivas suelen ser suficientes para promover el desarrollo de la competencia matemática. En cambio, el déficit en la DD es mucho más severo y persistente por lo que el abordaje también debe realizarse desde ámbitos especializados en dificultades específicas del aprendizaje.

 

¿CUÁL ES EL DÉFICIT NUMÉRICO ESPECÍFICO EN LA DD?

En la actualidad, dos posibles causas específicas del origen de la DD primaria están en plena investigación y debate¹¹.

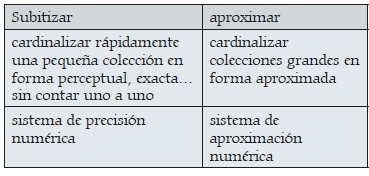
• un déficit en el sentido numérico: subitizar pequeñas cantidades de puntos o aproximar colecciones más grandes porque no hay comprensión del significado de las cantidades tanto en el sistema de precisión como en el de aproximación numérica⁵.

 

 

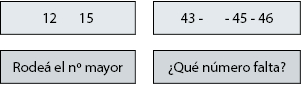
• un déficit para acceder a las representaciones numéricas mentales simbólicas (números en formato arábigo): comparar cantidades y ubicar arábigos en la recta numérica o hacer cálculos simples de suma y resta.

 

 

¿EXISTEN INDICADORES TEMPRANOS?

El conocimiento de los indicadores de dificultades en el desarrollo de una habilidad permite realizar intervenciones preventivas. Por ejemplo, un educador es clave en la detección y derivación temprana de un niño de 4 años que por ejemplo…

• no intenta etiquetar cada elemento de una colección con

• una palabra-número

• no separa hasta cinco objetos

• presenta dificultades para comparar números del intervalo 1-5

• adjudica siempre la misma etiqueta numérica (4, 2) a diferentes colecciones de elementos

• no cardinaliza adecuadamente

• falla al agrupar objetos de acuerdo con diferentes criterios (forma/color/tamaño)

• no reconoce patrones fácilmente.

 

¿EN QUÉ TAREAS ARITMÉTICAS SE OBSERVAN MAYORES DIFICULTADES?

• subitizar: reconocer el número de elementos de una pequeña colección (hasta 3) rápidamente y con exactitud ¡sin contar!

 

 

• estimar: aproximar la cantidad de elementos de una colección ¡sin contar!

 

 

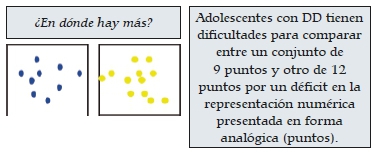
• contar

 

 

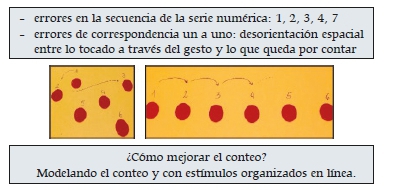
• aprender secuencias orales: contar hacia atrás, con diferentes intervalos

 

 

• reconocer las regularidades del sistema de numeración

 

 

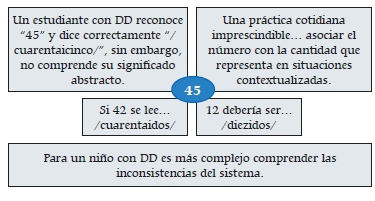
• comprender conceptos numéricos, reglas, secuencias y símbolos numéricos

• comparar números: ordenar numerosidades por tamaño

 

 

Comparar y ordenar números de menor a mayor (3º)

• cambiar con fluidez de una representación numérica a otra¹².

 

 

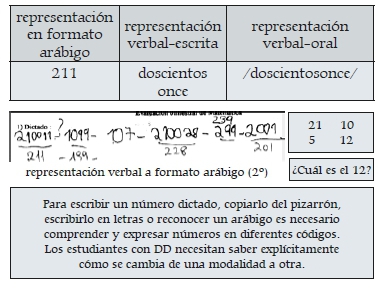
• organizar espacialmente cantidades (representación visoespacial)

 

 

• aplicar estrategias de cálculo

 

 

• recordar en forma automática (con fluidez) los hechos numéricos básicos

 

 

• resolver cálculos mentales

 

 

• resolver operaciones, especialmente restas y divisiones

 

 

• resolver problemas simples

 

 

• alternar procedimientos de resolución de problemas… (escasa flexibilidad cognitiva)

• leer mapas, gráficos, reconocer objetos en 3D desde diferentes perspectivas

• manejar el sistema monetario: comprender el concepto de "vuelto", comprender equivalencias, comprender cantidades con centavos.

• manejar magnitudes y proporciones: recordar secuencias temporales, estimar y comparar tiempo, velocidad y distancia, decir la hora (reloj analógico)

 

 

• autorregular y automonitorear: dificultades para evaluar habilidades para resolver un problema, seleccionar las estrategias necesarias, organizar la información y monitorear los resultados.

 

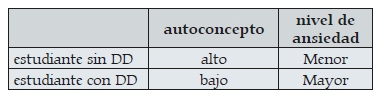
¿CÓMO IMPACTA LA DD EN LA CONSTRUCCIÓN DEL AUTOCONCEPTO DE LOS ESTUDIANTES?

 

 

El concepto de sí mismo y la motivación tienen una importante repercusión en el aprendizaje e inciden en el desempeño ante una tarea matemática. Los estudiantes con DD atribuyen sus éxitos académicos a la ayuda recibida, la facilidad de la tarea o simplemente a "la suerte". Sin embargo, cuando se trata de explicar errores, las causas son siempre internas: "no puedo, "no entiendo nada", "no me gusta" y evitan toda situación vinculada con "los números".

 

 

¿QUÉ ACCIONES PEDAGÓGICAS FAVORECEN A UN ESTUDIANTE CON DD?

 

 

Un niño o adolescente con DD necesita las mismas estrategias de intervención pedagógicas que todos los estudiantes para desarrollar la competencia matemática, pero significativamente más explícitas, más intensivas y más extensivas.

Algunas acciones concretas los favorecen especialmente:

• Desarrollar los conceptos matemáticos siguiendo la secuencia:

 

 

• Construir redes de conceptos para evitar "vacíos" en el conocimiento.

• Utilizar estrategias multisensoriales.

• Modelar cómo utilizar la matemática en la vida cotidiana: uso del sistema monetario, organización temporal de actividades, manejo del tiempo de estudio… elegir ejemplos concretos que conecten la matemática con la vida real.

• Comprobar la construcción de aprendizajes previos antes de continuar con un nuevo objetivo de estimulación.

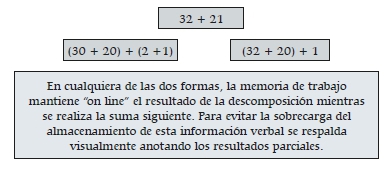
• Intervenir con explicaciones precisas y breves para no sobrecargar la memoria de trabajo.

• Promover la formulación de preguntas… si pregunta sobre un contenido es porque lo está entendiendo.

• Corroborar la adecuada comprensión del lenguaje matemático: ¿Sabés que quiere decir ordenar/agrupar/clasificar/trazar/tiene más que/…?

• Favorecer el "poner en palabras" las estrategias utilizadas, explicar qué hicieron y por qué lo hicieron de esa forma.

• Modelar con las propias estrategias de resolución.

• Practicar en forma contextualizada.

• Diseñar secuencias didácticas intensivas y extensivas que permitan consolidar el aprendizaje.

• Evitar la ejercitación reproductiva sin reflexión… NO asegura el aprendizaje.

• Extender en el tiempo la estimulación de las habilidades aritméticas básicas: subitización, aproximación, cálculos básicos, concepto de número, posicionalidad…

• Proponer frecuentemente actividades orientadas al desarrollo de procesos cognitivos básicos: memoria a largo plazo, memoria de trabajo, atención, percepción, lenguaje y organización visoespacial.

• Promover el desarrollo de estrategias de planificación y revisión en todas las actividades que se realicen (funciones ejecutivas).

• Analizar las ventajas y desventajas de diferentes procedimientos de resolución para optar por los más convenientes (toma de decisiones).

• Favorecer la comprensión de los procedimientos segmentando en los componentes más simples (sin perder el todo).

• Acompañar la identificación del error y promover la autocorrección inmediata. Las correcciones diferidas suelen no ser efectivas.

 

 

• Seleccionar flexiblemente los recursos de acuerdo con las necesidades de cada estudiante.

• Crear un ambiente de aprendizaje con soportes visuales diversos que sean funcionales al tema que se está desarrollando.

• Hablar con el estudiante sobre sus dificultades.

• Reforzar positivamente cada pequeño logro y expresar la alegría que genera su aprendizaje.

• Importante… formularse las siguientes preguntas y registrar las respuestas en algún formato simple que permita analizar la información y tomar decisiones pedagógicas.

 

 

Un estudiante con DD necesita una institución dispuesta a flexibilizar su organización para acompañar su proceso de aprendizaje: espacios, tiempos, recursos, metodologías, organización. También necesita un educador que conozca las características de las dificultades específicas del aprendizaje y que comprenda la singularidad de sus fortalezas y debilidades para diseñar una propuesta educativa de calidad.

El desarrollo cerebral es producto de un proceso de co-construcción entre lo genético y lo ambiental… una dinámica que se evidencia en la predisposición natural que tenemos para la matemática que el ambiente debe cultivar y enriquecer¹. Solo se puede estimular adecuadamente aquello que se conoce en profundidad, por esto, es importante la actualización permanente y la reflexión interdisciplinaria sobre el desarrollo típico de la competencia matemática y sus dificultades.

 

REFERENCIAS

1. Starr A, Libertus M, Brannon E. Number sense in infancy predicts mathematical abilities in childhood. Proc Natl Acad Sci U S A. 2013;110(45):18116-20.         [ Links ]

2. Roselli M, Matute E. La neuropsicología del desarrollo típico y atípico de las habilidades numéricas. Rev Neuropsicol Neuropsiq Neuroc. 2011;11(1):123-40.         [ Links ]

3. Dehaene S. The number sense: How the mind creates mathematics. New York: Oxford University Press; 2011.         [ Links ]

4. Geary DC. Consequences, characteristics, and causes of mathematical learning disabilities and persistent low achievement in mathematics. J Dev Behav Pediatr. 2011;32(3):250-63. DOI:10.1097/ DBP.0b013e 318209ede        [ Links ]

5. Butterworth B, Varma S, Laurillard D. Dyscalculia: from brain to education. Science. 2011;332(6033):1049-53. DOI:10.1016/j.cub. 2011.07.005        [ Links ]

6. Blakemore S, Frith U. Cómo aprende el cerebro: las claves para la educación. Ariel; 2011.         [ Links ]

7. Molko N, Cachia A, Rivière D, Mangin JF, Bruandet M, Le Bihan D, et al. Functional and structural alterations of the intraparietal sulcus in a developmental dyscalculia of genetic origin. Neuron. 2003;40(4):847-58.         [ Links ]

8. Rotzer S, Kucian K, Martin E, von Aster M, Klaver P, Loenneker T. Optimized voxel-based morphometry in children with developmental dyscalculia. Neuroimage. 2008; 39(1):417-22.         [ Links ]

9. Kucian K, Loenneker T, Dietrich T, Dosch M, Martin E, von Aster M. Impaired neural networks for approximate calculation in dyscalculic children: a functional MRI study. Behav Brain Funct. 2006;2:31.         [ Links ]

10. Wilson A, Dehaene S. Number sense and developmental dyscalculia. In: Coch D, Dawson G, Fischer K, eds. Human behavior, learning, and the developing brain: Atypical development. New York: Guilford; 2007. p.212-38.         [ Links ]

11. Piazza M, Facoetti A, Trussardi AN, Berteletti I, Conte S, Lucangeli D. Developmental trajectory of number acuity reveals a severe impairment in developmental dyscalculia. Cognition. 2010;116(1):33-41.         [ Links ]

12. McCloskey M, Caramazza A, Basili A. Cognitive mechanisms in number processing and calculation: evidence from dyscalculia. Brain Cogn. 1985;4(2):171-96.         [ Links ]

REFERENCIAS COMPLEMENTARIAS

American Psychiatric Association. Diagnostic and Statistical Manual of Mental Disorders. 5th ed. Washington: American Psychiatric Association; 2013.         [ Links ]

Chan WW, Au TK, Tang J. Developmental dyscalculia and low numeracy in Chinese children.         [ Links ]

Kaufmann L, Mazzocco MM, Dowker A, von Aster M, Göbel SM, Grabner RH, et al. Dyscalculia from a developmental and differential perspective. Front Psychol. 2013;4:516.         [ Links ]

Mazzocco MM, Feigenson L, Halberda J. Impaired acuity of the approximate number system underlies mathematical learning disability (dyscalculia). Child Dev 2011;82(4):1224-37. DOI: 10.1111/j.1467-8624.2011.01608.xdoi: 10.3389/fpsyg.2013.00516        [ Links ]

Rosselli M, Matute E, Pinto N, Ardila A. Memory abilities in children with subtypes of dyscalculia. Dev Neuropsychol. 2006;30(3):801-18. DOI: 10.1207/s15326942dn3003_3        [ Links ]

 

 

Dirección para correspondência:
Sandra Torresi
Palestina 646 - 1° 8
Buenos Aires, Argentina - CP 1182
E-mail: sptorresi@gmail.com

Artigo recebido: 3/10/2018
Aprovado: 18/10/2018

 

 

Trabalho realizado na Sociedad Iberoamericana de Neuroeducación, Buenos Aires, Argentina.
Conflito de interesses: A autora declara não haver.