ARTIGOS

 

Unidimensionalidade e a propriedade de invariância das estimativas da habilidade pela TRI

 

Unidimensionality and the invariance property of IRT ability estimates

 

 

Frederico Neves Conde ^*; Jacob Arie Laros ^**

Universidade de Brasília

Endereço para correspondência

 

 

---

RESUMO

A Teoria de Resposta ao Item (TRI) assume a propriedade de invariância dos parâmetros, que permite estimar a proficiência dos sujeitos independentemente da forma do teste administrado. O presente estudo investigou se estimativas da proficiência realmente independem da dificuldade do teste. As respostas de 18.806 alunos da 8ª série do Ensino Fundamental em um dos 26 cadernos do teste de Matemática foram analisadas. Encontrou-se uma dependência entre a dificuldade do caderno e a estimativa da proficiência, que ficou menos forte após a exclusão dos itens com baixas cargas fatoriais no fator único. Isso indica que quanto mais o pressuposto da unidimensionalidade é satisfeito, menos forte é a relação entre a dificuldade do teste e estimativa da proficiência. Conclui-se que a verificação do pressuposto da unidimensionalidade é de suma importância sempre que a TRI é utilizada, a fim de que a propriedade tão desejável da invariância dos parâmetros possa se manifestar.

Palavras-chave: Psicometria, Teoria de Resposta ao Item (TRI), Invariância dos parâmetros, Unidimensionalidade, SAEB.

---

ABSTRACT

Item Response Theory (IRT) assumes the property of invariance of parameters, which permits to estimate the proficiency of a person independently of the test form administered. The present study investigated if estimates of proficiency are really independent of the difficulty of a test. The answers of 18,806 pupils attending the 8th grade of basic education to one of 26 Mathematics test booklets were analyzed. Results showed a dependency between the difficulty of the test booklet and estimates of proficiency, which becomes less strong after exclusion of items with weak loadings on the unidimensional factor. This finding suggests that the more the assumption of unidimensionality is satisfied, the weaker the relation between the difficulty of a test and estimates of proficiency. It can be concluded that verification of the assumption of unidimensionality is of vital importance always when IRT is used, otherwise the very desirable invariance property of IRT might not apply.

Keywords: Psychometrics, Item Response Theory (IRT), Invariance of parameters, Unidimensionality, SAEB.

---

 

 

Introdução

A Teoria de Resposta ao Item (TRI) é um modelo estatístico que, em caso de itens dicotômicos, especifica a relação que existe entre a probabilidade de um indivíduo acertar o item e a habilidade latente ou traço latente requerida na sua resolução. A habilidade latente, que não pode ser diretamente mensurada, também é chamada teta ( ), e corresponde a dimensão psicológica que está sendo medida. Na TRI a probabilidade de acertar o item é modelada como função da habilidade latente do indivíduo e os parâmetros que representam algumas propriedades do item. A relação entre a habilidade latente e a probabilidade de acertar o item é descrita por uma equação monotônica crescente, chamada de Curva Característica do Item (CCI). A TRI se baseia em dois pressupostos principais: a unidimensionalidade e a independência local. O pressuposto da unidimensionalidade significa que apenas uma habilidade latente pode ser medida pelo conjunto de itens que compõem o teste. O pressuposto da independência local significa que quando a habilidade latente que está sendo mensurada pelo conjunto de itens é mantida constante, nenhum par de itens pode ser correlacionado. Este pressuposto implica que a probabilidade de acertar um item depende exclusivamente da habilidade do examinado, não da ordem do item dentro da prova, do cansaço etc. (Lord, 1980).

A TRI fornece modelos que atribuem parâmetros para itens e para indivíduos separadamente de forma a predizer probabilisticamente a resposta de qualquer indivíduo a qualquer item. Geralmente, os itens podem ser avaliados por meio de modelos de um, dois ou três parâmetros. O modelo de um parâmetro envolve apenas a dificuldade do item (parâmetro b); o de dois envolve a dificuldade e a discriminação (parâmetro a); e o de três parâmetros envolve a dificuldade, a discriminação e o acerto ao acaso (parâmetro c). Em todos estes modelos estima-se também o parâmetro teta, referente à habilidade de cada pessoa testada.

A TRI fornece contribuições na construção de testes, na identificação de viés de itens, na equalização de resultados de desempenho de examinandos em resposta a diferentes formas de um teste e na apresentação dos resultados por meio das escalas de desempenho (Van der Linden & Hambleton, 1997). Teoricamente, a TRI supera algumas limitações que a psicometria tradicional, baseada na Teoria Clássica dos Testes (TCT), contém. Se não a principal, uma das principais limitações da TCT é que as características dos examinandos e as características dos testes não podem ser separadas, sendo que uma só pode ser interpretada no contexto da outra (Andrade, 2000; Baker, 2001; Fernandez, 1990; Hambleton, Swaminathan & Rogers, 1991). Sob o enfoque da TCT, os escores totais que os examinandos obtiveram em resposta a uma prova dependem do teste utilizado. Sabe-se, assim, que o desempenho do examinando em um determinado teste pode variar em função da dificuldade de seus itens. Desta forma, geralmente, quando um teste é difícil, o examinando tende a apresentar um escore total baixo e, quando é fácil, tende a apresentar um escore total alto.

Por outro lado, a classificação da dificuldade de um teste ou de um item do teste depende da habilidade dos examinandos. Como o cálculo do índice de dificuldade dos itens se dá pelo percentual de examinandos que os acertou, um item é considerado difícil se esse percentual for baixo e fácil se esse percentual for alto. Se a habilidade da amostra de examinandos, representada pelo escore total, for, em média, maior que a de uma outra amostra de examinandos, gerarão diferentes índices de dificuldade.

Se, pela TCT, os índices de dificuldade dependem da habilidade dos examinados e a habilidade estimada depende da dificuldade dos itens da prova, verifica-se uma dependência circular entre eles. Uma das implicações práticas dos índices de dificuldade dos itens serem dependentes do grupo é que um mesmo conjunto de itens pode apresentar dois conjuntos diferentes de índices, se estes são calculados para duas amostras diferentes. Na administração de um banco de itens, por exemplo, isso é um problema de difícil solução. O Banco Nacional de Itens (BNI) do Instituto Nacional de Estudos e Pesquisas Educacionais Anísio Teixeira (INEP) armazena um conjunto de índices de cada item calculado pela TCT vinculado à avaliação que este item foi utilizado. Quando um item do SAEB é pré-testado nas capitais de cinco Estados, um de cada região, e posteriormente aplicado em uma avaliação estadual, por exemplo, é possível obter índices de dificuldade diferentes para um mesmo item. Um item receberá índices de dificuldade diferentes se a habilidade média dos estudantes em um determinado Estado for diferente da habilidade média dos estudantes das cinco capitais em que o pré-teste foi realizado. Um outro exemplo dessa "dupla identidade" do item (dois índices diferentes de dificuldade) pode ser encontrado na utilização de itens do SAEB 2001 em uma avaliação municipal de uma cidade do interior do Ceará. Um determinado item de Língua Portuguesa apresentou um índice de dificuldade (percentual de acertos) de 0,54 na aplicação nacional do SAEB, e de 0,45 quando aplicado no Município. No BNI, são registradas avaliações diferentes e armazenadas ambas as informações. O problema de obter vários índices de dificuldade dos itens pode ser minimizado se o plano amostral for bem delineado.

Por sua vez, a TRI assume a propriedade de invariância dos parâmetros, considerada como a sua maior distinção da TCT. Esse princípio afirma que quando um conjunto total de itens se adequa a um modelo da TRI, os parâmetros dos itens a, b, e c são independentes da habilidade dos examinandos (Baker, 2001) e a habilidade dos examinandos pode ser estimada independentemente da dificuldade do teste utilizado. Ou seja, os parâmetros dos itens a, b, e c independem do nível de habilidade dos examinandos que os responderam e a habilidade dos examinandos independe dos itens utilizados para determiná-la (Embretson & Herschberger, 1999).

Contudo, Fan (1998) alerta para a escassez de estudos empíricos que busquem verificar essa propriedade, anunciada pela TRI como uma de suas grandes vantagens sobre a TCT. O autor realizou uma investigação empírica que buscasse respostas (a) do quanto são comparáveis as estatísticas dos itens e dos examinandos geradas a partir da TCT e da TRI, e (b) do quanto essas estatísticas da TCT e da TRI são invariantes, quando calculadas por meio de amostras diferentes. Utilizando uma base de dados de um programa de avaliação em larga escala, o autor realizou a investigação empírica destas questões. O estudo apresentou, como resultados principais, que (a) as estatísticas dos examinandos pela TCT foram altamente comparáveis com as estimadas pela TRI, (b) os índices de dificuldades calculados pela TCT foram muito comparáveis com aqueles estimados pela TRI, e (c) o grau de invariância dos itens, pela TCT, foi altamente comparável com o grau de invariância em relação aos índices estimados pela TRI. Estes resultados não confirmam a superioridade teórica da TRI, com relação à invariância dos parâmetros dos itens.

Uma das condições necessárias para que haja a independência entre a habilidade estimada pela TRI e a dificuldade dos itens, de acordo com Baker (2001), Hattie (1985) e Kirisci, Hsu e Yu (2001), é que se esteja avaliando um mesmo traço latente, ou seja, que os itens do teste sejam unidimensionais. Para verificar a relação entre unidimensionalidade de um teste e a independência da habilidade estimada pela TRI e a dificuldade dos itens a pesquisa atual foi idealizada.

Os objetivos do presente estudo são: (a) verificar em que medida a estimativa da habilidade do aluno estimada pela TRI (teta) depende da dificuldade do teste, e (b) verificar o impacto da unidimensionalidade na relação entre a dificuldade do teste e a habilidade (teta) do aluno.

O Sistema Nacional de Avaliação da Educação Básica (SAEB)

O INEP vem obtendo informações sobre o desempenho dos alunos brasileiros desde 1990, por meio do Sistema Nacional de Avaliação da Educação Básica (SAEB). Esse sistema de avaliação em larga escala avalia o desempenho de estudantes do Ensino Fundamental e do Ensino Médio em disciplinas como Língua Portuguesa e Matemática, através da aplicação de testes educacionais. Realiza, ainda, um levantamento de informações de fatores associados ao desempenho mediante a aplicação de questionários.

A partir de 1995, o SAEB adotou uma metodologia de elaboração dos testes e de análise de dados baseada na TRI, com o modelo de três parâmetros (Baker, 2001; Lord, 1980; Van der Linden & Hambleton, 1997). O desempenho dos estudantes, sob esse enfoque teórico, é estimado conjuntamente entre as séries e anos de avaliação. Assim, uma série de procedimentos de análise é utilizada de forma que os resultados dos estudantes possam ser colocados em uma mesma métrica e representados em uma mesma escala. A escala única do SAEB varia teoricamente de 0 a 500, sendo que geralmente os resultados de desempenho dos estudantes variam, na prática, de 100 a 400. Uma das vantagens da utilização de uma escala comum entre anos é a possibilidade da criação de uma série histórica que permite o monitoramento dos resultados no decorrer do tempo.

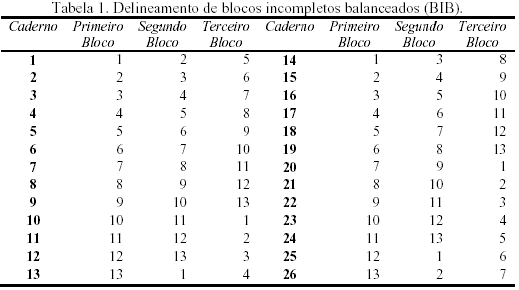
O SAEB adotou uma metodologia baseada na amostragem matricial de itens, que utiliza o esquema de montagem e aplicação de testes por Blocos Incompletos Balanceados (BIB). Sob esse delineamento, são montados, primeiramente, 13 blocos de itens. Desde 1999, o SAEB utiliza 13 itens por bloco, mas antes de 1999 utilizou tamanhos que variavam de 10 a 13 itens por bloco. São montados 26 cadernos a partir da combinação, três a três, desses blocos de itens, por meio da orientação fornecida pela matriz do BIB, apresentada na Tabela 1.

Esta distribuição de itens por blocos e combinação de blocos por cadernos permite que um mesmo conjunto de itens esteja localizado na primeira posição (primeiro bloco) em dois cadernos de teste, na segunda posição, em outros dois cadernos e na terceira posição, em outros dois. Por exemplo, o bloco 1 está localizado na primeira posição nos cadernos 1 e 14; na segunda posição nos cadernos 13 e 25; e na terceira posição nos cadernos 10 e 20. Esta observação vale para qualquer um dos 13 blocos.

Com o esquema amostral e o delineamento BIB adotado, consegue-se uma aplicação em que os estudantes que respondem a um determinado caderno apresentem, proporcionalmente, características semelhantes aos grupos que responderam aos outros cadernos, visto que a alocação dos cadernos aos alunos é aleatória. Em outras palavras, os grupos de estudantes que respondem a cada um dos 26 cadernos de teste do SAEB são equivalentes. A realização de análises pela TRI e a utilização de um delineamento no qual formas de testes diferentes são aplicadas a grupos de estudantes, com características semelhantes, faz dos resultados do SAEB um excelente material de pesquisa da propriedade de invariância do teta, em relação à dificuldade dos testes aplicados.

 

Método

Participantes

O teste da 8ª série do Ensino Fundamental (EF) de Matemática do SAEB 1997 foi respondido por uma amostra de 18.806 estudantes da rede pública e particular, delineada para produzir resultados de desempenho representativo para as 27 unidades da federação e, dentro delas, para sub-populações de interesse. A amostra do SAEB 1997 foi estratificada levando-se em conta as variáveis de escolas: zona (rural ou urbana), localização (capital ou interior) e rede administrativa (estadual, municipal e particular).

 

 

Instrumentos

Os 161 itens do teste foram construídos com base em uma matriz de referência (Pestana, 1997) de conteúdos e competências, validada em nível nacional em termos do currículo efetivo e com base no que estava sendo ensinado aos estudantes. Do conjunto total de itens selecionados foram montados 13 blocos de 11 ou 13 itens. Houve uma preocupação, da mesma forma, em montar cada bloco com itens baseados em descritores e complexidades variadas. A combinação dos 13 blocos de acordo com o delineamento BIB produziu 26 cadernos de teste. Seis cadernos foram compostos por 35 itens, doze por 37 itens e oito por 39 itens.

Procedimentos

Garantida a devida padronização nos procedimentos de aplicação, cada aluno respondeu a um único caderno do teste de Matemática. Esses cadernos foram distribuídos seqüencialmente dentro de uma turma. O primeiro aluno que respondeu ao teste de Matemática recebeu o caderno 1, o segundo aluno que respondeu ao teste de Matemática recebeu o caderno 2, e assim sucessivamente. Os cadernos desta disciplina foram distribuídos alternadamente com os cadernos das outras disciplinas aplicadas na 8ª série do EF (Língua Portuguesa e Ciência) no SAEB 1997. O teste foi aplicado por pessoal contratado que utilizou cerca de uma semana para cobrir toda a amostra. Anteriormente à aplicação do teste, foi aplicado um questionário sócio-demográfico. O tempo de aplicação do teste foi de 75 minutos, divididos em três períodos de 25 minutos para cada bloco. Os alunos de cada sala iniciavam ao mesmo tempo o preenchimento de cada bloco de itens.

Uma análise exploratória dos dados foi primeiramente realizada com o objetivo de identificar o grau de qualidade psicométrica dos itens que compunham o teste. Os coeficientes de correlação bisserial (uma correlação entre o item e o escore total no teste) foram utilizados para a definição da permanência ou não de cada um dos itens nas próximas fases de análise. Esperavam-se correlações positivas e altas na alternativa correta e negativas nos distratores (alternativas incorretas).

Para a estimação dos parâmetros dos itens e das habilidades pela TRI, foram mantidos apenas os itens que apresentaram correlação item-total maior que 0,20, tendo sido excluídos 4 dos 161 itens. Esse procedimento é justificado: aqueles itens que não apresentaram boa qualidade discriminativa poderiam prejudicar a estimação dos parâmetros por meio da TRI. Utilizou-se um critério até certo ponto leniente para que não se perdesse uma grande quantidade de itens.

Os seguintes parâmetros dos 157 itens mantidos foram estimados, por meio da TRI: a discriminação (parâmetro a), a dificuldade ou parâmetro de posição (parâmetro b), e o acerto ao acaso (parâmetro c). Também foram estimadas as habilidades dos estudantes (teta) por meio da TRI. Para tanto, foi utilizado o software BILOG-MG (Zimowski, Muraki, Mislevy & Bock, 1996), que implementa a Teoria dos Grupos Múltiplos (Bock & Zimowski, 1995). Essa teoria permite a estimação conjunta dos parâmetros em várias amostras não-equivalentes.

Os parâmetros dos itens do teste e das habilidades foram estimados conjuntamente aos dos parâmetros dos itens dos testes de Matemática da 4a Série do EF e 3a Série do Ensino Médio (EM) do SAEB 97 e dos testes de Matemática da 4a e 8a Séries do EF e da 3a Série do EM do SAEB 95. Essas estimativas, portanto, se encontram na mesma escala entre séries e anos do SAEB. Os parâmetros de dificuldade estimados pela TRI e o parâmetro de habilidade teta são registrados em uma escala que varia, geralmente, de -3 a 3 e que apresenta média 0, com desvio-padrão de 1. Para efeito de divulgação dos resultados do SAEB, eles são transformados para uma escala que varia de 0 a 500. Ressalta-se que, para efeitos do presente trabalho, os escores de habilidade teta serão sempre relatados na escala original da TRI (média 0, d.p. 1).

Para a estimação dos parâmetros dos itens e das proficiências, foram considerados os pesos amostrais normalizados. A normalização torna a soma dos pesos igual ao número de ocorrências da amostra, utilizando valores de pesos individuais substancialmente menores. Seguindo esse procedimento como uma opção de análise, foi realizada a normalização dos pesos amostrais originais (que chamaremos de peso_o). Para um examinando j, o valor de cada peso amostral normalizado (que chamaremos de peso_n) é

peso_n(j) = (18.806) · [peso_o(j) / 2.512.018].

Em que, peso_n(j) é o peso normalizado do examinando j e o peso_o(j), o peso original do examinando j. O valor 2.512.018 é a soma dos pesos originais (peso_o) e a estimativa do número de estudantes na população; e o valor 18.806 é o número de estudantes da amostra.

Duas condições foram fundamentais para a viabilização do estudo de verificação da invariância de teta com relação à dificuldade dos cadernos. Em primeiro lugar, foi fundamental, para nossa investigação, que os grupos que responderam aos cadernos de provas apresentassem características iguais em termos de habilidades, ou seja, que fossem equivalentes. Em segundo lugar, foi fundamental que os cadernos de provas apresentassem variabilidade em suas dificuldades, ou seja, que fossem de dificuldades diferentes.

A dificuldade dos cadernos foi representada pela estatística de dificuldade calculada pela TCT (valor p), que é o percentual de acertos do grupo de alunos que respondeu a cada um dos cadernos. Foram calculados os índices valor p médios dos cadernos, considerando os pesos amostrais, o que gerou 26 índices de dificuldade. As médias das habilidades estimadas por meio da TRI dos grupos de examinandos que responderam a cada um dos cadernos foram também calculadas.

Em posse dos 26 índices de dificuldade (valor p) médios e das 26 estimativas de habilidade da TRI (teta) médias para os estudantes que responderam a cada um dos cadernos, foram calculadas correlações (r de Pearson). Esperavam-se correlações baixas entre os índices de dificuldade e o teta.

Baker (2001) considerou que uma das condições básicas para a existência de invariância do teta é a de "todos os itens medirem o mesmo traço latente". Um outro aspecto que se procurou investigar no âmbito dessas correlações foi a influência de itens que praticamente não contribuíam para a unidimensionalidade na invariância do parâmetro de habilidade pela TRI.

Com base em uma análise prévia da unidimensionalidade das provas do SAEB 97 utilizando análise fatorial full information (Laros, Pasquali & Rodrigues, 2000), foi possível identificar os 26 itens da prova de Matemática da 8a série que apresentavam cargas fatoriais muito baixas no fator único (abaixo de 0,20). Assim, foram excluídos da análise clássica e da estimação dos parâmetros da TRI 30 itens: os 26 itens que praticamente não contribuíram na mensuração do fator único, e os 4 itens com correlação item-total menor que 0,20. Ressalta-se também que a prova apresentava, após a exclusão dos itens, um total de 131 itens, divididos em 26 cadernos que variaram de 19 a 39 itens.

Depois da exclusão dos 26 itens as novas percentagens de acerto foram calculadas e as novas habilidades (teta) estimadas. Na estimação do teta, todos os comandos do programa BILOG-MG foram mantidos os mesmos da primeira estimação, com exceção do comando groups, que indica os itens que entrariam nesta estimação. Justifica-se esse procedimento: esperava-se comparar as estimativas do teta sem a exclusão e, posteriormente, com a exclusão dos itens. Assim, quanto menor a influência de outros fatores que não essa eliminação de itens, melhor seria o controle dos fatores que poderiam influenciar os resultados.

Considerando as novas informações de médias, foram calculadas as médias, o desvio padrão e a amplitude entre elas. Também foram novamente calculadas as correlações (r de Pearson). Esperava-se que, se efetivamente a unidimensionalidade fosse uma condição para que ocorresse a invariância do parâmetro do teta, a correlação entre o teta e a dificuldade fosse menor que no caso sem a exclusão de itens.

 

Resultados

Após a verificação da equivalência das habilidades entre os 26 grupos de estudantes que responderam aos 26 cadernos, o levantamento de informações sobre as dificuldades dos cadernos de provas foi realizado, já que esta variável é fundamental para o alcance dos objetivos do estudo. Só se poderia investigar a influência da diferença de dificuldade entre os testes sobre a variável de habilidade estimada pela TRI se houvesse realmente variabilidade entre essas dificuldades.

Os resultados das estatísticas de dificuldade dos itens que compunham os cadernos e as estatísticas de habilidades dos estudantes que os responderam são apresentados na Tabela 2.

 

 

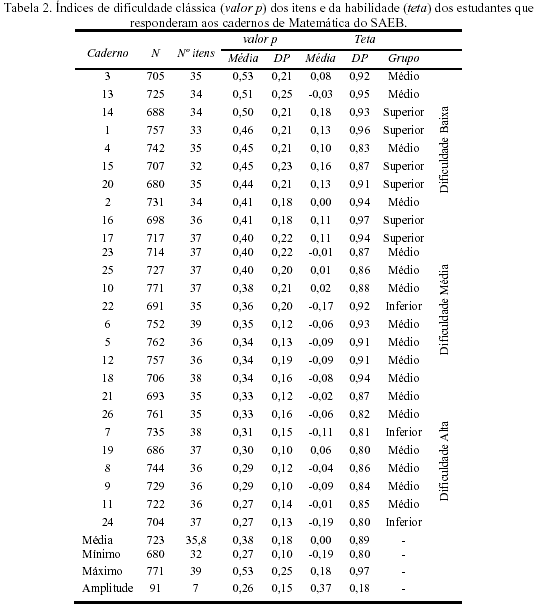
Ao inspecionar a Tabela 2 verifica-se que os 26 cadernos foram respondidos por, em média, 723 alunos. O caderno menos respondido foi o 20 (N = 680), enquanto que o 10 foi o caderno com maior número de respondentes (N = 771). O caderno com menor número de itens foi o 15 (32 itens); o caderno com maior número de itens foi o 6 (39 itens). A média dos índices de dificuldade dos 26 cadernos (valor p) foi de 0,38; o percentual de acertos aos itens que compõem os cadernos variou de 0,27 (cadernos 11 e 24, que são, em média, os mais difíceis) a 0,53 (caderno 3, o mais fácil). Levando estes resultados em consideração fica evidente que existem grandes diferenças em relação à dificuldade dos cadernos. O desvio-padrão médio do valor p dos 26 cadernos foi de 0,18. A diferença entre o caderno mais fácil e o mais difícil é de 0,26, que representa uma variabilidade de 1,44 d.p. (0,26/0,18 = 1,44), considerada uma diferença grande (Cohen, 1992).

A média dos resultados de teta dos estudantes foi de 0 (zero), o que equivale ao centro da escala. O desvio-padrão médio do teta dos 26 grupos de respondentes foi de 0,89. O teta médio dos 26 grupos variou de -0,19, referente ao grupo que respondeu ao caderno 24, a 0,18, referente ao grupo que respondeu ao caderno 14, o que representa uma amplitude de 0,37. O tamanho desta amplitude representa 0,42 DP. (0,37/0,89 = 0,42), considerada uma variabilidade pequena.

A associação entre o valor p e teta forneceu um coeficiente de correlação r de 0,68 (p < 0,01). Assim, pode-se concluir que a habilidade estimada pela TRI varia de forma semelhante à variação da dificuldade dos itens que são utilizados para estimá-la. A correlação de 0,68 indica que quase a metade da variância do teta (46%) está associada à variância da dificuldade dos cadernos. Assim, para grupos equivalentes em habilidade, cadernos de Matemática mais difíceis tendem a fornecer estimativas menores de habilidade que cadernos mais fáceis.

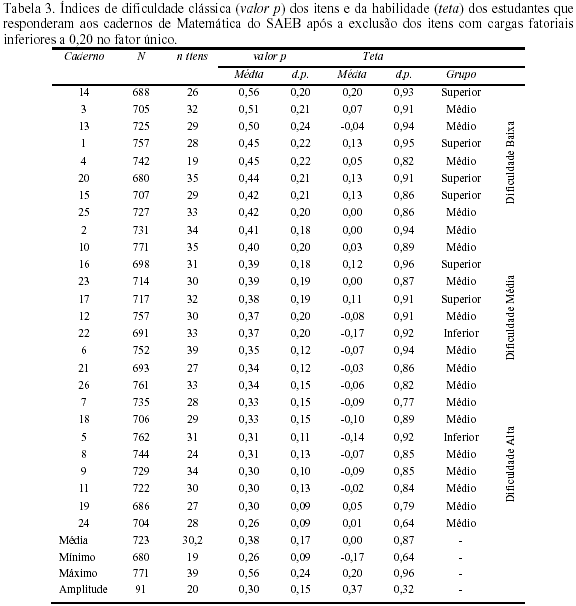
Após a exclusão dos itens que apresentaram cargas fatoriais iguais ou abaixo de 0,20 no fator único, a realização de novos cálculos das estatísticas de dificuldade e de uma nova estimação das habilidades dos estudantes nos 26 cadernos, os seguintes resultados foram observados (Tabela 3).

Sob essa configuração de análise, a média do índice de dificuldade dos cadernos pela TCT (valor p) foi de 0,38, o mesmo valor observado sem a exclusão dos itens. Observa-se também que as médias de valor para os 26 cadernos variam de 0,26 (caderno 24, que é o mais difícil) a 0,56 (caderno 14, que é o mais fácil). A amplitude do índice de dificuldade foi de 0,30, que representa uma variabilidade de 1,76 DP, maior que a variabilidade sem a exclusão dos itens que foi de 1,44 DP.

O teta médio foi de 0 (zero), e o desvio-padrão médio do teta dos 26 grupos de estudantes foi 0,87. Apresentou uma amplitude de valores média de teta de 0,37, ou seja, de 0,43 DP. Os estudantes que responderam ao caderno 14 (o mais fácil) obtiveram os maiores escores de proficiência (0,20) e os que responderam ao caderno 22 (de dificuldade média) obtiveram os menores (-0,17).

A associação entre valor p e teta forneceu um coeficiente de correlação de Pearson, r, de 0,59 (p < 0,01). A exclusão dos itens que não contribuem para a mensuração do fator único que pode ser interpretado como a proficiência em Matemática, resultou em uma diminuição da variância compartilhada entre a dificuldade do teste e a proficiência estimada pela TRI de 46% para 35%. Em outras palavras, este resultado indica que um aumento na satisfação do pressuposto da unidimensionalidade está associado a uma relação menos forte entre a dificuldade do teste e a proficiência estimada do aluno. Ou seja, os resultados indicam que quanto mais o pressuposto da TRI da unidimensionalidade do teste é satisfeito, mais a propriedade de invariância dos parâmetros da TRI se manifesta.

Para uma análise mais detalhada da relação da dificuldade dos cadernos com a habilidade dos estudantes que os responderam, os cadernos foram apresentados nas Tabelas 2 e 3 em ordem crescente de dificuldade e classificados em três níveis: (1) os de dificuldade baixa apresentam valor p e valor p que variam de 0,53 a 0,41, que totalizam 9 cadernos para cada índice; (2) os de dificuldade média apresentam valor p e valor p que variam de 0,40 a 0,34, num total de 9 cadernos para cada situação; e (3) os de dificuldade alta apresentam valor p que varia de 0,33 a 0,27 e valor p que varia de 0,33 a 0,26, ambos num total de 8 cadernos.

 

 

Observa-se também nas Tabelas 2 e 3 que o teta foi classificado em três níveis: os estudantes do Grupo Superior, os do Grupo Médio e os do Grupo Inferior. A faixa do Grupo Médio foi estabelecida de -0,10 a 0,10. O grupo de estudantes com um valor médio de teta abaixo de -0,10 recebeu a classificação inferior e o grupo com um valor médio de teta acima de +0,10 recebeu a classificação superior. A Tabela 4 apresenta sinteticamente o número de grupos de estudantes por classificação de teta para cada um dos níveis de dificuldade dos cadernos, antes e após a exclusão de itens que não contribuíram significativamente para o fator único.

 

 

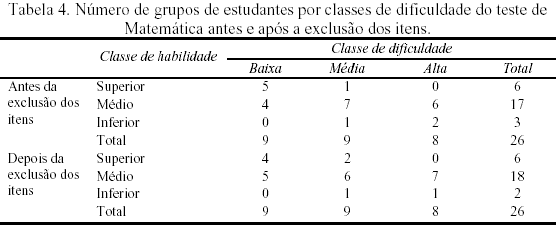
Inspeção da Tabela 4 revela que, antes da exclusão dos itens, praticamente todos os grupos superiores (5 dos 6 ou 83,3%) fizeram um dos cadernos de teste mais fácil. Dois dos três grupos inferiores (66,7%) fizeram um dos cadernos mais difíceis. Assim, fica mais claro que antes da exclusão dos itens existia uma relação considerável entre a dificuldade do caderno do teste de Matemática e a estimativa teta da proficiência dos alunos. É relevante ressaltar aqui novamente que por causa do delineamento usado no SAEB, a saber, a distribuição aleatória dos cadernos, todos os 26 grupos de alunos podem ser considerados equivalentes em termos de proficiência e deveriam ser classificados no mesmo grupo de proficiência.

A Tabela 4 revela ainda que depois da exclusão dos itens a percentagem dos grupos superiores que fizeram um dos cadernos de teste mais fácil diminuiu de 83,3% para 66,7%. A percentagem dos grupos inferiores que fizeram um dos cadernos de teste mais difícil diminuiu de 66,7% para 50%. Depois da exclusão dos itens menos grupos que receberam um dos cadernos do teste mais fáceis são classificados como grupos com desempenho superior. Estes resultados ilustram melhor o achado que o aumento da unidimensionalidade do teste está associado a um aumento da propriedade da invariância da TRI.

 

Discussão

O presente estudo investigou o quanto a estimativa da proficiência de sujeitos por meio da Teoria de Resposta ao Item depende da dificuldade do teste aplicado em condições de diferentes graus de falta de unidimensionalidade do teste. Uma vez que a unidimensionalidade do teste é um pressuposto da propriedade da invariância dos parâmetros da TRI é de suma importância investigar em que grau a falta de unidimensionalidade pode afetar esta propriedade. Muitos instrumentos nas ciências sociais não satisfazem o pressuposto de unidimensionalidade completamente, mas mensuram um fator dominante forte com um ou mais fatores fracos.

Para testar a relação entre a estimativa da proficiência dos sujeitos e a dificuldade do teste, foram utilizados os dados referentes ao teste de Matemática para a 8ª série do Ensino Fundamental do SAEB 1997. A escolha deste banco de dados foi motivada pelos resultados de um estudo anterior com os mesmos dados (Laros, Pasquali & Rodrigues, 2000) mostrando que: (1) os 26 cadernos do teste de Matemática têm índices de dificuldade bastante diferentes; (2) o teste de qui-quadrado da análise fatorial full information mostrou que o conjunto de 161 itens de Matemática é unidimensional, porém contendo vários itens que não contribuem na mensuração do fator único; (3) devido à designação aleatória dos cadernos do SAEB, os 26 grupos de alunos que fizeram o teste de Matemática podem ser considerados grupos equivalentes. Um argumento adicional para escolher este banco de dados foi que cada item do conjunto de 161 itens de Matemática foi respondido por um número elevado de estudantes, variando de 680 a 771.

Os resultados do presente estudo mostraram ainda uma correlação elevada (r = 0,68) entre a proporção média de itens corretos (valor p), indicador da dificuldade do caderno do teste de Matemática e a proficiência teta estimada pela TRI. Esta relação forte mostrou que a propriedade de invariância dos parâmetros da TRI não se aplica sempre. Este resultado corrobora os resultados de vários estudos internacionais (Fan & Ping, 1999; Fan 1998; McDonald & Paunonen, 2002; Rupp & Zumbo, 2004).

Para testar se a ausência da propriedade de invariância estava relacionada com o grau de falta de unidimensionalidade do teste de Matemática, os 26 itens com uma carga fatorial muita fraca ou negativa (< 0,20) foram excluídos do banco de dados e as análises foram refeitas. Dos 26 itens excluídos 18 tinham carga fatorial negativa e 8 apresentaram carga entre 0 e 0,20 no fator único.

As análises mostram que depois da retirada dos 26 itens acima referidos a correlação entre a estimação da proficiência em Matemática dos alunos e a proporção média de itens corretos (valor p) diminuiu de 0,68 para 0,59. Diminuindo o grau de falta de unidimensionalidade do teste de Matemática resultou em uma diminuição de 46% para 35% da variância compartilhada entre a dificuldade do teste e a proficiência estimada pela TRI. Em outras palavras, este estudo indicou que existe uma relação negativa entre a propriedade de invariância da TRI e o grau de falta da unidimensionalidade. A exclusão dos itens que apresentam carga fatorial negativa ou muito fraca no fator único é necessária para que a propriedade de invariância da TRI possa manifestar-se, mesmo se o teste de qui-quadrado na análise fatorial full information indicar que o teste como um todo é unidimensional.

Depois da retirada dos 26 itens que não contribuíram de forma significativa para a mensuração do fator único, observou-se ainda uma correlação positiva (r = 0,59) entre a proporção média de itens corretos do teste e a proficiência estimada pela TRI. Espera-se que quanto mais itens com cargas fracas sejam retirados a relação fique ainda mais fraca. O estudo de Laros, Pasquali e Rodrigues (2000) revelou que no teste de Matemática do SAEB 1997 existem mais 17 itens com cargas fatoriais entre 0,20 e 0,30. Um estudo futuro poderá mostrar se a propriedade da invariância da TRI manifesta-se melhor se estes itens forem retirados do banco de dados.

É relevante ressaltar aqui qual é a conseqüência de uma dependência entre a dificuldade de um teste e a habilidade estimada pela TRI: pessoas testadas com uma prova difícil receberão escores baixos e são prejudicadas quando comparadas com pessoas que fizeram uma prova mais fácil. Ou seja, quando existe uma relação entre a dificuldade de um teste e a estimativa da habilidade, pessoas só podem ser comparadas quando fizeram testes iguais ou estritamente paralelos.

Os resultados do presente trabalho mostram claramente que existe uma relação entre a dificuldade do teste e a proficiência estimada pela TRI quando existem itens com cargas fatoriais fracas (< 0,20) no fator único. Esta relação indesejada parece diminuir com a redução no grau de falta de unidimensionalidade de um teste. O presente estudo mostra ainda que a verificação da unidimensionalidade antes do uso da TRI seguida pela exclusão dos itens que não contribuem de forma positiva para a mensuração do fator único é de extrema importância para viabilizar a tão desejada propriedade da TRI, a invariância dos parâmetros.

 

Referências

Andrade, D.F., Taveres, H.R. & Valle, R.C. (2000). Teoria de Resposta ao Item: conceitos e aplicações. São Paulo: ABE - Associação Brasileira de Estatística.        [ Links ]

Baker, F. B. (2001). The basics of item response theory. Retirado em 23/04/2004 do Ericae (Eric clearinghouse assessment and evaluation), http//ericae.net/ftlib.htm.        [ Links ]

Bock, R. D. & Zimowski, M. F. (1995). Multiple group IRT. Em W. van der Linden & R. Hambleton (Orgs.), Handbook of item response theory. New York: Springer Verlag.        [ Links ]

Brogan, D. J. (1998). Software for analysis of sample surveys: Misuses of standard packages. Em P. Armitage & T. Colton (Orgs.), Encyclopedia of Biostatistics, vol. 5, (pp. 4167-4174). New York: John Wiley.         [ Links ]

Cohen, J. (1992). A power primer. Psychological Bulletin, 112, 155-159.         [ Links ]

Condé, F. N. (2002). A (in)dependência da habilidade estimada pela teoria de resposta ao item em relação à dificuldade da prova: um estudo com os dados do SAEB. Dissertação de Mestrado, Universidade de Brasília, Brasília.        [ Links ]

Embretson, S.E. & Herschberger, S.L. (1999). The new rules of measurement: What every psychologist and educator should know. Mahwah, NJ: Erlbaum.         [ Links ]

Fan, X. (1998). Item response theory and classical test theory: An empirical comparison of their item/person statistics. Educational and Psychological Measurement, 58, 357-381.        [ Links ]

Fan, X. & Ping, Y. (1999). Assessing the effect of model-data misfit on the invariance property of IRT parameter estimates. Trabalho apresentado em Reunião Anual (Annual Meeting) da American Educational Research Association.         [ Links ]

Fernandez, J. M. (1990). Teoria de Respuesta a los ítems: un nuevo enfoque en la evolución psicológica y educativa. Madrid: Ediciones Pirâmide.        [ Links ]

Hambleton, R.K., Swaminathan, H. & Rogers, H.J. (1991). Fundamentals of item response theory: measurement methods for the social sciences. Newbury Park, CA: Sage Publications, Inc.        [ Links ]

Hattie, J.A. (1985). Methodology Review: assessing unidimensionality of tests and items. Applied Psychological Measurement, 9, 134-164.        [ Links ]

Kirisci, L., Hsu T. & Yu, L. (2001). Robustness of item parameter estimation programs to assumptions of unidimensionality and normality. Applied Psychological Measurement, 25, 146-162.        [ Links ]

Laros, J. A., Pasquali, L. & Rodrigues, M.M.M (2000). Análise da unidimensionalidade das provas do SAEB. Brasília: Centro de Pesquisa em Avaliação Educacional - CPAE, UnB.        [ Links ]

Lord, F.M. (1980). Applications of item response theory to practical testing problems. Hillsdale (NJ): Lawrence Erlbaum.        [ Links ]

McDonald, P. & Paunonen S.V. (2002). A Monte Carlo comparison of item and person statistics based on item response theory versus classical test theory. Educational and Psychological Measurement, 62, 921-943.        [ Links ]

Pestana, M.I.G.S. (1997). Matrizes curriculares de referência para o SAEB. Brasília: Instituto Nacional de Estudos e Pesquisas Educacionais.        [ Links ]

Riether, M.M. & Rauter, R (2000). A Metodologia de amostragem do SAEB. Revista brasileira de estudos pedagógicos, 81, 143-153.        [ Links ]

Rupp, A.A. & Zumbo, B.D. (2004). A note on how to quantify and report whether IRT parameter invariance holds: When Pearson correlations are not enough. Educational and Psychological Measurement, 65, 588-599.        [ Links ]

Van der Linden, W.J. & Hambleton, R.K. (1997). Handbook of modern item response theory. New York: Springer-Verlag.         [ Links ]

Zimowski, M.F., Muraki, E., Mislevy, R.J. & Bock, R.D. (1996). BILOG-MG: multiple-group IRT analysis and test maintenance for binary items. Chicago: Scientific Software International (SSI).        [ Links ]

 

 

Endereço para correspondência
E-mail: jalaros@unb.br

Recebido em Janeiro de 2007
Reformulado em Agosto de 2007
Aceito em Novembro de 2007

 

 

Sobre os autores:

^* Frederico Neves Condé: é Graduado em Psicologia, habilitações Bacharel e Psicólogo (1997 e 1999), e Mestre em Psicologia pela Universidade de Brasília (2002). Cursa Doutorado no Departamento de Psicologia Social, do Trabalho e das Organizações por essa mesma Instituição. É professor do Instituto de Educação Superior de Brasília (IESB) e Conselheiro Suplente do Conselho Regional de Psicologia da 1ª Região.
^** Jacob Arie Laros: é Ph.D. em Personality and Educational Psychology pela University of Groningen - Holanda (1991), e, ainda Pós-Doutor (2002) em Educational Psychology pela mesma universidade. Atualmente, é professor adjunto III no Instituto de Psicologia da Universidade de Brasília (UnB), professor da pós-gradução em Psicologia Social, do Trabalho e das Organizações (PSTO) e bolsista de produtividade em pesquisa do CNPq.