Fatores que afetam o desempenho na prova de matemática do SEAB: Um estudo multinível¹

 

Factors that affect the performance on the SAEB mathematics test: A multilevel study

 

 

Jacob A. Laros^I; João Luiz Pereira Marciano^I; Josemberg Moura de Andrade^II

^IUniversidade de Brasília
^IIUniversidade Federal da Paraíba

 

 

---

Resumo

No presente estudo objetivou-se identificar quais características de alunos e escolas são associadas ao desempenho em Matemática. Foram analisados os dados de 35.929 alunos da 3ª série do Ensino Médio, distribuídos em 1.661 escolas brasileiras que fizeram o teste de Matemática do SAEB em 2001. Análise multinível mostrou uma correlação intraclasse (ICC) bruta de 0,43 e uma ICC corrigida pelas variáveis relacionadas com a composição e seletividade da escola de 0,15. Depois da entrada das variáveis de controle, sete indicadores no nível do aluno e cinco indicadores no nível da escola foram identificados como tendo efeito na proficiência em Matemática. No modelo final pelo menos 84,9% da variância total no nível da escola e 19,8% da variância total no nível do aluno foram explicadas. Os resultados do presente estudo corroboram outros estudos brasileiros com o uso de análise multinível sobre os fatores que afetam o desempenho em Matemática.

Palavras-chave: Avaliação educacional; Desempenho escolar; SAEB; Análise de regressão multinível.

---

Abstract

The main purpose of this study was to identify variables that affect proficiency in Mathematics of Brazilian students of the third grade of secondary school. To attain this goal we analyzed the data of 35,929 students of 1,715 schools who took the Mathematics test of the SAEB in 2001. Multilevel analysis showed a raw intraclass correlation (ICC) of .43 and an ICC corrected for variables related to the composition and selectivity of the school of .15. After the entry of the control variables seven indicators on student level and five indicators on school level were identified that affect achievement in Mathematics. The final model of this study explains at least 84.9% of the total variance on school level and 19.8% of the total variance on student level. The results of the present study confirm the results of other Brazilian studies related to factors affecting proficiency in Mathematics using multilevel analysis.

Keywords: Educational evaluation; School performance; SAEB; Multilevel regression analysis.

---

 

 

Introdução

A avaliação está presente em várias instâncias da ação humana e, especificamente no processo educacional, pode efetivar melhorias no ensino (Mello & cols., 2001). Embora a cultura de avaliação educacional esteja em vias de desenvolvimento no Brasil, é perceptível o avanço empreendido nessa área, seja por intermédio dos recursos metodológicos de que se dispõe, seja por meio das avaliações que vêm sendo operacionalizadas. Como exemplo de avaliações pode-se citar: o Sistema Nacional de Avaliação da Educação Básica (SAEB), o Exame Nacional do Ensino Médio (ENEM) (Rodrigues, 2002) e o Exame Nacional de Desempenho de Estudantes (ENADE).

A avaliação realizada pelo professor, no âmbito escolar, pode ser compreendida como uma das etapas do processo ensino-aprendizagem, na medida em que diagnostica as necessidades, os interesses e os problemas dos alunos. É a partir dos resultados observados que os professores podem planejar atividades de ensino mais adequadas às necessidades dos alunos. A avaliação educacional em larga escala, por sua vez, é normalmente implementada com finalidade similar, ou seja, fornece elementos para subsidiar políticas e diretrizes adequadas à realidade educacional nos contextos municipal, estadual e nacional (INEP, 2001a).

Nas avaliações educacionais, deve-se considerar, também, que o desempenho dos avaliados precisa ser contextualizado. Isto é relevante uma vez que as desigualdades sociais têm implicações diretas sobre a educação (INEP, 2001b). Como assinalam Jesus e Laros (2004), variáveis internas e externas à escola podem estar associadas ao desempenho escolar dos alunos. Corroborando essa afirmação, Rodrigues (2002) sugere que uma grande diversidade de fatores conduz o aluno a um bom ou mau desempenho escolar. Dessa forma, é relevante investigar quais fatores têm influência sobre o desempenho dos alunos, na tentativa de esclarecer o processo de produção das desigualdades educacionais (INEP, 2001b).

Na identificação das variáveis relacionadas ao desempenho escolar, deve-se conceber que as estruturas educacionais são construídas em torno de grupos de indivíduos, sejam eles famílias, escolas, bairros ou grupos de amigos. A partir desses agrupamentos, os indivíduos compartilham opiniões, atitudes ou realizações (Ferrão, 2003; Goldstein, 2001). Nesse contexto, pode-se dizer que o desempenho escolar é determinado por diversos fatores (Barbosa & Fernandes, 2001; Lüdke, 2001), dependendo do que o aluno traz consigo, bem como daquilo que a escola oferece em termos de ensino, de instalações e de ambiente. A partir da literatura nacional e internacional podem ser identificadas diversas variáveis contextuais relacionadas ao desempenho escolar (por exemplo, Andrade & Laros, 2007; Benbow, 1992; Brookhart, 1997; Caldas & Bankston III, 1997; Carvalho, 2004; Crane, 1996; Franco & Bonamino, 2001; Georgiou, 1999; Griffith, 1996; Jesus & Laros, 2004; Lüdke, 2001; Patto, 2000). Caso se queira pesquisar a complexidade de fatores relacionados ao desempenho escolar, é preciso dispor de instrumentos de modelagem que envolvam um nível comparável de complexidade. No entanto, mesmo dispondo desses instrumentos, dificilmente se chegará a descrições totalmente fidedignas (Goldstein, 2001).

Uma metodologia estatística que pode ser utilizada para esse fim é a da análise de regressão multinível. Nesse tipo de análise são considerados os níveis em que as variáveis estão inseridas (Kreft & De Leeuw, 1998; Natis, 2001). O modelo de regressão multinível incorpora, naturalmente e de maneira parcimoniosa, a estrutura hierárquica dos dados, tratando o intercepto e os coeficientes de inclinação como variáveis aleatórias (Ferrão, 2003). Isso significa que cada unidade do segundo nível pode ter seu próprio valor. Na medida em que leva em consideração a existência desses agrupamentos de dados, a análise multinível possibilita a estimação de erros padrão de mensuração, intervalos de confiança e testes de significância mais precisos (Rasbash, Steele, Browne & Prosser, 2004). Ainda, entre as vantagens de incorporação da estrutura hierárquica dos dados, pode-se citar: (1) obtenção de melhores estimativas para os parâmetros relativos a unidades específicas; (2) possibilidade de formular e testar hipóteses relativas a efeitos entre níveis; e, (3) partição da variância em componentes, verificando a importância específica dos níveis na explicação da variabilidade dos dados (Soares, César & Mambrini, 2001).

Nas análises multinível deve-se especificar a que nível a variável pertence e quais os efeitos diretos, bem como quais os efeitos de interação entre os níveis que são esperados. Em relação à medição das variáveis, estas podem ser feitas diretamente no próprio nível da variável e, também, por agregação ou desagregação. Agregar significa que uma variável de um nível mais baixo será movida para um nível mais elevado. Desagregar, por outro lado, significa mover variáveis de um nível mais alto para um nível mais baixo (Hox, 2002). Ressalta-se que o nível mais baixo de mensuração também é chamado de nível micro, enquanto o nível mais alto é chamado de nível macro. O nível macro muitas vezes é chamado de nível de contexto.

Outro aspecto a ser considerado é que na construção de teorias multinível, deve-se especificar a ordem de seleção das variáveis. São poucas as teorias que especificam a ordem de entrada das variáveis. Igualmente relevante, é que o uso de teorias nos estudos multinível é pouco freqüente (Van den Eeden, Hox & Hauer, 1990). A construção de modelos multinível guiada por uma teoria levará a modelos mais frutíferos e com maior aplicabilidade em comparação a modelos construídos com pouca ou nenhuma noção teórica.

No presente estudo, o modelo empírico apresentado por Jesus e Laros (2004) norteou a seleção das variáveis independentes que entraram nos modelos testados. Os referidos autores identificaram as variáveis preditoras do desempenho acadêmico de alunos da 8^a série do Ensino Fundamental de Língua Portuguesa avaliados no SAEB de 2001. A partir de análises de regressão multinível foi verificado que o nível socioeconômico da escola e a escolaridade dos pais foram as variáveis de controle mais relacionadas ao desempenho acadêmico. Os autores também observaram que quatro variáveis do nível do aluno afetavam o desempenho escolar. São elas: atraso escolar, se aluno trabalha ou não, apoio dos pais e aluno faz dever de casa. Considerando o nível da escola, verificou-se que as escolas que mais agregavam valor ao desempenho dos alunos possuíam as seguintes características: (1) recursos tecno-pedagógicos adequados; (2) professores que passam e corrigem a lição de casa; (3) instalações físicas em bom estado de conservação; (4) professores comprometidos com a aprendizagem dos alunos; (5) professores que têm altas expectativas em relação ao desempenho dos alunos, (6) alunos cujos pais apóiam, incentivam e conversam com eles sobre assuntos diversos e (7) alunos que não trabalham.

Diante da relevância de se estudar variáveis relacionadas ao desempenho escolar e considerando a análise de regressão multinível como a técnica estatística mais adequada para dados hierárquicos em avaliação educacional, o presente artigo teve como objetivo principal construir um modelo multinível indicando quais fatores afetam a proficiência em Matemática de alunos da 3ª série do Ensino Médio. A importância deste estudo é evidenciada na medida em que se buscou verificar quais são as características dos agentes envolvidos (alunos, pais, professores, diretores) e das escolas que justificam diferenças no desempenho escolar dos alunos.

Para atingir esse objetivo, foram considerados os alunos avaliados pelo Sistema Nacional de Avaliação da Educação Básica (SAEB) da 3ª série do Ensino Médio do ano de 2001. O SAEB foi implantado pelo Instituto Nacional de Estudos e Pesquisas Educacionais Anísio Teixeira (INEP), a partir de 1990. O objetivo do SAEB é de fornecer informações sobre o Ensino Fundamental e Médio brasileiro, com o intuito de contribuir para a melhoria da qualidade da educação brasileira e para a universalização do acesso à escola (INEP, 2001a).

 

Método

Participantes

A população de referência do SAEB 2001 correspondeu a todos os alunos matriculados, em 2001, na 4ª ou 8ª séries do Ensino Fundamental ou 3ª série do Ensino Médio, com exceção dos alunos das escolas federais, rurais ou de turmas multisseriadas. Somente para a 4ª série, foram mantidos os alunos das escolas rurais dos estados do Nordeste, Minas Gerais e Mato Grosso do Sul.

O estudo atual avaliou apenas os alunos da 3ª série do Ensino Médio que fizeram o teste de Matemática, a saber: 35.859 alunos alocados em 1.715 escolas. Em cada escola participaram de 1 a 181 alunos. Os participantes, com idades entre 14 e 22 anos, apresentaram a seguinte distribuição: sexo feminino 56%, sexo masculino 44%, etnia/cor autodeclarada branca 49%, negra 37%, demais etnias 14%. Ainda, os alunos proviam das seguintes regiões: Norte 15%, Nordeste 42%, Sudeste 18%, Sul 11% e Centro-Oeste 14%, freqüentando escolas particulares (44%) e públicas (56%).

Para a realização da análise multinível, foram agrupados os bancos de dados de alunos, professores, diretores e escolas. Para isso, foram considerados apenas os questionários de professores, diretores e escolas em que pelo menos um aluno respondeu ao teste.

Instrumentos

O desempenho dos estudantes em Matemática foi aferido por meio de um teste cognitivo composto de 39 itens de múltipla escolha. O SAEB adota a metodologia de construção de testes denominada Blocos Incompletos Balanceados (BIB), com distribuição em espiral. Essa metodologia permite a aplicação de 169 itens, o que possibilita cobrir as Matrizes de Referência. Para isso, esse conjunto total de itens é dividido em 13 blocos com 13 itens cada; em seguida, os blocos são agrupados de três em três, formando 26 cadernos diferentes. Cada aluno avaliado responde apenas a um caderno, o que equivale a 39 itens (INEP, 2001a).

Também foram considerados os questionários contextuais dos alunos, professores, diretores e escolas. Os alunos responderam dois questionários socioculturais. O primeiro era composto por 43 questões referentes à questões de caracterização sociodemográfica, enquanto o segundo era composto por dois tipos, uma para o aluno avaliado em Língua Portuguesa e outro para o aluno avaliado em Matemática. Esses continham questões referentes ao apoio familiar, trajetória escolar, motivação, autoestima, entre outras.

Os professores responderam um questionário composto por 98 questões sobre formação profissional, práticas pedagógicas, nível socioeconômico, entre outras. Os diretores responderam um questionário composto por 72 questões que abordavam os seguintes conteúdos: caracterização sociodemográfica, formação profissional, nível socioeconômico e cultural, estilos de liderança e formas de gestão. Por fim, o questionário da escola, composto por oito itens, foi respondido por um funcionário da secretaria de educação, designado pelo Ministério da Educação. Nesse questionário eram avaliadas as condições físicas da escola, segurança, conservação e biblioteca (INEP, 2001a).

Análise de dados

Com o intuito de estimar os parâmetros de grupos populacionais específicos, a população de referência foi dividida em estratos segundo variáveis de interesse: série, unidade da federação, dependência administrativa (estadual, municipal ou particular) e localização (capital ou interior). No total, 287.719 alunos de 6.935 escolas brasileiras foram pesquisados no SAEB/2001. Para mais informações sobre a amostra do SAEB 2001, ver Andrade, Silva e Bussab (2001) e Riether e Rauter (2002).

Por se tratar de uma amostra complexa (estratificada e com probabilidades desiguais de inclusão dos elementos), o uso dos pesos amostrais é indispensável (Pfeffermann, Skinner, Holmes, Goldstein & Rasbash, 1998). Os pesos amostrais são utilizados quando os sujeitos têm probabilidades diferentes de serem incluídos na amostra, como é o caso, especificamente, da amostra do SAEB. Ainda, os pesos amostrais também são recomendados quando se objetiva utilizar estatísticas descritivas de um nível agregado, tais como porcentagens e médias (Laros & van Batenburg, 2004). Sem o uso de pesos amostrais as estimativas pontuais dos parâmetros, a variância e os erros-padrão podem não ser corretos. Por isso, todas as estimativas produzidas nesse estudo consideraram os pesos amostrais.

Com o uso dos pesos brutos, o tamanho da amostra torna-se igual à soma desses pesos, que corresponde ao tamanho da população. Segundo Brogan (1998), esse valor alto impossibilita a realização adequada de testes estatísticos, que sempre tendem a ser significativos. Por isso, seguindo a recomendação da autora, o peso original das escolas foi multiplicado pela fração amostral (n/N, onde n é o tamanho da amostra e N é o tamanho da população). O novo peso amostral, chamado peso normalizado, foi utilizado em todos os procedimentos de análise dos dados. A soma dos pesos amostrais adotados resultou, então, no tamanho da amostra (e não mais da população) e a proporção de participação de cada escola nos dados foi respeitada.

Para a análise de regressão multinível utilizouse o programa MLwiN na sua versão 2.02, desenvolvido por Goldstein e colaboradores (1998). Inicialmente foi rodado o modelo nulo que, segundo a literatura (Ferrão, 2003; Kreft & De Leeuw, 1998; Snijders & Bosker, 1999), serve como base para comparação com os modelos subseqüentes. Em seguida, conforme sugere Fletcher (1998), pretendeuse controlar as características relacionadas ao nível socioeconômico do aluno e da escola, bem como as características de composição escolar (sexo e etnia), a fim de verificar quais eram as outras fontes de variação entre as escolas passíveis de intervenção. Posteriormente, atentando para os procedimentos propostos por Hox (2002), foram incluídas as variáveis explicativas do nível 1 com efeito fixo. O passo seguinte foi incluir as variáveis explicativas do nível 2. Em seguida, foi avaliado se alguns dos coeficientes de inclinação das variáveis explicativas do nível 1 possuíam componente de variância significativo entre as escolas. Em outras palavras, foi verificado se as variáveis tinham efeito diferenciado entre as escolas. Por fim, foram testadas possíveis interações das variáveis entre os níveis (efeito crosslevel).

 

Resultados e Discussão

Seguindo os passos de modelagem multinível propostos por Hox (2002), inicialmente foi estimado o modelo nulo, ou seja, o modelo sem variáveis explicativas. Nesse modelo, o desempenho escolar do aluno i que estuda na escola j é definido pelo intercepto (βoj) e pelo termo de erro (eij). O termo β oj é especificado aditivamente pelos termos: γ00, que representa a média global de desempenho, e uoj, que representa o afastamento do desempenho escolar da escola j à média global γ00. Admite-se que os efeitos aleatórios associados aos níveis 1 e 2 seguem distribuição normal com média 0 e variância σ² e e σ²u0, respectivamente, e são independentes (Ferrão, 2003; Hox, 2002). Vale salientar que o modelo nulo serve como base para a estimação da variância explicada versus variância não explicada em comparação aos modelos condicionais estimados a posteriori. Ainda, a estimação do modelo nulo é necessária para o cálculo do coeficiente de correlação intra-classe (intraclass correlation coefficient – ICC), também chamada de correlação intra-escola. A ICC é um coeficiente que pode variar de 0 a 1. Quando seu valor é nulo ou se aproxima de zero, isso significa que as escolas (em geral as unidades de nível macro) são homogêneas entre si e que o desempenho escolar do aluno é independente da escola que freqüenta (Ferrão, 2003). Quando o valor do ICC é zero o uso de análise multinível não é necessário. Podem ser observados na Tabela 1 o valor da ICC e outros resultados da estimação do modelo nulo (Modelo 0).

A partir das informações referentes à variância dos níveis 1 e 2, calculou-se uma ICC de 0,43. O resultado encontrado sugere que, a princípio, 43% da variância do desempenho escolar dos alunos estão associados à variabilidade entre as escolas, o que torna necessário o uso de modelos de regressão multinível.

Merece destaque o valor do intercepto (278,79) que representa o valor médio da proficiência em Matemática dos alunos da 3ª série do Ensino Médio. A proficiência está expressa na escala do SAEB, calibrada no desempenho em Matemática da 8a série em 1997 com um escore médio de 250 e desviopadrão de 50. É importante ressaltar que a escala assume valores interpretados de proficiência entre 100 e 500. O valor de desempenho médio esperado no teste de Matemática para o final da 3ª série de Ensino Médio é 400 (Soares & Alves, 2003). Podemos concluir que o desempenho dos alunos da 3ª série é consideravelmente menor que o esperado.

 

 

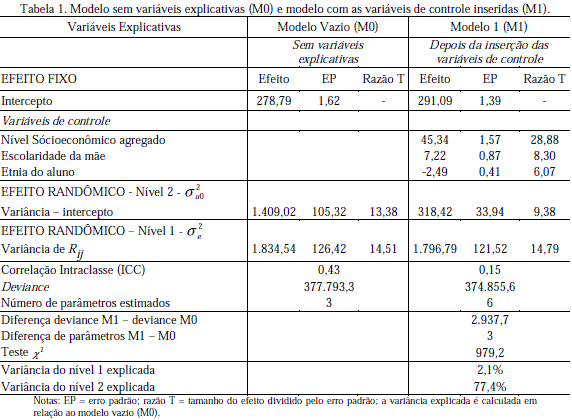
Ainda, a estimativa do deviance (–2log verossimilhança) para o modelo nulo foi igual a 377.793,3. Este valor é utilizado como referência para comparação com os modelos posteriores. O deviance reflete a falta de ajuste entre os dados e o modelo. Como regra para sua interpretação, deve-se comparar a magnitude das diferenças entre o seu valor e aquele encontrado no modelo seguinte (Snijders & Bosker, 1999). Se a diferença dos deviances for significativa, o modelo com o menor deviance é considerado melhor (Kreft & De Leeuw, 1998).

Em seguida, foram inseridas as variáveis de controle relacionadas à seletividade e composição escolar, a saber: nível socioeconômico da escola, escolaridade da mãe e etnia do aluno (Modelo 1). Como assinala Soares (2004), controlar estatisticamente o efeito dessas variáveis é absolutamente necessário, caso contrário estaríamos atribuindo às escolas um efeito que não é delas, e sim do capital econômico e cultural da família dos alunos. Os resultados do Modelo 1 podem ser observados na terceira coluna da Tabela 1. O que merece destaque especial na Tabela 1 é o efeito extremamente forte (45,34) e estatisticamente significativo do nível socioeconômico da escola (variável agregada). Neste contexto, Soares (2004) chegou à conclusão de que a associação entre o desempenho em Matemática e os fatores socioeconômicos é muito mais forte no nível da escola do que no nível de alunos individuais. Portanto, para prever o desempenho médio da escola o conhecimento do nível socioeconômico médio do alunado é extremamente importante.

Ainda na Tabela 1 outros resultados merecem destaque. A variável escolaridade da mãe tem um efeito positivo sobre o desempenho dos alunos em Matemática mesmo depois da inserção da variável nível socioeconômico da escola. Isso também é verificado em relação à variável etnia, indicando que estudantes brancos têm um desempenho melhor que estudantes não-brancos mesmo depois de controlar a influência do nível socioeconômico da escola e a escolaridade da mãe. Este resultado está em consonância com os achados do Soares e Alves (2003). Segundo os autores, a diferença de desempenho entre alunos brancos e negros não encontra explicação somente nas condições socioeconômica e cultural. Ainda, parece ser que devido a práticas e atitudes internas às escolas, os alunos negros não usufruem das melhorias da escola da mesma maneira que os alunos brancos.

Na Tabela 1 ainda pode ser verificado que mesmo controlando os efeitos de seletividade e de composição escolar a variância do intercepto continua relativamente alta (318,42) e estatisticamente significativa. A variabilidade do intercepto indica a existência de diferenças notáveis no desempenho médio em Matemática das escolas. Em outras palavras, existem diferenças na eficácia das escolas em torno da média nacional. Pode-se verificar que depois da inserção das variáveis de controle dos efeitos de seletividade e composição escolar a ICC corrigida tem um valor de 0,15. Ou seja, depois deste controle, 15% da variância do desempenho em Matemática podem ser atribuídos às escolas. Este valor é compatível com o valor da ICC corrigida de outros estudos elaborados com os bancos de dados do SAEB (Albernaz, Ferreira & Franco, 2002; Ferrão, 2003; Ferrão & Fernandes, 2003; Fletcher, 1998; Jesus & Laros, 2004; Soares, 2004).

Um outro resultado importante obtido da Tabela 1 é o ajuste do modelo aos dados. O valor do deviance do Modelo 1 diminuiu 2.937,7 pontos em comparação com o deviance do Modelo vazio, sendo estimados três parâmetros a mais no Modelo 1. Deste modo, o valor do teste χ² resultou em 979,2. Este valor é obtido pelo quociente da diferença entre os deviances dos dois modelos e a diferença entre o número de parâmetros estimados. Este quociente deve ser maior que 1,96 para possuir um nível de significância de 5%.

Foi calculada a quantidade de variância explicada do total de variância dos níveis 1 e 2 por causa da inserção de variáveis de controle. Os resultados indicam que 2,1% da variância total do nível 1 e 77,4% da variância total do nível 2 foram explicadas. O valor de 77,4% demonstra a grande importância do processo de seleção e da composição dos alunos nas escolas. Obviamente, escolas que recrutam alunos com nível socioeconômico e cultural elevado obtêm resultados melhores na prova de Matemática do que escolas que recrutam um alunado com um nível socioeconômico e cultural baixo.

De acordo com outros estudos de fatores associados (Albernaz, Ferreira & Franco, 2002; Soares, 2004), uma vez controlados os efeitos da seletividade e composição das escolas ainda existe variância que pode ser explicada tanto pelos efeitos do nível da escola quanto do nível do aluno. São estimados, primeiramente, os efeitos do nível do aluno, devido ao maior número de observações. As seguintes variáveis deste nível foram incluídas no modelo: atraso escolar, aluno gosta de estudar Matemática, auto-avaliação em Matemática, gênero masculino, cobrança e incentivo dos pais, repetência e, por fim, aluno faz dever de casa. Os resultados desse modelo (Modelo 2) podem ser observados na segunda coluna da Tabela 2.

A inspeção da Tabela 2 revela que todos os sete coeficientes de regressão das variáveis do nível de aluno incluídas no modelo são estatisticamente significativos (razão t > 2). A variável que mais afetou o desempenho escolar dos alunos foi atraso escolar, seguida de aluno gosta de estudar Matemática. Verifica-se que a cada aumento de uma unidade na escala de escore padrão de atraso escolar, o desempenho médio dos alunos diminuiu em -10,10 pontos (com erro padrão de 0,61). A contribuição das demais variáveis pode ser observada na Tabela 2. O modelo 2 conseguiu explicar 19,4% do total de variância do nível 1 e 79,7% do total de variância do nível 2. Em relação ao modelo anterior (M1) 17,7% da variância do nível 1 e 10,3% da variância do nível 2 foram explicadas.

Em seguida, foram incluídas no modelo as variáveis explicativas referentes ao nível da escola (Modelo 3). Algumas dessas variáveis foram mensuradas no nível do aluno e agregadas para o nível da escola, a saber: quantidade de faltas, repetência e recursos culturais. As variáveis originalmente mensuradas no nível da escola e consideradas nesse nível foram: trabalho colaborativo na escola e clima disciplinar na escola. Os resultados podem ser observados na terceira coluna da Tabela 2.

As variáveis incluídas no modelo que mais afetaram negativamente no desempenho escolar dos estudantes foram: quantidade de faltas e repetência, ambas agregadas para o nível da escola. As demais variáveis afetaram positivamente o desempenho escolar, tendo a variável recursos culturais agregados a maior contribuição. É importante ressaltar que o teste χ² resultou no valor de 72,2 indicando um melhor ajuste do Modelo 3 em comparação com o Modelo 2.

 

 

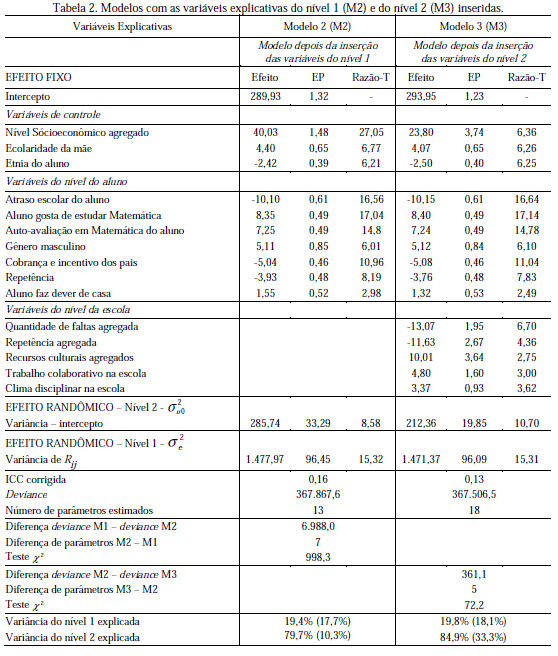
O modelo 3 é capaz de explicar 19,8% do total de variância do nível 1 e 84,9% do total de variância do nível 2. Considerando o modelo 1 como ponto de referência, o modelo 3 explica 18,1% da variância do nível 1 e 33,3% da variância do nível 2.

No modelo seguinte testado (Modelo 4), verificou-se o efeito randômico dos coeficientes de inclinação das variáveis do nível do aluno que já haviam entrado no modelo. Em outras palavras, procurou-se verificar se essas variáveis se comportam diferentemente entre as escolas. As variáveis que não apresentaram coeficiente de regressão com efeito randômico foram estimadas novamente com os coeficientes de regressão fixos. Os resultados da modelagem são apresentados na segunda coluna da Tabela 3.

Como pode ser observado na Tabela 3, a melhoria no ajuste deste modelo em comparação ao modelo anterior foi significativa (χ² igual a 190). Dessa forma, esse último modelo foi considerado mais adequado. As variáveis que apresentaram efeito randômico e que, portanto, comportam-se diferentemente entre as escolas foram: atraso escolar (-10,58), aluno gosta de estudar Matemática (8,02) e gênero masculino (10,17).

O último passo considerado foi o de verificar efeitos de interação entre os níveis (efeito crosslevel). Uma interação entre níveis na modelagem multinível refere-se ao efeito conjunto de uma variável de nível micro com uma variável de nível macro. Os resultados podem ser observados na terceira coluna da Tabela 3. Dois efeitos de interação foram encontrados: entre atraso escolar e repetência de alunos na escola (variável agregada), bem como entre atraso escolar e recursos culturais da escola (variável agregada). O primeiro efeito de interação indica que o atraso escolar tem um efeito maior em escolas que possuem uma maior quantidade de estudantes que repetem o ano do que em escolas que possuem poucos estudantes nessa situação. A segunda interação indica que o atraso escolar tem um efeito menor em escolas que possuem estudantes com uma maior quantidade de recursos culturais em comparação com escolas que possuem estudantes com poucos recursos culturais em casa. Como assinala Hox (2002), os efeitos da interação são de difícil compreensão e os pesquisadores devem tratar deles com cuidado. Dessa forma, os resultados aqui encontrados devem ser confrontados com resultados de outras pesquisas, a fim de que sejam corroborados ou refutados. A análise do deviance sugere que este último modelo é mais adequado que os anteriores. O Modelo 5 é representado esquematicamente pela Figura 1. Esta figura ilustra as variáveis componentes do modelo, bem como os respectivos coeficientes e o nível a que pertencem.

O modelo final representado na Figura 1 é composto de 18 variáveis: uma variável dependente e 17 variáveis independentes. A variável dependente, a proficiência em Matemática, está colocada na escala do SAEB. O valor da variável dependente no modelo final (287,99) é o valor médio dos alunos da 3ª série se todas as variáveis independentes assumirem o valor de zero.

As 17 variáveis independentes no modelo final podem ser classificadas da seguinte maneira: três variáveis de controle, sete variáveis do nível do aluno, cinco variáveis do nível da escola e duas variáveis de interação entre os níveis. Precisa-se ressaltar que nem todas as variáveis independentes são baseadas em um único item dos questionários. As seguintes variáveis são medidas multi-item (multiitem measures) baseadas na análise de componentes principais:

1. nível sócio-econômico (NSE): composta por 16 itens (alfa = 0,87, carga fatorial média = 0,59). Alguns exemplos de itens da medida NSE são: número de televisões em casa; quantidade de automóveis na residência; número de computadores em casa; número de banheiros na residência; quantidade de videocassetes em casa e número de empregadas domésticas em casa.

2. recursos culturais: composta por 12 itens (alfa = 0,75, carga fatorial média = 0,51). Alguns exemplos de itens desta variável composta são: o aluno tem acesso à internet em casa; número de livros em casa; na residência do aluno há revistas de informação em geral; o aluno fez ou faz curso de língua estrangeira fora da escola; possui dicionário em casa; tem acesso a um jornal diário e o aluno fez ou faz música, dança ou teatro fora da escola.

3. cobrança e incentivo dos pais: composta por 4 itens (alfa = 0,72, carga fatorial média = 0,69). Os quatro itens da variável composta são: os pais cobram a lição de casa do filho; os pais incentivam que o filho tire boas notas na escola; os pais procuram fazer com que o filho não atrase para a escola e os pais ajudam o filho a fazer a lição de casa.

4. clima disciplinar na escola: composta por 10 itens (alfa = 0,81; carga fatorial média = 0,61). Alguns exemplos de itens da variável composta são: a ocorrência de roubos e depredações; a ocorrência de violência contra alunos, professores e funcionários; a ocorrência de alto índice de faltas por parte dos professores; a ocorrência de alto índice de faltas por parte dos alunos.

5. trabalho colaborativo na escola: composta por 6 itens (alfa = 0,82; carga fatorial média = 0,68). Exemplos de itens desta variável composta são: o ensino da escola é influenciado pela troca de idéias entre os professores; a equipe de professores leva em consideração as idéias do diretor; o professor leva em consideração as idéias de outros colegas.

 

 

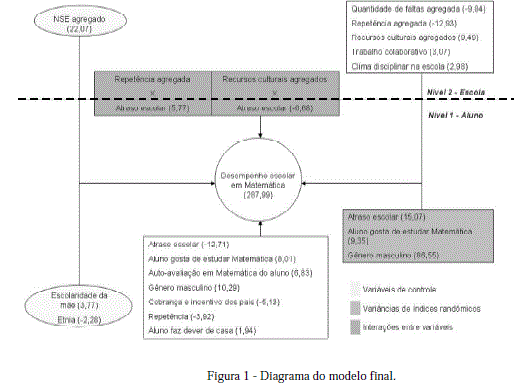
No modelo final, constam as três variáveis independentes cujos coeficientes de regressão são randômicos. O termo randômico significa que o coeficiente de regressão não é igual para todas as escolas. Com outras palavras, o impacto destas variáveis independentes é diferente para escolas diferentes. São elas: atraso escolar, aluno gosta de estudar Matemática e gênero masculino.

Por fim, existem ainda dois efeitos de interação entre os níveis: entre repetência agregada e atraso escolar, e entre recursos culturais agregados e atraso escolar. O primeiro efeito de interação, cujo sinal é positivo, indica que o atraso escolar tem um efeito maior em escolas que possuem uma maior quantidade de alunos que repetem o ano do que em escolas que possuem poucos alunos nessa situação. A segunda interação, cujo sinal é negativo, indica que o atraso escolar tem um efeito menor em escolas que possuem alunos com uma maior quantidade de recursos culturais em comparação com escolas que possuem alunos com poucos recursos culturais em casa.

Os resultados encontrados corroboram estudos prévios e, também, apontam para novas direções. Por exemplo, Andrade e Laros (2007), em estudo similar, objetivaram identificar quais variáveis explicativas afetam o desempenho dos estudantes da 3ª série do Ensino Médio nas disciplinas de Língua Portuguesa e Matemática no SAEB 2001. As variáveis do nível do aluno com efeito mais significativo foram atraso escolar e comparação do aluno com os colegas. Similarmente ao presente estudo, no nível da escola, as variáveis mais significativas foram recursos culturais agregado e atraso escolar agregado.

Pesquisas em outras culturas apresentam resultados similares. Em um estudo longitudinal com uma amostra de jovens norte-americanos, investigouse a relação entre fatores individuais e fatores da escola com os escores de um teste em ciências. Análises multinível indicaram que sucesso prévio teve influência efetiva sobre realizações subsequentes no escore do teste. Ainda, variáveis do nível individual como atitude científica, tempo dedicado aos estudos, ambiente de casa favorável e exposição à mídia foram significativamente determinantes para o bom desempenho em ciências (Young, Reynolds & Walberg, 1996).

Em um estudo realizado por Willms e Somers (2000), com amostras de 13 países da América Latina e que utilizou análise de regressão multinível, verificou a relação entre resultados escolares (desempenho em Linguagem, Matemática e tempo em que os alunos completavam o Ensino Fundamental) e relações familiares, práticas e políticas escolares. Foi verificado que as relações entre desempenho escolar e base familiar variaram entre os países. No entanto, em todos os países, as escolas mais efetivas apresentaram as seguintes características: recursos escolares satisfatórios, salas de aula onde os alunos não são agrupados por habilidade e não apresentam níveis de conhecimento muito diferenciados, alunos que são avaliados frequentemente, escolas com alto grau de envolvimento parental e salas de aula com clima positivo, ou seja, em que há respeito e disciplina. Como pode ser observado, os resultados encontrados no presente estudo são complementares aos de outros estudos, e não, excludentes.

 

Conclusão

O presente estudo teve como objetivo construir um modelo multinível de desempenho escolar, identificando quais variáveis explicativas afetam o desempenho dos estudantes da 3ª série do Ensino Médio na disciplina de Matemática. Ressalta-se que a identificação dessas variáveis é de grande importância na medida em que favorece a compreensão dos fatores que são associadas com um bom desempenho dos estudantes, bem como o processo de formação das desigualdades educacionais.

Em primeiro lugar, este estudo mostra que mesmo após o controle dos efeitos das variáveis relacionadas com a composição e seletividade da escola, ainda resta variância a ser explicada tanto no nível do aluno quanto no nível da escola. Isso significa que existem amplas possibilidades para a escola e para a família e os diversos atores responsáveis intervirem sobre o desempenho em Matemática do aluno.

Em segundo lugar, com base neste estudo são sugeridas algumas intervenções que a família pode realizar para aumentar o desempenho em Matemática dos seus filhos. Podemos citar as seguintes: incentivar desde a primeira infância, através de jogos e atividades lúdicas, a afinidade e o prazer pelos conceitos matemáticos; evitar que seus filhos ingressem e permaneçam na escola com distorção idade-série; oferecer para suas filhas brinquedos que incentivam o interesse por Matemática; estimular a auto-estima dos filhos com relação à aprendizagem escolar, dentre outras.

Em seguida, os resultados deste estudo permitem apontar algumas intervenções que podem ser desenvolvidas pelas escolas: aumentar o controle sobre a incidência de faltas na sala de aula; sanar as causas da repetência do ano letivo; estimular o trabalho colaborativo entre os professores; melhorar o clima disciplinar na escola prevenindo roubos, depredações e outros atos violentos. Ressalta-se, todavia, que ações isoladas tendem a não surtir efeito. Se forem adotadas isoladamente, é possível que cada uma das intervenções antes descritas não seja suficiente para melhorar consideravelmente o desempenho dos alunos em Matemática. Recomendase a implementação do conjunto de ações sugeridas, com a devida participação dos agentes governamentais.

Para interpretar corretamente os resultados deste estudo, deve-se considerar que a análise utilizada foi uma regressão multinível e que regressão, seja de forma tradicional ou de forma multinível, só permite formular conclusões em forma de relações ou associações entre variáveis e não em afirmativas causais. Afirmativas causais precisam de um delineamento experimental ou quaseexperimental na coleta de dados e de um referencial teórico que sustente uma relação causa-efeito. Neste sentido, não podemos afirmar que, por exemplo, o prazer em estudar Matemática causa um bom desempenho em Matemática. Ademais, pode ser que a relação causal ocorra ao contrário, que um bom desempenho causa o prazer em estudar Matemática. Talvez possamos esclarecer ainda melhor a interpretação de uma relação entre variáveis observando o sinal negativo no modelo final do nosso estudo entre a variável “cobrança e incentivo dos pais” e desempenho em Matemática. O sinal negativo entre estas duas variáveis não deve ser interpretado no sentido de que quanto mais os pais incentivam seu filho a ter um bom desempenho na escola, piores ficam seus resultados; é mais provável que um mau desempenho do aluno causa um aumento na cobrança e incentivo por parte dos pais. Portanto, convém observar-se que as únicas afirmações que podem ser feitas com base neste estudo são conclusões sobre a relação positiva ou negativa entre variáveis e não sobre relações causais.

Os resultados aqui encontrados reclamam por novas contribuições. Uma possibilidade de pesquisa é verificar em que grau o modelo final aqui proposto se ajusta em todas as regiões do Brasil. Um outro estudo pode verificar se o modelo final que foi elaborado neste estudo também se aplica à 4ª e 8ª séries do Ensino Fundamental. Dessa forma, espera-se que, cada vez mais, fique claro o que precisa ser operacionalizado para aumentar o nível de desempenho dos alunos em Matemática no Brasil.

 

Referências

Albernaz, A., Ferreira, F. H. & Franco, C. (2002). Qualidade e eqüidade da educação fundamental brasileira. Rio de Janeiro: PUC-Rio.         [ Links ]

Andrade, D. F., Silva, P.L.N. & Bussab, W.O. (2001). Plano amostral para o SAEB 2001. Relatório técnico, INEP.         [ Links ]

Andrade, J. M. de & Laros, J. A. (2007). Fatores associados ao desempenho escolar: um estudo multinível com dados do SAEB/2001. Psicologia: Teoria e Pesquisa, 23(1), 33-42.         [ Links ]

Barbosa, M. E. F. & Fernandes, C. (2001). A escola brasileira faz diferença? Uma investigação dos efeitos da escola na proficiência em matemática dos alunos da 4a série. In: C. Franco (Ed.). Avaliação, ciclos e promoção na educação (pp. 155-172). Porto Alegre: Artmed.         [ Links ]

Benbow, C. P. (1992). Academic achievement in mathematics and science of students between 13 and 23: are there differences among students in the top one percent of mathematical ability? Journal of Educational Psychology, 84(1), 51- 61.         [ Links ]

Brogan, D. J. (1998). Pitfalls of using standard statistical software packages for sample survey data. In: P. Armitage; T. Colton (Ed.). Encyclopedia of Biostatistics (pp. 4167-4174). New York: John Wiley.         [ Links ]

Brookhart, S. M. (1997). Effects of the classroom assessment environment on mathematics and science achievement. The Journal of Educational Research, 90(6), 323-330.         [ Links ]

Caldas, S. J. & Bankston III, C. (1997). Effect of school population socioeconomic status on individual academic achievement. The Journal of Educational Research, 90(5), 269-277.         [ Links ]

Carvalho, M. P. (2004). Quem são os meninos que fracassam na escola? Cadernos de Pesquisa, 34(121) 11-40.         [ Links ]

Crane, J. (1996). Effects of home environment, SES, and maternal test score on mathematics achievement. The Journal of Educational Research, 89(5), 305-314.         [ Links ]

Ferrão, M. E. (2003). Introdução aos modelos de regressão multinível em educação. Campinas: Editora Komedi.         [ Links ]

Ferrão, M. E. & Fernandes, C. (2003). O efeito escola e a mudança - dá para mudar? Evidências da investigação brasileira. Revista Electrónica Iberoamericana sobre Calidad, Eficácia y Cambio en Educación, 1(1), 1-13.         [ Links ]

Fletcher, P. R. (1998). À procura do ensino eficaz (Relatório Técnico). Brasília: MEC-DAEB.         [ Links ]

Franco, C. & Bonamino, A. (2001). Iniciativas recentes de avaliação da qualidade da educação no Brasil. In: C. Franco (Ed.). Avaliação, ciclos e promoção na educação (pp. 15-28). Porto Alegre: Artmed.         [ Links ]

Georgiou, S. N. (1999). Parental attributions as predictors of involvement and influences on child achievement. British Journal of Educational Psychology, 69(3), 409-429.         [ Links ]

Goldstein, H. (2001). Modelos da realidade: novas abordagens educacionais. In: C. Franco (Ed.). Avaliação, ciclos e promoção na educação (pp. 85-100). Porto Alegre: Artmed.         [ Links ]

Goldstein, H., Rasbash, J., Plewis, I., Draper, D., Browne, W. & Yang, M. (1998). A user’s guide to MLwiN. London: Institute of Education.         [ Links ]

Griffith, J. (1996). Relation of parental involvement, empowerment, and school traits to student academic performance. The Journal of Educational Research, 90(1), 33- 41.         [ Links ]

Hox, J. (2002). Multilevel analysis: techniques and applications. Mahwah, New Jersey: Lawrence Erlbaum Associates.         [ Links ]

Instituto Nacional de Estudos e Pesquisas Educacionais Anísio Teixeira – INEP. (2001a). SAEB 2001: novas perspectivas. Brasília: Ministério da Educação/INEP.         [ Links ]

Instituto Nacional de Estudos e Pesquisas Educacionais Anísio Teixeira – INEP (2001b). SAEB: relatório nacional 2001. Brasília: Ministério da Educação/INEP.         [ Links ]

Jesus, G. R. & Laros, J. A. (2004). Eficácia escolar: regressão multinível com dados de avaliação em larga escala. Avaliação Psicológica, 3(2), 93-106.         [ Links ]

Kreft, I. & De Leeuw, J. (1998). Introducing multilevel modeling. London: Sage Publications.         [ Links ]

Laros, J. A. & van Batenburg, T. A. (2004). O uso dos pesos amostrais. Manuscrito não publicado.         [ Links ]

Lüdke, M. (2001). Evoluções em avaliação. In: C. Franco (Ed.). Avaliação, ciclos e promoção na educação (pp. 29-34). Porto Alegre: Artmed.         [ Links ]

Mello, J. C., Leta, F., Fernandes, A., Vaz, M., Helena, M. & Barbejat, M. (2001). Avaliação qualitativa e quantitativa: uma metodologia de integração. Ensaio: avaliação e políticas públicas em educação, 9(31), 237-252.         [ Links ]

Natis, L. (2001). Modelos lineares hierárquicos: Construção e interpretação de escalas de conhecimento. Estudos em Avaliação Educacional, 23, 3-29.         [ Links ]

Patto, M. H. S. (2000). A produção do fracasso escolar: Histórias de submissão e rebeldia. 2 ed. São Paulo: Casa do Psicólogo.         [ Links ]

Pfeffermann, D., Skinner, C. J., Holmes, D. J., Goldstein, H. & Rasbash, J. (1998). Weighting for unequal selection probabilities in multilevel models. Journal of the Royal Statistical Society, 60, 23-40.         [ Links ]

Rasbash, J., Steele, F., Browne, W. & Prosser, B. (2005). A user’s guide to MLwiN Version 2.0. London: Centre for Multilevel Modeling, Institute of Education.         [ Links ]

Riether, M. M. & Rauter, R. (2002). A metodologia de amostragem do SAEB. Revista Brasileira de Estudos Pedagógicos, 81, 143-153.         [ Links ]

Rodrigues, M. M. M. (2002). Instrumentos de Avaliação Educacional: uma visão pedagógica e psicométrica integradas, estudo das provas do SAEB de Matemática 8^a série - 1997 e 1999. Dissertação de Mestrado, Instituto de Psicologia, Universidade de Brasília, Brasília.         [ Links ]

Snijders, T. A. B. & Bosker, R. (1999). Multilevel analysis: an introduction to basic and advanced multilevel modeling. London: Sage Publications.         [ Links ]

Soares, J. F. (2004). O efeito da escola no desempenho cognitivo de seus alunos. Revista Electrónica Iberoamericana sobre Calidad, Eficácia y Cambio en Educación, 2(2), 83-104.         [ Links ]

Soares, J. F. & Alves, M.T.G. (2003). Desigualdades raciais no sistema brasileiro de educação básica. Educação e Pesquisa, 29(1), 147-165.         [ Links ]

Soares, J. F., César, C. C. & Mambrini, J. (2001). Determinantes de desempenho dos alunos do ensino básico brasileiro: evidências do SAEB de 1997. In: C. Franco (Ed.). Avaliação, ciclos e promoção na educação (pp. 121-153). Porto Alegre: Artmed.         [ Links ]

Van Den Eeden, P., Hox, J. & Hauer, J. (1990). Theory and model in multilevel research: convergence or divergence? Amsterdam: SISWO.         [ Links ]

Young, D. J., Reynolds, A. J. & Walberg, H. J. (1996). Science achievement and educational productivity: a hierarchical linear model. The Journal of Education Research, 89(5), 272-278.         [ Links ]

Willms, J. D. & Somers, M. (2000). Family, classroom, and school effects on children’s educational outcomes in Latin America. School Effectiveness and School Improvement, 12(4), 409-445.         [ Links ]

 

 

Recebido em setembro de 2009
Reformulado em dezembro de 2009
Aceito em janeiro de 2010

 

 

Sobre os autores:

Jacob A. Laros: Doutor PhD em Personality and Educational Psychology pela University of Groningen (1991) e pós-doutorado pela University of Groningen (2001) e a Universitat de Valencia (2009). Atualmente é professor Adjunto IV da pós-graduação em Psicologia Social, do Trabalho e das Organizações (PSTO) da Universidade de Brasília (UnB) e bolsista de produtividade em pesquisa do CNPq. Suas áreas de expertise tanto para ensino como para pesquisa são: avaliação educacional, avaliação de programas educacionais e sociais, elaboração de testes de habilidades cognitivas, análise fatorial e análise multinível.
João Luiz Pereira Marciano: Doutor em Ciência da Informação. Ex-professor do programa de pós-graduacão da Universidade Católica de Brasília e ex-professor substituto da Universidade de Brasília, atualmente Analista Legislativo da Câmara dos Deputados. Áreas de interesse: segurança da informação, políticas de informação, epistemologia e hermenêutica, análise estatística.
Josemberg Moura de Andrade: Doutor em Psicologia Social, do Trabalho e das Organizações pela Universidade de Brasília (2008). É professor Adjunto do Departamento de Psicologia da Universidade Federal da Paraíba. Atua na área de avaliação e medidas com ênfase na elaboração, validação e adaptação de instrumentos psicológicos e educacionais.

¹Os autores agradecem o apoio financeiro do CNPq.
E-mail:
jalaros@gmail.com; marciano@unb.br;
josemberg.andrade@gmail.com