Medida psicológica: o debate entre as perspectivas conceituais representacionista e realista

 

Psychological measurement: The debate between representationalism and realism

 

Medición psicológica: el debate entre las perspectivas representacionista y realista

 

 

Nelson Hauck Filho^1,2

Universidade São Francisco

 

 

---

RESUMO

A possibilidade da medida dos fenômenos psicológicos é um tópico que suscita controvérsias conceituais e metodológicas desde os primórdios da Psicologia. O objetivo do presente trabalho é apresentar, criticamente, duas perspectivas teóricas nas quais a Psicometria tem se embasado para definir a medida: o representacionismo e o realismo. São discutidas as características e os problemas enfrentados por ambas as perspectivas conceituais, sendo avaliada a reivindicação, feita pelos dois lados do debate, de que os modelos de Rasch são testes de mensurabilidade dos atributos psicológicos. Argumenta-se que duas condições críticas ainda devem ser satisfeitas para uma solução satisfatória ao problema da medida psicológica. Não obstante, defende-se que é legítimo usar instrumentos psicométricos na avaliação psicológica, mesmo que ainda inexista uma resposta definitiva à questão da medida psicológica.

Palavras-chave: psicometria; filosofia da ciência; realismo; medida; teoria de resposta ao item.

---

ABSTRACT

The possibility of devising measures of psychological phenomena remains a contentious issue since the early days of Psychology as an independent science. The aim of this paper is to appraise two theoretical perspectives on which the boundaries of Psychometric measurement have been based: Representational Measurement Theory (RMT) and Realist Measurement Approach (RMA). This paper discusses distinctive features and specific problems faced by each conceptual approach, and evaluates claims by authors on both sides of the debate that the Rasch models consist of empirical tests of psychological attributes. Furthermore, the paper highlights two critical conditions that must be met for a satisfactory solution to the problem of psychological measurement. Notwithstanding, the paper defends the legitimacy of using psychometric instruments in psychological assessment in professional practice, even if definitive answers to the questions of psychological assessment do not yet exist.

Keywords: psychometrics; philosophy of science; realism; measurement; item response theory.

---

RESUMEN

La posibilidad de la medición de los fenómenos psicológicos es un tema que suscita controversias conceptuales y metodológicos desde lo inicio de la psicología como ciencia. El objetivo de este trabajo es presentar críticamente dos perspectivas teóricas desde donde Psicometría se ha basado para establecer el área de medición: representacionalismo y realismo. Se discuten las características y los problemas que enfrentan las dos perspectivas conceptuales, y se evalúa la afirmación de que los modelos de Rasch son pruebas de la capacidad de medición de atributos psicológicos. Se argumenta que hay dos condiciones críticas que aún deben cumplirse para una solución satisfactoria al problema de la medición psicológica. No obstante, se aboga por el uso de instrumentos psicométricos en la evaluación psicológica como una práctica legítima que es independiente de la existencia de una respuesta definitiva a la cuestión de la medición psicológica.

Palabras-clave: psicometría; filosofía de la ciencia; realismo; teoría representacional de la medida; teoría de respuesta al ítem.

---

 

 

Psicometria e Teoria da Medida

A Psicometria surgiu pelo esforço de pesquisadores, no século 19, para desenvolver procedimentos de medida dos fenômenos psicológicos. O interesse amplo desses autores pioneiros resultou em estratégias metodológicas de quantificação da experiência sensorial (Fechner, 1860; Galton, 1883), da inteligência (Binet & Simon, 1904; Spearman, 1904) e das atitudes (Thurstone, 1928), dentre outros aspectos. Isso aconteceu em contexto intelectual em que se acreditava que "a Psicologia não pode alcançar a certeza e a exatidão das ciências físicas a não ser que repouse em uma fundação sólida de experimentação e medida" (Cattell, 1890, p. 373, tradução livre). De fato, essa inspiração quantitativa parece ter surgido, ao menos em parte, do sucesso obtido pelas aplicações matemáticas no campo da Física e, em última instância, de uma visão pitagórica da natureza regida pela perfeição dos números (Michell, 2003).

Não obstante, esse "espírito quantitativo" também recebeu, desde cedo, duras críticas de alguns pesquisadores. Um marco histórico foi a publicação do relatório da British Association for the Advancement of Science de autoria do famoso físico Norman Campbell e de outros pesquisadores (Ferguson et al., 1940). O relatório apontou que, sendo inviável a concatenabilidade, a aditividade dos atributos psicológicos ainda não havia sido demonstrada, o que pôs em dúvida todos os procedimentos que visavam à mensuração na Psicologia (Michell, 2003). Em outras palavras, a principal crítica dirigia-se à dificuldade de demonstrar que magnitudes de atributos psicológicos são equivalentes à adição de porções menores desses mesmos atributos. Em contrapartida, essas e outras críticas fizeram surgir trabalhos voltados a uma melhor fundamentação teórica da medida na Psicologia e na ciência em geral, compondo a teoria da medida.

A teoria da medida é uma metateoria que busca um corolário ou uma justificativa racional para o uso dos procedimentos de mensuração nas ciências e, com isso, busca fornecer as bases para a quantificação em Psicologia. Para tanto, colocam-se questões fundamentais, por exemplo, "o que é medir?", "quais atributos da realidade empírica admitem medida?" e "como é possível construir medidas de atributos quantitativos?" No entanto, tendo em vista a complexidade de seu objeto de estudo, a área não é unânime quanto às suas premissas básicas, de modo que se subdivide em, pelo menos, duas correntes teóricas: a teoria representacional da medida (TRM) e a perspectiva realista da medida (PRM).

O objetivo do presente trabalho é apresentar, de maneira crítica, cada uma dessas abordagens como base conceitual para a Psicometria. A discussão também aborda quais seriam as contribuições, de fato, dos modelos Rasch para uma solução ao problema da medida psicológica. Os modelos Rasch são, eventualmente, considerados testes empíricos da mensurabilidade dos atributos psicológicos por ambos os lados do debate – atribuição avaliada criticamente neste trabalho. Por fim, argumenta-se que inventários, questionários e escalas psicológicas são imprescindíveis para a avaliação psicológica, independentemente de o problema da medida psicológica estar ou não resolvido.

 

A Teoria Representacional da Medida (TRM)

A TRM surgiu pelo operacionismo, de autoria do físico Percy Bridgman (1882-1961). O operacionismo é um ramo do positivismo lógico segundo o qual os conceitos científicos deveriam ser expressos em termos de operações físicas (Michell, 1997). Com o operacionismo, buscou-se banir da ciência as definições baseadas no significado intensional (com "s") dos conceitos, consideradas tautológicas e sem conexão com a realidade empírica. "Significado intensional" denota o conteúdo interno de um conceito, expresso em termos de outros conceitos cujos significados são dados como conhecidos previamente pelo leitor (Mari, 1996). Um exemplo de significado intensional é a definição encontrada em dicionários da palavra "cadeira". Essa definição poderia ser, grosseiramente, algo como "um móvel com encosto, com pernas ou rodinhas, que serve de assento para as pessoas". Ou seja, definições intensionais são abstrações que especificam características comuns a uma classe de objetos. Em contraste, o significado extensional equivale ao conjunto dos elementos abrangidos pelo conceito, como {a cadeira do meu escritório, as cadeiras da minha sala de jantar, as cadeiras da sala de aula onde leciono etc.}. A proposta do operacionismo foi que definições extensionais seriam mais afins à necessidade empiricista da observação dos fenômenos, pois os conceitos científicos equivaleriam a objetos ou a operações físicas feitas com objetos. Assim, somente os conceitos definidos pela via operacional interessariam à ciência.

Analogamente, a TRM define a mensuração também como operação empírica, ou seja, "atribuir numerais a objetos ou eventos de acordo com regras pré- -estabelecidas" (Stevens, 1946, p. 667). De fato, essa definição tem sido uma marca registrada da TRM, sendo bastante popular nos livros de introdução à Psicometria (para uma revisão, ver Michell, 1997). Desse processo operacional de atribuição numérica, surgem diversos níveis de medida ou "escalas", tradicionalmente conhecidas como nominal, ordinal, intervalar e de razão (para maiores detalhes, ver Pasquali, 2010). Contudo, a medida, de acordo com a TRM, não está garantida meramente ao serem atribuídos numerais a objetos, como poderia parecer. Um numeral é símbolo numérico que não necessariamente resguarda todas as propriedades dos números reais, como a ordem e a aditividade. Portanto, é necessário antes que sejam satisfeitos os axiomas de dois teoremas, conhecidos como o teorema da representação e o teorema da unicidade (Díez, 1997a; Finkelstein & Leaning, 1984).

Conceitualmente falando, o teorema da representação (ver detalhes técnicos em Finkelstein & Leaning, 1984; Krantz, Luce, Suppes, & Tversky, 1971) postula as condições para a correspondência (mapeamento) de um sistema relacional empírico (SRE) dentro de um sistema relacional numérico (SRN)3. Esse teorema é satisfeito se as relações qualitativas observáveis entre os elementos de um SRE (objetos, animais, pessoas) forem preservadas em termos de relações numéricas quantitativas dentro de um SRN. Por exemplo, dado um conjunto de barras de ferro de tamanhos variados, uma escala ordinal de avaliação do comprimento dessas barras implicaria que a ordem observada entre elas fosse preservada em uma representação numérica. Por sua vez, uma escala intervalar exigiria também a preservação das distâncias observadas. Nesse caso, obtém-se um mapeamento do domínio D de elementos empíricos (e.g., barras de metal) dentro de um domínio numérico R, estabelecendo uma correspondência de tipo "D ⇔ R". Essa correspondência é denominada homomorfismo, sendo a cardinalidade dos domínios D e R não necessariamente idêntica. Em outras palavras, se a escala é intervalar, mais de um elemento de D pode corresponder a um mesmo valor em R. Por exemplo, mais de uma barra de metal pode receber um valor de 50 cm.

O teorema da unicidade, por sua vez, busca demonstrar quais tipos de transformações matemáticas mantêm as propriedades da representação obtida (Rossi, 2007). O foco desse teorema é a estabilidade das escalas de medida obtidas após a satisfação dos axiomas do teorema da representação. Simplificadamente, para uma escala nominal, deve ser possível uma transformação mediante uma função biunívoca em que cada valor original recebe um novo valor, mantendo-se a identidade das representações originais. No caso da escala ordinal, deve ser possível uma função monotônica crescente, em que os novos valores preservam a ordem dos valores originais. Por sua vez, para as escalas intervalar e de razão, devem ser admissíveis transformações de tipo linear, sendo M'=αM+β para a escala intervalar e M'=αM para a escala de razão (para detalhes, ver Díez, 1997b; Finkelstein & Leaning, 1984). Ou seja, no caso da escala intervalar, as propriedades da representação devem ser mantidas após multiplicar o valor original por um valor qualquer e somar o produto a uma constante; no caso da escala de razão, as propriedades devem se manter após multiplicar o valor original por um valor qualquer.

Portanto, enquanto o teorema da representação aborda a qualidade da representação numérica dos elementos empíricos, o teorema da unicidade postula quais modificações são possíveis de realizar sem perder as propriedades escalares. Uma escala deve satisfazer ambos os conjuntos de exigências para ser "significativa" e "única", isto é, para que seja uma representação homomórfica estável após as devidas transformações teoricamente admissíveis (Díez, 1997a; Finkelstein & Leaning, 1984; Mari, 1996; Rossi, 2007). Vale ressaltar que, para a TRM, um atributo mensurado é uma mera abstração matemática de relações observáveis entre objetos, ou seja, esse atributo não necessariamente existe, mas é "criado" pelo procedimento de medida (Mari, 1996). Portanto, resumindo a perspectiva das escalas de Stevens (1946) e as propostas teóricas subsequentes sobre os teoremas da representação e da unicidade, é possível dizer que, na perspectiva representacionista, a medida é definida como a representação homomórfica de um sistema relacional de elementos empíricos observáveis por um sistema relacional numérico, mediante a atribuição de números, numerais ou símbolos aos elementos empíricos e às suas relações de acordo com uma regra.

 

A Perspectiva Realista da Medida (PRM)

A PRM contrasta substancialmente com a TRM, endossando pressupostos filosóficos realistas, em vez de operacionistas. O realismo filosófico pressupõe a existência de um mundo externo (realismo metafísico), cujo conhecimento é assumido como possível e independente de um observador (realismo epistemológico) (Michell, 2005). Uma perspectiva realista em ciência, usualmente, implica endossar pelo menos um dos três seguintes postulados: realismo das entidades teóricas, ou seja, os conceitos das teorias científicas não são meros "construtos teóricos", mas se referem a elementos que existem no mundo externo – sem necessidade de definições operacionais; realismo teórico, ou seja, as teorias científicas afirmam determinados estados de coisas cuja verdade ou falsidade pode ser testada empiricamente; e causalidade, ou seja, os fenômenos observados são causados por outros fenômenos da realidade empírica (Borsboom, 2005; Psillos, 2000).

Dentro da TRM, a mensurabilidade é uma questão ontológica, não condicionada à disponibilidade de escalas – como ocorre com a PRM. Na perspectiva realista, só é possível medir os atributos que, de fato, possuem uma estrutura interna quantitativa. Ocorre que alguns atributos são quantitativos e outros não, e essa situação é prévia à própria existência de escalas de medida. Assim sendo, a mensurabilidade é uma descoberta científica viabilizada pela natureza do atributo em questão, e não pela disponibilidade de definições operacionais ou de procedimentos de medida (escalas) (Michell, 1997). Medir, nesse contexto, implica a possibilidade de comparar uma magnitude desse atributo quantitativo Q com outra magnitude arbitrária de Q, que cumpre uma função de unidade de medida (Michell, 2005). Segundo a PRM, medidas não estão garantidas por meio de invenções matemáticas, mas apenas são autorizadas se o atributo em questão se conforma com certas condições de mensurabilidade.

Autores como Hermann von Helmholtz, Otto Hölder, Edward Huntington e Norman Campbell tentaram estabelecer definições formais para os atributos quantitativos ilimitados (cf. Díez, 1997b; Michell, 2003). O matemático alemão Otto Hölder (1859-1937) propôs uma axiomatização do conceito de estrutura quantitativa contínua, aplicável tanto nos atributos extensivos quanto nos intensivos (a tradução da obra para o inglês foi feita por Michell & Ernst, 1996, 1997). Com base no trabalho do autor, surgiu a proposta de que um atributo é quantitativo se não viola determinados axiomas que definem uma estrutura quantitativa. A ideia central é que essa não violação autoriza a inferência de que as magnitudes do atributo admitem as mesmas possibilidades que o conjunto dos números reais (Michell, 2003). Em outras palavras, o atributo em si apresenta uma natureza quantitativa com propriedades análogas às dos números reais, como ordem, aditividade e continuidade (para um resumo técnico dessas propriedades, ver Michell, 2005). Resumidamente, esses axiomas são:

H1 – Quaisquer duas magnitudes a e b de um mesmo atributo quantitativo Q devem ser idênticas (a=b) ou diferentes, sendo que, no último caso, deve existir uma terceira magnitude c que caracteriza a diferença entre ambas (a=b+c ou b=a+c).

H2 – Para toda magnitude a em Q, existe uma magnitude b em Q, de modo que b<a.

H3 – Para todo par de diferentes magnitudes a e b de um mesmo atributo quantitativo Q, existe uma magnitude c, de modo que a+b=c.

H4 – Para todo par de magnitudes a e b em Q, a+b>a e a+b>b.

H5 – Para todo par de magnitudes a e b em Q, se a<b, então existe uma magnitude c, de modo que a+c=b.

H6 – Para todo trio de magnitudes a, b e c em Q, a+(b+c)=(a+b)+c.

H7 – Dados dois conjuntos não-vazios de magnitudes A e B, em que cada magnitude pertence a um conjunto, mas não a ambos, e em que qualquer valor de A> qualquer valor de B, então existe um ponto Z, de modo que toda magnitude >Z pertence a A e toda magnitude <Z pertence a B.

Para a PRM, não é possível, portanto, considerar um atributo qualquer como "medido" antes de saber se axiomas como os de Hölder se aplicam (ver Michell, 2005). Essa postura contrasta com a noção propagada, na perspectiva representacionista, de que um atributo é sempre uma mera abstração matemática construída a partir das relações qualitativas observáveis entre os elementos empíricos. Por isso, "medida", na perspectiva realista, designa a estimação da razão entre duas magnitudes de um atributo quantitativo contínuo, sendo a primeira a magnitude mensurada e a segunda a unidade de medida arbitrária (Michell, 2003, 2005; Wright, 1997).

 

Apreciação Crítica das Perspectivas Realista e Representacionista

Realismo e representacionismo são diferentes posturas filosóficas frente ao problema da mensurabilidade. Das duas, podem ser derivados todos os conceitos formais relacionados à medida em ciência. Como revisado acima, há divergências entre ambas as posições quanto aos aspectos mais fundamentais da medida, incluindo a própria definição do que é medir. Portanto, enquanto os autores realistas endossam a ideia de que investigar a mensurabilidade é uma condição prévia à medida, os representacionistas buscam responder a essa questão pela via da construção de escalas. O propósito desta seção é apresentar uma análise crítica de ambas as perspectivas teóricas, aproximando-as de concepções atuais das variáveis latentes e dos atributos psicológicos. Como se verá, a TRM possui sérios problemas teóricos, embora a PRM também enfrente dificuldades de aplicação prática, que serão aprofundadas na próxima seção.

Como discutido, a TRM busca construir um homomorfismo entre um SRE e um SRN (Kyngdon, 2008). No entanto, essa correspondência ou mapeamento entre os conjuntos depende da disponibilidade de um conhecimento sobre esse SRE, que consiste nas relações qualitativas empiricamente observadas dos elementos entre si. Por exemplo, para construir uma escala de medida do comprimento de um conjunto de barras de metal, é antes necessário conhecer, qualitativamente (pela via dos sentidos), as relações de ordem de tamanho entre cada par de barras. Em outras palavras, o que a escala irá representar, em números, é justamente as relações qualitativas experienciadas ao comparar essas barras entre si. Um dos principais problemas, nessa situação, é que a TRM não esclarece como seria possível obter conhecimento sobre essas relações qualitativas que compõem o SRE – em vez disso, assume-as como estabelecidas. No caso de barras de metal com tamanho médio e diferenças macroscopicamente visíveis, é fácil, para um observador, estabelecer uma ordenação entre as barras e então construir uma representação numérica dessa ordenação empírica. Contudo, em outras circunstâncias, as comparações entre os elementos dependem, progressivamente, do quanto são acessíveis e evidentes a um observador externo, seja ele humano ou não.

Os problemas teóricos suscitados por uma abordagem baseada em sentenças derivadas de observações empíricas foram extensamente debatidos por Popper (1959). A principal dificuldade encontrada por esse tipo de empiricismo é o fato de que se sustenta em raciocínios indutivos. Especificamente, a indução é o processo inferencial mediante o qual leis gerais são obtidas a partir de observações singulares. Por exemplo, se 1000 cisnes da espécie A foram estudados e todos eram brancos, o raciocínio indutivo procederia à inferência de que ‘todos os cisnes da espécie A são brancos'. Contudo, como demonstrado por Popper (1959), a indução não é um método inferencial legítimo, pois sempre há a possibilidade de que o milésimo primeiro cisne seja preto ou de outra cor. Nesse caso, não há qualquer garantia de que seja verdadeira uma conclusão derivada de premissas assentadas em observações singulares.

Da mesma forma, sentenças como ‘a · b' ou ‘b · c" VER DEPOIS são derivadas das constatações indutivas de que ‘todos os objetos como a são perceptivelmente maiores do que ou equivalentes a objetos como b' e de que ‘todos os objetos como b são perceptivelmente maiores do que ou equivalentes a objetos como c'. Essas sentenças levam a uma redução ao infinito, uma vez que requerem intermináveis verificações para decidir sobre sua veracidade ou falsidade. Definir, claramente, as supostas relações qualitativas entre os elementos de um SRE é uma tarefa impossível do ponto de vista lógico.

A dependência de um observador para definir as relações qualitativas entre os elementos impõe sérias dificuldades teóricas até mesmo a tarefas simples como comparar o tamanho de dois objetos de tamanho médio. Em estudo clássico, Asch (1951) mostrou como as pessoas estão sujeitas a graves distorções cognitivas mesmo ao avaliar qual de duas figuras numa folha de papel é a maior. Além disso, existem limiares pelos quais as diferenças são percebidas, o que prejudica a identificação precisa das relações qualitativas entre os elementos (Gescheider, 1988). A menos que seja invocada a existência de uma entidade teórica metafísica com órgãos sensoriais perfeitamente acurados (e.g., o "demônio de Laplace"), a teoria é incompleta por não definir como se obtém conhecimento sobre as relações qualitativas do sistema empírico (Borsboom, 2005). Disso decorre que construir representações homomórficas e únicas de fenômenos psicológicos é um objetivo dificilmente alcançado.

Outra fragilidade da TRM diz respeito à própria natureza das definições invocadas para o conceito de "medida", a saber, que medir é o mesmo que "atribuir números ou numerais a coisas de acordo com uma regra" (e.g., Stevens, 1946; para uma revisão crítica, ver Michell, 1997). Suponha que, em determinada rua, por algum motivo, as plaquetas de numeração das casas fossem roubadas durante a noite, causando grandes problemas ao carteiro na manhã seguinte. Suponha também que, à tarde, os moradores contratassem um profissional para afixar novas plaquetas identificando o número de cada residência. Para essa situação hipotética, não seria incorreto dizer que esse profissional estaria "atribuindo numerais a objetos segundo uma regra". Assim, tendo em vista a definição tradicional na TRM, ele estaria "medindo" as casas do bairro, o que, certamente, não se aplica a esse caso. Uma definição (definiens) deve impor limites claros entre o determinado estado de coisas a que se refere (definiendum) e aqueles outros irrelevantes para essa situação. Por isso, verifica-se uma falta de especificidade na definição de medida proposta pela TRM.

Uma abordagem realista da medida não enfrenta esses problemas e, além disso, apresenta vantagens conceituais. A principal é requerer que o pesquisador adote uma visão realista dos próprios atributos psicológicos. Em uma abordagem realista, esses atributos não podem ser considerados meros "construtos teóricos" – termo com origem histórica ligada ao empiricismo lógico (cf. Michell, 2013). Ao contrário, na perspectiva realista, medir uma variável psicológica implica considerar a existência de algo que interaja causalmente com elementos observados. O foco nessa relação causal cria a necessidade de teorias aptas ao diálogo com áreas interessadas por níveis distintos de estudo dos fenômenos psicológicos, como a genética, as neurociências, a psicologia social e a antropologia. Não por acaso, algumas das teorias mais bem-sucedidas no campo da personalidade fazem isso e proporcionam investigações em todas essas áreas. Exemplos são a teoria de Krueger (2002) sobre as dimensões básicas da personalidade e da psicopatologia, as teorias fatoriais da personalidade (McCrae & John, 1992) e teorias neuropsicológicas sobre as diferenças individuais (Corr, 2008; Gray & McNaughton, 2000).

Outra vantagem da PRM é a coerência com a maioria dos modelos psicométricos, cuja formulação sintática expressa variáveis latentes como variáveis independentes causalmente relacionadas a indicadores comportamentais. Por exemplo, o modelo comum à TRI e à análise fatorial é o reflexivo, em que uma variável latente é a causa comum às respostas a um conjunto de indicadores, explicando as correlações observadas entre esses indicadores. Como visto na figura 1, em contraste com um modelo formativo (útil para construir índices, como na análise de componentes principais), um modelo reflexivo pressupõe causalidade no sentido variável latente → indicadores (Bollen & Lennox, 1991). Variáveis latentes não são apenas "rótulos" para conjuntos de indicadores ou "construtos teóricos": elas são entidades reais (propensões) probabilisticamente relacionadas a sentir, a pensar e a se comportar de determinadas maneiras (Bollen, 2002; Borsboom, 2008a; Krueger, 2002). Elas são ontologicamente distintas dos indicadores, e não são definidas por eles. Portanto, uma porção substancial das teorias e práticas metodológicas da ciência psicológica endossa uma visão realista dos atributos psicológicos, de maneira coerente com uma abordagem realista da medida. Assumir uma postura realista parece ser condição necessária para a própria existência de uma ciência psicológica com objeto de estudo definido (Pasquali, 2007).

 

 

Todavia, apenas endossar o realismo da medida e das teorias psicológicas não garante a mensurabilidade dos fenômenos psicológicos. Apesar da coerência teórica, a aplicabilidade prática da PRM persiste como uma das suas principais dificuldades. De fato, ambas as abordagens da TRM e da PRM carecem de método de investigação que permita testar a aplicação de seus axiomas teóricos. No caso da TRM, o teste deveria enfocar nos axiomas da representação e da unicidade, enquanto na PRM o foco deveria ser a mensurabilidade do atributo. Em virtude de os modelos Rasch serem, algumas vezes, interpretados como potenciais soluções práticas a ambos os lados do debate (cf. Borsboom & Scholten, 2008; Borsboom, 2005; Karabatsos, 2001), a seção a seguir apresenta uma apreciação crítica acerca do mérito dos modelos Rasch nesse sentido.

 

Modelo de Rasch: um Teste Empírico de Mensurabilidade?

Georg Rasch (1901-1980) foi um matemático dinamarquês interessado em obter estimativas paramétricas estáveis para pessoas e itens em avaliações educacionais. Para tanto, ele formalizou uma ideia bastante intuitiva em Psicometria, a saber, a de que a resposta de um indivíduo i a um item j depende, unicamente, do nível de habilidade (traço latente) desse indivíduo e da dificuldade desse item (cf. Guttman, 1944; Keats, 1967). Dessa forma, o modelo de teoria de resposta ao item (TRI) elaborado por Rasch (1960) expressa a probabilidade de acerto ou resposta positiva a um item dicotômico como uma função monotônica descrita por dois parâmetros: a habilidade θi do indivíduo com relação ao atributo medido e a dificuldade δj do item em questão (Andrich, 1988). Esse modelo, originalmente destinado a itens de natureza dicotômica, foi também estendido a itens politômicos por autores subsequentes (e.g., Andrich, 1978; Masters, 1982). No entanto, por motivos de economia e simplicidade, a presente discussão se restringirá ao modelo dicotômico de Rasch, embora se aplique, igualmente, aos referidos modelos derivados para itens politômicos.

O modelo de Rasch (1960), em escala logística, pode ser descrito como:

 

 

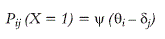
P_ij = probabilidade de o indivíduo i endossar ou responder corretamente ao item j;

Ψ = função de ligação logística;

θ_i = nível de habilidade ou posição do indivíduo i no traço latente;

δ_j = nível de dificuldade ou posição do item j no traço latente.

De acordo com alguns autores, a aditividade dos parâmetros θi e δj (ou seja, o fato de não interagirem, não serem multiplicados entre si no modelo) garantiria a eles uma série de propriedades análogas ao conjunto dos números reais. Essas propriedades incluiriam, por exemplo, ordem, aditividade e continuidade (para mais informações, ver Brogden, 1977; Keats, 1967; Perline, Wright, & Wainer, 1979). Em outras palavras, se os dados forem coerentes com o modelo, isso evidencia que as variáveis envolvidas possuem natureza quantitativa – além de que é possível uma representação numérica das relações entre pessoas, itens e pessoas e itens (Borsboom & Scholten, 2008). Nesse sentido, o modelo de Rasch (1960) se aproximaria tanto da PRM quanto da TRM, podendo ser considerado como ferramenta para o teste empírico dos axiomas dessas abordagens (Brogden, 1977; Keats, 1967; Perline, Wright, & Wainer, 1979; para uma opinião diversa, ver Michell, 2008).

Não obstante, há dois problemas teóricos para equivaler o ajuste dos dados à afirmação de que o parâmetro ?i representa uma variável aleatória com propriedades análogas às dos números reais. Em primeiro lugar, tanto o modelo como os procedimentos de estimação empregados nos programas estatísticos (e.g., Joint Maximum Likelihood e Marginal Maximum Likelihood) pressupõem que cada indivíduo possui um valor verdadeiro na variável latente θi. Ou seja, não há um teste de se os indivíduos, de fato, possuem valor fixo imutável, a fim de garantir a equivalência com uma reta análoga ao contínuo dos números reais. A única variabilidade admitida pelo modelo quanto aos valores estimados para ?i é entre indivíduos, e nunca intraindivíduo.

Uma preocupação na literatura diz respeito, precisamente, ao fato de que, embora relativamente estáveis temporalmente, muitas características psicológicas apresentam pequenas flutuações ao longo do tempo (Ferrando, 2004). Como ilustrado pela aplicação de um modelo de teoria de resposta ao item desenvolvido por Ferrando (2004), essas pequenas flutuações podem ocorrer mesmo durante a aplicação de um teste. Embora esse fenômeno ainda careça de novas investigações, se isso for verdadeiro para alguns atributos psicológicos, então modelos psicométricos com parâmetro ?i fixo para cada indivíduo podem não corresponder à verdadeira natureza dinâmica dos atributos psicológicos. Um teste legítimo, nessa situação, deveria comparar, de um lado, o ajuste de modelo com valores ?i fixos para os indivíduos e um modelo no qual há uma distribuição desse parâmetro em cada indivíduo ao longo das respostas aos itens. Essa situação não ocorre na prática e sua concretização impõe sérias dificuldades de estimação. Logo, é difícil dizer que o modelo de Rasch ou outro derivado representa um verdadeiro teste da mensurabilidade dos atributos psicológicos ou que permita uma representação homomórfica da relação entre itens, pessoas e itens e pessoas.

O segundo problema é conhecido na Filosofia da Ciência como "subdeterminação da teoria pelos dados". A subdeterminação da teoria pelos dados implica que o ajuste de um modelo não garante que esse modelo represente as verdadeiras entidades causais que produziram os dados observados (Borsboom, 2005). Isso ocorre porque outros infinitos modelos podem igualmente se ajustar aos dados sem, necessariamente, serem verdadeiros. Uma ilustração clássica desse obstáculo teórico é um experimento mental em que lançamentos de moedas (cara ou coroa) codificados binariamente poderiam obter um bom ajuste ao modelo de Rasch (Wood, 1978). Nesse caso, bons índices de ajuste não justificariam dizer que existe uma variável latente quantitativa subjacente aos dados, como descrito pela equação (1). Em virtude disso, é falacioso o argumento de que o ajuste de um modelo estatístico a bancos de dados únicos garante que uma variável latente seja quantitativa. A investigação da mensurabilidade dos atributos psicológicos deve, progressivamente, testar e esgotar explicações alternativas – por exemplo, a explicação de que esses atributos são meramente ordinais (cf. Michell, 2012).

Evidências empíricas individuais, em geral, não sustentam a inferência indutiva ou dedutiva de que o atributo é quantitativo, mas podem fornecer uma evidência abdutiva em favor de uma variável latente quantitativa (Haig, 2005). Uma "inferência abdutiva" se refere à explicação mais plausível (mais parcimoniosa) para um determinado fenômeno observado (Harman, 1965). Todavia, é importante constar que uma inferência abdutiva é viável apenas se houver também uma teoria psicológica substancial pela qual possa ser derivada, como necessária, a quantitatividade do atributo (Kyngdon, 2013). Ou seja, a investigação da mensurabilidade de um atributo psicológico depende não apenas de recursos metodológicos adequados, mas de uma teoria psicológica "forte" sobre esse atributo. Uma teoria dessa natureza pode requerer integrar conhecimentos disponíveis de diversas áreas, como a psicologia cognitiva, as neurociências, a genética e a psicologia evolucionista. Todas essas exigências implicam que, no estado atual do conhecimento, pode ser precipitado inferir (indutiva, dedutiva ou abdutivamente) em favor da natureza quantitativa dos atributos psicológicos (Michell, 2012). Não obstante, essa dificuldade não deve impedir pesquisadores de continuarem utilizando os melhores recursos teóricos e metodológicos disponíveis.

 

A Avaliação Psicológica Depende de Medidas Psicológicas?

Talvez não haja evidências suficientes para concluir que atributos psicológicos são quantitativos, em vez de simplesmente ordinais (Michell, 2012). É possível que variáveis psicológicas permitam, no máximo, inferências sobre quem tem mais ou menos do atributo, sem que seja possível definir unidades de medida (Michell, 2013). Contudo, em vez de limitar, a consciência dessa situação pode conduzir a novas possibilidade de pesquisa na Psicologia. Situada entre os dois extremos de modelos de variáveis latentes categóricas qualitativas e variáveis latentes contínuas quantitativas existe toda uma gama de possibilidades intermediárias – como os modelos mixture (Masyn, Henderson, & Greenbaum, 2010). Modelos mixture permitem combinar características qualitativas e quantitativas na explicação dos fenômenos psicológicos e, se utilizados em conjunto com hipóteses teóricas derivadas da teoria psicológica, podem contribuir à área (Leite & Cooper, 2009; Lubke & Muthén, 2005; Muthén, 2006). Em um dos exemplos possíveis, a análise de classes latentes ordenadas, assume-se que a variável latente é ordinal e composta por níveis discretos (Masyn et al., 2010). Portanto, a aplicação desses modelos possui um potencial para refinar a avaliação psicológica.

Outro ponto é, se um atributo psicológico for apenas ordinal e não quantitativo, a principal questão metodológica será obter instrumentos que permitam estimar, com a maior precisão possível, a verdadeira ordenação dos indivíduos, com vista à tomada de decisão clínica. Isso faz de inventários, questionários e escalas psicológicas excelentes recursos para obter informação a respeito de aspectos psicológicos na pesquisa ou na prática clínica. Todos esses instrumentos produzem escores ordinais que diferenciam os indivíduos em termos do atributo psicológico em questão, sendo que escores ordinais são suficientes para a maioria das aplicações práticas em avaliação psicológica (e.g., Sijtsma, 2012). Além disso, quando construídos visando a uma perspectiva de normatização referenciada no item, instrumentos psicométricos podem proporcionar informação clínica valiosa, comunicando cognições, afetos e pensamentos típicos de cada faixa crescente de escore (Primi, 2004). Por fim, existem métodos estatísticos que quantificam a informação de um instrumento psicométrico acerca de uma variável psicológica (Markon, 2013), o que permite tomar decisões devidamente embasadas sobre métodos de avaliação. Essas vantagens sustentam a defesa da continuidade da pesquisa psicométrica, bem como do desenvolvimento e da utilização de instrumentos psicométricos como métodos legítimos de avaliação psicológica.

 

Considerações Finais

O objetivo do presente estudo foi discutir criticamente duas teorias atuais sobre o problema da medida psicológica: a teoria representacionista da medida (TRM) e a perspectiva realista da medida (PRM). Enquanto a TRM deriva de um tipo de empiricismo conhecido como "operacionismo", a PRM endossa pressupostos realistas no que diz respeito à medida. Argumentou-se que a TRM conduz a problemas que a tornam uma abordagem controversa do problema da medida psicológica. Em contraste, uma perspectiva realista coloca o ônus da questão na investigação empírica da mensurabilidade dos atributos psicológicos. Uma postura realista da medida também se ajusta facilmente às teorias atuais sobre as variáveis latentes enquanto propensões reais a comportamentos. Nesse sentido, a PRM parece coerente com a ideia de modelos reflexivos de variáveis latentes, como ocorre com a TRI e a análise fatorial.

Se, por um lado, o realismo é mais facilmente defensável do que o representacionismo, por outro lado, um verdadeiro teste empírico da mensurabilidade de um atributo psicológico persiste como tópico controverso. Conforme debatido, há dificuldades que impedem considerar modelos estatísticos específicos como verdadeiros testes de mensurabilidade, como o modelo de Rasch. Com efeito, conclui-se que um verdadeiro teste de mensurabilidade requer: 1) um modelo psicométrico que estime aspectos tanto da variabilidade entre quanto da variabilidade intra indivíduos na variável latente ao responder a um conjunto de itens ou tarefas; e 2) uma teoria psicológica substancial que justifique considerar o atributo como quantitativo. Buscar atender a essas exigências poderia potencializar uma investigação mais aprofundada, complexa e abrangente dos fenômenos psicológicos, integrando conhecimentos filosóficos, psicológicos e estatísticos.

Ressalta-se que o propósito do presente trabalho não é apresentar uma crítica à avaliação psicológica ou à construção de instrumentos. Ao contrário, defende- -se que a avaliação psicológica é uma das práticas profissionais mais importantes da Psicologia, e inventários, questionários e escalas psicométricas são instrumentos adequados para obter informação acerca de um atributo psicológico. Consequentemente, os problemas conceituais aqui debatidos devem ser utilizados como uma inspiração para novas investigações científicas, e não como um empecilho a elas. A consciência dos problemas teóricos ainda presentes na medida psicológica pode levar a novas investigações que aprofundarão o conhecimento no campo da Psicologia.

 

Referências

Andrich, D. (1978). A rating formulation for ordered response categories. Psychometrika, 43(4), 561-573. doi:10.1007/BF02293814         [ Links ]

Andrich, D. (1988). Rasch models for measurement. Sage Publications, Inc.         [ Links ]

Asch, S. E. (1951). Effects of group pressure upon the modification and distortion of judgment. Em H. Guetzkow (Ed.), Groups, leadership and men. Pittsburgh: Carnegie Press.         [ Links ]

Binet, A., & Simon, T. (1904). Méthodes nouvelles pour le diagnostic du niveau intellectuel des anormaux. L'année Psychologique, 11(1), 191- 244. doi:10.3406/psy.1904.3675         [ Links ]

Bollen, K., & Lennox, R. (1991). Conventional wisdom on measurement: A structural equation perspective. Psychological Bulletin, 110(2), 305-314.         [ Links ]

Borsboom, D. (2005). Measuring the mind: Conceptual issues in contemporary psychometrics. Cambridge University Press.         [ Links ]

Borsboom, D. (2008). Latent Variable Theory. Measurement: Interdisciplinary Research & Perspective, 6(1-2), 25-53. doi:10.1080/15366360802035497         [ Links ]

Borsboom, D., & Scholten, A. Z. (2008). The Rasch Model and Conjoint Measurement Theory from the perspective of psychometrics. Theory & Psychology, 18(1), 111-117. doi:10.1177/0959354307086925         [ Links ]

Brogden, H. E. (1977). The rasch model, the law of comparative judgment and additive conjoint measurement. Psychometrika, 42(4), 631-634. doi:10.1007/BF02295985         [ Links ]

Cattell, J. M. (1890). Mental tests and measurements. Mind, 15, 373-381.         [ Links ]

Corr, P. J. (2008). The Reinforcement Sensitivity Theory of Personality. New York: Cambridge University Press.         [ Links ]

Díez, J. A. (1997a). A hundred years of numbers. An historical introduction to measurement theory 1887-1990: Part I: The formation period. Two lines of research: Axiomatics and real morphisms, scales and invariance. Studies in History and Philosophy of Science, 28(1), 167-185.         [ Links ]

Díez, J. A. (1997b). A hundred years of numbers. An historical introduction to measurement theory 1887-1990: Part II: Suppes and the mature theory: Representation and uniqueness. Studies in History and Philosophy of Science, 28(2), 237-265.         [ Links ]

Fechner, G. T. (1860). Elemente der psychophysik. Leipzig: von Breitkops Verlag.         [ Links ]

Ferguson, A., Myers, C. S., Bartlett, R. J., Banister, H., Bartlett, F. C., Brown, W., … Tucker, W. (1940). Quantitative estimates of sensory events: Final report of the committee appointed to consider and report upon the possibility of quantitative estimates of sensory events. Advancement of Science, 1, 331-349.

Ferrando, P. J. (2004). Person reliability in personality measurement: An item response theory analysis. Applied Psychological Measurement, 28(2), 126-140. doi:10.1177/0146621603260917         [ Links ]

Finkelstein, L., & Leaning, M. S. (1984). A review of the fundamental concepts of measurement. Measurement, 2(1), 25-34. doi:10.1016/0263- 2241(84)90020-4         [ Links ]

Galton, F. (1883). Inquires into human faculty and its development. London: Macmillan.         [ Links ]

Gescheider, G. A. (1988). Psychophysical scaling. Annual Review of Psychology, 39, 169-200. doi:10.1146/annurev.ps.39.020188.001125         [ Links ]

Gray, J. A., & McNaughton, N. (2000). The neuropsychology of anxiety: An enquiry into the functions of the septo-hippocampal system. (2.a Ed..). Oxford: Oxford University Press.         [ Links ]

Guttman, L. (1944). A basis for scaling qualitative data. American Sociological Review, 9(2), 139-150.         [ Links ]

Haig, B. D. (2005). Exploratory factor analysis, theory generation, and scientific method. Multivariate Behavioral Research, 40(3), 303-329. doi:10.1207/s15327906mbr4003_2         [ Links ]

Harman, G. H. (1965). The inference to the best explanation. The Philosofical Review, 74(1), 88-95.         [ Links ]

Karabatsos, G. (2001). The Rasch model, additive conjoint measurement, and new models of probabilistic measurement theory. Journal of Applied Measurement, 2(4), 389-423.         [ Links ]

Keats, J. A. (1967). Test Theory. Annual Review of Psychology, 18(1), 217-238. doi:10.1146/annurev.ps.18.020167.001245         [ Links ]

Krantz, D. H., Luce, R. D., Suppes, P., & Tversky, A. (1971). Foundations of measurement (Vol. I: Additive and polynomial representations). New York: Academic Press.         [ Links ]

Krueger, R. F. (2002). Personality from a realist's perspective: Personality traits, criminal behaviors, and the externalizing spectrum. Journal of Research in Personality, 36(6), 564-572. doi:10.1016/S0092-6566(02)00506-8         [ Links ]

Kyngdon, A. (2008). Conjoint Measurement, Error and the Rasch Model: A Reply to Michell, and Borsboom and Zand Scholten. Theory & Psychology, 18(1), 125-131. doi:10.1177/0959354307086927         [ Links ]

Kyngdon, A. (2008). The rasch model from the perspective of the representational theory of measurement. Theory & Psychology, 18(1), 89- 109. doi:10.1177/0959354307086924         [ Links ]

Kyngdon, A. (2013). Descriptive theories of behaviour may allow for the scientific measurement of psychological attributes. Theory & Psychology, 23(2), 227-250. doi:10.1177/0959354312468221         [ Links ]

Leite, W. L., & Cooper, L. A. (2009). Detecting social desirability bias using factor mixture models. Multivariate Behavioral Research, 45(2), 271-293. Recuperado de http://eric.ed.gov/?id=EJ887404         [ Links ]

Lubke, G. H., & Muthén, B. (2005). Investigating population heterogeneity with factor mixture models. Psychological Methods, 10(1), 21-39. doi:10.1037/1082-989X.10.1.21         [ Links ]

Mari, L. (1996). The meaning of "quantity" in measurement. Measurement, 17(2), 127-138. doi:10.1016/0263-2241(96)00022-X         [ Links ]

Markon, K. E. (2013). Information utility: Quantifying the total psychometric information provided by a measure. Psychological Methods, 18(1), 15-35.         [ Links ]

Masters, G. N. (1982). A rasch model for partial credit scoring. Psychometrika, 47(2), 149-174. doi:10.1007/BF02296272         [ Links ]

Masyn, K. E., Henderson, C. E., & Greenbaum, P. E. (2010). Exploring the latent structures of psychological constructs in social development using the dimensional-categorical spectrum. Social Development, 19(3), 470-493. doi:10.1111/j.1467-9507.2009.00573.x         [ Links ]

McCrae, R. R., & John, O. P. (1992). An introduction to the five-factor model and its applications. Journal of Personality, 60(2), 175-215. doi:10.1111/j.1467-6494.1992.tb00970.x         [ Links ]

Michell, J. (1997). Quantitative science and the definition of measurement in psychology. British Journal of Psychology, 88(3), 355-383. doi:10.1111/j.2044-8295.1997.tb02641.x         [ Links ]

Michell, J. (2003). Epistemology of measurement: The relevance of its history for quantification in the social sciences. Social Science Information, 42(4), 515-534. doi:10.1177/0539018403424004         [ Links ]

Michell, J. (2005). The logic of measurement: A realist overview. Measurement, 38(4), 285-294. doi:10.1016/j.measurement.2005.09.004         [ Links ]

Michell, J. (2008). Conjoint measurement and the rasch paradox: A response to kyngdon. Theory & Psychology, 18(1), 119-124. doi:10.1177/0959354307086926         [ Links ]

Michell, J. (2012). "The constantly recurring argument": Inferring quantity from order. Theory & Psychology, 22(3), 255-271. doi:10.1177/0959354311434656         [ Links ]

Michell, J. (2013). Constructs, inferences, and mental measurement. New Ideas in Psychology, 31(1), 13-21. doi:10.1016/j.newideapsych.2011.02.004         [ Links ]

Michell, J., & Ernst, C. (1996). The axioms of quantity and the theory of measurement. Journal of Mathematical Psychology, 40(3), 235-252. doi:10.1006/jmps.1996.0023         [ Links ]

Michell, J., & Ernst, C. (1997). The axioms of quantity and the theory of measurement. Journal of Mathematical Psychology, 41(4), 345-356. doi:10.1006/jmps.1997.1178         [ Links ]

Muthén, B. (2006). Should substance use disorders be considered as categorical or dimensional? Addiction, 101 Suppl, 6-16. doi:10.1111/ j.1360-0443.2006.01583.x         [ Links ]

Pasquali, L. (2007). Validade dos testes psicológicos: será possível reencontrar o caminho? Psicologia: Teoria E Pesquisa, 23(Esp.), 99-107. doi:10.1590/S0102-37722007000500019         [ Links ]

Pasquali, L. (2010). Teoria da medida. Em L. Pasquali (Org.). Instrumentação psicológica: fundamentos e práticas (pp. 56-78). Porto Alegre: Artmed.         [ Links ]

Perline, R., Wright, B. D., & Wainer, H. (1979). The Rasch Model as Additive Conjoint Measurement. Applied Psychological Measurement, 3(2), 237-255. doi:10.1177/014662167900300213         [ Links ]

Popper, K. R. (1959). The logic of scientific discovery. London, England: Routledge.         [ Links ]

Primi, R. (2004). Avanços na interpretação de escalas com a aplicação da Teoria de Resposta ao Item. Avaliação Psicológica, 3(1), 53-58.         [ Links ]

Psillos, S. (2000). Agnostic empiricism versus scientific realism: Belief in truth matters. International Studies in the Philosophy of Science, 14(1), 57-75. doi:10.1080/026985900111909         [ Links ]

Rasch, G. (1960). Probabilistic models for some intelligence and attainement tests. Copenhagen, Denmark: Danmarks Paedogogiske Institut.         [ Links ]

Rossi, G. B. (2007). Measurability. Measurement, 40, 545-562.         [ Links ]

Sijtsma, K. (2012). Psychological measurement between physics and statistics. Theory & Psychology. doi:10.1177/0959354312454353         [ Links ]

Spearman, C. (1904). "General intelligence," objectively determined and measured. The American Journal of Psychology, 15(2), 201-292.         [ Links ]

Stevens, S. S. (1946). On the theory of scales of measurement. Science, New Series, 103(2684), 677-680. doi:10.1126/science. 103.2684.677         [ Links ]

Thurstone, L. L. (1928). Attitudes can be measured. The American Journal of Sociology, 33(4), 529-554.         [ Links ]

Wood, R. (1978). Fitting the Rasch model-A heady tale. British Journal of Mathematical and Statistical Psychology, 31(1), 27-32. doi:10.1111/j.2044-8317.1978.tb00569.x         [ Links ]

Wright, B. D. (1997). A history of social science measurement. Educational Measurement: Issues and Practice, 16(4), 33-45. doi:10.1111/j.1745-3992.1997.tb00606.x        [ Links ]

 

 

Recebido em outubro de 2013
Reformulado em maio de 2014
Aprovado em maio de 2014

 

 

Sobre os autores

Adriana Cristina Boulhoça Suehiro: é Psicóloga. Doutora pelo Programa de Pós-Graduação Stricto Sensu em Psicologia da Universidade São Francisco. Docente da Universidade Federal do Recôncavo da Bahia – Santo Antônio de Jesus.
Vitória Lage Hohlenwerger: é Graduanda em Psicologia. Bolsista CNPq.

¹Endereço para correspondência: R. Rosalvo Fonseca, 225, São Cristóvão, 44571-037, Santo Antônio de Jesus-BA. E-mail: dricbs@yahoo.com.br