AVALIAÇÃO PSICOLÓGICA

Confiabilidade dos índices fatoriais da Wais-III adaptada para a população brasileira

 

Reliability of the factor index of the Wais-III adapted for the brazilian population

 

Fiabilidad de los índices factoriales Wais-III adaptada para la población brasileña

 

 

Felipe Valentini^I; Cristiano Mauro Assis Gomes^II; Monalisa Muniz^III; Tatiana Pontrelli Mecca^IV; Jacob Arie Laros^V; Josemberg Moura de Andrade^VI
I Universidade Salgado de Oliveira, Niterói – RJ – Brasil
^II Universidade Federal de Minas Gerais, Belo Horizonte – MG – Brasil
^III Universidade Federal de São Carlos, São Carlos – SP – Brasil
^IV Centro Universitário Fundação Instituto de Ensino para Osasco (Fieo), Osasco – SP – Brasil
^V Universidade de Brasília, Brasília – DF – Brasil
^VI Universidade Federal da Paraíba, João Pessoa – PB – Brasil

Endereço para correspondência

 

 

---

Resumo

Uma nova estratégia de avaliação da confiabilidade dos escores de instrumentos psicológicos é proposta por meio da ortogonalização das variáveis latentes e estimação de índices de confiabilidade composta destes. O presente trabalho utilizou-se dessa estratégia para investigar a confiabilidade dos índices fatoriais da Wais-III adaptada para a população brasileira. Diferentes modelos foram testados, e aquele com melhor ajuste foi o bifactor com um fator geral e quatro fatores específicos, correspondendo aos índices fatoriais da Wais-III. Os índices de confiabilidade foram altos para o fator geral: confiabilidade composta [CC] = 0,96; ômega hierárquico [ω] = 0,94; contudo, para as dimensões específicas, após controlar o efeito da dimensão geral, os índices foram baixos (CC ≤ 0,35; ω ≤ 0,14). Com base nesses resultados, sugere-se cautela na interpretação dos escores dos índices fatoriais da Wais-III, pois a maior parte da variância desses escores parece estar relacionada à dimensão geral.

Palavras-chave: modelo bifactor; precisão; confiabilidade composta; habilidades cognitivas; teste de inteligência.

---

Abstract

A new approach is presented for the assessment of the score reliability of psychological instruments by means of orthogonalization of the latent variables and the estimation of the corresponding coefficients of composite reliability. The present study used this approach to investigate the reliability of the Wais-III index scores, adapted for the Brazilian population. Various models were tested: the one with the best fit was the bifactor model with one general factor and four specific factors, corresponding to the Wais-III index scores. For the general factor, high reliability coefficients were found (composite reliability [CR] = .96; hierarchical omega [ω] = .94); yet the specific dimensions, after controlling the effect of the general dimension, showed low reliability coefficients (CR ≤ .35; ω ≤ .14). On basis of these findings, extreme caution is recommended concerning the interpretation of the Wais-III index scores, since most of the variance of those scores seems to be related to the general dimension.

Keywords: bifactor modes; accuracy; composite reliability; cognitive ability; intelligence test.

---

Resumen

Se ha propuesto una nueva estrategia de evaluación de fiabilidad de puntajes de instrumentos psicológicos por medio de la ortogonalización de variables latentes y de la estimación de los respectivos índices de confiabilidad compuesta. El presente trabajo utilizó esa estrategia para investigar la fiabilidad de los índices factoriales del Wais-III adaptada a la población brasileña. Fueron probados diferentes modelos, siendo los de mejor ajuste el de dos factores con un factor general y cuatro factores específicos, que corresponden a los índices factoriales del Wais-III. Los índices de fiabilidad fueron altos para el factor general: fiabilidad compuesta [CC] = 0,96; omega jerárquico [ω] = 0,94); sin embargo, para las dimensiones específicas, después de controlar el efecto de la dimen sión general, los índices fueron bajos (CC ≤ 0,35; ω ≤ 0,14). Con base en estos resultados, se recomienda cautela en la interpretación de los puntajes de los índices factoriales de la Wais-III, ya que la mayor parte de la varianza de los puntajes parece estar relacionada a la dimensión general.

Palabras clave: modelo de los factores; precisión; fiabilidade compuesta; habilidades cognitivas; teste de inteligência.

---

 

 

A terceira edição da escala Wechsler de inteligência para adultos (Wechsler adult intelligence scale – Wais), disponível para a população brasileira, é um dos instrumentos mais utilizados para avaliação nessa faixa etária. Trata-se de uma bateria de inte­ligência composta por 14 subtestes que avaliam habilidades distintas. Os estudos de análise fatorial confirmatória contidos no manual norte-americano e no brasileiro sustentam que a Wais-III mensura as habilidades de compreensão verbal, organização perceptual, memória operacional e velocidade de processamento (norte-americano, χ²[58] = 238,2; AGFI = 0,95; RMRS = 0,22; brasileiro, χ²[59] = 433,15; AGFI = 0,87; RMSR = 0,04) (Nascimento, 2004). A quantificação dessas habilidades tem sido frequentemente utilizada para a construção de inferências clínicas por diferentes campos da psico­logia. Por exemplo, a neuropsicologia emprega a Wais-III e seus escores relativos às habilidades supramencionadas com a finalidade de investigar grupos clínicos específicos com lesão cerebral (Fisher, Ledbetter, Cohen, Marmor, & Tulsky, 2000), traumatismo­ cranioencefálico (Donders, Tulsky, & Zhu, 2001), esquizofrenia (Nuechterlein et al., 2004), transtornos do espectro do autismo (Spek, Scholte, & Berckelaer-Onnes, 2008; Kanai et al., 2012), entre outros.

No entanto, vários estudos recentes têm investigado a estrutura multidimensional da Wais e indicado que os modelos bifactor se ajustam melhor aos dados do que os modelos tradicionais com quatro dimensões correlacionadas e do que os modelos de segunda ordem (Canivez, 2013, 2014; Gignac, 2005, 2006; Gignac & Watkins, 2013; Golay & Lecerf, 2011; Nelson, Canivez, & Watkins, 2013). Os modelos bifactor ganharam popularidade entre a comunidade científica nas últimas décadas, principalmente para estudos com variáveis cognitivas e no campo dos estudos da personalidade. Tais modelos configuram um fator geral que explica todas as variáveis observáveis (escores de testes ou itens, por exemplo), enquanto os fatores específicos explicam grupos determinados de variáveis observáveis. Nos modelos bifactor, os fatores são ortogonais, ou seja, as correlações entre as dimensões são fixadas em zero, e, portanto, um fator explica apenas a parte da variância que não é explicada pelos demais fatores, assim como pelo erro. Essa característica permite avaliações sobre a relevância e a precisão de uma variável latente após controlado o efeito explicativo das demais variáveis. Ademais, é possível compreender se determinada variável observável (item ou teste, por exemplo) é mais bem explicada por uma dimensão geral ou por uma dimensão específica (Reise, 2012; Reise, Moore, & Haviland, 2010; Reise, Scheines, Widaman, & Haviland, 2013; Rios & Wells, 2014). Explicações detalhadas sobre essa modelagem (inclusive­ com ilustrações gráficas) podem ser encontradas nas referências citadas.

As vantagens analíticas dos modelos bifactor têm subsidiado discussões relevantes na psicologia cognitiva. Especificamente para as escalas Wechsler, os pesquisadores Gignac e colaboradores trabalharam sistematicamente com a avaliação da estrutura e precisão dos escores da Wais-R, Wais-III e Wais-IV (respectivamente, Gignac, 2005, 2006; Gignac & Watkins, 2013). De acordo com os resultados desses estudos, os modelos bifactor apresentaram melhor ajuste aos dados, apontando para uma estrutura com um fator geral e três (Gignac, 2005) ou quatro (Gignac, 2006; Gignac & Watkins, 2013) específicos que correspondem aos índices fatoriais da Wais.

Entre os diversos resultados emergidos nessas pesquisas, os dados mais intrigantes estão relacionados aos subtestes: aritmética e dígitos (Gignac, 2005); aritmética, completar figuras, arranjo de figuras e raciocínio matricial (Gignac, 2006); aritmética, raciocínio matricial e completar Figuras (Gignac & Watkins, 2013). Os subtestes apresentaram betas muito baixos, não significativos ou negativos para compor o QI verbal (aritmética e dígitos), a memória operacional (aritmética) e a organização ou raciocínio perceptual (completar figuras, arranjo de figuras e raciocínio matricial). Além disso, todos os subtestes, em todos os estudos supramencionados, apresentaram betas altos para o fator geral, indicando que a maior parte da variância dos subtestes pode ser atribuída à dimensão geral.

Esses estudos foram replicados em diferentes contextos, e os resultados apontaram para a mesma conclusão: após removido o efeito da dimensão geral, pouca variância pode ser atribuída às dimensões específicas (índices fatoriais). Golay e Lecerf (2011), por exemplo, avaliaram a estrutura da Wais-III, a partir dos dados da normatização para a população francesa. Os pesquisadores observaram que a dimensão geral (proveniente de um modelo bifactor) explicou 63% da variância dos subtestes e que as dimensões específicas contribuíram pouco para o modelo (entre 4,7 e 15,9% da explicação da variância).

A interpretação dos escores específicos é ainda mais delicada quando se consideram­ os resultados de consistência interna. Estudos recentes sugerem que a confiabilidade dos escores das habilidades estimadas pela Wais pode estar sendo superestimada, em função da metodologia de estimação da confiabilidade das variáveis latentes (Canivez, 2014; Gignac & Watkins, 2013; Golay & Lecerf, 2011). Nesse contexto, Gignac e Watkins (2013) indicam que o índice alfa é inadequado para estimar a confiabilidade de testes multidimensionais, cujas variáveis latentes apresentam correlações altas. Eles propõem a utilização do modelo bifactor para que as variáveis latentes possam ser ortogonalizadas entre si e a variância explicada de cada variável latente em relação a cada variável observável não se superponha em relação a outras variáveis latentes do modelo. Por meio da ortogonalização, cada variável latente possui um papel específico e único na explicação da variância das variáveis observáveis, possibilitando uma estimativa precisa dos betas. Por consequência, Gignac e Watkins (2013) propõem que a estimativa de confiabilidade deve considerar os betas estimados para que de fato seja um indicador correto da confiabilidade da variável latente estimada.

Nesse contexto, por meio dos indicadores ômega hierárquico (ω) e confiabilidade composta (CC), por exemplo, é possível estimar a precisão dos escores de uma variável latente, considerando seus betas. Indicadores tradicionais (como alfa de Cronbach) têm sido criticados justamente por pressuporem que os betas das variáveis latentes são iguais, gerando um substancial viés na estimativa da confiabilidade (Rios & Wells, 2014). Ademais, o alfa estima o total de variância possivelmente atribuída à determinada dimensão, sem considerar as correlações entre as variáveis latentes. Isso pode, consequentemente, superestimar a precisão de escores específicos. Por exemplo, para duas dimensões altamente correlacionadas, é possível que a primeira dimensão explique a maior parte da variância das variáveis observáveis, o que respaldaria um indicador de precisão alto. Contudo, devido à correlação entre as variáveis, a precisão da segunda dimensão também tenderia a ser alta, mesmo que essa segunda dimensão explicasse muito pouco da variância das variáveis observáveis. Nesse sentido, é relevante a análise da consistência interna por meio de indicadores que possam isolar o efeito de qualquer variável latente sobre as demais (Reise, 2012; Reise et al., 2010; Reise et al., 2013; Rios & Wells, 2014).

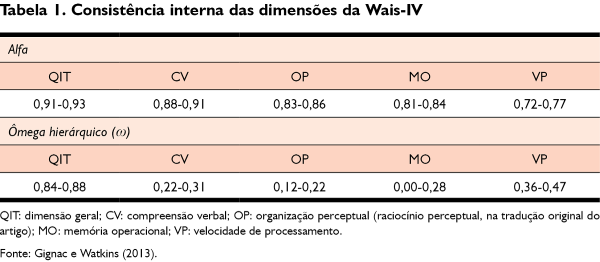
Sobre essa questão da confiabilidade, Gignac e Watkins (2013) reavaliaram a consistência interna dos escores da Wais-IV e compararam os resultados dos indicadores alfa e ômega. Na Tabela 1, é apresentado o resumo do estudo de precisão realizado por esses autores. Nesse trabalho, a consistência interna das dimensões geral e específicas foi estimada de maneira separada por faixa etária. Por esse motivo, na Tabela 1, são apresentados o mínimo e o máximo dos valores de precisão para cada dimensão latente. Um pesquisador (ou um clínico) poderia visualizar o alfa de Cronbach e concluir que todas as dimensões, geral e específicas, predizem escores com precisão aceitável para a prática clínica e de pesquisa. Contudo, se esse pesquisador não atentar para o fato de que dimensões são altamente correlacionadas, ele pode superestimar a precisão dos escores específicos. De acordo com os dados apresentados na Tabela 1, verifica-se que a consistência interna estimada para as dimensões específicas sofreu drástica redução ao controlar o efeito da dimensão geral. A consistência interna de velocidade de processamento, por exemplo, após controle do efeito da dimensão geral, é de, no máximo, 0,47; para memória de trabalho, esse valor pode chegar perto de zero. Ou seja, removendo a explicação da dimensão geral, apenas uma pequena parte da variância dos escores pode ser atribuída, de fato, às dimensões específicas. Tais resultados indicam que, quando se interpreta um escore específico, a maior parte da decisão do pesquisador (ou clínico) está embasada, na realidade, na dimensão geral.

 

 

Para a Wisc-IV, resultados semelhantes foram encontrados no recente estudo de Canivez (2014). Além do melhor ajuste do modelo bifactor, a consistência interna da dimensão geral foi maior (ω = 0,84) do que a das dimensões específicas (ω entre 0,10 e 0,33). Entretanto, uma pesquisa com população clínica apontou para indicadores de consistência interna menos discrepantes para a Wais-IV (Nelson et al., 2013): geral, ω = 0,74; e índices fatoriais, ω entre 0,11 e 0,64. Em que pese a menor discrepância, a precisão dos índices fatoriais também foi bastante limitada neste último estudo, principalmente para organização perceptual e memória de trabalho, cujos indicadores de consistência interna foram estimados abaixo de 0,40.

Inserido no contexto dessa questão, o presente estudo visa investigar a confiabilidade dos escores dos subtestes da Wais-III adaptada para a população brasileira (que é a versão disponível para uso dos psicólogos no Brasil), utilizando como estratégia o emprego do modelo bifactor e, consequentemente, a ortogonalização das variáveis latentes. Busca-se estimar a consistência interna das dimensões específicas, controlando o efeito da dimensão geral (e vice-versa). Ressalta-se que o foco do presente trabalho não é discutir qual é o melhor modelo estrutural para a Wais-III, mas apenas apresentar uma alternativa capaz de avaliar e comparar a contribuição das dimensões específicas e geral para a explicação da variância dos itens.

 

Método

Participantes

Os dados dos participantes foram analisados a partir da matriz de correlações dos resultados ponderados dos subtestes da Wais-III adaptada para a população brasileira. Para tanto, utilizou-se a matriz de correlações disponível no manual do instrumento (Nascimento, 2004, p. 177), conforme a Tabela 5.10 do referido manual.

Instrumento

A Wais-III, adaptação brasileira (Nascimento, 2004), é um instrumento, de aplicação individual, para avaliar a capacidade intelectual de adultos dentro da faixa etária de 16 a 89 anos. A amostra da Wais-III adaptada e padronizada foi constituída por 788 sujeitos, todos residentes na região metropolitana de Belo Horizonte-MG. Com o estudo de adaptação, algumas mudanças ocorreram, mas não foram significativas a ponto de descaracterizar o instrumento original.

Assim como na versão norte-americana, a adaptada manteve os 14 subtestes: completar figuras (CF), vocabulário (V), códigos (CD), semelhança (S), cubos (CB), aritmética (A), raciocínio matricial (RM), dígitos (D), informação (I), arranjo de figuras (AF), compreensão (C), procurar símbolos (OS), sequência de números e letras (SNL) e armar objetos (AO). A partir dos escores ponderados alcançados nos subtestes podem-se obter sete índices: QI verbal (QIV – somatório dos subtestes V, S, A, D, I, C e SNL), QI execução (QIE – somatório dos subtestes CF, CD, CB, RM, AF, PS e AO), QI total (QIT – somar QIV com QIE), índice de compreensão verbal (ICV – somatório dos subtestes V, S e I), índice de organização perceptual (IOP – CF, RM e C), índice de memória operacional (IMO – A, D e SNL), índice de velocidade de processamento (IVP – CD e OS).

Análise dos dados

A análise dos dados foi realizada por meio da matriz de correlação dos resultados ponderados dos subtestes e índices fatoriais da Wais-III adaptada (Nascimento, 2004). Para verificar a estrutura interna do instrumento, aplicou-se a modelagem por equações estruturais. Os parâmetros dos itens foram estimados por meio da máxima verossimilhança, com o auxílio do software Mplus (versão 7.11). Para verificar o ajuste do modelo aos dados, foram utilizados os seguintes indicadores de ajuste: qui-quadrado, root mean square error of approximation (RMSEA), standardized root mean square residual (SRMR), comparative fit index (CFI) e Tucker-Lewis index (TLI). Para compa­ração entre os modelos e os indicadores de ajuste Akaike criterion index (ACI) e Bayesian criterion index (BIC), adotaram-se os seguintes pontos de corte: CFI e TLI ≥ 0,95; RMSEA ≤ 0,06; SRMR ≤ 0,08 (Weston, Gore, Chan, & Catalano, 2008).

Para verificar a confiabilidade dos índices fatoriais, foram utilizados os índices de confiabilidade composta (CC), ômega hierárquico (ω) e variância média extraída (VME). A CC e a VME (Fornell & Larcker, 1981) são calculadas a partir dos betas entre a dimensão e os itens que a compõem. Em função de diferenças nas equações, a CC sofre influência do número de itens no modelo, e a VME sofre pequena influência da heterogeneidade dos betas. Ressalta-se que esses indicadores apresentam métricas distintas, e os seus valores nominais não podem ser comparados diretamente (Valentini & Damásio, no prelo). O ω, por sua vez, é um indicador de fidedignidade com base no modelo (model based reliabilities) e o seu cálculo é realizado por meio dos betas de um modelo bifactor. Assim, o ω é indicado para avaliar o grau em uma medida composta que pode ser explicada por um fator comum (McDonald, 1999, Reise, 2012; Rios & Wells, 2014).

 

Resultados

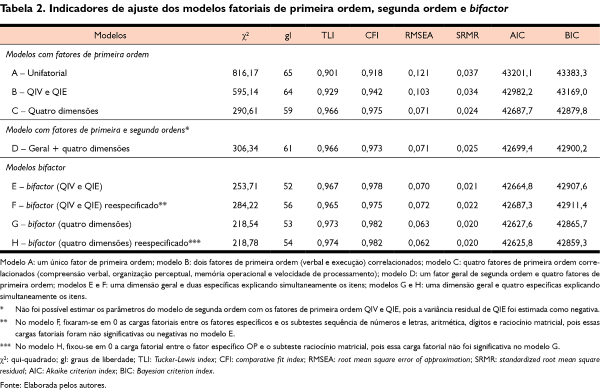
As análises fatoriais confirmatórias, por meio de equações estruturais, foram realizadas com base na matriz de correlações de Pearson disponibilizadas no manual do teste (Nascimento, 2004). Ressalta-se que as correlações dessa matriz foram calculadas com base nos escores normatizados, ponderando a faixa etária dos participantes. No manual, há tabelas de correlações separadas por faixa etária, no entanto a quantidade de sujeitos por grupo varia de 83 a 118, por isso optou-se por utilizar a tabela geral de idade que fornece maior quantidade de indivíduos. Nesse sentido, foi possível estimar os modelos discutidos neste artigo com base em apenas uma matriz de correlações. Na Tabela 2, são descritos os indicadores de ajuste de modelos hipotéticos de estrutura da Wais-III.

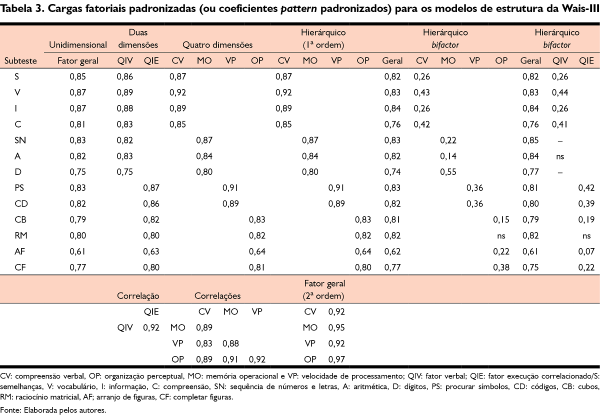
Nos modelos apresentados na Tabela 2, excluiu-se o subteste “armar objetos”, uma vez que ele não foi contabilizado nas estruturas fatoriais apresentadas no manual (Nascimento, 2004). No que se refere à comparação de estruturas, entre os modelos com fatores de primeira ordem, a extração de quatro dimensões (compreensão verbal, organização perceptual, memória operacional e velocidade de processamento) foi a solução mais bem ajustada. Contudo, ressalta-se que todas as correlações entre as quatro dimensões foram altas (r entre 0,83 e 0,92; ver Tabela 3) e, possivelmente, estão associadas a uma dimensão geral.

Considerando as altas correlações entre as dimensões de primeira ordem, buscou-se avaliar modelos de segunda ordem e bifactor. O modelo bifactor para uma dimensão geral e quatro específicas apresentou indicadores de ajuste levemente superiores aos demais. Nesse sentido, uma parte das variâncias dos itens pode ser explicada pela dimensão geral, e uma parte da variância remanescente, pelas quatro dimensões específicas.

 

 

 

Além disso, percebe-se, na Tabela 3, que, para os modelos bifactor, os betas fatoriais do fator geral são maiores do que os betas das dimensões específicas. Considerando que as dimensões são ortogonais nesses modelos, tais betas podem ser comparados diretamente, e as diferenças apontam que a dimensão geral explica mais variância dos itens do que as dimensões específicas. Ademais, a inspeção dos índices de modificação (modification index) oferecida pelo Mplus indica que apenas a correlação entre OP e VP continua com significância estatística no modelo bifactor. Ou seja, a estimação de uma dimensão geral explica a maior parte das correlações entre as dimensões específicas (observadas no modelo de quatro dimensões), bem como reduz de 0,90 para 0,43 (resultado não apresentado nas tabelas) a correlação entre OP e VP.

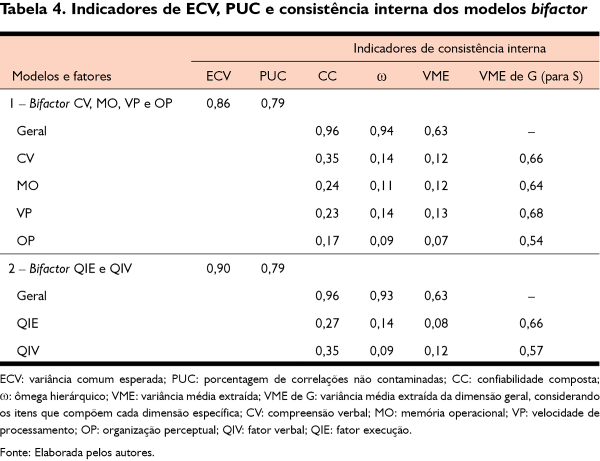
Os betas fatoriais também podem ser utilizados para avaliar a variância explicada pelas dimensões e a consistência interna. Os resultados dessas análises são descritos na Tabela 4. A variância comum esperada (expected common variance – ECV) indica a proporção da variância atribuída à dimensão geral sobre a variância explicada por todas as dimensões, incluindo a geral (sem contabilizar o erro). Assim, no modelo 1, 86% da variância dos itens, explicada pelas dimensões latentes, pode ser atribuída à dimensão geral; e, portanto, apenas 14% da variância é explicada pelas quatro dimensões específicas (CV, MO, VP e OP).

 

 

Na Tabela 4, também é indicado o valor da porcentagem de correlações não contaminadas (percentage of uncontaminated correlations – PUC). Tal indicador diz respeito à proporção das correlações da matriz utilizadas para estimar unicamente a dimensão geral. Valores de moderados a fortes (como os apresentados na Tabela 4) estão associados à maior robustez ao estimarem os coeficientes de regressão da dimensão geral (Reise, 2012). Os valores de PUC apresentados na Tabela 4 indicam que 79% das correlações da matriz foram utilizadas unicamente para estimar os betas fatoriais da dimensão geral (portanto, tais correlações não são “contaminadas” pelas dimensões específicas).

Conforme ressalta Reise (2012), ECV e PUC fortes não implicam, necessariamente, que as dimensões específicas não devam ser extraídas. Contudo, a dimensão geral parece mais relevante para o modelo, e, sem controlar o efeito da dimensão geral, a maior parte da variância estimada pelas dimensões específicas deve-se, na realidade, à dimensão geral. Nesse contexto, esperava-se que a consistência interna dos escores da dimensão específica fosse maior se comparada à consistência dos escores específicos. Essa hipótese também pode ser analisada na Tabela 4.

A confiabilidade composta (CC) e o ômega hierárquico (ω) possuem métricas semelhantes e ponderam os betas fatoriais ao estimarem a precisão dos escores. Contudo, no cálculo da CC, são contabilizadas apenas as cargas fatoriais da dimensão em questão; e o ω contabiliza a proporção de variância explicada pela dimensão sobre a não explicada, considerando, portanto, os betas fatoriais das demais dimensões do modelo. Consequentemente, o ω tende a maximizar as discrepâncias entre os fatores específicos e o geral; e a CC tende a apresentar valores maiores de consistência interna das dimensões específicas (se comparada ao ω). Ainda que esses indicadores tenham particularidades nas suas equações, ambos estimam a consistência interna dos escores de uma dimensão, controlando o efeito das demais dimensões. Nesse sentido, observa-se, na Tabela 4, que, mesmo controlando o efeito das dimensões específicas (de CV, MO, VP e OP ou QIE e QIV), a consistência interna dos escores da dimensão geral foi bastante alta (acima de 0,93). Para um modelo puramente unidimensional (sem estimar as dimensões específicas), a CC foi igual a 0,96 (resultado não apresentado nas tabelas). Assim, após controlar o efeito das dimensões específicas, a dimensão geral de inteligência apresentou leve (quase irrisória) redução de precisão.

Por sua vez, as precisões das dimensões específicas, após o controle do efeito da dimensão geral, são baixas (estimadas pelo CC e ω; ver Tabela 4). Esse resultado era esperado, uma vez que os betas fatoriais das dimensões específicas dos modelos bifactor apresentadas na Tabela 3 foram bem inferiores aos betas da dimensão geral. Portanto, ao prever (estimar) um escore específico da Wais-III (de CV, MO, VP, OP ou QIE e QIV), controlando o efeito da dimensão geral, a precisão desse escore específico será baixa. No entanto, caso não seja controlado o efeito da dimensão geral, a maior parte da precisão do escore específico poderá ser atribuída, na realidade, ao escore geral.

Finalmente, a variância média extraída (VME, apresentada na Tabela 4) diz respeito à média da variância explicada pela dimensão em questão. Diferentemente da CC e do ω, a VME não sofre influência relevante do número de itens do modelo (Valentini & Damásio, no prelo). Essa característica é importante, pois alguém poderia argumentar que a precisão da dimensão geral é mais alta do que a precisão das dimensões específicas por causa da diferença do número de itens. Conforme os resultados da VME, esse argumento não parece plausível. Ou seja, a VME da dimensão geral foi bastante superior às VMEs dos fatores específicos, indicando que, quando se controla o efeito das demais dimensões e sem a influência do número de itens, a dimensão geral explica a maior parte da variância dos itens. Em outras palavras, controlando o efeito da dimensão geral, as consistências internas das dimensões específicas foram baixas.

Na última coluna da Tabela 4, apresenta-se um cálculo adicional de VME da dimensão geral, no qual foram considerados apenas os itens de uma dimensão específica. Por exemplo, na linha CV (compreensão verbal), para o cálculo de VME da dimensão geral (última coluna), consideraram-se apenas as cargas fatoriais dos itens que compõem a CV (S, V, I e C). Esse cálculo é relevante, pois permite a comparação direta da explicação média da variância entre a dimensão geral e uma dimensão específica, a partir do conjunto de itens dessa dimensão específica. Os resultados indicaram que
a VME do fator geral foi superior à VME das dimensões específicas, mesmo quando foram computados apenas os itens que compõem a dimensão específica. Isso indica que a dimensão geral explica a maior parte da variância dos itens, e, controlado o efeito da dimensão geral, pouca variância remanescente é explicada pelas dimensões específicas. Considerando que a variância explicada está diretamente associada à consistência interna, tais resultados também são evidências adicionais da maior precisão dos escores da dimensão geral de inteligência.

 

Discussão

O presente artigo objetivou verificar a confiabilidade dos índices fatoriais da Wais-III, adaptada para a população brasileira, por meio de modelos bifactor, estimando a consistência interna das dimensões específicas e controlando o efeito da dimensão geral. Como já assinalado, o foco do presente estudo não foi analisar e discutir qual era o melhor modelo de estrutura dimensional para a Wais-III, e sim apresentar uma alternativa capaz de avaliar e comparar a contribuição das dimensões específicas e geral para a explicação da variância dos subtestes.

Especificamente sobre a estrutura das escalas Wechsler, nos estudos, até hoje, foram utilizados, principalmente, os modelos de fatores de primeira ordem correlacionados e os modelos hierárquicos (Gignac & Watkins, 2013). Um dos maiores problemas dos modelos de fatores de primeira ordem correlacionados (também denominados modelos oblíquos) é a ausência de um fator de segunda ordem, embora as correlações entre todos os fatores sejam altas. Outro problema desses modelos oblíquos na área de inteligência é teórico: não especificar um fator geral de inteligência é inconsistente com as pesquisas empíricas na área (Schneider & McGrew, 2012; Carroll, 1993). A tendência de dar mais valor aos fatores específicos do que ao geral é preocupante, uma vez que vários autores têm sugerido que a interpretação de fatores de primeira ordem pode ser enganosa, sem levar em consideração a influência de fatores de ordem superior (Canivez, 2014; Gignac & Watkins, 2013; Golay & Lecerf, 2011).

Todavia, nos modelos de segunda ordem, não é clara a importância dos fatores de primeira ordem (índices fatoriais na Wais-III), uma vez que os fatores de primeira ordem não são independentes do fator geral. Ademais, é difícil sustentar o pressuposto de mediação total dos fatores de primeira ordem sobre a relação entre a dimensão geral e os subtestes (Canivez, 2014). Assim, na interpretação dos resultados de um modelo de segunda ordem, existe a possibilidade de exagerar a importância dos fatores específicos.

O modelo bifactor, também chamado de modelo hierárquico direto, resolve esses problemas, uma vez que os fatores específicos podem ser estudados independentemente do fator geral (Reise, 2012; Rios & Wells, 2014). Nos modelos bifactor, todos os subtestes têm covariâncias diretas tanto com o fator geral quanto com seu fator específico. Os modelos bifactor também são particularmente apropriados para a estimação de índices de fidedignidade com base no modelo (model based reliabilities), tanto para os escores globais como para os escores nas subescalas. As estimativas de fidedignidade, portanto, representam a quantidade de consistência interna unicamente associada tanto com o escore geral (por exemplo, o QI geral) quanto com os escores das subescalas (por exemplo, as subescalas compreensão verbal e organização perceptual­).

Nesse contexto, os resultados do presente estudo indicam que o modelo bifactor para uma dimensão geral e quatro específicas apresentou-se mais bem ajustado aos dados, se comparado aos demais modelos. As quatro dimensões específicas correspondem aos índices fatoriais de compreensão verbal (CV), organização perceptual (OP), memória operacional (MO) e velocidade de processamento (VP). Isso significa que parte das variâncias dos itens pôde ser explicada pela dimensão geral, e uma parte da variância remanescente, pelas dimensões específicas.

Resultados semelhantes foram encontrados por estudos anteriores (Canivez, 2014; Gignac, 2005, 2006; Gignac & Watkins, 2013; Golay & Lecerf, 2011). Entre esses estudos­, destaca-se a relevância das investigações de Gignac (2006) e Golay e Lecerf (2011), pois utilizaram a terceira versão da Wais, e os resultados podem ser comparados diretamente com os da presente pesquisa. A pesquisa de Gignac (2006) apresentou média de betas dos modelos bifactor acima de 0,60 para a dimensão geral. No estudo de Golay e Lecerf (2011), os dados indicaram que 63% da variância comum foi explicada pela dimensão geral. Na presente pesquisa, os resultados de ECV indicaram que 86% da variância comum pôde ser atribuída à dimensão geral. Ademais, todos os subtestes apresentaram betas fatoriais maiores para a dimensão geral. Em outras palavras, a maior parte da variância pode ser atribuída à dimensão geral.

Os resultados mais importantes do presente estudo dizem respeito às estimações de consistência interna da dimensão geral, controlando o efeito das dimensões específicas (e vice-versa). Mesmo controlando o efeito das dimensões específicas (CV, OP, MO, e VP), a consistência interna dos escores da dimensão geral foi bastante alta. A confiabilidade composta (CC) do fator geral foi 0,96, e o coeficiente ômega hierárquico (ω), 0,94. Entretanto, para as dimensões específicas, após o controle do efeito da dimensão geral, os índices de fidedignidade foram muito baixos (CC ≤ 0,35; ω ≤ 0,14). Tais resultados têm implicações práticas e teóricas importantes. Por um lado, o escore da dimensão geral da Wais-III, considerando a sua alta precisão, tende a contribuir significativamente para diagnósticos cognitivos, bem como, na pesquisa, aumenta o poder estatístico dos testes de relações entre variáveis. Por outro lado, a interpretação dos índices fatoriais (CV, OP, MO, VP) deve ser realizada com cautela. Pesquisadores e usuários do instrumento devem considerar que a maior parte da precisão dos escores dos índices fatoriais advém, na realidade, da dimensão geral. Consequentemente, o usuário, se desconsiderar o efeito da dimensão geral, poderá subestimar o erro padrão de medida, interferindo na sua interpretação dos escores (principalmente no que se refere ao intervalo de confiança, que terá a sua amplitude subestimada). Nesse sentido, deve-se ter cuidado, por exemplo, ao interpretar as diferenças dos índices fatoriais entre grupos clínicos, pois, se o efeito da dimensão geral não for controlado, a sobreposição dos intervalos de confiança será subestimada. Assim, nesse exemplo, o pesquisador poderia concluir que existem diferenças entre esses grupos, quando, na realidade, ao se controlar o efeito da dimensão geral, tais diferenças não apresentam sustentação empírica.

Os resultados relativos à precisão oferecem suporte adicional às evidências encontradas por estudos internacionais. Ao utilizarem a amostra de normatização norte-americana da Wais-IV, Gignac e Watkins (2013) estimaram a precisão da dimensão geral levemente abaixo dos resultados do presente estudo. Ressalta-se que Gignac e Watkins (2013) avaliaram a quarta versão da Wais, cuja proposta é enfatizar os índices fatoriais. Nelson et al. (2013) avaliaram uma amostra clínica e estimaram a precisão da dimensão geral mais baixa se comparada aos demais estudos (ω = 0,74), embora a consistência interna da dimensão geral tenha sido maior do que das dimensões específicas. Tal diferença pode ser atribuída, hipoteticamente, a dois aspectos principais: 1. à variabilidade levemente reduzida da amostra clínica – conforme pode ser visualizado na Tabela 1 do artigo de Nelson et al. (2013); 2. a pequenas diferenças estruturais (hipoteticamente) da inteligência na população clínica. Ainda assim, no que se refere à validade incremental, no estudo de Nelson et al. (2013), o efeito individual dos índices fatoriais sobre a predição do desempenho acadêmico é trivial se comparado ao efeito da dimensão geral.

Considerando os baixos índices de fidedignidade dos escores específicos, uma reflexão é necessária sobre a adequação desses escores: na interpretação dos escores específicos da Wais-III, o escore geral deve ser sempre considerado. Contudo, ressalta-se, como principal limitação desta pesquisa, que se investigou apenas a amostra normativa­ da Wais-III. Estudos futuros devem ser conduzidos com amostras clínicas, com adultos­ com dificuldades cognitivas moderadas e graves, para os quais a estrutura de índices fatoriais pode ser, hipoteticamente, mais relevante. Ademais, a presente pesquisa restringiu a discussão principalmente às análises de confiabilidade. Nesse sentido, estudos futuros precisam ser realizados, no Brasil, para investigar a validade incremental dos escores específicos na predição de desempenho acadêmico, por exemplo.

Ressalta-se, ainda, que a Wais-III é um dos poucos instrumentos dedicados à avaliação de adultos que abarcam a inteligência sob diferentes tipos de tarefa. Nesse sentido, é possível afirmar que a Wais-III é um dos instrumentos mais completos para a avaliação cognitiva, abarcando-a de maneira complexa. Ressalta-se ainda a boa qualidade das pesquisas brasileiras de validação e de normatização desse instrumento (Figueiredo & Nascimento, 2007; Nascimento & Flores-Mendoza, 2007; Nascimento, 2004, entre outras). Portanto, a presente pesquisa não visa, sob nenhuma hipótese, desencorajar o uso do instrumento. Pelo contrário! Poucos instrumentos apresentam precisão de aproximadamente 0,95 (para os escores da dimensão geral de inteligência), e a Wais-III é um deles. No entanto, os resultados do presente estudo indicam que os usuários devem ter cautela ao interpretar os escores específicos (índices fatoriais), pois a maior parte da variância e precisão de tais escores parece estar associada à dimensão geral.

 

Referências

Canivez, G. L. (2013). Incremental validity of Wais-IV factor index scores: relationships with Wiat-II and Wiat-III subtest and composite scores. Psychological Assessment, 25(2), 484-495.         [ Links ]

Canivez, G. L. (2014). Construct validity of the Wisc-IV with a referred sample: direct versus indirect hierarchical structures. School Psychology Quarterly, i(1), 38-51.         [ Links ]

Carroll, J. B. (1993). Human cognitive abilities: A survey of factor-analytic Studies. New York: Cambridge University Press.         [ Links ]

Donders, J., Tulsky, D. S., & Zhu, J. (2001). Criterion validity of new Wais-III subtest scores after traumatic brain injury. Journal of the International Neuropsychological Society, 7(7), 892-898.         [ Links ]

Figueiredo, V. L. M., & Nascimento, E. (2007). Desempenhos nas duas tarefas do subteste dígitos do Wisc-III e do Wais-III. Psicologia: Teoria e Pesquisa, 23(3), 313-318.         [ Links ]

Fisher, D. C., Ledbetter, M. F., Cohen, N. J., Marmor, D., & Tulsky, D. S. (2000). Wais-III and WMS-III profiles of mildly to severely brain-injured patients. Applied Neuropsychology, 7(3), 126-132.         [ Links ]

Fornell, C., & Larcker, D. F. (1981). Evaluating structural equations models with unobservable variables and measurement error. Journal of Marketing, 18(1), 39-50.         [ Links ]

Gignac, G. E. (2005). Revisiting the factor structure of the Wais-R: insights through nested factor modeling. Assessment, 12(3), 320-329.         [ Links ]

Gignac, G. E. (2006). The Wais-III as a nested factor model: a useful alternative to the more conventional oblique and higher-order models. Journal of Individual Differences, 27(2), 73-86.         [ Links ]

Gignac, G. E., & Watkins, M. W. (2013). Bifactor modeling and the estimation of model-based reliability in the Wais-IV. Multivariate Behavioral Research, 48, 639-662.         [ Links ]

Golay, P., & Lecerf, T. (2011). Orthogonal higher order structure and confirmatory factor analysis of the French Wechsler adult intelligence scale (Wais-III). Psychological Assessment, 23(1), 143-152.         [ Links ]

Kanai, C., Tani, M., Hashimoto, R., Yamada, T., Ota, H., Watanabe, H., Iwanami, A., & Kato, N. (2012). Cognitive profiles of adults with Asperger’s disorder, high-functioning autism, and pervasive developmental disorder not otherwise specified based on the Wais-III. Research in Autism Spectrum Disorders, 6(1), 58-64.

McDonald, R. P. (1999). Test theory: a unified treatment. Mahwah, NJ: Erlbaum.         [ Links ]

Nascimento, E. (2004). Manual para administração e avaliação do Wais-III adaptado para a população brasileira. São Paulo: Casa do Psicólogo.         [ Links ]

Nascimento, E., & Flores-Mendonza, C. E. (2007). Wisc-III e Wais-III na avaliação da inteligência de cegos. Psicologia em Estudo, 12(3), 627-633.         [ Links ]

Nelson, J. M., Canivez, G. L., & Watkins, M. W. (2013). Structural and incremental validity of the Wechsler adult intelligence scale – fourth edition with a clinical sample. Psychological Assessment, 25(2), 618-630.

Nuechterlein, K. H., Barch, D. M., Gold, J. M., Goldberg, T. E., Green, M. F., & Heaton, R. K. (2004). Identification of separable cognitive factors in schizophrenia. Schizophrenia Research, 72(1), 29-39.         [ Links ]

Reise, S. P. (2012). The rediscovery of bifactor measurement models. Multivariate Behavioral Research, 47(5), 667-696.         [ Links ]

Reise, S. P., Moore, T. M., & Haviland, M. G. (2010). Bifactor models and rotations: exploring the extent to which multidimensional data yield univocal scale scores. Journal of Personality Assessment, 92(6), 544-559.         [ Links ]

Reise, S. P., Scheines R., Widaman, K. F., & Haviland, M. G. (2013). Multidimensionality and structural coefficient bias in structural equation modeling: a bifactor perspective. Educational and Psychological Measurement, 73(1), 5-26.         [ Links ]

Rios, J., & Wells, C. (2014). Validity evidence based on internal structure. Psicothema, 26(1), 108-116.         [ Links ]

Schneider, J. W., & McGrew, K. S. (2012). The Cattell-Horn-Carroll model of intelligence. In D. P. Flanagan & P. L. Harrison (Ed.). Contemporary intellectual assessment: theories, tests, and issues (3rd ed., pp. 99-144). New York: Guilford Press.         [ Links ]

Spek, A. A., Scholte, E. M., & Berckelaer-Onnes, I. A. van (2008). Brief report: the use of Wais-III in adults with HFA and Asperger syndrome. Journal of Autism and Developmental Disorders, 38(4), 782-787.         [ Links ]

Valentini, F., & Damásio, B. F. (no prelo). Variância média extraída e confiabilidade composta: indicadores de precisão. Psicologia: Teoria e Pesquisa. (no prelo).         [ Links ]

Weston, R., Gore Jr., P. A., Chan, F., & Catalano, D. (2008). An introduction to using structural equation models in rehabilitation psychology. Rehabilitation Psychology, 53(3), 340-356.

 

 

Endereço para correspondência:
Felipe Valentini
Laboratório de Medidas em Psicologia (Labmep), Universidade Salgado de Oliveira
Rua Marechal Deodoro, 217, Bloco A, 2º andar, Niterói
Rio de Janeiro – RJ – Brasil. CEP: 24030-060
E-mail: valentini.felipe@gmail.com

Submissão: 3.11.2014
Aceitação: 13.4.2015