Serviços Personalizados
Journal
artigo
Indicadores
Compartilhar
Actualidades en psicología
versão On-line ISSN 0258-6444
Actual. psicol. v.21 n.108 San José 2007
Teoría G: un futuro paradigma para el análisis de pruebas psicométricas
María Elena Zúñiga-BrenesI; Eiliana Montero-RojasI; II
IEscuela de Estadística, Universidad de Costa Rica
IIInstituto de Investigaciones Psicológicas, Universidad de Costa Rica
Dirección para correspondencia
RESUMEN
La teoría de la generalizabilidad (teoría G) permite medir la confiabilidad de una prueba por medio de la cuantificación de la importancia de cada una de sus fuentes de variabilidad. Se redefine el error, como condición o faceta de medición, utilizando el coeficiente de generalizabilidad como medida para estimar la confiabilidad. Este enfoque no contradice los planteamientos fundamentales de la teoría clásica de los tests, sino que puede ser visto como una extensión de ella. Se concluye que, si bien en muchos casos los instrumentos psicométricos se usan para tomar decisiones relativas (modelo con referencia a normas), siendo en esa situación suficiente la teoría clásica de los tests, otras instancias como las que involucran el uso de pruebas educativas, suelen requerir decisiones basadas en estándares absolutos de desempeño, donde la teoría G constituye una herramienta de gran utilidad y mucho más informativa que el enfoque clásico.
Palabras clave: Teoría G, Teoría de la generalizabilidad, Modelos de error de medición, Diseños de facetas, Componentes de varianza.
ABSTRACT
Generalizability Theory (G Theory) allows to measure the reliability of a test by means of the quantification of the importance of each one of its sources of variability. G Theory redefines the error as conditions or facets of measurement, using the Generalizability coefficient as an indicator to estimate the reliability. It is important to point out that this approach does not contradict the fundamental assumptions of Classical Test Theory. On the contrary, it can be seen as an extension of the latter. It is concluded that, even though in many cases the psychometric instruments are used to make relative decisions (norm referenced model), being Classical Test Theory sufficient for such situations; other instances, like those which involve the use of educational tests, often require decisions based on absolute standards of performance, where G Theory constitutes a very useful tool, much more informative than the classical approach.
Keywords: G Theory, Generalizability theory, Models for measurement error, Facet designs, Variance components.
Introducción
Este estudio tiene como propósito dar a conocer una teoría relativamente nueva en el área de la psicometría, llamada teoría de la generalizabilidad (teoría G).
Más específicamente, el objetivo es describir y valorar una de las más recientes aplicaciones de los métodos cuantitativos en la psicometría, la teoría de la generalizabilidad, y su relación con la teoría clásica de los tests.
Según Montero (2001) “la psicometría nos brinda un cuerpo de teoría y métodos para la medición de constructos en ciencias sociales. Uno de sus propósitos principales es el desarrollo de técnicas de aplicación empírica que permitan construir instrumentos de medición e indicadores, de alta confiabilidad y validez. Estas técnicas y métodos se basan en enfoques cuantitativos y utilizan conceptos, procedimientos y medidas derivado de la estadística y la matemática” (p. 218).
Por medio de la construcción de instrumentos psicométricos se intenta representar el constructo con un puntaje numérico derivado de la aplicación de un conjunto de reactivos (ítems, preguntas o estímulos) a la población de interés.
Andrade, Navarro y Yock (1999) afirman que “en el país se aplican gran cantidad de instrumentos de medición con diferentes propósitos; no obstante, muchos de ellos no han pasado por los procesos de validación necesarios para garantizar su calidad. Al no tener evidencia del grado de validez y confiabilidad del instrumento, se podrían estar tomando decisiones incorrectas” (p. 2).
Este artículo desarrolla y actualiza algunos conceptos referentes a los procedimientos asociados a la medición de la confiabilidad en el área de la psicometría. Pretende dar a conocer la importancia de utilizar nuevas herramientas para el análisis de pruebas utilizadas en Costa Rica. Si se cuenta con herramientas útiles para el análisis, se garantiza la calidad técnica de las pruebas, y con ello se contribuye a la toma de decisiones adecuadas, según las necesidades del (la) investigador(a) o del (la) usuario(a).
Primeramente se expondrán algunos elementos clave de la teoría clásica de los tests, la cual permite analizar los ítems de una prueba con respecto a su poder discriminatorio y medir la confiabilidad del instrumento, para establecer en cuánto se afecta la consistencia de la prueba por causa del error aleatorio. De esta teoría se deriva el alfa de Cronbach (α), medida que provee un indicador numérico del nivel de confiabilidad de la prueba.
Seguidamente se presentará la llamada teoría de la generalizabilidad (teoría G), que trata de descomponer e identificar fuentes de variación que la teoría clásica considera error aleatorio, para lograr una medición más precisa de las diferencias individuales entre las personas examinados(as) en el constructo de interés.
Luego de una exposición conceptual, se resumen los resultados más relevantes obtenidos a partir de la aplicación de las dos teorías mencionadas, en el caso de una prueba particular, llamada Escala Zurquí, utilizada para medir la calidad de vida en niños(as) con enfermedades terminales.
Finalmente se presentan las conclusiones de mayor importancia, producto de este trabajo, haciendo énfasis en una valoración comparativa de ambos modelos.
Psicometría y generalizabilidad
La psicometría brinda la herramienta teórica y metodológica para la medición de constructos en las ciencias sociales. Su correcta utilización permite asegurar la calidad técnica de las pruebas, ya sean tests de personalidad, pruebas de selección de personal, admisión, conocimientos u otras.
En la psicometría, como en otras áreas, es importante tener claro el concepto de medición. De acuerdo con Nunnally y Bernstein (1995) “la medición consiste en reglas para asignar símbolos a objetos, de manera que: 1) representen cantidades o atributos de forma numérica (escala de medición) y 2) definan si los objetos caen en las mismas categorías o en otras diferentes con respecto a un atributo determinado (clasificación) (...) es importante señalar que los objetos no pueden medirse, lo que se miden son sus atributos. Por ejemplo, no se mide a un niño(a) per se, si no más bien su inteligencia, estatura o socialización” (p. 3 y 5).
Andrade, Navarro y Yock (1999) expresan en su tesis de graduación que los tests psicológicos se crearon con el propósito de medir las diferencias entre las personas o sus reacciones en diferentes situaciones, constituyendo así una medida objetiva y tipificada de su conducta. Es objetiva en cuanto a la aplicación, la puntuación y la interpretación de las puntuaciones y tipificada en cuanto a la uniformidad del procedimiento en la aplicación del test (p. 36).
Los tests se utilizan en la solución de una amplia gama de problemas prácticos y de investigación, generalmente en el área de las ciencias sociales. Las pruebas son aplicadas para la selección de personal, evaluaciones psicológicas, valoración del rendimiento y de la aptitud académica, decisiones sobre la promoción estudiantil, medición de constructos en investigación social, entre otros.
Andrade, Navarro y Yock (1999) afirman que un test psicométrico se caracteriza porque:
1. Su resultado final es un puntaje numérico que se asigna al examinado(a) y ese puntaje indica el nivel que presenta en el constructo.
2. El test psicométrico tiene que pasar por ciertos procedimientos para garantizar su calidad técnica en términos de validez y confiabilidad.
3. Los puntajes en este test se tratan en una escala de intervalo, por lo que se pueden utilizar métodos paramétricos de análisis (p 36).
Una de las tareas fundamentales de la psicometría es determinar la confiabilidad en las pruebas para sus diversas aplicaciones. La teoría del error de medición establece que en cualquier medición existe un error, ya sea causado por el instrumento que se utilice, la forma cómo se aplica, el momento, el lugar, entre otros factores; todas estas circunstancias pueden generar error de medición. Este error puede producirse por un proceso sistemático donde se afectan todas las observaciones por igual y ser, por tanto, un error constante o sesgo, o puede ser generado por un proceso aleatorio. En este contexto, Nunnally y Bernstein (1995) definen la confiabilidad como la libertad del error aleatorio, es decir, cuán repetibles son las observaciones cuando diferentes personas hacen las mediciones, cuando se usan instrumentos alternativos que intentan medir lo mismo, y cuando hay variaciones incidentales en las condiciones de la medición (p. 238).
Se puede decir, entonces, que una medición es confiable si conduce a los mismos o similares resultados, sin importar las variaciones que puedan afectar la prueba. Entre los modelos de error de medición se encuentra, según Nunnally y Bernstein (1995) el modelo de dominio de muestreo, como uno de los más utilizados. En éste se considera que cualquier medida particular está compuesta de respuestas a una muestra aleatoria de reactivos (ítems) de un dominio o universo hipotético. Este modelo permite considerar la posibilidad de que los reactivos en el dominio varíen en diversas maneras, por ejemplo, por la condición física del objeto de medida, la habilidad de los(as) examinadores(as), el ambiente de la evaluación, y también en sus propiedades intrínsecas tales como dificultad y discriminación.
El primer modelo de análisis de datos que se utilizó para explicar y medir el error de una prueba se denomina teoría clásica de los tests. De acuerdo con Nunnally y Bernstein (1995) “la teoría clásica considera las mediciones basadas en combinaciones lineales de respuesta a reactivos individuales y puede contrastarse con el énfasis en la calificación de pruebas basadas en el patrón de respuestas a los reactivos” (p. 239). Utilizando la teoría clásica de los tests se pretende medir la confiabilidad de una prueba, considerando en cuánto se afecta la consistencia de ella por causa del error aleatorio.
El psicólogo inglés Charles Spearman, a principios del siglo XX, sentó las bases para el modelo de la teoría clásica. En este modelo, el error de medición es la discrepancia entre el puntaje observado en la prueba para el(la) examinado(a) y su puntaje verdadero. Una definición de puntaje verdadero es aquel valor que se obtendría como promedio si el(la) examinado(a) realizara la misma prueba, bajo las mismas circunstancias.
Esta teoría se fundamenta en los siguientes parámetros para caracterizar a los ítems y a las pruebas, de acuerdo con su calidad para la medición:
1. La dificultad del ítem, medida por el porcentaje de respuestas correctas.
2. La discriminación del ítem, medida generalmente por la correlación entre el puntaje en el ítem y el puntaje total en la prueba.
3. La estimación del puntaje total en la prueba como la suma o promedio simple de los puntajes obtenidos en los ítems.
4. La confiabilidad total de la prueba medida por el alfa de Cronbach (α).
Precisamente, el alfa de Cronbach (α) es una de las medidas empíricas más importantes derivadas de esta teoría, ya que proporciona estimaciones para medir la confiabilidad. El rango de este coeficiente generalmente está entre cero y uno; cuanto más cercano a uno, mayor es la confiabilidad de la prueba. El criterio para determinar cuáles valores para alfa son aceptables, depende tanto del juicio del(a) investigador(a), como de la naturaleza del constructo que se está midiendo y la población específica bajo estudio. Por ejemplo, si se van a tomar decisiones que afectan el futuro de los (las) examinados(as), como es el caso de una prueba de admisión, una confiabilidad de 0.9 o más, sería lo adecuado. Si es una prueba que se usa para investigación o diagnóstico, algunos autores como Nunnally y Bernstein (1995) consideran que un alfa mayor o igual a 0.7, sería suficiente.
La confiabilidad depende, principalmente, de dos factores: la correlación promedio entre los ítems del instrumento y el número de ítems que contenga éste. Cuanto más grande sea la correlación promedio entre los reactivos o cuanto mayor sea el número de ellos, menor será el error de medición y, por tanto, más alta será la confiabilidad.
La expresión matemática del Alfa de Cronbach es la siguiente:

Esta teoría supone que las observaciones se distribuyen normalmente y que el error de medición es aleatorio y del mismo tamaño para todas ellas.
El coeficiente de confiabilidad alfa de Cronbach también puede expresarse matemáticamente como la razón de la varianza de los puntajes observados a los puntajes verdaderos, de tal forma que representa la proporción de la varianza en los puntajes observados, que puede ser atribuida a la variación en los puntajes verdaderos.
En este modelo clásico se concibe el puntaje observado del(a) examinado(a) como una variable aleatoria. El puntaje particular de una persona en una prueba se ve como una muestra aleatoria, de tamaño uno, de muchos posibles puntajes que la persona podría obtener si se repitiera muchas veces la administración de la prueba, bajo las mismas condiciones. De manera que el puntaje observado resulta ser la suma del puntaje verdadero del(a) examinado(a) y el error aleatorio. Así, lo que le da el carácter aleatorio a esta variable es el término de error, pues el puntaje verdadero es un parámetro (valor fijo).
En realidad, el modelo de la teoría clásica no intentó originalmente explicar esas diversas fuentes de variación, ya que las asumió sencillamente como errores aleatorios, de manera que ese error era la única fuente de variación para los puntajes observados.
Por el contrario, en el caso de la teoría G, como será explicado seguidamente, se intenta identificar y cuantificar esas fuentes de variación de los puntajes observados. Por esta razón, la técnica estadística de análisis de varianza (ANOVA) es la idónea como herramienta para el estudio empírico de la confiabilidad de una prueba psicométrica. El llamado “error aleatorio” en la teoría clásica, es para la teoría G una variable que incluye diversos componentes de variabilidad, que necesitan ser identificados. Lo que en la teoría clásica se ve como un error aleatorio, es en realidad, para la teoría G, fuentes no explicadas de variación.
A continuación una ilustración de lo anterior. El puntaje de un(a) estudiante en una prueba estandarizada de conocimientos podría depender no solamente de las características de los ítems en esa prueba (su dificultad y discriminación), sino de otras características tanto de la administración misma de la prueba como contextuales, incluyendo hasta factores como la iluminación, el estado de ánimo del estudiante, la temperatura y el hacinamiento en el aula, entre otros. En una prueba de desarrollo, la influencia del(la) calificador(a) puede ser una fuente muy importante de variabilidad para los puntajes, pues es común que diferentes examinadores(as) provean diferentes calificaciones.
La teoría de la generalizabilidad se originó según Brennan (2001) a raíz de los trabajos realizados por Hoyt a inicios de los años 40s, y por Lindquist y Burt en los años 50s.
Es importante también señalar que el mismo Lee Cronbach, creador de la medida de confiabilidad de su mismo nombre (alfa de Cronbach), contribuyó a sentar las bases de la teoría de la generalizabilidad en un libro publicado en 1972 con el nombre de “The Dependability of Behavioral Measurements”. De hecho, en su artículo póstumo Cronbach (2004) señala que el coeficiente alfa cubre solamente una pequeña parte del rango de los usos de medición, para los cuales actualmente se requiere la información de confiabilidad. Entonces, α debe ser concebido como un elemento dentro de un sistema mucho más amplio de análisis de confiabilidad.
La teoría G es, así, una extensión de la teoría clásica de los tests. En la teoría G se aplican las técnicas de análisis de varianza para cuantificar la importancia de cada fuente de variabilidad, además de las diferencias individuales entre los(as) examinados(as).
Las autoras del presente artículo consideran que lo más relevante de la teoría G es esta nueva propuesta, donde se redefine el error como condición o faceta de medición.
Según Shavelson y Webb (1991) la confiabilidad se refiere a la exactitud al generalizar de un puntaje obtenido por una persona en una prueba u otra medida, al puntaje promedio que la persona habría recibido bajo todas las posibles condiciones de medición. Implícitos en esta noción de confiabilidad están los conocimientos de la persona, actitud, habilidad u otros atributos. Se asume que casi cualquier diferencia en los puntajes obtenidos por una persona en ocasiones diferentes de medición, es debida a una o más fuentes de variabilidad, y no necesariamente a los cambios sistemáticos de madurez o aprendizaje del individuo (p. 1).
Para Shavelson y Webb (1991) y Brennan (2001), en la teoría G la confiabilidad es medida en relación con las diferencias que existen entre las personas, las ocasiones en que se realice la prueba, los(las) observadores(as) o calificadores(as) que intervienen, los ítems que se utilicen y otras condiciones presentes en el estudio.
Así, un solo puntaje obtenido en una ocasión en particular, en una prueba con un(a) solo(a) observador(a) no es totalmente fidedigno; es decir, es improbable emparejar el puntaje promedio de esa persona en diversas ocasiones de medición, con diferentes formas de la prueba, y con diferentes administradores(as). Usualmente, el puntaje de una persona sería diferente en ocasiones diferentes, en otras formas de la prueba o con observadores(as) diferentes. Estas son algunas de las fuentes más serias de inconsistencias en los puntajes de los tests.
La teoría clásica de los tests puede estimar, separadamente, sólo una fuente de variabilidad en un momento en particular, mientras que la teoría G logra medir esas fuentes de variabilidad tomando en cuenta varios momentos, diferentes observadores(as), reactivos y otras situaciones.
Para Shavelson y Webb (1991), así como para Brennan (2001), lo relevante en la teoría G es que las múltiples fuentes de variabilidad pueden estimarse separadamente en un solo análisis, si se diseña apropiadamente el estudio de confiabilidad. Este modelo permite tomar en cuenta las múltiples fuentes de variabilidad, lo cual ayuda al (la) investigador(a) a determinar cuántas ocasiones, formas de la prueba y observadores(as) son necesarios para obtener puntajes de alta precisión. Como resultado de los análisis con la teoría G, se puede calcular un indicador sumario que es análogo al coeficiente de confiabilidad (alfa de Cronbach) de la teoría clásica de los tests; éste es llamado “coeficiente de generalizabilidad”.
Un propósito de la teoría G es evaluar las fuentes de mayor variabilidad, para que aquellos componentes de variabilidad no deseados puedan reducirse cuando se recolecten datos en el futuro. Por ejemplo, si en una prueba de ciencias no se desea que el conocimiento extra-curricular de los estudiantes sobre hámsters influya en la calificación de la prueba, los ítems que la componen no deberían contener enunciados que refieran a ese tema específico, puesto que si existieran tales reactivos, algunos(as) examinados(as) tendrían probablemente ventajas sobre otros(as), si poseen hámsters como mascotas o han tenido experiencias previas con ellos.
Las ideas expresadas en los siguientes párrafos son elaboraciones propias a partir de los textos de Shavelson y Webb (1991) y Brennan (2001).
El concepto de confiabilidad aplica a los universos simples o complejos en los cuales el(la) investigador(a) requiere generalizar. Primeramente, se expone el caso más simple, cuando el universo es definido por una fuente de variabilidad, el cual es denominado de “una faceta”.
Desde la perspectiva de la teoría G, una medición es una muestra de un universo de observaciones, que es usada por el(la) investigador(a) con el propósito de tomar una decisión. Esta decisión podría ser de carácter práctico, como la selección de los(as) estudiantes con puntajes más altos de un programa educativo, o podría ser una conclusión científica. Un universo de una faceta es definido por una fuente de variabilidad. Si el (la) investigador(a) intenta generalizar con un conjunto particular de ítems tomados como una muestra de un universo de muchos conjuntos de reactivos, entonces estos ítems constituyen una faceta de medición; el universo sería definido por todos los reactivos de la prueba.
Según Shavelson y Webb (1991) si todos los ítems en el universo son iguales en dificultad y el puntaje de una persona es el mismo de un reactivo al próximo, el desempeño de la persona en cualquier muestra de ítems, se podrá generalizar a todos los reactivos. Si la dificultad de los ítems varía, el puntaje de la persona dependerá de la muestra particular de reactivos en la prueba o test. En este último caso, la generalización de la muestra al universo es arriesgada. La variabilidad de los ítems representa una fuente potencial de inconsistencia en la generalización. Los reactivos constituyen una faceta de medida. Si es ésta la única faceta considerada, el conjunto de "ítems" es una sola faceta del universo. El(la) investigador(a) debe decidir cuáles ítems son aceptables.
Según la opinión de Shavelson y Webb, es el(la) investigador(a) quien debe decidir cuáles ítems son aceptables, tomando en cuenta el grado de dificultad de cada uno de ellos, ya que estos afectan el nivel de los puntajes de las personas.
Este autor menciona que el diseño de una faceta tiene cuatro fuentes de variabilidad:
1. La primera fuente de variabilidad se encuentra en las diferencias sistemáticas entre las personas en el rasgo o constructo que se desea medir; esto es, la variabilidad entre los objetos de medida (normalmente las personas), la cual se refleja en las diferencias de conocimiento, habilidades u otros atributos entre los examinados(as).
2. La segunda fuente de variabilidad es la diferencia en la dificultad de los ítems de la prueba. Algunos reactivos se consideran fáciles, intermedios o difíciles, según su nivel de dificultad, medido empíricamente, por ejemplo, en términos de la proporción de respuestas correctas para un grupo de examinados(as).
3. La tercera fuente de variabilidad se refleja en el nivel educativo y experiencias previas que las personas hayan tenido. Por ejemplo, un ítem de una prueba de ciencias que se refiera a hámsters, sería posiblemente más fácil para una persona que los ha tenido o tiene como mascota. Esto implica una interacción entre las personas y los ítems. Este emparejamiento entre las experiencias de una persona y un reactivo en particular, aumenta la variabilidad entre personas e incrementa la dificultad para generalizar, en términos del atributo específico que se desea medir.
4. La cuarta fuente de variabilidad se supone que es debida a otros factores sistemáticos no identificados o no conocidos.
En general, la tercera y cuarta fuente de variabilidad no pueden separarse estadísticamente, debido a que usualmente solo se cuenta con una observación y es prácticamente imposible poder controlar todos los factores asociados a las experiencias previas de las personas.
Para los estudiosos de este enfoque, la teoría G expresa la magnitud de variabilidad en términos de componentes de varianza. En el diseño de una faceta, según lo se que describe en la Tabla 1, los componentes de varianza son 

En el caso de los estudios de medición que se realizan en psicología y educación, se requiere usualmente más de una faceta, debido a su complejidad en términos de fuentes de variación.
Para un diseño de dos facetas, por ejemplo, el universo de observaciones podría estar definido por ítems y observadores(as), representando cada uno una faceta; es decir, el universo de puntajes sería definido por todos los posibles reactivos, con todos(as) los(as) posibles observadores(as). Otra ilustración de un diseño de dos facetas sería uno en donde las fuentes de variabilidad, además de las personas, sean los(as) observadores(as), y/o calificadores(as) y las ocasiones (o momentos) de medición, como podría ser el caso de una evaluación médica en la cual cada paciente es valorado por dos profesionales en dos momentos diferentes del día, obteniéndose cuatro mediciones en total para cada paciente. Un diseño de este tipo se ilustra en la Tabla 2.

Este diseño de dos facetas presenta específicamente las siguientes
fuentes de variabilidad:
Efectos principales
Personas (p): Varianza del puntaje-universo (objeto de medida).
Calificadores (c): Efecto constante en todas las personas, debido a la rigurosidad o laxitud en los puntajes otorgados por los calificadores(as).
Ocasiones (o): Efecto constante en todas las personas, debido a sus inconsistencias de comportamiento de una ocasión a otra.
Interacciones
p x c: Inconsistencias en la evaluación de los calificadores(as) u observadores(as) debidas al comportamiento particular de las personas.
p x o: Inconsistencias de una ocasión a otra en el comportamiento particular de las personas.
o x c: Efecto constante para todas las personas debido a diferencias en la rigurosidad de los calificadores(as) de una ocasión a otra.
p x c x o, e: Residuo. Consiste en todas las combinaciones únicas de p, c y o; facetas no medidas que afectan toda la medición; y/o eventos aleatorios.
En el caso de una muestra de dos calificadores(as) seleccionados(as) del universo de calificadores(as), las inconsistencias entre ellos(as) crean problemas en la generalización de la media de los puntajes obtenidos para cada objeto de medición. Por ejemplo, si se realizara un estudio en el que un grupo de niños(as) es evaluado por dos observadores(as) o calificadores(as), los puntajes obtenidos dependerán de la rigurosidad o laxitud de evaluación de cada calificador(a). La forma de calificar de cada observador(a) afecta igualmente a toda la población de interés. A esto se le llama "efecto principal", es un efecto constante para todos(as) los(as) niños(as). De igual manera ocurre con las ocasiones o momentos de medición, que afectan los puntajes de cada uno de ellos.
Los estudios de medición en educación y psicología, como en otras áreas, pueden tener tanta complejidad que no se logre capturar por medio de dos facetas. Por ejemplo, puede darse el caso de una prueba con cierto número de ítems que difieren en dificultad, con varios(as) observadores(as), y aplicada en varias ocasiones, la cual sería una prueba en un universo de tres facetas. Este tipo de estudios no se analizarán a profundidad en este artículo, pero debe entenderse que existen, y que su complejidad es mayor.
De la misma forma como el (la) investigador(a) intenta identificar y estimar los efectos de variables independientes potencialmente importantes, el (la) especialista que utiliza la teoría G intenta identificar y estimar la magnitud de las fuentes potenciales de variabilidad en una medida u observación, la variabilidad debida al universo y otras fuentes.
La teoría G utiliza el ANOVA para distinguir las fuentes de variación entre una y otra observación. En las aplicaciones tradicionales se usa el ANOVA para identificar fuentes de variación en una variable de respuesta o dependiente, según los efectos de ciertas variables independientes, sus combinaciones (interacciones), y el error. En el caso de la teoría G, el ANOVA se emplea para conocer el efecto de cada faceta o fuente de variabilidad sobre las observaciones (efectos principales) y el efecto de cada combinación de estas facetas (interacciones). El ANOVA logra esta partición trabajando con componentes de varianza. En consecuencia, en investigaciones sustantivas, la varianza total se divide en las fuentes independientes de variabilidad, debida a cada variable independiente, sus interacciones y el residuo.
En un diseño factorial con dos variables independientes A y B, el ANOVA divide la variabilidad entre los puntajes, en un efecto para A, un efecto para B, su interacción (A x B), y otras fuentes de variabilidad no identificadas. En el caso específico del diseño de una faceta, de igual manera, el ANOVA puede ser aplicado para dividir la variabilidad en el efecto de las personas, el efecto de los reactivos (variabilidad debida a la dificultad del ítem) y un residuo que incluye la interacción de persona-ítem.
Se denotan las observaciones para cualquier persona (p) en cualquier ítem (i) como Xpi. Cualquier puntaje Xpi, puede expresarse como una suma que involucra tres parámetros: μp, μi y μ. El universo de puntajes, denotado como μp, se define como el puntaje promedio de una persona para todo el universo de reactivos. Se toma este promedio para caracterizar el desempeño de una persona, a partir de su estimación, con una muestra de ítems del universo.
Formalmente, el puntaje del universo se define en el objeto de estudio (personas) como μp, que es el valor esperado (E) de la variable aleatoria, Xpi, incluyendo todos los ítems:

El valor p μ es aproximado a infinito en términos de, k, el número de ítems:
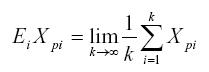
El segundo parámetro, μi, representa el promedio de la población de ítems i. Éste se define como el valor esperado de Xpi para todo el universo de personas:

En este caso, lo que hace tender a infinito es el número de personas y no el número de ítems.
El tercer parámetro, μ, es:
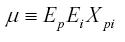
Y tanto el número de reactivos como el número de personas debe aproximarse a infinito. Este es el parámetro que representa el gran promedio de todas las observaciones en el universo.
Los parámetros μp, μi y μ no son observables. Las respuestas de todos los examinados(as) a todos los ítems en el universo nunca están disponibles, pero sí es posible descomponer la observación de una persona en cada ítem (Xpi) de la siguiente forma:

Shavelson y Webb (1991) y Brennan (2001) explican que el puntaje observado de una persona en una prueba, en el diseño de una faceta, puede dividirse en los cuatro componentes presentados arriba:
1. El efecto principal o gran promedio, que es constante para todas las personas.
2. El efecto de las personas, que muestra la distancia entre los puntajes de los individuos del universo y el efecto principal (μp- μ). Un efecto positivo para una persona particular, indica que el puntaje de la persona está por encima del gran promedio y un efecto negativo, indica que está por debajo del gran promedio.
3. El efecto para un ítem en particular (μi-μ). Un efecto positivo indica que el reactivo es más fácil que el promedio y un efecto negativo indica que es más difícil que el promedio.
4. Finalmente, el efecto del residuo que consiste en la interacción persona-ítem y otras fuentes de variabilidad no identificadas: (Xpi - μp - μi + μ).
En la teoría G se analiza la variabilidad de los puntajes observados según fuentes separadas de variabilidad. Por ejemplo, en un diseño (p x i) la variabilidad se divide en tres fuentes: personas, ítems y el residuo. Así, la teoría G define los componentes de varianza  para cada fuente de variabilidad de los puntajes observados. En este caso, éstos se denominan el componente de varianza de las personas
para cada fuente de variabilidad de los puntajes observados. En este caso, éstos se denominan el componente de varianza de las personas 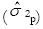 , ítems
, ítems  y el residuo
y el residuo  .
.
El cálculo de los componentes de varianza para un diseño de una faceta se presenta en la Tabla 3.

El diseño de dos facetas para ítems y calificadores(as) (u observadores(as)) se descompone de la siguiente manera:

El cálculo de los componentes de varianza para un diseño de dos facetas, como el descrito, se presenta en la Tabla 4.

Interpretación de resultados en un estudio de generalizabilidad
Para llevar a cabo el análisis con esta teoría, debe considerarse el tipo de decisión que se requiere tomar con base en los puntajes observados, debido a que afecta directamente la interpretación de los resultados. Se debe distinguir entre decisiones basadas en interpretaciones referentes a normas y decisiones basadas en interpretaciones referentes a criterios.
En el primer caso se habla de interpretaciones relativas, donde el resultado se expresa de acuerdo con la posición relativa que ocupa el desempeño de una persona particular, comparado con los otros(as) examinados(as). Por ejemplo, en un examen de Español de sexto grado, el desempeño de un(a) estudiante particular se puede describir como igual o mayor al del 80% de los(as) estudiantes que realizaron la prueba.
En el segundo caso se dice que se trata de interpretaciones absolutas, las cuales son utilizadas para describir lo que una persona puede o no hacer, sin tomar como referencia el desempeño de otros(as). Por ejemplo, describir tareas de aprendizaje específicas de un(a) estudiante con respecto a un desempeño óptimo o aceptable (memorizar el alfabeto, deletrear correctamente el 70% de las palabras de una lista, etc.).
A partir de estas dos interpretaciones se derivan dos tipos de pruebas o tests, que según Linn y Gronlund (2000) son los siguientes:
• Test referido a normas: es un test diseñado para suministrar una medida del desempeño que es interpretada en términos de la posición relativa de la persona en un grupo conocido.
• Test referido a criterios: es un test diseñado para suministrar una medida del desempeño que es interpretada en términos del grado de dominio de la persona sobre un conjunto claro y delimitado de tareas.
Como se afirmó anteriormente, el(a) investigador(a) o tomador(a) de decisiones desea generalizar el puntaje observado de una muestra de medidas hacia el universo de puntajes. La inexactitud de la generalización es llamada error de medición.
Los componentes de varianza contribuyen de diferentes formas al error de medición, según se trate de decisiones relativas o absolutas. Para decisiones relativas, todos los componentes de varianza que influyen en la posición relativa de los individuos contribuyen al error. Estos componentes son las interacciones de cada faceta con el objeto de medida (personas). Para decisiones absolutas, todos los componentes de varianza, excepto el objeto de medida (personas), contribuyen al error. Estos componentes incluyen todas las interacciones y los efectos principales, excepto el de personas.
El diseño de una faceta (p x i) se denomina de esta manera porque todas las personas que realizan la prueba responden a los mismos reactivos. Si se toma como referencia este diseño, el único componente de varianza que contribuye al error relativo es la interacción entre las personas y los ítems  . Esta interacción claramente influye en su posición relativa. Un componente de varianza
. Esta interacción claramente influye en su posición relativa. Un componente de varianza  grande, indica que la posición relativa de las personas cambia de un reactivo a otro (Shavelson & Webb, 1991).
grande, indica que la posición relativa de las personas cambia de un reactivo a otro (Shavelson & Webb, 1991).
El componente de varianza para los ítems  , no afecta la posición relativa de las personas en un diseño de una faceta, ya que todos los sujetos responden a los mismos reactivos.
, no afecta la posición relativa de las personas en un diseño de una faceta, ya que todos los sujetos responden a los mismos reactivos.
En el caso del modelo referido a criterios, en el diseño de una faceta, los componentes de varianza que contribuyen al error absoluto son 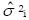 y
y  . Si los ítems difieren en dificultad, al escoger un grupo de ellos para un test, estos reactivos específicos influyen en los niveles absolutos de desempeño de las personas. Si se escogen ítems fáciles, las personas obtendrán puntajes altos; si se escogen reactivos difíciles, los puntajes serán bajos.
. Si los ítems difieren en dificultad, al escoger un grupo de ellos para un test, estos reactivos específicos influyen en los niveles absolutos de desempeño de las personas. Si se escogen ítems fáciles, las personas obtendrán puntajes altos; si se escogen reactivos difíciles, los puntajes serán bajos.
La información acerca de la posición relativa de las personas (mostrada por la magnitud de  ) también influye en los puntajes absolutos de ellas. Si la posición relativa de las personas cambia de un ítem a otro, los puntajes absolutos individuales dependerán de los reactivos escogidos.
) también influye en los puntajes absolutos de ellas. Si la posición relativa de las personas cambia de un ítem a otro, los puntajes absolutos individuales dependerán de los reactivos escogidos.
En resumen, para un diseño de una faceta el único componente de varianza que contribuye al error relativo es  y, para el error absoluto son dos:
y, para el error absoluto son dos: 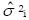 y
y  .
.
En el diseño de dos facetas (p x i x c) donde p son las personas, i los ítems y c los(as) calificadores(as) u observadores(as), cada persona es evaluada por dos calificadores(as) en cada una de las preguntas de la prueba, y, para tomar decisiones relativas, los componentes de varianza de las interacciones con el objeto de medida (personas) contribuyen al error; éstos son  . Si
. Si  es grande, entonces los calificadores(as) afectan la posición relativa de las personas, y la escogencia de los calificadores puede afectar los puntajes. Si
es grande, entonces los calificadores(as) afectan la posición relativa de las personas, y la escogencia de los calificadores puede afectar los puntajes. Si  es grande, entonces la posición relativa de las personas cambia de un reactivo a otro, y la escogencia de los ítems influye en los puntajes. Si el componente de varianza
es grande, entonces la posición relativa de las personas cambia de un reactivo a otro, y la escogencia de los ítems influye en los puntajes. Si el componente de varianza 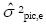 es grande, la posición relativa de las personas cambia en cada combinación calificador(a)-ítem y, por tanto, al escoger esta combinación los puntajes podrían verse influenciados. Los componentes de varianza de los calificadores(as) u observadores(as) (
es grande, la posición relativa de las personas cambia en cada combinación calificador(a)-ítem y, por tanto, al escoger esta combinación los puntajes podrían verse influenciados. Los componentes de varianza de los calificadores(as) u observadores(as) ( ), ítems
), ítems  , y su interacción (
, y su interacción ( ) no contribuyen al error relativo en un diseño de dos facetas, porque no influyen en la posición relativa de las personas.
) no contribuyen al error relativo en un diseño de dos facetas, porque no influyen en la posición relativa de las personas.
Para decisiones absolutas, los componentes de varianza que contribuyen al error en este diseño son 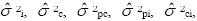 y
y 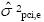 . Se incluye el componente de varianza de los observadores(as) (
. Se incluye el componente de varianza de los observadores(as) ( ), ya que éste puede producir variabilidad en el desempeño de las personas y con ello modificar su posición absoluta. También se incluye el componente de varianza de los ítems (
), ya que éste puede producir variabilidad en el desempeño de las personas y con ello modificar su posición absoluta. También se incluye el componente de varianza de los ítems (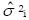 ), donde el nivel de dificultad puede ser diferente e intervenir en el desempeño de la persona, igualmente ocurre con su interacción (
), donde el nivel de dificultad puede ser diferente e intervenir en el desempeño de la persona, igualmente ocurre con su interacción ( ).
).
La varianza del error para la toma de decisiones ( ) se definirá aquí como
) se definirá aquí como  para decisiones relativas y para decisiones absolutas como
para decisiones relativas y para decisiones absolutas como 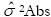 .
.
Para el diseño de una faceta (p x i), se tiene que la varianza del error  es:
es:

donde ni es el número de ítems.
Para el diseño de dos facetas con ítems y calificadores(as) la varianza del error  es:
es:
Diseño p x c x i
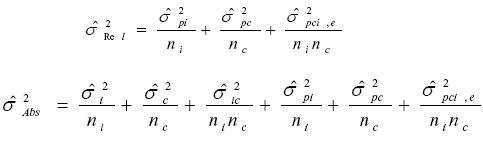
donde ni es el número de ítems y nc es el número de calificadores(as).
La teoría G también proporciona un coeficiente de confiabilidad llamado “coeficiente de generalizabilidad o coeficiente G”. Según la opinión de Shavelson y Webb (1991) el coeficiente de generalizabilidad refleja la proporción de variabilidad en los puntajes de los individuos, atribuible a sus diferencias sistemáticas en conocimiento, habilidades y experiencias (p. 83).
El coeficiente de generalizabilidad se expresa de la siguiente forma:

Cuando el coeficiente de generalizabilidad se calcula para decisiones relativas se conoce como  , y cuando se calcula para decisiones absolutas se denomina Φ (Shavelson & Webb, 1991).
, y cuando se calcula para decisiones absolutas se denomina Φ (Shavelson & Webb, 1991).
Comparación de la teoría de la generalizabilidad y la teoría clásica de los tests
Los métodos basados en la teoría clásica de los tests no son suficientes para analizar la confiabilidad de los puntajes cuando el (la) investigador(a) está interesado(a) en obtener decisiones absolutas, ya que la variabilidad en dificultad de un reactivo a otro contribuye al error. En opinión de Shavelson y Webb (1991), a consecuencia de lo anterior, se asume que la teoría clásica es primariamente una teoría de diferencias individuales (p. 94).
Este autor también nos recuerda que la teoría clásica de los tests divide la varianza en solo dos fuentes de variabilidad, los puntajes verdaderos y la varianza del error. Entonces, en el diseño de una faceta, el coeficiente de confiabilidad (alfa de Cronbach) de la teoría clásica es comparable con el coeficiente de generalizabilidad, solo para el caso donde se pretende tomar decisiones relativas.
En un diseño de dos facetas (p x c x i) y aplicando la teoría clásica, se tendría que examinar separadamente cada una de las fuentes de variabilidad para considerar las dos facetas de este diseño, ya que con esta teoría no se logran estimar los efectos de los(as) calificadores(as) y los ítems en un solo análisis, tal como lo hace la teoría de la generalizabilidad.
En resumen, la teoría clásica de los tests no fue concebida para identificar fuentes de variabilidad diferentes a la variación de persona a persona, tampoco fue concebida pensando en decisiones absolutas; mientras que la teoría G sí se plantea estos problemas desde su inicio y hace una propuesta para su medición y control empírico.
Aplicación de la teoría clásica y la teoría G a un instrumento específico
Para tener un mejor panorama sobre la utilidad y alcances de cada uno de los dos enfoques bajo estudio, a continuación se presentan los resultados obtenidos en un instrumento construido en el país, la prueba Zurquí, elaborada como parte de una consultoría para medir la calidad de vida en niños con enfermedades terminales.
La construcción y el análisis de la prueba Zurquí fueron realizados por un equipo de investigadores(as) del Albergue San Gabriel, entidad privada encargada de atender a menores que sufren enfermedades terminales y sus familias, que pertenece a la Fundación Pro-Unidad de Cuidados Paliativos del Hospital Nacional de Niños. El equipo estuvo encabezado por el doctor Juan Carlos Irola y contó con la asesoría de una de las autoras, en términos de la validación psicométrica del instrumento. La escala incluye una dimensión de aspectos médicos, los cuales fueron calificados por profesionales de esta área, y por una dimensión de aspectos de la cuidador(a) del(a) niño(a), calificados por trabajadores(as) sociales y psicólogos(as) (Irola, 2001). Estas dos dimensiones, aspectos médicos y aspectos de la cuidadora, fueron analizadas separadamente con la teoría clásica y con la teoría G.
El instrumento consta de 10 reactivos para la evaluación de los aspectos médicos y 10 reactivos en los aspectos del(a) cuidador(a). Todos estos ítems se responden en una escala de medición ordinal de 0 a 3, donde 3 es el valor más alto para cada ítem, representando el máximo valor de calidad de vida en el contexto y para el tipo de población meta del instrumento. El 0 representa, por su parte, el valor más bajo.
En el estudio piloto de validación psicométrica participaron 63 niños, de ambos sexos y menores de 18 años, que padecían diversas formas de enfermedades terminales y que eran atendidos(as), junto con su madres o cuidadoras, en el Albergue San Gabriel. La gran mayoría de ellos pertenecen a estratos socioeconómicos bajos y medios y residen en el Gran Área Metropolitana del Valle Central. Debido a que eran menores de edad y muchos(as) no estaban en pleno uso de sus facultades mentales, sus encargados fueron quienes autorizaron su inclusión en el estudio, bajo los estándares de ética que rigen el cuidado de pacientes en condición terminal y con la supervisión del personal de planta del albergue. Los(as) calificadores(as) fueron profesionales capacitados para tratar a este tipo de población. Las áreas de especialización de estos profesionales fueron medicina, enfermería, trabajo social y psicología.
Los niños y niñas fueron evaluados(as) por dos diferentes calificadores(as) en cada una de las dimensiones de la prueba (aspectos médicos y aspectos del(a) cuidador(a), de manera que cada niño(a) fue calificado cuatro veces, dos veces para cada aspecto.
A continuación, se mostrarán algunos resultados obtenidos por las investigadoras, aplicando la teoría clásica de los tests y la teoría de la generalizabilidad. Los hallazgos según la teoría clásica, ya habían sido reportados previamente por el grupo constructor del instrumento.
En el análisis con la teoría clásica para los 10 reactivos que conforman los aspectos médicos se obtuvo un alfa de Cronbach igual a 0.7163. Los ítems 2 y 9 resultaron con índices de discriminación por debajo de 0.30 y contribuyendo al error de medición, por lo tanto, fueron eliminados. El ítem 7 no fue eliminado debido a un criterio sustantivo médico, a pesar de que su índice de discriminación fue de 0.1363.
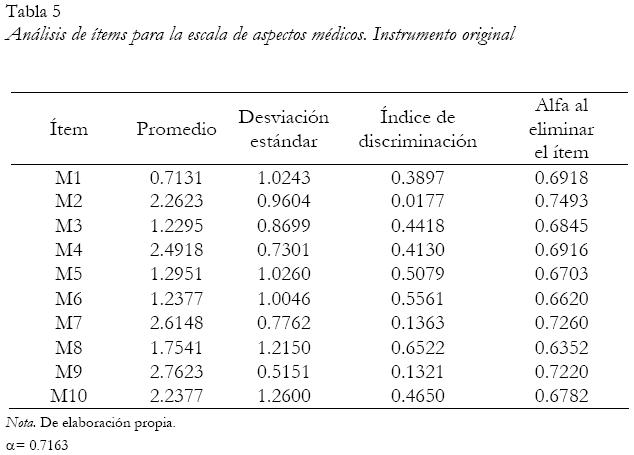


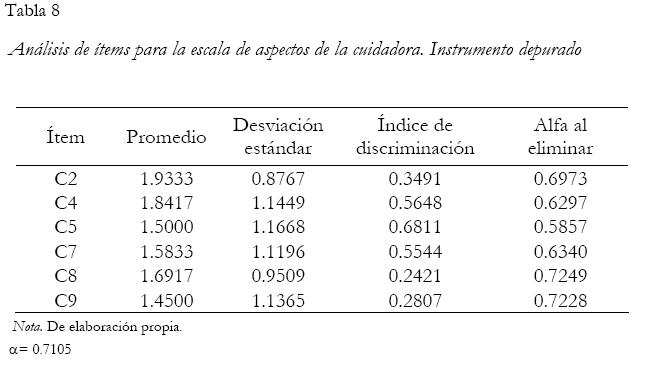
Mediante el análisis con la teoría clásica, se seleccionaron finalmente ocho reactivos para los aspectos médicos y seis reactivos en los aspectos de la cuidadora.
Desde el punto de vista de la teoría G, la prueba Zurquí es un diseño de dos facetas, en el cual se presentan las siguientes fuentes de variabilidad: personas, ítems, calificadores(as) u observadores(as), la interacción personaítem, la interacción persona-calificador(a), la interacción ítem-calificador(a), la interacción persona-calificador(a)-ítem y las otras fuentes de variabilidad no identificadas.
Como se dijo antes, para realizar el análisis de componentes de varianza de la prueba Zurquí se utilizaron las dos sub-escalas: aspectos médicos y aspectos del (a) cuidador(a).
Primeramente, para cada una, se debió ingresar la información en el SPSS tal como se muestra en la Tabla 9.
Se utiliza la opción modelo general lineal en el SPSS para realizar el análisis, y se incluyen los puntajes obtenidos como la variable dependiente y los datos de identificación de las personas, los ítems y calificadores(as) como factores aleatorios. Las Tablas 10 y 11 presentan los resultados obtenidos en términos del análisis de componentes de varianza para las escalas de aspectos médicos y aspectos de la cuidadora, respectivamente.


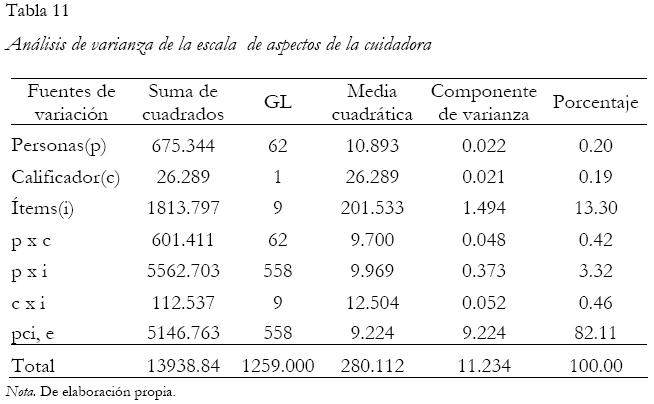
Con base en las tablas anteriores, si se considera que la prueba Zurquí debe interpretarse usando un modelo referido a normas, los componentes de varianza que contribuyen al error son  . Así, en la escala de aspectos médicos, se obtendría una varianza del error relativo igual a 0.0657 dando como resultado un coeficiente de generalizabilidad de 0.7342. Este resultado se debe, principalmente, a que el porcentaje de varianza residual
. Así, en la escala de aspectos médicos, se obtendría una varianza del error relativo igual a 0.0657 dando como resultado un coeficiente de generalizabilidad de 0.7342. Este resultado se debe, principalmente, a que el porcentaje de varianza residual 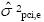 es bajo, correspondiente a un 13.7% de la varianza total.
es bajo, correspondiente a un 13.7% de la varianza total.
Por su parte, la escala de aspectos de la cuidadora presenta una varianza del error relativo igual a 0.5225. El coeficiente de generalizabilidad es de 0.0410, un valor bastante bajo. Esto se debe, principalmente, a que el porcentaje de variabilidad debida al componente de la interacción más el residuo es 82%, valor muy alto que provoca falta de precisión en la estimación de los puntajes.
Si por el contrario, la prueba Zurquí fuera referida a criterios, dado que interesa medir el nivel de calidad de vida de los niños(as), la varianza del error absoluto para los aspectos médicos sería igual a 0.1565. El coeficiente de generalizabilidad tendría un valor de 0.5369. Para la escala de aspectos de la cuidadora, se obtendría una varianza del error igual a 0.685, produciendo un coeficiente G de 0.0316, lo que constituye nuevamente una medida muy baja de confiabilidad. A este valor tan bajo no solo contribuye el componente de varianza de la interacción y residuo, sino también el componente de variabilidad de los ítems, el cual explica un 13% de la variabilidad total.
Conclusiones
Uno de los aportes de la teoría de la generalizabilidad (teoría G) es que permite la evaluación, en un solo análisis, de múltiples fuentes de variabilidad de los puntajes de una prueba o instrumento, tales como personas, observadores(as) o calificadores(as), ítems, las interacciones entre ellos y otras fuentes de variabilidad no identificadas.
En esta teoría se logra obtener una medida de la confiabilidad representada en el coeficiente de generalizabilidad (coeficiente G), el cual se puede ver como análogo al coeficiente de confiabilidad alfa de Cronbach de la teoría clásica de los tests.
Antes de realizar el análisis de confiabilidad de un instrumento con cualquiera de estos modelos, se debe determinar, de acuerdo con el propósito de la prueba, si las decisiones derivadas a partir de los puntajes son relativas o absolutas. En los estudios de decisiones relativas interesa, comparar entre sí las personas. Se busca identificar la posición relativa de un examinado(a) particular, en relación con el grupo de examinados(as). Por el contrario, en los estudios de decisiones absolutas se desea medir una característica o varias características de la persona y compararlo contra un estándar absoluto de desempeño, situación para la cual es especialmente relevante el cálculo del coeficiente G.
De acuerdo con la opinión de las investigadoras, una posible desventaja de la teoría G en relación con la teoría clásica, es que no permite medir individualmente el poder discriminatorio de cada reactivo, solo calcula el porcentaje de variabilidad explicada por los componentes de varianza de los ítems y sus interacciones. Dada esta debilidad, se puede considerar un uso complementario de ambas teorías, empleando la clásica para eliminar de previo reactivos que no contribuyan a la precisión en términos del alfa de Cronbach.
Tradicionalmente, las pruebas psicológicas se han usado para tomar decisiones relativas, por eso, en muchos casos la teoría clásica puede ser suficiente para el análisis de su confiabilidad. Sin embargo, las pruebas educativas suelen requerir decisiones basadas en estándares absolutos de desempeño (como el logro de ciertos objetivos de aprendizaje). Un caso típico son las decisiones de promoción (pasar-perder un curso). En este tipo de contextos educativos, la teoría de la generalizabilidad puede constituir una herramienta muy útil para analizar y controlar las diversas fuentes de variabilidad en los puntajes de las pruebas. Debe recordarse que lo que interesa aquí es maximizar el componente de varianza debido a las personas examinados(as) y minimizar las otras fuentes de variabilidad en los puntajes.
En la aplicación realizada en este estudio, con fines ilustrativos, es claro que en el caso de aspectos de la cuidadora, no hay evidencia para poder emplear la escala con un grado aceptable de precisión. En cuanto a los aspectos médicos, la situación no es tan clara y dependerá del investigador(a) determinar si acepta este nivel de confiabilidad como adecuado para los fines del instrumento. Si se desea mejorar este nivel de precisión, se debería poner énfasis en el componente de la interacción persona-ítem, ya que es relativamente alto (explica un 38% de la varianza total). Este componente puede disminuirse modificando reactivos existentes o construyendo otros para la prueba, aumentando así la confiabilidad del instrumento en este aspecto.
Referencias
Andrade, X., Navarro, O. & Yock, I. (1999). Construcción y validación de una prueba para medir inteligencia emocional. Tesis de Licenciatura en Estadística. San José, Costa Rica: Escuela de Estadística, Universidad de Costa Rica. [ Links ]
Brennan, Robert L. (2001). Generalizability Theory. New York: Springer-Verlag. [ Links ] Cronbach, L. J. (2004). My current thoughts on coefficient Alpha and successor procedures. Educational and Psychological Measurement, 64, 391-418. [ Links ]
Linn, R., & Gronlund, N. (2000). Measurement and evaluation in teaching. (octava edición). NJ: Merrill, Prentice Hall. [ Links ]
Irola, J.C. (2001). Escala Zurquí: proyecto de investigación para construir una prueba para medir la calidad de vida en niños con enfermedades terminales. Manuscrito no publicado. San José, Costa Rica: Fundación de Cuidados Paliativos del Hospital Nacional de Niños. [ Links ]
Nunnally J.C. & Bernstein, I.H. (1995). Teoría Psicométrica. Mc Graw Hill.México, D.F. [ Links ]
Montero, E. (2001). La teoría de respuesta a los ítems: una alternativa para el análisis psicométrico de instrumentos de medición. Revista de Matemáticas: Teoría y aplicaciones, 7 (1-2), 217-228. [ Links ]
Shavelson, R. J. & N.M., Webb. (1991). Generalizability Theory: A Primer. Newbury Park: SAGE Publications. [ Links ]
 Dirección para correspondencia
Dirección para correspondencia
María Elena Zúñiga-Brenes
686-1100 Tibás
Ce: elenazb@costarricense.cr
Eiliana Montero-Rojas
Ce: emontero@cariari.ucr.ac.cr
Recibido: 10 de diciembre de 2004
Aceptado: 10 de enero de 2006














