DOI: 10.22491/1678-4669.20190024

PSYCHOBIOLOGY E COGNITIVE PSYCHOLOGY

 

Prediction of arithmetic competence: role of cognitive abilities, socioeconomic variables and the perception of the teacher in Early Childhood Education

 

Predição da competência aritmética: papel das habilidades cognitivas, variáveis socioeconômicas e percepção do professor na Educação infantil

 

Predicción de la competencia aritmética: papel de las habilidades cognitivas, variables socioeconómicas y percepción del profesor en la Educación infantil

 

 

Talita de Cassia Batista Pazeto^I; Natália Martins Dias^II; Cristiano Mauro Assis Gomes^III; Alessandra Gotuzo Seabra^I

^IUniversidade Presbiteriana Mackenzie
^IIUniversidade Federal de Santa Catarina
^IIIUniversidade Federal de Minas Gerais

Endereço para correspondência

 

 

---

ABSTRACT

The study investigated, in a longitudinal cohort, predictive models of arithmetic competence (AC) in the 1st year from language and executive functions assessed at preschool age. A total of 71 children were evaluated in oral language skills, preliminary writing abilities and executive functions. In the 1st year, the children were also evaluated in AC. Parents provided information on the socioeconomic level and teachers indicated children with difficulties. Language, oral (phonological awareness and vocabulary) and preliminary writing (knowledge of letters, reading and writing of words) abilities, together with indications of difficulty by the teacher in the ECE, were able to explain a mean of 62% of the variability in AC in the 1st year. The findings reveal predictive variables for the performance in arithmetic in the initial stage of Elementary Education, which can assist in early identification and the design of preventive intervention models.

Keywords: academic performance; childhood assessment; arithmetic competence; mathematics; prevention.

---

RESUMO

O estudo investigou, em um recorte longitudinal, modelos preditivos da competência aritmética (CA) no 1º ano a partir de habilidades de linguagem e funções executivas avaliadas em idade pré-escolar. Participaram 71 crianças que foram avaliadas em habilidades de linguagem oral, habilidades preliminares de escrita e funções executivas. No 1º ano, as crianças foram também avaliadas em CA. Pais proveram informações sobre nível socioeconômico e professores indicaram crianças com dificuldades no curso da EI. Habilidades de linguagem, oral (consciência fonológica e vocabulário) e preliminares de escrita (conhecimento de letras, leitura e escrita de palavras), juntamente com indicação de dificuldade pelo professor na EI, foram capazes de explicar média de 62% da variabilidade em CA no 1º ano. Os achados revelam variáveis preditoras do desempenho em aritmética em etapa inicial do Ensino Fundamental e estendem seu impacto para a identificação precoce e delineamento de modelos preventivos de intervenção.

Palavras-chave: desempenho escolar; avaliação infantil; competência aritmética; matemática; prevenção.

---

RESUMEN

El estudio investigó, en un recorte longitudinal, modelos predictivos de la competencia aritmética (CA) en el primer año a partir de habilidades de lenguaje y funciones ejecutivas evaluadas en edad preescolar. Participaron 71 niños que fueron evaluados en habilidades de lengua oral, habilidades preliminares de escritura y funciones ejecutivas. En el primer año, los niños también se evaluaron en CA. Los padres proporcionaron información sobre NSE y los profesores indicaron a los niños con dificultades en el curso de la EI. Las habilidades de lenguaje, oral (conciencia fonológica y vocabulario) y preliminares de escritura (conocimiento de letras, lectura y escritura de palabras), junto con indicación de dificultad por el profesor en la EI, fueron capaces de explicar media del 62% de la variabilidad en CA en 1er año. Los hallazgos revelan variables predictoras del desempeño en aritmética en etapa inicial de la Enseñanza Fundamental y expiden su impacto para la identificación precoz y delineamiento de modelos preventivos de intervención.

Palabras clave: rendimiento escolar; evaluación infantil; la cognición; matemáticas; la prevención.

---

 

 

In addition to reading and writing, mathematics is an important acquisition of the school phase

(Menon, 2010), although, compared to the first two, it receives less attention in the literature. This point can be illustrated by the investment made in research in the area of specific learning disorders. Thus, from 2000 to approximately 2009, the National Institute of Healthspent about US$107 million on reading disorder research and about 2% of this on research into mathematics disorder (Bishop et al., 2010; Butterworth, Varma, & Laurillard, 2011). This fact is also reflected in the knowledge currently available regarding precursors of reading/writing and mathematics abilities. In relation to reading/writing, the role of linguistic skills, especially phonological processing, has been well established in the acquisition of word recognition (Melby- Lervåg, Lyster, & Hulme, 2012; Seabra & Dias, 2012c); as has the participation of other skills, such as executive functions, in more complex processes, such as those involved in reading comprehension (Borella, Carretti, & Pelegrina, 2010; Kendeou, van den Broek, Helder, & Karlsson, 2014). With regard to mathematics, studies exist (e.g. Bull & Lee, 2014; Lopes-Silva et al., 2016), however, there are still no consistent conclusions in some areas, as the participation of inhibition and switching in math performance or the role of phonemic awareness in numerical tasks, for example.

The concept of mathematics involves arithmetic, which refers to the study of numbers, their properties and operations (Novick & Arnold, 1988). Models of neuropsychology and cognitive psychology have sought to understand arithmetic competence (AC), which has been understood as a complex skill that includes different components, among which are more basic elements of number processing and others, more complex, as the application of procedures and calculation (Menon, 2010). One of these is that of McCloskey, Caramazza and Basili (1985), described in Seabra, Dias and Macedo (2010), which delimits a 'numerical processing' component, which involves numerical comprehension and production, knowledge of symbols and quantities and a 'calculation' component, which refers to the processing of the symbols and execution of the calculation itself.

More recently, Menon (2010) presented a model that complements that of McCloskey et al. (1985). The model recognizes three levels of processing: basic numerical processing, which includes knowledge of numbers, symbols, quantities and magnitude; simple mathematical computation, the ability to solve simple calculations and to retrieve arithmetic information; and complex mathematical computing, which includes processing complex operations.

From these models it is possible to analyze which cognitive abilities are relevant for each component. For example, the most basic component of number processing is associated with more elementary mathematical abilities, which allow the understanding of magnitude, for example, number sense (Feigenson, Libertus, & Halberda, 2013; Jordan, Kaplan, Locuniak, & Ramineni, 2007). In addition, even naming or writing numbers involves accessing their symbolic representations and demands verbal processes, such as those that occur in the retrieval of arithmetic facts or in problem solving (Lopes-Silva et al., 2016; Zhang & Lin, 2015). Finally, the performance of more complex calculations requires the application of strategies and procedures, involving the important participation of executive functions¹ (Menon, 2010).

Some associations are well established in the literature, such as number sense and mathematical skills, with evidence that the former is an important predictor of future competence in the second (Feigenson et al., 2013, Jordan et al., 2007), as well as evidence which support a causal relationship between them (Park & Brannon, 2014). In a similar way, there are studies showing the association between performance in arithmetic and executive functions at different ages (Borella et al. 2010; Duncan et al., 2007; Gathercole, Pickering, Knight, & Stegmann, 2004; Toll, Van der Ven, Kroesbergen, & Van Luit, 2011). However, a relatively recent review has shown that, in general, working memory has been evidenced as the sole predictor of mathematical performance, so that findings related to inhibition and flexibility seem less conclusive (Bull & Lee, 2014).

The participation of the verbal processes in AC seems to be of more recent interest, although, already in the 1990s, the triple-code model of Dehaene and Cohen (1995) supported this association. In the model, three types of numerical representation systems are considered: an analog representation of magnitude, therefore, non-verbal (example ●●●●●); a visual symbolic representation (5) and a verbal symbolic representation (five). The interactions between these representations occurs through the process of transcoding, which reveals the relation between verbal and non-verbal codes.

In fact, several language skills are associated with mathematical development. For example, LeFevre et al. (2010) stated that cognitive skills in general, such as spatial and linguistic skills, are essential and function as a basis for learning arithmetic. The study revealed that the ability to count sequences is related to arithmetic competence and language skills. Also Zhang and Lin (2015) argued that language skills (phonology, word meaning and writing) relate to arithmetic problem solving, mathematical writing and the non-symbolic system.

In a longitudinal study, with preschool children up to the 3rd grade, phonological awareness, knowledge of letters, vocabulary, visuospatial skills and AC (assessed by addition and subtraction calculations) were evaluated. It was verified that linguistic and visuospatial skills act in the preschool as predictors of good arithmetic performance in Elementary Education. Furthermore, knowledge of letters has been shown to be a predictor of arithmetic performance (Zhang et al., 2014) and studies have suggested that children with reading difficulties also have difficulties in arithmetic (Duncan et al., 2007; Landerl & Moll, 2010; Zhang et al., 2014).

Relationships between arithmetic performance and phonological processing skills have been evidenced, more specifically phonological awareness (PA; the ability to reflect on speech sounds). For example, phonological processing deficits in dyslexic people may impair aspects of mathematics that depend on the manipulation of verbal codes (e.g. counting, retrieval of arithmetic facts) (Simmons & Singleton, 2008) and PA was a significant predictor of both reading and numerical writing in a sample of the 2nd to 4th grade students, suggesting this ability as a module shared between abilities of reading and writing and mathematics (Lopes-Silva et al., 2016). Another point to consider is that school requirements in relation to mathematics vary in each grade, therefore, cognitive demands for task resolution may also vary (Dias & Seabra, 2013; Menon, 2010).

This article focuses on whether and which linguistic and executive skills assessed in Early Childhood Education (ECE) can predict AC and by how much (considering numeracy and calculation processing skills) in the first year of this acquisition, that is, at the end of the 1st grade of Elementary Education. Among the linguistic abilities, PA, short-term phonological memory, vocabulary and preliminary reading and writing skills (knowledge of letters and their sounds, reading and writing isolated words) were selected. Among the executive abilities, inhibition and cognitive flexibility were selected, as there is a larger amount of evidence already published in relation to working memory. Finally, also taking into account the influence of other factors on the learning and performance of arithmetic, the individual history and socioeconomic level (SEL) variables were considered in the analyses, as well as early indicators of difficulties (learning and/or behavior) in the preschool, from the perception of the teacher.

The aim of this study was to investigate, in a longitudinal cohort, predictive models of arithmetic competence in the 1st grade from the linguistic and executive abilities assessed at preschool age, also considering the predictive power of other variables, including those of SEL and the perception of the teacher regarding the child's difficulties. The findings may contribute by listing predictive abilities and variables that aid in understanding the processes involved in AC, as well as in the early identification of children in ECE at risk for difficulties in this area of academic performance.

 

Method

Participants

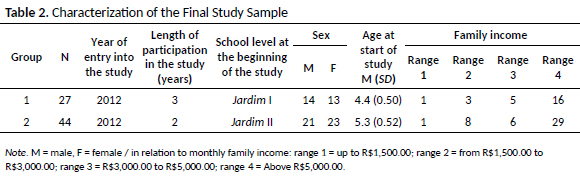
The final study sample consisted of 71 children who entered the study in ECE and were followed up to the 1st grade. These participants entered into the study at different periods, so that they composed 2 groups: Group 1, composed of 27 children (age at start of the study: M = 4.4 years; SD = 0.50) recruited for the study when they attended Jardim I (Jd-I) and who participated in three years of evaluation; and Group 2, composed of 44 children (age at start of the study: M = 5.3 years; SD = 0.52) recruited for the study when attending Jardim II (Jd-II) and who participated in two years of evaluation. Table 1 shows the time course, with the entry of both groups, over the years of the study.

 

 

The exclusion criteria were presence of diagnosis of intellectual deficiencies or medical diagnosis of genetic or neurodevelopmental diseases, evidenced by medical report, with this information obtained from the school management and from a questionnaire sent to the parents/guardians. Four children were excluded because they were within this criterion. All the children had ages appropriate to the grade they attended and there were no cases of repetition. Table 2 summarizes the characteristics of the sample for groups 1 and 2. The school is private, located in a middle to high class region and uses the phonics approach as the literacy method.

 

 

Instruments

Questionnaires (Application in the Child's First Year in the Study, Jd-I Or Jd-II)

Questionnaire for Parent Identification (Qpa). Itis completed by the parents and has questions about aspects of the child, his/her history, development and health, as well as information for characterization of the family. The variables selected for analysis were: prematurity; age at initiation of school; age and schooling of the mother; age and schooling of the father; and family income.

Questionnaire for Teachers (Qtch). The teachers were asked to indicate which students, in their judgment, had some type of difficulty (without specifying whether it was academic or behavioral) when compared to their class peers.

Evaluation of Executive Functions (Application In Jd-I And Jd-II)

Semantic Stroop Test (SST; Trevisan, 2010). It evaluates the ability of inhibitory control. It is computerized and divided into two parts. In the first part, the child has to name the figures presented, one by one, on the screen (boy, girl, moon and sun) and, in the second, say the opposite noun of the semantic pair (Example: say "boy" for the figure of the "girl"). Each part has 16 items, presented in a time of 300 ms. For the analyses, the correct responses and reaction time (RT) in part 2 of the test were used. Evidence of validity can be found in the study by Trevisan (2010).

Trail Making Test for preschool children (TMT-PS; Trevisan & Seabra, 2012). It evaluates the cognitive flexibility ability. In condition A the child has to connect the stimuli (figures of five puppies) in order of size. In condition B, figures of bones the same sizes as the dogs are introduced, and the child must match the puppies with their appropriate bones, in order of size, connecting them alternately. The score of sequences (i.e., items connected correctly in an uninterrupted sequence) in part B of the test was used. Evidence of validity and normative data have been published for preschool children (Seabra & Dias, 2012a).

Attention by Cancellation Test (ACT; Seabra & Dias, 2012a). It evaluates the selective and alternating attention. In the first part, a target stimulus among the other distracter must be cancelled. The same is requested in the second part, however, two target stimuli must be canceled when they appear together. In the last part, the target stimulus changes with each line, requiring the ability to alternate attention. There is a time limit of 1 minute for each part. The number of correct responses in the total of the test was used. The instrument has evidence of validity and standards available (Seabra & Dias, 2012a).

Assessment of Language Skills (Oral and Preliminary Writing, Application in Jd-I And Jd-II)

Phonological Awareness Test by Oral Production (PATO; Seabra & Capovilla, 2012). It evaluates the ability to manipulate speech sounds. It consists of 10 subtests that measure different levels of phonological awareness: syllabic and phonemic synthesis, judgment of rhyme and alliteration; segmentation, manipulation, and syllabic and phonemic transposition. Evidence of validity, accuracy data and standards have been published by Seabra and Dias (2012b). The total score in the test was used.

Peabody Picture Vocabulary Test (PPVT; Capovilla & Capovilla, 1997). It evaluates the receptive vocabulary. It is computerized and composed of 125 test items. Each item is composed of four black line drawings on white backgrounds. The program emits a word and the child has to point to the picture that corresponds to the word being emitted. Evidence of validity and reliability data in a sample of Brazilian children were presented by Ferracini, Capovilla, Dias and Capovilla (2006). The total score of the test was used.

Word and Pseudoword Repetition Test (WPRT; Seabra, 2013). It evaluates short-term phonological memory. The applicator pronounces sequences of 2 to 6 words for the child, with the child's task being to repeat the words in the same sequence. Subsequently, sequences with pseudowords are presented. One point is computed for each sequence that is repeated correctly. The total score in the test was used. Evidence of validity and normative data were presented by Seabra and Dias (2012b).

Letter and sound recognition task (LSRT; Pazeto, Seabra, & Dias, 2014). It evaluates the knowledge of the child regarding the names of the letters and their sounds. The letters are randomly presented in capital letter format to the child, one at a time. In the first application, the child has to name the letter; then the procedure is repeated, however, the child is instructed to say the sound of the letter. Scoring can range from 0 to 26 points in the letters and in the sounds. The total in each part of the test, letters and sounds, were used as scores. A national study has already used the task in a sample of preschool children (Pazeto et al., 2014).

Reading and Writing Task (RWT; Pazeto et al., 2014). It assesses preliminary reading and writing abilities. It consists of two phases: in the first, the child receives a sheet with 8 words and two pseudowords to read, and in the second, eight words and two pseudowords are dictated for the child to write. The percentage of correct responses (ranging from 0 to 100%) in each part of the test was used. A national study has already used the RWT in a sample of preschool children (Pazeto et al., 2014).

Assessment of Arithmetic Competency (application in 1st grade)

Arithmetic Test (AT, Seabra, Montiel, & Capovilla, 2013). It evaluates different aspects of arithmetic competence. It has six subtests that allow for the evaluation of aspects that include writing by extension of numbers presented algebraically and writing the algebraic form of numbers pronounced by the applicator, writing increasing and decreasing numerical sequences, comparing numerical quantities, calculating written and orally presented operations and solving mathematical problems. In this way, the instrument covers the domains of numerical processing and calculation. The total score in the instrument was used. Evidence of validity, reliability and normative data are available in Seabra, Dias and Capovilla (2013).

Procedure

The project was approved by the Research Ethics Committee (CAAE 02631312.3.0000.0084). Data collection took place at the school over three years. Thus, in year 1, the letters of presentation of the study and the consent forms were sent to those responsible for the participating children. The previously authorized children participated in the second and third years of the study.

In the three years of the study, the collection began in the second semester, in mid-August and finished in mid-October. In each year, all evaluations took place in a reserved room provided by the school during the regular class period. When the children were in Jd-I and Jd-II, they were withdrawn from the room individually for short periods of time, ranging from 10 to 30 minutes, with the teacher's permission and the consent of the student, for the application of the language and executive functions tests. Each participant was withdrawn at least 6 times to apply the tests, individually. When the children were in the 1st grade, the AT was applied collectively, in a single session with an average duration of 40 minutes. In addition, at the time of the entry of the child into the study (Jd-I and Jd-II for groups 1 and 2, respectively), the parents were asked to respond to the Qpa and the teachers asked to complete to the Qtch.

Data Analysis

The database preparation stage was started from the data imputation process. This statistical procedure is used in studies with missing data, aiming to complete the data. The procedure starts from the number of initial subjects and estimates a value for the missing results of each of the subjects (from their performance at other times and the performance of children of the same level at the same time), so that, at the end of the imputation, the database is complete. The imputation process was repeated five times, creating five complete databases, with this being considered a sufficient number to obtain acceptable properties, to guarantee greater effectiveness and reliability of the data. The tree regression, specifically the M5 algorithm, which was used in this study, is interesting to use because it breaks the data into parts, in a non-linear way, and then performs line-res regressions in each of the parts. This non-linear break is advantageous because it maximizes prediction and allows trawling with samples of different sizes. Details of the tree technique in educational studies can be found in Gomes and Almeida (2017), specifically the method of tree regression. This process is suggested for use in longitudinal studies, allowing predictive analyses to be conducted in a relatively robust way (Carpenter & Kenward, 2013). The R program, version 3.2.2 (R CORE TEAM, 2015) was used.

A descriptive analysis of the performances of the participants in the different measures in the different periods of the study and the Linear Regression Tree analysis was carried out, in order to verify which cognitive abilities and other variables, measured in ECE, were important predictors of the performance in arithmetic in the 1st grade. The Linear Regression Tree analysis performed in the R Program, in the RWeka package, using the M5 algorithm, was conducted to verify which cognitive abilities and other variables, measured in ECE, act as predictors of arithmetic competence in the 1st garde, deriving models of the importance of each variable for the prediction of the outcome variable. The "leave-one-out cross-validation" method was used, which is a control strategy that aims to minimize overfitting. This method has the advantage of being non-parametric and non-linear. According to Golino and Gomes (2014), these methods are especially interesting for the area of educational research because they allow the analysis of which set of variables best predicts a certain outcome. In the present study, this analysis was conducted from the general worksheet derived from the five imputations performed.

In order to select the independent variables that actually had incremental validity for the explanation of the dependent variables, the Boruta package (Kursa & Rudnicki, 2010) was used, this being a package of the R program (R Core Team 2015) that performs, through the Random Forest approach, the selection of variables to compose a predictive model to be tested (Kursa & Rudnicki, 2010). This process allowed more parsimonious models to be derived, with predictor variables selected according to their importance in the model.

The Root Mean Square Error (RMSE) was used to compare the samples (indicates how much the sample is not able to explain the outcome variable) and the R2, coefficient of determination, associated with the variability of the outcome variable explained by the variability of the predictors (fit of the model).

 

Results

The preparation of the database for the prediction analysis started with the imputation process. All the imputations generated presented the Rhat index < 1.1, which suggests that the data estimated for all the imputed spreadsheets were reliable estimates and could be used for the subsequent analyses. This process prepared the database for the regression tree analysis, which allowed the analysis of the importance of the variables and abilities evaluated in ECE to predict arithmetic competence in the 1st grade of Elementary Education. Table 3 presents the descriptive statistics, with the performances of the children in the AT in the 1st grade and in the other language measures (oral and preliminary writing) and executive functions in Jd-I and Jd-II. For the prediction from the Regression Tree, the results are presented for each of the five imputations.

 

 

The analysis was conducted with the Boruta package in order to verify which independent variables would have incremental validity to explain the outcome variable. This analysis was performed for each of the five samples generated by the imputation process. These variables, in the order of importance in the prediction of the outcome, are presented in Table 4. Note that for each predictor variable there is a percentage of importance, which indicates how relevant this variable was for the outcome. The Boruta analysis was conducted in sequence, to confirm which variables were more relevant for each imputed sample. The confirmed variables, in order of importance in the prediction of arithmetic competence, are presented in Table 5.

 

 

 

 

Seven variables were maintained in the models, with the most important being the performance in PA tasks in Jd-II, preliminary reading and writing abilities in Jd-II, difficulty highlighted by the teacher, performance in the knowledge of letters task also in Jd- II (all in five imputations); performance in vocabulary, in both Jd-I (four imputations) and Jd-II (three imputations) and, again, knowledge of letters, however, in Jd-I (three imputations). Table 4 presents the regression analysis values, including the RMSE and R². It also presents the confidence interval values for each of the samples imputed. All the imputations presented predictor variables capable of explaining the performance in arithmetic, with a mean R² = 0.62. That is, up to 62% of the variance in performance in arithmetic in the 1st grade can be explained by the predictor variables selected, evaluated in the course of ECE.

 

Discussion

The aim of the study was to investigate predictive models of AC in the 1st grade from language (oral and preliminary written) abilities and executives functions evaluated in the course of ECE, jointly considering the predictive power of other variables, including those of SEL and the perception of the teacher regarding difficulties of the child, also in ECE. The findings revealed variables relevant to the subsequent performance in AC, in this order: performance in the tasks of PA in Jd-II, preliminary skills of reading and writing in Jd-II, difficulty highlighted by the teacher, and performance in the knowledge of letters task also in Jd-II. Four of the five models also featured the vocabulary performance in Jd-I and three models featured the vocabulary performance in Jd-II and knowledge of letters in Jd-I. Even in the variables unconfirmed for all five models/samples, it was considered that there was consistency in their selection (they were evidenced in three or four of the five models). The models generated explained a mean of 62% of the variance in the AC performance in the 1st grade.

In summary, the data show that AC in the 1st grade can be consistently and robustly predicted from language skills in ECE, both oral language abilities (especially PA, but also vocabulary) as well as preliminary written language abilities, specifically reading and writing of words and knowledge of letters. It should be noted that some of these abilities have some predictive power over AC when evaluated in both Jd-I and Jd-II (as was the case with vocabulary and knowledge of letters), which suggests some fairly early predictors of AC, already in children of 4 years of age. Other abilities figure as predictors only from Jd-II. It may be the case that, as the various measures were included together in the analysis, the performances in Jd-II totally mediated any possible effect of these same variables in Jd-I. However, the study analysis does not allow this hypothesis to be directly tested. In general, however, the study corroborates the important predictive role of language in relation to AC (LeFevre et al., 2010; Lopes-Silva et al., 2016; Zhang et al., 2014; Zhang & Lin, 2015).

Studies, such as that of Lopes-Silva et al. (2016), have already demonstrated the role of PA in the prediction of reading skills and numerical writing. The present findings broaden those of Lopes-Silva et al. by showing that the PA is predictive not only of numerical reading and writing, but also of AC evaluated in a more comprehensive way. These results corroborate previous findings regarding the association between phonological, semantic and writing skills, including knowledge of letters, calculation, arithmetic problem solving, mathematical writing, and functioning of the non-symbolic system (Zhang et al., 2014; Zhang & Lin, 2015). It is possible to raise some hypotheses related to the role of these abilities in AC, such as that of PA in the process of transcoding between Arabic and verbal representations (for example, in the Dehaene and Cohen model (1995). At the same time, knowledge of numbers, of operations, and even the understanding of the enunciation of arithmetical tasks require vocabulary. For example, when listening to a mathematical problem, the child has to access the semantic representations involved, transform the verbal information into mathematical concepts, and then solve the problem (Novick & Arnold, 1988).

Furthermore, it is possible that the underlying mechanisms for letter recognition are at some level shared with number recognition (for example, in the Dehaene and Cohen model (1995), occipito-temporal regions are considered in the visual analysis of the number; and specialized adjacent areas in the left hemisphere are involved in letter and word recognition). However, this association may reflect the effect of a third variable, underlying the learning of both letters and numbers, such as intelligence. In addition, the association with reading and writing skills is supported by studies that have shown that children with reading difficulties also have difficulties in arithmetic (Duncan et al., 2007; Landerl & Moll, 2010; Zhang et al., 2014).

In addition, the difficulty highlighted by the teacher variable reached importance in the model, suggesting its role in the consideration and early detection of children who, in ECE, may present risk of poor AC in the 1st grade. Other studies have highlighted that the perception and expectations of the teacher seem to be sensitive in the identification of children with difficulties (Hinnant, O'Brien, & Ghazarian, 2009; Salles & Parente, 2007), with the present study corroborating this association and reinforcing its predictive power.

It should be noted that other variables considered in the analysis were not included in the predictive models, as was the case with the various SEL variables. However, this result may be related to the limited variability of these variables, since the sample was recruited from a single school and was, therefore, relatively homogeneous. In addition to the other skills evaluated, it is interesting to note that measures of executive functions did not appear to be significant predictors for AC, contrary to part of the literature (Borella et al., 2010; Duncan et al., 2007; Gathercole et al., 2004; Toll et al., 2011).

Some hypotheses may be raised for this fact, including: 1) the possibility of the tests used not being discriminatory for this age group; 2) that executive functions were predictors of oral and written language abilities and these, in turn, were predictors of AC, that is, the effect of the executive functions would be mediated by other skills that comprised the predictive models (this is corroborated by the relationship between oral and written language skills and executive functions already observed in preschool children, as in Pazeto et al., 2014); 3) the study outcome was AC in the 1st grade, that is, at this school level, this ability still presents itself at a very initial level, where the language skills may be more relevant. However, it is expected that for more complex abilities (such as more complex calculations) the executive functions may have greater predictive power. This is consistent with the idea that school requirements for mathematics vary in each grade and that cognitive demands for the resolution of the tasks may also vary (Dias & Seabra, 2013; Menon, 2010); and 4) studies indicate working memory as a predictor of mathematical performance, although results are inconclusive with respect to inhibition and flexibility (Bull & Lee, 2014). Corroborating this idea, the results of the present study may suggest that inhibition and flexibility are not, in fact, predictor abilities for AC, at least at the end of the 1st grade.

Given these hypotheses, it is suggested that future studies could investigate the role of executive functions as intermediate predictors of AC (predictors of oral and written language skills, which in turn predict AC) or as predictors of more complex outcomes, in more advanced school levels. Some limitations of the study should be overcome in the future, such as the small number of participants that could be monitored over the years of the study (although the statistical techniques used are specific to minimize sample difficulties), absence of the assessment of intelligence and sampling by convenience, selected from a single private school. The results indicate some new directions for studies in the field and draw some practical conclusions, suggesting the important predictive role of language (oral and preliminary written) abilities and the perception of the teacher, in relation to AC in the 1st grade. Such variables should be considered in the course of ECE, aiming for the early detection of children at risk of poor performance in arithmetic.

 

Final considerations

The results allowed the clarification of the demands and predictive variables of performance in arithmetic in the 1st grade. Thus, it is suggested that the perception of the teacher and language skills in ECE should be considered in the identification of children who may, in the future, present difficulties in arithmetic. Implications of the findings include their consideration in the delimitation of theoretical models of AC that consider abilities and processes relevant to performance in the different school levels, as well as in the formation of teachers, orientation of pedagogic teams and structuring of the curricular with a focus on the early identification and delineation of preventive models of intervention.

 

References

Bishop, D. V. M., Al-Shahi, R., Will, R., Warlow, C., Gross, C., Anderson, G., ... Rutter, M. (2010). Which neurodevelopmental disorders get researched and why? PLoS ONE, 5(11), e15112. doi: 10.1371/journal.pone.0015112        [ Links ]

Borella, E., Carretti, B., & Pelegrina, S. (2010). The specific role of inhibition in reading comprehension in good and poor comprehenders. Journal of Learning Disabilities, 43(6), 541-552. doi: 10.1177/0022219410371676        [ Links ]

Bull, R., & Lee, K. (2014). Executive functioning and mathematics achievement. Child Development Perspectives, 8(1), 36-41. doi: 10.1111/cdep.12059        [ Links ]

Butterworth, B., Varma, S., & Laurillard, D. (2011). Dyscalculia: From brain to education. Science, 332(6033). doi: 10.1126/science.1201536        [ Links ]

Capovilla, F. C.; & Capovilla, A. G. S. (1997). Desenvolvimento linguístico na criança dos dois aos seis anos: tradução e estandardização do Peabody Picture Vocabulary Test de Dunn & Dunn, e da Language Development Survey de Rescorla. Ciência Cognitiva: Teoria, Pesquisa e Aplicação, 1(1), 353-380.         [ Links ]

Carpenter, J. R., & Kenward, M. G. (2013). Multiple imputation and its application. Chichester, UK: John Wiley & Sons.         [ Links ]

Dehaene, S., & Cohen, L. (1995). Towards an anatomical and functional model of number processing. Mathematical Cognition, 1(1), 83-120. Retrieved from http://www.unicog.org/publications/DehaeneCohen_TripleCodeModelNumberProcessing_MathCognition1995.pdf        [ Links ]

Dias, N. M., & Seabra, A. G. (2013). Competência aritmética sob a perspectiva do processamento da informação: compreensão, desenvolvimento e subsídios para a avaliação. In A. G. Seabra, N. M. Dias, & F. C. Capovilla (Eds.), Avaliação neuropsicológica cognitiva: leitura, escrita e aritmética (pp. 76-85). São Paulo: Memnon.         [ Links ]

Duncan, G. J., Dowsett, C. J., Claessens, A., Magnuson, K., Huston, A. C., Klebanov, P., ... Japel, C. (2007). School readiness and later achievement. Developmental Psychology, 43(6), 1428-1446. doi: 10.1037/0012-1649.43.6.1428        [ Links ]

Feigenson, L., Libertus, M. E., & Halberda, J. (2013). Links between the intuitive sense of number and formal mathematics ability. Child Development Perspectives, 7(2), 74-79. doi: 10.1111/cdep.12019        [ Links ]

Ferracini, F., Capovilla, A., Dias, N., & Capovilla, F. (2006). Avaliação de vocabulário expressivo e receptivo na educação infantil. Revista Psicopedagogia, 23(71), 124-133. Retrieved from http://pepsic.bvsalud.org/scielo.php?script=sci_arttext&pid=S0103-84862006000200006&lng=pt&tlng=pt        [ Links ]

Gathercole, S. E., Pickering, S. J., Knight, C., & Stegmann, Z. (2004). Working memory skills and educational attainment: Evidence from national curriculum assessments at 7 and 14 years of age. Applied Cognitive Psychology, 18(1), 1-16. doi: 10.1002/acp.934        [ Links ]

Gomes, C. M. A., & Almeida, L. S. (2017). Advocating the broad use of the decision tree method in education. Practical Assessment, Research & Evaluation, 22, 1-10. Retrieved from https://pareonline.net/getvn.asp?v=22&n=10        [ Links ]

Hinnant, J. B., O'Brien, M., & Ghazarian, S. R. (2009). The longitudinal relations of teacher expectations to achievement in the early school years. Journal of Educational Psychology, 101(3), 662-670. doi: 10.1037/a0014306        [ Links ]

Jordan, N. C., Kaplan, D., Locuniak, M. N., & Ramineni, C. (2007). Predicting first-grade math achievement from developmental number sense trajectories. Learning Disabilities Research & Practice, 22(1), 36-46. doi: 10.1111/j.1540-5826.2007.00229.x        [ Links ]

Kendeou, P., van den Broek, P., Helder, A., & Karlsson, J. (2014). A cognitive view of reading comprehension: Implications for reading difficulties. Learning Disabilities Research & Practice, 29(1), 10-16. doi: 10.1111/ldrp.12025        [ Links ]

Kursa, B. M., & Rudnicki, W. R. (2010). Feature selection with the boruta package. Journal of Statistical Software, 36(11). doi: 10.18637/jss.v036.i11        [ Links ]

Landerl, K., & Moll, K. (2010). Comorbidity of learning disorders: prevalence and familial transmission. Journal of Child Psychology and Psychiatry, 51(3), 287-294. doi: 10.1111/j.1469-7610.2009.02164.x        [ Links ]

LeFevre, J.-A., Fast, L., Skwarchuk, S.-L., Smith-Chant, B. L., Bisanz, J., Kamawar, D., & Penner-Wilger, M. (2010). Pathways to mathematics: Longitudinal predictors of performance. Child Development, 81(6), 1753-1767. doi: 10.1111/j.1467-8624.2010.01508.x        [ Links ]

Lopes-Silva, J. B., Moura, R., Júlio-Costa, A., Wood, G., Salles, J. F., & Haase, V. G. (2016). What is specific and what is shared between numbers and words? Frontiers in Psychology, 7(22). doi: 10.3389/fpsyg.2016.00022        [ Links ]

McCloskey, M., Caramazza, A., & Basili, A. (1985). Cognitive mechanisms in number processing and calculation: Evidence from dyscalculia. Brain and Cognition, 4(2), 171-96. doi: 10.1016/0278-2626(85)90069-7        [ Links ]

Melby-LervÃ¥g, M., Lyster, S.-A. H., & Hulme, C. (2012). Phonological skills and their role in learning to read: A meta-analytic review. Psychological Bulletin, 138(2), 322-352. doi: 10.1037/a0026744        [ Links ]

Menon, V. (2010). Developmental cognitive neuroscience of arithmetic: Implications for learning and education. The International Journal on Mathematics Education, 42(6), 515-525. doi: 10.1007/s11858-010-0242-0        [ Links ]

Novick, B. Z.; & Arnold, M. M. (1988) Fundamentals of clinical child neuropsychology. Philadelphia, PA: Grune & Stratton.         [ Links ]

Park, J., & Brannon, E. M. (2014). Improving arithmetic performance with number sense training: An investigation of underlying mechanism. Cognition, 133(1), 188-200. doi: 10.1016/j.cognition.2014.06.011        [ Links ]

Pazeto, T. C. B., Seabra, A. G., & Dias, N. M. (2014). Executive functions, oral language and writing in preschool children: Development and correlations. Paidéia, 24(58), 213-221. doi: 10.1590/1982-43272458201409        [ Links ]

R Core Team (2015) The R Project for Statistical Computing (Computer software). Retrieved from https://www.r-project.org        [ Links ]

Salles, J. F.; & Parente, M. A. M. P. (2007). Relação entre desempenho infantil em linguagem escrita e percepção do professor. Cadernos de Pesquisa, 37(132), 687-709. doi: 10.1590/S0100-15742007000300009        [ Links ]

Seabra, A. G. (2013). Teste de repetição de palavras e pseudopalavras. In A. G. Seabra & N. M. Dias (Eds.), Avaliação neuropsicológica cognitiva: linguagem oral (pp. 97-99). São Paulo: Memnon.         [ Links ]

Seabra, A. G., & Capovilla, F. C. (2012). Prova de consciência fonológica por produção oral. In A. G. Seabra & N. M. Dias (Eds.), Avaliação neuropsicológica cognitiva: linguagem oral (pp. 117-122). São Paulo: Memnon.         [ Links ]

Seabra, A. G., & Dias, N. M. (2012a). Avaliação neuropsicológica cognitiva: atenção e funções executivas (1st ed.). São Paulo: Memnon.         [ Links ]

Seabra, A. G., & Dias, N. M. (2012b). Avaliação neuropsicológica cognitiva: linguagem oral. São Paulo: Memnon.         [ Links ]

Seabra, A. G., & Dias, N. M. (2012c). Reconhecimento de palavras e compreensão de leitura : dissociação e habilidades linguístico-mnemônicas preditoras. Revista Neuropsicologia Latinoamericana, 4(1), 43-56. doi: 10.5579/rnl.2012.0101        [ Links ]

Seabra, A. G., Dias, N. M., & Capovilla, F. C. (2013). Avaliação neuropsicológica cognitiva: leitura, escrita e aritmética. São Paulo: Memnon.         [ Links ]

Seabra, A. G., Dias, N. M., & Macedo, E. C. (2010). Desenvolvimento das habilidades aritméticas e composição fatorial da prova de aritmética em estudantes do ensino fundamental. Interamerican Journal of Psychology, 44(3), 481-488. Retrieved from http://www.redalyc.org/articulo.oa?id=28420658010        [ Links ]

Seabra, A. G., Montiel, J. M., & Capovilla, F. C. (2013). Prova de aritmética. In A. G. Seabra, N. M. Dias, & F. C. Capovilla (Eds.), Avaliação neuropsicológica cognitiva: leitura, escrita e aritmética (pp. 97-104). São Paulo: Memnon.         [ Links ]

Simmons, F. R., & Singleton, C. (2008). Do weak phonological representations impact on arithmetic development? A review of research into arithmetic and dyslexia. Dyslexia, 14(2), 77-94. doi: 10.1002/dys.341        [ Links ]

Toll, S. W., Van der Ven, S. H., Kroesbergen, E. H., & Van Luit, J. E. (2011). Executive functions as predictors of math learning disabilities. Journal of Learning Disabilities, 44(6), 521-532. doi: 10.1177/0022219410387302        [ Links ]

Trevisan, B. T. (2010). Atenção e controle inibitório em pré-escolares e correlação com indicadores de desatenção e hiperatividade (Dissertação de Mestrado, Universidade Presbiteriana Mackenzie). Retrieved from http://tede.mackenzie.br/jspui/handle/tede/1537        [ Links ]

Trevisan, B. T., & Seabra, A. G. (2012). Teste de trilhas para pré-escolares. In A. G. Seabra & N. M. Dias (Eds.), Avaliação neuropsicológica cognitiva: atenção e funções executivas (pp. 92-100). São Paulo: Memnon.         [ Links ]

Zhang, X., Koponen, T., Räsänen, P., Aunola, K., Lerkkanen, M.-K., & Nurmi, J.-E. (2014). Linguistic and spatial skills predict early arithmetic development via counting sequence knowledge. Child Development, 85(3), 1091-1107. doi: 10.1111/cdev.12173        [ Links ]

Zhang, X., & Lin, D. (2015). Pathways to arithmetic: The role of visual-spatial and language skills in written arithmetic, arithmetic word problems, and nonsymbolic arithmetic. Contemporary Educational Psychology, 41, 188-197. doi: 10.1016/j.cedpsych.2015.01.00        [ Links ]

 

 

Endereço para correspondência:
Avenida Interlagos, 800 – c1 – 81 Jardim Marajoara
São Paulo, SP
Cep 04.660000
Telefone: (11) 97657.1956
Email: talita.psicopedagoga@hotmail.com

Recepted in 26.jun.18
Revised in 08.apr.19
Accepted in 10.jul.19

 

 

1. These are complex skills that allow top-down control of behavior. They include skills such as inhibition (ability to inhibit inappropriate actions and the person's attention to distractors), working memory (ability to mentally manipulate information), and flexibility (ability to take different perspectives, consider different alternatives). See the review of Diamond (2013) for a review of Executive Functions.
Talita de Cassia Batista Pazeto, Doutora em Distúrbios do Desenvolvimento pela Universidade Presbiteriana Mackenzie (UPM), é Professora convidada do curso de Pós-Graduação em Psicopedagogia da Universidade Presbiteriana Mackenzie (UPM).
Natália Martins Dias, Doutora e Pós-doutora em Distúrbios do Desenvolvimento. Universidade Presbiteriana Mackenzie (UPM), é Professora do Departamento de Psicologia da Universidade Federal de Santa Catarina – UFSC. Email: natalia.m.dias@ufsc.br
Cristiano Mauro Assis Gomes, Doutor em Educação pela Universidade Federal de Minas Gerais (UFMG), Pós-Doutor em Psicologia da Educação pela Universidade do Minho (UMinho), Portugal, é Professor Associado da Universidade Federal de Minas Gerais (UFMG). Email: cristianomaurogomes@gmail.com
Alessandra Gotuzo Seabra,Doutora e Pós-doutora em Psicologia Experimental pela Universidade de São Paulo (USP), é Docente e pesquisadora do Programa de Pós-graduação em Distúrbios do Desenvolvimento pela Universidade Presbiteriana Mackenzie (UPM). Email: alessandragseabra@gmail.com