O uso da teoria de resposta ao item em avaliações educacionais: diretrizes para pesquisadores

 

The use of item response theory in educational assessment: directions for researchers

 

 

Josemberg Moura de Andrade^{1, I}; Jacob Arie Laros^II; Valdiney Veloso Gouveia^I

^IUniversidade Federal da Paraíba
^IIUniversidade de Brasília

 

 

---

Resumo

A Teoria de Resposta ao Item (TRI) tem sido considerada por muitos especialistas como um marco para a Psicometria moderna. A TRI é um conjunto de modelos matemáticos que considera o item como unidade básica de análise e procura representar a probabilidade de um examinando dar uma certa resposta a um item como função dos parâmetros do item e do(s) traço(s) latente(s) do indivíduo. No presente artigo objetivou-se discutir os pressupostos, modelos e aplicações da TRI em avaliações educacionais de larga escala. Também são feitas algumas considerações sobre a utilização do software Bilog-MG 3.0. Diante da complexidade do tema tratado, não se teve a intenção de esgotá-lo, e sim, oferecer aos pesquisadores e avaliadores educacionais diretrizes para a tomada de decisões no momento de operacionalização de análises psicométricas por meio da TRI.

Palavras-chave: Psicometria; Teoria do traço latente; Testes educacionais de larga escala.

---

Abstract

Item response theory (IRT) is considered as a landmark of modern psychometrics by a great number of specialists. IRT is a set of mathematical models that considers the item like the basic unit of analysis and that relates the probability of a correct response of an examinee on an item in function of the item parameters and underlying latent trait of the evaluated person. This current paper aims to discuss the assumptions of IRT, the various models and applications in large scale educational assessment. Also, the utilization of the software program Bilog-MG is commented. Taking the complexity of the exposed topic into consideration, we do not intend to exhaust it, but are trying to offer support to researchers when making decisions in the process of performing psychometric analyses using IRT.

Keywords: Psychometrics; Latent trait theory; Large scale educational tests.

---

 

 

Introdução

Joana é professora da 4ª série do Ensino Fundamental da rede pública de ensino do Rio Grande do Sul. Na sua última avaliação de Língua Portuguesa, Joana elaborou um teste de dez itens de múltipla escolha e aplicou em sua turma de 30 alunos. Atenciosa com o desempenho escolar dos seus alunos, a professora Joana estava particularmente interessada nas notas de dois alunos específicos: o Tadeu e a Mariana. O primeiro, considerado "aluno problema", era repetente, pouco esforçado e tinha dificuldades de concentração. Mariana, por sua vez, apesar do baixo nível socioeconômico da sua família, era uma aluna dedicada que se esforçava bastante nos seus estudos para obter bons resultados. O resultado da avaliação deixou a professora Joana um tanto frustrada e inquieta. Os dois alunos obtiveram exatamente a mesma nota. Inconformada, ela analisou cada um dos itens que compunham o teste. A professora Joana observou que os itens, elaborados por ela própria, não possuíam o mesmo grau de dificuldade. Dos cinco itens que Mariana acertou, dois eram de dificuldade baixa, um de dificuldade mediana e dois de alta dificuldade que exigiam um grau de raciocínio mais elevado. Tadeu, por outro lado, acertou os três itens mais fáceis do teste e dois de dificuldade mediana. Outro fato observado pela professora foi que Tadeu acertou um item cujo textobase era sobre futebol, enquanto Mariana e quase todas as outras meninas da turma erraram esse item. A professora Joana concluiu ter favorecido os meninos da turma em detrimento das meninas, já que os primeiros possuem maior familiaridade com o tema futebol. Intrigada, a professora Joana se questionou sobre a possibilidade de elaborar testes mais válidos, precisos e que não privilegiem grupos específicos de alunos.

O presente artigo objetiva discutir os questionamentos da professora Joana, personagem fictício da história anteriormente apresentada. Existe alguma maneira de elaborar testes educacionais mais válidos, fidedignos e que não privilegiem grupos específicos de alunos? Em outras palavras, objetivase discutir o uso da Teoria de Resposta ao Item nas avaliações educacionais, a fim de oferecer diretrizes para pesquisadores e avaliadores educacionais.

Há tempos, pedagogos, psicólogos e educadores em geral, se preocupam em conceber, desenvolver e aplicar métodos avaliativos que representem de forma mais fiel possível os resultados da aprendizagem. Nesse âmbito, a teoria da medida tem tido implicações diretas no delineamento, interpretação e resultados de pesquisas e avaliações educacionais (Allen & Yen, 2002). Tal teoria desenvolve uma discussão epistemológica em torno da utilização dos números no estudo científico dos fenômenos naturais (Pasquali, 2003).

A mensuração – objeto da teoria da medida – pode ser definida como um conjunto de regras para representar o comportamento em categorias ou números. Construir um instrumento para medir uma variável nas ciências sociais é uma tarefa árdua e inclui uma série de etapas que deve ser seguida rigorosamente. Entre essas etapas pode-se citar: (a) conceituação dos comportamentos que definem operacionalmente o construto em questão, (b) elaboração de itens que acessem o construto, (c) administração dos itens elaborados para amostras pré-definidas, (d) refinamento do instrumento baseado em análises dos itens e (e) realização de estudos de validade e confiabilidade. Essas etapas são necessárias para se garantir que os escores em um instrumento são consistentes e realmente acessam o construto que se pretende avaliar. Duas aproximações teóricas são dominantes no campo da medição, a saber: a Teoria Clássica dos Testes (TCT) e a Teoria de Resposta ao Item (TRI) (Mathison, 2005).

De acordo com a TCT, que durante muito tempo orientou o desenvolvimento dos testes psicológicos e educacionais (Embretson & Reise, 2000; Hambleton, Swaminathan & Rogers, 1991), a pontuação obtida por um examinando em um teste representa o nível do atributo que está sendo avaliado como o somatório das respostas em cada um dos itens (Nunnally & Bernstein, 1995). Apesar da ampla utilização da TCT, a mesma padece de algumas limitações teóricas. Exemplo disso é que, na TCT, os parâmetros dos itens dependem estritamente da amostra de sujeitos utilizada para estabelecê-los. Em outras palavras, isto quer dizer que o teste será considerado fácil, mediano ou difícil, dependendo da aptidão do grupo de respondentes que se submeteu ao teste. Ainda, examinandos que acertam a mesma quantidade de itens (como na história fictícia apresentada no início do artigo), porém de propriedades psicométricas (discriminação, dificuldade e probabilidade de acerto ao acaso) diferentes, apresentam o mesmo escore total ou desempenho (Andrade, Tavares & Valle, 2000; Cortada de Kohan, 2004; Crocker & Algina, 1986; Hambleton & colaboradores, 1991; Pasquali, 2003; Pasquali, 2007). Voltando à história fictícia, a professora Joana não sabia que comumente fazia uso em sala de aula de uma medida por teoria, a TCT.

É nesse contexto que especialistas em Psicometria desenvolveram um conjunto de modelos matemáticos que procura responder as limitações da TCT, a saber: a TRI. Esta vem ganhando espaço e é cada vez mais utilizada em avaliações educacionais (Andrade & colaboradores, 2000), bem como em avaliações psicológicas. Por meio da TRI é possível identificar itens com funcionamento diferencial em grupos diferentes (Differential Item Functioning – DIF), equalizar escores de diferentes testes ou formas alternativas de um mesmo teste, e descrever e interpretar escores de testes em uma única escala (Hambleton & colaboradores, 1991). Ressalta-se, todavia, que a TCT não tem sido abandonada, e sim, utilizada em combinação com a TRI, a fim de oferecer informações adicionais. A TRI pode ser considerada como uma extensão da TCT e os conceitos das duas teorias estão relacionados uns com os outros (Bechger, Maris, Verstralen & Béguin, 2003). Na verdade, a TCT continua sendo utilizada uma vez que apresenta resultados consistentes até mesmo quando seus pressupostos são ligeiramente violados (Crocker & Algina, 1986).

A presente revisão da literatura tem como objetivo discutir os pressupostos, modelos e aplicações da TRI em avaliações educacionais de larga escala. Procurou-se oferecer ao leitor diretrizes que orientem a tomada de decisões no momento da operacionalização de análises psicométricas de itens por meio da TRI. A seguir são discutidos os pressupostos da TRI – a unidimensionalidade e a independência local – e os modelos logísticos de 1, 2 e 3 parâmetros para itens dicotômicos. Também são feitas algumas considerações sobre a utilização do software Bilog-MG 3.0 (Bock & Zimowski, 1997).

Teoria de Resposta ao Item

A TRI tem sido considerada hoje por muitos especialistas como um marco para a Psicometria moderna (Nunes & Primi, 2005). Também conhecida como Teoria da Curva Característica do Item ou Teoria do Traço Latente, a TRI é um conjunto de modelos matemáticos que considera o item como unidade básica de análise (e não o escore total como na TCT) e procura representar a probabilidade de um indivíduo dar uma certa resposta a um item como função dos parâmetros do item e do(s) traço(s) latente(s) do indivíduo (Andrade & colaboradores, 2000). O traço latente (qualificados na TRI com a letra grega teta – θ) é uma característica não observável do sujeito, que determina sua forma de responder ao teste que é apresentado, enquanto o θ é uma medida do nível do traço latente. Um modelo de traço latente especifica a relação entre o rendimento observável de um examinando em um teste e o traço latente não observável ou habilidade, que se supõe subjacente ao rendimento no teste (Gaviria Soto, 1998).

A TRI assume dois postulados básicos. Um deles é de que o desempenho do examinando em um item pode ser predito a partir de um conjunto de fatores ou variáveis hipotéticas (traços latentes). Outro postulado é de que a relação entre o desempenho e os traços latentes pode ser descrita por uma função matemática monotônica crescente, cujo gráfico é chamado de Curva Característica do Item – CCI (Pasquali, 2007). O modelo matemático padrão da CCI é a forma cumulativa da função logística. A função logística foi inicialmente descoberta em 1844 e tem sido largamente utilizada nas ciências biológicas para modelar o crescimento de plantas e animais do nascimento à maturidade. A função logística foi introduzida na Psicometria por Birnbaum e por causa da sua simplicidade tornou-se preferida em relação à função da ogiva normal, utilizada pelos pioneiros da TRI (Baker, 2001; Lord & Novick, 1968). As duas funções, tanto a normal quanto a logística, são funções não lineares. A expressão da função da ogiva em termos logísticos evita trabalhar com integrais, o que permite um tratamento matemático mais simples. Essa função considera o método da máxima verossimilhança em vez dos mínimos quadrados, sendo matematicamente mais fácil de ser processada (Pasquali, 2007).

No contexto da TRI é comumente utilizado os termos estimação do nível de habilidades e estimação ou calibração dos itens. Estimar habilidades significa determinar o nível do teta (θ) para cada um dos examinandos no teste (Hambleton & cols., 1991). O θ pode ser, por exemplo, o nível de habilidade/proficiência em Leitura, Matemática e/ou Ciências. A estimação ou calibração dos itens, por sua vez, diz respeito à tarefa de caracterizar os itens por meio dos valores numéricos de seus parâmetros (Baker & Kim, 2004). Do ponto de vista teórico, existem três situações de estimação: (1) quando os parâmetros dos itens são conhecidos e se pretende estimar apenas o nível de habilidades dos respondentes; (2) quando se conhece o nível de habilidades dos respondentes e se pretende estimar apenas os parâmetros dos itens; e (3) quando se deseja estimar simultaneamente os parâmetros dos itens e os níveis de habilidades dos respondentes (Andrade & colaboradores, 2000).

A TRI tem sido amplamente utilizada nas últimas décadas na elaboração de testes de avaliações educacionais de larga escala, calibração de itens, construção de escalas de habilidades e de bancos de itens, investigação do funcionamento diferencial dos itens, entre outros processos referentes ao desenvolvimento de testes (Hambleton & cols, 1991). Tal método passou a ser conhecido, principalmente, a partir do ano de 1968 com o trabalho de Lord e Novick intitulado de “Statistical Theories of Mental Tests Scores”. Alguns exemplos de avaliações em larga escala que utilizam a TRI são o teste TOEFL (Test of English as a Foreign Language) e o teste GRE (Graduate Record Examination), aplicados via testagem adaptativa por computador (computerized adaptative testing - CAT) pelo Educational Testing Service – ETS (Nunes & Primi, 2005). No Brasil, a TRI passou a ser mais divulgada a partir da sua utilização no Sistema Nacional de Avaliação da Educação Básica, o SAEB. O SAEB é um dos mais importantes sistemas de avaliação educacional do Brasil e tem como propósito avaliar a qualidade, eqüidade e a eficiência da educação brasileira. Nessa avaliação, o uso da TRI favoreceu a construção de uma escala de habilidades comum entre séries e entre anos que permite o acompanhamento da evolução do sistema educacional brasileiro ao longo dos anos (INEP, 2005).

Entre as vantagens do uso da TRI, quando os dados se ajustam ao modelo, pode-se citar: (1) diferentes pessoas ou a mesma pessoa em diferentes ocasiões podem ter suas habilidades comparadas a partir de itens comuns nos testes – técnica da equalização; (2) os parâmetros obtidos por meio da TRI são medidas estatisticamente independentes da amostra de respondentes (propriedade da invariância); e (3) a estimativa da habilidade de examinandos que acertaram o mesmo número de itens, porém diferentes itens, é diferenciada (Nunnally & Bernstein, 1995). Esta última vantagem faria com que os alunos Mariana e Tadeu da história fictícia não recebessem a mesma nota, o que certamente levaria a um resultado mais fidedigno.

Alguns pressupostos devem ser assegurados para que se possa fazer uso dos modelos da TRI. Um desses pressupostos, no caso dos modelos unidimensionais da TRI, é de que o teste deve avaliar apenas um único traço latente. Em outras palavras, espera-se que haja apenas uma aptidão responsável pela realização de um conjunto de itens. Ressalta-se, todavia, que há muitas controvérsias em relação à unidimensionalidade dos testes. Esse pressuposto nunca pode ser plenamente satisfeito uma vez que vários fatores cognitivos (habilidade para responder rapidamente), de personalidade (ansiedade, motivação, etc.) e de testagem podem afetar o desempenho do examinando no teste. Geralmente, para satisfazer tal postulado, é suficiente que haja um fator dominante responsável pelas respostas dos avaliados a um conjunto de dados (Hambleton & colaboradores, 1991; Laros, Pasquali & Rodrigues, 2000; Pasquali, 2003). Em uma revisão das principais definições e métodos de avaliação da dimensionalidade, Vitória, Almeida e Primi (2006) assinalam que diante da falta de critérios empíricos consensuais para avaliar a dimensionalidade dos testes, a unidimensionalidade é uma questão de grau. Algumas avaliações, seja pela construção dos itens ou pela própria finalidade da aplicação, não podem, a princípio, ser consideradas unidimensionais (Nojosa, 2001). Devido a esses fatos, modelos multidimensionais da TRI são discutidos na literatura internacional (por exemplo, Bryant, 2005; Reckase, 1997; Segall, 2001) e contribuições no âmbito nacional são requeridas.

Apesar da dificuldade de se avaliar a unidimensionalidade dos testes, ressalta-se que é de extrema importância assegurar esse pressuposto. Em recente pesquisa, Condé e Laros (2007) investigaram se estimativas do nível de proficiência realmente independem da dificuldade do teste. Encontrou-se uma dependência entre a dificuldade do caderno de teste (SAEB) e a estimativa do nível de proficiência, que ficou menos forte após a exclusão dos itens com baixas cargas fatoriais no fator único. Os autores concluíram que quanto mais o pressuposto da unidimensionalidade é satisfeito, menos forte é a relação entre a dificuldade do teste e a estimativa da proficiência. Dessa forma, a verificação do pressuposto da unidimensionalidade é de suma importância sempre que a TRI é utilizada, a fim de que a propriedade da invariância dos parâmetros possa se manifestar.

No caso de itens dicotômicos do tipo certo/errado em que pode ser gerada uma matriz de correlações do tipo tetracórica, a análise fatorial de informação plena (Full Information Factor Analysis – FIFA) é comumente utilizada para se avaliar a dimensionalidade dos testes. Essa técnica trabalha com padrões distintos de resposta ao item em vez das intercorrelações, utilizando o modelo multifatorial de Thurstone baseado em estimativas de máxima verossimilhança marginal e no algoritmo EM (Expectation – Maximization) (Wilson, Wood & Gibbons, 1991). A FIFA oferece vantagens sobre os métodos convencionais de demonstração da unidimensionalidade, a saber: (1) considera toda a informação empírica do teste; (2) leva em consideração o acerto dado ao acaso; (3) proporciona tratamento específico aos casos omissos; e (4) é capaz de contornar os problemas da matriz não positiva-definida (Laros e colaboradores, 2000; Pasquali, 2003). A FIFA também proporciona um teste de significância estatístico baseado no qui-quadrado para testar a dimensionalidade do conjunto de itens, bem como fornece a significância estatística da contribuição do último fator adicionado ao modelo. Critérios que podem ser utilizados como índices complementares de unidimensionalidade e que podem ajudar na tomada de decisões do pesquisador ou usuário da técnica são: (1) a porcentagem de variância explicada pelo primeiro fator; (2) a média das correlações bisseriais item-total de um teste; e (3) a média das correlações tetracóricas entre os itens (Hattie, 1985). Outro critério que pode ser utilizado de maneira complementar é o da correlação entre os fatores encontrados depois da rotação oblíqua. Correlações muito altas entre os fatores podem sugerir unidimensionalidade (Kirisci, Hsu & Yu, 2001).

Para operacionalização da FIFA utiliza-se o software TESTFACT (http://www.ssicentral. com) com a inclusão de estimativas dos parâmetros de acerto ao acaso (parâmetro c) de cada um dos itens, obtidas, por exemplo, a partir do software BILOG-3 for Windows/Bilog-MG. Os itens com cargas fatoriais negativas ou positivas baixas devem ser abandonados, pois não contribuem adequadamente para avaliar o traço latente em questão. Na literatura (Erthal, 2003; Pasquali, 2003; Tabachnick & Fidell, 2007) é comumente utilizado como critério de aceitação do item no fator cargas fatoriais iguais ou superiores a 0,32. Todavia, como assinalam Andrade (2005) e Ribeiro (2004), as cargas fatoriais obtidas pela FIFA ficam mais infladas em comparação com os métodos comumente utilizados em análise fatorial. Uma sugestão é utilizar carga fatorial maior ou igual a 0,40.

No caso de itens do tipo ordinal das escalas atitudinais comumente utilizadas na Psicologia e na Educação pode-se realizar análise fatorial pelo software SPSS (Statistical Package for Social Sciences) para verificar a adequação do pressuposto da unidimensionalidade. A literatura tanto estatística quanto psicológica sobre análise fatorial é vasta. Por exemplo, Laros (2005) afirma que sempre que um pesquisador realizar uma análise fatorial, ele deverá decidir várias questões, entre elas: (a) a natureza e o tamanho da amostra que formará a base de dados da análise fatorial; (b) a seleção de variáveis a serem submetidas à análise fatorial; (c) o número de fatores a ser extraído; (d) o tipo de análise fatorial a ser utilizado para extrair os fatores; (e) o procedimento de rotação a ser utilizado a fim de direcionar os fatores; (f) a interpretação dos resultados da análise fatorial; e (g) a investigação de uma solução hierárquica. Os modelos da TRI para itens ordinais podem ser estimados utilizando-se o software PARSCALE. O foco do presente artigo é a estimação dos modelos da TRI para itens dicotômicos do tipo certo/errado ou corrigidos como certo/errado.

No momento da verificação do pressuposto da unidimensionalidade, o pesquisador ou usuário da TRI se depara com uma primeira questão prática, a saber: a quantidade mínima de sujeitos necessária para uma análise fatorial. Crocker e Algina (1986) sugerem como regra geral usar 10 sujeitos por variável ou item, com um mínimo de 100 sujeitos na amostra total. Pasquali (1999) indica, como regra geral, 100 sujeitos por fator medido. Comrey e Lee (1992) classificam amostras de 50 como muito inferiores, de 100 como inferiores, de 200 como razoáveis, de 300 como boas, de 500 como muito boas e de 1.000 ou mais como excelentes. No que se refere ao tamanho da amostra para estimação dos modelos da TRI, Nunes e Primi (2005), a partir de nove sub-amostras de diferentes tamanhos retiradas de um banco de dados com respostas de 44 mil examinandos, verificaram que os parâmetros dos itens e a habilidade dos avaliados podem ser estimados adequadamente em amostras a partir de 200 participantes. Amostras menores geram estimativas menos estáveis. Essa condição sinaliza para o uso da TRI em avaliações de larga escala. No exemplo fictício do início do artigo, a professora Joana só poderia estimar os níveis de habilidades dos seus alunos pela TRI se os parâmetros dos itens do teste tivessem sido previamente estimados com uma amostra suficientemente grande de alunos (Nunes & Primi, 2005). Nesse caso, os níveis de habilidades dos 30 alunos seriam estimados a partir da técnica da equalização, considerando-se os parâmetros dos itens conhecidos.

Outro pressuposto da TRI é o da independência local. Tal pressuposto diz respeito ao fato de que, mantidas constantes as aptidões que afetam o teste, menos o θ dominante, as respostas dos sujeitos aos itens são estatisticamente independentes. Isso implica que o desempenho do avaliado em um item não afeta o desempenho nos demais itens; cada item é respondido exclusivamente em função do tamanho do θ dominante (Hambleton & colaboradores, 1991; Lord, 1980; Pasquali, 2003; Pasquali, 2007). A independência local não é assegurada, por exemplo, quando um item contém informação para a resposta correta ou fornece informação que ajuda a responder um outro item posterior. Neste caso, alguns examinandos irão detectar a informação, enquanto outros não. A habilidade para detectar a informação é uma dimensão além da habilidade sendo testada (Lord, 1980). A suposição da independência local é importante e útil, porque sendo ela verdadeira, a seqüência de respostas do examinando a uma série de itens será o produto das probabilidades de cada item individual (Pasquali, 2007).

Com base na literatura, Pasquali (2007) assinala que, embora pareça improvável que as respostas de um mesmo examinando não estejam correlacionadas, a independência local sugere que, se houver correlação, esta se deve à influência de fatores estranhos e não devido ao fator dominante avaliado. Se os fatores estranhos forem controlados, ou seja, mantidos constantes, o fator dominante será a única fonte de variação e, nesse caso, as respostas se tornam independentes já que o examinando responde exclusivamente em função da magnitude do seu θ. Embretson e Reise (2000) apresentam, com base na literatura, técnicas estatísticas (G², Q³) para se avaliar a independência local, no entanto, assinalam que a melhor maneira de lidar com a dependência local é prevenindo sua ocorrência. Geralmente, quando o pressuposto da unidimensionalidade é satisfeito, o pressuposto da independência local também é satisfeito.

Embora a TRI apresente uma série de vantagens em relação à TCT, ressalta-se que essa última não tem sido abandonada. Como já assinalado anteriormente, a TCT tem sido utilizada em combinação com a TRI, a fim de oferecer informações adicionais sobre a qualidade do teste (Bechger & colaboradores, 2003). As análises clássicas continuam sendo importantes ferramentas de apoio que auxiliam na análise exploratória dos itens, bem como possibilitam identificar inconsistências nos dados e itens problemáticos. Por exemplo, no caso do SAEB, os parâmetros dos itens são estimados primeiramente pela TCT. Por meio da análise das correlações bisseriais são identificados itens com problemas de gabarito. Por exemplo, de acordo com os procedimentos adotados no SAEB no ano de 2005, os itens com coeficiente bisserial do gabarito menor ou igual a 0,15; itens com dois coeficientes bisseriais de distratores (alternativas erradas) maiores que 0,10 ou coeficiente bisserial de um distrator maior que a bisserial da alternativa correta são encaminhados para a análise pedagógica (INEP, 2005). Após uma análise pedagógica realizada por especialistas da área, itens identificados como problemáticos podem ter seu gabarito corrigido ou ser abandonado nas análises subseqüentes. Feitas as alterações de gabarito pertinentes, as análises clássicas são recalculadas e os itens que ainda continuam com índices psicométricos inadequados são abandonados antes mesmo da estimação pela TRI.

Segundo Nunnally e Bernstein (1995) os vários modelos de TRI propostos na literatura dependem fundamentalmente (1) do número de atributos ou dimensões assumidas (uma ou mais); (2) do formato dos itens (por exemplo, múltipla escolha/resposta aberta, dicotômico/politômico) e (3) do número de parâmetros dos itens a serem estimados. Na educação prevalecem os modelos logísticos de 1, 2 e 3 parâmetros para itens dicotômicos.

O modelo logístico de 1 parâmetro avalia somente a dificuldade dos itens ou parâmetro b (também identificado como location ou threshold). Esse parâmetro é medido na mesma escala da habilidade e corresponde ao valor do θ para o qual a probabilidade de acerto é de 0,50. Quanto maior o valor do parâmetro b do item, maior a habilidade requerida para um examinando ter 50% de chance de acertá-lo e, dessa forma, mais difícil será (Hambleton & colaboradores, 1991). No caso do modelo logístico de 3 parâmetros (apresentado a seguir), a probabilidade que define a dificuldade é tipicamente superior a 0,50, devido à possibilidade de acerto ao acaso. Comumente os parâmetros dos itens e o nível de habilidade dos respondentes são estimados na métrica (0,1), ou seja, com média igual a 0 (zero) e desvio-padrão igual a 1 (um). Após a estimação, pode-se fazer uma transformação linear das estimativas para qualquer outra escala de habilidade. Por exemplo, no SAEB a escala de habilidade considerada possui média de, aproximadamente, 250, e desvio padrão de, aproximadamente, 50. Nesse caso, a transformação linear é feita multiplicando-se cada escore de desempenho pelo desvio-padrão desejado (50 no caso do SAEB) e somando a nova média (250). Uma observação se faz necessária aqui. Quando se qualifica o nível do traço latente de interesse, é de fundamental importância saber qual é a métrica ou medida utilizada, a fim de se poder entender o significado do valor atribuído. Por exemplo, quando se diz que um examinando obteve 9 em um teste de desempenho, sendo este um desempenho excelente, está-se supondo que a métrica utilizada é uma escala que vai de 0 a 10. Se a escala utilizada fosse de 0 a 100, então a nota 9 indicaria um péssimo desempenho (Pasquali, 2007).

O modelo de 1 parâmetro, inicialmente criado por Rasch em 1960 e posteriormente descrito para um modelo logístico por Wright em 1977, é definido como segue:

 

 

i = 1,2,...., n

No qual:

Uij é uma variável dicotômica que assume os valores 1, quando o indivíduo j responde corretamente o item i, ou 0 quando o indivíduo j não responde corretamente o item i;

θj valor do traço latente de um indivíduo j;

P(Uij=1/θj) é a probabilidade de um indivíduo j com habilidade θ responder corretamente o item i e é chamada Função de Resposta ao Item – FRI;

e é um número transcendental cujo valor é 2,718; base dos logaritmos neperianos;

D é um fator introduzido para tornar a função logística mais próxima possível da função da ogiva normal; D = 1,7.

b_i é o parâmetro de localização relativo à dificuldade do item i;

n é o número de itens no teste (Hambleton & colaboradores, 1991).

O modelo de 2 parâmetros avalia, além da dificuldade, a discriminação do item ou o parâmetro a (também identificado como slope). A discriminação é definida como o poder do item para diferenciar sujeitos com magnitudes próximas do traço latente que está sendo aferido. Esse parâmetro é representado pelo ângulo formado entre a inclinação da curva e o ponto de inflexão, onde a probabilidade de resposta correta é de 50%. Assim, o parâmetro a refere-se à inclinação da curva (Hambleton & colaboradores, 1991; Pasquali, 2003). Itens com curvas características dos itens mais inclinadas são mais úteis para diferenciar alunos com habilidades diferentes do que itens com curvas mais achatadas. Os valores do parâmetro a podem variar teoricamente de - 8 a +8, todavia, na prática, esses valores comumente estão entre 0,0 e 2,0 (Baker, 2001). Ressalta-se que o item não discrimina igualmente em toda a escala de habilidade. Isto pode ser observado quando se analisa a Curva de Informação do Item (CII). Por meio da CII é observada a precisão do item para os diferentes níveis de θ (Nunes & Primi, 2005). A CII é discutida adiante.

O referido modelo é descrito a seguir:

 

 

i = 1,2,...., n

Acrescenta-se à função anterior:

a_i é o parâmetro de inclinação do item, também chamado de parâmetro de discriminação (Hambleton & colaboradores, 1991).

Itens com parâmetro a negativo não são esperados, uma vez que indicariam que a probabilidade de responder corretamente o item diminui com o aumento da habilidade. Baixos valores de a indicam que o item tem pouco poder de discriminação, ou seja, tanto alunos com baixa habilidade quanto alunos com alta habilidade têm praticamente a mesma probabilidade de responder corretamente o item. Valores muito altos do parâmetro a, por sua vez, indicam itens com curvas características muito “íngremes”, que discriminam os alunos basicamente em dois grupos: os que possuem habilidade abaixo do valor do parâmetro b e os que possuem habilidades acima do parâmetro b (Andrade & colaboradores, 2000). Baker (2001) apresenta a seguinte classificação do parâmetro de discriminação por faixa de valores: Nenhuma discriminação: 0,0; discriminação muito baixa: de 0,01 até 0,34; discriminação baixa: de 0,35 até 0,64; discriminação moderada: de 0,65 até 1,34; discriminação alta: de 1,35 até 1,69; discriminação muito alta: maior que 1,70. Se o usuário quiser interpretar os parâmetros de discriminação do item sob o modelo da ogiva normal (discutido anteriormente), deve dividir esses valores por 1,7.

Por fim, o modelo logístico de 3 parâmetros desenvolvido por Lord (1980), acrescentou às análises o parâmetro c ou a probabilidade de acerto ao acaso (também identificado como chute ou asymptote). Esse parâmetro avalia a resposta correta dada ao acaso, ou seja, a probabilidade de um aluno com habilidade muito baixa de acertar o item. Esse parâmetro é definido pela assíntota da CCI: se ela cortar a ordenada acima do ponto 0, então houve chute, isto é, há respostas corretas por parte dos sujeitos que não poderiam conhecer a resposta correta. Os valores de c podem variar de 0 a 1,0. Em geral são recomendáveis probabilidades iguais ou inferiores a 0,20 para itens com cinco opções (alternativas) de marcação, 0,25 para itens com quatro opções (Andrade & colaboradores, 2000; Hambleton & colaboradores, 1991; Pasquali, 2003) e, 0,50 para itens com duas opções.

A expressão Matemática do modelo logístico de 3 parâmetros é apresentada a seguir:

 

 

i = 1,2,...., n

Acrescenta-se à função anterior:

c_i é o parâmetro de probabilidade de acerto ao acaso do item i; reflete as chances de um examinando de proficiência muito baixa selecionar a opção de resposta correta (Hambleton & colaboradores, 1991).

A seguir, na Figura 1 é apresentada a Curva Característica de um item qualquer de um teste de Matemática obtido nos exemplos do Bilog-MG. Os parâmetros desse item foram estimados a partir do modelo logístico de 3 parâmetros.

 

 

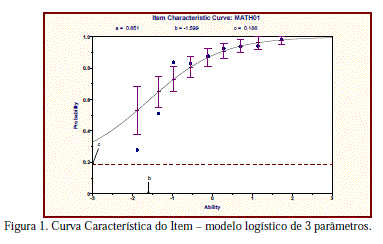
Pode-se observar na Curva Característica do Item (CCI), apresentada na Figura 1, a relação entre a probabilidade de responder corretamente ao item (eixo da ordenada) e o nível de habilidade ou θ dos respondentes. Na figura vê-se que, à medida que aumenta o θ, aumenta também a probabilidade de acertar o item (relação monotônica crescente entre aptidão e probabilidade de acerto). Como já discutido anteriormente, nos modelos de 1 e 2 parâmetros a dificuldade do item corresponde ao valor do θ para o qual a probabilidade de acerto é de 0,50. No caso do modelo logístico de 3 parâmetros, a probabilidade que define a dificuldade é tipicamente superior a 0,50, devido a possibilidade de acerto ao acaso. Dessa forma é feita a seguinte correção da probabilidade de acerto para definição da dificuldade do item No caso do item da Figura 1, que apresenta parâmetro c igual a 0,186, a probabilidade de acerto é igual a 0,593, ou seja, (Pasquali, 2007).

O parâmetro a, por sua vez, é proporcional à derivada da tangente da curva no ponto de inflexão. Baixos valores desse parâmetro não são esperados e indicam que o item tem pouco poder de discriminação, ou seja, alunos com diferentes habilidades têm aproximadamente a mesma probabilidade de responder corretamente o item. Na Figura 1, o parâmetro a igual a 0,651 indica um item de discriminação moderada, segundo a classificação do Baker (2001). Ressalta-se que no modelo de 1 parâmetro, assume-se que todas as inclinações dos itens são iguais (uniformemente igual a 1,0).

Por fim, o local onde a assíntota inferior corta o eixo das ordenadas refere-se à probabilidade de acerto ao acaso, o chute. O chute do item apresentado na Figura 1 é igual a 0,186. Em geral, os valores do parâmetro c devem ser menores do que a probabilidade aleatória de acerto (Hambleton & colaboradores, 1991). Lord (1980) interpretou que o parâmetro c não é o parâmetro de acerto aleatório, mas sim a representação de um fenômeno genuíno do item em desenvolver atratividade. Nos modelos de 1 e 2 parâmetros, assume-se que os parâmetros de probabilidade de acerto ao acaso são zero.

Na Figura 2 é apresentada a curva de informação do mesmo item apresentado na Figura 1. Também é apresentada a curva de informação de um segundo item com padrão diferenciado de informação nos vários níveis da escala de habilidade.

 

 

A Curva de Informação do Item (CII), apresentada na Figura 2, permite analisar quanto um item contém de informação psicométrica para a medida de habilidade. Segundo Pasquali (2007), a função de informação do item é estatisticamente definida como o montante de informação psicométrica que um item contém em todos os pontos ao longo do contínuo do traço latente que ele representa. Baker (2001) discute sobre a importância relativa dos parâmetros do item para a função de informação dos mesmos, como segue:

(I) Discriminação do item (a_i): quanto maior for a discriminação do item, maior será a informação que ele traz para o θ. Itens com maior valor do parâmetro a têm a curva característica com inclinação mais acentuada;

(II) Dificuldade do item (b_i): a informação do item é maior quando o valor do parâmetro b for igual ao valor do θ; porque assim a diferença θ - b_i é igual a zero;

(III) probabilidade de acerto ao acaso (c_i): quanto menor for o acerto ao acaso do item, maior será a informação que ele traz para o θ;

Assim, a CII de um item produz a máxima quantidade de informação sobre o θ quando θ = b e quando ele for muito discriminativo e pouco acertado ao acaso. Na medida em que o chute aumenta, o máximo da CCI do item ocorre acima do ponto de sua dificuldade.

Na Figura 2 é possível observar a curva de informação de dois itens obtidos a partir dos exemplos do software Bilog-MG. No primeiro item da figura (Item MATH 01), verifica-se que o ponto máximo da CII é obtido em torno da habilidade de - 1,559 (valor do parâmetro b). Essa precisão vai diminuindo à medida que se caminha para os extremos da CII. Nos extremos dos níveis de teta, o teste produz mais erro de informação do que informação legítima, pois a curva do erro supera a curva de informação. O segundo item (MATH 11), por sua vez, apresenta o máximo de informação em torno da habilidade 0,177. A partir de uma inspeção visual é possível verificar claramente que o segundo item apresenta maior quantidade de informação do que o primeiro. O Bilog-MG fornece a curva de informação para cada um dos itens, bem como para o teste total. A curva de informação do teste representa o somatório das informações de todos os itens. A Figura 3 apresenta a curva de informação total de um teste apresentado nos exemplos do Bilog-MG.

 

 

A curva da informação do teste é representada pela linha contínua (de cor azul), enquanto a linha pontilhada (de cor vermelha) representa a curva do erro padrão da medida. Chama atenção, o fato de que nos extremos dos níveis de θ, o teste produz mais erro de informação do que informação legítima, pois a curva do erro supera a curva de informação. Após a estimação do modelo faz-se necessário avaliar a adequação do seu ajuste aos dados empíricos. Esse tópico, como assinalam Embretson e Reise (2000), é uma área ativa de pesquisa em que respostas definitivas ainda não existem. Existe uma bateria de testes estatísticos de ajuste para indicar em que grau um dado modelo da TRI se ajusta adequadamente aos dados. Essas estatísticas são chamadas de índices de bondade de ajuste (goodness of fit). Um fraco ajuste do modelo não pode assegurar que os parâmetros dos itens e das habilidades são invariantes (Spencer, 2004). Por exemplo, no caso do modelo de um parâmetro ou modelo Rasch, o software WINSTEPS calcula dois índices: o INFIT e o OUTFIT. A magnitude desses índices é diretamente proporcional à existência de respostas inesperadas. Em outras palavras, quanto mais freqüentes forem os erros e acertos inesperados mais altos serão esses índices. Especificamente, o INFIT atenua a importância dos resíduos extremos, enquanto o OUTFIT é mais sensível aos resíduos extremos (Ziviani & Primi, 2005). Hambleton e colaboradores (1991), com base na literatura, sumarizam os enfoques para (1) avaliação das suposições do modelo, (2) características esperadas do modelo (invariância das estimativas dos parâmetros dos itens e dos níveis de habilidades) e (3) predições do modelo. Nesse último, por exemplo, os autores sugerem que a investigação dos resíduos de adequação do modelo aos dados pode orientar o pesquisador na escolha do modelo de TRI que melhor se adéqua aos dados. O leitor interessado deve recorrer à literatura em questão (Embretson & Reise, 2000; Hambleton e colaboradores, 1991; Pasquali, 2007) para aprofundamento dessa área da TRI.

Outro tema que tem atraído bastante atenção dos psicometristas e avaliadores educacionais é o DIF. A sigla DIF é originária do termo em inglês Differential Item Functioning. As técnicas de DIF passaram a ser investigadas a partir da campanha dos Direitos Civis dos Estados Unidos na década de 60 e, atualmente, são empregadas para identificar itens que funcionam diferentemente em relação a subgrupos específicos dentro da população de interesse (Camilli & Shepard, 1994; Cortada de Kohan, 2004). Uma definição de DIF bastante aceita é a de que um item apresenta DIF quando examinandos que possuem a mesma habilidade, mas são oriundos de diferentes subgrupos, não têm a mesma probabilidade de respondê-lo corretamente. O DIF é a evidência empírica de que os subgrupos não apresentam a mesma probabilidade de acerto no item. Ressalta-se, todavia, que essa evidência empírica não é suficiente para se assumir que existe viés do item; esta conclusão envolve uma inferência que vai além dos dados (Hambleton & colaboradores, 1991).

Entre as principais causas de DIF apontadas pelo ETS, pode-se citar a familiaridade ou o interesse do respondente em relação ao tema abordado no item do teste. No exemplo fictício da professora Joana, apresentado no início do capítulo, levanta-se a hipótese de que o item cujo texto base era sobre futebol teria favorecido os meninos da turma. Esse item provavelmente apresentava funcionamento diferencial.

Comumente, nos estudos sobre DIF são investigadas as interações entre subgrupos étnicos (brancos, negros, amarelos etc.), subgrupos demográficos (avaliados oriundos de diferentes regiões) ou subgrupos diferenciados pelo gênero (masculino e feminino). No entanto, ressalta-se que qualquer classificação de respondentes de uma população pode ser investigada (du Toit, 2003). Na análise de DIF operacionalizada pelo Bilog-MG é considerada, especificamente, a interação do parâmetro b (dificuldade) do item com os grupos prédeterminados. Além disso, assume-se que o parâmetro de discriminação dos itens (a) é homogêneo entre os grupos e, por isso, não tem implicação sobre o DIF (du Toit, 2003). Conforme assinala Muñiz (1997), não existem itens de testes inteiramente isentos de DIF. Trata-se então de detectar a quantidade de DIF aceitável em um determinado item ou teste, segundo os objetivos do processo de avaliação.

Apesar de existir uma grande variedade de métodos para investigar DIF, os mesmos padecem de limitações. Alguns autores aconselham complementar as análises estatísticas obtidas pelo uso de mais de um procedimento de detecção do DIF, com a opinião de especialistas da área e, assim, aumentar a validade dos resultados (Adriola, 2001). A partir da TRI, o DIF pode ser investigado comparando-se os parâmetros que descrevem as curvas características dos itens (Cortada de Kohan, 2004). O item não apresentará DIF quando a CCI for idêntica para os grupos comparados em um mesmo nível ou magnitude da variável medida (Lord, 1980).

Ao fazer uma revisão dos principais métodos de detecção de DIF, Adriola (2001) assinala que a lógica subjacente à detecção do DIF consiste em (1) estimar os parâmetros dos itens para os grupos de interesse definindo o grupo de referência; (2) colocar esses parâmetros em uma mesma escala; (3) representá-los por meio das CCIs; (4) comparar as referidas CCIs nos grupos escolhidos e, finalmente, (5) observar a significância estatística das possíveis discrepâncias entre as CCIs. A análise de DIF pela TRI pode ser implementada pelo software Bilog-MG. Quando uma análise de DIF é solicitada, o Bilog-MG fornece as estimativas dos parâmetros de dificuldade dos itens ajustados e não ajustados para cada grupo considerado com seus erros padrão. Uma referência 430 Andrade, Laros & Gouveia Avaliação Psicológica, 2010, 9(3), pp. 421-435 que pode ser utilizada como base para o estudo do DIF é o livro de Camilli e Shepard (1994).

Utilização do software Bilog-MG 3.0

Um dos fatores que mais contribuíram para o uso generalizado da TRI foi o avanço da informática. Como a complexidade matemática no campo da TRI é grande, o progresso dos processadores e, conseqüentemente, o desenvolvimento de softwares apropriados nos anos 80 para operacionalização de tais cálculos, foi decisivo para o uso da TRI (Pasquali, 2007). A aplicação e o desenvolvimento da TRI em muito dependem da disponibilização de programas computacionais que possam facilitar ou viabilizar sua utilização (Nojosa, 2001). O Bilog-MG é um software que pode ser utilizado para a estimação dos modelos da TRI (http://www.ssicentral. com). O Bilog-MG é uma extensão do Bilog 3 for Windows e é designado para análises de itens dicotômicos, incluindo itens de múltipla escolha ou itens de resposta curta pontuados como certo, errado, omisso ou não apresentado. Uma facilidade desse software é que todos os outputs (saídas com resultados) são apresentados em arquivos do tipo TXT o que facilita a elaboração de relatórios, bem como a seleção de parâmetros de itens, no caso de fixação de parâmetros para equalização ou exportação para outros softwares como, por exemplo, o Testfact.

O Bilog-MG utiliza uma extensão da TRI para múltiplos grupos de respondentes. Aplicações da TRI de múltiplos grupos incluem: (a) equalização de grupos não equivalentes a fim de manter a comparabilidade de escores quando novas formas de testes são desenvolvidas; (b) equalização vertical de formas alternativas de um teste entre séries ou grupos de idade; (c) análise de funcionamento diferencial do item associada à diferenças demográficas ou grupais; (d) detecção e correção de tendência dos parâmetros dos itens associado ao tempo (DRIFT); (e) calibração e atribuição de escores (scoring) dos testes em aplicações de duas etapas com a finalidade de reduzir o tempo total de aplicação; e (f) estimação da habilidade latente ou distribuição de proficiência de estudantes em escolas, comunidades ou outras agregações (Zimowski, Muraki, Mislevy & Bock, 1996).

Uma das maiores vantagens no Bilog-MG é que sintaxes podem ser geradas ou adaptadas usando menus e caixas de diálogo. Os usuários podem especificar, por exemplo, os dados, modelos, técnicas etc. por meio dos menus. Cada opção de menu fornece acesso a um número de caixas de diálogo em que especificações podem ser feitas pelo usuário. Arquivos de sintax em formato TXT continuam sendo utilizados e o próprio software já traz exemplos para cada tipo de análise (Zimowski & colaboradores, 1996). A Figura 4 apresenta a janela do Bilog-MG.

 

 

No exemplo de janela da Figura 4, foi acessado o menu setup e o submenu general. Nessa opção pode-se definir o título da sintax, comentários, número total de itens, examinandos, grupos, formas alternativas de testes, além de se poder especificar o grupo de referência (quando necessário). As demais caixas de diálogo devem ser acessadas para definição de todas as especificações do modelo. Finalizada essa etapa, o usuário deve acessar o menu run e o submenu build sintax. A sintax será construída. Ressalta-se que o arquivo de dados deve ser cuidadosamente construído em formato do tipo TXT ou DAT. Os dados de cada observação (examinando) devem conter identificação do sujeito, número da forma do teste respondido (opcional), número do grupo respondente (opcional), peso amostral (opcional) e respostas aos itens. As respostas dos examinandos aos itens consistem de um caractere para cada item. O número de colunas do arquivo de dados deve ser rigorosamente igual ao disposto na sintax. Ainda, os códigos para o gabarito, itens não apresentados e itens omissos (quando utilizado) são lidos exatamente no mesmo formato das observações. Respostas omissas (deixadas em branco) podem ser tratadas como “erradas”, “parcialmente corretas” ou omitidas do cálculo da habilidade dos respondentes (Zimowski & colaboradores, 1996).

Ainda por meio do menu run, após a construção da sintax, pode-se rodar apenas as estatísticas clássicas (fase 1), apenas a calibração dos itens (fase 2) ou apenas os escores dos examinandos (fase 3). Também é dada a opção para rodar as três fases juntas (stats, calibration and scoring). Os resultados podem ser acessados por meio do menu output (Zimowski & colaboradores, 1996).

Os resultados da fase 1 são apresentados no arquivo do tipo *.ph1. Esses arquivos incluem a identificação do item e do teste, além das estatísticas clássicas dos itens, tais como índice de dificuldade também chamado de facilidade do item (percentual de respostas corretas), correlações item-total (bisserial e ponto-bisserial) e número de respondentes que tentaram cada item. Os resultados da fase 2 são apresentados em arquivo do tipo *.ph2. Eles incluem as distribuições assumidas a priori, parâmetros dos itens estimados, erros padrão e estatísticas de bondade de ajuste dos itens, parâmetros de DRIFT (quando solicitado), estimações de funcionamento diferencial do item (quando solicitado), médias dos grupos e desviospadrão e estimativas dos seus erros-padrão, entre outros. Os resultados da fase 3, por sua vez, são apresentados em arquivo do tipo *.ph3. Eles incluem as habilidades dos examinandos, correlações entre os escores dos subtestes, constantes de transformação, parâmetros dos itens transformados, entre outros. Os parâmetros estimados na fase 3 podem ser transformados de acordo com a convenção escalar selecionada pelo usuário (Zimowski & colaboradores, 1996).

Na Figura 5 é apresentada a janela do Bilog- MG que apresenta as opções de gráficos oferecidas pelo software.

 

 

Por meio do menu run e submenu plot, o usuário tem acesso as opções de gráficos disponibilizadas pelo Bilog-MG. São disponibilizados, na seqüência, (a) os gráficos da Curva Característica do Item (ICC) e (b) a Curva de Informação do Item (information) para cada um dos itens, (c) as curvas características e de informação plotadas simultaneamente em um único gráfico (ICC and info), (d) a curva de informação total do teste (Total info), (e) um conjunto de gráficos das CCIs (matrix plot), (f) o gráfico de regressão de habilidade sobre a porcentagem de resposta correta (bivariate plot), e (g) o histograma das habilidades (histogram) (Zimowski & colaboradores, 1996). Maiores informações podem ser obtidas no menu help do próprio software Bilog-MG.

 

Discussão e Conclusões

Um teste educacional, como outro teste qualquer, é um instrumento que funciona de forma semelhante a uma régua que mede o comprimento de um objeto. Esse instrumento deve ser válido e preciso para que resultados inconsistentes não sejam emitidos. Em avaliações educacionais de larga escala, nas quais decisões de grandes proporções são tomadas e políticas públicas são operacionalizadas, resultados inválidos e imprecisos podem ser muito onerosos e sugerir caminhos desastrosos, seja para uma rede educacional específica, seja para o país como um todo.

Como em qualquer outra abordagem baseada em modelagem para interpretação de dados, as vantagens dos modelos da TRI são obtidas à medida que as suposições subjacentes a sua aplicação são garantidas (Embretson & Reise, 2000). Dessa forma, os pressupostos da TRI devem ser atendidos pelo pesquisador. O não atendimento dos pressupostos levará fatalmente a resultados inconsistentes.

A pergunta inicial feita no início do capítulo, instigada pela professora Joana, foi se existe alguma maneira de se elaborar testes educacionais válidos, fidedignos e que não privilegiem grupos específicos de alunos. A TRI parece responder a essa questão a partir do conjunto de técnicas que dispõe. É nítido o avanço proporcionado pela TRI ao campo da avaliação educacional no âmbito brasileiro. No entanto, como assinala Nojosa (2001), a TRI, em comparação com outras áreas da psicometria, ainda está na sua infância. Vários problemas ainda precisam ser solucionados, enquanto novas metodologias precisam ser desenvolvidas para ajudar na solução desses problemas. A área de adequação de ajuste dos modelos aos dados empíricos, por exemplo, requer novas contribuições uma vez que o conhecimento já disponível parece pouco sistematizado. Ainda, o uso de modelos multidimensionais da TRI no Brasil é escasso, enquanto que em outras culturas está em franco desenvolvimento. Além da Educação e Psicologia, a TRI tem sido largamente aplicada em várias outras áreas, entre elas pode-se citar: qualidade de vida (Mesbah, Cole & Lee, 2002), satisfação do consumidor (Costa, 2001), genética (Tavares, Andrade & Pereira, 2004), psiquiatria (Schaeffer, 1988), entre outras. Diante da complexidade do tema tratado no presente artigo, não se teve a intenção de esgotá-lo, e sim, oferecer aos pesquisadores e avaliadores diretrizes para a tomada de decisões no momento de operacionalização de análises psicométricas por meio da TRI.

 

Referências

Andriola, W. B. (2001). Descrição dos principais métodos para detectar o funcionamento diferencial dos itens (DIF). Psicologia: Reflexão e Crítica, 14(3), 643-652.         [ Links ]

Allen, M. J. & Yen, W. M. (2002). Introduction to measurement theory. Illinois: Waveland Press.         [ Links ]

Andrade, D. F. de, Tavares, H. R. & Valle, R. da C. (2000). Teoria de resposta ao item: conceitos e aplicações. São Paulo: ABE – Associação Brasileira de Estatística.         [ Links ]

Andrade, J. M. de (2005). Construção de um modelo explicativo de desempenho escolar: um estudo psicométrico e multinível com dados do SAEB. Dissertação de Mestrado não-publicada, Curso de Pós-Graduação em Psicologia Social, do Trabalho e das Organizações, Universidade de Brasília. Brasília, DF.         [ Links ]

Baker, F. B. (2001). The basics of item response theory (2^a ed). Washington: Eric Clearinghouse on Assessment and Evaluation.         [ Links ]

Baker, F. B. & Kim, S. (2004). Item response theory: parameter estimation techniques. Nova York: Marcel Dekker.         [ Links ]

Bechger, T. M., Maris, G., Verstralen, H. H. F. M. & Béguin, A. A. (2003). Using classical test theory in combination with item response theory. Applied Psychological Measurement, 27(5), 319-334.         [ Links ]

Bock, R. D. & Zimowski, M. F. (1997). Multiple group IRT. Em Wim J. Van der Linden e Ronald K. Hambleton (Orgs.): Handbook of modern item response theory. (pp. 433-448). New York: Springer.         [ Links ]

Bryant, D. U. (2005). A note on item information in any direction for the multidimensional threeparameter logistic model. Psychometrika, 70(1), 213-216.         [ Links ]

Camilli, G. & Shepard, L. A. (1994). Methods for identifying biased test items. California: Sage Publications.         [ Links ]

Comrey, A. L. & Lee, H. B. (1992). A first course in factor analysis (2ª ed.). Hillsdale: Erlbaum.         [ Links ]

Condé, F. N. & Laros, J. A. (2007). Unidimensionalidade e a propriedade de invariância das estimativas da habilidade pela TRI. Avaliação Psicológica, 6(2), 205-215.         [ Links ]

Cortada de Kohan, N. (2004). Teoría de respuesta al ítem: supuestos básicos. Evaluar, 4(setiembre), 95-110.         [ Links ]

Costa, M.B.F. (2001). Técnica derivada da teoria da resposta ao item aplicada ao setor de serviços. Dissertação de Mestrado não-publicada, PPGMUE, Universidade Federal do Paraná. Curitiba/PR.         [ Links ]

Crocker, L. & Algina, J. (1986). Introduction to classical and modern test theory. Orlando: Harcourt Brace Jovanovich College Publishers.         [ Links ]

du Toit, M. (2003). IRT from SSI: Bilog-mg, Multilog, Parscale, Testfact. Lincolnwood: Scientific Software International.         [ Links ]

Embretson, S. E. & Reise, S. P. (2000). Item response theory for psychologists. New Jersey: IEA.         [ Links ]

Erthal, T. C. (2003). Manual de psicometria (7^a ed). Rio de Janeiro: Jorge Zahar Editor.         [ Links ]

Gaviria Soto, J. L. (1998). Breve introducción a la psicometria. Principales teorías. Manuscrito não publicado. Madrid: Universidade Complutense de Madrid.         [ Links ]

Hambleton, R. K., Swaminathan, H. & Rogers, H. J. (1991). Fundamentals of item response theory. California: Sage Publications.         [ Links ]

Hattie, J. (1985). Methodology review: assessing unidimensionality of tests and items. Applied Psychological Measurement, 9(2), 139-164.         [ Links ]

Instituto Nacional de Estudos e Pesquisas Educacionais Anísio Teixeira - INEP (2005). Relatório técnico da análise da teoria de resposta ao item. Brasília: INEP.         [ Links ]

Kirisci, L., Hsu, T. & Yu, L (2001). Robustness of item parameter estimation programs to assumptions of unidimensionality and normality. Applied Psychological Measurement, 25(2), 146-162.         [ Links ]

Laros, J. A. (2005). O uso da análise fatorial: algumas diretrizes para pesquisadores. Em L. Pasquali (Org.), Análise fatorial para pesquisadores (pp. 163-184). Brasília: LabPAM.         [ Links ]

Laros, J. A., Pasquali, L & Rodrigues, M. M. M. (2000). Análise da unidimensionalidade das provas do SAEB. Relatório Técnico. Brasília: Centro de Pesquisa em Avaliação Educacional – Universidade de Brasília.         [ Links ]

Lord, F. M. (1980). Applications of item response theory to practical testing problems. New Jersey: IEA.         [ Links ]

Lord, F. M. & Novick, M. R. (1968). Statistical theories of mental scores. Massachusetts: Addison-Wesley Publishing Company.         [ Links ]

Mathison, S. (2005). Encyclopedia of evaluation. Thousands Oaks: Sage Publications.         [ Links ]

Mesbah, M., Cole, B.F. & Lee, M. L. T. (2002). Statistical methods for quality of life studies: design, measurements and analysis. Boston: Kluwer Academic Publishers        [ Links ]

Muñiz, J (1997). Introducción a la teoría de respuesta a los items. Madrid: Psicología Pirámide.         [ Links ]

Nojosa, R. T. (2001). Modelos multidimensionais para a teoria de resposta ao item. Dissertação de mestrado não-publicada. Mestrado em Estatística, Universidade Federal de Pernambuco. Recife, PE.         [ Links ]

Nunes, C. H. S. da S. & Primi, R. (2005). Impacto do tamanho da amostra na calibração de itens e estimativa de escores por Teoria de Resposta ao Item. Avaliação Psicológica, 4(2), 141-153.         [ Links ]

Nunnally, J. C. & Bernstein, I. H. (1995). Psychometric theory (3^a ed). New York: McGraw-Hill.         [ Links ]

Pasquali, L. (1999). Instrumentos psicológicos: manual prático de elaboração. Brasília: LabPAM/UnB.         [ Links ]

Pasquali, L. (2003). Psicometria: teoria dos testes na psicologia e na educação. Petrópolis: Editora Vozes.         [ Links ]

Pasquali, L. (2007). Teoria de resposta ao item: teoria, procedimentos e aplicações. Brasília: LabPAM/UnB.         [ Links ]

Reckase, M. D. (1997). The past and future of multidimensional item response theory. Applied Psychological Measurement, 21(1), 25-36.         [ Links ]

Ribeiro, A. F. (2004). A qualidade psicométrica da prova de Matemática do SAEB – 2001 para a 4ª série do ensino fundamental. Dissertação de Mestrado não-publicada, Curso de Pós- Graduação em Psicologia Social, do Trabalho e das Organizações, Universidade de Brasília. Brasília, DF.         [ Links ]

Schaeffer, N. C. (1988). An Application of Item Response to the Measurement of Depression. Sociological Methodology, 18, 271–307.         [ Links ]

Segall, D. O. (2001). General ability measurement: an application of multidimensional item response theory. Psychometrika, 66(1), 79-97.         [ Links ]

Spencer, S. G. (2004). The strength of multidimensional item response theory in exploring construct space that is multidimensional and correlated. Tese de Doutorado não-publicada. Department of Instructional Psychology and Technology. Brigham Young University. Provo, Utah.         [ Links ]

Tabachnick, B. G. & Fidell, L. S. (2007). Using multivariate statistics (5^a ed.). Boston: Pearson Education.         [ Links ]

Tavares, H. R, Andrade, D. F. & Pereira, C. A. (2004). Detection of determinant genes and diagnostic via item response theory. Genetics and Molecular Biology, 27(4), 679-685.         [ Links ]

Vitória, F., Almeida, L. S. & Primi, R. (2006). Unidimensionalidade em testes psicológicos: conceito, estratégias e dificuldades na sua avaliação. Revista de Psicologia da Vetor Editora, 7(1), 1-7.         [ Links ]

Wilson, D. T., Wood, R. & Gibbons, R. (1991). Testfact: test scoring, item statistics, and item factor analysis. Chicago: Scientific Software.         [ Links ]

Zimowski, M. F., Muraki, E., Mislevy, R. J. & Bock, R. D. (1996). BILOG-MG – Multiple-group IRT analysis and test maintenance for binary itens. Chicago: Scientific Software International, Inc.         [ Links ]

Ziviani, C. & Primi, R. (2005). Teoria da resposta ao item e o modelo rasch de mensuração: uma análise do provão de psicologia. Em R. Primi (Org.), Temas em avaliação psicológica (pp. 255- 287). São Paulo: Casa do Psicólogo.         [ Links ]

 

 

Recebido em agosto de 2009
Reformulado em fevereiro de 2010
Aceito em março de 2010

 

 

Sobre os autores:

Josemberg Moura de Andrade: Professor Adjunto do Departamento de Psicologia da Universidade Federal da Paraíba, João Pessoa. Doutor em Psicologia Social, do Trabalho e das Organizações pela Universidade de Brasília (2008). Atua na área de avaliação e medidas com ênfase na elaboração, validação e adaptação de instrumentos psicológicos e educacionais. Endereço para correspondência: Núcleo de Avaliação e Medidas Psicológicas (NAMP).
Jacob Arie Laros: Professor Adjunto do Instituto de Psicologia da Universidade de Brasília. É PhD em Personality and Educational Psychology pela University of Groningen - Holanda (1991). Atua nas áreas de avaliação de programas sociais e educacionais, avaliação educacional em larga escala, análise de dados e elaboração de testes de habilidades cognitivas.
Valdiney Veloso Gouveia: Professor Associado da Universidade Federal da Paraíba. Doutor em Psicologia Social pela Universidade Complutense de Madri (1998). Atua nas áreas de Psicologia social (estruturas sociais; indivíduos) e avaliação psicológica (construção e adaptação de escalas e testes).

¹Contato:
Email: josemberg.andrade@gmail.com