ORIGINAL RESEARCH

 

Higuchi fractal dimension applied to RR intervals in children with Attention Deficit Hyperactivity Disorder

 

 

Rubens Wajnsztejn^I; Tatiana Dias de Carvalho^{II, III}; David M. Garner^IV; Rodrigo Daminello Raimundo^III; Luiz Carlos Marques Vanderlei^V; Moacir Fernandes Godoy^VI; Celso Ferreira^II; Vitor E. Valenti^VII; Luiz Carlos de Abreu^III

^INúcleo Especializado em Aprendizagem da Faculdade de Medicina do ABC, FMABC, Santo André, SP, Brazil
^IIDepartamento de Medicina, Disciplina de Cardiologia, Universidade Federal de São Paulo, UNIFESP, São Paulo, SP, Brazil
^IIILaboratório de Delineamento de Estudos e Escrita Científica da Faculdade de Medicina do ABC, FMABC, Santo André, SP, Brazil
^IVCardiorespiratory Research Group, Department of Biological and Medical Sciences, Faculty of Health and Life Sciences, Oxford Brookes University, Gipsy Lane, Oxford OX3 0BP, United Kingdom
^VDepartamento de Fisioterapia da Faculdade de Ciências e Tecnologia, Universidade Estadual Paulista, UNESP, Presidente Prudente, SP, Brazil
^VINúcleo Transdisciplinar de Estudos do Caos e da Complexidade, Faculdade de Medicina de São José de Rio Preto, FAMERP, São José do Rio Preto, SP, Brazil
^VIIDepartamento de Fonoaudiologia da Faculdade de Filosofia e Ciências, Universidade Estadual Paulista, UNESP, Marília, SP, Brazil

 

 

---

ABSTRACT

BACKGROUND: Attention deficit hyperactivity disorder (ADHD) is categorized by a lowered attention span, recklessness, and hyperactivity. Autonomic nervous system inequality has previously been studied using the same data by chaotic global techniques. We aim to compare the autonomic function of children with ADHD and controls by analyzing heart rate variability (HRV)
METHODS: 28 children with ADHD (22 boys, mean age 10.0 years ± 1.9 years) and 28 controls (15 boys, mean age 9.9 years ± 1.8 years) rested in supine position with spontaneous breathing for 20 minutes. Heart rate was recorded beat by beat. HRV analysis was performed by Higuchi Fractal Dimension technique.
RESULTS: ADHD promoted an increase in the Higuchi Fractal Dimension. The optimum value of K_max was 10.
CONCLUSION: ADHD significantly altered cardiac autonomic modulation as measured by the Higuchi fractal dimension of HRV. It can therefore be stated that ADHD has increased the complexity of the HRV signal through cardiac autonomic modulation.

Key words: attention deficit hyperactivity disorder, children, fractal physiology, heart rate variability, higuchi fractal dimension.

---

RESUMO

INTRODUÇÃO: O transtorno de deficit de atenção e hiperatividade (TDAH) é caracterizado por um período reduzido de atenção, impulsividade e hiperatividade. O desequilíbrio na função do sistema nervoso autônomo (SNA) tem sido previamente estudado utilizando-se técnicas globais da teoria do caos.
OBJETIVO: comparar a função autonômica de crianças com TDAH e controles por meio da análise da variabilidade da frequência cardíaca (VFC)
MÉTODO: 28 crianças com TDAH (22 meninos, com média de idade de 10,0 anos ± 1,9 anos) e 28 controles (15 meninos, com média de idade de 9,9 anos ± 1,8 anos) permaneceram em decúbito dorsal, com respiração espontânea por 20 minutos. A frequência cardíaca foi registrada batimento a batimento e a análise da VFC foi realizada pela técnica de Dimensão Fractal Higuchi.
RESULTADOS: TDAH promoveu um aumento na Dimensão Fractal Higuchi. O valor ideal de Kmax foi 10.
CONCLUSÃO: O TDAH alterou significantemente a modulação autonômica cardíaca, como demonstrado pela Dimensão Fractal Higuchi da VFC. Assim, pode-se afirmar que crianças com TDAH apresentaram aumento das respostas caóticas neste tipo de análise da modulação autonômica cardíaca.

Palavras-chave: transtorno de déficit de atenção e hiperatividade, criança, fisiologia fractal, variabilidade da frequência cardíaca, dimensão fractal Higuchi.

---

 

 

INTRODUCTION

Attention deficit hyperactivity disorder (ADHD) is a well-known mental condition in children¹. It is typified by lowered levels of cognitive ability, impulsiveness, and hyperactivity^{2, 3}. The exact pathological mechanisms of these psychiatric indications is unclear⁴. Nevertheless, ADHD has proven more prevalent and associated with cardiac abnormalities. Pharmacological treatment of these symptoms in children can affect their heart rate and blood pressure^3,5. Considering that cardiac function is synchronized by the autonomic nervous system (ANS); mediated through the sinus (SA) node⁶, heart rate variability (HRV) can be used to assess variation in autonomic modulation. It is an easy, non-invasive and low-cost method of monitoring the ANS and is used extensively in the research laboratory and clinically.

The apparent benefit for testing the correlation with HRV in subjects with ADHD is that it can offer a benchmark to the risk of the so called "dynamical diseases"⁷. We are assuming that the ADHD subjects RR-intervals behave in a non-linear way akin to other medical conditions such as asthma⁸, cardiac failure^9,10 and epilepsy^11-14. In addition, fractal indices are also able to detect slight changes in the dynamics of RR intervals better than conventional spectral analyses¹⁵. Further information on such "complex" conditions can be found in the article by Seely and Macklem¹⁶.

In this study the cardiac autonomic modulation was examined by the Higuchi Fractal Dimension algorithm^11-19. In previous studies, a similar computation, correlation dimension (D₂)^20-23 had been applied. These proved significant in mainly neurological assessments in Schizophrenia²⁴, Parkinson's disease²⁵, and Creutzfeldt-Jakob disease²⁶.

 

METHODS

Population

Twenty-eight children with ADHD (22 boys, mean age 10.0 ± 1.9 years) and 28 controls (15 boys, mean age 9.9 ± 1.8 years) were recruited from the Núcleo Especializado em Aprendizagem da Faculdade de Medicina do ABC (Learning Disabilities Center of Medicine ABC University), Santo André, Brazil, where they are treated by a multidisciplinary team. All volunteers in this study had the medical diagnosis of ADHD, according to the Diagnostic and Statistical Manual of Mental Disorders, 4^th edition, published by the American Psychological Association^27,28, and the following inclusion criteria were satisfied by all subjects: i) absence of congenital anomalies such as congenital heart disease, pulmonary malformations, diaphragmatic hernia, and defects of abdominal wall closure; ii) absence of central nervous system malformations and/or neurological syndromes; iii) absence of metabolic disorders; iv) absence of medication such as methylphenedite that influences cardiac autonomic modulation since that drug treatment has effects on cardiovascular parameters such as heart rate and blood pressure. The control group consisted of healthy children without a diagnosis of ADHD. Parents of the children were asked for consent. The study received approval from the Ethics Committee of Faculdade de Medicina do ABC (protocol number 312/11) and was in compliance with Resolution 196/96 of the Conselho Nacional de Saúde.

Procedure

Datasets were collected under controlled temperature (21°C - 23°C) and humidity (40%-60%). Participants attended the laboratory each time between 8:00 and 11:00 to avoid circadian influences. They were instructed to avoid consuming ANS stimulants for 24 hours before evaluation. Parents and guardians of the children stayed in the room during the entire protocol. Demographics and anthropometric measurements were obtained following the standard recommendations proposed by Lohman et al²⁹. A heart monitor strap was placed on the chest, over the distal third of the sternum, and the heart rate receiver (Polar RS800 CX monitor; Polar, Kempele, Finland) was placed on the wrist. This type of equipment has been previously validated for beat-by-beat measurements and for HRV analysis^30-32. Children rested in supine position with spontaneous breathing for 20 minutes and were instructed to avoid talking during data collection.

For HRV analysis, the heart rate was recorded beat-by-beat with a sampling frequency of 1000 Hz. The data series was first digitally filtered using Polar Precision Performance SW software (version 4.01.029; Polar), in which only series with more than 95% sinus rhythm beats were included³³. It was then manually complemented, and the visual inspection of the time series on the computer showed absence of artifacts. 1000 RR intervals were selected for data analysis.

Higuchi's Fractal Dimension

Previously, Higuchi developed a new algorithm for measuring the fractal dimension of discrete time sequences¹⁹. It is applied directly to the time-series; rather than power spectra. It can quantify self-similarity and complexity of the signal and has been applied to brain^33-35 and other biological signals^36,37. Higuchi's algorithm is described by Khoa et al¹⁷ below. It is based on a measure of length, L(k), of the curve that represents the considered time series while using a segment of k samples as a unit, if L(k) scales like:

L(k)~k^-Df

The curve is said to show fractal dimension D_f. A simple curve has dimension equal to 1.Nevertheless, a plane has a dimension equal 2. This, the value of D_f is always between 1 and 2. D_f measures complexity of the curve and so of the time series this curve represents on a graph.

From a given time series, X(1), X(2), ... , X(N), the algorithm constructs k new time series:

 

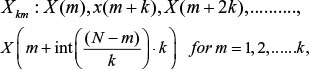
where m is initial time, k is interval time, int(r) is integer part of a real number r.

For example, for k = 4 and N = 1000, the algorithm produces 4 time series:

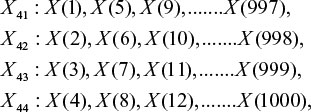
The "length" L_m(k) of each curve Xkm is then calculated as:

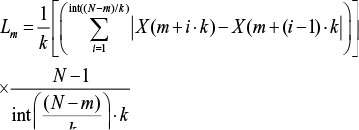
Where, N is total number of samples.

L_m(k) is not "length" in Euclidean sense, it represents the normalized sum of absolute values of difference coefficient in ordinates of pair of points distant k (with initial point m). The "length" of curve for the time interval k, L(k), is calculated as the mean of the k values L_m(k) for m = 1, 2, ... , k:

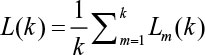
The value of fractal dimension, D_f, is calculated by a least-squares linear best-fitting procedure as the angular difference coefficient of the linear regression of the log-log graph.

So, when L(k) is plotted against 1/k on a double logarithmic scale, with k = 1,2,...,kmax, the data should fall on a straight line, with a slope equal to the Fractal Dimension of X. Thus, Higuchi fractal dimension is defined as the slope of the line that fits the pairs 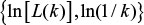in a least-squares sense. In order to choose an appropriate value for the parameter kmax, Higuchi fractal dimension values were plotted against a range of kmax. The point at which the Fractal Dimension plateaus is considered a saturation point and that kmax value should be selected.

With a = D_f, according to the following formulae:

y = ax + b

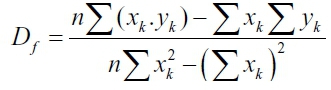
where y_k=ln L(k), x(k)=ln(1/k).

k = k₁, ... , k_max, and n denotes the number of k values for which the linear regression is calculated (2 ≤ n ≤ k_max).

 

Table 1

 

 

Figure 1

 

 

Table 2

 

 

Figure 2

 

 

Table 3

 

RESULTS

Normalization of the data is important so we know which statistical test of significance to apply. So, we applied the Anderson-Darling³⁸, and Lilliefors tests³⁹. The Anderson-Darling test for normality applies an empirical cumulative distribution function. The Lilliefors test is suitable when the number of subjects is short. In this study there are 28 subjects per category. The results from both tests are inconclusive. Consequently, we must apply both the parametric one-way analysis of variance; ANOVA1 and the non-parametirc Kruskal-Wallis⁴⁰ test of significance. Differences were considered significant when the probability of a type I error was less than 1% (p < 0.01). Here, for Higuchi fractal dimension we found significant reduced values in subjects with ADHD (p ≈ 0.004). The Kruskal-Wallis test of significance provided a p-value of 0.0035 and ANOVA1 provided a p-value of 0.0044. Both optimum values were obtained at a value of K_max of 10.

 

DISCUSSION

The ANS plays an important role in regulation of physiological mechanisms, such as cardiac and metabolic systems; and alterations in autonomic activity in children with ADHD have been investigated in several studies^1,3. HRV analysis using nonlinear methods is useful because mechanisms involved in cardiovascular regulation likely interact between each other in a nonlinear way^9,11. To the best of our knowledge, this is the first study to examine the effect of ADHD on cardiac autonomic modulation using Higuchi Fractal Dimension analysis of HRV.

A literature search revealed three studies that addressed the effect of ADHD on cardiac autonomic modulation using a nonlinear analysis of HRV. In the first investigation⁴¹, according to the frequency and time domains and the Poincaré plot, the indexes that indicate parasympathetic component were higher in children with ADHD than in children without the disorder. The second study investigated the effect of ADHD⁴² on the RR-intervals using the chaotic global techniques⁴³; and thus cardiac autonomic modulation therein.

In another study⁵ that evaluated ANS functioning and the effects of methylphenidate in stimulant-free children with ADHD and controls, the authors also found that stimulant-free children with ADHD have a parasympathetic dominance of the autonomic balance relative to control subjects. We could suggest that increased parasympathetic is related to increased chaosity found in this work.

A recent investigation⁴⁴ analyzed heart rate asymmetry as a qualitative profile of heart rate complex dynamics in ADHD untreated children at rest and in response to postural change manoeuvre (orthostatic stimulation). Opposite to our results, the authors reported atypical complex autonomic cardiac regulatory system. In this sense, there are important issues to be raised. Tonhajzerová et al⁴⁴ studied only severe ADHD, while we did not divide the ADHD group based on disorder degree.

There are other techniques which could be applied such as approximate entropy^45-47 and sample entropy^48-50. However considerable skill and expertise is required with these techniques to set the appropriate parameters for run length m and, tolerance window r.

Studies on changes in fractal properties dynamics of HRV help clinical professionals to manage disease development, since some of them indicate that the loss of fractal dynamics represents autonomic dysfunction⁵¹. This study is the first to apply Higuchi fractal dimension analysis of HRV in ADHD patients. In this context, this information is useful to further investigations to raise innovations into and to the advance of therapies for this disorder.

In conclusion, the chaotic response measured by Higuchi Fractal Dimension of HRV in child subjects with ADHD increases. This is useful in the risk assessment as a benchmark of dynamical diseases associated with ADHD.

 

COMPETING INTERESTS

The authors declare that there is no conflict of interests regarding the publication of this article.

 

REFERENCES

1. Tonhajzerova I, Ondrejka I, Adamik P, Hruby R, Javorka M, Trunkvalterova Z, et al. Changes in the cardiac autonomic regulation in children with attention defi cit hyperactivity disorder (ADHD). Indian J Med Res. 2009;130(1):44-50.         [ Links ]

2. Negrao BL, Bipath P, Van der Westhuizen D, Viljoen M. Autonomic correlates at rest and during evoked attention in children with attention-defi cit/hyperactivity disorder and effects of methylphenidate. Neuropsychobiology. 2010;63(2):82-91. DOI: http://dx.doi.org/10.1159/000317548        [ Links ]

3. Meijer WM, Faber A, van den Ban E, Tobi H. Current issues around the pharmacotherapy of ADHD in children and adults. Pharm World Sci. 2009;31(5):509-16. DOI: http://dx.doi.org/10.1007/s11096-009-9302-3        [ Links ]

4. Husarova V, Ondrejka I, Tonhajzerova I. Potential pathomechanisms of ADHD based on neurometabolite changes. Neuro Endocrinol Lett. 2010;31(4):438-45.         [ Links ]

5. Negrao BL, Crafford D, Viljoen M. The effect of sympathomimetic medication on cardiovascular functioning of children with attention-defi cit /hyperactivity disorder: cardiovascular topic. Cardiovascular J Africa. 2009;20(5):296-9.         [ Links ]

6. Task Force of the European Society of Cardiology and the North American Society of Pacing and Electrophysiology. Heart rate variability: standards of measurement, physiological interpretation and clinical use. Circulation. 1996;93(5):1043-65. DOI: http://dx.doi.org/10.1161/01.CIR.93.5.1043        [ Links ]

7. Mackey MC, Milton JG. Dynamical diseases. Ann New York Acad Sci. 1987;504(1):16-32. DOI: http://dx.doi.org/10.1111/j.1749-6632.1987.tb48723.x        [ Links ]

8. Que CL, Kenyon CM, Olivenstein R, Macklem PT, Maksym GN. Homeokinesis and short-term variability of human airway caliber. J Appl Physiol (1985). 2001;91(3):1131-41.         [ Links ]

9. Goldberger AL, Peng CK, Lipsitz LA. What is physiologic complexity and how does it change with aging and disease? Neurobiol Aging. 2002;23(1):23-6.         [ Links ]

10. Goldberger AL, Rigney DR, Mietus J, Antman EM, Greenwald S. Nonlinear dynamics in sudden cardiac death syndrome: heartrate oscillations and bifurcations. Experientia. 1988;44(11-12):983-7.         [ Links ]

11. Skinner JE, Molnar M, Vybiral T, Mitra M. Application of chaos theory to biology and medicine. Integr Physiol Behav Sci. 1992;27(1):39-53.         [ Links ]

12. Stead M, Worrell GA, Litt B. Frequency and dependence of long range temporal correlations in human hippocampal energy fl uctuations. Complexity. 2005;10(5):35-44. DOI: http://dx.doi.org/10.1002/cplx.20088        [ Links ]

13. Ponnusamy A, Marques JL, Reuber M. Comparison of heart rate variability parameters during complex partial seizures and psychogenic nonepileptic seizures. Epilepsia. 2012;53(8):1314-21. DOI: http://dx.doi.org/10.1111/j.1528-1167.2012.03518.x        [ Links ]

14. Ponnusamy A, Marques JL, Reuber M. Heart rate variability measures as biomarkers in patients with psychogenic nonepileptic seizures: potential and limitations. Epilepsy Behav.. 2011;22(4):685-91. DOI: http://dx.doi.org/10.1016/j.yebeh.2011.08.020        [ Links ]

15. Tulppo MP1, Kiviniemi AM, Hautala AJ, Kallio M, Seppänen T, Mäkikallio TH, et al. Physiological background of the loss of fractal heart rate dynamics. Circulation. 2005;112(3):314-19. DOI: http://dx.doi.org/10.1161/CIRCULATIONAHA.104.523712        [ Links ]

16. Seely AJE, Macklem PT. Complex systems and the technology of variability analysis. Crit Care. 2004;8(6):R367-84. DOI: http://dx.doi.org/10.1186/cc2948        [ Links ]

17. Khoa TQD, Ha VQ, Toi VV. Higuchi fractal properties of onset epilepsy electroencephalogram. Computational Mathematical Methods Med. 2012;1-6. DOI: http://dx.doi.org/10.1155/2012/461426        [ Links ]

18. Anier A, Lipping T, Melto S, Hovilehto S. Higuchi fractal dimension and spectral entropy as measures of depth of sedation in intensive care unit. Conf ProcI EEE Eng Med Biol Soc. 2004;1:526-9. DOI: http://dx.doi.org/10.1109/IEMBS.2004.1403210        [ Links ]

19. Higuchi T. Approach to an irregular time series on the basis of the fractal theory. Physica D. 1988;31(2):277-83. DOI: http://dx.doi.org/10.1016/0167-2789(88)90081-4        [ Links ]

20. Skinner JE, Carpeggiani C, Landisman CE, Fulton KW. Correlation dimension of heartbeat intervals is reduced in conscious pigs by myocardial ischemia. Circ Res. 1991;68(4):966-76.         [ Links ]

21. Molnar M, Skinner JE. Correlation dimension changes of the EEG during the wakefulness-sleep cycle. Acta Biochim Biophys Hung. 1991-1992;26(1-4):121-5.         [ Links ]

22. Molnar M, Skinner JE, Csepe V, Winkler I, Karmos G. Correlation dimension changes accompanying the occurrence of the mismatch negativity and the P3 event-related potential component. Electroencephalogr Clin Neurophysiol. 1995;95(2):118-26.22.         [ Links ]

23. Van Leeuwen P, Bettermann H, An der HU, Kummell HC. Circadian aspects of apparent correlation dimension in human heart rate dynamics. Am J Physiol. 1995;269(1 Pt 2):H130-4.         [ Links ]

24. Kotini A, Anninos P. Detection of non-linearity in schizophrenic patients using magnetoencephalography. Brain Topogr. 2002;15(2):107-13.         [ Links ]

25. Anninos PA, Adamopoulos AV, Kotini A, Tsagas N. Nonlinear analysis of brain activity in magnetic infl uenced Parkinson patients. Brain Topogr. 2000;13(2):135-44.         [ Links ]

26. Babloyantz A, Destexhe A. The Creutzfeld-Jakob disease in the hierarchy of chaotic attractors. In: Markus M, Muller S, Nicolis G. From chemical to biological organization. Springer; 1988. p. 307-16.         [ Links ]

27. Park S, Kim JW, Yang YH, Hong SB, Park MH, Kim BN, et al. Possible effect of norepinephrine transporter polymorphisms on methylphenidate-induced changes in neuropsychological function in attention-defi cit hyperactivity disorder. Behav Brain Funct. 2012;8:22. DOI: http://dx.doi.org/10.1186/1744-9081-8-22        [ Links ]

28. Cantwell DP. Attention defi cit disorder: a review of the past 10 years. J Am Acad Child Adolesc Psychiatry. 1996;35(8):978-87. DOI: http://dx.doi.org/10.1097/00004583-199608000-00008        [ Links ]

29. Lohman TG, Roche AF, Martorell R. Anthropometric standardization reference manual. Champaign; 1988.         [ Links ]

30. Vanderlei LCM, Silva RA, Pastre CM, Azevedo FM, Godoy MF. Comparison of the Polar S810i monitor and the ECG for the analysis of heart rate variability in the time and frequency domains. Braz J Med Biol Res. 2008;41(10):854-9. DOI: http://dx.doi.org/10.1590/S0100-879X2008005000039        [ Links ]

31. Gamelin FX, Baquet G, Berthoin S, Bosquet L. Validity of the polar S810 to measure R-R intervals in children. Int J Sports Med. 2008;29(2):134-8. DOI: http://dx.doi.org/10.1055/s-2007-964995        [ Links ]

32. Gamelin FX, Berthoin S, Bosquet L. Validity of the polar S810 heart rate monitor to measure R-R intervals at rest. Med Sci Sports Exerc. 2006;38(5):887-93. DOI: http://dx.doi.org/10.1249/01.mss.0000218135.79476.9c        [ Links ]

33. Godoy MF, Takakura IT, Correa PR. Relevância da análise do comportamento dinâmico não linear (Teoria do Caos) como elemento prognóstico de morbidade e mortalidade em pacientes submetidos à cirurgia de revascularização miocárdica. Arq Ciênc Saúde. 2005;12(4):167-71.         [ Links ]

34. Accardo A, Affinito M, Carrozzi M, Bouquet F. Use of the fractal dimension for the analysis of electroencephalographic time series. Biol Cybern. 1997;77(5):339-50. DOI: http://dx.doi.org/10.1007/s004220050394        [ Links ]

35. Ferenets R, Lipping T, Anier A, Jantti V, Melto S, Hovilehto S. Comparison of entropy and complexity measures for the assessment of depth of sedation. IEEE Trans Biomed Eng. 2006;53(6):1067-77. DOI: http://dx.doi.org/10.1109/TBME.2006.873543        [ Links ]

36. Doyle TL, Dugan EL, Humphries B, Newton RU. Discriminating between elderly and young using a fractal dimension analysis of centre of pressure. Int J Med Sci. 2004;1(1):11.         [ Links ]

37. Acharya R, Bhat PS, Kannathal N, Rao A, Lim CM. Analysis of cardiac health using fractal dimension and wavelet transformation. ITBM-RBM. 2005;26(2):133-9. DOI: http://dx.doi.org/10.1016/j.rbmret.2005.02.001        [ Links ]

38. Anderson TW, Darling DA. A test of goodness of fit. J Am Statistical Associat. 1954;49(268):765-9.         [ Links ]

39. Razali NM, Wah YB. Power comparisons of shapiro-wilk, kolmogorov-smirnov, lilliefors and Power comparisons of shapiro-wilk, kolmogorov-smirnov, lilliefors and Anderson-Darling tests. J Statist Modeling Analytics. 2011;2(1):21-33.         [ Links ]

40. Kruskal WH, Wallis WA. Use of ranks in one-criterion variance analysis. J Ame Statist Associat. 1952;260(47):583-621.         [ Links ]

41. de Carvalho TD, Wajnsztejn R, de Abreu LC, Marques Vanderlei LC, Godoy MF, Adami F, et al. Analysis of cardiac autonomic modulation of children with attention defi cit hyperactivity disorder. Neuropsychiatr Dis Treat. 2014;10:613-8. DOI: http://dx.doi.org/10.2147/NDT.S49071        [ Links ]

42. Wajnsztejn R, Carvalho TD, Garner DM, Vanderlei LCM, Godoy MF, Raimundo RD, et al. Heart rate variability analysis by chaotic global techniques in children with attention deficit hyperactivity disorder. Complexity. 2016;21(6):412-19. http://dx.doi.org/10.1002/cplx.21700        [ Links ]

43. Garner DM, Ling BWK. Measuring and locating zones of chaos and irregularity. J Syst Sci Complexity. 2014;27(3):494-506. DOI: http://dx.doi.org/10.1007/s11424-014-2197-7        [ Links ]

44. Tonhajzerová I, Ondrejka I, Farský I, Višňovcová Z, Mešťaník M, Javorka M, et al. Attention defi cit/hyperactivity disorder (ADHD) is associated with altered heart rate asymmetry. Physiol Res. 2014;63(Suppl 4):S509-19.         [ Links ]

45. Pincus S. Approximate entropy (ApEn) as a complexity measure. Chaos. 1995;5(1):110-7.         [ Links ]

46. Van Leeuwen P1, Cysarz D, Edelhäuser F, Grönemeyer D. Heart rate variability in the individual fetus. Auton Neurosci. 2013;178(1-2):24-8. DOI: http://dx.doi.org/10.1016/j.autneu.2013.01.005        [ Links ]

47. Hornero R, Escudero J, Fernandez A, Poza J, Gomez C. Spectral and nonlinear analyses of MEG background activity in patients with Alzheimer's disease. IEEE Trans Biomed Eng. 2008;55(6):1658-65.         [ Links ]

48. Lake S. Approximate Entropy and Sample Entropy. [cited 2015 Oct 08] Available from: http://tug.org/pipermail/texhax/attachments/20100616/9225924f/attachment-0007.doc.         [ Links ]

49. Richman JS, Lake DE, Moorman JR. Sample entropy. Methods Enzymol. 2004;384:172-84. DOI: http://dx.doi.org/10.1016/S0076-6879(04)84011-4        [ Links ]

50. Vuksanovic V, Gal V. Nonlinear and chaos characteristics of heart period time series: healthy aging and postural change. Auton Neurosci. 2005;121(1-2):94-100. DOI: http://dx.doi.org/10.1016/j.autneu.2005.06.004        [ Links ]

51. Carvalho TD, Pastre CM, Godoy MF, Ferreira C, Pitta FO, Abreu LC, et al. Fractal correlation property of heart rate variability in chronic obstructive pulmonary disease. Int J Chron Obstruct Pulmon Dis. 2011; 6:23-28. DOI: http://dx.doi.org/10.2147/COPD.S15099        [ Links ]

 

 

Manuscript submitted: Jun 18 2016
Accepted for publication Jun 27 2016

 

 

Corresponding author: David M. Garner. E-mail: davidmgarner1@gmail.com