Estimación de la validez predictiva de las pruebas de bachillerato en educación media

 

Estimation on the predictive validity of the graduating high school test

 

 

Tania Moreira Mora

División de Control de Calidad y Macroevaluación del Sistema Educativo, Ministerio de Educación Pública, San José, Costa Rica

Dirección para correspondencia

 

 

---

RESUMEN

Objetivo. El propósito de este estudio fue determinar el grado de validez predictiva de las pruebas de bachillerato de educación media con respecto al éxito o fracaso de los estudiantes que ingresaron a la Universidad de Costa Rica (UCR).Método. Esta medida de la validez predictiva consistió en relacionar las puntuaciones obtenidas por los estudiantes en estas pruebas en el año 1998 con los promedios ponderados de los cursos de la Escuela de Estudios Generales y de Matemáticas de la UCR, durante el trienio 1999 – 2001. La investigación fue descriptiva, transversal y correlacional. La estimación del grado predictivo de las pruebas se realizó mediante el modelo de regresión múltiple y la correlación producto – momento, r de Pearson. La muestra es representativa de los estudiantes que ingresaron a todas las sedes de la Universidad de Costa Rica en 1999. Resultados. Las variables independientes que explicaron la variabilidad en los cursos de estudios generales son el sexo, la provincia y el promedio de las pruebas. En el caso de los cursos de matemáticas lo hicieron el sexo, el horario del colegio y el promedio de las pruebas. La variabilidad del promedio ponderado fue explicada por el promedio de las pruebas, el sexo, la provincia, la modalidad y el tipo de colegio.

Palabras clave: Validez predictiva, Percepciones, Análisis correlacional, Expectancia y pruebas de bachillerato.

---

ABSTRACT

Objective. The purpose of this study was to determinate the predictive validity of graduating high school tests according to the success or failure of students that were admitted at the University of Costa Rica (UCR). Method. This measure of predictive validity consisted of relating the scorings obtained by the students in these tests in 1998 with the averages praised of the courses of School of General Studies and Mathematics, at UCR during the triennium 1999-2001. The investigation was descriptive-transactional with a correlation focus, and the estimation of the predictive degree of the tests, was carried out by means of the multiple regression models and the correlation product-moment, r of Pearson. It was formed with a representative sample of students that entered to all the headquarters in the University of Costa Rica in 1999. Results. Independent variables that explained the variability of General Studies’s courses are sex, providence and test average. In the case of matematic’s classes, variability was explained by sex, school schedule and test average.

Keywords: Predictive validity, Perceptions, Correlation’s analysis, Expectability and secondary school’s tests.

---

 

 

Introducción

En Costa Rica las pruebas de bachillerato en educación media son instrumentos de medición que permiten acreditar el dominio de conocimientos básicos de los estudiantes egresados de la educación diversificada. En el Informe Nacional de Bachillerato 1997 (Ministerio de Educación Pública) se señala que en el ámbito internacional se ha generado la necesidad de instaurar controles de calidad del sistema educativo para cuantificar su eficacia y brindar información para la toma de decisiones. En Costa Rica esta tendencia se ha fortalecido y se define como una de las estrategias para efectuar un control de salida, con el fin de mejorar el rendimiento académico puesto que las pruebas de bachillerato, como instrumentos de medición, permiten tanto acreditar el dominio de los conocimientos básicos, como brindar información para la toma de decisiones y realimentar el proceso educativo.

Asimismo, en nuestro contexto educativo y social estas pruebas han sido constantemente criticadas, ya sea por aspectos técnicos, administrativos o por sus consecuencias sociales y, pocas veces, se ha reconocido algún valor o mérito. Por tanto, interesa en este estudio encontrar evidencias de la utilidad o valor agregado de estas pruebas como instrumentos predictivos.

Este tipo de análisis predictivo es relevante porque se utiliza información de una variable (notas de las pruebas de bachillerato) para predecir las probabilidades de éxito o fracaso de los sujetos que ingresan a la educación superior. Asimismo, favorece el seguimiento del desempeño académico de los estudiantes graduados de la educación diversificada en 1998, cuando ingresaron a la Universidad de Costa Rica, específicamente en el trienio 1999 - 2001.

Se seleccionó la Universidad de Costa Rica por ser la principal universidad estatal del país y con mayor trayectoria histórica. Así también por contar, además de la sede Rodrigo Facio, con nueve sedes regionales ubicadas en casi todas las regiones del país. Por consiguiente se garantiza una muestra representativa de los estudiantes que ingresaron a esta universidad.

Además, están considerados los cursos de la Escuela de Estudio Generales por ser básicos e iniciales en la formación académica de los estudiantes de la Universidad de Costa Rica. Estos se dividen en dos tipos: la opción regular y la opción de un seminario participativo. La primera se constituye por los cursos de historia de la cultura, comunicación y lenguaje, filosofía del pensamiento y guía académica. En la segunda opción se añaden cursos de la rama artística y otros cursos complementarios. También se consideraron los cursos introductorios (matemática elemental y cálculo) de la Escuela de Matemáticas, ya que estos cursos han sido históricamente, tanto en la enseñanza secundaria como en la Universidad de Costa Rica, los de más bajo rendimiento.

 

Las pruebas estandarizadas de logro

Las pruebas estandarizadas de logro son aquellas que se administran y califican siguiendo un procedimiento tipificado predeterminado y se aplican para evaluar la eficacia del centro educativo, así como el desempeño académico de los estudiantes (Popham, 1999). Levin (1998) manifiesta que las puntuaciones de las pruebas estandarizadas de logro han sido el "patrón de oro" del pasado y constituye la forma predominante de evaluación de los estudiantes y centros educativos.

En varios países se administran las pruebas estandarizadas por varias razones, tales como evaluar programas, comparar los sistemas educativos regionales, diagnosticar a los estudiantes, evaluar a los futuros profesionales y determinar el valor agregado de un programa educativo (Levinson, 2000). También afirma que, a menudo, estas pruebas han sido un mecanismo para promover el currículo.

Según Popham (1999), las pruebas estandarizadas de logro muestrean los conocimientos o destrezas de un dominio de contenidos. Generalmente, este instrumento de medición proporciona interpretaciones válidas referidas a normas, sobre la situación de un estudiante respecto a una porción sustancial de contenidos. Además, si se asume que el grupo normativo (promedio) nacional es genuinamente representativo del país, los educadores y padres pueden hacer inferencias útiles sobre los estudiantes.

De acuerdo con este autor, una de las principales inferencias se refiere a las fortalezas y debilidades relativas de los estudiantes entre las distintas asignaturas y entre las diversas áreas o temas de cada una de las asignaturas; aunque estas pruebas contienen pocos ítem como para permitir una comparación significativa en el interior de una misma asignatura. Un segundo tipo de inferencia se relaciona con el mejoramiento del estudiante a través del tiempo en diferentes asignaturas.

Por otra parte, para lograr una política de evaluación más justa, en función de las pruebas de alta implicancia, se debe (Achieve, s.f.):

• valorar si todos los estudiantes tuvieron iguales oportunidades de una escolaridad de alta calidad y, sobre todo, si poseen los conocimientos y habilidades necesarias para tener éxito en la vida;

• medir verdaderamente lo que se espera que los alumnos aprendan;

• demostrar que las pruebas ofrecen información vital para las reformas educacionales;

• ofrecer oportunidades adicionales de aprendizaje a los estudiantes que no pasan la prueba en el primer intento.

• Además, se destaca que las consecuencias ligadas a los resultados de las pruebas son necesarias para crear incentivos que favorezcan a los estudiantes e instituciones.

Los aspectos relacionados con la justicia y la equidad son cuestionamientos importantes hacia las pruebas estandarizadas. Algunos sugieren que las pruebas están siendo utilizadas para privar de oportunidades a algunos alumnos. Los datos más recientes indican que a muchos estudiantes, especialmente los de bajos ingresos, se les está negando actualmente oportunidades de acceso a la educación. Además, las inequidades educativas probablemente persistirían sin que los diseñadores de políticas educativas, docentes, padres de familia y público se enteraran de su existencia. Por tanto, si no hubiera consecuencias ligadas a los resultados de las pruebas estandarizadas, serían pocos los incentivos para que los centros educativos disminuyan las brechas actuales en el logro académico.

Asimismo, se considera que los sistemas de atribución de responsabilidades no asignan consecuencias injustas al desempeño estudiantil porque es un hecho que los alumnos confrontan consecuencias todo el tiempo, por ejemplo, cuando egresan de secundaria y descubren que carecen de la preparación necesaria para la universidad o una carrera. Para muchos el sistema educativo ha sido un camino hacia puertas cerradas (Achieve, 2000).

Entre las recomendaciones señaladas a las pruebas estandarizadas y de alto desempeño, Haertel (1999) manifiesta en primer lugar, que no es posible encontrar una solución de retorno a los errores del pasado. Lo esencial es reconsiderar el argumento de las pruebas para la responsabilidad. También señala que, no debería desvirtuarse el valor real de las pruebas utilizadas con fines instruccionales.

Schomoker (2000) resalta que las pruebas estandarizadas se emplean porque proveen información a las escuelas y al sistema educativo y son una guía para orientar su superación. Además, promueven una instrucción común focalizada y el abandono de prácticas inefectivas. Asimismo, destaca que a pesar de sus deficiencias, las pruebas estandarizadas proporcionan información numérica y comprensible sobre qué tan bien un niño, un docente, o una escuela se desempeña o se supera. Además ofrece información vital acerca de los patrones de debilidades y fortalezas entre los estudiantes de una clase, o una escuela.

En resumen, estas pruebas ayudan a los centros educativos a valorar su actividad educativa y cuáles áreas específicas necesitan mejorar. Si no hay mérito, poco a poco, la gente pierde su sentido de responsabilidad y empiezan a dar excusas por su desempeño deficiente (Covey citado por Schomoker, 2000).

 

Calidad de las pruebas estandarizadas de logro.

Por otra parte, estas pruebas estandarizadas deben ser de una alta calidad técnica, lo que implica una construcción de acuerdo con estrictos criterios de confiabilidad y validez. Tradicionalmente la validez se ha conceptuado en tres sentidos: contenido, constructo y criterio.

La validez de contenido se refiere a qué tan adecuadamente los contenidos o las respuestas de la prueba muestrean un universo de situaciones y/o el campo cubierto por la materia examinada. La validez de constructo es el grado en el cual las puntuaciones de una prueba pueden verificarse mediante ciertos conceptos explicativos de la teoría psicológica. La validez de criterio consiste en la relación existente entre las puntuaciones obtenidas en las pruebas y las medidas externas independientes (criterios). Sin embargo, sobre la cuestión de la validez de criterio hay diferentes puntos de vista. Algunos autores establecen una distinción entre dos tipos de validez de criterio: la concurrente y la predictiva. La principal diferencia práctica entre ambas radica en el periodo en que se reúnen los datos-criterio. Cuando se recolectan simultáneamente con los datos de la prueba, se habla de validez concurrente y cuando se realiza en una fecha posterior, se tiene una medida de validez predictiva. Sin embargo, para Anastasi y Urbina (1998) esta distinción se basa en los objetivos: la validación concurrente es adecuada para diagnosticar el estado actual más que para predecir los resultados futuros. Esta diferencia la ejemplifican con las siguientes interrogantes: “¿califica Ortega como un buen piloto?” (concurrente) o “¿posee Ortega los requisitos para convertirse en buen piloto?” (predictiva).

También Kerlinger (1998) destaca que se predice si existe o no alguna relación. Se caracteriza por la predicción para un criterio externo y por la verificación de un instrumento de medición, ya sea en el presente o futuro, contra algún resultado o medición. En cierto sentido, todas las pruebas son predictivas de cierto tipo de resultado, ya sea un estado actual o futuro. Su única dificultad es el criterio mismo, puesto que su obtención es difícil.

Nunnally y Bernstein (1995) señalan que la validez de los instrumentos predictivos se determina por métodos correlativos bivariados y multivariados. En el caso de las correlaciones basadas en un solo predictor, salvo en algunos escenarios altamente dominados por la inteligencia, rara vez exceden de 0.30 a 0.40 (una cifra típica en la predicción del éxito académico). Por una parte, debido a que las personas son muy complejas como para permitir una estimación altamente precisa de su destreza a partir de algunas pruebas y, por otra parte, también son complejas las perturbaciones que afectan las medidas de criterio, por ejemplo, la cantidad de variables involucradas en la determinación de las calificaciones promedio de los estudiantes universitarios.

Las medidas de criterio más usadas incluyen calificaciones escolares, puntuaciones de las pruebas de aprovechamiento, expedientes de promoción y de graduación entre otros (Anastasi & Urbina, 1998). Sin embargo, la predicción puede ser afectada por factores no cognoscitivos que pueden influir en la continuidad de la educación (factores económicos, sociales y motivacionales). Por ejemplo, un mismo criterio -como el rendimiento académico- en los cursos universitarios puede diferir por aspectos como el contenido, el método de enseñanza, las características del docente, y los criterios de calificación. En consecuencia, lo que parece ser un mismo criterio puede representar una combinación muy diversa de rasgos en situaciones distintas.

Nunnally y Bernstein (1995) consideran que las pruebas de aprovechamiento y otros instrumentos que dependen principalmente de la validez de contenido no son construidos para correlacionarse con otras variables, pero con frecuencia suelen ser excelentes predictores de criterios específicos, como el éxito en la educación superior. Además, si una prueba predictiva (como es el caso de las pruebas de bachillerato) tiene evidencias de validez de contenido en el sentido de derivarse de un dominio de contenido bien delimitado y muestrea bien ese dominio y lo mide de manera sensible, proporciona evidencia circunstancial adicional de la utilidad de la prueba predictiva, más allá de la pura correlación con el criterio.

 

Método

Cuestiones preliminares.

En el caso particular de este estudio, se consideraron las pruebas de bachillerato en educación media aplicadas en la convocatoria ordinaria de 1998 con la finalidad de predecir las probabilidades de aprobar los cursos universitarios de formación general y humanística. Con respecto a los cursos de matemática, se incluyeron los de Matemática elemental, Cálculo I para ingenierías, Cálculo I para ciencias biológicas y otras ciencias, Matemáticas para ciencias económicas I, Matemática básica 1, Matemática para computación I, Principios de matemática y Laboratorio de matemática I así como cursos de los niveles siguientes.

Esta evaluación es transversal, correlacional y descriptiva. Se mide el grado de asociación existente entre las variables y permite indagar cómo las alteraciones de una dependen de los cambios de otra. La magnitud de la relación se calcula mediante un coeficiente de correlación que se expresa como un índice numérico, cuyo nivel de confianza para determinar su significancia fue de 0.95 y 0.99 para tener una seguridad razonable de que el coeficiente obtenido no se debe a fluctuaciones aleatorias del muestreo.

Para Hopkins, Hopkins & Glass (1997) los coeficientes de correlación resumen la magnitud y la dirección de una asociación entre dos variables. La primera se indica con un valor absoluto. Así pues, cuanto más alto es este valor, mayor es la relación y la predicción de “γ” a partir de "χ" o viceversa; mientras que la segunda se marca por los signos “+” o “-”. Una asociación positiva indica una tendencia a mantener relaciones directas en ambas medidas, es decir, las puntuaciones altas están asociadas con las altas y las bajas con las bajas. Una relación negativa indica una relación inversa, o sea, quienes calificaron alto en una variable "χ" tienden a calificar bajo en una variable “y” o viceversa. Además, estos mismos autores apuntan que los valores diferentes de cero indican que “γ” puede predecirse, con mayor o menor precisión, si conocemos “χ” pero la predicción por sí misma no presupone una relación causal.

Al respecto, Runyon y Haber (1992), señalan que el término predicción en estadística no implica ninguna deducción hacia el futuro, sino que se refiere al uso de la información de una variable para obtener información respecto a otra. Cuando se encuentran correlaciones bajas, según estos autores, se cae en la tentación de concluir que la asociación es débil o no existe ninguna relación. Sin embargo, puede tratarse de una falta de evidencia debida a que las dos variables no están relacionadas o la relación no es lineal.

En este aspecto, Anastasi y Urbina (1998) señalan que una prueba puede mejorar apreciablemente la eficacia predictiva si se correlaciona significativamente con el criterio, por baja que sea. En estas circunstancias, incluso un coeficiente de la validez tan reducido como 0.20 o 0.30 puede justificar la inclusión del test en un programa de selección. En ciencias sociales una r ≥ 0.30 señala que la relación es muy importante.

En este estudio se utilizó el coeficiente de correlación producto momento (r de Pearson), ya que las calificaciones obtenidas por los y las estudiantes en las pruebas de bachillerato y en los cursos universitarios corresponden a una escala de intervalo. También se utilizó el método de análisis de la regresión lineal múltiple, que consiste en predecir la variable dependiente (y) a partir de valores conocidos de dos o más variables independientes (χ¹, χ²,...χ^k) que influyen mutua y simultáneamente. Se asume que existe una relación lineal entre ambas variables. Cuando la correlación es 1, la predicción es perfecta. El coeficiente de regresión indica el cambio de “y” por unidad de cambio en “χ”, es decir, cuánto disminuye o aumenta la variable dependiente cuando la independiente aumenta en una unidad. Para Kerlinger (1998) la regresión trata con relaciones, pero la dirección es en un solo sentido: de las variables independientes a la dependiente.

Según Lind, Mason y Marchal (2001) se trata de probar cuál es la capacidad de las variables independientes χ¹, χ²,...χ^k para explicar el comportamiento de la variable dependiente “y”. En forma interrogativa sería: ¿se puede estimar la variable dependiente sin tomar en cuenta a las independientes?

 

Participantes

Muestra.

La muestra de estudiantes de la Universidad de Costa Rica fue representativa de quienes ingresaron en sus diez sedes, cuya base de datos fue proporcionada por la Oficina de Información y Registro de la misma Universidad. En 1999 se admitieron un total de 4 484 estudiantes de la educación formal, sin embargo, se perdieron 1 775 casos debido a las siguientes razones:

• No se logró empatar todos los números del carné universitario con la respectiva cédula de identidad.

• Hubo errores en la digitación del número de cédula, por tanto no se identificaron totalmente los apellidos y nombres de estudiantes que realizaron las pruebas de bachillerato en 1998. En ese año la base de datos de la División de Control de Calidad del Ministerio de Educación Pública no disponía del número de cédula de todos los estudiantes que realizaron estas pruebas.

• Se excluyeron estudiantes que no realizaron las cinco pruebas de bachillerato en esta convocatoria ordinaria de 1998 y a quienes no ingresaron efectivamente a la Universidad de Costa Rica, pese a que habían logrado aprobar la prueba de admisión a este centro de educación superior.

También esta muestra fue representativa de los estudiantes provenientes de cada una de las diferentes categorías de colegios: oficiales, semioficiales y privados (dependencia); diurnos y nocturnos (horario); y académicos, técnicos y artísticos (modalidad); así como también de las siete provincias.

Finalmente, cabe subrayar la representatividad de la muestra, pues al estar compuesta por 2 709 participantes están presentes las características relevantes de la población, así también, los datos estadísticos calculados son más exactos que los de una muestra pequeña.

 

Resultados

Análisis correlacional

En la estimación de los coeficientes de validez predictiva se analizó el grado de asociación estadística existente entre el promedio de las calificaciones obtenidas por los y las estudiantes en las cinco pruebas de bachillerato de 1998 (no se consideró el 40% correspondiente a la nota de presentación, calculada como un promedio de las calificaciones obtenidas por los/las estudiantes en todas las asignaturas de la educación diversificada) con los promedios ponderados de estudios generales y los cursos seleccionados de matemática realizados entre 1999 y el 2001. En esta universidad se calcula el promedio ponderado multiplicando la calificación obtenida por el número de créditos correspondiente a cada curso y luego estas puntuaciones (de todos los cursos realizados en la Escuela de Estudios Generales o los cursos de matemáticas considerados en la investigación) se suman y se dividen por el respectivo total de créditos. Finalmente, es relevante destacar que estos promedios ponderados fueron calculados con base en los cursos aprobados e improbados, así como tomando en cuenta las veces que el/la estudiante matriculó un mismo curso durante el periodo en estudio (ver Tabla 1).

 

 

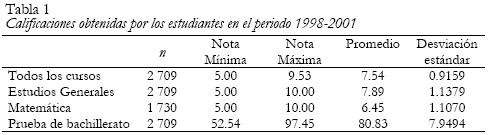
En 1998 la nota mínima de aprobación en las pruebas de bachillerato era de 65 (en escala de 1 a 100) y en los cursos universitarios de 7 (en escala de 1 a 10). En la muestra constituida por 2 709 estudiantes, 1 730 realizaron cursos en la Escuela de Matemáticas. Los valores mínimo y máximo corresponden a la puntuación más baja y más alta de cada variable. En cuanto a los promedios, el de matemáticas fue el más bajo (6.45) lo cual se debe probablemente, a que sólo el 33% (569) aprobaron estos cursos.

En este punto cabe destacar que la estimación del promedio o la media aritmética es muy sensible a las mediciones extremas, cuando no están equilibradas en ambos lados de ella, como es el caso de estos cursos.

Con respecto a la desviación estándar (medida de la variabilidad de las calificaciones con respecto al promedio) las puntuaciones de las pruebas de bachillerato fueron las más dispersas con respecto a su promedio (80.83); mientras que las calificaciones de todos los cursos universitarios seleccionados (calculado con los promedios ponderados de los cursos de estudios generales y los cursos de matemática) presentaron menor variabilidad.

También es necesario subrayar que el propósito cardinal de las pruebas de bachillerato es acreditar el dominio de los conocimientos básicos. Sin embargo, sus resultados pueden utilizarse para pronosticar el desempeño de los estudiantes en la educación superior (ver Tabla 2).

 

 

Los/las estudiantes provenientes de colegios privados lograron el promedio más alto en las pruebas de bachillerato, sin embargo, su rendimiento en los cursos universitarios es semejante al de otros/as alumnos/as. Asimismo, los/las estudiantes con el menor promedio en las pruebas de bachillerato y en los cursos universitarios provienen de los colegios nocturnos, demostrándose cierta desventaja con respecto a los otros. Por ejemplo, sólo el 8% de estos/as alumnos/as aprobaron los cursos seleccionados de matemáticas. También se observó que el mejor rendimiento en todos los cursos universitarios fue logrado por las mujeres.

De acuerdo con lo definido en el marco metodológico, se correlacionaron la media aritmética de las pruebas de bachillerato (sin incluir la nota de presentación) con los promedios ponderados de los cursos de estudios generales y los seleccionados de matemáticas, cuyos coeficientes se presentan en la Tabla 3.

 

 

En general los coeficientes significativos en el nivel 0,01 (examen bilateral) fueron débiles, ya que oscilaron entre 0.16 y 0.33. Es decir, existe en la población una asociación positiva entre las calificaciones obtenidas en las pruebas de bachillerato con los promedios ponderados de los cursos universitarios seleccionados, pero con una dispersión considerable de las puntuaciones. Al respecto, Anastasi y Urbina (1998) señalan que existen diversas circunstancias que afectan a los coeficientes de validez.

Primero, una prueba podría tener una validez muy alta para predecir cierto criterio en una población y muy poca o ninguna validez en otra, debido a diferencias como sexo, nivel educativo, edad o cualquier característica afín. En este estudio, no hubo evidencias de validez predictiva de las pruebas de bachillerato para los estudiantes provenientes de colegios nocturnos, semioficiales, técnicos y artísticos (en este sólo en los cursos de matemáticas). Probablemente esto se debe a que las muestras son muy pequeñas, de 35 a 64 estudiantes, por lo tanto, es necesario determinar una muestra más apropiada de esta subpoblación.

Segundo, la heterogeneidad de la muestra puesto que, en igualdad de circunstancias, cuanto mayor sea el rango de las puntuaciones, más alta será la correlación. Sin embargo, cuando existe una preselección (como en este caso, la prueba de admisión de la UCR), es muy probable que la amplitud total del grupo en las puntuaciones de la prueba y en las medidas de criterio se reduzca en el extremo inferior de la distribución como efecto de la preselección y descienda el coeficiente de validez.

Los coeficientes de validez pueden cambiar con el tiempo a causa de cambios en la selección de estándares cambiantes. Por ejemplo, la nota mínima de aprobación para las pruebas de bachillerato en 1998 fue de 65, pero a partir de 1999 es de 70. Asimismo, la puntuación mínima para que un estudiante sea elegible para ingresar a un plan de formación en la Universidad de Costa Rica ha sido de 442 puntos (aún se mantiene) de un máximo de 800, aunque esta puntuación varía según la carrera o plan de formación.

El cálculo del coeficiente de correlación de Pearson, da por sentado que la relación es lineal y uniforme a lo largo de todo el rango de la distribución bivariante, es decir, presupone la homoscedasticidad. Sin embargo, es posible que exista una variabilidad más amplia en el criterio de desempeño entre los estudiantes con puntuaciones altas que entre los que obtienen puntuaciones más bajas.

Finalmente, se destaca lo planteado por esta autora, en cuanto que si la correlación es significativa con el criterio, por baja que sea (de 0,20 a 0,30) puede justificarse la inclusión de la prueba en un programa de selección.

 

Análisis de expectancia

Para comprender mejor el sentido de la validez predictiva se elaboraron los gráficos de expectancia que, según Anastasi y Urbina (1998), muestran las probabilidades de que un individuo con cierta puntuación en la prueba obtenga un nivel especificado de desempeño en el criterio. Específicamente en esta evaluación se estimaron las probabilidades para cada intervalo de puntuación de las pruebas de bachillerato con respecto a los cursos universitarios seleccionados, cuyos promedios ponderados se clasificaron en improbados (puntuaciones inferiores a 7) y aprobados (igual o superior a 7).

 

Escuela de Estudios Generales.

La promoción general de los estudiantes en los cursos de la Escuela de Estudios Generales realizados entre 1999 y 2001 se resume en la Figura 1.

 

 

En este gráfico se representa el porcentaje de estudiantes que aprobaron o improbaron los cursos de la Escuela de Estudios Generales, en el cual se comprobó que conforme aumentaba las puntuaciones en las pruebas de bachillerato, el porcentaje de fracasos disminuyó en forma consistente. Basándose en estos datos, cabe predecir, por ejemplo, que aproximadamente el 97% de estudiantes con calificaciones entre 90 y 99.99 en las pruebas de bachillerato aprobarán los cursos de Estudios Generales.

Además, hubo una tendencia de mayor aprobación conforme aumentaban las calificaciones de las pruebas de bachillerato en la mayoría de los estudiantes provenientes de los colegios públicos académicos diurnos y de los privados. En la promoción total el 91% de las mujeres y el 84% de los varones aprobaron los cursos de Estudios Generales.

Con la finalidad de obtener más evidencias estadísticas se estimó el coeficiente de regresión múltiple, considerándose como variable dependiente la promoción en los cursos de la Escuela de Estudios Generales (y) y seis variables independientes: sexo de los estudiantes (β₁), provincia (β₂), horario (β₃), modalidad (β₄), tipo de colegio (β₅) y promedio de pruebas (β₆). El coeficiente de determinación, estimado por el modelo de regresión, midió el porcentaje de variación en y que es explicable por la variación de los seis predictores. En este caso fue muy bajo: 6.8%; debido, en parte, al bajo coeficiente de correlación (0.26) entre las variables independientes y el promedio ponderado de Estudios Generales.

También se probaron las hipótesis de los coeficientes de regresión en el nivel 0.05 con el estadístico de la prueba t de Student. La hipótesis nula (H₀) establecía que el coeficiente de regresión era cero y la alternativa (H₁) que era diferente a cero (examen bilateral). Si no se rechaza la H₀ la variable independiente no sería de valor para explicar la variación en la dependiente. De los seis predictores resultaron significativos tres y se rechazaron sus hipótesis nulas; por lo tanto, se aceptan las alternativas. Desde el punto de vista práctico, esto significa que las variables sí pueden explicar la variación en la promoción de los cursos de la Escuela de Estudios Generales. Estas variables independientes fueron el sexo de los estudiantes, la provincia y el promedio de pruebas.

Según los coeficientes de regresión muestrales, en promedio las mujeres obtuvieron en la nota en Estudios Generales 0.4 puntos más que los hombres. También en promedio, los estudiantes de otras provincias lograron una nota que fue 0.09 puntos más alta que los de San José; ésta, aunque es una diferencia mínima resultó significativa.

El promedio de pruebas fue la variable independiente con mayor importancia relativa y mostró una relación positiva con el promedio ponderado en la Escuela de Estudios Generales. Según el coeficiente de regresión, por cada punto que aumentó el promedio de las pruebas de bachillerato, la nota de Estudios Generales aumentó en 0.3 puntos. En otras palabras, conforme aumentó el promedio de las pruebas, la nota en los cursos de Estudios Generales se incrementó.

 

Escuela de Matemáticas.

El análisis se basó únicamente en los resultados logrados por los estudiantes en los siguientes cursos: Matemática Elemental, Cálculo I para Ingenierías (MA1001), Cálculo I para Ciencias Biológicas y otras Ciencias (MA1210), Matemáticas para Ciencias Económicas I, Matemática Básica 1, Matemática para Computación I, Principios de Matemática y Laboratorio de Matemática I y cursos de niveles siguientes de la Escuela de Matemática, cuyos porcentajes de promoción generales se presentan en la Figura 2.

 

 

El número de estudiantes que realizaron cursos de matemáticas fue de 1 730 (64% de la muestra), de los cuales aprobaron únicamente el 33% (569). De acuerdo con los datos de la Figura 2, los mayores porcentajes de aprobación se presentaron en los estudiantes que obtuvieron puntuaciones iguales o superiores a 90 en las pruebas de bachillerato.

Es importante destacar que los porcentajes de aprobación aumentaron conforme se incrementaban las puntuaciones en las pruebas; con la excepción de quienes puntuaron entre un 50 a un 59.99. En este intervalo se ubicaron solamente 22 estudiantes (equivalente al 1.3% de esta muestra), de los cuales 9 aprobaron los cursos de matemáticas, de ahí el 41% de aprobación. La mayoría de los estudiantes (47.5%) se ubicaron en el intervalo de 80 a 89.99, por lo que de acuerdo con los resultados obtenidos, se puede predecir que los estudiantes de colegios públicos con calificaciones entre 90 y 99.99 tendrán mayores probabilidades de aprobar (72%) los cursos de matemáticas que los de instituciones privadas (60%).

Un dato relevante fue la menor matrícula de mujeres en la Escuela de Matemáticas: 56% de varones y 44% de mujeres, situación contraria a la Escuela de Estudios Generales y a la de la totalidad de los cursos universitarios. Pese a esta diferencia, la promoción fue mayor en las mujeres (41%) con respecto a los varones (26%). Se puede predecir que las mayores probabilidades de éxito, tanto para mujeres como para varones, en los cursos de la Escuela de Matemáticas, serán en aquellos que obtengan calificaciones iguales o superiores a 90 en las pruebas de bachillerato.

En relación con el coeficiente de determinación, resultó que sólo el 11% de la variación ocurrida en la promoción de los cursos de matemáticas fue explicada por los predictores. Este valor se explica por la débil asociación (0.33) entre las variables independientes y la promoción en matemáticas. Los predictores que resultaron significativos fueron: sexo de los estudiantes, horario del colegio y promedio de pruebas. Sus hipótesis nulas se rechazaron, por tanto, sí explicaron una proporción de la variabilidad en la variable dependiente. Según los coeficientes de regresión muestrales, en promedio las mujeres obtuvieron una nota 0.3 puntos más alta que los hombres en los cursos de matemáticas. Asimismo, los estudiantes de colegios diurnos lograron una nota que fue 0.43 más alta que los de instituciones nocturnas.

También en estos cursos el promedio de pruebas fue la variable independiente con mayor importancia relativa. Según el coeficiente de regresión, por cada punto que aumentó el promedio de las pruebas de bachillerato, la nota en los cursos de matemáticas aumentó en 0.4 puntos; es decir, se mantuvo una relación directa y positiva entre ambas medidas.

 

Todos los cursos universitarios.

En esta sección se muestran sumados los promedios ponderados obtenidos por los estudiantes en cursos de la Escuela de Estudios Generales, de la Escuela de Matemáticas y de otras escuelas. Los resultados generales se presentan en la Figura 3.

 

 

En general, las probabilidades de éxito en todos los cursos seleccionados entre 1999 y 2001 aumentaron significativamente en los estudiantes que obtuvieron calificaciones iguales o superiores a 90 en las pruebas de bachillerato. Sin embargo, los porcentajes de promoción fueron superiores y más consistentes en los cursos de la Escuela de Estudios Generales.

En el caso de los estudiantes que obtuvieron las más bajas calificaciones en las pruebas de bachillerato (de 50 a 69.99) sus probabilidades de fracasar en la universidad fueron mayores: 29% y 31% de reprobación. Por otra parte, los porcentajes de promoción fueron semejantes en las poblaciones provenientes de colegios públicos y privados, con excepción en la categoría de 70 a 79.99, ya que los estudiantes de instituciones públicas superaron en 17 puntos porcentuales a los de colegios privados.

En general, las mujeres superaron a los varones en la aprobación total de los cursos seleccionados, con excepción de la primera categoría (50 a 59.99). Las mayores probabilidades de éxito para las mujeres y los varones, se presentaron entre las puntuaciones de 80 y 99.99. Estos resultados se reflejaron en la promoción final: 85% de las mujeres y el 68% de los varones aprobaron los cursos.

El coeficiente de determinación calculado en el modelo de regresión fue de 12%; esto significa que el 12% de la variabilidad en la promoción de todos los cursos seleccionados fue explicada por los predictores. Esta proporción tan baja se debió a que la asociación entre las variables independientes y la dependiente fue débil (0.35). Los predictores significativos fueron sexo, provincia, modalidad, tipo y promedio de pruebas, cuyas hipótesis nulas se rechazaron. Consecuentemente, sí explicaron una proporción de la variabilidad en la promoción de los estudiantes en todos los cursos universitarios.

De acuerdo con los coeficientes de regresión muestrales, en promedio las mujeres mostraron un aumento de 0.5 puntos en su promedio ponderado total con respecto a los varones; además fue el predictor con mayor importancia relativa. También, en promedio los estudiantes de otras provincias obtuvieron 0.085 puntos más que los de San José en su promedio ponderado total. Otro coeficiente significativo fue el horario, donde en promedio los estudiantes de colegios diurnos obtuvieron un promedio ponderado que fue 0.199 puntos más alto que los de nocturnos. Asimismo, en promedio, los estudiantes de colegios públicos lograron 0.142 puntos más en el promedio ponderado con respecto a los de centros privados.

Finalmente, el promedio de pruebas mostró una relación positiva con el promedio ponderado total, cuyo coeficiente de regresión mostró que por cada punto de aumento en el promedio de las pruebas de bachillerato, el promedio ponderado aumentó en 0.25 puntos. Este resultado evidenció, una vez más, que las pruebas de bachillerato son un buen predictor del rendimiento académico en los cursos seleccionados de la Universidad de Costa Rica.

 

Discusión

El propósito cardinal de esta evaluación fue obtener algunas evidencias estadísticas de la validez predictiva de las pruebas de bachillerato, aunque el objetivo de éstas es muy diferente: medir y certificar el dominio de los conocimientos básicos logrado por los estudiantes al concluir la educación diversificada. Sin embargo, es usual en la evaluación e investigación educativa emplear las pruebas de logro estandarizadas para predecir el desempeño académico en niveles superiores.

Uno de los análisis estadísticos empleados fue el coeficiente de correlación producto momento de Pearson, cuyos valores fueron positivos, bajos (oscilaron entre 0.16 y 0.37) y la mayoría significativos y por ende se pueden generalizar a toda la población. Estos coeficientes significan que hubo una tendencia a mantener puntuaciones similares, aunque con muchas excepciones, entre el promedio de las pruebas de bachillerato de 1998 y las calificaciones en cursos de estudios generales, matemáticas y el promedio ponderado de otros cursos seleccionados entre 1999 y 2001 en la Universidad de Costa Rica.

En relación con estos resultados es importante destacar que las pruebas de bachillerato son aproximaciones gruesas del estatus del estudiante con respecto al dominio de un conjunto de contenidos delimitados en el curriculum nacional. Por lo tanto, la estimación y la predicción del rendimiento académico puede afectarse por factores económicos, culturales, sociales, educativos, motivacionales y por la capacidad intelectual.

Por otra parte, las calificaciones de los cursos universitarios de una misma asignatura pueden diferir en contenidos, métodos de enseñanza, personalidad del docente y criterios evaluativos, entre muchos otros aspectos. En consecuencia, estos múltiples factores asociados al desempeño académico afectaron los coeficientes de correlación.

También se recurrió al método de la regresión múltiple para obtener más evidencias estadísticas, como el coeficiente de determinación que estimó el porcentaje de variación en la promoción de los cursos universitarios que fue explicada por la variación de seis predictores (variables independientes): sexo de los estudiantes, provincia, horario, modalidad, tipo de colegio y promedio de pruebas. Los coeficientes fueron muy bajos: entre 6.8% y 12%, debido, en parte, a que la correlación entre las variables independientes y la dependiente es débil, de 0.26 a 0.35. Sin embargo, algunos de estos predictores resultaron significativos y sus hipótesis nulas se rechazaron. Esto significa que las variables sí explicaron una proporción de la variación en la promoción de los estudiantes en los cursos universitarios.

En los cursos de la Escuela de Estudios Generales las variables independientes que explicaron el 6.8% de la variabilidad en la promoción fueron el sexo de los estudiantes, la provincia y el promedio de pruebas. En los cursos seleccionados de la Escuela de Matemática, el 11% de la variabilidad fue explicada por el sexo del estudiante, horario del colegio y el promedio de las pruebas. En el promedio ponderado de los cursos realizados por los estudiantes, incluyendo los de la Escuela de Estudios Generales y la de Matemáticas, el 12% de la variabilidad fue explicada por el promedio de pruebas, el sexo de los estudiantes, la provincia, la modalidad y el tipo de colegio.

De acuerdo con la tendencia de los resultados se presentó una mayor promoción en los estudiantes provenientes de colegios diurnos, aunque sólo 64 alumnos de la muestra eran de instituciones nocturnas. También resultó relevante que los estudiantes de colegios académicos lograron porcentajes de promoción más altos en relación con los colegios técnicos y artísticos. Además, se evidenció que las mujeres en promedio obtuvieron una nota que fue de 0.3 a 0.5 puntos más alta que los varones.

También resultó interesante que en promedio los estudiantes de otras provincias obtuvieran entre 0.09 y 0.085 puntos más en sus calificaciones que los de San José. También cabe destacar, que los estudiantes provenientes de colegios privados obtuvieron un mejor promedio en las pruebas de bachillerato; sin embargo, los alumnos de instituciones públicas en promedio obtuvieron 0.14 puntos más en el promedio ponderado de los cursos universitarios que los de instituciones privadas.

El predictor que resultó con mayor importancia relativa en la promoción de todos los cursos seleccionados de la Universidad de Costa Rica fue el promedio de las pruebas de bachillerato. De acuerdo con los análisis, se presentó la tendencia de mayor promoción en estos cursos conforme aumentaba el promedio de las pruebas de bachillerato. Por tanto, se puede considerar un buen predictor del rendimiento universitario en los cursos seleccionados y las mayores posibilidades de éxito las tendrán aquellos estudiantes que obtuviesen calificaciones iguales o superiores a ochenta en las pruebas de bachillerato.

En suma, el análisis correlacional y la regresión lineal multivariable proporcionaron evidencias estadísticas de la asociación entre la promoción en los cursos seleccionados de la Universidad de Costa Rica y las pruebas de bachillerato, cuyos coeficientes fueron bajos y débiles. Sin embargo, estos resultados son valiosos en la medida que proporcionan información relevante para mejorar el desempeño académico de estudiantes y centros educativos, especialmente aquellos provenientes de colegios nocturnos, semioficiales, técnicos y artísticos. Además, todas las pruebas son predictivas de cierto tipo de resultado, de algún estado actual o futuro.

Finalmente, una limitación importante del estudio fue la prueba de admisión a la Universidad de Costa Rica, puesto que genera una condición especial de selectividad inicial que favorecería el éxito universitario. Asimismo, la mayoría de los criterios son heterogéneos en su estructura factorial y sus medidas son parcialmente confiables. Otra limitación fue no considerar las demás universidades estatales, sin embargo, este ha sido un primer acercamiento a la validez predictiva de las pruebas de bachillerato, que se podría ampliar con otros análisis estadísticos y muestras.

 

Referencias

Achieve (s.f.). Estándares altos: dando a todos los estudiantes una oportunidad justa. Biblioteca PREAL [En línea]. Recuperado el 12 de junio de 2002 de www.Preal.el/GTEE/pdf/:Achieve2.pdf        [ Links ]

Achieve (s.f.). Las pruebas de logro: aclarando las cosas. Biblioteca PREAL [En línea]. Recuperado el 12 de junio del 2002 de: www.preal.org/GTEE/pdf/Achieve.pdf

Anastasi, A. & Urbina, S. (1998). Test psicológicos. México: Prentice Hall.

Ary, D., Jacobs, L. Ch. & Razaviech, A. (1998). Introducción a la investigación pedagógica. México: McGraw Hill.

Haertel, E. (1999). Pruebas de desempeño y reforma educativa. Biblioteca PREAL [En línea]. Recuperado el 12 de junio de 2002 de: www.preal.org/GTEE/articulosdifusión.pdf.18k

Hopkins, K, Hopkins, B. R. & Glass, G. (1997). Estadística básica para las ciencias sociales y del comportamiento. México: Prentice-Hall Hispanoamericana.

Kerlinger, F. (1998). Investigación del comportamiento. México: McGraw-Hill.

Levin, H. (1998). Educational performance standards and the economy. Educational Leadership, 27 (4), pp. 4-10. United States of America: Association for Supervision and Curriculum Development.

Levinson, C. (2000). Student assessment in eight countries. Educational Leadership, 57 (5), pp. 58-61. United States of America: Association for Supervision and Curriculum Development.

Lind, D., Mason, R. & Marshall, W. (2001). Estadística para administración y economía. México: McGraw-Hill.

Mehrens, W. & Lehmann, I. (1982). Medición y evaluación en la educación y en la psicología. México: Continental.

Ministerio de Educación Pública. (1999). Informe nacional de resultados de bachillerato 1998. San José, Costa Rica: Ministerio de Educación Pública.

Nunnally, J. & Berstein, I. (1995). Teoría psicométrica. México: McGraw-Hill.

Popham, W.J. (1999). ¿Por qué las pruebas estandarizadas no miden la calidad educativa? Biblioteca PREAL [En línea]. Recuperado el 12 de junio de 2002 de: http://www.preal.org/GTEE/pdf/Popham.pdf

Popham, W. J. (2001). The truth about testing. An educator´s call to action. United States of America: Association for Supervision and Curriculum Development

Runyon, R. & Haber, A. (1992). Estadísticas para las ciencias sociales. United States of America: Addison-Wesley Iberoamericana.

Schomoker, M. (2000). The results we want. Educational Leadership, 57 (5), 62-65. United States of America: Association for Supervition and Curriculum Development.

 

 

Dirección para correspondencia
Dirección postal: 1437-1100 Tibás, San José;
Ce:tmoreira@costarricense.cr.

Recibido: 8 de marzo de 2004
Aprobado: 8 de noviembre de 2004