ARTIGOS

 

Análisis de consistencia interna mediante Alfa de Cronbach: un programa basado en gráficos dinámicos

 

Internal consistency analysis by means of Cronbach’s Alpha: a computer program based on dynamic graphics

 

 

Rubén Ledesma^{*, 1}; Gabriel Molina Ibañez^**; Pedro Valero Mora^***

 

 

---

RESUMEN

En este trabajo se presenta una herramienta informática original que permite realizar análisis de consistencia interna (modelo Alfa de Cronbach) utilizando métodos gráficos dinámicos. Se trata de un módulo basado en la filosofía del Análisis Exploratorio de Datos y en métodos de visualización estadística, diseñado para asistir al analista en el proceso de construcción de pruebas psicológicas. La herramienta permite analizar la consistencia interna de la prueba, las propiedades de los ítems que la componen, los patrones de respuesta de los sujetos a los ítems, y el efecto de la eliminación de los ítems y del incremento en la longitud de la prueba sobre su fiabilidad. En comparación con otros programas existentes, el beneficio del módulo es la incorporación de gráficos estadísticos dinámicos como complemento a la presentación de resultados convencionales en formato texto.

Palabras claves: Alfa de Cronbach, Visualización estadística, Gráficos dinámicos.

---

ABSTRACT

This paper describes a computer software that provides dynamic graphics to perform internal consistence analysis by means of Cronbach’s Alpha. This software, based on Exploratory Data Analysis philosophy and statistical visualization methods, is designed to assist the process of psychological test and scale construction. It allows carry out internal consistency analysis, as well as exploring statistical properties of items, subject responses patterns, and the effect of item deletion and test length increase on reliability coefficient. Comparing with other statistical software, the benefit of this program is to use dynamic graphics complementing statistical output.

Keywords: Cronbach’s Alpha, Statistical visualization, Dynamic graphics.

---

 

 

Introducción

Análisis de consistencia interna mediante Alfa de Cronbach

Dentro de la Teoría Clásica de los Tests (TCT) el método de consistencia interna es el camino más habitual para estimar la fiabilidad de pruebas, escalas o test, cuando se utilizan conjuntos de ítems o reactivos que se espera midan el mismo atributo o campo de contenido. La principal ventaja de ese método es que requiere solo una administración de la prueba; además, los principales coeficientes de estimación basados en este enfoque son sencillos de computar y están disponibles como opción de análisis en los programas estadísticos más conocidos, como SPSS, Statistica o SAS.

Dentro de esta categoría de coeficientes, Alfa de Cronbach es, sin duda, el más ampliamente utilizado por los investigadores. Alfa estima el límite inferior del coeficiente de fiabilidad y se expresa como:

Donde k es el número de ítems de la prueba, es la varianza de los ítems (desde 1...i) y es la varianza de la prueba total. El coeficiente mide la fiabilidad del test en función de dos términos: el número de ítems (o longitud de la prueba) y la proporción de varianza total de la prueba debida a la covarianza entre sus partes (ítems). Ello significa que la fiabilidad depende de la longitud de la prueba y de la covarianza entre sus ítems.

Históricamente, la importancia y popularidad del trabajo de Cronbach (1943, 1946, 1947, 1951) puede atribuirse, entre otras cosas, al progreso realizado con respecto a los enfoques existentes en el momento. En relación con el método de división por mitades (Spearman, 1910; Brown, 1910), el coeficiente a ofrecía una estimación única de fiabilidad, consistente en la media de las estimaciones para todas las posibles mitades; y en relación con los métodos desarrollados por Kuder y Richardson (1937), Cronbach extendía la estimación al caso de datos no binarios. Desde entonces, el coeficiente a ha sido permanente objeto de estudio, siendo analizado en lo relativo a sus formas de derivación (Novick & Lewis, 1967; Feldt, 1965), sus propiedades estadísticas (Angoff, 1953; Lord, 1955; Pandey & Hubert, 1975; Callender & Osburn, 1979; Feldt, Woodruff & Salih, 1987; Zimmerman, Zumbo & Lalonde, 1993), su relación con el análisis factorial clásico (Kaiser & Caffrey, 1965; Bentler, 1968; Heise & Bohrnstedt, 1970; Armor, 1974; Greene & Carmines, 1979; Bacon, Sayer & Young, 1995) y desde los modelos de ecuaciones estructurales (Fleishman & Benson, 1987; Reuterberg & Gustafsson, 1992), entre otros aspectos.

Alfa de Cronbach en los programas estadísticos convencionales

Además del permanente interés teórico que el coeficiente ha despertado entre los especialistas, en la práctica, su uso se ha extendido ampliamente entre los investigadores. Por tal razón, se han desarrollado herramientas que permiten realizar el análisis de forma automatizada, existiendo una gran variedad de programas informáticos que incluyen el cálculo de a entre sus opciones de análisis. Dentro del software disponible, los programas más utilizados son los denominados “paquetes estadísticos de propósitos múltiples”, como SPSS, Statistica o SAS.

La ventaja de estos programas es que pueden utilizarse para desarrollar procesos completos de gestión y tratamiento de datos, proporcionando al investigador una amplia gama de métodos, modelos y herramientas de análisis. No obstante, también pueden señalarse algunas limitaciones en este tipo de software. En primer lugar, se trata de productos comerciales, por lo que se plantean ciertas limitaciones de acceso para aquellos usuarios o instituciones que disponen de recursos económicos limitados o escasos. En segundo lugar, el diseño lineal de los programas (imput-análisis-output) conlleva ciertas dificultades en la ejecución de determinadas tareas de análisis. Especialmente en momentos exploratorios, donde se requieren procesos basados en acciones cíclicas o iterativas por parte del analista (Young & Smith, 1991). Este punto es importante ya que los procesos iterativos son algo común en la dinámica del análisis psicométrico. Por ejemplo, cuando se realizan comparaciones sucesivas de escalas basadas en sub conjuntos de ítems, sea para maximizar la fiabilidad o reducir la longitud de la prueba. En los programas disponibles, cada “ciclo” supone la ejecución completa de un nuevo análisis, lo cual lentifica la ejecución de la tarea y dificulta la interpretación y comparación de resultados. Por último, los programas convencionales solo proporcionan, para estos análisis, salidas numéricas en formato texto (listado). Cuando se trabaja con pruebas extensas estas salidas pueden ser excesivamente largas y difíciles de interpretar. Además, en momentos exploratorios, puede ser importante interpretar los índices o resúmenes estadísticos sin perder en ese proceso otros detalles de la información, como las distribuciones empíricas de los ítems o los patrones de respuesta de los sujetos. En todo caso, mediante salidas numéricas, resultará difícil lograr el equilibrio necesario entre resumir y perder información (Yu & Behrens, 1995). En este sentido, debe reconocerse la utilidad comparativa de los métodos gráficos en determinadas situaciones de análisis, sobre todo, en la categoría de los denominados gráficos dinámicos o interactivos (Cleveland & McGill, 1988).

Propuesta de una herramienta basada en gráficos dinámicos

Algunas de las limitaciones mencionadas pueden superarse utilizando entornos estadísticos y arquitecturas de programación menos convencionales. En este trabajo se propone un software de este tipo, un módulo experimental que forma parte de un proyecto de desarrollo de métodos psicométricos basados en gráficos dinámicos. El módulo, diseñado para realizar análisis de consistencia interna mediante el modelo Alfa de Cronbach, tiene algunas características que los diferencian claramente de los programas disponibles. En primer lugar, se trata de una herramienta gratuita, abierta y extensible, integrada a un programa estadístico mayor de libre distribución denominado ViSta “The Visual Statistics System” (Young, 2002). En segundo lugar, el módulo proporciona salidas con gráficos dinámicos diseñados para visualizar los resultados del análisis de consistencia interna y otras propiedades psicométricas de los ítems y el test. Por último, con respecto a la ejecución del análisis, el programa ofrece un entorno flexible y más apropiado para realizar sesiones de análisis que involucran actividades cíclicas o iterativas. Esto último se logra utilizando una arquitectura gráfica no convencional denominada “Spreadplots” (Young, Valero Mora, Faldowsky & Bann, 2000). A continuación, se describe con mayor detalle el fundamento metodológico de la propuesta y el funcionamiento del sistema.

 

Método

Gráficos dinámicos

El aspecto metodológico más distintivo de la herramienta es la utilización de gráficos estadísticos dinámicos, interactivos o de manipulación directa (Cleveland & McGill, 1988). Los gráficos dinámicos son imágenes o representaciones estadísticas que pueden cambiar en tiempo real como respuesta a una acción directa del usuario. Estas acciones se aplican al gráfico de forma sencilla, utilizando el ratón o el teclado de la computadora, y producen una respuesta gráfica inmediata. La respuesta del gráfico depende del tipo de representación y de la acción que el usuario ha realizado, pudiendo tratarse de movimientos, animaciones o variaciones producidas por relaciones con otros gráficos.

Entre las características de los gráficos dinámicos, una de las más interesantes es la propiedad de ‘ligado’, o sea, la posibilidad de programar los gráficos de modo que estos se relacionen mediante vínculos empíricos, algebraicos o estadísticos (Young et al., 2000). Cuando dos gráficos están ligados, las manipulaciones que el usuario ejerce sobre uno de ellos producen cambios instantáneos en el otro. La ventaja de esta metodología es que permite combinar diferentes gráficos para obtener visualizaciones más detalladas y completas de la estructura de los datos (Wills, 2000), lo cual resulta de gran utilidad cuando se trata de visualizar datos o modelos multivariados o comparar resultados de diferentes modelos.

Es llamativo que a pesar de sus ventajas comparativas, los gráficos dinámicos no hayan sido incorporados en toda su extensión por los programas estadísticos comerciales. Sin embargo, existe software experimental y de libre distribución basado íntegramente en la utilización de este tipo de gráficos, como ViSta y ARC (Cook & Weisberg, 1999). Estos programas, escritos en lenguaje LispStat (Tierney, 1990), proporcionan poderosos recursos de visualización basados en gráficos dinámicos; además, pueden ser utilizados como plataforma para el desarrollo de nuevos métodos.

Gráficos dinámicos extendidos “spreadplots”

Los mencionados “spreadplots” o gráficos extendidos maximizan la utilidad de los gráficos dinámicos utilizando sus capacidades de ligado como elemento básico de visualización. Un “spreadplot” es una estructura gráfica compuesta de múltiples gráficos dinámicos ligados entre sí, diseñados para visualizar de forma interactiva determinado tipo de datos, transformación o modelo estadístico. Eventualmente, los spreadplots pueden ser utilizados como entorno para ejecutar los análisis, siendo particularmente útiles en el desarrollo de tareas iterativas.

En este trabajo se extiende la metodología de los spreadplots al caso del análisis psicométrico, introduciendo una herramienta diseñada específicamente para aplicar y visualizar análisis de consistencia interna mediante el modelo Alfa de Cronbach. La herramienta está pensada para asistir al analista en la selección de ítems que maximicen la consistencia interna de la prueba, sin perder en ese proceso otros aspectos importantes para el análisis, tales como las distribuciones de los ítems, los perfiles de respuesta de los sujetos o la distribución de las puntuaciones totales. A continuación se discute en detalle el funcionamiento de la herramienta y se presenta un ejemplo de aplicación.

 

Descripción del programa y ejemplo de aplicación

Características técnicas y capacidades generales

El módulo ha sido desarrollado en lenguaje XLISP-STAT y funciona integrado a ViSta 7.5 para Windows (95 o superior). El programa no corre bajo Windows 3.x y tampoco está disponible actualmente para los entornos Macintosh y Unix, aunque existen versiones previas de ViSta que funcionan en tales plataformas.

En términos generales, el módulo permite importar, crear, editar, gestionar y transformar los datos para el análisis; computar y reportar los resultados del análisis en formato texto convencional; visualizar resultados y utilizar gráficos para realizar nuevos análisis; y, finalmente, guardar los resultados como nuevos datos para posteriores análisis. A continuación, se describen esas capacidades básicas.

Datos

Los datos para el análisis deben estar dispuestos en una matriz con variables numéricas. En esa matriz, las filas representan sujetos y las columnas son ítems de una escala cuyos valores brutos se computarán como suma simple de los ítems. Los datos pueden ser creados utilizando la planilla de datos de ViSta o importarse en formato texto desde otros programas. La Figura 1 muestra una imagen de ViSta con un archivo de datos apropiados para el análisis. Se trata de datos parciales provenientes de un estudio sobre satisfacción laboral en profesionales de salud. En este estudio se administró un ‘Inventario de Satisfacción Laboral’ (ISL) compuesto por 16 ítems tipo likert (Terroni, 2002). En este archivo, las filas representan los sujetos del estudio y las columnas los ítems del ISL. En la imagen puede observarse parcialmente la planilla de datos y la interfaz de usuario del programa ViSta.

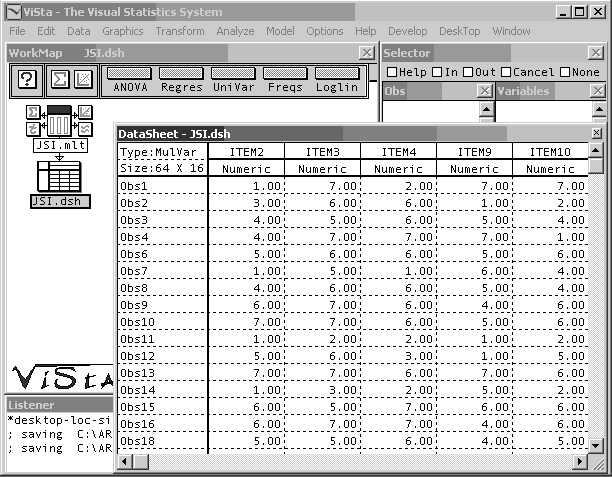
Figura 1 - Imagen parcial de un archivo de datos en el programa ViSta “The Visual Statistics System”.

Reporte

Seleccionando la opción Item Analysis en el menú principal de ViSta, y dentro de ella la alternativa Cronbach’s Alpha, el programa computará el coeficiente y varios estadísticos para los ítems y la escala. El resultado puede reportarse en formato numérico o visualizarse mediante un spreadplot. El reporte numérico completo incluye estadísticos descriptivos para los ítems y las puntuaciones totales; matrices de correlación entre ítems e ítems-total; estimaciones de errores de medida e información sobre el modelo Alfa de Cronbach. La Figura 2 muestra una imagen parcial de los resultados obtenidos para los datos del ejemplo, donde se lista el valor del coeficiente a (.85), el error estándar de medida (6.49), el error estándar de estimación (5.99) y una tabla de resultados que muestra los cambios en los estadísticos del ISL si cada ítem fuera eliminado del mismo. La últimacolumna de esa matriz indica el cambio en el valor de a si los ítems son eliminados (Alpha-if). Puede observarse que al eliminar el ítem 1 del inventario el valor de a se incrementa a .863. El caso contrario se presenta para el ítem 10, cuya eliminación haría decrecer a a .834. Esta información es útil al momento de depurar la escala o seleccionar grupos óptimos de ítems.

No obstante, cuando el número de ítems es grande o la escala se encuentra en una etapa incipiente de desarrollo, puede ser más ágil utilizar el spreadplots del análisis para explorar los cambios que se producen al eliminar o agregar ítems. Como se detalla a continuación, en el spreadplot la selección y eliminación de ítems resulta sencilla de ejecutar. Además, el analista podrá disponer de información detallada sobre el comportamiento de los ítems, los perfiles de respuesta de los sujetos y el comportamiento de la escala total.

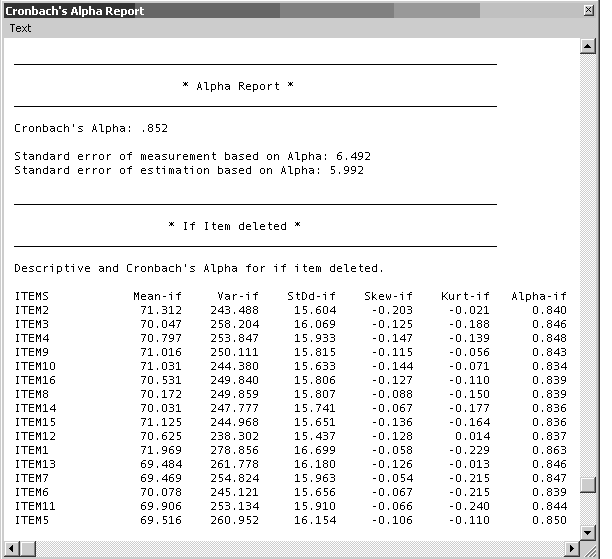
Figura 2- Imagen parcial del listado de resultados para el análisis de consistencia interna aplicado a los datos del ejemplo.

Visualización y análisis gráfico

El spreadplot del análisis está compuesto por seis ventanas gráficas ligadas que permiten visualizar resultados y ejecutar nuevos análisis (Figuras 3 y 4). En estos spreadplots los gráficos están ligados empíricamente, de modo que al seleccionar un sujeto en cualquier gráfico el mismo se iluminará automáticamente en el resto de los gráficos. Un vínculo más sofisticado existe entre la Lista de los ítems (a la izquierda del spreadplot) y el resto de las ventanas: si bien por defecto el spreadplot se inicia con el modelo de escala computada con todos los ítems (Figura 3), al seleccionar un nuevo conjunto en la Lista de ítems, el Spreadplot se acomoda a dicha la selección (Figura 4). La selección de los ítems en la lista se realiza utilizando los métodos convencionales del ratón de la PC.

Para entender la naturaleza y funcionamiento del método, describiremos con mayor detalle la estructura básica del spreadplot, utilizando para ello las Figura 3 y 4 correspondientes a los datos del ejemplo. El gráfico incluye seis ventanas, las cuales se comentan a continuación.

Lista de los ítems. La ventana izquierda muestra los nombres o etiquetas de los ítems y funciona como panel de control y selección de los mismos. Eso significa que si se selecciona con el ratón un conjunto de ítems en la lista, el resto de los gráficos se adecuan a dicha selección. Los ítems seleccionados constituyen el input para calcular una nueva escala y analizar su fiabilidad. En la Figura 4 puede verse una selección en la cual se han eliminado los ítems 4, 1, 13, 7 y 5, de modo que el spreadplot permite visualizar los resultados para la escala sin esos ítems.

Lista de las observaciones. La ventana izquierda presenta los nombres o etiquetas de los sujetos del análisis y funciona como panel de control y selección. Al seleccionar un sujeto o conjunto de sujetos en dicha lista estos se identificarán automáticamente en el resto de los gráficos. La lista resulta de utilidad cuando se quiere visualizar el comportamiento específico de un sujeto o conjunto de sujetos. En la Figura 3 se puede observar que el sujeto 8 (Obs8) ha sido seleccionado y aparece identificado en el histograma de la prueba total y en el gráfico de cajas paralelas correspondiente a los ítems.

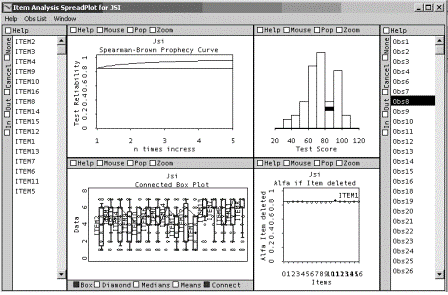
Figura 3 - Imagen de spreadplot para visualizar los resultados del análisis aplicado a los datos del ejemplo.

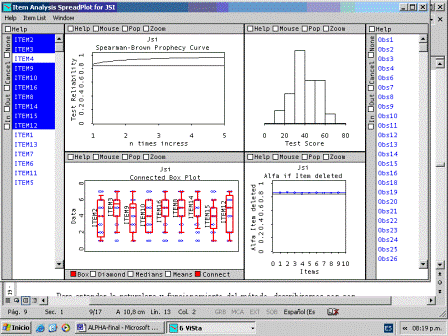
Figura 4 - Imagen del spreadplot del análisis habiendo modificado la selección de ítems en la “Lista de Ítems”.

Gráfico de fiabilidad. El gráfico superior central derecho esta diseñado para visualizar la fiabilidad de la escala y evaluar como el incremento en su longitud podría incrementar dicha propiedad. En esta representación, se utiliza la fórmula de Spearman-Brown, que relaciona longitud y fiabilidad bajo el supuesto de que los ítems son medidas paralelas:

La fórmula profetiza el coeficiente de fiabilidad R que tendrá una prueba con fiabilidad inicial r si se aumenta o disminuye su longitud n veces, permitiendo determinar cuantos ítems paralelos habría que añadir o quitar para lograr un determinado valor de fiabilidad. Esa función crece rápidamente y se desacelera siendo asintótica para r = 1, como se puede ver en el gráfico. La línea gris (horizontal) representa la fiabilidad de la escala computada para todos los ítems originales, estimada mediante el coeficiente a. La línea negra representa la profecía de Spearman-Brown para incrementos de n veces en la longitud de la escala, con origen en la fiabilidad de la escala basada en todos los ítems (por defecto). Al seleccionar cualquier conjunto de ítems esa función se ajusta a la escala computada sobre los ítems seleccionados. Comparando dicha función con la línea de base original se pueden evaluar los cambios en la fiabilidad de la escala a través de los subconjuntos de ítems. Si se compara el gráfico de la Figura 3 con el homólogo de la Figura 4, puede observarse un incremento en la fiabilidad de la prueba basada en el subconjunto de ítems seleccionados.

Histograma de frecuencias para la escala total. La ventana central superior izquierda muestra un histograma con la distribución de frecuencias del test objeto de análisis, en nuestro caso el ISL. El gráfico permite visualizar la distribución de la prueba y examinar cambios a través de diferentes grupos de ítems. El histograma está ligado empíricamente con el gráfico de cajas paralelas y la lista de observaciones. Como puede verse en la Figura 3, el elemento “iluminado” indica la posición en la escala total que ocupa el sujeto “Obs8” seleccionado en la lista de observaciones. Alternativamente, el usuario puede ejercer selecciones directas sobre el histograma; por ejemplo, seleccionar el conjunto de sujetos de “mayor” o “menor” rendimiento.

Gráfico de puntos, cajas y diamantes paralelos para los ítems. La ventana inferior central izquierda es un gráfico de puntos, cajas y/o diamantes paralelas para los ítems. Cada caja o diamante representa la distribución empírica de un ítem, los sujetos son posicionados como puntos de acuerdo a su correspondiente valor de respuesta (de 1 a 7 según los valores originales de los ítems del ISL). Por defecto, el gráfico se inicia con todos los ítems y cambia según la selección efectuada en la lista de ítems. En la Figura 3, puede verse la representación con todos los ítems, mientras que en la Figura 4 solo se muestra los ítems seleccionados en la lista. Los diamantes están conectados entre sí y con el resto de las ventanas por las observaciones (sujetos), de modo que al seleccionar un punto sujeto (o conjunto de puntos sujetos) se obtendrá su perfil de respuesta y su posición en la escala total (histograma), como se muestra para el sujeto 8 en la Figura 3. Este gráfico posee gran utilidad desde el punto de vista exploratorio, permite analizar y comparar las distribuciones de los ítems, visualizar patrones de respuesta, detectar valores fuera de rango e identificar clusters entre otras utilidades.

Gráfico de fiabilidad si el ítem es eliminado. Este diagrama, ubicado en la parte inferior central derecha del spreadplot, muestra cómo el coeficiente Alfa es afectado por cada uno de los ítems. Se trata de una representación gráfica equivalente a la columna ‘Alpha-if’ del reporte numérico. El eje horizontal representa el número del ítem según su posición en la escala y el eje vertical representa el valor de a si el ítem es eliminado. Los ítems son representados como puntos azules y están etiquetados con sus respectivos nombres. La línea horizontal en negro indica el valor de a basado en todos los ítems y sirve como referencia para comparar los valores de Alfa que se obtendrían si los ítems fueran eliminados de la escala. En la Figura 3 puede verse que el ítem 1 se ubica por encima de la línea negra, lo cual indica que su eliminación incrementará el valor de a, como ya se ha comentado. Cuando el usuario aplica una nueva selección en la lista de ítems se muestra además una línea horizontal (azul) que representa el valor de a para los ítems seleccionados, la cual puede compararse con el modelo original basado en todos los ítems. Obsérvese que en la Figura 4 se ha logrado una selección de ítems cuya consistencia interna es superior a la original, puesto que la línea azul (superior) se ubica por encima de la línea negra (inferior).

Los gráficos anteriores admiten diversas manipulaciones directas, apropiadas para que el analista pueda interactuar con cada una de las representaciones según sus necesidades. No obstante, en este trabajo solo queremos destacar la funcionalidad del spreadplot como estructura gráfica única. En ese sentido, el aspecto más interesante es que los distintos gráficos estén ligados empírica y estadísticamente. De ese modo, la comparación secuencial de las propiedades de la escala y de los ítems resulta sumamente sencilla de ejecutar.

Crear datos

Finalmente, es posible crear y guardar resultados como nuevos archivos de datos, los cuales pueden utilizarse en posteriores análisis. Estos datos pueden ser puntuaciones totales brutas o normalizadas, intervalos de confianza para puntaciones observadas, etc. (ver Figura 5). Otras transformaciones específicas pueden ser aplicadas sobre el archivo de datos utilizando las funciones del menú “Transformaciones” de Vista.

Figura 5 - Imagen del cuadro del diálogo con las opciones para la creación automática de datos.

 

Discusión

Entre los coeficientes de estimación de fiabilidad basados en el método de consistencia interna, Alfa de Cronbach es el más utilizado por los investigadores. Por esta razón, los paquetes estadísticos más conocidos, como SPSS, Statistica o SAS, lo incluyen entre sus opciones de análisis. En este trabajo se ha presentado una herramienta informática alternativa, que permite aplicar Alfa de Cronbach de una manera más dinámica y flexible que en el software convencional. El mayor dinamismo y flexibilidad del software se logra complementando los reportes numéricos con salidas gráficas interactivas, desde donde pueden ejecutarse nuevos análisis y visualizarse los resultados obtenidos.

Como metodología básica de trabajo se ha utilizado la arquitectura gráfica de los spreadplots, la que se ha aplicado al desarrollo de una opción de análisis para Alfa de Cronbach. El resultado final es una interface gráfica que permite realizar análisis de fiabilidad de forma interactiva y visualizar los resultados en tiempo real. Mediante dicho método, se agiliza la comparación secuencial de escalas basadas en subconjuntos de ítems y se facilita la selección de ítems que maximicen la consistencia interna de la prueba. A su vez, el usuario dispone de información gráfica relacionada con otros aspectos importantes del análisis, como las distribuciones de los ítems, los perfiles de respuesta de los sujetos o la distribución de las puntuaciones totales de la prueba. La ventaja comparativa con respecto a los entornos convencionales es el mayor dinamismo que el Spreadplot otorga a la tarea de análisis y su mejor prestación en términos exploratorios.

Cabe señalar que la aplicación Alfa de Cronbach, tal como la hemos presentado, forma parte de un módulo psicométrico mayor integrado a su vez al programa ViSta. Este software psicométrico, basado en gráficos dinámicos, permite analizar ítems y test desde la perspectiva de la Teoría Clásica de los Tests (TCT), incluyendo métodos estadísticos descriptivos para ítems y puntuaciones totales, estimaciones de fiabilidad, análisis de dimensionalidad y creación automatizada de puntajes. En el futuro, se espera ampliar las capacidades del software incluyendo procedimientos de corrección automatizada de pruebas y modelos basados en Teoría de Respuesta al Ítem.

 

Referencias

Angoff, W. H. (1953). Test reliability and effective test length. Psychometrika, 18 (1), 1-14.        [ Links ]

Armor, D. J. (1974). Theta reliability and factor scaling. En: Costner, H. L. (Eds.). Sociological Methodology. San Francisco: Jossey-Bass, p. 17-50.        [ Links ]

Bacon, D. R., Sayer, P. L. & Young, M. (1995). Composite reliability in structural equations modeling. Educational and Psychological Measurement, 55 (4), 394-406.        [ Links ]

Bentler, P. M. (1968). Alpha-maximized factor analysis (alphamax): its relation to alpha and canonical factor analysis. Psychometrika, 33 (3), 335-345.         [ Links ]

Brown, W. (1910). Some experimental results in the correlation of mental abilities. British Journal of Psychology, 3 (3), 296-322.        [ Links ]

Callender, J. C. & Osburn, H. G. (1979). An empirical comparison of coefficient alpha, Guttman’s Lambda-2, and MSPLIT maximized split-half reliability estimates. Journal of Educational Measurement, 16 (1), 89-99.        [ Links ]

Cleveland, W. S. & McGill, M. E., (1988). Dynamic Graphics for Statistics. Belmont, CA: Wadsworth.        [ Links ]

Cleveland, W. S. (1993). Visualizing Data. Murray Hill, New Jersey: AT&T Bell Lab.        [ Links ]

Cook, R. D. & Weisberg, S. (1999). Arc [software]. [On-line] Disponible: URL: http://www.stat.umn.edu/arc/software.html        [ Links ]

Cronbach, L. J. (1943). On estimates of test reliability. The Journal of Educational Psychology, 34 (4), 485-494.        [ Links ]

Cronbach, L. J. (1946). A case study of the split-half reliability coefficient. The Journal of Educational Psychology, 37 (3), 473-480.        [ Links ]

Cronbach, L. J. (1947). Test “reliability”: its meaning and determination. Psychometrika, 12 (1), 1-16.        [ Links ]

Cronbach, L. J. (1951). Coefficient alpha and the internal structure of tests. Psychometrika, 16 (2), 297-334.        [ Links ]

Feldt, L. S. (1965). A test of the hypothesis that Cronbach’s alpha or Kuder-Richardson coefficient twenty is the same for two tests. Psychometrika, 34 (3), 363-373.        [ Links ]

Feldt, L. S., Woodruff, D. J. & Salih, F. A. (1987). Statistical inference for coefficient alpha. Applied Psychological Measurement, 11 (1), 93-103.        [ Links ]

Fleishman, J. & Benson, J. (1987). Using LISREL to evaluate measurement models and scale reliability. Educational and Psychological Measurement, 47 (5), 925-939.        [ Links ]

Greene, V. L. & Carmines, E. G. (1979). Assessing the reliability of linear composites. En: Schuessler, K. (Ed.). Sociological Methodology. San Francisco: Jossey-Bass, p. 160-175.        [ Links ]

Heise, D. R. & Bohrnstedt, G. W. (1970). Validity, invalidity and reliability. En: Borgatta, E. F. & Bohrnstedt, G. W. (Eds.), Sociological Methodology. San Francisco: Jossey-Bass, p. 104-129.        [ Links ]

Kaiser, H. & Caffrey, J. (1965). Alpha factor analysis. Psychometrika, 30 (1), 1-14.        [ Links ]

Kuder, G. F. & Richardson, M. W. (1937). The theory of the estimation of test reliability. Psychometrika, 2 (1), 151-160.        [ Links ]

Lord, F. M. (1955). Sampling fluctuations resulting from the sampling of test ítems. Psychometrika, 20 (1), 1-22.        [ Links ]

Novick, M. R. & Lewis, C. (1967). Coefficient alpha and the reliability of composite measurements. Psychometrika, 32 (1), 1-13.        [ Links ]

Pandey, T. N. & Hubert, L. (1975). An empirical comparison of several interval estimation procedures for coefficient alpha. Psychometrika, 40 (1), 169-181.        [ Links ]

Reuterberg, S. & Gustafsson, J. E. (1992). Confirmatory factor analysis and reliability: testing measurement model assumptions. Educational and Psychological Measurement, 52 (4), 795-811.        [ Links ]

Spearman, C. (1910). Correlation calculated from faulty data. British Journal of Psychology, 3 (2), 271-295.        [ Links ]

Terroni, N. (2002). El nivel de satisfacción de los trabajadores de una institución de salud pública. Su relación con el ausentismo y la salud psicofísica. (Tesis de Maestría en Psicología Social). Argentina: Facultad de Psicología de la UNMdP.        [ Links ]

Tierney, L. (1990). Lisp-Stat An Object-Oriented Environment for Statistical Computing and Dynamic Graphics. New York: John Wiley & Sons.        [ Links ]

Wills, G. (2000). Linked Data Views. Statistical Computing and Statistical Graphics Newsletter, 10, 20-24.        [ Links ]

Young, F. (2002). ViSta “The Visual Statistics System”. [computer software] [On-line] Disponible: URL: http://forrest.psych.unc.edu/research/index.html        [ Links ]

Young, F. & Smith, J. (1991). Towards a Structured Data Analysis Environment: A Cognition-Based Design. En: Buja, A. & Tukey, P. A. (Eds.). Computing and Graphics in Statistics, New York: Springer-Verlag, 36, 253-279.        [ Links ]

Young, F., Valero Mora, P., Faldowsky, R. A. & Bann, C. (2000). Spreadplots. The Visual Statistic project, Report Number 2000-4. L. L. Thurstone Psychometric Lab, Univ. N. Carolina, Chapel Hill, May 2000.        [ Links ]

Young, F., Ledesma, R., Molina, G., Valero, P. & Llorens, A. (2001). ViSta “The Visual Statistics System”. Revista Métodos de Encuesta, 3 (1), 127-133.        [ Links ]

Yu, Ch. H. & Behrens, J. (1995). Applications of Multivariate Visualization to Behavioral Sciences. Behavior Research Methods, Instruments and Computers, 27 (2), 264-271.        [ Links ]

Zimmerman, D. W., Zumbo, B. D. & Lalonde, C. (1993). Coefficient alpha as an estimate of test reliability under violation of two assumptions. Educational and Psychological Measurement, 5 (1), 33-49.        [ Links ]

 

 

Recebido em 25/09/2002
Revisado em 06/11/2002
Aceito em 10/12/2002

 

 

¹ Endereço para Correspondência:
Funes 3280 - cuerpo V - nivel 3 (7600) Mar del Plata - Argentina
E-mail: rledesma@mdp.edu.ar
^* Rubén Ledesma - Becario en la Categoría Posdoctoral por el Consejo Nacional de Investigaciones Científicas y Tecnológicas - CONICET (Argentina). Docente e Investigador de la Facultad de Psicología de la Universidad Nacional de Mar del Plata. Miembro del Grupo de Investigación en “Psicología Cognitiva y Educacional”.
^** Gabriel Molina Ibáñez - Profesor Titular Regular con dedicación Exclusiva en el Departamento de Metodología de las Ciencias del Comportamiento de la Facultad de Psicología de la Universitat de València (España). Miembro del Grupo de Investigación: “Proceso de Datos en Psicología”.
^*** Pedro Valero Mora - Profesor Titular Regular con dedicación Exclusiva en el Departamento de Metodología de las Ciencias del Comportamiento de la Facultad de Psicología de la Universitat de València (España). Miembro del Grupo de Investigación: “Proceso de Datos en Psicología”.