ORIGINAL RESEARCH

 

Heart rate dynamics by novel chaotic globals to HRV in obese youths

 

 

Franciele Marques Vanderlei^I; Luiz Carlos M. Vanderlei^I; David M. Garner^II

^IFranciele Marques Vanderlei & Luiz Carlos M. Vanderlei, Department of Physiotherapy, UNESP - Univ Estadual Paulista - Presidente Prudente, São Paulo, Brazil
^IIDepartment of Biological and Medical Sciences, Faculty of Health and Life Sciences, Oxford Brookes University, Gipsy Lane, Oxford OX3 0BP, United Kingdom

 

 

---

ABSTRACT

OBJECTIVE: this study aimed to assess the heart rate dynamics in young obese subjects by novel chaotic globals to HRV
METHODS: eighty-six young subjects were distributed in two equal groups (n = 43) according to the nutritional status: obese and control following Body Mass Index. For the analysis of HRV indexes, the heart rate was recorded heartbeat to heartbeat with the young resting in dorsal (prone) position for 30 minutes
RESULTS: after Anderson-Darling and Lilliefors tests, the data was deemed non-normal. So, Kruskal-Wallis test of significance was applied for the statistical analysis, level set at (p < 0.01). Principal Component Analysis (PCA) identified two components represented 100% of total variance. The algorithm which applies all three parameters is suggested as the most influential and statistically very significant at the level (p < 0.001); it also elevates the chaotic response
CONCLUSION: youth obesity increases the chaotic response. The reasons for the study include quantitative assessment to allow effective dietary, pharmacological or even surgical intervention in the condition

Key words: obese youths, complexity, chaotic globals, multi-taper method, high spectral.

---

 

 

INTRODUCTION

Heart rate recorded by Electrocardiograph (ECG) can oscillate in a chaotic and complex way^1-4. Traditionally, methods derived from statistical physics and thermodynamics have allowed researchers to study such systems⁵. Heart rate variability (HRV) is a cheap and non-invasive method of monitoring the sympathetic and parasympathetic ratio. In addition, the HRV is considered a functional marker of human development⁶ and can be used to identify phenomena related to the autonomic nervous system (ANS) in healthy subjects and patients with diseases^7-9. High HRV is a signal characterizing a healthy person with efficient autonomic mechanisms. Whilst lower HRV is frequently an indicator of atypical and insufficient adaptation of the ANS; causing the subject low physiological function.

In general spectral entropy¹⁰ and techniques termed spectral detrended fluctuation analysis (sDFA) and spectral multi-taper method (sMTM) are based on 'chaotic globals'¹¹. Spectral entropy applies the standard Shannon entropy^12,13 algorithm to a Welch power spectrum¹⁴. Whereas, sDFA applies the DFA algorithm in the same manner to the same power spectrum. This attempts to overcome the disadvantage of limited time-series; since only phase information is misplaced. sMTM applies the responsive and adaptive multi-taper method (MTM)^15,16 to the data. sMTM is the value of the area between the MTM spectrum and the baseline. If spectral entropy and sDFA previously applied to Welch power spectra were applied to multi-taper spectra which do not have fixed windows but are adaptive and sensitive - the results may have greater chaotic parametric response. We would then term these parameters high spectral entropy (hs Entropy) and high spectral detrended fluctuation analysis (hsDFA).

These computations are useful clinically in patients undergoing surgery^17,18; or unable to communicate distress as in sleep apnea¹⁹ or dyspnea^20-22 and the potential risk associated with diabetes mellitus²³ and obese children²⁴ has been studied using these methods. This study aimed to assess the heart rate dynamics in young obese subjects by novel chaotic globals to HRV. Understanding the obesity, causal factors, consequences and repercussions, it is important and reinforces its status as a public health problem, and such studies are essential to establish the intensity of the changes promoted by obesity and stimulating programs of prevention and treatment of obesity include changes in lifestyle, particularly changes in eating habits and regular physical activity, which come against the precepts of public health that works to improve health and quality of life through prevention and treatment of disease and through promotion of healthy behaviors²⁵.

 

METHODS

Population and Sample

In this study, we reviewed data of 86 young volunteers of both sexes, with a mean age of 20.58 ± 1.48 years. The subjects were assigned as one of two equal groups: obese (23 male and 20 female; 20.45 ± 1.57 years; 102.30 ± 20.82 Kg; 1.70 ± 0.10 m; BMI = 34.67 ± 3.87 Kg/m²) or control (22 male and 21 female; 20.70 ± 1.39 years; 62.89 ± 10.47 Kg; 1.68 ± 0.10 m; BMI = 21.91 ± 1.86 Kg/m²). The classification criteria adopted for the formation of the groups was the value of body mass index (BMI). Excluded from the study were the subjects who had at least one of the following features: smokers, drinkers (ANS stimulants), subjects who use narcotics, medications or presented any infections, metabolic diseases or known cardiorespiratory system diseases, which could affect the cardiac autonomic control.

All participants received explanations regarding the procedures and objectives of the study and upon agreement they signed a consent letter. The study received approval from the Ethics Committee of Institution (Proc. N° 11/2011).

Data Collection

The data collection was undertaken in a room with the temperature between 21°C and 23°C and relative humidity between 40 and 60%. The subjects were instructed not to drink alcohol and caffeine for 24 hours before evaluation. Datasets were collected on an individual basis, between 8:00 and 11:00 a.m. to minimize the interference of the circadian rhythm. All procedures necessary for the data collection were explained on an individual basis and the subjects were instructed to remain at rest and avoid talking during the collection. Prior to initiating the experimental procedure, the participants were identified by age, height, weight and BMI. Anthropometric measurements were obtained following the standard recommendations proposed by Lohman et al.²⁶ BMI was computed using the formula: weight (kg)/height² (m).

The heart monitor strap was placed on the thorax over the distal third of the sternum. The heart rate receiver of the Polar S810i monitor (Polar Electro OY, Kempele, Finland) was placed on the wrist. This equipment has been previously validated for beat-by-beat measurements and, the use of the results for HRV analysis²⁷. The participants were instructed to recline in the face-up position on a bed and rest with spontaneous breathing for 30 minutes. For the HRV analysis, the heart rate was recorded beat-by-beat throughout the period at a sampling frequency of 1000 Hz. For data analysis, 1000 consecutive RR intervals were applied, after digital filtering and complemented with a manual procedure for the elimination of premature ectopic heartbeats and artifacts. Only series with more than 95% sinus rhythm were included²⁸. All measurements were performed by fully trained staff.

Chaotic global parameters

Multi-Taper Method: Power Spectrum

Disparagement exists in previous studies with respect to chaotic global parameters. Analysis could be more responsive if we applied the Shannon entropy and DFA algorithms to the multi-taper spectrum rather than the Welch power spectrum. Thus the spectra applied in all three chaotic global parameters would be the same.

MTM^15,16 provides a useful tool for spectral estimation and signal reconstruction, of a time series of a spectrum that may contain broadband and line components. MTM is non-parametric since it does not apply an a priori, parameter dependent model of the process that generated the time series under analysis. MTM reduces the variances of spectral estimates by using a small set of tapers. Data is pre-multiplied by orthogonal tapers created to minimize the spectral leakage owing to the finite length of the time series. A set of independent approximations of the power spectrum is calculated. Functions known as Discrete Prolate Spheroidal Sequences (DPSS) are a set of functions which optimize the tapers. They are defined as eigenvectors of a Rayleigh-Ritz minimization problem.

MTM has the following features (1) Efficient in detecting periodic components; (2) A random signal may generate many false peaks which may or may not be significant; (3) There are two ways of testing the spectrum (red-noise²⁹ and harmonic tests).

Chaotic Globals

High spectral entropy is a function of the irregularity of amplitude and frequency of the power spectrums peaks. It is derived by applying Shannon entropy^12,13 to the MTM power spectrum (Figure 1).

This output is then normalized so that the sum of the magnitude is equal to unity; giving a normalized power spectrum. We then calculate an intermediate parameter which is the median Shannon entropy of the value obtained from three different power spectra using the MTM power spectra under three test conditions: a perfect sine wave, uniformly distributed random variables, and finally the experimental oscillating signal. These values are then again normalized mathematically so that the sine wave gives a value of zero, uniformly random variables give unity, and the experimental signal between zero and unity. It is this final value that corresponds to high spectral entropy.

The standard DFA algorithm^30,31 can be applied to datasets where statistics such as mean, variance and autocorrelation vary with time. To obtain hsDFA we calculate the spectral adaptation in exactly the same way as for high spectral entropy using a MTM power spectrum with the same settings; but DFA rather than Shannon entropy is the algorithm applied. Spectral Multi-Taper Method (sMTM) is founded on the increased intensity of broadband noise in power spectra generated by irregular and chaotic signals. sMTM is the area between the MTM power spectrum and the baseline (Figure 1).

Chaotic Forward Parameter

The parameter [CFPx 1-7] is referred to as Chaotic Forward Parameter for the functions 1 to 7 below where it is applied to non-obese and obese youth datasets. Since hsDFA responds to chaos in the opposite way to the others we subtract its value from unity when applying here. All three chaotic global values have equal weightings.

 

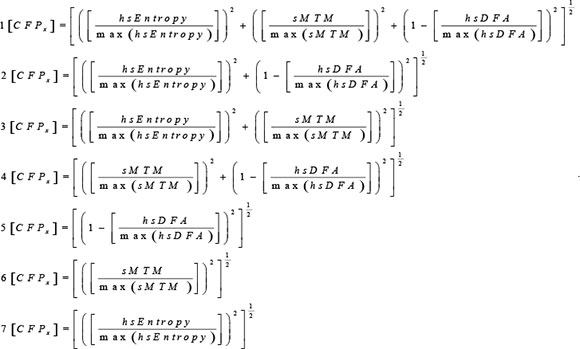
RESULTS

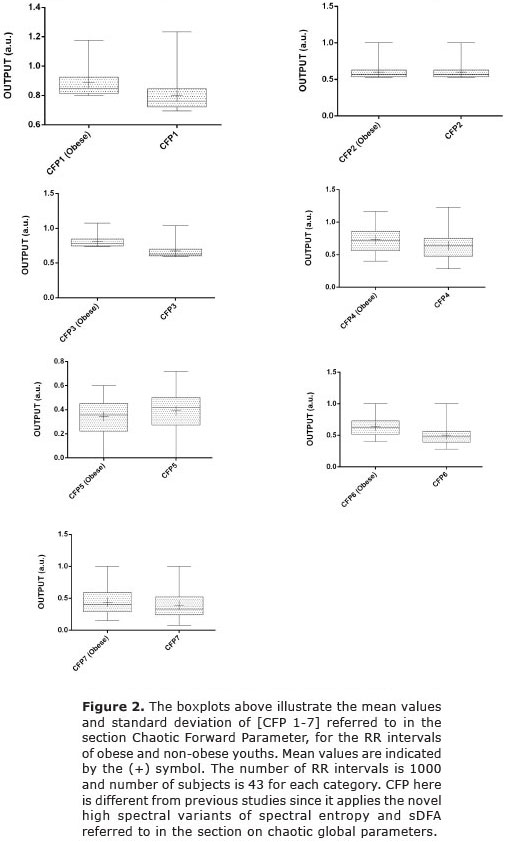
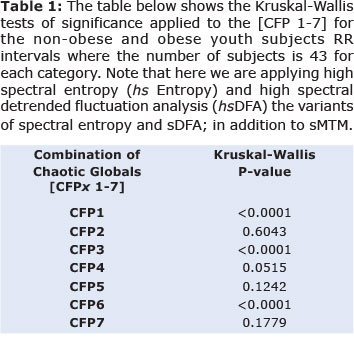
Results illustrate that there is a wide variation in both the mean values and standard deviation for both non-obese and obese youths (Figure 2). The algorithm computes a significant statistical result for three of the seven combinations (p < 0.01) (Table 1). These are combinations [CFPx 1, 3 & 6]. In all cases there is a increase in chaotic response when going from non-obese to obese youth subjects. There is a considerable improvement in significance applying high spectral techniques compared to a similar previous study²⁴.

 

 

 

 

DISCUSSION

Parametric statistics generally assume the data are normally distributed, hence the use of the mean as a measure of central tendancy. If we cannot normalize the data we should not compare means. To test our assumptions of normality we apply the Anderson-Darling³² test and the Lilliefors test³³. The Anderson-Darling test for normality applies an empirical cumulative distribution function. The Lilliefors test is useful in studies with small sample sizes. In the majority of cases the p<0.05; for both tests so we cannot pronounce that the observations follow a normal distribution. Therefore we have a probability plot of mainly non-normal data and so we must apply the Kruskal-Wallis³⁴ test of significance.

A multivariate technique termed principal component analysis (PCA) is beneficial here (Table 2). We have the values of [CFP] for seven groups for 43 subjects who are obese youths; hence a grid of 7 by 43 to be assessed. The First Principal Component (PC1) has a variance (eigenvalue) of 4.7758 and accounts for 68.2% of the total variance. The Second Principal Component (PC2) has an eigenvalue of 2.2185 accounting for 99.9% of cumulative total variance. PC2 accounting for 31.7% of its proportion of the variance. Therefore we can assume that most variance is acheived in the first two components. Only [CFPx 1, 3 & 6] are significantly different when tested by Kruskal-Wallis test (p < 0.01).

[CFPx1] has the First Principal Component (0.326) and the Second Principal Component (-0.470); whereas, [CFPx3] has the First Principal Component (0.149) and the Second Principal Component (-0.634). [CFPx6] has the First Principal Component (0.456) and the Second Principal Component (-0.049). Only the first two components need be considered due to the steep scree plot. [CFPx1] which applies all three chaotic globals techniques is the proposed best overall combination with regards to influencing the correct outcome. It is the most robust statistically when compared by p-value and PCA.

Additionally, there is evidence to apply [CFPx 1] as the most robust function as in the optimization problem posed by Garner and Ling¹¹. This in addition to forward problems in childhood obesity²⁴, diabetes mellitus²³ and chronic obstructive pulmonary disease³⁵.

We have developed three robust functions which can take short-times series of HRV and deduce which time-series is from a non-obese and obese youth subjects. There is a high level of significance for these algorithms (p<0.001). The first algorithm parameters is suggested as the most robust algorithm. Referring to Garner and Ling¹¹; which applies the Duffing, Brusselator and Lorenz models for the purposes of optimization; [CTF] a variant of [CFPx] is the most reliable objective function assessed by multivariate analysis. The same conclusion reached here as PCA is applied to the seven combinations of three parameters for obese youths. Here 100% of influence is achieved by the first two Principal Components. The combination with all three chaotic globals applied testing as most influencial algorithm.

By applying these novel functions there has been a significant increase in chaotic response of HRV for obese youths. In a previous study by Vanderlei²⁴ with obese children the same relationship was found. The relationship between obesity and complexity measures is useful in the risk assessment of diseases associated with youth obesity. It identifies severity from an inexpensive and reliable method of monitoring the ANS. This is helpful in treatments, such as determination of the level of dietary or pharmacological intervention especially in related dynamical diseases. Nevertheless, proceeding cautiously, since the subject's autonomic modulation may be critical. It is noted that there are other conditions which could cause the complexities correlation.

Further improvement for future study could involve modifying the DPSS of the MTM to optimize the final level of significance. In addition the weighting of the three chaotic global parameters could be adjusted since here they have only equal weightings of unity. It would also be statistically favourable to have larger, but equal datasets for both non-obese and obese youths.

 

CONCLUSIONS

Young obese subjects have increased the chaotic response and the algorithm which applies all three parameters (CFP1) is suggested as the most influential and statistically significant for this analysis. These results are atypical in that usually diseased states decrease the chaosity of the datasets and thus HRV. However there are still advantages of such analysis. These include quantitative assessment and suitable dietary, pharmacological or even surgical intervention in the condition.

Competing interests

The authors declare that there is no conflict of interests regarding the publication of this article

Acknowledgements

The authors are grateful to CNPq (National Council of Scientific and Technological Development) financial support for this study (Proc. n° 307361/2011-0).

 

REFERENCES

1. Seely AJ, Macklem P. Fractal variability: an emergent property of complex dissipative systems. Chaos. 2012; 22(1): 013108. DOI: http://dx.doi.org/10.1063/1.3675622        [ Links ]

2. Goldberger AL, West BJ. Chaos and order in the human body. MD Comput. 1992; 9(1): 25-34.         [ Links ]

3. Goldberger AL. Cardiac chaos. Science. 1989; 243(4897):1419.         [ Links ]

4. Elbert T, Ray WJ, Kowalik ZJ, Skinner JE, Graf KE, Birbaumer N.Chaos and physiology: deterministic chaos in excitable cell assemblies. Physiol Rev. 1994; 74(1):1-47.         [ Links ]

5. Ho MW. The rainbow and the worm: The physics of organisms. Singapore: World scientific, 2008.         [ Links ]

6. Abreu LC. Heart rate variability as a functional marker of development. J Hum Growth Dev. 2012; 22(3): 279-282.         [ Links ]

7. Souza NM, Rossi RC, Vanderlei FM, Vitor ALR, Bernardo AFB, Gonçalves ACCR, Ferreira LL, Vanderlei LCM. Heart rate variability in obese children. J Hum Growth Dev. 2012; 22(3): 328-333.         [ Links ]

8. Vanderlei FM, Rossi RC, Souza NM, Sá DA, Gonçalves TM, Pastre CM, Abreu LC, Valenti VE, Vanderlei LCM. Heart rate variability in healthy adolescents at rest. J Hum Growth Dev. 2012; 22(1): 173-178        [ Links ]

9. Vanderlei LCM, Pastre CM, Hoshi RA, Carvalho TD, Godoy MF. Basic notions of heart rate variability and its clinical applicability. Rev Bras Cir Cardiovasc. 2009; 24(2): 205-17. DOI: http://dx.doi.org/10.1590/S0102-76382009000200018        [ Links ]

10. Johnson RW, Shore JE. Which is the better entropy expression for speech processing: -S logS or log S? IEEE Trans Acoust. 1984; 32(1): 129-137.         [ Links ]

11. Garner DM, Ling BWK. Measuring and locating zones of chaos and irregularity. J Syst Sci Complex. 2014; 27(3): 494-506. DOI: http://dx.doi.org/10.1007/s11424-014-2197-7        [ Links ]

12. Shannon CE. A Mathematical Theory of Communication. Bell System Technical J. 1948; 27(3): 379-423.         [ Links ]

13. Zyczkowski K. Renyi extrapolation of Shannon entropy. Open Sys Information Dyn. 2003; 3(10): 297-310.         [ Links ]

14. Alkan A, Kiymik MK. Comparison of AR and Welch methods in epileptic seizure detection. J Med Sys. 2006; 6(30): 413-419.         [ Links ]

15. Ghil M. The SSA-MTM Toolkit: Applications to analysis and prediction of time series. Proc SPIE. 1997; 3165: 216-230. DOI: http://dx.doi.org/10.1117/12.279594        [ Links ]

16. Percival DB, Walden AT. Spectral Analysis for Physical Applications: Multitaper and Conventional Univariate Techniques. New York: Cambridge University Press, 1993.         [ Links ]

17. Kawaguchi M, Takamatsu I, Kazama T. Rocuronium dose-dependently suppresses the spectral entropy response to tracheal intubation during propofol anaesthesia. Br J Anaesth. 2009; 102(5):667-72. DOI: http://dx.doi.org/10.1117/12.279594        [ Links ]

18. Morgaz J, Granados MD, Dominguez JM, Navarrete R, Fernandez A, Galan A, et al. Evaluation of spectral entropy to measure anaesthetic depth and antinociception in sevoflurane-anaesthetised Beagle dogs. Vet J. 2011; 188(3): 352-355. DOI: http://dx.doi.org/10.1016/j.tvjl.2010.06.001        [ Links ]

19. Alvarez D, Hornero R, Marcos J, Del Campo F, Lopez M. Spectral analysis of electroencepha-logram and oximetric signals in obstructive sleep apnea diagnosis. Conf Proc IEEE Eng Med Biol Soc. 2009; 2009: 400-403. DOI: http://dx.doi.org/10.1109/IEMBS.2009.5334905        [ Links ]

20. Moosavi SH, Topulos GP, Hafer A, Lansing RW, Adams L, Brown E et al. Acute partial paralysis alters perceptions of air hunger, work and effort at constant P(CO(2) and V(E). Respir Physiol. 2000; 122(1): 45-60.         [ Links ]

21. Banzett RB, Lansing RW, Reid MB, Adams L, Brown R. Air hunger' arising from increased PCO2 in mechanically ventilated quadriplegics. Respir Physiol. 1989; 76(1):53-67.         [ Links ]

22. Binks AP, Vovk A, Ferrigno M, Banzett RB. The air hunger response of four elite breath-hold divers. Respir Physiol Neurobiol. 2007; 159(2):171-177. DOI: http://dx.doi.org/10.1016/j.resp.2007.06.014        [ Links ]

23. Souza NM, Vanderlei LCM, Garner DM. Risk evaluation of diabetes mellitus by relation of chaotic globals to HRV. Complexity. 2015; 20(3): 84-92. Doi: 10.1002/cplx.21508.         [ Links ]

24. Vanderlei FM, Vanderlei LCM, Garner DM. Chaotic global parameters correlation with heart rate variability in obese children. J Hum Growth Dev. 2014; 24(1):24-30.         [ Links ]

25. Atrash HK, Carpentier R. The evolving role of public health in the delivery of health care. J Hum Growth Dev. 2012; 22(3): 396-399.         [ Links ]

26. Lohman TG, Roche AF, Martorell R. Anthropometric standardization reference manual. 1988.         [ Links ]

27. Vanderlei LCM, Silva RA, Pastre CM, Azevedo FM, Godoy MF. Comparison of the Polar S810i monitor and the ECG for the analysis of heart rate variability in the time and frequency domains. Braz J Med Biol Res. 2008; 41(10): 854-859. DOI: http://dx.doi.org/10.1590/S0100-879X2008005000039        [ Links ]

28. Godoy MF, Takakura IT, Correa PR. Relevância da análise do comportamento dinâmico não linear (Teoria do Caos) como elemento prognóstico de morbidade e mortalidade em pacientes submetidos à cirurgia de revascularização miocárdica. Arq Ciênc Saúde. 2005; 12(4):167-171.         [ Links ]

29. Mann ME, Lees JM. Robust estimation of background noise and signal detection in climatic time series. Climatic Change. 1996; 33(3):409-445. DOI: http://dx.doi.org/10.1007/BF00142586        [ Links ]

30. Donaldson GC, Seemungal TA, Hurst JR, Wedzicha JA. Detrended fluctuation analysis of peak expiratory flow and exacerbation frequency in COPD. Eur Respir J. 2012; 40(5): 1123-1129. DOI: http://dx.doi.org/10.1183/09031936.00180811        [ Links ]

31. Peng CK, Havlin S, Stanley HE, Goldberger AL. Quantification of scaling exponents and crossover phenomena in nonstationary heartbeat time series. Chaos. 1995; 5(1): 82-87. DOI: http://dx.doi.org/10.1063/1.166141        [ Links ]

32. Anderson TW, Darling DA. A test of goodness of fit. J Am Stat Assoc. 1954; 49(268): 765-769.         [ Links ]

33. Jolliffe IT. Principal Component Analysis, Series: Springer Series in Statistics. New York: Springer, 2002.         [ Links ]

34. Kruskal WH, Wallis WA. Use of ranks in one-criterion variance analysis. J Am Stat Assoc. 1952; 260(47): 583-621.         [ Links ]

35. Bernardo AFB, Vanderlei LCM, Garner DM. HRV Analysis - A clinical and diagnostic tool in Chronic Obstructive Pulmonary Disease. Int Schol Res Notices. 2014; 2014: 6. Doi: http://dx.doi.org/10.1155/2014/673232.         [ Links ]

 

 

Manuscript submitted Jun 08 2014
Accepted for publication Dec 12 2014

 

 

Corresponding author: dgarner@brookes.ac.uk.