Serviços Personalizados
Journal
artigo
Indicadores
Compartilhar
Revista Psicopedagogia
versão impressa ISSN 0103-8486
Rev. psicopedag. vol.31 no.94 São Paulo 2014
ARTIGO ORIGINAL
Intervenção no uso de procedimentos e estratégias de contagem com alunos dos anos iniciais com baixos desempenho em matemática
Intervention in the use of counting procedures and strategies with students in the first years of school with low performance in mathematics
Yasmini Lais Spindler Sperafico
Doutoranda pela Universidade Federal do Rio Grande do Sul (UFRGS), Psicopedagoga Clínica e Institucional pelo Centro Universitário La Salle (UNILASALLE) e Licenciada em Matemática pela Universidade do Vale do Rio dos Sinos (UNISINOS)
RESUMO
A contagem é uma habilidade essencial ao desenvolvimento de todo o conhecimento numérico, sendo um aspecto preditor do desempenho matemático posterior. Dentre as habilidades de contagem, encontram-se os procedimentos e estratégias de contagem que tratam de conhecimentos procedurais aplicados à resolução de problemas aritméticos. O presente estudo teve como objetivo avaliar os efeitos de uma intervenção psicopedagógica nos procedimentos e estratégias de contagem, verificando a evolução desses procedimentos e estratégias e a possibilidade de generalização dos efeitos a outros contextos matemáticos, com um grupo heterogêneo com cinco estudantes. Verificou-se uma evolução no uso de procedimentos e estratégias de contagem, sendo que a maior parte dos alunos passou a recuperar diversos fatos da memória. Observou-se, ainda, uma evolução no conhecimento numérico, em habilidades não abordadas durante as intervenções, evidenciando que o conhecimento de contagem traz benefício na aprendizagem de outros conceitos matemáticos.
Unitermos: Estudos de intervenção. Matemática. Conceitos matemáticos. Transtornos de Aprendizagem.
SUMMARY
Counting is an essential skill for the development of the whole numerical knowledge being a predictor aspect of later math performance. Among counting skills, there are counting procedures and strategies which deal with procedural knowledge applied to solve arithmetic problems. The present study aimed to evaluate the effects of a psychoeducational intervention in the counting procedures and strategies checking the evolution of these procedures and strategies and the possibility of generalization of the effects in other mathematical contexts, with a heterogeneous group with five students. It was identified an evolution in the use of counting procedures and strategies, and most students recovered several facts from memory. It was also observed an evolution in numerical knowledge, even in the skills not addressed during interventions, showing that counting knowledge brings benefits in learning other mathematical concepts.
Keywords: Intervention studies. Mathematics. Mathematical concepts. Learning disorders.
INTRODUÇÃO
A contagem é uma habilidade essencial ao desenvolvimento de todo o conhecimento numérico do sujeito, sendo um dos conhecimentos de base da área da matemática1. Alguns estudos abordam essa habilidade como um preditor significativo do desempenho matemático nos anos posteriores do ensino1,2.
Dentre a gama de conhecimentos conceituais e procedurais de contagem, encontram-se os procedimentos e estratégias de contagem. São formas de realizar a contagem de duas ou mais parcelas na resolução de problemas aritméticos que evoluem e desenvolvem-se ao longo dos anos, em ritmo ditado pelas condições biológicas e ambientais da criança.
Estudos têm evidenciado que crianças com desenvolvimento atípico desenvolvem procedimentos e estratégias de contagem de forma semelhante a estudantes com desenvolvimento típico, entretanto, em ritmo diferenciado3-7. Pesquisas têm demonstrado que intervenções focadas nesses aspectos da contagem auxiliam os estudantes de desenvolvimento atípico a desenvolver procedimentos e estratégias de contagem mais desenvolvidas. Isso foi demonstrado em dois estudos com grupos mais homogêneos de estudantes, um com crianças com transtorno de déficit de atenção/hiperatividade e outro com crianças com deficiência intelectual.
O presente estudo tem como objetivo verificar os efeitos de uma intervenção psicopedagógica de curta duração, focada no uso de procedimentos e estratégias de contagem, em um grupo de cinco estudantes com características heterogêneas, verificando a possibilidade de generalização dos efeitos a outros contextos matemáticos. Para isso, inicialmente apresenta-se uma revisão de estudos que abordam a habilidade de contagem e a sua importância para a aprendizagem matemática posterior. Em seguida, conceituam-se os procedimentos e estratégias de contagem identificados nas crianças, bem como se discute a forma como esses evoluem e as diferenças de desenvolvimento dessa habilidade entre crianças de desenvolvimento típico e atípico. Na sequência, aborda-se brevemente o pequeno corpo de estudos descrevendo os efeitos de intervenções nesse aspecto matemático e os resultados obtidos com grupos específicos de crianças. Por fim, apresenta-se o método utilizado e os resultados obtidos que são discutidos à luz dos estudos revisados.
Desenvolvimento da habilidade de contagem
A contagem é uma habilidade fundamental para o desenvolvimento da capacidade de compreensão numérica1. Possuir a habilidade de contagem significar estar apto a estabelecer relações de um-para-um entre objetos de uma série e suas representações numéricas1.
Estudos têm evidenciado que a habilidade de contagem é capaz de predizer o aprendizado matemático posterior1,2. Dessa forma, alunos que possuem uma maior capacidade de contagem, bem como fazem bom uso desse recurso, são melhor sucedidos nos conteúdos aritméticos e apresentam maior facilidade em realizar cálculos simples e complexos.
Nunes & Bryant8 evidenciam que diversas pesquisas têm discutido que as primeiras experiências matemáticas da criança ocorrem muito antes dessas ingressaram na vida escolar. A psicologia vem apresentando resultados empíricos que evidenciam a capacidade dos bebês para perceber a numerosidade, ou seja, demonstram sensibilidade à mudança da quantidade de um conjunto numérico com poucos elementos9. Essa capacidade foi verificada em diversos estudos experimentais, com numerosidades até três, sendo que a mudança na quantidade de objetos no conjunto foi identificada pelos bebês quando foram adicionados ou retirados objetos10,11.
Geary12, entretanto, alerta que, embora os bebês apresentem essa capacidade de detectar pequenas quantidades, isso não significa que identifiquem que um conjunto de três objetos é maior que um conjunto de dois objetos, isto é, não possuem a capacidade de comparar e ordenar quantidades. Costa5 ainda questiona se possuir a capacidade de perceber a mudança de quantidades de um objeto significa identificar que foram retirados ou adicionados itens a ele. A autora destaca que essa questão foi respondida por um estudo realizado, em 1992, por Wynn, com bonecos Mickey Mouse, que demonstrou que os bebês de 5 meses sustentavam por mais tempo o olhar quando a quantidade de bonecos era inesperada, ou seja, quando surgiam ou desapareciam bonecos, fornecendo evidências de uma competência aritmética elementar.
Esse conjunto de evidências empíricas sustenta a existência de uma capacidade inata de abstração numérica - capacidade para formar representações sobre as numerosidades, também encontrada nos animais5. E são essas capacidades que, conforme Costa5, dão origem aos princípios de contagem que são desenvolvidos posteriormente em contexto cultural. Ainda não há consenso quanto à origem inata ou não das habilidades numéricas, mas há consenso na literatura quanto aos cinco princípios da contagem que são desenvolvidos pelas crianças5.
Os cinco princípios da contagem foram inicialmente formulados por Gelman & Gallistel13 e discutidos em diversos estudos posteriores3,4,8,14. São eles: 1) correspondência termo a termo (cada objeto deve ser contado apenas uma vez, sendo utilizado um nome de número); 2) ordem estável (a ordem das palavras de contagem é invariante, seguindo a sequência um, dois, três, e assim por diante); 3) Cardinalidade (o total de objetos de um conjunto corresponde ao último nome de número, sendo que este envolve todos os números da sequência); 4) Abstração (objetos de qualquer tipo podem ser colocados juntos e contados); e 5) irrelevância da ordem (objetos de um dado conjunto podem ser contados em qualquer ordem).
Grande parte desses princípios é compreendida e aplicada pelas crianças de 5-6 anos de idade, exceto os princípios de abstração e irrelevância da ordem, que são adquiridos entre o primeiro e o segundo ano escolar3,15. Entretanto, estudos demonstram que crianças que apresentam desenvolvimento atípico têm atrasos na aquisição desses princípios. Geary et al.3,4,14 demonstraram que crianças com dificuldades na matemática ou na matemática e na leitura demoram mais tempo que crianças sem dificuldades ou apenas com dificuldades na leitura para compreender o princípio de irrelevância da ordem, podendo chegar ao segundo ano sem a compreensão desse princípio.
Desenvolvimento dos procedimentos e estratégias de contagem
Geary3 afirma que o desenvolvimento das competências procedurais é influenciado, em parte, pelo progresso das crianças na compreensão da contagem e reflete na passagem gradual de procedimentos de contagem mais imaturos (contar todos) para procedimentos mais desenvolvidos (contar a partir de, contar a partir do maior). Do mesmo modo, o uso dos procedimentos de contagem resulta no desenvolvimento da representação dos fatos básicos na memória, possibilitando sua recuperação imediata.
Os procedimentos de contagem mais descritos na literatura são3-6:
• Contar todos: representar todas as parcelas e realizar a contagem começando por 1. Assim, para 3+2, representar-se-ia o 3 e o 2, contando, na sequência, a totalidade (1,2,3,4,5);
• Contar a partir de: percepção da não necessidade de realizar a contagem de todas as parcelas, sendo assim, a contagem é realizada a partir da primeira parcela ou a partir da maior parcela identificada. Assim, 2+3 poderia ser resolvido com a contagem a partir de 2 (primeira parcela), com 3,4,5 ou, a partir da maior parcela (3), 4,5.
Esses procedimentos de contagem são executados, frequentemente, com o apoio de estratégias de contagem nos dedos (ou em outro material concreto) ou com a contagem verbal ou silenciosa.
Costa5 afirma que, apesar dos procedimentos de contar possuírem uma característica evolutiva, "as crianças, na prática, usam simultaneamente diversos deles, o que acaba resultando no desenvolvimento da representação desses fatos básicos na memória de longo prazo. Uma vez formada, a representação permite o uso desses processos de resolução apoiados na memória".
Dois procedimentos apoiados na memória são descritos na literatura3-6:
• Recuperação imediata da memória: a resposta é recuperada imediatamente da memória de longo prazo;
• Decomposição: Reconstrução de respostas baseadas na recuperação de uma parte da soma. Por exemplo, o fato aritmético 6+7 pode ser decomposto em 6+6+1, sendo 6+6 recuperado imediatamente da memória, sob o resultado 12, basta acrescentar 1, para obter a resposta 13.
O uso de procedimentos apoiados na memória resulta na solução rápida dos problemas e na redução de demanda da Memória de Trabalho (MT). A menor demanda da MT, por sua vez, facilita a resolução de problemas mais complexos (problemas verbais) com menos erros3.
O progresso dos procedimentos de contagem para os apoiados na memória não ocorre em etapas, havendo coexistência de diversos procedimentos. Isso ocorre por dois motivos. O primeiro se refere ao emprego do procedimento que varia conforme o objetivo do cálculo e o tipo de problema. Se a criança quer ser rápida, utiliza os procedimentos apoiados na memória; se quer ser precisa, pode preferir os procedimentos de contagem3. O segundo diz respeito ao fato desse progresso entre os tipos de procedimento ser um processo gradual, caracterizado por Hopkins & Lawson16 em três grandes mudanças:
1) Passagem do uso de procedimentos menos desenvolvidos para outros mais eficientes;
2) Desenvolvimento da confiança na recuperação (para alguns problemas) com base na prática bem sucedida e continuada no uso de procedimentos mais eficientes;
3) Substituição de procedimentos eficientes pela decomposição, sendo que a prática bem sucedida na decomposição auxilia no desenvolvimento da confiança na recuperação (para outros problemas).
Sendo assim, o procedimento de decomposição parece ser um mediador entre o procedimento contar a partir de e a recuperação imediata para problemas com parcelas maiores que 4. Costa5, com base em uma revisão de literatura, afirma que "para a construção da representação dos fatos básicos na memória de longo prazo entre o problema e a resposta é importante que ambos sejam ativados ao mesmo tempo na memória de trabalho". As crianças sem dificuldades desenvolvem a confiança na recuperação dos fatos para problemas com parcelas menores que 4, usando esse conhecimento para derivar as parcelas maiores16. Isso torna essas crianças mais eficientes na resolução de problemas mais complexos, sendo que, aos poucos, passam a automatizar fatos com parcelas maiores. Entretanto, crianças com velocidade de contagem lenta, que apresentam desenvolvimento atípico, não apresentam essa evolução em tempo semelhante3-6.
Estudo de Geary3 evidencia que crianças com dificuldades na matemática e na leitura e apenas na matemática utilizam estratégias de contagem semelhantes às utilizadas por crianças de desenvolvimento típico na resolução de problemas aritméticos simples, mas diferem no uso do procedimento. No 1o e 2o ano, essas crianças cometiam mais erros na contagem e utilizavam um procedimento imaturo (contar todos) com mais frequência que as crianças com dificuldades apenas na leitura ou sem dificuldades. Estudo de Costa et al.6 investigou o desenvolvimento dos procedimentos de contagem em estudantes com transtorno de déficit de atenção/ hiperatividade (TDAH), verificando que esses permanecem por mais tempo utilizando procedimentos menos eficientes, o que caracteriza um atraso no desenvolvimento dessa habilidade em relação a crianças de desenvolvimento típico. Esse atraso no desenvolvimento também foi evidenciado em estudantes com deficiência intelectual7.
Embora não haja consenso quanto às causas desse atraso no desenvolvimento dos procedimentos e estratégias de contagem, a literatura apresenta três paradigmas que apontam explicações para tal fato:
1) Senso numérico pobre: alguns autores defendem a existência de um déficit no senso numérico2,17. O senso numérico pode ser definido como a habilidade de trabalhar com números, o que envolve a compreensão do seu significado e das ideias a ele relacionadas. Assim, déficits nessa habilidade seriam responsáveis por dificuldades nas aquisições matemáticas posteriores;
2) Déficit de Memória de Trabalho (MT): a MT é a habilidade de armazenar temporariamente uma informação, manipulando-a18. Se a recuperação dos fatos básicos só é possível se o problema e a resposta estivem ativos simultaneamente na MT, déficits nessa habilidade prejudicariam o desenvolvimento da recuperação imediata3. Em alguns casos, o limite e o tempo de armazenamento da informação pela MT podem estar preservados, mas o estudante excede esse limite por ser lento na contagem;
3) Lentidão na velocidade de processamento das informações: alguns autores têm observado que crianças com dificuldades aritméticas são mais lentas na contagem, processando a informação de forma mais demorada que crianças sem dificuldades ou se perdem durante a contagem4,16. Essa lentidão possibilita que ocorra o esquecimento antes que a sequência de cálculo seja completada.
Sendo assim, há fortes evidências empíricas que confirmam que muitos grupos de crianças com desenvolvimento atípico apresentam certa lentidão no desenvolvimento de procedimentos e estratégias de contagem se comparadas a seus pares de desenvolvimento típico. Entretanto, evidências da possibilidade de auxiliar essas crianças a desenvolver procedimentos e estratégias de contagem mais desenvolvidos ainda são escassas.
Intervenção no uso de procedimentos e estratégias de contagem
Estudos têm demonstrado que intervenções focadas no desenvolvimento das habilidades de contagem trazem benefícios a estudantes de diferentes grupos5,7. Costa5 desenvolveu um estudo interventivo com sete estudantes entre 9 e 13 anos (3o a 4o ano), com TDAH. Todos os estudantes apresentavam QI acima de 80.
Os estudantes realizaram uma avaliação dos procedimentos e estratégias de contagem, sendo designados, aleatoriamente, para dois grupos, intervenção (n=4) e controle (n=3). O grupo de intervenção recebeu 10 sessões de uma hora de intervenção de ensino explícito de procedimentos e estratégias de contagem, sendo que o grupo controle trabalhou apenas com jogos que não envolviam a prática de procedimentos e estratégias de contagem.
Os resultados evidenciaram um ganho no número de fatos básicos recuperados da memória nos dois grupos do pré para o pós-teste. Entretanto, o grupo experimental apresentou maior frequência no uso de procedimentos apoiados na memória em relação ao grupo controle, que permaneceu mais nos procedimentos de contagem. Essa melhora se manteve após três meses. Esses resultados trazem evidências de que o ensino explícito de procedimentos e estratégias de contagem auxilia no desenvolvimento da recuperação de fatos básicos.
A intervenção apresentada no estudo de Costa5 foi replicada por Cechin et al.7, com três estudantes com deficiência intelectual, entre 8 e 12 anos de idade. Os resultados também evidenciaram o progresso dos estudantes que passaram a utilizar o procedimento contar a partir de, substituindo o contar todos. A evolução para o uso de um procedimento mais desenvolvido também teve efeitos sobre a média de acertos dos alunos no pós-teste, que aumentou significativamente.
Apesar da evidência empírica de que intervenções que visem ao desenvolvimento de procedimentos e estratégias de contagem beneficiam estudantes ao auxiliar no desenvolvimento de procedimentos mais evoluídos, ainda são escassas pesquisas nessa área. Dessa forma, o presente estudo buscou desenvolver uma intervenção no desenvolvimento dos procedimentos e estratégias de contagem, com um grupo diferenciado de 5 alunos do 2o ao 4o ano do Ensino Fundamental, por meio do uso de jogos diversificados.
MÉTODO
O presente estudo caracteriza-se como uma pesquisa qualitativa-quantitativa que teve como objetivo verificar os efeitos de uma intervenção psicopedagógica nos procedimentos e estratégias de contagem, com foco no uso de procedimentos e estratégias mais desenvolvidos e no desempenho na resolução de problemas aritméticos simples por estudantes dos anos iniciais do Ensino Fundamental, com queixa de baixo desempenho matemático. Optou-se por essa abordagem pela possibilidade de complementação dos resultados quantitativos pelos resultados qualitativos, gerando informações em diferentes níveis de análise19.
A amostra para o estudo foi composta por cinco estudantes que frequentam o 2o e o 4o ano de uma escola privada do município de Canoas. Dois desses estudantes (duas meninas - Ju e Eda) possuem diagnóstico TDAH e três estudantes (três meninos - Rog, Dav e Mar) apresentam dificuldades na matemática (relatadas pelas professoras, dado o baixo desempenho escolar). Os estudantes possuem entre 8 e 10 anos de idade.
Avaliação
Realizou-se uma avaliação inicial em duas sessões, aplicando-se um instrumento em cada uma delas, e uma avaliação final, uma semana após a última sessão de intervenção.
Como instrumentos na avaliação inicial, utilizou-se o Teste de Conhecimento Numérico20 e um jogo de memória de quantidades. Ambos os procedimentos permitiram a identificação dos procedimentos e estratégias de contagem dois estudantes. O primeiro instrumento também permitiu verificar o desempenho na resolução de problemas aritméticos. Já o jogo de memória forneceu indícios da compreensão dos princípios de contagem13 pelos estudantes, por meio dos questionamentos realizados durante a interação com o material do jogo. Para a avaliação final, reaplicou-se o Teste de Conhecimento Numérico20 e realizou-se o Teste de Estratégias e Procedimentos de Contagem e de Recuperação da Memória4, conforme instruções utilizadas no estudo de Corso21.
Intervenção
A intervenção foi realizada ao longo de quatro sessões, nas quais foram utilizados jogos diversificados e organizadas atividades estruturadas com base nas situações de jogo. Os encontros tiveram entre uma hora e uma hora e meia de duração cada.
A cada sessão era realizada a exploração de um ou dois jogos coletivos, sendo realizadas a problematização do jogo e, para alguns jogos, representações de situações em atividades estruturadas com lápis e papel. Na primeira sessão, explorou-se o jogo Faça 105. Na segunda sessão, utilizou-se um jogo de tabuleiro5 e o Tux of Math Comand, um jogo de computador com cálculos aritméticos envolvendo os fatos básicos da adição. Na terceira sessão, explorou-se o jogo Circo Faça 105, desenvolvendo uma atividade com lápis e papel de exploração do jogo e utilizou-se novamente o jogo de computador (Tux of Math Comand). Na quarta sessão, utilizou-se os jogos Batalha dos Duplos e Duplo Problemático5, sendo realizada novamente uma atividade de lápis e papel de exploração da estratégia de decomposição.
RESULTADOS E DISCUSSÃO
Na avaliação inicial, utilizou-se um jogo de memória de quantificação, para verificar se os estudantes possuíam os princípios de contagem desenvolvidos, bem como verificar as estratégias e procedimentos de contagem predominantemente utilizados. Essa última habilidade também foi avaliada por meio do Teste de Conhecimento Numérico20 que, ainda, forneceu evidências da habilidade dos estudantes na resolução de problemas aritméticos simples.
Verificou-se que o procedimento mais utilizado foi o contar a partir de, sendo que apenas um estudante (Rog) oscila entre o contar todos e esse procedimento mais desenvolvido. Para a utilização desse procedimento, os estudantes adotam, predominantemente, a estratégia de contagem nos dedos, sendo que apenas Dav utilizou, em alguns momentos, a contagem silenciosa.
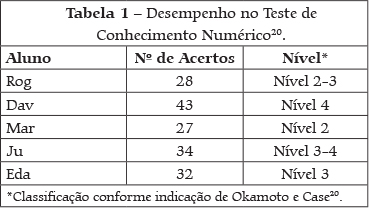
Quanto à competência no Teste de Conhecimento Numérico com resolução de problemas aritméticos simples, pode-se verificar o resultado de cada aluno na Tabela 1. Verificou-se uma média de 29,83 acertos (de um total de 51 problemas), sendo que a maior parte dos estudantes encontra-se no Nível 3 (classificação de Okamoto & Case20) de conhecimento numérico ou em transição do Nível 2 para o 3. Apenas Mar se encontra no Nível 2, apresentando resultado um pouco inferior aos colegas. Já Dav alcançou o Nível 4 (último nível), apresentando conhecimento numérico bem desenvolvido.
No pós-teste, aplicou-se o Teste de Estratégias e Procedimentos de Contagem e de Recuperação da Memória4. O teste totalizava 14 problemas. A maior parte dos alunos utilizou o contar a partir do maior, com o uso da estratégia de contagem silenciosa e a recuperação imediata da memória. Os resultados de cada aluno podem ser visualizados na Tabela 2.
Os resultados demonstram que os alunos apresentaram evolução no uso de procedimentos e/ou estratégias de contagem. Dav foi o que teve maior evolução, passando a utilizar, predominantemente, procedimentos apoiados na memória, em especial a recuperação imediata. Já Ju apresentou o menor crescimento, necessitando ainda de procedimentos de contagem, sendo capaz de recuperar da memória, apenas fatos com, pelo menos, uma das parcelas menor ou igual a três. Rog também recupera apenas fatos com parcelas pequenas, mas passou a utilizar uma estratégia mais desenvolvida, a contagem silenciosa. Os demais estudantes retornavam ao uso de estratégias menos desenvolvidas nos problemas em que as parcelas eram maiores que cinco ou quando tinham dúvidas quanto ao resultado recuperado.
Sendo assim, verifica-se que todos os estudantes evoluíram em seus procedimentos de contagem, sendo que alguns já utilizam procedimentos apoiados na memória com maior frequência. O desenvolvimento observado nos alunos é semelhante ao descrito em estudos3,4,9 que evidenciam que os estudantes progridem, inicialmente, nos procedimentos de contagem (contar todos para contar a partir de) para então utilizarem procedimentos apoiados na memória, sendo que essa evolução é processual.
Os estudantes também apresentaram crescimento nos escores do Teste de Conhecimento Numérico20 do pré-teste para o pós-teste, como evidenciam os dados da Tabela 3. Entre os estudantes que apresentaram maior evolução está Mar, que evoluiu do Nível 2 para o Nível 4, em relação ao seu conhecimento numérico. Já Eda permaneceu na classificação de Nível 3, apesar de ter obtido pontuação maior. Tem-se como hipótese que as dificuldades da aluna estejam associadas aos prejuízos na atenção, ocasionados pelo TDAH, já que a atenção é um importante aspecto do aprendizado matemático22.
Sendo assim, parece que o desenvolvimento de procedimentos e estratégias de contagem contribui para a melhora em outros aspectos do senso numérico, já que os estudantes obtiveram progressos em habilidades numéricas que não foram trabalhadas nas sessões, como operações com multidígitos e computação de distâncias, evidenciadas por meio dos resultados do Teste de Conhecimento Numérico.
CONSIDERAÇÕES FINAIS
O presente estudo teve como objetivo avaliar os efeitos de uma intervenção psicopedagógica nos procedimentos e estratégias de contagem no uso de procedimentos e estratégias mais evoluídos e na verificação de generalização dos efeitos a outros contextos matemáticos. Verificou-se evolução no uso de procedimentos e estratégias de contagem, sendo que a maior parte dos alunos passou a recuperar diversos fatos da memória. Observou-se, ainda, evolução no conhecimento numérico em habilidades não abordadas durante as intervenções, evidenciando que o conhecimento de contagem traz benefício à aprendizagem de outros conceitos matemáticos.
Esses resultados corroboram a evidência empírica de que intervenções no uso de procedimentos e estratégias de contagem são eficazes ao auxiliarem os alunos na realização de tarefas matemáticas de forma mais eficiente, resultando em melhora do desempenho matemático.
REFERÊNCIAS
1. Passolunghi MC, Vercelloni B, Schadee H. The precursors of mathematics learning: working memory, phonological ability and numerical competence. Cognitive Development. 2007; 22(2):165-84. [ Links ]
2. Corso LV, Dorneles BV. Senso numérico e dificuldades de aprendizagem na matemática. Rev Psicopedag. 2010;27(83):298-309. [ Links ]
3. Geary DC. Mathematical disabilities: cognitive, neuropsychological and genetic components. Psychol Bull. 1993;114(2):345-62. [ Links ]
4. Geary DC, Hamson CO, Hoard MK. Numerical and arithmetical cognition: a longitudinal study of process and concept deficits in children with learning disability. J Exp Child Psychol. 2000;77(3):236-63. [ Links ]
5. Costa AC. Ensino de fatos básicos aditivos para crianças com transtorno de déficit de atenção/hiperatividade (TDAH): possibilidades de intervenção pedagógica na aritmética [Tese de Doutorado]. Porto Alegre: Universidade Federal do Rio Grande do Sul; 2009. [ Links ]
6. Costa AC, Dorneles BV, Rohde LAP. Identificação dos procedimentos de contagem e dos processos de memória em crianças com TDAH. Psicol Reflex Crit. 2012;25(4):791-801. [ Links ]
7. Cechin MBC, Costa AC, Dorneles BV. Ensino de fatos aritméticos para escolares com deficiência intelectual. Rev Bras Ed Esp. 2013; 19(1):79-92. [ Links ]
8. Nunes T, Bryant P. Crianças fazendo matemática. Porto Alegre: Artmed; 1997. [ Links ]
9. Butterworth B. The development of arithmetical abilities. J Child Psychol Psychiatry. 2005; 46(1):3-18. [ Links ]
10. Starkey P, Cooper RG. Perception of numbers by human infants. Science. 1980;210(4473): 1033-5. [ Links ]
11. Starkey P, Spelke ES, Gelman R. Numerical abstraction by human infants. Cognition. 1990;36(2):97-128. [ Links ]
12. Geary DC. Development of mathematical understanding. In: Kuhl D, Siegler R, eds. Cognition, perception and language: handbook of child psychology. New York: John Wiley & Sons; 2006. p.777-810. [ Links ]
13. Gelman R, Gallistel CR. The child's understanding of number. Cambridge: Harvard University Press; 1978. [ Links ]
14. Geary DC, Hoard MK, Hamsom CO. Numerical and arithmetical cognition: patterns of functions and deficits in children at risk for a mathematical disability. J Exp Child Psychol. 1999;74(3):213-39. [ Links ]
15. Dorneles BV. Princípios da contagem numérica: uma construção progressista. In: Seminário de Pesquisa em Educação: Região Sul, 5, 2004, Curitiba. Anais. Curitiba: PUCRS; 2004. Cd-Rom. [ Links ]
16. Hopkins SL, Lawson MJ. Explaining the acquisition of a complex skill: methodological and theoretical considerations uncovered in the study of simple addition and the moving-on process. Educ Psychol Rev. 2002; 14(2):121-54. [ Links ]
17. Jordan N, Hanich L, Kaplan D. A longitudinal study of mathematical competence in children with specific mathematical difficulties versus children with co-morbid mathematical and learning difficulties. Child Development. 2003;74(3):834-50. [ Links ]
18. Baddeley A. Memória de trabalho. In: Memória. Trad. Stolting C. Porto Alegre: Artmed; 2011. p.54-82. [ Links ]
19. Creswell J. Projeto de pesquisa: métodos qualitativo, quantitativo e misto. Porto Alegre: Artmed; 2007. [ Links ]
20. Okamoto Y, Case R. Exploring the microstructure of children's central conceptual structures in the domain of number. Monogr Soc Res Child Dev. 1996;61(1-2):27-58. [ Links ]
21. Corso LV. Dificuldades na leitura e na matemática: um estudo dos processos cognitivos em alunos da 3a a 6a série do Ensino Fundamental [Tese Doutorado]. Porto Alegre: Universidade Federal do Rio Grande do Sul; 2008. [ Links ]
22. Zentall SS. Math performance of students with ADHD: cognitive and behavioral contributors and interventions. In: Berch DB, Mazzocco MMM, eds. Why is math so hard for some children? Maryland: Brookes; 2007. p.219-43. [ Links ]
 Endereço para correspondência:
Endereço para correspondência:
Yasmini Lais Spindler Sperafico
Av. Protásio Alves, 1320, apto. 12 - Petrópolis
Porto Alegre, RS, Brasil
CEP: 90410-005
E-mail: yasmini182@hotmail.com
Artigo recebido: 4/2/2014
Aprovado: 21/3/2014
Trabalho desenvolvido no Centro Universitário La Salle - UNILASALLE, Canoas, RS, Brasil.













