ARTIGO ORIGINAL

 

Intervenção construtivista: saber geométrico, jogo e os possíveis e o necessário

 

Constructivist intervention: Geometric knowledge, games the possible and the necessary

 

 

Lilian Alves Pereira Peres^I; Geiva Carolina Calsa^II

^IDoutora em Educação - Universidade Estadual de Maringá (UEM/PR); Professora da Universidade Estadual de Maringá (UEM/PR); Membro do Grupo de Estudos e Pesquisa em Psicopedagogia, Aprendizagem e Cultura (GEPAC/UEM), Maringá, PR, Brasil
^IIDoutora em Educação - Universidade Estadual de Campinas (UNICAMP); Professora da Universidade Estadual de Maringá (UEM/PR); Professora Líder do Grupo de Estudos e Pesquisa em Psicopedagogia, Aprendizagem e Cultura (GEPAC/UEM), Maringá, PR, Brasil

Endereço para correspondência

 

 

---

RESUMO

Este trabalho tem por objetivo apresentar parte da pesquisa realizada entre os anos de 2013 a 2017 para a tese de doutorado em educação, apresentada ao Programa de Pós-graduação em Educação da Universidade Estadual de Maringá, cujo objetivo foi investigar os efeitos de uma intervenção pedagógica construtivista com jogos e construção de possíveis e do necessário em relação à aprendizagem de conteúdos escolares sobre noções espaciais. Para tanto, foi utilizado como principal referencial teórico os estudos de Piaget e Inhelder e Piaget. A pesquisa, apoiada no método clínico-crítico piagetiano, teve a seguinte configuração: antes e depois de um processo de intervenção pedagógica foram realizadas provas operatórias sobre noções espaciais, o possível e o necessário e conceitos espaciais. Além disso, realizamos, antes e depois do processo de intervenção, a aplicação de uma avaliação sobre conteúdos geométricos, mais especificamente atividades que envolviam as noções de Espaço e Forma. Resultados apontaram que o uso do jogo Katamino contribuiu para a construção de possíveis nas estratégias dos estudantes, bem como para a melhoria de seu desempenho em todas as provas realizadas após as intervenções. Concluímos que esses resultados estão relacionados à metodologia utilizada durante as intervenções pedagógicas, em especial, o uso do jogo de regras acompanhado de mediação pedagógica da professora-pesquisadora. Esses dados afirmam a importância do jogo de regras em um contexto educativo, como desencadeador de reflexão nos sujeitos, proporcionando construções significativas do ponto de vista cognitivo.

Unitermos: Educação. Jogos de Regras. Possível e Necessário. Espaço e Forma. Intervenção Pedagógica Construtivista.

---

ABSTRACT

Current paper presents a section of the research work developed between 2013 and 2017 for a doctoral degree in Education at the Universidade Estadual de Maringá. It investigates the effects of a constructivism pedagogical intervention with games and the construction of the possible and the necessary with regard to the learning of spatial notions. Studies by Piaget and Inhelder and Piaget foregrounded the main theoretical references. The research, based on Piaget´s clinical and critical method, comprised the following design: operatory tests on spatial notions, the possible and the necessary, and spatial concepts were performed prior to and after pedagogical interventions. In addition, we perform before and after to the above question could be given, assessment on geometry, specifically activities on the notions of Space and Form, was performed. Results showed that the use of the game Katamino contributed towards the construction of the possible within the students´ strategies and improvement in all post-evaluation tests. Results are related to the methodology used during pedagogical interventions, especially, the use of games of rules plus teacher-researcher´s pedagogical mediation. Data underline the importance of games of rules within an educational context due to the fact that they trigger thoughts in the agents, providing significant constructions from the cognitive point of view.

Keywords: Education. Games of Rules. The Possible and the Necessary. Space and Form. Constructivism Pedagogical Intervention.

---

 

 

INTRODUÇÃO

Apesar de estar presente nos Parâmetros Curriculares Nacionais: Matemática (PCNs)¹, nas Diretrizes Curriculares da Educação Básica: Matemática², no Currículo Básico para as Escolas Públicas do Estado do Paraná³ e no Currículo da Educação Infantil e Anos Iniciais do Ensino Fundamental⁴, a prática pedagógica e a organização do ensino de Espaço e de Forma e/ou Geometria^* continuam se constituindo uma prática escolar distorcida, equivocada e conceitualmente desvinculada da realidade dos alunos na escola, bem como distante da reflexão e do estudo do professor.

Assim, um dos problemas apontados por pesquisas, como a de Melo⁵, refere-se ao fato de o saber cotidiano, lúdico e científico não se integrar no processo escolar, promovendo problemas pedagógicos de não aprendizagem, para os quais os docentes e a escola parecem não se sentir preparados. Para a autora, nenhuma atividade deve ser introduzida na escola sem antes ser estudada e refletida por parte do docente quanto aos aspectos intelectuais, sociais, emocionais e afetivos envolvidos.

Ainda, segundo a autora, quando usadas, as brincadeiras e jogos o são de forma não lúdica, provocando sua "escolarização" e tornando-as mais um instrumento pedagógico para ensinar outros conteúdos. Nesse processo, ao se perder o caráter lúdico, essas atividades são transformadas em exercícios e mais uma tarefa a ser cumprida de forma reprodutora e memorística.

Foi a partir do trabalho, como professora de Educação Infantil e na formação de professores, e da observação desse cenário da Educação Básica que percebi a incoerência sobre a literatura^6-9 e a prática escolar, ao ensinar os conteúdos curriculares, dentre eles, as noções espaciais. A saber, os estudos mostram que, na maioria das vezes, já na Educação Infantil, prioriza-se o processo de alfabetização com atividades sistematizadas de leitura e de escrita e relacionada com números em detrimento de atividades espaciais, isso porque "o ensino da matemática continua reduzido às noções numéricas"¹⁰ (p. 8), e a geometria acaba tornando-se um complemento da prática escolar.

Nesse sentido, pode-se dizer que, com a ênfase da alfabetização (ler e escrever) sobre a alfabetização matemática, o conteúdo ligado às noções espaciais, como a geometria, agrava-se. Um dos problemas apontados pela autora pode estar situado na defasagem da formação acadêmica, que não envolve uma proposta de ensino da matemática de qualidade, em que a teoria se alie à prática, para auxiliar no processo pedagógico do professor de modo que se possa promover "um trabalho significativo para o desenvolvimento do conhecimento geométrico infantil"¹⁰ (p. 9).

Várias pesquisas^5,6,8,10-17 também têm concluído que os estudantes continuam mantendo distância entre os conhecimentos ensinados na escola e os que vivenciam em seu cotidiano. Dessa forma, as noções espaciais, quando ensinadas, apresentam-se de forma intuitiva e experimental e parecem não se integrar às atividades de seu dia a dia, pois, muitas vezes, os professores utilizam apenas a identificação das quatro figuras: quadrado, retângulo, triângulo e círculo; para depois trabalhar a parte métrica, como o perímetro e área.

Além disso, nos anos iniciais do Ensino Fundamental, o ensino das noções espaciais, como Espaço e Forma e/ou Geometria, tem ficado em segundo plano nas aulas de matemática. Quando ensinada, porém, geralmente, aparece como um tópico isolado, sem conexão com os outros conteúdos da matemática, em atividades com folha de papel e lápis.

Com relação às noções geométricas, as pesquisas de Piaget e de Inhelder¹⁸, bem como estudos posteriores com o mesmo referencial teórico-metodológico^14,16,19-21, demonstram que o processo de construção espacial inicia pela construção topológica e, na sequência, as relações projetivas e euclidianas. Apesar disso, o ensino de conteúdos que envolvem Espaço e Forma e/ou Geometria continua iniciando pelas relações projetivas e euclidianas antes das topológicas, ou seja, o ensino das figuras geométricas antes dos sólidos geométricos demonstra como esse ensino não é adequado para a construção do conhecimento espacial na Educação Infantil e nos primeiros anos do Ensino Fundamental.

Como consequência, segundo esses estudos, a falta de um trabalho efetivo que envolva inicialmente os espaços topológicos e, posteriormente, os projetivos e euclidianos tem provocado lacunas na construção do espaço tridimensional, prejudicando as atividades geométricas sistematizadas que envolvem a bidimensionalidade.

Levando em consideração tais aspectos, o presente artigo pretende demonstrar parte dos resultados de uma pesquisa realizada entre os anos de 2013 a 2017 para a tese de Doutorado em educação, apresentada ao Programa de Pós-graduação em Educação (PPE) da Universidade Estadual de Maringá (UEM), cujo objetivo foi investigar os efeitos de uma intervenção pedagógica construtivista com jogos e construção de possíveis e do necessário em relação à aprendizagem de conteúdos escolares sobre noções espaciais.

Assim, com o intuito de buscarmos respostas para o problema levantado de que: "a aprendizagem de noções espaciais pode ser favorecida por meio de intervenção pedagógica construtivista com jogos de regras e formação de possíveis e do necessário?", é que, apoiados no método clínico-crítico piagetiano, realizamos, antes e depois do processo de intervenção pedagógica construtivista, a aplicação de provas operatórias sobre noções espaciais, o possível e o necessário e uma avaliação sobre conteúdos geométricos, mais especificamente atividades que envolviam as noções de Espaço e de Forma e/ou Geometria.

Portanto, neste trabalho iremos demonstrar os dados obtidos com relação à avaliação sobre conteúdos geométricos (noções de Espaço e de Forma), aplicados antes e depois do processo de intervenção pedagógica construtivista.

 

A CONSTRUÇÃO DO ESPAÇO, O JOGO E A FORMAÇÃO DE POSSÍVEIS E DO NECESSÁRIO

Neste tópico, apresentamos o desenvolvimento da noção de espaço a partir do referencial teórico piagetiano. Apoiamo-nos principalmente em Piaget & Inhelder¹⁸. Além disso, apresentamos o processo de formação de possíveis e do necessário²² como parte essencial da construção de noções espaciais.

Em sua obra "A representação do espaço na criança", Piaget & Inhelder¹⁸ apresentam os resultados de seus estudos sobre o espaço e é possível concluir que o espaço é construído segundo uma ordem de sucessão, que vai de relações topológicas iniciais a relações mais complexas, como as projetivas e as euclidianas. Essa sucessão evidencia a presença dos processos de abstração empírica e reflexionante nesse desenvolvimento. Para isso, os autores mostram que a construção do "espaço infantil começa por intuições topológicas elementares, bem antes de tornar-se gradativamente e simultaneamente projetivo e euclidiano"¹⁸ (p. 12).

Reforçam, ainda, que a construção do espaço não é "[...] uma leitura das propriedades dos objetos, mas, antes, desde o início, uma ação exercida sobre eles [...]"¹⁸ (p. 469), ou seja, depende tanto dos objetos físicos com os quais o sujeito interage como dos esquemas assimilativos de que se utiliza. Em outras palavras, a leitura do objeto em sua relação espacial depende da abstração, empírica ou reflexionante, realizada pelo sujeito.

Com os progressos das estruturas espaciais "[...] quantidades crescentes das propriedades dos corpos e das ações tornam-se observáveis depois de terem sido, anteriormente, ou negligenciadas ou sistematicamente deformadas"²³ (p. 288). O conhecimento físico é abstraído dos objetos de conhecimento, enquanto o conhecimento lógico-matemático é abstraído da coordenação das ações que o sujeito exerce sobre os objetos. Assim, enquanto os objetos constituem a fonte do conhecimento físico, o sujeito constitui a fonte do conhecimento lógico-matemático.

Para Piaget²³, a abstração reflexionante é o princípio comum da formação de novidades cognitivas, pois diferentemente da abstração empírica, que produz conhecimento de forma indutiva ou extensiva, a abstração reflexionante conduz a generalizações. Nesse sentido, a cooperação entre as abstrações empíricas e reflexionantes é que permitirá a evolução de ambas, pois uma serve de suporte para a outra, já que as abstrações empíricas e reflexionantes envolvem deduções que proporcionam melhor compreensão sobre si e sobre o mundo.

É pertinente expor que deduções são produtos de construções do sujeito, ou seja, são novidades criadas pelo sistema cognitivo, como síntese entre possíveis criados e o necessário escolhido. Piaget²² destaca "que na medida em que uma escolha não é imposta e tende a tornar-se consciente enquanto escolha, os termos não retidos constituem, em razão disso, possíveis logo atualizáveis"²² (p. 101). A formação do necessário depende, assim, das possibilidades criadas pelo sujeito em sua interação com os objetos de conhecimento.

Na obra "O possível e o necessário: evolução dos possíveis na criança", Piaget²² procurou compreender o mecanismo formador de novos possíveis e seus experimentos permitiram comprovar que uma ideia ou possibilidade organizada pelo sujeito é capaz de desencadear novas ideias e possibilidades em um processo contínuo.

Nesse processo distinguiu três tipos de esquemas: os presentativos, os de procedimentos e os operatórios. Os esquemas presentativos são criados para compreensão do real; os esquemas de procedimentos consistem em meios orientados para um fim; já os esquemas operatórios integram as duas criações precedentes e organizam a forma de pensar dos sujeitos. Dessa forma, os sujeitos possuem dois grandes sistemas cognitivos que se complementam, os de possíveis, formados pelos esquemas presentativos, que se caracterizam por serem fechados, com esquemas e estruturas estáveis, e os gerados pelo sistema de procedimentos, que apresentam mobilidade contínua.

A formação de possíveis resulta, portanto, "de uma atividade acomodatícia em busca de sua forma de atualização, dependendo esta ao mesmo tempo da flexibilidade e solidez dos esquemas e das resistências do real"²² (p. 10). Nesse processo, os possíveis organizam-se de forma lógica e estrutural.

Se lógica, tem-se o possível hipotético, que envolve ensaios válidos e de erros; o possível atualizável, selecionado a partir dos resultados obtidos ou de esquemas presentativos; o possível dedutível, produto de variações intrínsecas; o possível exigível, quando o sujeito acredita que pode realizar novas construções, mas ainda não encontra os procedimentos adequados. Se estrutural, tem-se o possível analógico, no qual o sujeito realiza pequenas mudanças no objeto; o co-possível concreto, em que diversos possíveis a serem atualizados são simultaneamente antecipados; o co-possível abstrato, em que as atualizações são exemplos de outros concebíveis; o co-possível qualquer, em que são ilimitados e extinguem definitivamente as pseudonecessidades.

As pseudonecessidades constituem-se em limitações da formação de possíveis e se "prendem a uma indiferenciação inicial entre o real, o possível e o necessário", isto é, todo objeto ou ideia de esquemas que aparecem para o sujeito, não aparecem somente como sendo o que são, mas como necessariamente deveriam ser²² (p. 9). A ocorrência de pseudonecessidades evidencia o quanto a formação de possíveis não é consequência de associações livres e simples, mas consiste em aberturas reais que exigem liberação de limitações em graus diversos. Assim, "[...] para atingir novos possíveis não é suficiente imaginar em processos que visam a um objetivo qualquer [...]"²² (p. 10), pois é preciso a compensação da resistência do real, concebido como pseudonecessário.

As etapas de construção da noção espacial serão, portanto, produto dos processos cognitivos acima descritos. Sabemos que a formação de possíveis e a escolha de um necessário em cada momento do desenvolvimento do indivíduo fica evidente na constituição gradual, mas contínua dessa noção.

O desenvolvimento da inteligência humana, bem como o desenvolvimento das noções espaciais são descritos e classificados por Piaget²⁴ e seus colaboradores em quatro estádios: sensório-motor (0 a 2 anos), pré-operatório (2 a 7 anos), operatório concreto (7 a 11-12 anos) e operatório formal (11-12 anos em diante).

Primeiramente, o estádio sensório-motor tem início com o nascimento do indivíduo e estende-se mais ou menos até os 2 anos de vida. Em relação ao espaço, caracteriza-se pela diferenciação crescente entre seu corpo e os demais objetos de conhecimento com os quais convive, pessoas e coisas. Segundo Piaget²⁴, nesse estádio, o espaço não é único, pois existem tantos espaços quanto os movimentos que a criança realiza, como espaço bucal, tátil, visual, auditivo e postural. À medida que esses espaços se coordenam entre si, ocorre a organização de grupos de deslocamentos que permitem a construção de sequências reversíveis de ações coordenadas de seu corpo para atingir um fim. Esses grupos de deslocamentos vão permitindo gradualmente ao indivíduo situar-se e compreender o espaço.

Em "A construção do real na criança", Piaget²⁵ descreve o desenvolvimento do campo espacial no estádio sensório-motor, por meio das características de cinco grupos de deslocamento. O grupo prático ou heterogêneo (desde o nascimento até por volta dos 3 a 6 meses): comporta as características das duas primeiras etapas do período sensório-motor - exercícios dos puros reflexos, as primeiras adaptações adquiridas e a reação circular primária. Esse grupo é caracterizado pelo espaço prático, em que a criança ainda não compreende a permanência dos objetos sem sua ação. Ações pouco coordenadas, mas que permitem a ela executar movimentos e adaptar-se a formas e a dimensões. São as relações espaciais mais elementares denominadas topológicas.

O grupo de deslocamento denominado subjetivo (entre 4 a 9 meses) comporta as características da terceira e início da quarta etapa do estádio sensório-motor: reações circulares secundárias e as primeiras condutas inteligentes. Inicia-se com a coordenação dos grupos práticos, no qual, por exemplo, tudo que o bebê enxerga tende a ser agarrado. Essa coordenação visão-preensão possibilita a organização de vários esquemas de manipulação que favorecem o desenvolvimento da permanência dos objetos.

Os grupos de deslocamento objetivos (9 a 12 meses) comportam características da quarta etapa do período sensório-motor, em que a criança passa a se valer de meios já conhecidos para resolver situações novas para ela. Dos 12 a 18 meses tem-se o desenvolvimento de outro grupo objetivo, que comporta as características da quinta etapa do período sensório-motor: reações circulares terciárias, nas quais os objetos já podem ser compreendidos em seus deslocamentos, conforme a sucessão temporal dentro de seu campo de visão. Além disso, a criança passa a compreender a diferença entre seu movimento e o do objeto, tornando-se capaz de procurá-lo quando desaparece de sua visão.

O grupo representativo (18 a 24 meses) comporta características da sexta etapa do período sensório-motor: primeiras coordenações de ação interiorizadas. Nisso, o estabelecimento de relações dos objetos entre si e entre ela mesma torna o espaço representativo, uma vez que toma consciência dos movimentos de seu corpo e da ocorrência de movimentos de objetos fora do seu campo de percepção.

Mais tarde, Piaget & Inhelder¹⁸ utilizam as características dos cinco grupos de deslocamento como base para a descrição dos seis estádios de desenvolvimento do período sensório-motor descritos na obra "O nascimento da inteligência na criança"²⁴. Vale citar que os autores organizaram esses estádios em três grandes períodos, para explicar a construção da noção espacial descritos na sequência.

O primeiro dos três períodos de desenvolvimento do espaço contempla o primeiro e o segundo estádio do período sensório-motor (exercícios dos puros reflexos, primeiras adaptações adquiridas e reação circular primária). Caracteriza-se pela não coordenação dos diversos espaços sensoriais entre si, principalmente pela falta de coordenação entre o espaço visual e o espaço tátil-cinestésico, bem como pela não permanência do objeto sólido e a constância perceptiva das formas e grandezas. São, portanto, relações espaciais elementares, que dependem da estrutura perceptiva, e a relação de vizinhança entre os objetos faz parte desse primeiro período, que depende da proximidade ou da distância dos elementos percebidos em um mesmo campo.

A segunda relação espacial do primeiro período de desenvolvimento da noção de espaço é a separação. Nela, dois elementos vizinhos podem confundir-se, mas, quando se introduz o conceito de separação, é possível dissociá-los ou produzir um meio de distingui-los. A terceira a relação construída é de ordem espacial, que é estabelecida ao mesmo tempo que as relações de vizinhança e de separação. Ocorre quando o indivíduo segue ou realiza uma sequência de movimentos, ordenados tanto no espaço como no tempo.

As relações de interioridade podem ser dadas em uma, duas ou três das dimensões. Quando em uma sequência ordenada ABC, o elemento B é percebido entre seus vizinhos, A e C, daí tem-se a relação de interioridade de uma dimensão. Em duas dimensões, a relação de interioridade ocorre quando um elemento é percebido quando está rodeado por outros, por exemplo, o nariz enquadrado pelo rosto. A relação de interioridade em terceira dimensão demanda organizações mais elaboradas e requer a constituição das três relações constituídas anteriormente (vizinhança, separação e ordem). Essa relação possibilita que o bebê consiga encontrar um objeto dentro de uma caixa fechada, por exemplo, sem considerar que tal utensílio tenha sumido.

A relação espacial de continuidade e de descontinuidade é, ao mesmo tempo, síntese das relações anteriores e fator da construção das outras, desde o início da elaboração dessas relações. Nessa perspectiva, o sujeito começa a ter noção de continuidade, por meio dos deslocamentos, e essa percepção vai se modificando em função do aperfeiçoamento das atividades sensorimotrizes. Nisso, o objeto não é procurado em seu ponto de partida, mas conforme seus deslocamentos no espaço. O indivíduo, portanto, mantém sua atenção voltada única e exclusivamente ao objeto, que, consequentemente, serve de referência a ele para estabelecer relações espaciais com o seu meio.

O segundo período de desenvolvimento do espaço refere-se ao terceiro e ao quarto estádio do desenvolvimento sensório-motor (reações circulares secundárias e as primeiras condutas inteligentes), caracterizados pela coordenação da visão e da preensão e correspondem ao segundo período do desenvolvimento do espaço. No terceiro estádio, os esquemas de manipulação são controlados visualmente e, no quarto estádio, temos o início das relações inteligentes de meios e fins, sendo possível ocorrer a coordenação das ações entre si. Percebe-se, então, uma transformação profunda no espaço perceptivo, devido à sistematização dos movimentos guiados pela visão e pela preensão. Com a coordenação das ações, a permanência do objeto é elaborada, e a partir desse momento ocorre a coordenação simultânea das relações euclidianas (constância das dimensões) e projetivas (coordenação dos pontos de vista) sobre os objetos.

Para Piaget & Inhelder¹⁸, neste período (4 a 5 até 10 a 12 meses) ocorre a elaboração das figuras com a constância perceptiva. Os autores consideram que a percepção das formas euclidianas simples desenvolve-se com a idade, em função da atividade sensório-motriz, os movimentos do olhar, a exploração tátil, a análise imitativa, as transposições ativas, entre outros, e essas atividades desempenham um papel fundamental nessa construção. Ainda neste período, a forma e a grandeza tornam-se constantes, pois as duas pressupõem a organização simultânea das relações projetivas e das relações euclidianas.

Como explicam Piaget & Inhelder¹⁸, as relações projetivas e euclidianas são construídas juntas e apoiam-se umas nas outras, em razão da constância das formas ser resultado tanto das atividades sensório-motrizes como da coordenação de perspectivas. Assim, durante o primeiro período, as mudanças de perspectiva só são percebidas como transformações do próprio objeto e não como uma transformação dos pontos de vista relativos ao sujeito e o objeto.

O terceiro período do desenvolvimento do espaço refere-se ao quinto e sexto estádio do período sensório-motor (reações circulares terciárias e primeiras coordenações interiorizadas). Nesse ponto, inicia-se a coordenação das relações dos objetos entre si e as coordenações de ações tornam-se interiorizadas. Aparece a imagem mental como um prolongamento da imitação e os primeiros esboços de representação. Em seguida, torna-se possível a aquisição da função simbólica, da linguagem e do sistema dos signos coletivos, ou seja, o espaço puramente perceptivo torna-se representativo. E é por meio das coordenações sensório-motoras que se organizam os esquemas entre si, e a compreensão do espaço representativo somente existirá a partir do momento em que a criança conseguir entender o objeto em sua ausência.

Por não conhecer o espaço representativo, nesse período prevalece para a criança a vivência de situações corporais ligadas ao desenvolvimento espacial. Como explicam Piaget & Inhelder¹⁸ (p. 29), "[...] não existe nenhum movimento inserido numa "conduta" qualquer que não se apoie em percepções, nem alguma percepção que não seja inserida numa atividade que comporta elementos motores". Sendo assim, não é a percepção ou o movimento isolado que constituem o ponto de partida da análise das condutas, mas sim esquemas sensório-motores. Desse modo, a tomada de consciência da organização desses esquemas e da coordenação das ações levará a criança a novas aquisições em termos operacionais.

Dando sequência, o estádio pré-operatório realiza a transição entre a inteligência sensório-motora e a representativa e ocorre entre os 2 e os 6/7 anos, lembrando que essas transformações são lentas e sucessivas. Para Piaget & Inhelder¹⁸, somente após as relações estabelecidas pela criança em nível sensório-motor é que ela será capaz de partir para as conquistas futuras da representação espacial. Segundo os autores, somente ao atingir o pensamento representativo que a criança terá condições de reconstruir o objeto, o tempo, o espaço, as categorias lógicas de classes e as relações entre esses objetos. Essa representação se processará por meio de uma reconstrução que não envolverá mais as atividades perceptivas, mas a função simbólica.

No estádio operatório concreto, que se inicia em geral por volta dos 7 anos de idade, a atividade cognitiva da criança é operatória. Ela tem condições de descentrar-se ao acompanhar as transformações sucessivas do objeto para apreendê-lo como um todo. Essa interiorização da ação possui características de reversibilidade que a ajudará na construção de novos invariantes cognitivos: conservação de comprimento, de distâncias, de quantidades discretas e contínuas, de quantidades físicas (peso, substância, volume etc).

Nesse estádio, as relações espaciais tornam-se projetivas e reversíveis, e isso significa que a interiorização das ações físicas começa a ser considerada operação mental, podendo ser representada. Pode-se dizer que a incapacidade de se colocar no ponto de vista de outros é superada e a criança começa a estabelecer relações e a coordenar pontos de vista diferentes e integrá-los de modo lógico e coerente. Essa crescente compreensão da conservação das propriedades físicas dos objetos, como quantidade, peso e volume, das classificações e das seriações, permitirá mais tarde à criança operar com as noções de número e de espaço, porém, a criança ainda precisa do mundo concreto para relacionar diferentes aspectos e abstrair dados da realidade.

Com o estádio operatório formal (12 anos em diante), o adolescente torna-se capaz de raciocinar e deduzir, não somente sobre objetos manipuláveis, mas sobre hipóteses e proposições. Torna-se, ainda, capaz de manipular hipóteses de maneira formal e hipotético-dedutiva, bem como raciocinar a partir do ponto de vista do outro. No que diz respeito às noções espaciais, as relações topológicas, projetivas e euclidianas tendem a estar plenamente elaboradas e prontas para formalização.

Desse modo, retomamos as conclusões de Piaget & Inhelder¹⁸ de que a topologia é um dos primeiros dados da construção geométrica, seguidos das noções projetivas e euclidianas. Além disso, as pesquisas citadas ao longo desse trabalho destacam que a compreensão espacial é necessária para que o indivíduo possa ter diversas oportunidades de exploração de tamanho, de direção e de posição no espaço, permitindo a ele interpretar e compreender os objetos, classificando-os e organizando-os, de acordo com suas propriedades.

Durante a coleta de dados realizada para essa pesquisa, foi possível observar que os conhecimentos geométricos propostos pelo Currículo Básico para escolas públicas do Estado do Paraná³ tanto para Educação Infantil como para o Ensino Fundamental, em sua maioria, são fundamentados no domínio espacial de campos mais reduzidos como uma folha de papel.

Com base na teoria piagetiana podemos afirmar que essa sequência não é adequada para a construção do conhecimento espacial. Como mostram as pesquisas de Piaget¹⁸ e seus colaboradores, esse processo se inicia pela construção topológica e, na sequência, as relações projetivas e euclidianas. Apesar disso, o ensino de geometria continua iniciando o ensino de geometria pelas relações projetivas e euclidianas antes das topológicas que envolvem as relações entre o corpo e o meio que o rodeia. Como consequência, a falta de um trabalho que envolva inicialmente os espaços topológicos tem provocado lacunas na construção do espaço tridimensional e prejudica as atividades geométricas que envolvem a bidimensionalidade, como as de lápis e papel.

A partir do referencial teórico adotado entendemos que os jogos de regras, por meio de sua estrutura e funcionamento, desenvolvem conceitos, estratégias de pensamento e princípios morais, tornando os indivíduos mais conscientes de suas soluções. Além disso, com as intervenções pedagógicas desenvolvidas é possível investigar como os sujeitos constroem as noções espaciais. Dessa forma, o jogo Katamino, além de possibilitar o desenvolvimento de habilidades geométricas, foi capaz de oferecer condições de promover a evolução da criatividade lógica por meio da construção dos possíveis e do necessário.

Consideramos que ao organizar novas estratégias as crianças criam procedimentos de acordo com sua capacidade de antecipação e atualização. Para Brenelli²⁶ (p. 176), "como os jogos permitem à criança inventar novos procedimentos, constituem contextos excelentes para a construção do possível e do necessário". Nesse sentido, os possíveis "dizem respeito aos diferentes meios de se alcançar o resultado, e a necessidade à coerência e à integração dos meios em função dos resultados".

Encontramos em Piaget²² reforço à nossa posição quando ressalta que a cada novo procedimento realizado pelo sujeito em situação de jogo surge uma nova criação, isto quer dizer que novas possibilidades se atualizam. Sabe-se que a cada contato com o objeto de conhecimento o sujeito realiza interpretações abstraindo as propriedades desse objeto. Assim, a cada novo possível as interpretações dos sujeitos se tornam cada vez maiores e mais complexas. Podemos dizer que o jogo de regra, ao exigir estratégias na resolução de situações-problema, relaciona-se com a formação de possíveis na medida em que exige do sujeito diversos procedimentos para ganhar a partida.

Estudos como o de Amaral²⁷ evidenciam a necessidade de que professores e estudantes sejam capazes de solucionar criativamente situações-problema da vida escolar contemporânea. Isto significa criar novidades, produzir novos conhecimentos e também saber lidar com os saberes novos produzidos pelo outro. Dentro da teoria piagetiana, as condições intelectuais para a abertura dos indivíduos ao novo, ao diferente e, portanto, aos pontos de vista diferentes dos seus estão presentes no conceito de criação de possíveis. Criar possíveis infinitos prepara intelectualmente o indivíduo para criar e aceitar a novidade.

Desse modo, o jogo oportuniza os dois tipos de perturbações prováveis no sistema intelectual: as que se opõem às acomodações que são responsáveis pelos erros e fracassos e aquelas que consistem em lacunas que deixam as necessidades insatisfeitas, pois os esquemas assimilativos são insuficientemente alimentados. Ao agir sobre o objeto de conhecimento, incluindo o pensar sobre, o sujeito pode vir a tornar sua ação ou ideia possível, desde que seja capaz de compreender que existem essas possibilidades e que tais possibilidades precisam enfrentar os limites do que é necessário naquele momento ou situação tendo em vista o contexto.

 

PROCEDIMENTOS METODOLÓGICOS

De abordagem qualitativa, a pesquisa caracterizou-se como descritiva. Valentim²⁸ reporta que com essa abordagem é possível observar, registrar, correlacionar e descrever os fatos ou fenômenos de uma determinada realidade sem manipulá-los. Na pesquisa descritiva por meio da descrição e análise de observações advindas de uma situação experimental, no caso proporcionada pelo contexto do jogo, os problemas podem ser resolvidos e as práticas podem ser melhoradas. Dessa forma, a perspectiva de pesquisa adotada é compatível com o método clínico crítico piagetiano. Assim, dentre as possibilidades de se problematizar e de interpretar a realidade, adotamos a perspectiva teórico-metodológica da Epistemologia Genética de Jean Piaget, que concebe o conhecimento como uma construção psicossocial e contínua. Assumimos, assim, que os resultados, as discussões e as conclusões produzidas nessa pesquisa poderiam ser outros, se não fossem fundamentados na perspectiva piagetiana, da qual derivou nosso problema, bem como o delineamento da investigação.

O presente estudo tem como hipótese conceitual de que a aprendizagem de noções espaciais pode ser favorecida por meio de intervenção pedagógica construtivista com jogos de regras e formação de possíveis e do necessário. Para verificação da hipótese, antes e depois do processo de intervenção pedagógica construtivista, foi realizada uma bateria de provas sobre noções espaciais adaptados de Piaget & Inhelder¹⁸. As provas aplicados foram "O relacionamento das perspectivas", "Os sistemas de referência e as coordenadas: a horizontal e a vertical" e "Os esquemas topográficos e o mapa da aldeia". Também foi aplicada a prova de Piaget²² "A construção de arranjos espaciais e equidistâncias". Além disso, com o intuito de buscarmos respostas para o problema levantado e verificarmos nossa hipótese, realizamos antes e depois do processo de intervenção pedagógica a aplicação de uma avaliação com nove exercícios sobre conteúdos matemáticos, mais especificamente atividades que envolviam noções de Espaço e Forma e/ou Geometria.

Participaram da pesquisa 10 alunos do 5^o ano do Ensino Fundamental com faixa etária entre 9 e 10 anos que frequentam a sala de acompanhamento pedagógico de uma escola do município de Maringá-PR, devidamente matriculados. Esses sujeitos participaram do processo de intervenção pedagógica e foram organizados individualmente, em duplas e quintetos.

Foram oito sessões de intervenção pedagógica^**, organizada com o jogo Katamino e adaptação do método clínico, sistematizado por Jean Piaget²⁹ e contou com questões específicas de possíveis e necessários²². Vale ressaltar que, todos os procedimentos referentes ao critério de inclusão e exclusão de participantes, instrumento de aferição dos resultados, organização dos grupos de participantes para análise dos dados, avaliação das perdas do estudo, o consentimento de pós-informado e a descrição da avaliação estatística das variáveis do estudo são descritas na tese já mencionada. Além de que, os princípios éticos do referido estudo envolvendo seres humanos foram preservados e constam no parecer consubstanciado de aprovação do comitê de ética de pesquisa envolvendo seres humanos da Universidade Estadual de Maringá - (UEM), com o nº 3.766.034 e CAAE n^o 33175814.8.0000.0104.

 

RESULTADOS E DISCUSSÕES

Em relação ao desempenho escolar, podemos evidenciar crescimento dos alunos em seu desempenho quanto ao aumento da quantidade de acertos das questões relativas às noções espaciais (Gráfico 1). Os resultados mostram que os alunos-participantes melhoraram seu desempenho em solução de problemas sobre espaço e forma, passando de dois para oito acertos em uma avaliação com nove questões. Tais dados levam-nos a supor que o crescimento dos resultados desses alunos deve-se ao uso do jogo Katamino, que envolve noções espaciais, acompanhado de intervenção pedagógica com abordagem construtivista, e, portanto, reflexão, verbalização e reorganização de seus procedimentos de jogo.

 

 

No pré-teste, três crianças acertaram duas questões; duas acertaram três; três acertaram quatro e duas acertaram cinco. No pós-teste, percebe-se um movimento bastante intenso de migração de crianças apresentando um número maior de acertos, no qual uma criança passou a acertar cinco questões; cinco crianças, seis questões; duas passam a sete questões e duas passaram a acertar oito questões.

Comparando os resultados do pré-teste com os do pós-teste, verificamos acréscimo de acertos em praticamente todas as questões de parte do conjunto de estudantes-participantes da pesquisa. Além desse aumento da quantidade de acertos, também constatamos modificações na forma como as crianças passaram a resolver as atividades propostas. Mais uma vez supomos que o progresso de seu desempenho, agora nas provas sobre conteúdos geométricos, ocorrido no intervalo de tempo compreendido entre o pré-teste e o pós-teste, pode ter sido favorecido pelo uso do jogo acompanhado da mediação clínica da pesquisadora. Consideramos que o uso do jogo Katamino cujo conteúdo envolve noções espaciais bi e tridimensionais acabou por favorecer o estabelecimento de novos sentidos aos conceitos geométricos aprendidos na escola. Sobre esse aspecto podemos ressaltar as condutas de STE (9,7) ao resolver a seguinte atividade

Paulo está fazendo uma reforma em um salão de festa e precisa cobrir toda a superfície com cerâmicas. Cada cerâmica possui 1 metro quadrado (1m²), veja a figura abaixo: Quantos metros quadrados (m²) de cerâmica ele precisará para revestir a superfície toda contando com a parte já preenchida?

 

 

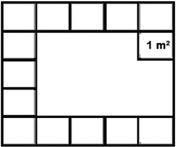
Para resolver esse exercício, no primeiro teste, STE (9,7) termina de fazer os quadrinhos com o lápis, conta todas as partes e responde que precisará de 25 m² de cerâmica para revestir a superfície. Mesmo acertando a questão, questionamos sobre o que ela fez para resolver a atividade: "Eu pensei que cada quadradinho tem 1 (um) metro e se a gente terminar de fazer os quadradinhos e contar os quadradinhos vai dar 25 quadradinhos" STE (9,7).

Entretanto, no pós-teste STE (9,7) também acerta a questão respondendo que precisará de 25 m² de cerâmica para revestir a superfície, no entanto, utiliza outra forma de realizar a atividade. Faz a contagem da quantidade de quadrados da base e multiplica-os pela altura. Ao ser perguntada sobre como ela fez para resolver a atividade, responde: "Eu fiz assim porque é mais fácil eu contar as colunas e as linhas e fazer uma conta de vezes" STE (9,7). A modificação da estratégia de resolução da tarefa proposta não modificou o resultado correto da questão proposta, mas sugere um dar-se conta de outras maneiras de resolver um mesmo problema.

Essa conduta de STE (9,7) pode ser considerada relevante se levamos em conta o conjunto de suas atividades na quais apresentou o mesmo movimento. O que também foi observado entre o grupo de crianças pesquisadas que não somente melhoraram seu desempenho quanto a quantidade de acertos (Gráfico 1), mas também modificaram procedimentos de resolução das tarefas no segundo teste tendo ou não acertado no primeiro.

Esses resultados nos levam a concordar com Piaget²² quando afirma que não é possível conceber esses processos em termos de simples transferências a situações novas, mas sim um processo que demanda uma reorganização mental. Entendemos que não basta a criança ser submetida à resolução de problemas, mas é de fundamental importância que se dê a ela a oportunidade de pensar sobre as suas ações, de estabelecer relações entre o contexto específico de resolução e outros contextos mais ou menos semelhantes a ele, como foi o caso do jogo Katamino.

Nossa hipótese explicativa para a elaboração de novas estratégias de resolução das atividades de geometria por parte dos estudantes é de que atividades lúdicas como o jogo Katamino, desde que mediadas por uma abordagem construtivista, contribuem para o estabelecimento de relações entre um contexto (jogo) e outro (atividades geométricas escolares). Parece-nos ter ocorrido a construção de novos esquemas procedimentais que ao se consolidarem como presentativos disponíveis no sistema cognitivo das crianças favoreceram a melhor resolução das tarefas escolares sobre geometria.

Concluindo, destacamos que os resultados vão ao encontro dos encontrados por Bonon¹⁹, Kobayashi²⁰, Rodrigues¹⁴, Pereira¹⁶ e Moniz²¹ que, fundamentados no construtivismo, mostram as defasagens das crianças na área espacial. Devido a isso, enfatizam a necessidade de a escola modificar sua forma de abordar essas noções, uma vez que nesses estudos identificaram uma contradição na sequência em que o domínio espacial é apresentado. Convencionalmente, a escola inicia esse tema pelas relações projetivas e euclidianas (figuras geométricas) e, na maioria das vezes, não desenvolve noções topológicas.

Dessa forma, os resultados das provas de problemas escolares sobre Geometria e/ou Espaço e Forma confirmam a hipótese da presente pesquisa sobre a possibilidade de melhoria do desempenho em noções espaciais por parte de alunos submetidos a intervenção pedagógica com as características apresentadas em nosso estudo. Destacamos que as crianças investigadas não somente melhoraram seu desempenho em termos de aumento quantitativo de acertos nos problemas, como também ampliaram suas estratégias de resolução. Os alunos que, no início da pesquisa (pré-teste), resolveram as atividades por meio de tentativa ou erro e/ou de forma intuitiva, no pós-teste manifestaram ampliação de suas estratégias de resolução, isto é, ampliaram sua criação de possíveis - sua criatividade lógica.

Ainda, os dados demonstram que o aumento do número de acertos realizados pelas crianças investigadas foi decorrente da variável controlada na pesquisa, a intervenção pedagógica construtivista, realizada com o jogo Katamino.

Vale ressaltar que, entre os alunos-participantes, ao final da nossa intervenção, três haviam sido liberados das atividades de acompanhamento pedagógico indicado para crianças com dificuldades de aprendizagem, principalmente dificuldades nos conteúdos que envolvem tratamento de informações. Para esses alunos, a apresentação das situações problemas, proporcionadas pelo jogo Katamino, parece ter oferecido melhores condições de aprendizagem do que a oferecida no ambiente de sala de aula. Os resultados confirmam a possibilidade de modificação dos procedimentos de resolução de alunos que receberam conceitos próprios do conteúdo de Espaço e de Forma e/ou Geometria, por meio da intervenção pedagógica. Os resultados gerais dos participantes viabilizam nossa hipótese de que a melhoria de desempenho desses três alunos deveu-se em parte ao processo de intervenção pedagógica do qual participaram, confirmando resultados de pesquisas anteriores, como as de Fávero^6,7, Saladini¹³, Rodrigues¹⁴, Pereira^16,30, Rabassi¹⁷ e Melo⁵, e na qual alunos com dificuldades de aprendizagem se beneficiaram de uma intervenção de caráter construtivista, com o objetivo de desenvolvimento cognitivo.

Além disso, o nível de acertos obtidos pelas crianças no pré-teste não foi compatível com os dados fornecidos pela Avaliação Nacional do Rendimento Escolar - PROVA BRASIL³¹ dos alunos da Região Sul, local em que foi realizada a pesquisa. De acordo com esses dados, 21,17% das crianças apresentam o desempenho em matemática identificado no nível cinco (desempenho maior ou igual 225 e menor que 250 pontos). Com essa pontuação, no que diz respeito aos conteúdos de Espaço e de Forma e/ou Geometria, as crianças são capazes de reconhecer a planificação de um cubo dentre um conjunto de planificações apresentadas. Foi somente no pós-teste que a maioria das crianças conseguiram realizar as atividades que envolviam essas características. Podemos dizer que, ainda, esse desempenho obtido pelas crianças tem se mantido em um nível de rendimento abaixo do esperado para o final do quinto ano do Ensino Fundamental, já que a classificação máxima dessa avaliação é de nível dez.

 

CONSIDERAÇÕES FINAIS

Os dados coletados e analisados neste trabalho confirmam a hipótese do estudo de que os conteúdos de Espaço e Forma e/ou Geometria de estudantes pode ser desenvolvida por meio da construção do possível e do necessário com uso do jogo Katamino mediado por um processo de intervenção pedagógica construtivista da pesquisadora.

Os resultados apontam que o uso do jogo de regra Katamino contribuiu para mudanças nas condutas de construção de possíveis favorecendo mudanças estruturais, com evolução de estádios em todas as crianças investigadas. Subentende-se que essas mudanças foram provocadas pelo uso do jogo Katamino e das características da intervenção pedagógica realizada, que baseada no método clínico exigiu a reflexão e a verbalização dos procedimentos de jogo por parte das crianças.

Esses dados sugerem também que uma metodologia baseada no método clínico com desenvolvimento do possível e do necessário aplicada ao jogo Katamino foi capaz de contribuir para a construção de estruturas procedimentais e presentativas dos estudantes, bem como facilitar a aprendizagem de conceitos geométricos. Essa conclusão é comprovada pelos resultados dos estudantes nas provas escolares sobre conceitos espaciais em que o aumento da quantidade de acertos mostrou-se significativa. Além da significância estatística do aumento de acertos, as explicações e justificativas dos estudantes sobre as respostas fornecidas na prova de conteúdos geométricos após as intervenções pedagógicas mostraram-se qualitativamente importantes.

Os resultados de nossa pesquisa reforçam os de estudos anteriores de que as dificuldades de aprendizagem em geometria se devem ao não respeito da escola e dos livros didáticos ao desenvolvimento das noções espaciais das crianças, iniciando-o pelas relações espaciais projetivas e euclidianas antes das noções topológicas. Concordamos com Souza¹⁰ que a geometria deve ser desenvolvida de forma a promover "experiências de aprendizagem com a intenção de oportunizar uma forma específica de ação/pensamento, próprio da geometria" (p. 46).

Diante dos resultados, fica evidente que promover uma forma de trabalho com base nos pressupostos construtivista utilizando jogos na escola é algo possível. Mas, é necessário que o professor compreenda as características dessa intervenção e reconheça todas as potencialidades do jogo. Para reestruturamos nossa prática pedagógica com os alunos, devemos rever nossas concepções teóricas.

Como mostram estudos recentes, as práticas educativas vêm enfatizando conteúdos numéricos em detrimento dos geométricos, atividades de lápis e papel em detrimento daquelas de jogo. Analisamos que essa conduta se deve, em parte, ao desconhecimento e a má formação dos docentes sobre a construção das noções geométricas, levando-os a uma abordagem empirista de ensino-aprendizagem. Há, portanto, limitação de atividades de manipulação (espaço perceptivo) e insuficientes para o alcance de níveis operatórios nos conhecimentos espaciais.

Como professores, faz-se necessário compreendermos que um conteúdo geométrico está ligado a noções espaciais de cunho topológico. Essas noções são progressivamente construídas, até a elaboração das estruturas projetivas e euclidianas. Dessa forma, devemos considerar como prioridade a construção desses elementos espaciais mais primitivos, com atividades investigativas, desde os anos iniciais, para que haja a consolidação das ideias mais complexas.

Sabemos que a escola tem como uma das funções mais importantes ensinar e sistematizar conhecimentos científicos, porém, para a criança, essa função, muitas vezes, torna-se abstrata e distante da sua realidade. De acordo com Macedo³² (p. 10), a escola deve permitir que os alunos e os professores sejam criativos para com a construção do seu conhecimento. Por essa razão, na concepção construtivista, o jogo é considerado uma prática educativa importante para este fim, uma vez que os professores podem ensinar os conteúdos escolares como conceitos e formas de pensar com maior sentido para os estudantes. Os jogos oferecem situações-problema impregnadas de desafios e de estratégias para resolução que exploram a ludicidade, a função simbólica, regras, competição, cooperação e operatoriedade, entre outros conteúdos relevantes para a formação dos indivíduos.

 

REFERÊNCIAS

1. Brasil. Ministério da Educação. Secretaria de Educação Fundamental. Parâmetros curriculares nacionais. Brasília, DF: MEC/SEF; 1997.         [ Links ]

2. Paraná. Secretaria de Estado da Educação. Diretrizes curriculares da educação básica: matemática. Curitiba: Secretaria de Estado da Educação do Paraná; 2008.         [ Links ]

3. Paraná. Secretaria de Estado da Educação. Currículo básico para a escola pública do estado do Paraná. Curitiba: Secretaria de Estado da Educação do Paraná; 2003 [acesso 2014 Ago 20]. Disponível em: https://www.fasul.edu.br/portal/app/webroot/files/links/legislacao_educacional/CURRICULO_ BASICO_PARA_A_ESCOLA_PUBLICA_DO_ESTADO_DO_PARANA.pdf        [ Links ]

4. Maringá. Prefeitura do Município de Maringá. Secretaria de Educação. Currículo da educação infantil e anos iniciais do ensino fundamental. Maringá, PR: SEDUC; 2012.         [ Links ]

5. Melo KMS. A tomada de consciência das estratégias do jogo Sudoku por parte de docentes do Ensino Fundamental [Dissertação]. Maringá: Universidade Estadual de Maringá; 2012.         [ Links ]

6. Fávero MTM. Desenvolvimento psicomotor e aprendizagem da escrita [Dissertação]. Maringá, PR: Universidade Estadual de Maringá; 2004.         [ Links ]

7. Fávero MTM. Comportamento psicomotor, dificuldades de aprendizagem em escrita e habilidades cognitivas verbais e não verbais: contribuições de um programa de intervenção psicomotora em crianças [Tese]. Maringá, PR: Universidade Estadual de Maringá; 2016.         [ Links ]

8. Fonseca V. Desenvolvimento Psicomotor e Aprendizagem. Porto Alegre, RS: Artmed; 2008.         [ Links ]

9. Pereira K. Perfil psicomotor: caracterização de escolares da primeira série do ensino fundamental de colégio particular [Dissertação]. São Carlos, SP: Universidade Federal de São Carlos; 2005.         [ Links ]

10. Souza S. Geometria na educação infantil: da manipulação empirista ao concreto piagetiano [Dissertação]. Maringá, PR: Universidade Estadual de Maringá; 2007.         [ Links ]

11. Oliveira GC. Psicomotricidade: Um estudo em escolares com dificuldades em leitura e escrita [Dissertação]. Campinas, SP: Universidade Estadual de Campinas; 1992. 277 f.         [ Links ]

12. Porto IMR. Brinquedos e brincadeiras na Educação Infantil: Construindo conhecimento em geografia [Dissertação]. São Luís, MA: Universidade Federal do Maranhão; 2003.         [ Links ]

13. Saladini AC. A educação física e a tomada de consciência da ação motora da criança [Tese]. Marília, SP: Universidade Estadual Paulista (UNESP); 2006.         [ Links ]

14. Rodrigues MCP. O ensino-aprendizagem em dança na construção das noções de espaço e de tempo [Dissertação]. Porto Alegre, RS: Universidade Federal do Rio Grande do Sul (UFRS); 2007.         [ Links ]

15. Cezar KPL. Acentolândia: criação e aplicações de um jogo de regras sobre acentuação gráfica para séries iniciais do ensino fundamental [Dissertação]. Maringá, PR: Universidade Estadual de Maringá; 2009.         [ Links ]

16. Pereira LA. Prevenção de dificuldades na construção do espaço topológico por meio de intervenção pedagógica com ênfase na área psicomotora e tomada de consciência com alunos da educação infantil [Dissertação]. Maringá, PR: Universidade Estadual de Maringá; 2009. 145 p.         [ Links ]

17. Rabassi LKBC. Brincadeiras cantadas: uma intervenção pedagógica para a construção da estrutura ritma binária [Dissertação]. Maringá, PR: Universidade Estadual de Maringá; 2011. 145 f.         [ Links ]

18. Piaget J, Inhelder B. A representação do espaço na criança. Porto Alegre, RS: Artes Médicas; 1993.         [ Links ]

19. Bonon LHP. O processo de construção das noções espaciais topológicas na interação da criança com o seu meio ambiente [Dissertação]. Campinas, SP: Universidade Estadual de Campinas, Faculdade de Educação; 1987.         [ Links ]

20. Kobayashi MCM. A construção da geometria pela criança. Bauru, SP: EDUSC; 2001.         [ Links ]

21. Moniz CMV. Visualização espacial na perspectiva da Epistemologia Genética [Dissertação]. Porto Alegre, RS: Universidade Federal do Rio Grande do Sul; 2013.         [ Links ]

22. Piaget J. O possível e o necessário: evolução dos possíveis na criança. Volume 1. Porto Alegre, RS: Artes Médicas; 1985.         [ Links ]

23. Piaget J. Abstração reflexionante: relações lógico aritméticas e ordem das relações espaciais. Porto Alegre, RS: Artmed; 1995.         [ Links ]

24. Piaget J. El nacimiento de la inteligencia em el niño. Buenos Aires: Crítica; 2009.         [ Links ]

25. Piaget J. A construção do real na criança. Tradução: Ramon Américo Vasques. São Paulo, SP: Ática; 2006.         [ Links ]

26. Brenelli RP. O jogo como espaço para se pensar: a construção de noções lógicas e aritméticas. Campinas, SP: Papirus; 1996.         [ Links ]

27. Amaral TC. Descentração cognitiva e esfera pública dialógica nas primeiras séries escolares? Um estudo exploratório [Dissertação]. Maringá, PR: Universidade Estadual de Maringá; 2013.         [ Links ]

28. Valentim MLP. Métodos de Pesquisa em Ciência da Informação. São Paulo, DP: Polis; 2005.         [ Links ]

29. Piaget J. A representação do mundo na criança. Aparecida, SP: Idéias e Letras; 2005.         [ Links ]

30. Pereira-Peres LA. "Eu jogo fazendo todas as maneiras que eu consigo": como criar possibilidades de novas relações espaciais por meio do jogo Katamino [Tese]. Maringá, PR: Universidade Estadual de Maringá; 2017. 155 p.         [ Links ]

31. Brasil. Ministério da Educação. Instituto Nacional de Estudos e Pesquisas Educacionais (INEP). Boletim de desempenho da avaliação do rendimento escolar: Prova Brasil. Brasília, DF: Ministério da Educação; 2015.         [ Links ]

32. Macedo L. Os jogos e sua importância na escola. Cad Pesqui. 1995;93:5-10.         [ Links ]

 

 

Endereço para correspondência:
Lilian Alves Pereira Peres
Rua Diogo Zuliani, 798 - Maringá, PR, Brasil
CEP 87033-030
E-mail: lilianalvespereira@hotmail.com

Artigo recebido: 28/12/2019
Aprovado: 17/10/2020

 

 

Trabalho realizado Universidade Estadual de Maringá (UEM); Escola Municipal de Ensino Fundamental Silvino Dias, Maringá, PR, Brasil.
Conflito de interesses: As autoras declaram não haver.
* Nessa pesquisa adotaremos o termo Espaço e Forma e/ou Geometria como bloco de conteúdos matemáticos, pois essa nomenclatura está presente nos documentos oficiais.
** Para verificar o detalhamento completo da intervenção ler Pereira-Peres LA. "Eu jogo fazendo todas as maneiras que eu consigo": como criar possibilidades de novas relações espaciais por meio do jogo Katamino [Tese]. Maringá, PR: Universidade Estadual de Maringá; 2017. 155 p. Disponível em: http://www.ppe.uem.br/teses/2017/2017%20-%20Lilian%20Alves%20Pereira%20Peres.pdf