Psico
ISSN 1980-8623
Psico (Porto Alegre) vol.47 no.1 Porto Alegre 2016
https://doi.org/10.15448/1980-8623.2016.1.18924
ARTIGO ORIGINAL
http://dx.doi.org/10.15448/1980-8623.2016.1.18924
Relação entre habilidades cognitivas de processamento visual e inteligência fluida com o desempenho em aritmética
Relationship between cognitive abilities of visual processing and fluid intelligence with arithmetic performance
Relación entre las habilidades cognitivas del procesamiento visual y inteligencia fluida con el rendimiento en aritmética
Tatiana Pontrelli MeccaI; Natália Martins DiasI; Alessandra Gotuzo SeabraII; Tatiana Abrão JanaII; Elizeu Coutinho de MacedoII
ICentro Universitário Fieo. Osasco, SP, Brasil
IIUniversidade Presbiteriana Mackenzie. São Paulo, SP, Brasil
RESUMO
O objetivo deste estudo foi verificar a relação entre habilidades cognitivas de processamento visual e inteligência fluida, avaliadas pela Leiter-R, e desempenho em aritmética de estudantes do Ensino Fundamental I. Foram avaliadas 51 crianças entre 7 e 8 anos de idade (52,94% meninos e 47,06% meninas), pertencentes ao 2º e 3º ano de escolas pública e privada. Correlações positivas, significativas e de magnitude moderada foram observadas entre os subtestes de Analogias e Sequências com habilidades de processamento numérico e cálculo da Prova de Aritmética. Ambos explicaram 25% da variância em aritmética. Ao analisar os dados separadamente por tipo de escola, resultados semelhantes foram verificados para escola particular, porém poucas correlações foram observadas com crianças de escola pública. Os achados corroboram a literatura no que tange às relações entre habilidades cognitivas e desempenho em aritmética, ressaltando a importância do tipo de escola como variável a ser considerada nestes estudos.
Palavras-chave: Inteligência; Raciocínio indutivo; Discriminação visual; Processamento numérico; Cálculo.
ABSTRACT
The aim of this study was to investigate the relationship between cognitive skills like visual processing and fluid intelligence assessed by the Leiter-R and arithmetic performance in elementary school students. 51 children were evaluated between 7 and 8 years of age (52.94% boys and 47.06% girls), belonging to the 2nd and 3rd years of public and private schools. Positive, significant and moderate correlations were observed between the Analogies and Sequential Order Subtests of the Leiter-R with arithmetic skills like numerical processing and calculation. Both explained 25% of variance in arithmetic. By analyzing the data separately by school, similar results were obtained for private school, but few correlations were observed with children in public school. The findings of this study support the literature regarding the relationship between cognitive abilities and performance in arithmetic, emphasizing the importance of school type as the variable to be considered in these studies.
Keywords: Intelligence; Inductive reasoning; Visual discrimination; Numeric processing; Calculation.
RESUMEN
El objetivo de este estudio fue investigar la relación entre la inteligencia fluida y procesamiento visual, evaluado por el Leiter-R, y aritmética de los estudiantes de Escuela Elemental I. 51 niños fueron evaluados entre 7 y 8 años de edad (52,94% hombres; 47.06% mujeres), pertenecientes a la 2º y 3º años de escuelas públicas y privadas. Se observaron correlaciones positivas, significativas y de magnitud moderada entre los subtests Secuencias y Analogías con habilidades de procesamiento numérico y cálculo. Tanto explicó 25% de la varianza en la aritmética. Al analizar los datos por tipo de escuela, se obtuvieron resultados similares para la escuela privada, pero pocas correlaciones se observaron con los niños en escuela pública. Los hallazgos apoyan la literatura sobre la relación entre las capacidades cognitivas y el rendimiento en aritmética, haciendo hincapié en la importancia de la escuela como el tipo de variable a considerar en estos estudios.
Palabras clave: Inteligencia; Raciocinio inductivo; Discriminación visual; Procesamiento numérico; Cálculo.
Introdução
O modelo psicométrico vigente sobre a estrutura da inteligência, denominado Cattell-Horn-Carroll (C-H-C), a compreende como multifatorial, ou seja, composto por habilidades cognitivas distintas, porém interrelacionadas e dispostas em níveis de generalidade. De acordo com o modelo CHC, atualmente existem 16 dimensões ou fatores amplos: Inteligência Fluida (Gf), Memória de Curto Prazo (Gsm), Memória de Longo Prazo (Glr), Rapidez Cognitiva (Gs), Velocidade de Reação e Decisão (Gt), Velocidade Psicomotora (Gps), Conhecimento/Compreensão (Gc), Conhecimento Específico (Gkn), Leitura e Escrita (Grw), Conhecimento Quantitativo (Gq), Processamento Visual (Gv), Processamento Auditivo (Ga), Habilidades Olfativas, (Go) Táteis (Gh), Cinestésicas (Gk) e Psicomotoras (Gp). Cada dimensão ampla é abarcada por fatores específicos. No caso da Gf, por exemplo, fazem parte habilidades específicas de raciocínio indutivo, sequencial e quantitativo, enquanto que na dimensão Conhecimento/Compreensão (semelhante ao que se denominava Inteligência Cristalizada) estão subjacentes fatores específicos como informação verbal geral, desenvolvimento da linguagem e conhecimento lexical (Schneider & McGrew, 2012).
Há uma vasta literatura a respeito das relações entre inteligência e o desempenho acadêmico (Alloway & Gregory, 2013; Gomes, 2010; Lu, Weber, Spinath & Shi, 2011; Mól & Wechsler, 2008; Pereira & Almeida, 2010; Primi, Ferrão & Almeida, 2010). De acordo com Gomes e Golino (2012) há evidências de que tanto habilidades específicas, quanto habilidades amplas e o fator geral predizem em torno de 30 a 60% do desempenho acadêmico geral.
No entanto, alguns estudos especificam a relação entre inteligência e desempenho acadêmico em aritmética (Lu et al., 2011; Primi, Santos & Vendramini, 2002; Stock, Desoete & Roeyers, 2009). Gomes e Golino (2012) verificaram que inteligência fluida explica, de maneira indireta (mediada pelo desenvolvimento acadêmico), cerca de 34% da variância das diferenças de desenvolvimento em matemática. Considerando estes aspectos do desenvolvimento, Stock et al. (2009) verificaram que raciocínio sequencial (ou habilidade de seriação) e classificação na pré-escola são preditores importantes das habilidades aritméticas nos anos iniciais do Ensino Fundamental I. Ao final desta etapa de escolarização, inteligência, juntamente com memória de trabalho, explicam 36% da variância nos escores em matemática (Lu et al., 2011). Já em estudantes universitários, a inteligência fluida se correlacionou de forma positiva, significativa e com magnitude moderada com o desempenho de alunos nos cursos de Matemática, Engenharia Civil e Medicina (Primi et al., 2002). Neste sentido, a inteligência fluida tem se mostrado relacionada ao desempenho em matemática durante fases distintas do desenvolvimento acadêmico.
A competência aritmética abarca habilidades distintas. O modelo de McCloskey, Caramazza e Basili (1985) sugere dois componentes, ‘Processamento Numérico’ e ‘Cálculo’. O primeiro é responsável pelo conhecimento dos símbolos numéricos e quantidades, inclui a leitura, escrita e contagem de números, abarcando, desta forma, compreensão e produção. Já o segundo, Cálculo, está relacionado à recuperação de fatos aritméticos da memória, processamento dos símbolos matemáticos e realização das operações aritméticas. Mais recentemente, e guardando algumas similaridades com o modelo de McCloskey et al., Menon (2010) sugeriu três níveis de processamento da informação aritmética, sendo ‘Processamento Numérico Básico’, análogo ao Processamento Numérico do modelo anterior; ‘Computação Matemática Simples’, responsável pela recuperação de fatos aritméticos da memória e habilidade de cálculo; e ‘Computação Matemática Complexa’, que exige a realização de cálculo, em geral em situações com maiores demandas sobre a memória de trabalho.
Frente a estes modelos, Dias e Seabra (2013a) sugerem uma modificação de modo que a recuperação de fatos aritméticos seja compreendida como habilidade do módulo ‘Processamento Numérico’, uma vez que a demanda envolvida seria basicamente de acesso à memória de longo prazo, enquanto que nos módulos de ‘Cálculo’ haveria demanda sobre processos de manipulação da informação propriamente. Com base nisso, os módulos ‘Computação Matemática Simples’ e ‘Computação Matemática Complexa’ poderiam também ser condensados em um único, uma vez que a diferença entre eles se dá em termos da complexidade da tarefa, não necessariamente da natureza do processamento envolvido.
De acordo com Primi et al. (2002), as habilidades aritméticas são fundamentais para o processo de escolarização, mas também são necessárias para resolver problemas cotidianos que requerem raciocínio, percepção, domínio de conhecimentos específicos e capacidade de adaptação e assimilação frente a novas informações. Desta forma, justifica-se a importância de compreender sua relação com o funcionamento intelectual do indivíduo.
O desempenho em aritmética está associado a distintas dimensões do modelo CHC (Flanagan, Ortiz, Alfonso & Mascolo, 2006; Geray, Hoard & Bailey, 2011; McGrew & Wedling, 2010). Estudos apontam uma relação consistente com conhecimento/compreensão (Floyd, Evans, & McGrew, 2003; Gelman & Butterworth, 2005; Swanson & Jerman, 2006), velocidade de processamento (Floyd et al., 2003; McGrew & Wedling, 2010), memória de curto prazo e memória operacional (Fuchs et al., 2008; Geary, 2007;) bem como inteligência fluida (Flanagan et al., 2006; Geray, 2007; Hale et al., 2007) e processamento visual (Geary, 2007; Hale et al., 2008).
Uma série de estudos nacionais investigou a relação entre inteligência e o desempenho em matemática. De modo geral, participaram destes estudos indivíduos a partir de 9 anos de idade, sendo que os estudos com crianças mais novas são escassos e nenhum estudo recente nacional avaliou nível de inteligência e habilidades acadêmicas em crianças nas séries iniciais da escolarização, ou seja, com 7 ou 8 anos de idade (Gomes, 2010; Mól & Wechsler, 2008; Primi et al., 2002). Um instrumento que possibilita a avaliação desta faixa etária é a Bateria de Visualização e Raciocínio da Escala Internacional de Inteligência Leiter-R (Roid & Miller, 1997).
A Leiter-R é uma escala de avaliação não-verbal de inteligência composta por estímulos considerados universais, minimizando aspectos culturais específicos e o efeito de variáveis linguísticas (Anastasi & Urbina, 2000). Em função das instruções e formas de resposta não verbais, também é amplamente utilizada em indivíduos com transtornos do desenvolvimento (Antonio, Mecca, & Macedo, 2012). Este instrumento avalia duas dimensões amplas: o Processamento Visual (Gv) e a Inteligência Fluida (Gf). Há tradução e adaptação para o Brasil (Mecca, 2010), além de estudos psicométricos com evidências de validade e precisão para pré-escolares (Mecca, Antônio, Rabelo, Valentine, & Macedo, 2014; Mecca, Antônio, Seabra, & Macedo, 2014), crianças de Ensino Fundamental I (Mecca, 2013), indivíduos com autismo (Mecca, Orsati, & Macedo, 2014) e com Síndrome de Down (Mecca, 2013).
Testes não verbais, como a Leiter-R, que avaliam a capacidade geral de raciocínio apresentam correlações moderadas, em torno de 0,50, com testes de desempenho acadêmico (Pereira & Almeida, 2010). Entretanto, são escassos os estudos que investigam a relação ou a predição da Leiter-R em habilidades aritméticas. Algumas correlações são apresentadas no manual técnico da Leiter-R com o Wechsler Individual Achievement Test (WIAT), Woodcock-Johnson (WJ), Wide Range Achievment Test (WRAT), California Achievement Test (CAT), Comprehensive Test of Basic Skills (CTBS) e do Stanford Achievement Test (SAT). Os resultados indicaram correlações positivas e de alta magnitude entre a Leiter-R e os índices de matemática do WIAT e WJ, correlações de magnitude moderada com a prova de aritmética do WRAT e com os índices de matemática do CAT e do SAT. Apenas o índice de matemática do CTBS apresentou correlação de baixa magnitude com o QI na Leiter-R, indicando uma relação consistente do funcionamento intelectual com as habilidades de aritmética (Roid & Miller, 1997). Roberts et al. (2005) realizaram um estudo cujo objetivo foi avaliar preditores de habilidades acadêmicas em crianças entre 4 e 13 anos de idade com Síndrome do X-Frágil. Os resultados deste estudo não indicaram predição do QI obtido pela Leiter-R no aumento dos escores nos subtestes da WJ.
Mecca, Carvalho, Simões e Macedo (2016) verificaram uma correlação positiva, significativa e de magnitude moderada entre o desempenho total na Leiter-R e na Prova de Aritmética (Seabra, Montiel, & Capovilla, 2013). No entanto, não foram realizadas análises específicas com as distintas habilidades aritméticas. Neste sentido, outros estudos são necessários para elucidar a relação entre desempenho em aritmética e as habilidades mensuradas pela Leiter-R. O objetivo do presente estudo foi verificar a relação entre as habilidades cognitivas distintas avaliadas pela Leiter-R e os componentes do modelo de competência aritmética, incluindo as habilidades específicas avaliadas nos subtestes da Prova de Aritmética em escolares de 7 e 8 anos de idade. De forma exploratória, o estudo também investigou se as relações entre habilidades aritméticas e cognitivas variam em função do tipo de escola, particular e pública.
Método
Participantes
Foram avaliadas 51 crianças, estudantes do 2º e 3º ano do Ensino Fundamental I, entre 7 e 8 anos de idade (M=7,66; DP=0,47), sendo 30 pertencentes a uma escola pública (58,82%) e 21 a uma escola particular (41,18%), ambas localizadas na zona norte da cidade de São Paulo. Participaram do estudo 27 meninos (52,94%) e 24 meninas (47,06%). A amostra foi selecionada por conveniência, de acordo com a disponibilidade e autorização das instituições e responsáveis pelas crianças. Foram excluídas crianças com deficiências sensoriais conhecidas e não corrigidas de acordo com as informações obtidas nas próprias escolas.
Instrumentos
Foram aplicados os seis subtestes da Bateria de Visualização e Raciocínio da Leiter-R que compõem o QI Total para crianças na faixa etária dos 7 aos 8 anos de idade, a saber: Figura-Fundo, Analogias, Formas Completas, Sequências, Padrões Repetidos e Dobra de Papel. A bateria completa é composta por dez subtestes, sendo apenas seis necessários ao cálculo do QI nesta faixa etária. Dos outros quatro subtestes não aplicados, três correspondem a faixa etária dos 2 aos 5 anos e um corresponde a um índice fatorial específico de raciocínio visuo-espacial. Isto auxilia no tempo demandado para a aplicação, cuja duração é em torno de 30 minutos (Roid & Miller, 1997). Um estudo realizado com escolares da cidade de São Paulo mostrou que a Leiter-R é composta por dois fatores, sendo o primeiro (Fator 1) composto pelos subtestes Figura-Fundo, Formas Completas e Padrões Repetidos, enquanto que o segundo fator (Fator 2) é composto pelos subtestes Analogias, Sequências e Dobra de Papel (Mecca, 2013).
O subteste Figura-Fundo avalia habilidades de exploração e discriminação visuais. O objetivo é encontrar o estímulo-alvo em uma prancha na qual estão presentes diversos estímulos distratores. Em Formas Completas avalia-se a capacidade de síntese visual, cuja tarefa é encontrar, em uma prancha com diversos estímulos, aquele que representa a figura completa referente ao estímulo-alvo apresentado em fragmentos. No subteste Sequências é avaliada a habilidade de completar sequências que progridem em uma determinada ordem, selecionando os estímulos corretos. Em Padrões Repetidos, os estímulos são apresentados em determinada ordem e o participante deve completar a prancha descobrindo a regra subjacente à sequência, utilizando raciocínio indutivo. No subteste Analogias, há uma matriz em que faltam estímulos e o indivíduo deve descobrir a relação entre as figuras da matriz para escolher a figura correta que a preencha de forma adequada. Por fim, em Dobra de Papel, avalia-se habilidade de manipulação mental de estímulos visuais, uma vez que o objetivo é escolher qual figura representa o estímulo-alvo, caso este estivesse dobrado (Mecca, 2010; Roid & Miller, 1997).
Foi também utilizada a Prova de Aritmética – PA (Seabra, Montiel, & Capovilla, 2013), que possibilita a avaliação da competência aritmética de forma relativamente ampla, incluindo os componentes ‘Processamento Numérico’ e ‘Cálculo’ (Seabra, Dias, & Macedo, 2010). O instrumento possui 6 subtestes, sendo que o primeiro avalia a escrita por extenso e algébrica de números ditados pelo avaliador; o segundo, a escrita de sequências numéricas crescente e decrescente; o terceiro, relação de grandeza; o quarto e quinto subtestes mensuram a habilidade de cálculo envolvendo as quatro operações aritméticas, porém, no quarto subteste as contas são dadas montadas e, no quinto, são apresentadas oralmente e o participante deverá montá-las e solucioná-las; por fim, o sexto subteste avalia a resolução de problemas escritos. O instrumento oferece um escore total, podendo ainda ser extraído escore para os índices fatoriais ‘Processamento numérico’, a partir da soma dos subtestes 1 e 3, e ‘Cálculo’, a partir dos subtestes 4, 5 e 6, delineados a partir do estudo prévio de Seabra et al. (2010). O subteste 2 não compõe nenhum fator específico, sendo contemplado apenas na pontuação total do teste. O instrumento possui dados de evidências de validade e normatização para amostra de crianças e adolescentes brasileiros dos 6 aos 11 anos de escolas públicas (Dias & Seabra, 2013b).
Procedimentos
O presente estudo foi submetido e aprovado pelo Comitê de Ética da Universidade onde foi realizado (CAAE nº 0112.0.272.000-10). A coleta de dados ocorreu nas próprias escolas, após assinatura do Termo de Consentimento Livre e Esclarecido pelos responsáveis, durante o período de aula conforme combinado previamente de forma a não prejudicar as atividades escolares dos alunos. Os instrumentos foram aplicados individualmente, em dois encontros com cada criança. No primeiro encontro foi feita a aplicação da Leiter-R (com duração de 30 minutos) e no segundo encontro foi aplicada a Prova de Aritmética (duração de 20 minutos).
Foi realizado teste de Kolmogorov Smirnov Z para verificação da distribuição normal dos dados para o desempenho na Leiter-R e na Prova de Aritmética. A homogeneidade das variâncias foi investigada a partir do teste de Levene. Como critérios para distribuição normal e homogeneidade das variâncias foram considerados valores de p ≥ 0,05.
Foram realizadas análises de variância para comparação do desempenho na Leiter-R e na Prova de Aritmética entre crianças de escolas públicas e particulares, Correlação de Pearson entre os instrumentos, bem como análises de Regressão Linear para verificar o valor preditivo da Leiter-R no desempenho em aritmética. Optou-se por utilizar os dados referentes aos pontos brutos, pois a normatização da Leiter-R está em andamento. Para a PA também foram utilizados os totais brutos, uma vez que os dados normativos encontram-se disponíveis somente para crianças de escolas públicas. Para análise dos resultados foi utilizado o programa IBM Statistical Package for Social Sciences® versão 21.0 para Windows.
Resultados
Como justificativa à escolha dos testes paramétricos, o teste de Kolmogorov-Smirnov indicou distribuição normal dos dados na Leiter-R (z = 0,474; p = 0,978) e na PA (z = 0,740; p = 0,643). O teste de Levene mostrou homogeneidade das variâncias tanto na Leiter-R (F = 0,043; p = 0,836) quanto na PA (F = 2,652; p = 0,110). Desta forma, optou-se por utilizar testes paramétricos.
Primeiramente o desempenho entre crianças de escolas públicas e particulares foram comparados na Leiter-R e a na Prova de Aritmética. As estatísticas descritivas de média e desvio-padrão, bem como os resultados obtidos a partir da análise de variância univariada (ANOVA) são apresentados na Tabela 1.
Conforme os dados apresentados na Tabela 1, de modo geral médias superiores são observadas em crianças de escolas particulares tanto no teste de inteligência quanto em aritmética. No primeiro caso, diferenças significativas foram observadas entre os grupos no desempenho em Analogias, Sequências e Dobra de Papel, bem como no escore total. Na PA, diferenças estatisticamente significativas ocorreram em todas as medidas específicas, bem como nos índices fatoriais e pontuação geral.
Em seguida foram verificadas as relações entre o desempenho na PA, considerando o escore nos subtestes específicos, nos índices fatoriais ‘Processamento Numérico’ e ‘Cálculo’ e total, e os escores obtidos na Leiter-R, incluindo desempenho nos subtestes e total, a partir de Correlações de Pearson. Os resultados obtidos estão apresentados na Tabela 2.
Os dados apresentados na Tabela 2 mostraram que o Subteste 1, que avalia a capacidade de escrita algébrica e por extenso de números, e o Subteste 5, que avalia a capacidade de elaborar uma operação aritmética a partir de uma instrução verbal e resolvê-la, se correlacionaram de forma positiva e estatisticamente significativa com os Subtestes Figura-Fundo, Analogias, Sequências e Dobra de Papel, bem como com o desempenho total na Leiter-R. Já o Subteste 2, que avalia a escrita de sequências numéricas crescente e decrescente, se correlacionou com o subteste Sequências. O Subteste 4, caracterizado por cálculo de operações apresentadas por escrito se correlacionou de forma positiva, significativa e com magnitude moderada com os Subtestes Analogias e Sequências, bem como com o escore total da Leiter-R. Não foram observadas correlações entre os subtestes 3 e 6 da PA com os subtestes da Leiter-R. Correlações significativas, de magnitude baixa a moderada, também foram observadas entre os escores em Processamento Numérico, Cálculo e total na PA e nos subtestes Analogias, Sequências, Dobra de Papel e Total na Leiter-R, havendo também relação entre Processamento Numérico e Figura-Fundo.
Considerando os dois fatores que compõem a Leiter-R, os resultados indicaram correlações positivas, em sua maioria significativas e de magnitude moderada, do Fator 2 da Leiter-R (composto pelos subtestes Figura-Fundo, Formas Completas e Padrões Repetidos) com os subtestes 1, 4 e 5, com os índices de processamento numérico e cálculo bem como o Total na PA. Ainda considerando o Fator 2 da Leiter-R, observaram-se correlações positivas, significativas, mas de baixa magnitude com os subtestes 2 e 6 da PA. Já em relação ao Fator 1 da Leiter-R (composto por Analogias, Sequências e Dobra de Papel), foram observadas correlações significativas e de baixa magnitude com os subtestes 1, 4 e 5, com os índices de processamento numérico e cálculo, assim como uma tendência com o total na PA (p = 0,055).
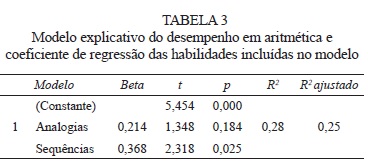
A partir destes resultados, observou-se que, de modo geral, os subtestes Analogias e Sequências são aqueles que estabeleceram maior número de correlações (sobretudo considerando aquelas maiores que 0,40) com os desempenhos nos subtestes da PA. Desta forma, procedeu-se a análise de regressão linear múltipla para verificar a predição destes dois subtestes no desempenho em aritmética. As estatísticas de resíduo (Centered Leverage Value = 0,039; Cook’s Distance = 0,020) não demonstram a existência de outliers. Também, as estatísticas de diagnóstico de multicolinearidade (Tolerance = 0,595; VIF = 1,68; Condition Index entre 1,00 e 6,928) não identificaram variáveis colineares, de modo que julgou-se que os resultados da análise de regressão podem ser interpretados com relativa segurança. O modelo resultante, que é apresentado na Tabela 3, obteve ajuste satisfatório (p < 0,001) e mostrou-se capaz de explicar até 25% da variância no desempenho em aritmética. Porém, dentre as variáveis preditoras incluídas, apenas o coeficiente de regressão de Sequências obteve significância estatística.
Exploratoriamente foram também conduzidas análises de correlação entre os desempenhos nas diversas medidas da PA e Leiter-R considerando separadamente o tipo de escola. Os resultados das correlações por tipo de escola, pública e particular, encontram-se descritos nas Tabelas 4 e 5 respectivamente.
De acordo com os dados apresentados na Tabela 4 referentes à escola pública, apenas duas relações significativas foram observadas, ambas de magnitude baixa, sendo positiva entre o desempenho no subteste 5 da PA e no total da Leiter-R e negativa entre desempenho no subteste 6 da PA e no subteste Figura-Fundo da Leiter-R. Houve uma tendência de correlação entre o Subteste 1 da PA e o total na Leiter-R (p = 0,058).
No grupo de crianças pertencentes a escolas particulares, foram observadas correlações positivas, significativas e de magnitude moderada entre o subteste 4 da PA com os subtestes de Analogias e Sequências da Leiter-R, bem como com o total. O subteste 5 se correlacionou de forma positiva, significativa e também com magnitude moderada com o subteste de Analogias da Leiter-R. Também foram observadas correlações entre os índices fatoriais da PA, Processamento Numérico e Cálculo, com o subteste de Sequências da Leiter-R. O índice de Cálculo se correlacionou com o subteste Analogias. Uma tendência foi verificada entre Analogias da Leiter-R e o subteste1 (p = 0,056), o índice de processamento numérico (p = 0,056) e o total na PA (p = 0,054). Em suma, considerando esta amostra de escola particular, os desempenhos nos subtestes de Analogias e Sequências da Leiter-R estiverem mais associados ao desempenho em habilidades aritméticas.
Discussão
O principal objetivo deste estudo foi verificar a relação entre as habilidades cognitivas de processamento visual e inteligência fluida avaliadas pela Leiter-R e as habilidades e componentes da competência aritmética baseadas no modelo de McCloskey e colaboradores (1985), avaliados pela PA. De fato, a literatura já aponta para a relação entre inteligência e desempenho em aritmética (Lu et al., 2011; Primi, Santos, & Vendramini, 2002; Stock, Desoete, & Roeyers, 2009).
Os resultados aqui encontrados, considerando, sobretudo as relações entre os totais em ambos os instrumentos, eram esperados, uma vez que estudos prévios reportam relações de magnitude moderada entre desempenho em aritmética e testes não-verbais de inteligência (Pereira & Almeida, 2010). Tais estudos discutem a relação e predição das habilidades de cognitivas como inteligência fluida e processamento visual no desempenho acadêmico utilizando medidas que avaliam tais dimensões amplas (Floyd et al., 2003) ou que utilizam apenas os escores totais em testes de inteligência (Lu et al., 2011). Entretanto são escassos os estudos que se debruçam sobre as habilidades específicas de cada dimensão. O presente estudo investigou a relação de habilidades específicas tais como raciocínio sequencial, raciocínio indutivo, discriminação visual, raciocínio visuo-espacial, entre outras avaliadas pela Leiter-R, com habilidades específicas de aritmética.
Verificou-se que crianças com melhores habilidades de raciocínio tendem a se desempenhar melhor em uma tarefa de aritmética, corroborando achados prévios (Flanagan et al., 2006; Geray, 2007; Hale et al., 2007). Isto pode ser observado quando considerado o desempenho tanto no componente Processamento Numérico, quanto em Cálculo, apesar de relação ligeiramente maior com este último. Este achado é coerente dada à natureza da tarefa envolvida, ou seja, Processamento Numérico refere-se a habilidades de compreensão e produção numéricas, enquanto que Cálculo envolve a realização de operações e manipulação da informação propriamente (Dias & Seabra, 2013a; McCloskey et al., 1985), o que de fato eleva a demanda de raciocínio da tarefa. Os subtestes 4 e 5 da PA, que envolvem a resolução de operações aritméticas, foram os subtestes que travaram relações mais elevadas (algumas na ordem de 0,50) com o total e subtestes da Leiter-R. Estes achados corroboram a literatura à medida que Gf aparece como um dos construtos mais proeminentes em estudos sobre o desenvolvimento de habilidades matemáticas. Isto pode ser observado nos esquemas de resolução de problemas, utilização e mudanças de estratégias (Floyd et al., 2003).
Com relação aos subtestes da Leiter-R que apresentaram maiores correlações com as medidas de aritmética, verificou-se que Analogias e Sequências, ambos com demandas de inteligência fluida (Roid & Miller, 1997; Mecca, 2013), estabeleceram relações mais consistentes com os desempenhos na PA. Este dado é sugestivo de uma associação diferencial em que a habilidade de inteligência fluida, mais do que de processamento visoespacial, relaciona-se ao desempenho escolar em aritmética. Maior relação de provas que avaliam inteligência fluida com desempenho em aritmética é consistente com o próprio modelo teórico CHC, no qual o raciocínio quantitativo faz parte da dimensão Gf (Schneider & McGrew, 2012). Isto indica que parte do desempenho em tarefas de raciocínio quantitativo, raciocínio indutivo e sequencial são explicadas por um fator comum denominado Gf (Floyd et al., 2003).
O modelo derivado da análise de regressão, no entanto, revelou que apenas Sequências contribui com variância única ao desempenho em aritmética. Este subteste demanda que a criança escolha qual estímulo completa uma sequência corretamente seguindo uma progressão lógica (Mecca, 2010). Além do raciocínio sequencial, Roid e Miller (1997), destacam que neste subteste está presente a capacidade de abstração, como criar e perceber relações entre estímulos. Os dados obtidos a partir da análise de regressão também corroboram a literatura, pois apenas parte do desempenho em aritmética pode ser explicado pelo raciocínio fluido e processamento visual. Outras habilidades cognitivas, como compreensão, velocidade de processamento e memória estão relacionadas com o desempenho em aritmética (Fuchs et al., 2008; McGrew & Wedling, 2010).
Apesar das relações observadas entre o subteste Analogias e os índices e os subtestes específicos na PA, a análise de regressão mostrou que não há uma contribuição significativa deste subteste da Leiter-R em aritmética de maneira geral. Uma hipótese possível para esta ausência de contribuição única é que talvez as relações entre Analogias e aritmética poderiam ser mediadas por habilidades mais específicas de raciocínio indutivo e sequencial avaliado pelo subteste Sequências, uma vez que o subteste Analogias, além do raciocínio, demanda também habilidades visuo-espaciais, que por sua vez não estão fortemente relacionadas ao desempenho em aritmética (Floyd et al., 2003).
De forma exploratória, o estudo também mostrou que as relações entre habilidades aritméticas e cognitivas variam em função do tipo de escola, particular e pública. Optou-se por explorar estas relações separadamente, pois crianças pertencentes a escolas públicas apresentam desempenho significativamente inferior a crianças de escolas particulares na Leiter-R (Mecca, Jana, Simões e Macedo, 2015). De modo geral, o que se observou das correlações entre PA e Leiter-R em crianças de escolas públicas foi tendência de ausência de correlações significativas. Houve apenas uma relação baixa entre subteste que exige montagem e solução de operações aritméticas e o total na Leiter-R. Observou-se também uma relação negativa inesperada entre subteste de solução de problemas da PA e Figura-Fundo da Leiter-R, uma vez que estudos prévios apontam para relações positivas entre desempenho aritmético e habilidades de processamento visual (Geary, 2007; Hale et al., 2008). Estes resultados mostram que, nestas crianças de escola pública, não há uma relação entre o desempenho em aritmética e habilidades de processamento visual e raciocínio fluido. Por outro lado, considerando as crianças da escola particular, relações foram encontradas, de modo geral, entre as tarefas que exigem a habilidade de cálculo (subtestes 4 e 5 e índice fatorial Cálculo da PA) e os subtestes Semelhanças e Analogias, além do total, na Leiter-R.
Uma possível explicação para este resultado seria de que, para as crianças da escola pública, a PA foi de mais difícil realização. Nos subtestes 2, 5 e 6 algumas crianças de escola pública apresentaram pontuação ‘zero’ havendo tendência a efeito de piso em alguns subtestes, o que influenciaria as relações estabelecidas. O tipo de estimulação ou instrução que é oferecida nas escolas públicas e particulares, bem como a familiaridade dos alunos das diferentes instituições com o conteúdo da PA podem ter influenciado o desempenho dos participantes neste instrumento. Outra hipótese seria que talvez as crianças de escolas públicas estejam em fase inicial de aquisição dos conhecimentos aritméticos em que outras habilidades cognitivas sejam mais relevantes do que processamento visual ou inteligência fluida.
Estudos prévios como o de Floyd et al. (2003) apontam que o desempenho em cálculo e raciocínio matemático no início do Ensino Fundamental estão mais associados a outras habilidades tais como conhecimento/compreensão e velocidade de processamento quando comparados a inteligência fluida. Esta apresenta relações mais fortes com matemática a partir dos 12 anos. Portanto, as diferenças observadas entre crianças de escolas públicas e particulares na PA podem refletir diferenças na aquisição de conhecimento formal, não avaliado pela Leiter-R.
Ao realizar estudos de validade e normatização de instrumentos que avaliam habilidades cognitivas e desempenho acadêmico, o tipo de escola deve ser considerado como uma importante variável a ser investigada ou controlada. Conforme observado nos resultados no presente estudo, trata-se de um fator que poderá influenciar na busca por evidências de validade, considerando inteligência e desempenho em aritmética como construtos relacionados, ou até mesmo em estudos que objetivam verificar evidências de validade preditiva da inteligência no desempenho em aritmética.
Dentre as limitações observadas no presente estudo, pode-se mencionar o número reduzido de sujeitos por tipo de escola. Neste sentido, sugere-se que estudos futuros considerem um aumento da amostra, ampliando a faixa etária para além das séries iniciais do Ensino Fundamental, com um número mais equilibrado entre participantes de escolas públicas e particulares. Ressalta-se também a importância de estudos que investiguem a relação entre desempenho aritmético e habilidades cognitivas a partir de modelos mais recentes de competência aritmética, bem como outras dimensões amplas do modelo CHC.
Considerações Finais
O presente estudo verificou relações de magnitude moderada entre habilidades aritméticas específicas de processamento numérico e cálculo com habilidades cognitivas relacionadas à inteligência fluida. Estes resultados refletem mais especificamente a amostra de crianças pertencentes à escola particular. Dentre as habilidades cognitivas avaliadas pela Leiter-R, observou-se que raciocínio sequencial e por analogias estão mais associados ao desempenho em aritmética, sendo apenas o primeiro considerado um preditor significativo deste último.
Referências
Alloway, T. P., & Gregory, D. (2013). The predictive ability of IQ and Working Memory scores in literacy in an adult population. International Journal of Educational Research, 57, 51-56. http://dx.doi.org/10.1016/j.ijer.2012.10.004
Anastasi, A. & Urbina, S. (2000). Testagem Psicológica. Porto Alegre: Artmed.
Antonio, D. A. M., Mecca, T. P., & Macedo, E. C. (2012). O uso do teste não-verbal Leiter-R na avaliação de inteligência em distúrbios do desenvolvimento. Cadernos de Pós-graduação em Distúrbios do Desenvolvimento, 12(2), 9-15.
Carroll, J. B. (1993). Human Cognitive Abilities: A Survey of Factor Analytic Studies. New York: Cambridge University Press.
Cohen, J. (1988). Statistical power analysis for the behavioral sciences (2ª ed.). Hillsdale, New Jersey: Lawrence Erbaum.
Dias, N. M. & Seabra, A. G. (2013a). Competência aritmética sob a perspectiva do processamento da informação: compreensão, desenvolvimento e subsídios para avaliação. In A. G. Seabra, N. M. Dias, & F. C. Capovilla (Orgs.). Avaliação Neuropsicológica Cognitiva (Vol. 3: Leitura, escrita e aritmética) (pp. 76-84). São Paulo: Memnon Edições Científicas.
Dias, N. M. & Seabra, A. G. (2013b). Evidências de validade e fidedignidade da Prova de Aritmética. In A. G. Seabra, N. M. Dias & F. C. Capovilla (Orgs.). Avaliação Neuropsicológica Cognitiva (Vol. 3: Leitura, escrita e aritmética) (pp. 85-91). São Paulo: Memnon Edições Científicas.
Flanagan, D. P., Ortiz, S. O., Alfonso, V. C., & Mascolo, J. T. (2006). The Achievement Test Desk Reference (ADRT): A Guide to Learning Disability Identification. Boston: Allyn & Bacon.
Floyd, R. G., Evans, J. J., & McGrew, K. S. (2003). Relations between measures of Cattell-Horn-Carroll (CHC) cognitive abilities and mathematics achievement across the school-age years. Psychology in the Schools, 40(2), 155-171. http://dx.doi.org/10.1002/pits.10083
Fuchs, L. S., Fuchs, D., Stuebing, K., Fletcher, J. M., Hamlett, C. L., & Lambert, W. (2008). Problem solving and computational skill: Are they shared or distinct aspects of mathematical cognition? Journal of educational psychology, 100(1), 30-47. http://dx.doi.org/10.1037/0022-0663.100.1.30
Geary, D. C. (2007). An evolutionary perspective on learning disability in mathematics. Developmental Neuropsychology, 32(1), 471-519. http://dx.doi.org/10.1080/87565640701360924
Geary, D. C., Hoard, M. K., & Bailey, D. H. (2011). How SLD manifests in mathematics. In Flanagan, D. P. & Alfonso, V. C. (Eds.). Essentials of Specific Learning Disability Identification (pp. 43-64). Hoboken, NJ: Wiley.
Gelman, R. & Butterworth, B. (2005). Number and language: how are they related? Trends in cognitive sciences, 9(1), 6-10. http://dx.doi.org/10.1016/j.tics.2004.11.004
Gomes, C. M. A. (2010). Avaliando a Avaliação Escolar: Notas Escolares e Inteligência Fluida. Psicologia em Estudo, Maringá, 15(4), 841-849. http://dx.doi.org/10.1590/S1413-73722010000400020
Gomes, C. M. A. & Golino, H. F. (2012). O que a inteligência prediz: diferenças individuais ou diferenças no desenvolvimento acadêmico? Psicologia: teoria e prática, 14(1), 126-139.
Hale, J. B., Fiorello, C. A., Dumont, R., Willis, J. O., Rackley, C., & Elliott, C. (2008). Differential Ability Scales-Second Edition (neuro) psychological predictors of math performance for typical children and children with math disabilities. Psychology in the Schools, 45(9), 838-858. http://dx.doi.org/10.1002/pits.20330
Hale, J. B., Fiorello, C. A., Kavanagh, J. A., Holdnack, J. A., & Aloe, A. M. (2007). Is the demise of IQ interpretation justified? A response to special issue authors. Applied Neuropsychology, 14(1), 37-51. http://dx.doi.org/10.1080/09084280701280445
Lu L., Weber H. S, Spinath F. M., & Shi, J. (2011). Predicting school achievement from cognitive and non-cognitive variables in a Chinese sample of elementary school children. Intelligence, 39(2-3), 130-140. http://dx.doi.org/10.1016/j.intell.2011.02.002
McCloskey, M., Caramazza, A., & Basili, A. (1985). Cognitive mechanisms in number processing and calculation: evidence from Dyscalculia. Brain and Cognition, 4, 171-196. http://dx.doi.org/10.1016/0278-2626(85)90069-7
McGrew, K. S. & Wedling, B. J. (2010). Cattell-Horn-Carroll cognitive-achievement relations: What we have learned from the past 20 years of research. Psychology in theSchools, 47, 651-675. http://dx.doi.org/10.1002/pits.20497
Mecca, T. P. (2010). Tradução, adaptação, fidedignidade e evidências de validade da Bateria de Visualização e Raciocínio da Leiter International Performance Scale-Revised. [Dissertação Mestrado em Distúrbios do Desenvolvimento], Universidade Presbiteriana Mackenzie, São Paulo.
Mecca, T. P. (2013). Verificação das Propriedades Psicométricas da Bateria de Visualização e Raciocínio da Leiter-R em Crianças dos 2 aos 8 Anos e nos Distúrbios do Desenvolvimento. [Tese Doutorado em Distúrbios do Desenvolvimento], Universidade Presbiteriana Mackenzie, São Paulo.
Mecca, T. P., Antônio, D. A. M., Rabelo, I., Valentine, F., & Macedo, E. C. (2014). Avaliação de Inteligência em Crianças Pré-escolares. In A. G. Seabra., J. A. Laros, E. C. Macedo., & N. Abreu (Orgs.). Inteligência e Funções Executivas: avanços e desafios para a avaliação neuropsicológica. São Paulo, SP: Memnon Edições Científicas. pp. 174-193.
Mecca, T. P., Antonio, D. A. M., Seabra, A. G., & Macedo, E. C. (2014). Parâmetros Psicométricos da Escala Internacional de Inteligência Leiter-R para Crianças Pré-Escolares. Avaliação Psicológica [Online], 13, 125-132.
Mecca, T. P., Carvalho, L. F., Simões, M. R., & Macedo, E. C. D. (2016). Evidências de validade e fidedignidade da Escala Internacional de Inteligência Leiter-R para crianças dos 6 aos 8 anos. Psicologia Teoria e Pesquisa, 32(1), 51-60. http://dx.doi.org/10.15900102-37722016012222051060
Mecca, T. P., Jana, T. A., Simões, M. R., & Macedo, E. C. D. (2015). Relação entre habilidades cognitivas não-verbais e variáveis presentes no contexto educacional. Psicologia Escolar e Educacional, 19(2), 329-339. http://dx.doi.org/10.1590/2175-3539/2015/0192844
Mecca, T. P., Orsati, F. T., & Macedo, E. C. (2014). Non-Verbal Cognitive Profile of Young Children with Autism Spectrum Disorders. Psychology (PSYCH), 5, 1404-1417. http://dx.doi.org/10.4236/psych.2014.511151
Menon, V. (2010). Developmental cognitive neuroscience of arithmetic: implications for learning and education. Mathematics Education, 42, 515-525. http://dx.doi.org/10.1007/s11858-010-0242-0
Mól, D. A. R. & Wechsler, S. M. (2008). Avaliação de crianças com indicação de dificuldades de aprendizagem pela bateria Woodcock-Johnson III. Psicologia Escolar e Educacional, 12(2), 391-399.
Pereira, M. & Almeida, L. (2010). Predição do rendimento académico no final do ensino secundário na base dos testes de QI na infância. Revista Galego-Portuguesa de Psicología e Educación, 18(1), 239-249.
Primi, R., Ferrão, M. E., & Almeida, L. S. (2010). Fluidintelligence as a predictoroflearning: A longitudinal multilevel approach appliedtomath. Learning and Individual Differences, 20(5), 446-451. http://dx.doi.org/10.1016/j.lindif.2010.05.001.
Primi, R., Santos, A. D., &Vendramini, C. M. (2002). Habilidades básicas e desempenho acadêmico em universitários ingressantes. Estudos de Psicologia, 7(1), 47-55.
Roberts, J. E., Schaaf, J. M., Skinner, M., Wheeler, A., Hooper, S., Hatton, D. D., & Bailey Jr, D. B. (2005). Academic Skills of Boys with Fragile X Syndrome: Profiles and Predictors. American Journal on Mental Retardation, 110(2), 107-120.
Roid, G. H. & Miller, L. J. (1997). Leiter International Performance Scale-Revised. Wood Dale, IL: Stoelting.
Schneider, W. J. & McGrew, K. S. (2012). The Cattell-Horn-Carroll Model of Intelligence. In D. P. Flanagan, P. L. Harrison (Org). Contemporary Intellectual Assessment: Theories, Tests and Issues (3rd ed.). New York, NY: The Guilford Press. pp. 553-581.
Seabra, A. G., Dias, N. M., & Macedo, E. C. (2010). Desenvolvimento das habilidades aritméticas e composição fatorial da Prova de Aritmética em estudantes do Ensino Fundamental. Interamerican Journal of Psychology, 44(3), 411-418.
Seabra, A. G., Montiel, J. M., & Capovilla, F. C. (2013). Prova de Aritmética. In A. G. Seabra, N. M. Dias, & F. C. Capovilla. Avaliação Neuropsicológica Cognitiva: Leitura, escrita e aritmética (pp. 97-104). São Paulo: Memnon Edições Científicas.
Stock, P., Desoete, A., & Roeyers, H. (2009). Predicting Arithmetic Abilities: The Role of Preparatory Arithmetic Markers and Intelligence. Journal of Psychoeducational Assessment, 27, 237-251. http://dx.doi.org/10.1177/0734282908330587
Swanson, H. L. & Jerman, O. (2006). Math disabilities: A selective meta-analysis of the literature. Review of Educational Research, 76(2), 249-274. http://dx.doi.org/10.3102/00346543076002249
Recebido em: 14.10.2014
Aceito em: 16.01.2016
Endereço para correspondência:
Tatiana Pontrelli Mecca
Rua Jacofer, 161, ap. 74, bloco 2
02712-070 São Paulo, SP, Brasil
Autores:
Tatiana Pontrelli Mecca – Doutor, Centro Universitário Fieo - Unifieo.
Natália Martins Dias – Doutor, Centro Universitário Fieo - Unifieo.
Tatiana Abrão Jana – Iniciação Ciêntífica, Universidade Presbiteriana Mackenzie.
Alessandra Gotuzo Seabra – Doutor, Universidade Presbiteriana Mackenzie.
Elizeu Coutinho de Macedo – Doutor, Universidade Presbiteriana Mackenzie.














