ARTÍCULOS

 

Variabilidade Comportamental Operante e o Esquema de Reforçamento Lag-N

 

Operant Behavioral Variability and the Lag–N Schedule of Reinforcement

 

 

Lourenço de Souza Barba¹

Universidade Ibirapuera, São Paulo, Brasil

 

 

---

RESUMO

Pesquisadores afirmam que a variabilidade constitui uma dimensão operante do comportamento. O estudo presente analisou a consistência dessa posição, adotando um conceito de operante que distingue classes descritivas e classes funcionais. O reforçamento diferencial modela operantes modificando a correlação entre as duas classes. A variação positiva da correlação representa o processo de diferenciação. As classes descritivas são definidas sobre parâmetros do comportamento. Definido um parâmetro, pode-se definir um parâmetro secundário, o tempo de recorrência (TR), que mede recência. Os esquemas Lag–N defi nem classes sobre o parâmetro TR. Muitos estudos sobre variabilidade operante empregaram esquemas Lag–N e reforçaram diferencialmente a emissão de diferentes sequências de respostas. Esses estudos adotaram como principal variável dependente um índice (U), que mede previsibilidade de eventos. Eram registradas as frequências em que era emitida cada uma das diferentes sequências. O índice U refletia a uniformidade da distribuição dessas frequências. Como o esquema Lag–N não define sua classe descritiva sobre U, não se pode medir a variação da correlação sobre esse índice. A variação de U não representa, portanto, o processo de diferenciação que os esquemas Lag-N promovem. Essa circunstância traz dificuldades à tese de que a variabilidade é uma dimensão operante do comportamento.

Palavras-chave: variabilidade comportamental, variabilidade operante, comportamento operante, esquema Lag–N, sequências comportamentais.

---

ABSTRACT

There are two groups of studies that investigated variability of responding. One group includes the studies that investigated the behavioral variability without reinforcing it differentially. Another group of studies investigated the behavioral variability generated by differential reinforcement. According to some researchers, studies of later group produced data showing that variability is an operant dimension of behavior. So there would be an operant variability. The present study analyses the pertinence of such point of view. Controlling by consequences is the basic feature of operant behavior. Some authors that examined the concept of operant distinguished two classes of behavior: the class of behavior that produces consequences (descriptive class) and the class of behavior that is affected by consequences produced (functional class). The present work adopted this perspective. The relationship between both classes, measured by the standard correlation coeffi cient (r), defi nes operant behavior. The differential reinforcement usually changes the correlation coeffi cient between classes over the time. Positive variation of r represents the differentiation process. Descriptive classes are defi ned upon some parameter of behavior (like force, duration, location and so on). Such parameters were called primary parameters. It is possible defi ne, upon such primary parameter, a secondary parameter, the recurrence time parameter (RT), that refl ects the recency of a certain value of the primary parameter. Lag–N schedule defi nes descriptive classes upon the secondary parameter RT. Many studies of operant behavioral variability employed Lag–N schedules and reinforced differentially response sequences. Responses on two manipulanda (left manipulandum and right manipulandum) composed sequences of R and L components. Such studies took behavioral variability as synonym of unpredicability and chose as main dependent variable the U measure, a value that refl ects predicability of events. From this point of view, variable responding is responding with low predicability level. The studies show that Lag– N schedule increases the U values (when the values are compared with the baseline U values). However, because Lag–N schedule does not defi ne descriptive class upon the U values, it is not possible measure the variation of correlation upon U. Moreover, the U represents a property of a population of events (responses or sequences). It does not refl ect the property of an unique response or sequence. Defi ning a descriptive class upon the U measure might be conceptually problematic. The traditional employment of U takes into account frequencies at which different sequences are emitted. The present work argues that this procedure represents an arbitrary choice. The determination of U can take into account other universes of events and distribution of other variables. The same behavioral pattern can be said to be highly variable or lowly variable depending on the universe regarded for the calculation of U. The present study concludes that Lag–N schedule produces effects on behavior that do not concern the RT parameter. The variation of U is among these effects. Particularly, the variation of U does not represent the differentiation process that Lag–N schedule generates. This fact debilitates the point of view that variability is an operant dimension of behavior.

Key words: behavioral variability, operant variability, operant behavior, Lag–N schedule, behavioral sequences.

---

 

 

Muitos estudos têm investigado a variabilidade comportamental. A análise desses trabalhos permite distinguir duas linhas básicas de estudo. Alguns deles elegeram uma dimensão do comportamento (localização, duração, intervalo entre respostas), manipularam certas variáveis (esquemas de reforçamento, magnitude do reforço, administração de drogas, grau de privação) e mediram os efeitos dessa manipulação sobre a variabilidade da dimensão eleita (Antonitis, 1951; Boren, Moerschbaecher, & Whyte, 1978; Carlton, 1962; Carlton, 1962; Dale & Roberts, 1986; Eckerman & Lanson, 1969; Ferraro & Hayes, 1967; Ferraro & Branch, 1968; Lachter & Corey, 1982; McCray & Harper, 1962; McSweeney, 1974; Newberry, 1971; Tremont, 1984). Outro grupo de trabalhos reforçou diferencialmente comportamentos que apresentavam certo nível de variabilidade (Barba & Hunziker, 2003; Cohen, Neuringer, & Rhodes, 1990; Cruvinel & Sério, 2008; Denney & Neuringer, 1998; Hunziker, Caramori, Silva, & Barba, 1998; Hunziker, Saldana, & Neuringer, 1996; Mook & Neuringer, 1994; Morgan & Neuringer, 1990; Morris, 1987; Morris, 1989; Neuringer, 1991; Neuringer, 1992; Neuringer & Huntley, 1992; Neuringer, Deiss, & Olson, 2000; Page & Neuringer, 1985; Schoenfeld, Harris, & Farmer, 1966; Schwartz, 1982; Stokes, 1995; Van Hest, van Haaren, & van de Poll, 1989). Os resultados de Page e Neuringer (1985), um dos primeiros trabalhos desse último grupo, mostraram que comportamentos mais variados apareceram com mais frequência, quando foram submetidos a reforçamento diferencial. Page e Neuringer (1985) propuseram, com base em tais resultados, que a variabilidade constitui uma dimensão operante do comportamento. Desde então, tem crescido a literatura dedicada ao assunto, e os resultados de Page e Neuringer (1985) têm-se replicado (Neuringer, 2002). Este artigo pretende examinar a pertinência da tese de que a variabilidade constitui uma dimensão operante do comportamento (Page & Neuringer, 1985).

Essa tarefa exige um conceito bem estabelecido de comportamento operante. Adotou-se o conceito que propôs Catania (1973) em seu artigo "The Concept of the Operant in the Analysis of Behavior". O conceito que Catania (1973) oferece permite analisar novos aspectos dos desempenhos obtidos sob o esquema Lag - N. Esse autor relacionou o conceito de comportamento operante ao conceito estatístico de correlação. A correlação estatística envolve duas ou mais variáveis. Considere-se um par de variáveis (variável A e variável B) e os valores que elas assumem sob determinadas condições (se A assume o valor a₁, B assume o valor b₁; se A assume o valor a₂, B assume o valor b₂;...; se A assume o valor a_n, B assume o valor b_n). Esse registro casado dos valores de A e B pode revelar o grau de dependência entre as duas variáveis. A evolução de A pode não guardar nenhuma relação com a evolução de B. Em outras palavras, os valores que assume a variável A podem não constituir bons preditores dos valores que assume a variável B. Essa circunstância produziria correlação nula. Também pode ocorrer que a evolução da variável A acompanhe, de alguma forma, a evolução da variável B. Ter-se-ia, então, correlação não nula. Quer isso dizer que os valores de A constituem, em alguma medida (dada pelo grau de correlação), preditores dos valores de B.

É vasta a literatura dedicada ao tema da variabilidade. Selecionaram-se, por essa razão, trabalhos experimentais que usaram a metodologia de Page e Neuringer (1985), pesquisadores que propuseram o caráter operante da variabilidade comportamental e adotaram o procedimento Lag-N. Muitos estudos adotaram posteriormente esse esquema de reforçamento (Neuringer, 2002). O presente trabalho analisou, à luz do conceito que propôs Catania (1973), os resultados que esses estudos produziram. Essa análise permitiu discutir a consistência da tese que defendem Page e Neuringer (1985), quando a variabilidade é obtida sob o esquema Lag-N.

 

COMPORTAMENTO OPERANTE E CORRELAÇÃO

O controle do comportamento pelas consequências que ele produz constituiu o elemento fundamental que caracteriza o operante (Skinner, 1953, 1969, 1974). Catania (1973) observa que essa conceituação, historicamente consolidada, pode sofrer objeções de natureza lógica e empírica. Esse autor pretendeu oferecer uma definição de operante que conciliasse a caracterização historicamente estabelecida e as exigências de caráter lógico e empírico. Catania (1973) analisou o comportamento operante recorrendo ao conceito estatístico de correlação. Esse pesquisador distinguiu duas classes de respostas: aquelas que produzem uma determinada consequência e aquelas que são afetadas pela consequência produzida. A relação entre ambas as classes é o que define comportamento operante. As duas classes não coincidem necessariamente. O grau em que coincidem pode variar. O coeficiente de correlação linear, usualmente representado por r, (Bussab & Moretin, 2002) constitui uma medida possível do grau em que as duas classes se sobrepõem.

A relação entre respostas e consequências envolve o conceito de contingência. Toda contingência de reforçamento condiciona a ocorrência de um evento ambiental (o estímulo conseqüente) à ocorrência de respostas que apresentam certas propriedades particulares (Catania, 1999; Skinner, 1969). Pressionar uma barra ou pressionar um disco são atividades que apresentam certas propriedades ou dimensões. Cada pressão particular imprime uma força específica à barra, envolve uma duração específica, é aplicada em uma região específica da barra e sob um ângulo específico. Nem todas as pressões que envolvem contato com a barra produzem seu deslocamento. A pressão exercida sobre a barra produz a consequência somente se ela imprime uma força mínima sobre o dispositivo. O ângulo também importa. Somente quando aplicada sob certos ângulos, é que a pressão verga a barra. Somente as pressões que apresentam certos valores dessas propriedades produzem, portanto, a consequência programada. Apenas as pressões que impingem à barra uma força mínima de x gramas produzem a consequência programada, por exemplo. As características da barra podem determinar o valor de x. O experimentador pode também determinar arbitrariamente esse valor. Basta que o equipamento registre a força aplicada e somente apresente a consequência programada quando a intensidade da força aplicada igualar ou superar o valor x.

A mais elementar relação de contingência divide, portanto, em duas classes a gama completa de valores que uma propriedade pode assumir: valores que produzem a consequência programada (CP) e valores que não produzem a consequência programada (CP). O conceito de probabilidade condicional oferece uma forma de descrever relações de contingência (Catania, 1999). A divisão que a mencionada contingência instaura encontra uma expressão possível na seguinte forma:

P (CP / força aplicada à barra < x) = 0

P (CP / força aplicada à barra ≥ x) = 1

Ou seja:

Se a força aplicada à barra não atingir o valor x, a consequência programada certamente não ocorrerá (probabilidade = 0).

Se a força aplicada à barra igualar ou exceder o valor x, a consequência programada certamente ocorrerá (probabilidade = 1).

Um experimentador que instituísse essa contingência reforçaria diferencialmente pressões cuja força igualasse ou excedesse o valor x. Esse procedimento ilustra um caso em que o reforçamento diferencial ocorre com base em um parâmetro da própria pressão. Podem-se também reforçar diferencialmente as pressões com base em propriedades do ambiente em que as pressões ocorrem. A este trabalho interessam, em particular, procedimentos do primeiro tipo.

As contingências de reforçamento podem instituir duas ou mais classes de valores e podem atribuir-lhes diferentes probabilidades de reforçamento.

O parâmetro ´localização´ pode também defi nir um critério de reforçamento. Podese, por exemplo, equipar um caixa experimental com seis chaves. Chaves ímpares ocupam certas regiões do espaço. Chaves pares ocupam outras regiões do espaço. Esse equipamento permitiria instituir, por exemplo, a seguinte contingência: somente pressões exercidas sobre as chaves ímpares produzem a consequência programada. Em termos probabilísticos, poderia escrever-se:

P (CP / pressão exercida sobre chaves pares) = 0

P (CP / pressão exercida sobre chaves ímpares) = 1

As contingências mencionadas relacionam, portanto, dois grupos de valores: os valores que a propriedade força (ou localização) pode assumir (grupo I) e certos valores de probabilidades - probabilidades de que a consequência programada ocorra (grupo II). A qualquer valor do grupo I, a contingência associa somente um valor de II. Essa característica permite que uma função represente adequadamente a contingência (função que será denominada função S). Reforçar diferencialmente implica estabelecer uma função S. Esse procedimento elege respostas que produzirão a consequência programada em uma manipulação. Estabelecer a função S equivale a definir uma classe descritiva. Catania (1999) dá o nome de classe descritiva ou classe nominal ao conjunto de respostas que produzem a consequência programada. Respostas que não pertencem à classe descritiva não produzem a consequência programada. A definição da função S precede o reforçamento diferencial. Essa definição independe completamente, portanto, dos efeitos que a contingência produz sobre o comportamento do organismo. O procedimento que reforça diferencialmente pressões sobre as chaves ímpares institui uma função S. A Figura 1 mostra a representação gráfica dessa função S.

 

 

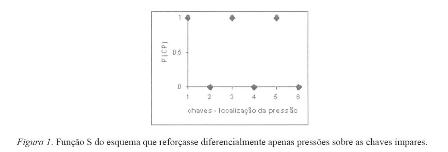
Os analistas do comportamento manipulam variáveis ambientais. Essas manipulações alteram a probabilidade de que ocorra uma determinada porção de comportamento. Essas alterações constituem os processos comportamentais estudados (Skinner, 1969). A probabilidade de que uma determinada parte do comportamento ocorrerá em um determinado instante constitui, portanto, o dado básico da ciência do comportamento (Skinner, 1969). Em qualquer momento da história de um organismo, pode-se supor que há uma probabilidade de que certa resposta ocorra. Respostas que certamente ocorrerão em determinado instante têm probabilidade 1. Respostas que certamente não ocorrerão em determinado instante têm probabilidade 0. A resposta pressionar a barra pode ter alta probabilidade de ocorrer em certas ocasiões e pode ter baixa probabilidade de ocorrer em outras ocasiões.

Mais especificamente, pode-se supor que esses valores de probabilidade se relacionem a propriedades da resposta, ou a valores particulares que essas propriedades assumem. Na terminologia de Catania (1973), essas propriedades são chamadas parâmetros da resposta. Uma pressão que imprima à barra uma força menor que x pode ter alta probabilidade de ocorrer, por exemplo. Uma pressão que imprima à barra uma força maior que x pode ter baixa probabilidade de ocorrer. Podem-se, portanto, relacionar dois outros grupos de valores: Aqueles valores que um parâmetro da resposta pode assumir (grupo I) e certos valores de probabilidades - probabilidades de que ocorram respostas cujos parâmetros assumam determinados níveis (grupo II). Também aqui, a qualquer valor do grupo I, a condição do organismo relaciona apenas um valor de II em um dado instante. Também aqui se pode, portanto, postular uma função que represente adequadamente a relação (função que será denominada função R).

Frequência e taxa são os dados primários que fundamentam o conceito de probabilidade (Skinner, 1969). As probabilidades são inferidas dos valores de frequência (Skinner, 1950, 1953). A ciência que Skinner propõe adota, portanto, uma concepção frequentista de probabilidade. Ao definir funções R, Catania (1973, p.108) emprega valores hipotéticos de frequência relativa. Catania acolhe, portanto, a concepção frequentista de probabilidade que Skinner propõe. As probabilidades associadas às respostas (ou, mais especificamente, aos valores que certo parâmetro assume) são, portanto, inferidas da frequência relativa em que esses valores ocorrem.

O procedimento hipotético mencionado acima elegeu o parâmetro localização e definiu uma função S sobre ele. Somente pressões exercidas sobre as chaves ímpares produziriam a consequência programada. À medida que opera sobre o comportamento, o reforçamento diferencial modifica a função R definida sobre o mesmo parâmetro. Pode ocorrer inicialmente que pressões exercidas sobre chaves pares comecem a ocorrer com maior frequência. Essas pressões não produziriam a consequência programada. Ainda assim, o reforçamento diferencial poderia aumentar a probabilidade de que essas pressões ocorressem. Esse resultado mostraria que os efeitos do reforçamento diferencial não se limitam às localizações que pertencem à classe descritiva. Esse efeito dispersivo do reforçamento diferencial é denominado indução (Catania, 1999).

À medida que o tempo corre, contudo, o reforçamento diferencial pode produzir um afunilamento das localizações registradas. Pressões exercidas sobre as chaves pares podem tornar-se menos e menos freqüentes. Ou seja, pressões cuja localização não pertence à classe descritiva começam a rarear. Esse efeito concentrador do reforçamento diferencial é denominado diferenciação de respostas (Catania, 1999). Existe uma função R, definida sobre o parâmetro localização, que descreve a condição do organismo antes que o reforçamento diferencial tenha início (uma função R de linha-de-base). Pode acontecer que essa função R inicial mostre o seguinte: o sujeito pressiona as seis chaves com igual frequência. A Figura 2 mostra a função R correspondente a esse dado.

 

 

A função S e a função R iniciais apresentariam correlação zero (r=0). Essa seria a medida de correlação inicial (r inicial). Em algum ponto, o procedimento poderia produzir um estado estável. Esse estado geraria uma nova função R (uma função R final). Dentre os resultados possíveis, há três casos notáveis:

1) – O sujeito ainda distribui as pressões igualmente sobre as seis chaves. As funções R inicial e R final seriam idênticas. O coeficiente de correlação final também assumiria o valor zero. Não haveria, portanto, diferença entre o r inicial e o r final. Não teria havido diferenciação.

2) – O sujeito concentra suas pressões sobre as chaves pares. Esse resultado poderia gerar a função R representada pela Figura 3.

 

 

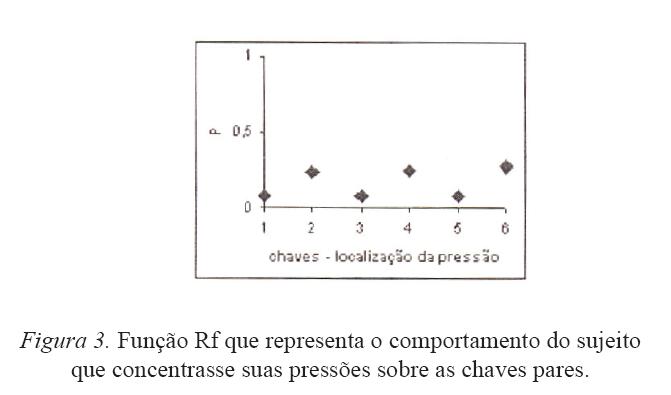
O caso 2 geraria um r final negativo (r = -1). A variação de r assumiria, portanto, um valor negativo (-1 – 0 = -1). Não teria havido diferenciação.

3) - O sujeito concentra suas pressões sobre as chaves ímpares. Esse resultado poderia gerar a função R representada pela Figura 4.

 

 

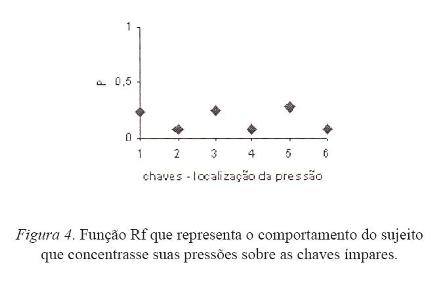
O caso 3 geraria um r final positivo (r = 1). A variação de r assumiria, portanto, um valor positivo (1 – 0 = 1). Teria havido diferenciação. Somente o caso 3 apresenta uma variação positiva de r. Essa variação refletiria a concentração do efeito do reforçamento diferencial. Ela representaria o processo de diferenciação.

O conceito de operante que propõe Catania (1973) implica, em resumo, uma definição operacional do processo de diferenciação. Essa definição envolve certos procedimentos e medidas. O pesquisador que produz e mede diferenciação segue um roteiro. Ao cumprir esse roteiro, o pesquisador:

1. Elege um ou mais parâmetros do comportamento;

2. Define, sobre o parâmetro escolhido, uma relação de contingência (define uma função S);

3. Obtém uma função R inicial (função Ri);

4. Mede a correlação inicial (ri), obtida entre Ri e S;

5. Procede ao reforçamento diferencial;

6. Obtém uma função R final (função Rf);

7. Mede a correlação final (rf), obtida entre Rf e S;

8. Mede a variação da correlação (Dr).

A variação positiva da correlação representa a diferenciação. A taxa de resposta constitui a medida usual do processo de diferenciação. Catania (1973) propõe uma análise que concilia a taxa de resposta e o índice de correlação (r).

A função R é instável. O reforçamento diferencial é um dos procedimentos que usualmente modificam a função R ao longo do tempo. A função S, ao contrário, é estável. Essa é condição essencial. Essa estabilidade é que permite comparar os índices de correlação. A função S constitui um referencial fixo em relação ao qual se mede a variação da função R (ou a variação da correlação) no tempo.

 

ESQUEMA LAG – N E PARÂMETROS DE SEGUNDA ORDEM

Schoenfeld, Harris e Farmer (1966) reforçaram diferencialmente pressões que ratos exerciam sobre um manipulandum. Há um intervalo de tempo que separa duas pressões consecutivas. Esse intervalo constitui um parâmetro das pressões. Schoenfeld et al. (1966) dividiram o espectro de intervalos em classes e definiram o seguinte esquema: uma pressão produzia a consequência programada somente se apresentasse um intervalo que recaísse em uma classe distinta da classe em que recaíra o intervalo da pressão imediatamente anterior.

Cruvinel e Sério (2008) usaram ratos em um experimento que investigou variabilidade e empregaram caixas equipadas com dois manipulanda: uma barra de pressão e um orifício de focinhar. Pressões à barra e introdução do focinho no orifício acionavam o contador. As durações de ambos os eventos foram inicialmente registradas. Em seguida, as autoras dividiram a gama de durações em oito intervalos. Uma pressão (ou uma introdução do focinho) produzia a consequência programada somente se apresentasse uma duração que pertencesse a uma classe distinta das classes em que haviam recaído as durações das três ultimas pressões ocorridas (treino de variabilidade).

Ambos os trabalhos realizaram reforçamento diferencial. Definiram, portanto, uma função S. A função S requer um parâmetro. Os parâmetros ‘intervalo´ (em Schoenfeld et al., 1966) e ´duração´ (em Cruvinel & Sério, 2008) não definiriam satisfatoriamente a função S, pois o intervalo ou a duração que os esquemas exigiam variavam ao longo do tempo. Um mesmo valor de intervalo ou duração podia levar a diferentes probabilidades de reforçamento, a depender do momento em que ocorresse. A função S constitui um referencial fixo. A definição da função S exige, portanto, que se considere um outro parâmetro. O exemplo abaixo permite que se defi na esse parâmetro.

Considere-se o parâmetro duração da pressão à barra (parâmetro P). Podem-se dividir os valores que P assume em cinco classes contíguas (fechadas à esquerda e abertas à direita). Seriam elas:

Classe 1 - 0 a 100ms (p1)

Classe 2 - 100 a 200ms (p2)

Classe 3 - 200 a 300ms (p3)

Classe 4 - 300 a 400ms (p4)

Classe 5 - 400ms ou mais (p5)

Toda pressão emitida teria sua duração registrada. Se a pressão n apresenta um valor que recai dentro da classe 0 a 100ms, diz-se que o parâmetro P assumiu, relativamente à pressão n, o valor p₁. (Embora a duração apresente um caráter contínuo, esse procedimento ´discretiza´ o universo de valores que P pode assumir). P assume, em cada ocorrência da pressão, um número finito de valores (p₁, p₂, p₃, p₄, ou p₅). Pode-se então associar, a cada pressão emitida, um valor p₁, p₂, p₃, p₄, ou p₅. A toda sequência de pressões emitidas corresponde, portanto, uma única sequência de valores p.

A partir da segunda ocorrência de um valor de P, é possível definir e atribuir valor a um novo parâmetro, que será denominado tempo de recorrência de P [TR(P)]. TR(P) corresponde ao número de ocorrências que separam a atual ocorrência de um valor de P e a sua ocorrência passada mais recente. A Tabela 1 apresenta uma sequência possível de pressões, assim como, as durações, o valor de P e o valor de TR(P) respectivos.

 

 

O parâmetro tempo de recorrência (TR) aparece em Machado (1989). Esse parâmetro é exemplo de um parâmetro que se define sobre outros parâmetros. Os parâmetros que não se definem sobre outros parâmetros (força, duração, localização etc...) serão denominados parâmetros primários. Os parâmetros que se definem sobre parâmetros primários serão chamados parâmetros secundários.

Este trabalho examina alguns efeitos dos esquemas denominados esquemas Lag– N. Esquemas Lag–N reforçam diferencialmente unidades de análise do comportamento que difiram, em algum aspecto, das N últimas unidades emitidas. Trata-se de esquemas que, ao definir suas funções S, adotam o parâmetro secundário TR. Schoenfeld et al. (1966) usaram um esquema Lag–N. A Figura 5 mostra a função S que os pesquisadores instituíram (sobre o parâmetro TR).

 

 

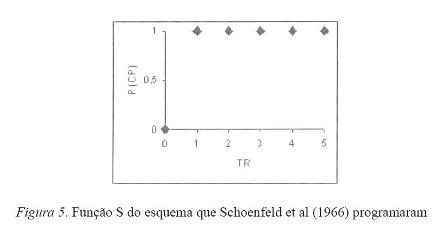
SEQÜÊNCIAS

A delimitação da unidade de análise do comportamento é, em princípio, arbitrária. Quaisquer unidades de análise do comportamento apresentam propriedades. Muitos estudos que investigaram a variabilidade operante empregaram caixas experimentais equipadas com dois manipulanda (duas barras de pressão ou dois discos): um deles instalado à esquerda de uma posição central e outro instalado à direita da posição central. Pressões (ou bicadas) sobre o manipulandum esquerdo e pressões (ou bicadas) sobre o manipulandum direito eram registradas de maneira independente. Pressões emitidas em série compunham sequências. Pressões (ou bicadas) sobre o manipulandum esquerdo constituíam o componente E da sequência. Pressões (ou bicadas) sobre o manipulandum direito constituíam o componente D da sequência (Barba & Hunziker, 2003; Cohen et al., 1990; Denney & Neuringer, 1998; Hunziker et al., 1996; Hunziker et al., 1998; Mook & Neuringer, 1994; Morgan & Neuringer, 1990; Morris, 1987; Morris, 1989; Neuringer, 1991; Neuringer, 1992; Neuringer & Huntley, 1992; Neuringer et al., 2000; Page & Neuringer, 1985; Schwartz, 1982). Duas pressões sucessivas sobre o manipulandum esquerdo, seguidas de duas pressões sucessivas sobre o manipulandum direito, compunham a sequência de pressões EEDD, por exemplo. Essa sequência contém quatro elementos constituintes: dois componentes E e dois componentes D. A sequência apresenta somente uma mudança de manipulandum durante a emissão da sequência (essa mudança ocorre entre a segunda e a terceira pressão). Essas mudanças de manipulandum são denominadas ´alternações´ e tiveram papel central em alguns trabalhos (Barba & Hunziker, 2003; Machado 1997).

Sequências assim constituídas formaram a unidade de análise desses trabalhos. Em sua maioria, esses estudos adotaram o regime de tentativas. Um antecedente ambiental assinalava as ocasiões em que as pressões, se ocorressem, eram efetivas. Uma sequência de n pressões (ou n bicadas) produzia a consequência programada somente se ela atendesse às exigências impostas pelo esquema. Sequências que não atendiam aos critérios do esquema produziam um time-out.

Quatro pressões à barra, emitidas consecutivamente, podem definir uma tentativa e constituem uma unidade de análise possível. Essa unidade possui propriedades mensuráveis. Algumas delas são: duração (intervalo temporal que separa a primeira e a última pressão), força média com que são exercidas as pressões, intervalo entre sequência (IES), número de componentes E, número de componentes D, número de alternações, posição em que ocorrem as alternações, posições de ocorrência dos componentes E, posições em que ocorrem os componentes D. Quaisquer dessas propriedades podem definir um parâmetro da sequência. Os parâmetros número de componentes E, número de componentes D, número de alternações, posições em que ocorrem as alternações, posições em que ocorrem os componentes E e posições em que ocorrem os componentes D apresentam uma característica particular. Eles definem a configuração da sequência. Tomem-se, por exemplo, as três sequências seguintes:

1 – EEDE

2 – EDDD

3 – EEDE

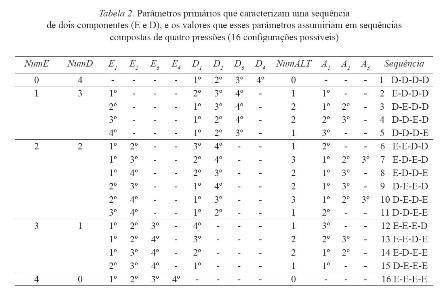
Quando emitidas, as sequências 1 e 3 podem apresentar diferentes durações. Apresentam, entretanto, configurações idênticas. As sequências 1 e 2 diferem, porém, em suas configurações. Elas apresentam diferentes números de componentes E e D, diferentes números de alternações entre os manipulanda, e as alternações ocorrem em posições distintas. Os parâmetros que afetam a configuração das sequências serão denominados parâmetros configurativos. Sequências de quatro pressões consecutivas à barra apresentam 16 diferentes configurações possíveis. A análise de combinação dos parâmetros configurativos permite construir a Tabela 2. Ela mostra os valores que cada parâmetro assume em cada uma das 16 configurações. Os parâmetros são os seguintes:

NumE: número de componentes E que a sequência contém (esse parâmetro pode assumir os valores 0, 1, 2, 3 e 4).

NumD: número de componentes D que a sequência contém (esse parâmetro pode assumir os valores 0, 1, 2, 3 e 4).

E1: posição do primeiro componente E (pode assumir os valores 1º , 2º , 3º e 4º).

E2: posição do segundo componente E (pode assumir os valores 2º , 3º e 4º ).

E3: posição do terceiro componente E (pode assumir os valores 3º e 4º ).

E4: posição do quarto componente E (pode assumir o valor 4º ).

Descrição análoga vale para os parâmetros (D₁, D₂, D₃, D₄).

NumALT: número de alternações ocorridas durante a emissão da sequência. (esse parâmetro pode assumir os valores 0, 1, 2 e 3).

A1: posição da primeira alternação. (pode assumir os valores 1º , 2º e 3º )

A2: posição da segunda alternação. (pode assumir os valores 2º e 3º)

A3: posição da terceira alternação. (pode assumir o valor 3º)

Os parâmetros NumE, NumD e NumALT assumem valores em qualquer uma das 16 sequências. O mesmo não ocorre aos demais parâmetros. Os parâmetros E₁, E₂, E₃, E₄, D₁, D₂, D₃, D₄ , A₁, A₂ e A₃ não assumem valores em todas as sequências. E₂, por exemplo, só assume valor, se o parâmetro NumE assumir valor igual ou superior a 2. A₃, por sua vez, só assume valor, se o parâmetro NumALT assumir o valor 3.

 

 

Qualquer parâmetro da sequência pode gerar uma função S. Um esquema poderia reforçar diferencialmente sequências cuja duração assumisse um valor mínimo, por exemplo. Esquemas que reforçam diferencialmente a emissão de sequências podem não impor nenhuma exigência adicional. Qualquer sequência de pressões à barra (ou bicadas em discos) produz a consequência programada. A emissão de uma sequência é condição necessária e suficiente, nesse caso, para que ocorra a consequência programada. Os sujeitos submetidos a esses esquemas produzem, predominantemente, sequências que não contêm alternações entre os manipulanda. Hunziker et al. (1996) e Hunziker et al. (1998) mostram que esse padrão de emissão predomina, quando o esquema não impõe exigências adicionais. Esse padrão será denominado padrão ALT-0 (emissão predominante ou exclusiva de sequências que não contêm alternação entre os manipulanda).

Interação e combinação de parâmetros: Podem-se definir funções S sobre parâmetros configurativos. Machado (1997) treinou pombos a emitir sequências de oito bicadas sobre dois manipulanda. O experimentador instituiu esquemas que exigiam um número mínimo de alternações em cada sequência emitida. O experimentador definiu, portanto, sua função S sobre o parâmetro NumALT.

Contingências definidas sobre parâmetros configurativos levantam, porém, um problema. Suponha-se um esquema Lag–4 que exija a emissão de sequências compostas por quatro pressões à barra. Uma sequência produz a consequência programada somente se apresentar exatamente três componentes E. A contingência exige explicitamente apenas que o parâmetro NumE assuma o valor 3. Esse esquema definiria, portanto, sua função S sobre o parâmetro NumE.

Ocorre que o parâmetro NumE interage com outros parâmetros configurativos. Sequências que contêm zero ou três alternações certamente não produziriam a consequência programada. Portanto, nem todo valor do parâmetro NumALT produziria a consequência programada com igual probabilidade. Logo, o experimentador também teria definido, indiretamente, uma função S´ sobre o parâmetro NumALT. A probabilidade de que ocorra a conseqüência programada, dado que a sequência contenha uma única alternação [P(CP/ NumALT = 1)], corresponde à probabilidade de que a sequência contenha exatamente três componentes E, dado que ela contenha uma única alternação [P(NumE = 3/ NumALT = 1)], o que, por sua vez, corresponde à razão E3 / ALT1, onde:

ALT1 é o número total de sequências que apresentam NumALT = 1 (seis sequências). E3 é o número de sequências que apresentam NumE = 3, dentre as seis que apresentam NumALT = 1, (duas sequências).

Portanto, pode-se escrever que P(CP/ NumALT = 1) = 2/6.

O mesmo procedimento de cálculo levaria às seguintes probabilidades de ocorrência da consequência programada:

P(CP/ NumALT = 0) = 0/6.

P(CP/ NumALT = 2) = 2/6.

P(CP/ NumALT = 3) = 0/6.

A Figura 6 representa graficamente a função S e a função S´ que esse esquema definiria.

 

 

Caso semelhante ocorreria se o experimentador exigisse um número exato de alternações por sequência emitida. Se o esquema reforçasse exatamente duas alternações, a função S estaria definida sobre o parâmetro NumALT, e estaria definida indiretamente uma função S´ sobre o parâmetro NumE. A Figura 7 representa graficamente a função S e a função S´ que esse esquema estabeleceria.

 

 

Esses casos mostram que os parâmetros configurativos são dependentes. Eles não variam livremente.

Além disso, ao instituir uma classe descritiva, um esquema de reforçamento pode combinar, de diferente maneiras, as propriedades da unidade de análise (Catania, 1999). Um esquema que reforça diferencialmente a emissão de sequências pode combinar parâmetros de maneira disjuntiva: uma sequência produz a consequência programada, somente se apresentar exatamente dois componentes E ou apresentar uma única alternação (exemplo de uma combinação disjuntiva dos parâmetros NumE e NumALT). O esquema pode combinar parâmetros de maneira conjuntiva: uma sequência produz a consequência programada, somente se contiver exatamente dois componentes E e apresentar uma única alternação (exemplo de uma combinação conjuntiva dos parâmetros NumE e NumALT). O esquema pode combinar parâmetros de maneira relacional: uma sequência produz a consequência programada, somente se o seu número de componentes E exceder o seu número de alternações (exemplo de uma combinação relacional dos parâmetros NumE e NumALT).

Um esquema pode reforçar diferencialmente sequências que apresentam exatamente dois componentes E ou uma única alternação (combinação disjuntiva dos parâmetros NumE e NumALT). Esse esquema define explicitamente duas funções S: uma função S sobre o parâmetro NumE [S(NumE)] e uma função S sobre o parâmetro NumALT [S(NumALT)]. A Figura 8 mostra a representação gráfica dessas funções. Os pontos destacados (quadrados) revelam claramente a interação dos parâmetros. A função S(NumALT) mostra que a emissão de uma sequência contendo três alternações produziria a consequência programada com 100% de probabilidade. As 16 configurações possíveis contêm somente duas sequências com três alternações, e ambas apresentam exatamente dois componentes E.

 

 

Nessas condições, o esquema poderia produzir efeitos distintos sobre cada um dos parâmetros. Ele poderia afetar diferentemente as funções R de cada um deles. O procedimento poderia gerar, entre outros, dois resultados extremos: o organismo emitiria apenas sequências com uma única alternação (mas variaria o valor de NumE entre 1 e 3). Ou, ao contrário, emitiria apenas sequências que contivessem exatamente dois componentes E (mas variaria o valor de NumALT entre 1 e 3)².

Alguns estudos que investigaram a variabilidade comportamental formaram grupos em que foi conduzido um treino de repetição. Nesses grupos, foi reforçada diferencialmente a emissão de uma mesma sequência (Mook & Neuringer, 1994; Neuringer, 1991). Esse treino envolve uma combinação conjuntiva de parâmetros.

 

SEQUÊNCIAS E ESQUEMA LAG – N

A contingência Lag-N pode operar sobre quaisquer unidades de análise do comportamento. Pode operar sobre sequências de pressões a barras ou bicadas sobre discos. Pode operar sobre um único parâmetro, confi gurativo ou não. O experimentador pode dividir em classes os valores do intervalo entre sequências (IES), como fizeram Schoenfeld et al. (1966), e impor a seguinte condição: uma sequência produz a consequência programada somente se o IES dessa sequência recair em um intervalo distinto do intervalo em que recaíram os IES das N últimas sequências emitidas. Pode-se também escolher um parâmetro configurativo: uma sequência produz a consequência programada somente ela contiver um número de alternações diferente do número que apresentaram as N últimas sequências emitidas. Também aqui se pode definir, sobre cada um dos parâmetros primários, um parâmetro secundário TR. Pode-se definir o parâmetro secundário TR sobre o parâmetro primário IES [TR(IES)], pode-se definir o parâmetro secundário TR sobre o parâmetro primário NumE [TR(NumE)], pode-se definir o parâmetro secundário TR sobre o parâmetro primário E1 [TR(E1)] e assim por diante.

Muitos trabalhos que investigaram a variabilidade comportamental empregaram o esquema Lag–N (Neuringer, 2002). Esse esquema operava da maneira seguinte: uma sequência produzia a consequência programada somente se ela diferia ao menos das N últimas sequências emitidas. Diferir equivale a apresentar outra configuração. Uma série hipotética de sequências pode ilustrar o critério de reforçamento que adota o esquema Lag–N. Suponha-se que as dez primeiras sequências emitidas em uma sessão de esquema Lag–4 foram as seguintes:

EEEE (1) – EEED (2) – EDDD (3) – EEED (4) – EEEE (5) – DEEE (6) – DEEE (7) – DDEE (8) – DDDE (9) – DEEE (10).

Apenas as sequências 1, 2, 3, 6, 8 e 9 produziriam a consequência programada.

Todo parâmetro primário permite definir um TR específico. O parâmetro NumE dá origem ao parâmetro secundário TR(NumE), que assume um valor em cada uma das sequências emitidas. O mesmo ocorre aos demais parâmetros primários. A Tabela 3 mostra os valores que assumiriam os parâmetros primários e os respectivos parâmetros TR na série hipotética de dez sequências apresentada acima.

Os parâmetros E₁, E₂, E₃, E₄, D₁, D₂, D₃, D₄ , A₁, A₂ e A₃ não assumem valores em todas as sequências. Se uma sequência contiver dois ou mais componentes E, podem-se atribuir a E₂ os valores 2º, 3º ou 4º. Se a sequência apresentar zero ou um único componente E, não se podem atribuir valores a E₂. Todavia, sempre é possível atribuir um valor a TR(E₂), como mostra a Tabela 3. A sequência 9 (que contém um único componente E) apresenta TR(E₂) = 5. O valor 5 descreve a seguinte circunstância: o número de sequências que separam a atual ocorrência desse evento (sequência que apresenta menos de dois componentes E) e a ocorrência passada mais recente de uma sequência que apresenta essa mesma característica é cinco.

O esquema Lag–N sempre reforça as sequências que ocorrem pela primeira vez, já que elas diferem de todas as sequências emitidas anteriormente. Excluídas essas sequências, pode-se definir, para toda sequência emitida, um parâmetro TR mais geral, que considera a configuração da sequência. O valor que esse TR assume corresponde ao número de sequências que separam a atual ocorrência da configuração e a ocorrência passada mais recente dessa mesma configuração. O valor que esse parâmetro TR atinge corresponde ao maior valor de TR que cada sequência apresenta (VmaxTR, na Tabela 3). Os valores de TR de cada parâmetro primário permitem, portanto, definir um novo parâmetro TR: o parâmetro TR terciário (TRt).

 

 

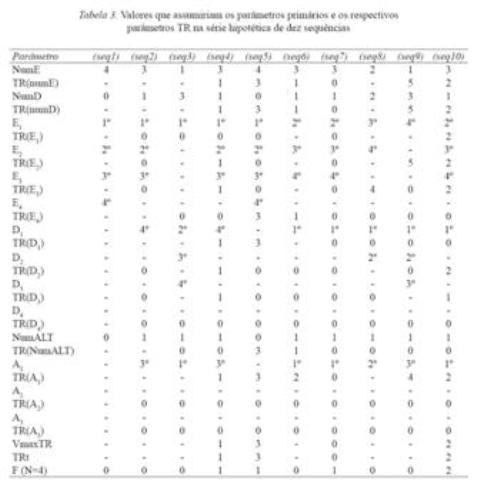
Esquema Lag-N e seleção dependente da frequência: O esquema Lag–4 que opera sobre sequências reforça diferencialmente a emissão de sequências cujo TRt iguale ou supere quatro e reforça as sequências inéditas (aquelas em que o parâmetro TRt não assume valor). O esquema Lag–4 reforça diferencialmente a emissão da sequência S, na tentativa n, somente se a sequência S não tiver sido emitida nas tentativas n-1, n-2, n-3, e n-4. O universo das quatro últimas sequências emitidas constitui um conjunto que o esquema considera ao programar a liberação da consequência. Se S ocorre com frequência zero nesse conjunto, a consequência programada ocorre na tentativa n. Se S ocorre com frequência superior a zero nesse conjunto, a consequência programada não ocorre na tentativa n. Essa característica permite que a propriedade frequência constitua um parâmetro sobre o qual se pode estabelecer a função S. O valor de N (em Lag-N) representa a extensão do conjunto de sequências. Se N assume o valor quatro, o conjunto inclui as quatro últimas sequências emitidas. O valor atribuído ao parâmetro frequência (F) é função do valor atribuído a N. O parâmetro TRt não apresenta essa característica. O valor que o parâmetro TRt assume não depende do valor atribuído a N (em Lag-N). A Tabela 3 mostra os valores do parâmetro F (para N = 4). O esquema Lag–4 apresenta a consequência programada somente quando F assume o valor zero.

Se uma sequência apresenta TRt maior ou igual 4, então ela apresenta F = 0 (para N=4), e vale a recíproca. Aumentando a emissão de sequências cujo TRt iguala ou excede quatro, o esquema Lag–4 aumenta, em igual proporção, a emissão de sequências com F = 0. A variação da correlação pode, portanto, medir-se sobre qualquer dos dois parâmetros.

O esquema Lag–N pertence ao grupo dos esquemas em que a propriedade frequência constitui a base do reforçamento diferencial (Machado, 1992). Trata-se de esquemas que promovem alguma forma de seleção dependente da frequência.

O esquema Lag–N que opera sobre sequências define, portanto, sua função S sobre o parâmetro TRt. Alternativamente, pode-se dizer o esquema Lag–N define sua função S sobre o parâmetro F. Quando se trata de medir a variação da correlação, os dois parâmetros se equivalem.

 

ESQUEMA LAG–N E VARIABILIDADE

Page e Neuringer (1985) mediram variabilidade empregando um índice oriundo da teoria da informação, o índice U (Attneave, 1959). Muitos outros trabalhos recorreram ao mesmo índice (Neuringer, 2002). Convém examinar algumas propriedades do índice U e relacioná-las ao conceito de variabilidade. Essa análise limita-se aos estudos que empregaram o esquema Lag–N e que adotaram o índice U (Barba & Hunziker, 2003; Cohen et al., 1990; Hunziker et al., 1996; Hunziker et al., 1998; Morgan & Neuringer, 1990; Neuringer, 1991; Neuringer, 1992; Neuringer & Huntley, 1992). Esses estudos instituíram esquemas que reforçavam diferencialmente a emissão de sequências formadas pelos componentes E e D. Essas sequências continham um número x de elementos constituintes. O valor de x determina o número total de diferentes configurações possíveis. Se quatro elementos constituintes formam a sequência, têm-se 16 (2⁴) configurações possíveis. Ao fim de uma sessão, os experimentadores obtinham conjuntos de sequências emitidas. Pode-se calcular, dentro do conjunto obtido, a frequência relativa em que foi emitida cada uma das diferentes configurações. Pode-se obter, portanto, uma distribuição das frequências em que ocorria cada uma das configurações. O índice U foi calculado com base nos valores de frequência relativa e refletiu a uniformidade dessa distribuição. Esse índice assumia o seu valor mínimo (0) se o sujeito emitisse apenas uma das diferentes configurações, e assumia o valor máximo (1) se o animal emitisse, com frequência idêntica, todas as diferentes configurações.

Tome-se o exemplo de um esquema que reforça diferencialmente a emissão de sequências contendo quatro elementos constituintes (16 configurações distintas). Se um sujeito emite apenas a sequência EEDD durante toda uma sessão, tem-se, ao fim, um conjunto de sequências que contém apenas a configuração EEDD. Desse conjunto podese tomar ao acaso uma sequência (sequência S). Pode-se afirmar, nesse caso, que S é seguramente a sequência EEDD. É 100% provável que S seja a sequência EEDD. Se o animal emite todas as sequências com igual frequência, o conjunto contém todas as configurações em igual quantidade. Nesse caso, tem-se uma (1) chance em 16 de que S (a sequência tomada ao acaso) seja a sequência EEDD. Ou seja, a probabilidade de que S seja a sequência EEDD assume o valor 1/16. O primeiro exemplo ilustra um caso em que o comportamento do sujeito é altamente previsível. O segundo caso mostra uma situação em que o comportamento é bem menos previsível.

O índice U mede previsibilidade de eventos. Sentenças que expressam previsibilidade podem tomar a forma de enunciados probabilísticos. O exemplo apresentado acima pode ganhar a forma: P (S = EEDD) = 1, no primeiro caso e P (S = EEDD) = 1/16, no segundo caso.

Além das frequências em que cada uma das sequências ocorre, a ordem em que são emitidas também afeta a previsibilidade. Se o sujeito emitiu todas as 16 sequências com igual frequência, tem-se P (S = EEDD) = 1/16. Suponha-se, no entanto, que o sujeito tenha emitido as 16 sequências em ordem perfeitamente regular. A emissão da sequência EDDE sempre antecedia a emissão da sequência EEDD. Se a sequência EDDE ocorria na tentativa n, então a sequência EEDD sempre ocorria na tentativa seguinte n +1. Esse padrão de emissões gera um conjunto de sequências. Desse conjunto pode-se tomar ao acaso uma sequência S. Se se constata que S é a sequência EDDE, pode-se afirmar, com certeza, que a sequência emitida na tentativa seguinte (tentativa n + 1) foi a sequência EEDD. A sequência emitida na tentativa n + 1 é, portanto, totalmente previsível, desde que se conheça a sequência que foi emitida na tentativa n. Em termos de probabilidade, pode-se afirmar que é 100% provável que a sequência emitida na tentativa n + 1 seja EEDD, desde que a sequência emitida na tentativa n tenha sido a sequência EDDE. Ou, resumidamente:

P (S_(n+1) = EEDD / EDDE_(n)) = 1

Essa série de sequências apresentaria a seguinte característica: as sequências emitidas são altamente imprevisíveis, se tomadas isoladamente, mas são totalmente previsíveis, se tomadas aos pares. O registro das frequências pode indicar essa previsibilidade. Nesse caso, porém, a frequência em que cada sequência é emitida isoladamente não mostra essa característica. Se forem registradas, contudo, as frequências em que são emitidos os pares de sequências, pode-se identifi car essa previsibilidade. Nesse caso, a frequência em que o sujeito emitiu a dupla EDDE–EEDD superaria a frequência em que ocorreram outras duplas. O comportamento desse sujeito é altamente previsível em algum nível. O índice U pode considerar essa variável, a depender do nível em que é calculado.

A previsibilidade que o índice U mede considera apenas as propriedades do conjunto de sequências (as frequências e, eventualmente, a ordem em que as sequências ocorrem). Page e Neuringer (1985, p. 438) informam que o cálculo de U não considerou reforçamentos e time-outs. Os trabalhos que seguiram Page e Neuringer (1985) e usaram o índice U mantiveram esse procedimento (Neuringer, 2002). O cálculo de U não considera os eventos ambientais que o esquema programa. O exemplo que segue ilustra essa propriedade do índice U. Imagine-se que o pesquisador tenha registrado, ao fim de uma sessão, k ocorrências da sequência EEDD. O cálculo de U considera o valor k e, a depender do nível de análise, considera também as sequências que antecederam e sucederam a emissão da sequência EEDD dentro daquele conjunto. Mas a sequência EEDD terá produzido a consequência programada em algumas de suas ocorrências e não a terá produzido em outras. Os dados talvez mostrem que a sequência EEDD ocorre com maior frequência imediatamente depois de ter sido reforçada diferencialmente. O conjunto de dados mostraria o seguinte: A frequência em que ocorre a série de eventos EEDD-CPEEDD (ocorrência em que a primeira sequência EEDD atendeu ao critério Lag-N e produziu a consequência programada (CP)) supera a frequência em que ocorre a série de eventos EEDD ¾ EEDD (ocorrência em que a sequência EEDD não atendeu ao critério Lag-N e produziu o time-out). Esse dado revelaria que é mais provável a ocorrência da sequência EEDD na tentativa n + 1, se a mesma EEDD produziu a consequência programada na tentativa n. Formalmente, poder-se-ia escrever que:

P (S_(n+1) = EEDD / EEDD produziu CP em n) > P (S_(n+1) = EEDD / EEDD não produziu CP em n)

Esse elemento do ambiente permitiria prever, com maior precisão, a ocorrência da sequência EEDD (aumentaria a previsibilidade do comportamento do sujeito). O cálculo do índice U, tal como é realizado nos estudos em questão, não leva em conta, porém, esse elemento. O índice U indica se o sujeito emite sequências de maneira mais previsível ou menos previsível, considerando-se apenas as frequências individuais e, a depender do nível de análise, a ordem em que são emitidas as sequências. O índice U (tal como é calculado nos estudos que empregam o esquema Lag–N) apresenta, portanto, um caráter estrutural³.

Ao escolherem a variável U, Page e Neuringer (1985) adotaram um conceito possível de variabilidade, dentre outros (Barba, 2006; Neuringer, 2002). Muitos trabalhos que empregaram o procedimento Lag–N adotaram o mesmo conceito (Barba, 2006; Neuringer, 2002). Comportamento mais variável corresponde, nessa perspectiva, a comportamento menos previsível.

 

REFORÇAMENTO DIFERENCIAL DO NÚMERO DE ALTERNAÇÕES

Os sujeitos de Page e Neuringer (1985) emitiam sequências de oito bicadas consecutivas. Sequências de oito bicadas apresentam um número de alternações que varia entre zero e sete. As sequências produziam a consequência programada somente se atendessem à exigência do esquema Lag–N. Quando N assume um alto valor, o esquema exige que o sujeito emita um grande número de sequências diferentes. Ocorre que existem somente duas configurações que apresentam zero alternações. O número de configurações que apresentam uma única alternação é maior que dois. E o número de configurações que apresentam duas alternações é ainda maior. Ou seja, o número de configurações disponíveis aumenta à medida que se consideram as sequências com números intermediários de alternações (três e quatro alternações). Quando N assume altos valores, o esquema Lag–N reforça diferencialmente, portanto, a emissão de sequências que contêm números intermediários de alternações. A variabilidade que o esquema gera poderia constituir um sub-produto do reforçamento diferencial de sequências que encerram números médios de alternações. Machado (1997) formulou e testou essa hipótese conduzindo experimentos. Machado treinou pombos a emitir sequências de oito bicadas sobre dois manipulanda. O primeiro experimento instituía um esquema que reforçava diferencialmente sequências que continham ao menos uma (grupo 1) ou duas (grupo 2) alternações. O segundo experimento reforçava diferencialmente sequências que apresentavam números intermediários de alternações. Nenhuma variação era exigida em nenhum dos dois experimentos.

Os esquemas de Machado (1997) geraram alguma variabilidade. Os índices não atingiram, contudo, os níveis alcançados em Page e Neuringer (1985). Além disso, os esquemas de Machado (1997) não sustentaram os níveis de variabilidade ao longo do tempo.

Os resultados que Machado (1997) obteve importam pouco aos argumentos que o trabalho presente desenvolve. Mas a hipótese de Machado, confirmada ou não, interessa diretamente a essa análise. Essa hipótese distingue duas classes de sequências: 1 - uma classe de sequências que produzem a consequência programada (classe que define a contingência); 2 – uma classe de sequências afetadas pela contingência. Trata-se da distinção que Catania (1973) estabeleceu ao definir comportamento operante. Em Machado (1997), a classe 1 foi definida sobre o parâmetro NumALT (função S).

O esquema de Machado (1997) incidiu naturalmente sobre uma linha-de-base. Inicialmente cada uma das 256 diferentes sequências era emitida com alguma frequência. Essas frequências geravam uma função Ri sobre o parâmetro NumALT. O reforçamento diferencial presumivelmente alterou a função R ao longo do tempo, dando origem a uma função Rf (sobre o parâmetro NumALT). Essas funções permitiriam calcular a variação da correlação sobre esse parâmetro. Essa variação representaria o processo de diferenciação que o esquema produziu. Ainda que os esquemas tivessem gerado e mantido altas proporções de diferentes sequências, não se poderiam medir correlações sobre esse efeito, pois as funções S foram definidas sobre o parâmetro NumALT. Essa circunstância reforça a tese de Machado (1997). A variabilidade gerada pelo esquema constituiria um derivativo do reforçamento diferencial. O aumento da variabilidade não representaria diferenciação.

A hipótese de Machado (1997) aplica-se, em princípio, a qualquer dos parâmetros configurativos. O número de configurações que contêm três, quatro ou cinco componentes E (182 das 256 configurações) supera grandemente o número de configurações que contêm zero, um, sete ou oito componentes E (18 das 256 confi gurações). Se N assume valores altos, o esquema Lag–N reforça diferencialmente sequências que apresentam um número intermediário de componentes E. Um esquema que reforçasse diferencialmente um número médio de componentes E (3≤ NumE ≤ 5) talvez gerasse alta variabilidade (embora não a exigisse), segundo a hipótese de Machado (1997). Esse procedimento estabeleceria sua função S sobre o parâmetro NumE. Ainda que o esquema engendrasse altos níveis de variabilidade, não se poderia afirmar que a variabilidade obtida representasse o processo de diferenciação.

 

REFORÇAMENTO DIFERENCIAL DE SEQUÊNCIAS DIFERENTES

O esquema Lag–N estabelece sua função S sobre o parâmetro TR. Em particular, os esquemas que reforçam diferencialmente a emissão de sequências definem sua função S sobre o parâmetro TRt. A medição de Dr exigiria, portanto, que se obtivessem funções R (Ri e Rf ) definidas sobre o parâmetro TRt. A variação da correlação mostraria o processo de diferenciação.

Os resultados de Neuringer e Huntley (1991) mostram que o esquema Lag–N gera uma variação positiva da correlação. Esses autores submeteram ratos ao esquema Lag–4 e empregaram um delineamento ABA. Os sujeitos foram expostos à contingência que exigia variabilidade (Lag-4). Em seguida, foram submetidos a uma contingência que permitia, mas não exigia, variabilidade (esquema yoke). E, finalmente, foram novamente expostos ao esquema Lag-4. Os autores mostraram a porcentagem de variação (sessão a sessão), que correspondia à razão número de sequências que atendiam à exigência do esquema Lag–4 / número total de sequências emitidas na sessão. Durante as fases Lag–4, essa porcentagem coincidia com a porcentagem de sequências reforçadas. Os resultados mostraram que o esquema afetou essa variável. Sob o esquema Lag-4, os animais produziram números acima de 50%. Sob o esquema yoke, esses valores declinaram visivelmente. O esquema Lag–4 elevou, portanto, a proporção em que eram emitidas sequências que apresentavam TRt maior ou igual a quatro. Logo, o esquema Lag–4 produziu um aumento da correlação (medida sobre o parâmetro TRt). Esse dado indica que o esquema produziu diferenciação. O esquema Lag–N modelou um operante.

Esse resultado levanta, porém, duas questões: 1 - Pode-se falar em variabilidade operante? 2 – Se é a variação da correlação (medida sobre o parâmetro TRt) que representa o processo de diferenciação, que efeito mostraria a variação do índice U?

Não é possível medir a variação da correlação sobre U, pois a contingência Lag–N não estabelece sua função S sobre esse índice. Isto é, ainda que o esquema Lag–N produza um aumento do índice U (quando age sobre a linha-de-base ALT-0), essa variação de U não reflete o processo de diferenciação. A variação de U não atesta, portanto, a formação de um operante, segundo o conceito que Catania (1973) propõe.

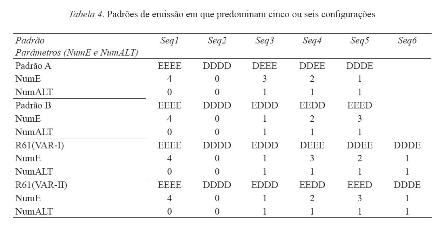
Quando opera sobre o padrão ALT-0, o esquema Lag–N eleva, de fato, o valor de U (Hunziker et al., 1996; Hunziker et al, 1998). Hunziker et al. (1998) instituíram um esquema Lag–4. Quatro pressões consecutivas às barras compunham a unidade de análise. Os autores apresentaram a frequência em que cada sujeito emitiu cada uma das 16 diferentes sequências. Foram apresentadas, sujeito a sujeito, as frequências registradas na 10º sessão de cada fase (um dos grupos foi submetido a duas fases de Lag–N: fase VAR-I e fase VAR-II). Na última sessão das fases em que vigorava o esquema Lag–4, boa parte dos sujeitos emitiu preferencialmente cinco ou seis sequências distintas. Esse pequeno número de sequências produz alta porcentagem de reforço, sob o esquema Lag–4, se as emissões obedecem a uma ordem regular. Onze sujeitos foram mantidos até o fim do experimento. Alguns sujeitos apresentaram um padrão de emissão em que prevaleceram cinco sequências distintas. Outros sujeitos mostraram um padrão de emissão em que predominaram seis sequências distintas. A Tabela 4 mostra alguns desses padrões. O sujeito R62 (em VAR-I e em VAR-II), o sujeito R64 (em VAR-I e em VAR-II) e o sujeito R66 (em VAR-II) exibiram o padrão A. O sujeito R63 (em VAR-II), o sujeito 71 e o sujeito 72 apresentaram o padrão B. O sujeito R61 emitiu predominantemente seis sequências distintas em ambas as fases VAR (as seis sequências emitidas em VAR-II não repetiram, contudo, as seis sequências emitidas em VAR-I).

 

 

ESSES PADRÕES NÃO INCLUÍRAM OS SUJEITOS R65, R67, R68 E R70.

Hunziker et al. (1996) também submeteram ratos a um esquema Lag–4. Quatro pressões às barras constituíam a unidade de análise. Esses autores também apresentam as frequências em que cada sujeito emitiu cada uma das diferentes sequências. Em Hunziker et al. (1996), foram usados 20 sujeitos. Os sujeitos SI.2, SI.5, WE.4 e WE.5. exibiram claramente um dos padrões apresentados acima.

Essas cinco ou seis sequências, emitidas em ordem regular, produzem um TRt (por sequência) superior a quatro em todas as emissões. Em um esquema Lag–4, esse padrão rende 100% de reforçamento. Agindo sobre a linha-de-base ALT-0, o esquema que engendra esses padrões produz uma variação positiva da correlação. Esse padrão representa, porém, um comportamento altamente previsível.

Se, ao contrário, as cinco ou seis sequências são emitidas aleatoriamente, há maior imprevisibilidade. Mas muitas emissões poderiam apresentar um TRt inferior a quatro. Logo, a porcentagem de reforçamento não atingiria 100%. Em relação à linha-de-base ALT-0, esse padrão aleatório poderia engendrar uma variação positiva da correlação. Mas essa variação poderia assumir valores muito diferentes em cada caso. Cada replicação do procedimento poderia produzir valores de Dr muito distintos. A emissão aleatória das sequências geraria, portanto, uma medida instável do processo de diferenciação.

A rigor, o esquema Lag-N não reforça diferencialmente a variabilidade. Ele reforça diferencialmente a emissão de sequências cujo valor do parâmetro TRt seja maior ou igual a N. Quando atua sobre a linha-de-base ALT-0, o esquema Lag-N gera um processo de diferenciação. Ele eleva o TRt médio das sequências e produz uma variação positiva da correlação. O Lag–N engendra, portanto, um operante. A variação do índice U não representa, porém, esse processo.

O esquema Lag-N afeta indiretamente a distribuição das frequências em que são emitidas as diferentes sequências. O índice U mede o efeito que o esquema Lag-N produz sobre essa distribuição. Operando sobre a linha-de-base ALT-0, o esquema gera uma distribuição menos concentrada das frequências em que são emitidas as sequências. O esquema Lag–N produz, portanto, um incremento nos valores que assume o índice U. Todavia, ainda que o esquema Lag–N produza uma distribuição perfeitamente uniforme das frequências (e leve, portanto, o índice U ao seu valor máximo), não se pode medir a variação da correlação sobre esse efeito, pois o esquema define sua função S sobre o parâmetro TRt (e não sobre U). Logo, segundo o conceito de operante que propõe Catania (1973), não se pode afirmar que a variação do índice U represente um processo de diferenciação. A variação desse índice constituiria um efeito secundário do reforçamento diferencial de sequências cujos valores de TRt igualam ou superam N.

Os trabalhos que empregaram o esquema Lag–N e adotaram o U como principal variável dependente relacionaram ´variabilidade´ a esse efeito secundário do esquema sobre a distribuição das frequências em que foram emitidas as sequências. Maior variabilidade implica distribuição mais uniforme das frequências (Barba, 2006; Neuringer, 2002). O efeito do esquema sobre os índices de U mostraria que a variabilidade constitui uma dimensão operante do comportamento (Page & Neuringer, 1985). Se a variação do índice U não representa o processo de diferenciação, não se poderia concluir que o esquema Lag–N produz variabilidade operante. Nessa perspectiva, a variação do índice U oferece evidências precárias à tese de Page e Neuringer (1985).

Índice U e dependência de parâmetros

O esquema Lag–N que opera sobre sequências exige que o sujeito emita sequências cujos valores de TRt sejam iguais ou superiores a N. A depender do valor de N, o esquema Lag-N exige indiretamente que o sujeito emita um número mínimo de diferentes sequências. O esquema exige, portanto, que o sujeito apresente uma distribuição de frequências menos concentrada que a distribuição de frequências do padrão ALT-0. Incidindo sobre a linha-de-base ALT-0, o esquema Lag–N exige diretamente que os sujeitos emitam sequências cujos valores de TRt superem ou igualem N e exige indiretamente que os sujeitos distribuam mais uniformemente as sequências emitidas. O parâmetro TRt e o índice U apresentariam, portanto, alguma dependência. Não se poderia, então, afirmar que o esquema Lag–N define indiretamente uma função S´ sobre o índice U? Essa tese encontra duas dificuldades. Primeiramente, o índice U não constitui um parâmetro de sequências. Ele mede propriedades de conjuntos de sequências. Em segundo lugar, as contingências estabelecem funções S. Isso implica que o reforçamento diferencial associa, a cada valor do parâmetro adotado, um único valor de probabilidade de ocorrência da consequência programada. O esquema Lag–N não associa, a cada valor de U, um único valor de probabilidade de ocorrência da consequência programada. A dependência que relaciona o parâmetro TRt e o índice U é distinta da dependência que relaciona os parâmetros NumE e NumALT do exemplo mencionado anteriormente. Portanto, o esquema Lag-N não estabelece, nem indiretamente, uma função S sobre o índice U.

Variabilidade e indução

O reforçamento diferencial pode elevar a frequência em que ocorrem valores do parâmetro que não produzem a consequência programada, se esses valores estão próximos de valores que a produzem. Ele pode gerar indução (Catania, 1999). Incidindo sobre o padrão ALT-0, o esquema Lag–4 pode aumentar a frequência em que são emitidas sequências cujo valor do parâmetro TRt é igual a três. Essas sequências não produzem a consequência programada, mas apresentam um valor de TRt próximo ao valor mínimo que a produz. Esse efeito atende à definição de indução. Note-se que essa definição de indução restringe seu conceito a efeitos que o reforçamento diferencial produz sobre o parâmetro em que foi definida a função S.

A literatura mostra que o esquema Lag–N eleva o valor de U, quando a referência é o padrão ALT-0 (Hunziker et al., 1996; Hunziker et al., 1998). A variação de U não corresponderia, porém, àquilo que se denomina indução, pois o esquema Lag–N estabelece sua função S sobre o parâmetro TRt.

Caráter arbitrário do cálculo do índice U

Em muitos trabalhos, o cálculo do índice U considera as frequências em que são emitidas as diferentes configurações de sequências. Esse cálculo leva em conta o universo de todas as configurações possíveis (Barba & Hunziker, 2003; Cohen et al., 1990; Hunziker et al., 1996; Hunziker et al., 1998; Morgan & Neuringer, 1990; Neuringer, 1991; Neuringer, 1992; Neuringer & Huntley, 1992). Hunziker et al. (1998) escolheram sequências de quatro elementos constituintes. Logo, o cálculo de U considerou o universo das 16 (24) configurações distintas. Nada impede, porém, que o cálculo do índice U considere um conjunto menor de configurações ou considere outras distribuições de frequência. Esses procedimentos podem produzir resultados diferentes. O sujeito R62 de Hunziker et al. (1998), que apresentou, na fase VAR-I, o padrão A de emissão (Tabela 4), é um exemplo. Embora tenha emitido predominantemente cinco sequências diferentes, o sujeito as emitiu em frequências bastante próximas.

O cálculo de U que considerasse apenas essas frequências renderia um alto valor do índice. Embora o sujeito tenha concentrado suas emissões em um universo restrito de cinco sequências, as frequências em que elas foram emitidas mostraram um desenho bastante uniforme. O cálculo de U examinado até aqui considera a distribuição das frequências em que foram emitidas as configurações de sequências. Mas o cálculo de U poderia, em princípio, tomar a distribuição de qualquer variável. As cinco sequências que o sujeito R62 (de Hunziker et al., 1998) emitiu apresentam diferentes quantidades de componentes E. A Tabela 4 mostra que cada uma das cinco sequências contém um número diferente de componentes E. Nota-se que ocorrem todos os valores que o parâmetro NumE pode assumir (0, 1, 2, 3 e 4). Esse é o universo de valores possíveis do parâmetro NumE. Considerado esse universo, o sujeito R62 apresentou uma distribuição bastante uniforme desse parâmetro. O cálculo de U poderia considerar essa distribuição. O índice U poderia também refletir a distribuição do parâmetro NumALT do mesmo sujeito R62. O universo de valores que esse parâmetro assume é o seguinte: 0, 1, 2 e 3. O sujeito R62 apresentou apenas os valores 0 e 1 dentre as sequências em que se concentrou, como demonstra a Tabela 4. Calculado sobre esse universo, o índice U mostraria uma distribuição mais concentrada.

Essas considerações mostram que o cálculo do índice U, tal como se efetua nos estudos que empregam o esquema Lag–N, apresenta um caráter arbitrário. A depender da variável e do universo considerados, um mesmo padrão comportamental pode apresentar diferentes valores de U.

 

ESQUEMA LAG –N E PARÂMETROS CONTÍNUOS

Os procedimentos que adotaram Schoenfeld et al. (1966) e Cruvinel e Sério (2008) atendem à definição de esquema Lag-N, embora não tenham analisado sequências. Ambos investigaram variabilidade comportamental operante. O presente trabalho deve, portanto, incluir uma análise dos resultados de ambos.

Se os dois estudos instituíram esquemas Lag–N, os autores definiram suas função S sobre o parâmetro TR. Em ambos os trabalhos, o parâmetro TR foi definido sobre parâmetros primários que apresentam caráter contínuo (intervalo e duração). O conceito de operante que adota o trabalho presente se aplicaria aos procedimentos e resultados se os pesquisadores:

• Obtivessem uma função Ri sobre TR;

• Medissem a correlação inicial ri;

• Procedessem ao reforçamento diferencial;

• Obtivessem uma função Rf sobre TR;

• Medissem a correlação final rf;

• Determinassem a variação da correlação.Essa medida mostraria o processo de diferenciação.

Os resultados de Schoenfeld et al. (1966) mostraram apenas o desempenho dos sujeitos nas sessões finais do experimento. Os animais exibiram um padrão regular de emissões. Esse padrão compreendia uma alternação simples entre intervalos longos e intervalos curtos. Esse desempenho satisfazia à contingência. Os autores concluíram que o reforçamento diferencial pode produzir variabilidade comportamental.

Pode-se inferir que o procedimento de Schoenfeld et al. (1966) produziu uma variação positiva da correlação, se, ao início, os sujeitos apresentavam pressões cujos intervalos recaíam majoritariamente sobre uma mesma classe (pressões com TR = 0). Esse resultado mostraria o processo de diferenciação. Todavia pode-se também discutir se, e em que grau, o padrão gerado pelo esquema apresenta variabilidade. O padrão de alternações sistemáticas mostra um elevado grau de previsibilidade. Logo, os resultados não oferecem fortes evidências em favor da tese dos autores.

Cruvinel e Sério (2008) também mostraram apenas o desempenho dos sujeitos nas sessões finais do experimento. Além de submeterem ratos ao esquema Lag–3 (treino de variabilidade), essas autoras também formaram outro grupo de sujeitos em que reforçaram diferencialmente pressões que apresentavam duração de uma mesma classe (treino de repetição). A seção de Resultados compara basicamente os resultados desses dois grupos (treino de variabilidade e treino de repetição). São mostradas as distribuições de frequência (expressas em porcentagens) ao longo das classes de duração definidas no estudo. O esquema Lag-3 produziu uma distribuição de frequência visivelmente mais uniforme que a distribuição gerada pelo treino de repetição. As autoras não apresentaram medidas que refletissem essa diferença. Pode-se, contudo, supor que o desvio padrão ou o índice U mostrariam as acentuadas discrepâncias entre os dois grupos. Embora menos concentradas, as distribuições de frequência do grupo submetido ao esquema Lag-3 mostraram uma maior incidência em algumas classes. Predominaram, ao fim do experimento, as pressões que apresentavam durações menores. Os dados não revelam a organização temporal dessas pressões. Um padrão de repetição regular de classes (classe 1, classe 2, classe 3, classe 4, classe 1, classe 2, classe 3, classe 4,..... ) atenderia perfeitamente à exigência de um esquema Lag–3. Apresentaria, porém, alto grau de previsibilidade.

Ainda que os dados não permitam afirmá-lo, pode-se admitir que o esquema de Cruvinel e Sério (2008) tenha produzido variação positiva da correlação (e, portanto, diferenciação), se a função Ri, relativa aos sujeitos do esquema Lag–3, mostrava predomínio de pressões cujas durações incidiam em uma mesma classe (pressões com TR = 0).

Em ambos os trabalhos, pode-se, portanto, presumir que o reforçamento diferencial tenha gerado um processo de diferenciação. Mas o padrão de comportamento gerado pode apresentar alto grau de previsibilidade.

Duração é parâmetro primário e contínuo. Parâmetros TR definidos sobre ela constituem parâmetros secundários. Schoenfeld et al. (1966) e Cruvinel e Sério (2008) definiram, portanto, suas funções S sobre parâmetros secundários. Esquemas que reforçam a emissão de sequências diferentes definem suas funções S sobre o parâmetro terciário TRt. O parâmetro TRt é definido sobre os parâmetros secundários TR. Estes são, por sua vez, definidos sobre parâmetros primários configurativos, que apresentam caráter discreto. Embora todos esses trabalhos tenham buscado produzir variabilidade operante, suas metodologias diferem significativamente. Um esquema que envolvesse sequências e definisse sua função S sobre um parâmetro secundário permitiria uma comparação mais direta dos resultados. Um esquema Lag–N poderia impor a seguinte condição: uma sequência produz a consequência programada somente se ela apresentar um número de alternações distinto do número de alternações que apresentaram as N últimas sequências emitidas. Esse esquema definiria uma função S sobre o parâmetro TR(NumALT), um parâmetro secundário. Esse procedimento enfrentaria, porém, o problema da forte dependência que vigora entre os parâmetros que caracterizam as sequências.

 

CONSIDERAÇÕES FINAIS

O esquema Lag–N pode afetar diversas propriedades do comportamento. Muitas delas não guardam relação direta com os parâmetros TR ou TRt. Exigindo que o sujeito emita sequências diferentes, o esquema Lag–N exige que o sujeito alterne entre os manipulanda (se o valor de N for superior a um). Alternar entre os manipulanda demanda mais tempo. Logo, o esquema Lag–N exige indiretamente que o sujeito amplie a duração média das sequências emitidas (considerando-se a referência da linha-de-base ALT-0). O esquema Lag–N não impõe, contudo, nenhuma condição explícita sobre a duração das sequências. Particularmente, ele não associa, a cada valor de duração, um único valor de probabilidade de que ocorra a consequência programada. Ou seja, o esquema Lag–N não define, nem indiretamente, uma função S sobre o parâmetro primário duração. Não se poderia, portanto, medir variação da correlação sobre esse parâmetro. Algo semelhante ocorre ao índice U.

O esquema Lag-N poderia também aumentar a variabilidade da duração das sequências emitidas (medida pelo desvio padrão). Todavia, esse aumento da variabilidade também não representaria o processo de diferenciação que o esquema engendra.

Trata-se, em qualquer caso, de efeitos que acompanham o processo de diferenciação. Todos constituem efeitos secundários do reforçamento diferencial de sequências diferentes.

Page e Neuringer (1985) defendem que a variabilidade constitui uma dimensão operante do comportamento, comparável à força, duração, localização, etc...A presente análise estabelece uma hierarquia de parâmetros. Força, duração, localização representam parâmetros primários da unidade de análise. Medidas que representam variabilidade (medidas de dispersão, medidas de uniformidade distributiva, medidas de incerteza) descrevem propriedades de conjuntos de unidades de análise. Não pertenceriam ao grupo dos parâmetros que caracterizam uma unidade de análise.

Pode-se, em princípio, conceber um esquema em que a variação de U representasse o processo de diferenciação. Esse procedimento exigiria que o esquema estabelecesse sua função S sobre os valores desse índice. Ocorre que o índice U mede propriedades de um conjunto de eventos. Ele não constitui parâmetro de uma sequência. Ainda assim, um esquema que reforçasse a emissão de sequências poderia definir uma função S sobre o valor acumulado de U. A cada sequência emitida, o equipamento calcularia o valor de U referente ao conjunto de sequências emitidas até aquele ponto. A apresentação da consequência programada seria contingente à ocorrência de um valor mínimo de U. Operando sobre a linha-de-base ALT-0, esse esquema talvez produzisse um aumento do índice U e um aumento do TRt médio das sequências. Note-se que aqui não se poderia medir a variação da correlação sobre o parâmetro TRt, pois a função S não teria sido definida sobre ele. O caso representaria uma inversão do que ocorre ao esquema Lag-N. Nesse último, pode-se medir a variação da correlação sobre o parâmetro TRt (pois a função S é estabelecida sobre ele), e a variação do índice U representa um efeito secundário do esquema. O oposto ocorreria ao esquema que instituísse a função S sobre o índice U. Neste, a variação do TRt médio é que representaria um efeito secundário.

Essas circunstâncias reforçam o conceito de operante que Catania (1973) propõe. O reforçamento diferencial pode produzir efeitos diversos sobre o comportamento. O processo de diferenciação, que dá consistência à noção de operante, representa um desses efeitos. A variação da correlação constitui uma medida adequada desse processo. Examinando o esquema Lag–N e seus efeitos, este trabalho procurou identifi car o processo de diferenciação que o esquema Lag–N gera e relacioná-lo ao conceito de variabilidade comportamental. Constatou-se que a principal medida de variabilidade que esses esquemas empregam não representa esse processo. Essa circunstância traz dificuldades ao conceito de variabilidade comportamental operante.

 

REFERÊNCIAS

Antonitis, J. J. (1951). Response variability in the rat during conditioning, extinction, and reconditioning. Journal of Experimental Psychology, 42, 273-281.         [ Links ]

Attneave, F. (1959). Applications of information theory to psychology: A summary of basic concepts, methods and results. New York: Holt-Dryden Book: Henry Holt.         [ Links ]

Barba, L. S. (2006). Variabilidade Comportamental: uma Taxonomia Estrutural. Acta Comportamentalia, 14 (1), 23-46.         [ Links ]

Barba, L. S., & Hunziker, M. H. L. (2003). Variabilidade comportamental produzida por dois esquemas de reforçamento. Acta Comportamentalia, 10 (1), 5-22.         [ Links ]

Boren, J. J., Moerschbaecher, J. M., & Whyte, A. A. (1978). Variability of response location on fixed-ratio and fixed-interval schedules of reinforcement. Journal of the Experimental Analysis of Behavior, 30, 63-67.         [ Links ]

Bussab, W. O., & Morettin, P. A. (2002). Estatística Básica. São Paulo: Saraiva.         [ Links ]

Carlton, P. L. (1962). Effects on deprivation and reinforcement magnitude of response variability. Journal of the Experimental Analysis of Behavior, 5, 481-486.         [ Links ]

Catania, A. C. (1973). The Concept of the Operant in the Analysis of Behavior. Behaviorism, 1 (2): 103 – 116.

Catania, A. C. (1999). Aprendizagem: Comportamento, linguagem e cognição (D. Souza, Trad.). Porto Alegre: Artmed.         [ Links ]

Cohen, L., Neuringer, A., & Rhodes, D. (1990). Effects of ethanol on reinforced variations and repetitions by rats under a multiple schedule. Journal of the Experimental Analysis of Behavior, 54, 1-12.         [ Links ]

Cruvinel, A. C., & Sério, T. M. A. P. (2008). Variabilidade Comportamental: a Produção de Variabilidade da Duração da Resposta. Acta Comportamentalia, 16 (1), 5-23.         [ Links ]

Dale, R. H. I., & Roberts, W.A. (1986). Variations in radial maze performance under different levels of food and water deprivation. Animal Learning & Behavior, 14, 60-64.         [ Links ]

Denney, J., & Neuringer, A. (1998). Behavioral variability is controlled by discriminative stimuli. Animal Learning & Behavior, 26, 154-162.         [ Links ]

Eckerman, D., & Lanson, R. (1969). Variability of response location for pigeons responding under continuous reinforcement intermittent reinforcement, and extinction. Journal of the Experimental Analysis of Behavior, 12, 73-80.         [ Links ]

Ferraro D. P., & Hayes K. M. (1967). Variability of response duration during punishment. Psychological Reports, 21, 121 - 127         [ Links ]

Ferraro, D. P., & Branch, K. H. (1968). Variability of response location during regular and partial reinforcement. Psychological Reports, 23, 1023-1031.         [ Links ]

Hunziker, M. H. L., Saldana, L., & Neuringer, A. (1996). Behavioral variability in SHR and WKY rats as a function of rearing environment and reinforcement contingency. Journal of the Experimental Analysis of Behavior, 65, 129-144.         [ Links ]

Hunziker, M. H. L., Caramori, F. C., Silva, A. P., & Barba, L. S. (1998). Efeitos da história de reforçamento sobre a variabilidade comportamental. Psicologia: Teoria e Pesquisa, 14, 149-159.         [ Links ]

Lachter, G. D., & Corey, J. R. (1982). Variability of the duration of an operant. Behaviour Analysis Letters, 2, 97-102.         [ Links ]

Machado, A. (1989). Operant conditioning of behavioral variability using percentil reinforcement schedule. Journal of the Experimental Analysis of Behavior, 52, 155-166.         [ Links ]

Machado, A. (1992). Behavioral variability and frequency-dependent selection. Journal of the Experimental Analysis of Behavior, 58, 241-263.         [ Links ]

Machado, A. (1997). Increasing the variability of response sequences in pigeons by adjusting the frequency of switching between two keys. Journal of the Experimental Analysis of Behavior, 68, 1-25.         [ Links ]

McCray, C. L., & Harper, R. S. (1962). Some relationships of schedules of reinforcement to variability of response. Journal of Comparative and Physiological Psychology, 55, 19-21.         [ Links ]

McSweeney, F. K. (1974). Variability of responding on a concurrent schedule as a function of body weight. Journal of the Experimental Analysis of Behavior, 21, 357-359.         [ Links ]

Mook, D. M., & Neuringer, A. (1994). Different effects of amphetamine on reinforced variations versus repetitions in spontaneously hypertensive rats. Physiology & Behavior, 56, 939-944.         [ Links ]

Morgan, L., & Neuringer, A. (1990). Behavioral variability as a function of response topography and reinforcement contingency. Animal Learning & Behavior, 18, 257-263.         [ Links ]

Morris, C. J. (1987). The operant conditioning of response variability: Free-operant versus discrete-response procedures. Journal of the Experimental Analysis of Behavior, 47, 273-277.         [ Links ]

Morris, C. J. (1989). The effects of lag value on the operant control of response variability under freeoperant and discrete-response procedures. The Psychological Record, 39, 263-270.         [ Links ]

Neuringer, A. (1991). Operant variability and repetition as functions of interresponse time. Journal of Experimental Psychology: Animal Behavior Processes, 17, 3-12.         [ Links ]

Neuringer, A. (1992). Choosing to vary and repeat. Psychological Science, 3, 246-250.         [ Links ]

Neuringer, A. (2002). Operant variability: Evidence, functions, and theory. Psychonomic Bulletin & Review, 9 (4), 672 – 705.

Neuringer, A., & Huntley, R. W. (1992). Reinforced variability in rats: Effects of gender, age and contingency. Physiology & Behavior, 51, 145-149.         [ Links ]

Neuringer A, Deiss, C., & Olson, G. (2000). Reinforced variability and operant learning. Journal of Experimental Psychology: Animal Behavior Processes, 26, 98-111.         [ Links ]

Newberry, B. H. (1971). Response variability and the partial reinforcement effect. Journal of Experimental Psychology, 89, 137-141.         [ Links ]

Page, S., & Neuringer, A. (1985). Variability is an operant. Journal of Experimental Psychology: Animal Behavior Processes, 11, 429-452.         [ Links ]

Schoenfeld, W. N., Harris, A. H., & Farmer, J. (1966). Conditioning response variability. Psychological Reports, 19, 551-557.         [ Links ]

Schwartz, B. (1982). Failure to produce response variability with reinforcement. Journal of the Experimental Analysis of Behavior, 37, 171-181.         [ Links ]

Skinner, B. F. (1950). Are Theories Of Learning Necessary? Psychological Review, 57, 193-216.         [ Links ]

Skinner, B. F. (1953). Science and Human Behavior. New York: The MacMillan Company.         [ Links ]

Skinner, B. F. (1969) Contingencies of Reinforcement: A Theoretical Analysis. New York: Appleton-Century- Crofts.         [ Links ]

Skinner, B. F. (1974). About Behaviorism. New York: Appleton-Century-Crofts.         [ Links ]

Stokes, P. (1995). Learned variability. Animal Learning and Behavior, 23, 164-176.         [ Links ]

Tremont, P. J. (1984). Variability of force and interresponse time under random interval reinforcement schedules. Behavioural Processes, 9, 413-420.         [ Links ]

Van Hest, A., van Haaren, F., & van de Poll, N. E. (1989). Operant conditioning of response variability in male and female Wistar rats. Physiology & Behavior, 45, 551-555.         [ Links ]

 

 

Received: December 15, 2009
Accepted: February 22, 2010

 

 

¹ Endereço para correspondência: Rua Brazeliza Alves de Carvalho, 522. CEP: 02510-030. São Paulo – SP. Endereço eletrônico: lourenbarba@yahoo.com.br
² Catania (1999, p.140) faz referência a esse ponto discutindo o ´problema de alternação dupla´.
³ O índice U calcula-se pela fórmula U = (-Spi.log2pi )/ log2N, com i variando de 1 a N. N representa o número de elementos do universo analisado. pi representa a frequência relativa em que ocorreu cada confi guração. Em Hunziker et al. (1998), por exemplo, N assumiu o valor 16 (número de diferentes confi gurações em sequências de quatro elementos constituintes)