ARTIGOS

 

Relações entre a percepção da estrutura de um problema, a memória e a memória matemática

 

Relations among mathematical memory, memory and perception of a problem structure

 

 

Érica Valeria Alves^I; Márcia Regina Ferreira de Brito^II

^IUniversidade Federal de Alfenas
^IIUniversidade Estadual de Campinas

 

 

---

RESUMO

Este estudo partiu do pressuposto que, ao solucionar um problema matemático, o indivíduo, inicialmente, percebe seus elementos componentes, analítica e sinteticamente, isolando-os, estabelecendo hierarquia, combinações e relações entre eles. Considerando algumas relações teóricas entre a percepção da estrutura de um problema, a memória e a memória matemática, buscou-se estudar tais relações empiricamente. Trinta e dois sujeitos foram selecionados dentre 177 estudantes de quinta e oitava séries do Ensino Fundamental e terceira série do Ensino Médio, mediante o desempenho em uma prova matemática e uma prova para avaliar a memória matemática. Esses sujeitos foram submetidos ao teste das figuras complexas de Rey. Por meio de análise de correlação, foi obtido coeficiente de Pearson 0,54 entre os desempenhos na prova para avaliar a memória matemática e o teste de reprodução das figuras complexas. A análise qualitativa das relações entre os resultados obtidos por dois sujeitos mostrou que um deles, tendo percebido os elementos do mais geral aos mais específicos, tanto nos problemas matemáticos, como na figura complexa, teve maior facilidade em representá-los, retê-los e recuperá-los. O outro sujeito, entretanto, percebia na figura elementos justapostos sem que fosse estabelecida relação entre eles. Essa dificuldade de percepção e recuperação também foi observada na prova para avaliar a memória matemática.

Palavras-chave: Memória matemática, Percepção, Habilidades matemáticas, Solução de problemas.

---

ABSTRACT

This study assumed that during a mathematical problem solving the person, at the beginning, perceive synthetically and analytically their elements. The analytic perception is characterized by the problem elements isolate, differentiate accessing and hierarchy establishing. The synthetic perception happens during relations and combinations establishing between problem elements by the person. Considering the theoretical relations between mathematical memory, memory and perception, this research aimed to study this relationship empirically. For that, 32 students were selected among 177 students from basic education, considering their performance in a mathematics test and a mathematical memory test. These students were submitted to the reproduction and copy test of Rey complex figures. Through correlation analysis it was obtained the Pearson coefficient 0,54 between reproduction complex figures test and mathematical memory test performance. The qualitative analysis of relations between individual results in complex figures test and the performance in mathematical memory test showed that when a person perceives the elements from the general toward specific, either in mathematical problems or in complex figures, the person recovered, retrieved and represented it easily. Otherwise, when the person perceived juxtaposed elements in the figure, without relations establishing, this retrieving and perception difficulty was observed also in mathematical memory test.

Keywords: Mathematical memory, Perception, Mathematical abilities, Problem solving.

---

 

 

A atividade de solução de problemas matemáticos pode evidenciar diversas reações e processos cognitivos superiores a ela subjacentes, dentre eles: a percepção, a representação, a imagem, a retenção e a recuperação de informações contidas na memória. Ao elaborar a representação de um problema, indivíduos habilidosos são capazes de diferenciar claramente três elementos em um problema: as relações que possuem significado matemático básico; as quantidades não essenciais para aquele tipo de problema, mas que são essenciais naquela variante; e as quantidades supérfluas para aquele problema específico. Assim, percebem o material matemático contido no enunciado verbal de um problema de forma analítica (isolando diferentes elementos da estrutura, acessando-os de maneira diferenciada, sistematizando-os e determinando sua hierarquia) e de forma sintética (combinando os elementos, estabelecendo relações matemáticas e funções de dependência entre eles), simultaneamente (Krutetskii, 1976). Dentre os determinantes da representação de um problema, estão os conhecimentos prévios do indivíduo. Ao formar a representação de um problema, este recupera na memória, os procedimentos adequados aplicáveis àquela situação e é exatamente essa representação que vai orientar a recordação de tais procedimentos (Chi & Glaser, 1992).

De acordo com a afirmação anterior, durante a solução de problemas, alguns processos cognitivos superiores podem ser evidenciados, dentre eles: a percepção, a representação, e a memória.

A percepção consiste em um conjunto de processos psicológicos, pelos quais as pessoas reconhecem, organizam, sintetizam e fornecem significação, em nível cognitivo, às sensações recebidas dos estímulos ambientais, através dos órgãos dos sentidos . Em particular, a percepção da estrutura de um problema matemático, refere-se ao reconhecimento, à organização, à síntese e à significação de elementos do problema, relacionando-os a elementos da memória matemática. A percepção pode ser tratada de acordo com duas perspectivas e pode ser vista como percepção construtiva ou percepção direta. A percepção construtiva, ou inteligente, admite que o sujeito crie a percepção (a compreensão cognitiva) usando, a partir do estímulo, a informação sensorial, vista como fundamento da estrutura perceptual, além de utilizar outras fontes de informação. Na teoria da percepção construtiva, o pensamento de ordem superior é relevante na construção da percepção e, durante essa construção, várias hipóteses são testadas. Existe, portanto, uma interação entre a inteligência e os processos perceptivos, sendo por isso também chamada de percepção inteligente. Na teoria da percepção direta, as informações e o contexto são necessários e suficientes para a formação da percepção e os indícios necessários à construção da percepção são estritamente inerentes ao estímulo (Sternberg, 2000).

A representação do conhecimento, segundo Sternberg (2000), é a forma pela qual o sujeito conhece objetos, eventos e idéias que são externos a sua estrutura cognitiva. A representação compreende várias formas do pensamento e permite criar e modificar as estruturas do conhecimento declarativo e de procedimento que o sujeito possui. Esse processo cognitivo difere de acordo com a natureza do conhecimento, que pode ser classificado em declarativo (corpo organizado de informações factuais), ou de procedimentos (algoritmos de execução de uma tarefa).

A representação do conhecimento declarativo é baseada no constructo de esquemas (estruturas mentais que representam o conhecimento, abrangendo uma série de conceitos inter-relacionados em uma organização significativa). Os esquemas caracterizam-se pela inclusão de outros esquemas, pela abrangência de fatos típicos gerais, pela variação em graus de abstração, pela inclusão de informações sobre relações entre conceitos e pela inclusão de informações que podem ser usadas para extrair inferências (Pozo, 1994).

Uma forma bastante utilizada de representar o conhecimento de procedimento é o uso de um conjunto de regras de produção, do tipo "se-então". A cláusula "se" da regra inclui um conjunto de condições que devem ser atendidas a fim de levar o sistema a executar a cláusula "então". A cláusula "então" corresponde a uma ação, ou um conjunto de ações (Sternberg, 2000).

Memória, segundo Baddeley (1999), é um sistema de armazenamento e recuperação de informação, obtida através dos sentidos. Embora a palavra memória sugira a existência de um termo unitário, trata-se de um sistema múltiplo, pois não existe um único sistema, mas muitos, e estes "variam em armazenamento desde pequenos armazenamentos momentâneos ao sistema de memória de longo prazo, que parece exceder extensamente em capacidade e flexibilidade ao maior ordenador disponível". Segundo Arroyo (1992), trata-se de um mecanismo capaz de realizar a retenção de conhecimentos de qualquer natureza, com os quais, em algum momento, o sujeito estabeleceu qualquer relação. Além da capacidade aparentemente ilimitada, suas características fundamentais são a persistência duradoura de seus conteúdos e a pluralidade de códigos (devido à capacidade de retenção de conhecimentos de naturezas distintas, por diferentes meios para a aquisição), ainda que exista um predomínio de codificações semânticas.

Como conclusão de estudos sobre a percepção, a representação e a memória, Bartlett (1932/1995), afirmou que "perceber alguma coisa é a mais simples, imediata e mais fundamental, das reações cognitivas humanas". Além disso, propõe que:

Recordar pode então ser definido como uma reconstrução imaginativa, ou como uma construção, fora da relação ou de nossos propósitos em relação a toda massa ativa de organização de reações passadas ou experiências, e com um proeminente detalhe que comumente aparece em imagem visual ou em forma de linguagem (p.213).

A memória matemática é um componente da habilidade matemática, relacionado ao terceiro estágio da solução de problemas (a retenção da informação matemática). Trata-se de uma retenção generalizada e operante, e uma rápida elaboração de representações de problemas e relações, no domínio dos símbolos numéricos e verbais. A memória matemática é notavelmente seletiva, ou seja, a estrutura cognitiva não retém toda a informação matemática disponível na situação, mas "refina" os dados concretos que representam estruturas abreviadas e generalizadas. Esse tipo de retenção torna o método mais econômico e conveniente, pois, ao reter a informação deste modo, não sobrecarrega a estrutura cognitiva com informações desnecessárias, permitindo que mais informações sejam retidas e, conseqüentemente, que sejam acessadas mais facilmente (Krutetskii, 1976).

Para acessar a memória matemática, o autor propôs algumas séries de problemas. Dentre estas, a série XXII é composta por problemas com termos difíceis de recordar. Nesta série, a "complexidade é introduzida deliberadamente, a fim de que o sujeito não tenha a possibilidade de memorizar o problema completo após uma leitura". De acordo com o autor, sob essas condições experimentais, podem ser reveladas "não apenas características da função mnemônica, mas também algumas características da percepção e generalização" (Krutetskii, 1976, p.155).

Considerando as relações teóricas entre a percepção, a memória e a memória matemática, este estudo teve como objetivo estudar tais relações empiricamente, propondo como problema de pesquisa a questão: Existe relação entre a forma como os indivíduos percebem e recuperam os elementos no teste das Figuras Complexas de Rey e a memória matemática?

 

Método

Cento e setenta e sete estudantes de quinta e oitava séries do ensino fundamental e terceiro ano do ensino médio foram solicitados a responder aos seguintes instrumentos:

a) uma prova matemática para avaliar o desempenho e os procedimentos empregados na solução de problemas matemáticos, abordando os conteúdos matemáticos: multiplicação e divisão entre números naturais, decimais e fracionários.

b) uma prova para avaliar a memória matemática, elaborada a partir dos testes aritméticos da série XXII (problemas com termos que são difíceis de se recordar) de Krutetskii (1976). Os problemas eram apresentados aos sujeitos, um a um e era solicitado que, após a leitura atenta, reproduzissem imediatamente o problema lido. Em cada um dos seis problemas da prova para avaliar a memória matemática foram atribuídos de 1 a 4 pontos, conforme a Tabela 1.

A partir dos resultados conseguidos com o uso desses instrumentos, foram selecionados trinta e dois sujeitos, com as notas mais altas e mais baixas em cada série. Esses trinta e dois sujeitos foram submetidos ao teste das figuras complexas de Rey. Trata-se de um teste de cópia e de reprodução de memória de figuras geométricas complexas. Cada sujeito, em sessão individual, recebia uma folha de papel em branco e era solicitado a copiar uma figura impressa em um cartão, trocando periodicamente a cor do lápis, de forma intencional, a fim de verificar a ordem de sucessão dos elementos da figura percebidos pelo sujeito.

Após a conclusão da cópia, eram recolhidos o cartão com a figura original e a folha. Após um intervalo, não superior a três minutos, o sujeito recebia outra folha em branco e era solicitado a reproduzir a figura anteriormente vista. Novamente eram modificadas as cores dos lápis a fim de constatar se houve melhora em relação à cópia (Rey, 1999). Este teste foi utilizado por permitir observar a ordem em que os elementos (gerais e específicos) de uma figura complexa são observados e, comparar com a ordem em que os elementos do enunciado de um problema matemático (estrutura do problema e dados numéricos) são percebidos.

Nesse instrumento, foram inicialmente pontuadas a cópia e a reprodução elaborada por cada sujeito, de acordo com as orientações do manual de aplicação (Rey, 1999). Para tanto, a figura era decomposta em dezoito elementos e, para cada elemento, eram consideradas a precisão e a localização, atribuindo a cada elemento de zero a 2,0 pontos. Desse modo, cada sujeito recebia uma pontuação variando entre zero e 36,0 no teste de cópia e no teste de reprodução.

Através da utilização de cores distintas e sucessivas durante a cópia e a reprodução, os sujeitos também foram classificados de acordo com o tipo de cópia. Os tipos de cópia são classificados no manual de aplicação dos mais aos menos racionais, conforme hierarquia apresentada a seguir:

I. Construção a partir da armação.
II. Detalhes incluídos na armação.
III. Contorno geral.
IV. Justaposição de detalhes.
V. Detalhes sobre fundo confuso.
VI. Redução a um esquema familiar.
VII. Garatuja

 

Resultados

As notas dos 177 sujeitos na prova matemática variaram entre zero e 8,86, com média 3,82 e desvio padrão 1,99. A média dos sujeitos da quinta série foi 2,50, da oitava foi 3,97 e do terceiro ano do ensino médio 4,95. A partir da ANOVA, foi constatada a inferioridade da média da quinta série em relação aos demais grupos. Entre a oitava série e o terceiro ano do ensino médio, não foram encontradas diferenças de média significativas.

Na prova para avaliar a memória matemática, a nota mínima obtida pelos sujeitos foi zero, a máxima foi 24 e a média da amostra foi 11,10, com desvio padrão 5,32. Comparando o desempenho em relação às séries, as médias foram 8,42 na quinta, 10,48 na oitava e 13,99 no terceiro ano. A ANOVA indicou que entre as séries do ensino fundamental não havia diferença significativa de médias e que o terceiro ano diferia dos demais grupos (p<0,001).

Com a ajuda de um diagrama de dispersão (Figura 1), é possível observar a concentração de sujeitos da quinta série com notas menos elevadas nos dois instrumentos e de sujeitos do terceiro ano do ensino médio com notas mais elevadas em ambos. A análise de correlação bivariada entre o desempenho nos dois instrumentos obteve coeficiente de Pearson de 0,610 (p<0,001). Esse resultado ratifica a afirmação de Krutetskii (1976) de que a habilidade é um dos fatores que favorecem o sucesso na realização de atividades matemáticas.

Os trinta e dois sujeitos selecionados para participar da segunda etapa do estudo obtiveram notas na prova matemática variando entre zero e 8,8 e pontuação na prova para avaliar a memória matemática variando entre zero e 24,0, distribuídos como mostra a Figura 2. No teste de Riqueza e exatidão da cópia, as notas variaram entre 17,0 e 36,0, com média 28,48 (sd=4,37). No teste de Riqueza e exatidão da reprodução, as notas foram inferiores, variando entre 5,0 e 33,0 (sd=6,93). O teste-T mostrou que não foram encontradas diferenças significativas de média atribuídas ao gênero ou à série.

Para analisar as relações entre os resultados obtidos na primeira e segunda etapa do estudo, foram realizadas análises de correlação para verificar as possíveis associações entre as variáveis. Inicialmente, entre a pontuação obtida no teste de Riqueza e exatidão da cópia e no teste de Riqueza e exatidão da reprodução, o coeficiente de correlação de Pearson obtido foi 0,54, indicando uma alta correlação entre as variáveis (p=0,001). Este resultado ratifica alguns elementos apresentados na fundamentação teórica do presente estudo, de que a percepção, a representação e a recuperação são processos cognitivos intimamente relacionados.

Com a mudança de cores dos lápis utilizados durante o teste, foi possível classificar as cópias realizadas pelos sujeitos, com base nos critérios estabelecidos por Osterrieth (1944, citado por Rey, 1999). Esses critérios diferenciavam a cópia de um nível mais racional a um nível menos racional. Os trinta e dois sujeitos da segunda etapa do estudo distribuíram-se entre os sete tipos de cópia, conforme mostra a Tabela 2.

 

 

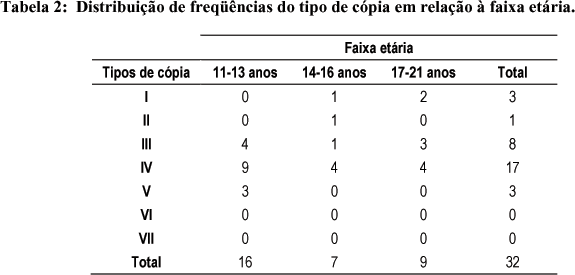
É possível observar que o tipo de cópia que ocorreu mais freqüentemente foi o IV: justaposição de detalhes. De acordo com Osterrieth (1944, citado por Rey, 1999), a característica fundamental desta categoria é a ausência de um traçado de base, culminando em um conjunto razoavelmente coerente. De acordo com o autor, esta é uma "reação dominante de 5 a 10 anos. Sua freqüência cresce dos 4 aos 7 anos, atinge seu máximo aos 8 anos (70%), para diminuir em seguida de maneira bastante regular até a idade adulta, quando atinge seu mínimo". De acordo com o manual de aplicação do teste, era esperado, para as três faixas etárias, maior freqüência dos tipos I e II, uma vez que são categorias mais elaboradas, caracterizando uma percepção mais completa da figura.

A partir dessa estratégia de análise das cópias, foram selecionados os sujeitos com maior e menor pontuação nos testes de cópia e reprodução, de ambos os gêneros. Foi realizada uma análise qualitativa das relações entre os resultados obtidos para cada um dos sujeitos a partir de todos os instrumentos utilizados no presente estudo e comparados os resultados obtidos por dois desses sujeitos na prova para avaliar a memória matemática e no teste das figuras complexas de Rey, com a finalidade de relacionar a percepção e a memória com a memória matemática.

O sujeito 91 era estudante do terceiro ano do ensino médio e era do gênero feminino. Na prova para avaliar a memória matemática, dos seis problemas, em apenas um deles a estudante não foi capaz de reproduzir o problema integralmente, sendo que sua pontuação nessa prova foi 21 (o máximo era 24 pontos). No teste de riqueza e exatidão de detalhes da cópia, o sujeito 91 foi classificado pelo tipo de cópia na categoria I: construção a partir da armação. É possível observar, na Figura 3, que o sujeito percebe inicialmente o retângulo grande central e todos os demais elementos são associados posteriormente a ele. Ou seja, primeiramente o sujeito percebeu a estrutura da figura e, a seguir, foi atentando para os detalhes.

 

 

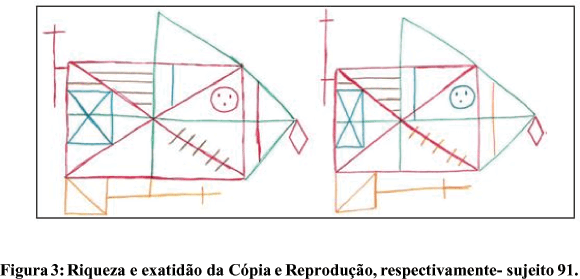
Nesta etapa do teste, o sujeito obteve 36 pontos, uma vez que foi capaz de copiar todos os elementos da figura, com precisão e localização consideradas boas. Na reprodução da figura, o sujeito obteve 33,0 pontos, sendo que não foi capaz de reproduzir com exatidão apenas três elementos da figura (a linha pequena perpendicular no quadrante superior, em azul; a cruz no extremo inferior do retângulo, em laranja e; a inversão da diagonal no quadrado no extremo inferior esquerdo, em laranja), conforme pode ser observado na Figura 3.

Comparando os resultados obtidos pelo sujeito no teste das figuras complexas e na prova para avaliar a memória matemática, é possível afirmar que esses resultados ratificam as afirmações de Bartlett (1932/1995) de que "perceber alguma coisa é a mais simples e imediata, e também mais fundamental das reações cognitivas humanas". Ou seja, tendo percebido os elementos do mais geral aos mais específicos, tanto nos problemas matemáticos, como na figura complexa, o sujeito teve maior facilidade em representá-los, retê-los e recuperá-los.

Estudante da quinta série do ensino fundamental do gênero masculino, o sujeito 40, obteve nota 1,67 na prova matemática. Na prova para avaliar a memória matemática, o sujeito elaborou reprodução de todos os problemas, sendo que todas as reproduções foram parciais e contendo erros, demonstrando não ter percebido a estrutura de nenhum dos problemas. A Figura 4 apresenta a reprodução elaborada pelo sujeito para o problema 5 (Quatro canos são conectados num tanque. Quando os canos 1, 2 e 3 estão abertos o tanque enche em 12 minutos; quando os canos 2, 3 e 4 estão abertos, leva 15 minutos; quando apenas os canos 1 e 4 estão abertos, demora 20 minutos. Quanto tempo levará para encher o tanque se os quatro canos estiverem abertos?). É possível observar que o sujeito não foi capaz de perceber dados numéricos, informações ou relações no problema, como pode ser observado na reprodução do problema 5 do instrumento, apresentada na Figura 4.

No teste das figuras complexas de Rey, a cópia realizada pelo sujeito foi classificada como tipo IV, denominada por Rey (1999, p. 21) como "justaposição de detalhes". Neste tipo de cópia "o sujeito justapõe os detalhes uns aos outros, procedendo pouco a pouco como se estivesse montando um quebra-cabeça. Não há elemento diretor da reprodução. O conjunto, terminado mais ou menos bem, é reconhecível e pode inclusive estar perfeitamente realizado." Nesta prova, o sujeito obteve 22,5 pontos (Figura 5). Na reprodução da figura, o sujeito obteve 5,5 pontos, sendo que o único elemento reproduzido com precisão e localização consideradas boas foi o losango no vértice extremo do triângulo isósceles, em vermelho (Figura 5).

 

 

As observações realizadas sobre o sujeito 40, baseadas no teste de Riqueza e exatidão da cópia, indicaramque o sujeito percebia elementos justapostos sem que fosse estabelecida uma relação entre eles. Provavelmente, essa percepção desprovida de uma diretriz dificultou a recordação da figura, como foi observado no teste de reprodução. Essa dificuldade de percepção e recuperação também foi observada na prova para avaliar a memória matemática, onde o sujeito em nenhum dos problemas foi capaz de perceber sua estrutura ou, sequer, relações entre elementos do problema.

 

Considerações Finais

Considerando que para a obtenção de sucesso na execução de atividades matemáticas faz-se necessário que o sujeito disponha de um conjunto de fatores, dentre eles, a habilidade matemática, as atitudes positivas em relação à atividade, os traços de personalidade, além de conhecimentos, destrezas e hábitos, este estudo buscou levantar evidências acerca da influência da memória nessas situações.

De acordo com as teorias que fundamentaram este estudo, a memória não é um elemento isolado na estrutura cognitiva, mas compõe um sistema complexo, relacionando-se com todos os demais processos cognitivos superiores. Assim, a percepção, a representação e a atenção foram consideradas como processos cognitivos superiores altamente relevantes durante a solução de um problema matemático.

Também foi apresentada na fundamentação teórica deste trabalho a relevância da percepção nos processos de solução de problemas (Krutetskii, 1976). Ao solucionar um problema, um sujeito habilidoso percebe simultaneamente os elementos que compõem a situação, de maneira analítica e sintética. A percepção analítica ocorre à medida que o sujeito é capaz de isolar os diferentes elementos do problema, acessá-los de forma diferenciada e estabelecer relação de hierarquia entre esses elementos. A percepção sintética ocorre à medida que o sujeito vai estabelecendo combinações e relações entre os elementos que compõem o problema. Através do teste das Figuras Complexas de Rey, utilizado neste estudo, foi possível observar a influência da percepção sobre a memória. Os sujeitos que percebiam a figura complexa a partir de sua estrutura mais geral em direção aos aspectos mais específicos apresentavam maior facilidade de recuperação no momento de reproduzir a figura. Já os sujeitos que percebiam os elementos da figura sem estabelecer uma hierarquia entre os elementos não eram capazes de recuperar todos os elementos componentes da figura. No teste para avaliar a memória matemática, foi possível verificar que os sujeitos que apresentaram dificuldade na percepção dos elementos da figura complexa apresentavam dificuldade em recuperar informações sobre as relações entre os elementos do problema. Provavelmente, esses sujeitos atentavam para o aspecto externo do problema, deixando de perceber sua estrutura e relação entre elementos.

Assim, tão relevante como a memória no desempenho na solução de um problema matemático, a percepção do sujeito desempenha um papel fundamental nos processos cognitivos superiores. Trata-se da mais imediata das reações humanas diante de uma situação inédita. Antes de representar, reter, ou recuperar uma informação na memória, o sujeito a percebe: "Nada pode ser reconhecido ou recordado sem antes ter sido percebido" (Bartlett, 1932/1995).

 

Referências

Arroyo, F. V. (1992). Estructuras y procesos en la memoria. In J. Mayor e J. L. Pinillos (Ed), Memoria y Representación(pp.41 - 83). Madrid: Alhambra Longman.        [ Links ]

Baddeley, A. (1999). Memória humana. Teoria e prática. (G. N. Navarro, Trad.) Madrid: Mc Grall-Hill.        [ Links ]

Bartlett, F. C. (1932-1995). Remembering: A Study in Experimental and Social Psychology. Cambridge: Cambridge University Press.        [ Links ]

Chi, M. T. H., & Glaser, R. A. (1992). Capacidade para a solução de problemas. In R. J. Sternberg (Ed), As Capacidades Intelectuais Humanas: Uma Abordagem em Processamento de Informações (pp. 249 - 275). Porto Alegre: ArtMed.        [ Links ]

Krutetskii, V. A. (1976) The Psychology of Mathematical Abilities in Schoolchildren. Chicago: The University of Chicago Press.        [ Links ]

Pozo, J. I. (1994). Teorías cognitivas del aprendizaje. Madrid: Ediciones Morata.        [ Links ]

Rey, A. (1999). Teste de cópia e reprodução de memória de figuras geométricas complexas: manual. São Paulo: Casa do Psicólogo.        [ Links ]

Sternberg, R. J. (2000). Psicologia Cognitiva. (M. R. B. Osório, Trad.) Porto Alegre: ArtMed.        [ Links ]

 

 

Enviado em Maio de 2008
Revisado em Março de 2009
Aceite final em Maio de 2009
Publicado em Outubro de 2009