ARTIGOS

 

O resgate das demonstrações: uma contribuição da Informática à formação do professor de Matemática

 

The recovery of the demonstrations: a contribution of the computer science to the teachers of mathematics formation

 

El rescate de las demostraciones: una contribución de la informática a la formación del profesor de matemática

 

 

Emilia Barra Ferreira ^{I, *}; Adriana Benevides Soares ^{II, **}; Josefino Cabral Lima ^{III, ***}

I Fundação Centro de Ciências e Educação Superior à Distância do Estado do Rio de Janeiro
II Universidade Salgado de Oliveira
III Universidade Federal do Rio de Janeiro

 

 

---

RESUMO

Este trabalho teve por objetivo investigar a contribuição dos ambientes de geometria dinâmica num processo de formação continuada de professores de Matemática, no sentido de incentivá-los ao uso das demonstrações. Nessa direção, foi desenvolvida uma engenharia didática, em ambiente de geometria dinâmica, buscando a formação dos professores participantes tanto em aspectos conceituais quanto didáticos. Oito professores em exercício do ensino de Matemática participaram dos trabalhos e os instrumentos utilizados para coleta de dados foram: questionários de sondagem, produção dos participantes na forma de material escrito, registro das manifestações dos professores durante a discussão de textos, seqüência didática elaborada pelos participantes para aplicação com seus alunos. Os resultados revelaram que o trabalho, nesse ambiente, se constitui numa alternativa eficiente no processo de formação de professores no sentido de incentivá-los ao uso das demonstrações.

Palavras-chave: Formação de professores, Demonstrações, Geometria dinâmica.

---

ABSTRACT

The objective of this work was to investigate the dynamic geometry environment contribution in a process of Mathematics' teachers continuous formation, in order to motivate them to use demonstrations. In that direction, a didactic engineering was developed, in a dynamic geometry environment, seeking the participants' formation in both conceptual and didactic aspects. Eight in service Mathematics teachers participated in the activities and the instruments used for data collection were: survey questionnaires, the participants' production in the form of written material, registration of teachers' manifestations during the discussion of texts, and the didactic sequence elaborated by the participants to be applied to their students. The results revealed that the work in that environment, constitutes an efficient alternative in the process of teacher preparation in order to motivate them to use demonstrations.

Keywords: Teacher preparation, Demonstrations, Dynamic geometry.

---

RESUMEN

Este trabajo tuvo como objetivo investigar la contribución de los ambientes de geometría dinámica en un proceso de formación continuada de profesores de Matemáticas, como una forma de incentivarlos a usar las demostraciones. En ese sentido, fue desarrollada una ingeniería didáctica en ambiente de geometría dinámica, buscando la formación de los profesores participantes, tanto en aspectos conceptuales como didácticos. Participaron de los trabajos ocho profesores de Matemáticas en actividad y los instrumentos utilizados para la cosecha de datos fueron: cuestionarios de sondeo, producción de los participantes en la forma de material escrito, registro de las manifestaciones de los profesores durante la discusión de textos, secuencia didáctica elaborada por los participantes para aplicar con sus alumnos. Los resultados mostraron que el trabajo, en ese ambiente, se constituye como una alternativa eficiente en el proceso de formación de profesores como una forma de incentivarlos al uso de las demostraciones.

Palabras clave: Formación de profesores, Demostraciones, Geometría dinámica.

---

 

 

Introdução

A Matemática, de forma ímpar, é uma ciência derivada do pensamento puro, constituindo-se essencialmente em um processo de construção mental. Dessa maneira, suas atividades caracterizam-se pela formulação de conjecturas que se validam quando acompanhadas das devidas demonstrações. Parte-se de alguns conceitos, tomados sem definição, e de algumas proposições aceitas sem demonstração: os axiomas. A partir destes, propriedades são derivadas e teoremas são demonstrados, seguindo-se as regras da lógica matemática. É natural, portanto, que se considere de suma importância, no processo educativo, a convivência e a prática das demonstrações por professores e estudantes.

Entretanto, a realidade nas escolas não reflete essas concepções. Dentre as causas apontadas para a não utilização ou, até mesmo, para a tradicional abordagem¹ das demonstrações no ensino-aprendizagem da Geometria, cita-se o fato de os professores não possuírem os conhecimentos geométricos necessários para a realização de tal prática. Segundo Vianna (1988), Pavanello (1993) e Gouvea (1998), tem-se observado a ausência da Geometria nas escolas, principalmente nas públicas. Essa ausência se reflete nos saberes dos professores em atuação, pois os conteúdos não aprendidos não são ensinados, dando origem a um círculo vicioso que acaba afetando gerações de alunos que não aprendem Geometria. Pesquisas apontam sérios problemas com a formação de professores de Matemática, sobretudo quanto à Geometria (Belfort, Guimarães & Barbastefano, 1999; Gouvêa, 1998; Lorenzato, 1995).

Ponte (1994), além de reconhecer a relevância do domínio dos conteúdos ensinados pelo professor, destaca a importância do conhecimento didático desse conteúdo, que seria a capacidade de compreensão das matérias de ensino, permitindo encontrar maneiras mais adequadas de apresentá-las aos alunos. Nessa direção, muitos recursos são oferecidos pelas Tecnologias da Informação e da Comunicação que vêm, nos últimos anos, provocando uma verdadeira revolução na maneira de se trabalhar e de se aprender. Especificamente, no âmbito de aplicação da tecnologia informática em educação matemática, o potencial dos ambientes de geometria dinâmica (GD) é investigado e discutido nacional e internacionalmente por diversos pesquisadores, como por exemplo: Alves (2004), Barra Ferreira, Soares e Lima (2005a, 2005b), Belfort e cols. (1999), Gravina (2001), Hanna (2000), Hoyles e Jones (1998), Laborde (2000), Laborde e Capponi (1994).

Esses ambientes computacionais são direcionados à aprendizagem da Geometria oferecendo recursos que viabilizam as ações mentais dos alunos e podem ajudar na superação de dificuldades inerentes ao processo dessa aprendizagem, tais como: visualização, construção e raciocínio geométrico. Eles criam condições para que se aprenda investigando, conjecturando, testando, analisando e concluindo acerca de um fenômeno estudado. Nesses ambientes, o aluno se transforma de mero expectador em agente do processo educativo, em alguém que pensa, reflete, dirige, decide e atua.

Para a viabilização dessas propostas transformadoras, a formação dos professores é reconhecida como um dos fatores de fundamental importância. Assim, o objetivo desta pesquisa traduziu-se nas seguintes hipóteses: a utilização de ambientes de GD, no processo ensino-aprendizagem da Geometria, pode estimular a evolução dos níveis de pensamento geométrico com simultâneo desenvolvimento do raciocínio lógico-dedutivo dos professores envolvidos, permitindo uma melhor compreensão do significado das demonstrações, bem como desenvolvendo competências para sua elaboração; a utilização desses ambientes, num processo de formação de professores, através de competências desenvolvidas e da prática de novas metodologias, pode contribuir para uma reflexão sobre as demonstrações e seu ensino, favorecendo uma retomada de posição favorável a sua prática pedagógica.

Considerando a complexidade do processo ensino-aprendizagem das demonstrações, não só para o aluno, mas também para o professor, o embasamento teórico do estudo contemplou uma reflexão sobre as demonstrações em seus aspectos cognitivo e didático. Apoiou-se, para isso, em dois suportes teóricos: nos estudos sobre os processos de construção do pensamento da Psicologia Construtivista de Piaget (1983, 1995) e na Didática da Matemática Francesa, representada por Brousseau (1986), Balachef (1988), Chevallard (1985) e Duval (1995).

A abordagem cognitiva traduziu uma preocupação com os processos cognitivos direcionados à construção do conhecimento de um modo geral e, particularmente, da Geometria. Quando se pretende, em situações de aprendizagem, um processo semelhante ao da produção do saber matemático², os subsídios teóricos da Psicologia Cognitiva são valiosos para a compreensão da dinâmica que se estabelece entre funcionamentos cognitivos e a construção do conhecimento. Adotou-se, de acordo com Piaget, que toda aprendizagem depende fundamentalmente de ações coordenadas do sujeito, quer sejam de caráter concreto ou caráter abstrato.

Segundo Gravina (2001), os ambientes de GD oferecem, à luz da teoria de Piaget, recursos que dão suporte às ações do sujeito e que conseqüentemente favorecem a construção do conhecimento matemático. Na aprendizagem da Matemática, este suporte possibilita o "fazer matemático", isto é, experimentar, visualizar múltiplas facetas, generalizar, conjecturar e enfim, demonstrar. A escolha desses ambientes para o trabalho da investigação foi coerente com o entendimento de uma proposta educacional na qual o conhecimento é resultado de um processo de construção.

Os objetos geométricos construídos nesses ambientes, segundo suas propriedades, podem ser manipulados diretamente na tela do computador dinamizando-se as configurações. Tal manipulação é propiciada pelo "arrastar", recurso específico desses software, em que através do mouse, selecionando-se um ponto do objeto construído, é possível arrastá-lo pela tela, criando um movimento que provoca uma mudança em sua configuração. Com a dinâmica do desenho, uma coleção de desenhos em movimento revela certos invariantes geométricos a esse mesmo objeto, decorrentes implicitamente da construção feita. Assim, como afirma Gravina (2001), ao permitir a construção e a manipulação de objetos concretos-abstratos³, os ambientes de GD desencadeiam algumas das primeiras ações mentais características do pensar matemático: o estabelecer relações e conjecturar, o que faz de forma contundente se comparado com as possibilidades apresentadas pelo desenho estático, em papel.

Embora os ambientes de GD evidenciam-se como ferramentas de grande potencial no processo de construção do conhecimento geométrico, não se pode deixar de levar em consideração a forma do "fazer pedagógico", em consonância com estratégias didáticas adequadas e planejadas para que este diferencial possa efetivamente contribuir qualitativamente com o processo ensino-aprendizagem.

No desenvolvimento das atividades da pesquisa em questão, o professor participante atuou como aluno e o pesquisador como professor ou orientador. A expectativa era de que o professor, como aluno, além de ter a oportunidade de rever, consolidar e/ou evoluir em seus conhecimentos geométricos, tivesse a oportunidade de vivenciar e dimensionar situações que favorecessem a aprendizagem em Geometria, particularmente no desenvolvimento de habilidades em trabalhar com as demonstrações.

Conceitos da Escola Francesa foram adotados no sentido de orientar as escolhas didáticas a serem aplicadas na investigação, tais como: a teoria das Situações Didáticas (Brousseau, 1986) e a da Transposição Didática (Chevallard, 1985). Nessa Escola, são encontradas investigações consistentes sobre as dificuldades dos alunos em situação de ensino aprendizagem da Matemática e uma de suas características principais é a formalização conceitual de suas constatações práticas e teóricas. Tais investigações caracterizam-se pela integração de três grandes eixos: os funcionamentos cognitivos que permeiam o processo de aprendizagem; a natureza do meio que propicia a aprendizagem e a natureza do saber matemático.

A teoria das Situações Didáticas, proposta por Guy Brousseau (1986), apresenta um estudo sobre fatos que devem ser levados em consideração ao se preparar e apresentar atividades sobre determinados conteúdos matemáticos, visando realizar uma educação matemática mais significativa para o aprendiz. Nesse modelo, a situação didática se desenvolve em três fases: a fase da contextualização e devolução (o professor apresenta um problema ou atividade aos alunos despertando-lhes o desejo de resolvê-lo); a fase da situação adidática⁴, compreendendo os momentos de ação, formulação e validação em que o aluno, na busca da solução do problema, realiza ações mais imediatas que produzem conhecimento de natureza experimental do conhecimento e que, no momento da formulação, deve ser corroborado por uma validação semântica e sintática; e a terceira fase, da institucionalização, que ocorre quando os alunos são levados a assumir o significado socialmente estabelecido de um saber que foi por eles elaborado.

Entretanto, o saber que se trabalha em sala de aula não reflete exatamente o que foi produzido na comunidade científica. Ele passa por uma série de transformações para que possa se transformar em um saber a ser ensinado. Chevallard (1985) denomina esse processo de Transposição Didática. Num primeiro momento, o conhecimento científico sofre uma transformação que envolve os elementos responsáveis por estabelecer o que deve ser ensinado na escola (professores, pedagogos, técnicos de instituições do Governo). Os objetos de ensino geralmente são organizados em propostas curriculares oficiais que servem de orientação aos livros didáticos e de parâmetros para os professores. O momento final da transformação sofrida pelo saber científico é aquele que acontece na sala de aula tendo no professor o elemento humano responsável por tal transposição. Em sala de aula é, portanto, diretamente através do professor que o aluno se apossa do saber científico.

A formação do professor é ponto estratégico dentro de um projeto educacional de melhoria da qualidade de ensino. E, essa formação no contexto da Informática na Educação, necessita ser mais sólida e mais ampla, tanto no domínio do currículo escolar como dos aspectos computacionais. Sem esses conhecimentos é muito difícil o professor saber integrar e saber tirar proveito do computador no desenvolvimento dos conteúdos (Borba & Penteado, 2001; Perrenoud, 1999; Ponte, 2003; Valente, 1996).

 

Metodologia

A metodologia da pesquisa foi inspirada na Engenharia Didática desenvolvida pela Escola Francesa de Didática da Matemática. A Engenharia Didática se constitui numa forma de organizar a pesquisa em didática da Matemática a partir da criação de uma seqüência de aulas planejadas, com a finalidade de obter informações que permitam interpretar processos de ensino-aprendizagem da Matemática, esclarecendo assim o fenômeno investigado. Enquanto procedimento metodológico, ela se fundamenta em registros de estudos de casos, cuja validade é interna, circunscrita ao contexto da experiência realizada e baseada na confrontação entre a análise a priori e a análise a posteriori. Por meio da análise a priori é indicado de que maneira as atividades propostas podem contribuir para a aprendizagem pretendida e, por outro lado, são fornecidos os critérios para observação dos participantes durante o processo de trabalho (Pais, 2001). A metodologia compreendeu, também, uma análise das impressões dos participantes acerca das demonstrações e de seu ensino, antes e depois das atividades do estudo de campo.

Participantes

Trinta professores de Matemática, da rede pública ou particular dos Ensinos Fundamental e Médio de uma cidade do estado do Rio de Janeiro, foram convidados, através de carta, a participar dos trabalhos do estudo de campo desta pesquisa. O único critério de inclusão como participante no grupo foi o de ser professor atuante de Matemática. Assim, o trabalho realizado congregou oito dos professores convidados e que aceitaram o convite. Todos revelaram ter experiência no ensino da Geometria e utilizar demonstrações neste ensino, com exceção de um dos professores para ambos os casos. O tempo de atuação no magistério de cada um oscilou entre: de 2 a 5 anos (um professor), de 5 a 10 anos (um professor), de 10 a 20 anos (um professor) e mais de 20 anos (cinco professores). Quanto à utilização do computador em suas aulas, apenas um declarou já tê-lo feito, de forma eventual. Registra-se que três desses oito professores nunca haviam usado o computador até aquela ocasião. Todos os professores cumpriram as etapas previstas para a investigação.

Instrumentos

Os dados analisados foram coletados durante os encontros e os instrumentos utilizados foram: questionários de sondagem, inicial e final; produção dos participantes na forma de material escrito (construções, resolução de problemas, elaboração de demonstrações); registro das manifestações dos professores durante a discussão de textos, através de gravação em fita; seqüência didática elaborada pelos professores participantes para uma eventual aplicação com seus alunos.

O questionário inicial teve o objetivo de traçar um perfil individualizado dos professores e, ao mesmo tempo, de colher dados sobre suas concepções acerca da Geometria e, particularmente, das demonstrações e de seu ensino para um confronto posterior com as respostas obtidas na aplicação do questionário final, com o intuito de verificar se ocorreu alguma mudança nas concepções dos professores. O questionário final coletou depoimentos dos professores sobre sua participação no experimento e sobre possíveis influências dessa participação em suas concepções acerca das demonstrações.

A produção dos professores participantes, durante a execução das atividades da seqüência em ambiente de GD, foi registrada na forma de material escrito. Essa produção englobou o encaminhamento e o desenvolvimento de seu processo de resolução dos problemas apresentados, fornecendo dados sobre sua forma de raciocinar, sobre suas dificuldades e seus avanços. Esses dados se constituíram em fonte para o confronto entre a análise a priori e a análise a posteriori dos fenômenos de aprendizagem observados. As atividades propostas na seqüência, em número de oito, compreenderam as de expressão e as de exploração, envolvendo conceitos e propriedades relacionados às figuras: circunferência, triângulos, retângulos e quadrados. Nas atividades de expressão, em número de cinco, os professores, seguindo etapas de um roteiro de trabalho, construíram figuras, identificaram e demonstraram propriedades destas e, ao mesmo tempo, tiveram a oportunidade de se familiarizar com o programa utilizado, o Tabulae⁵. As três atividades de exploração foram realizadas em torno de construções já prontas e que tinham de ser exploradas segundo um objetivo, como a solução para os problemas propostos.

Os depoimentos dos professores ocorridos durante a discussão de textos e registrados em gravador de voz foram utilizados na análise de suas concepções acerca das demonstrações. Para isso, paralelamente aos trabalhos no laboratório, foram desenvolvidas discussões acerca de temas relacionados ao assunto da investigação, buscando-se uma reflexão sobre as demonstrações e o seu ensino de forma a estimular nos professores uma retomada de posição favorável à sua prática pedagógica.

A seqüência didática elaborada pelo professor para seus alunos, em ambiente de GD, foi utilizada como um outro instrumento para avaliação de seus avanços dentro dos objetivos pretendidos por esta referenciada pesquisa, observando-se a influência dos trabalhos nas concepções dos professores através da maneira como ele conseguia relacionar a experiência vivida com a sua prática. Foram itens sugeridos para a elaboração da atividade: série a que se destina, assunto, objetivos, número de aulas necessárias, recurso utilizado, forma de desenvolver o trabalho e avaliação. Duas das últimas sessões foram destinadas à realização desse trabalho, pelos professores.

Procedimentos

O estudo de campo foi implementado em um laboratório de informática de uma escola da rede particular da cidade sede do projeto. O projeto foi desenvolvido em 15 sessões semanais de 90 minutos cada uma, perfazendo um total de 22 horas.

As atividades da seqüência didática foram realizadas sob a orientação do pesquisador com o apoio de um profissional da área da Informática para auxiliá-lo no acompanhamento e na superação das possíveis dificuldades técnicas (relacionadas ao uso do computador e do software) encontradas pelos professores participantes. Conforme planejado, as atividades foram executadas individualmente, com cada participante trabalhando em sua máquina para a conquista da desenvoltura necessária no uso do programa (domínio da técnica) e para que seu particular desempenho pudesse ser avaliado. Apesar do necessário estabelecimento do uso individual do computador pelo professor, as discussões em grupo em torno da leitura de textos apresentados se constituíram em momentos efetivos e marcantes de compartilhamento de experiências e idéias pelos professores, dentro da execução do projeto.

Os trabalhos compreenderam, portanto, além da seqüência didática: a aplicação de questionários de sondagem, a discussão de textos e a elaboração de uma seqüência didática, em ambiente de GD. Na 1ª sessão, foram feitas as apresentações iniciais, estabeleceu-se o contrato didático entre pesquisador e participantes e foi aplicado o questionário de sondagem. Na sessão seguinte, o ambiente Tabulae foi apresentado aos professores, juntamente com a exposição de telas com trabalhos já prontos e efetuados nesses ambientes. Nessa segunda sessão, o professor teve espaço para fazer uso, inicialmente dirigido e depois livre, do Tabulae. Da 3ª à 12ª sessão, foram efetuadas pelos professores as atividades programadas, sendo estas intercaladas pelas discussões já mencionadas. As 13ª e 14ª sessões foram reservadas para a complementação dos trabalhos e a elaboração da seqüência didática para os alunos. No último encontro, foi feita uma avaliação global dos trabalhos e foi aplicado o questionário final, quando se encerraram as atividades do estudo.

 

Resultados e Discussão

De acordo com as hipóteses, a análise do processo era composta de duas partes: uma referente ao desenvolvimento do pensamento geométrico dos professores e a outra relacionada às suas concepções acerca das demonstrações e de seu ensino. Para melhor compreensão do trabalho realizado e de uma de suas análises, é aqui relatado um exemplo concreto do processamento de validação, pelo confronto entre a análise a priori e a a posteriori, de uma das oito atividades realizadas, por determinado professor X. Trata-se da atividade de expressão do triângulo retângulo, a quinta na ordem de aplicação, selecionada por se situar numa etapa intermediária do processo.

O objetivo dessa atividade era oferecer ao participante a oportunidade de efetuar a construção de um triângulo retângulo inscrito numa circunferência, de fazer verificações empíricas e de produzir demonstrações a respeito das propriedades relacionadas a esse triângulo.

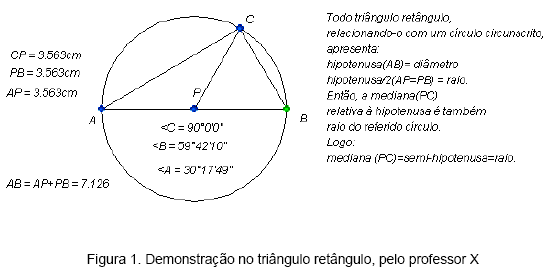
Definiu-se na análise a priori da atividade do triângulo retângulo que, inicialmente, um triângulo deve ser construído de modo que um dos seus lados coincida com o diâmetro de uma circunferência. A partir de medidas registradas na tela do Tabulae e da análise do comportamento das mesmas com a movimentação da figura, verificou-se o estabelecimento de um triângulo retângulo como conseqüência das condições de construção. Para justificar esse fato, o professor deve fazer uma reinterpretação do desenho, percebendo fatos estáveis implícitos decorrentes dos fatos declarados na construção. Isso significa perceber que o ângulo oposto ao lado coincidente com o diâmetro é um ângulo inscrito num semicírculo e, portanto de medida igual a 90°. A verificação sobre a medida da mediana relativa à hipotenusa ser equivalente à medida da metade desta, também é feita através da análise do comportamento das medidas provocado pelo dinamismo da figura. A justificativa para essa propriedade é simples e se baseia na própria construção, onde a mediana e as seções médias da hipotenusa são raios do mesmo círculo, apresentando, assim, a mesma medida.

Na análise a posteriori, com base na produção escrita e nos depoimentos do professor X acerca dessa atividade, pode-se observar que a construção do triângulo, apresentando um dos lados coincidindo com o diâmetro da circunferência inicialmente construída, não apresentou grande dificuldade para ele, mesmo sendo iniciante na técnica informática. Ocorreu, no entanto, a necessidade de acompanhamento constante do pesquisador no momento de suas dúvidas e dificuldades e de um tempo maior para que ele conseguisse completar a tarefa. A caracterização do triângulo retângulo, pelo fato da hipotenusa coincidir com o diâmetro da circunferência, foi um passo que se mostrou favorável ao enriquecimento das representações desse professor, o que pode ser percebido pelos seus comentários a respeito. A justificativa dada para esse fato baseou-se, como previsto na análise a priori, em conceito de ângulo inscrito num semicírculo.

Na etapa final do trabalho, com a construção da mediana relativa à hipotenusa, foram processadas novas investigações a partir da movimentação da figura. Com a observação do movimento e da conseqüente alteração no comportamento das medidas registradas na tela, novos fatos implícitos foram observados ou constatados por esse professor que pode, então, concluir sobre a relação entre as medidas da mediana e da hipotenusa.

A demonstração dessa relação foi feita com base na sua condição de raios da circunferência e pode ser vista na Figura 1. Foi uma validação mais simples em relação às anteriores devido, inclusive, a uma sensível melhora no desempenho desse professor na resolução dos problemas, decorrente do trabalho na investigação.

Na aplicação da seqüência didática, as produções dos professores e os possíveis conseqüentes progressos na compreensão e elaboração de demonstrações, foram analisados através da confrontação entre a análise a priori e o que foi produzido efetivamente no desenrolar do experimento e que se sistematizou pela análise a posteriori. Assim, a avaliação do nível de desenvolvimento do pensamento geométrico dos participantes, paralelamente ao desenvolvimento de competências para a elaboração de demonstrações, permitiu sugerir que os professores, de um modo geral, avançaram em seus conhecimentos em Geometria, particularmente nas demonstrações, pois demonstraram compreender: o tratamento do desenho como uma instância de representação do objeto geométrico, contribuindo muito para isso, as atividades de construção realizadas em que o desenho fica subordinado às apreensões seqüenciais, favorecendo a devida fusão dos componentes figurais e conceituais do objeto geométrico; a importância e necessidade das demonstrações para explicar logicamente propriedades das figuras e para resolver problemas; a ordenação das informações que compõem a prova, entendendo que imposições de construção (as hipóteses) acarretam fatos estáveis implícitos (a tese) que exigem explicações e que se revelam no dinamismo do desenho; o processo das demonstrações, desenvolvendo competências na habilidade em construí-las.

 

 

Quanto à verificação de possíveis mudanças nas concepções dos professores em relação às demonstrações e ao seu ensino, esta foi baseada em alguns fatores, conforme já mencionado. Na análise comparativa dos dados dos questionários (antes e depois da seqüência), foram estabelecidas categorias para representar as concepções inicial e final dos participantes a respeito das demonstrações. Pelo grande número de categorias iniciais estabelecidas, percebeu-se que não havia uma concepção comum a esses professores acerca das demonstrações. Muitas idéias foram colocadas que, embora se relacionassem com as demonstrações, se revelaram individualmente insuficientes ou incompletas para explicá-las. Após os trabalhos, verificou-se, de um modo geral, um novo olhar para as demonstrações entendidas, então, como um processo e não simplesmente como um resultado. Processo que pode e deve ser desenvolvido paralela e gradativamente ao ensino da Geometria, com um formalismo adaptado aos níveis de desenvolvimento do aluno.

Os professores identificaram os ambientes de GD como um rico e eficiente recurso que pode contribuir para a efetivação de uma proposta de ensino que privilegia uma aprendizagem interativa, onde o sujeito é o agente maior de sua aprendizagem. Os depoimentos dos professores durante a discussão de textos reforçaram essas idéias.

A natureza das atividades elaboradas pelos professores sugeriu, também, uma postura em relação à Matemática que busca propiciar aos alunos um ambiente de aprendizagem onde eles tenham a oportunidade de investigar, conjecturar, experimentar, redescobrir, argumentar, e elaborar demonstrações.

 

Considerações Finais

Tendo em vista o objetivo de investigar a contribuição dos ambientes de GD na formação de professores de Matemática, no sentido de adequar e intensificar o uso das demonstrações no ensino da Geometria, a metodologia adotada nesta pesquisa procurou alcançar a formação do professor em aspectos que se relacionassem com essas necessidades. Concebeu-se uma situação em que ele pudesse vivenciar dois momentos: um primeiro, na posição de aluno, assumindo e resolvendo problemas concebidos por outra pessoa, sentindo e superando eventuais dificuldades através de um processo de construção do conhecimento voltado para as demonstrações em Geometria; e um segundo momento vivenciando a prática de uma nova metodologia de ensino, percebendo-a como uma nova e eficiente proposta metodológica para o ensino das demonstrações.

Assim, com base na reflexão teórica, a situação didática em ambiente informatizado realçou: a importância do meio na superação das dificuldades apontadas para o ensino das demonstrações, permitindo que o processo de desequilíbrio x reflexão x ação x reequilíbrio acontecesse provocando novas aprendizagens e a evolução do pensamento geométrico; o potencial da tecnologia informática no desenvolvimento cognitivo do professor; o desenvolvimento da habilidade do professor em utilizar esses novos recursos tecnológicos; e a importância da seleção de conteúdos de acordo com a realidade do professor e em consonância com as orientações curriculares.

A utilização do modelo de situação didática proposto pela Escola Francesa de Didática da Matemática, ao permitir que fossem contemplados os papéis reservados a aluno e professor no processo ensino-aprendizagem, possibilitou uma realização didática em que se aplicaram os pressupostos da teoria piagetiana. Pois, dessa maneira, os alunos (professores participantes) foram os construtores de seu conhecimento, tendo no professor (pesquisador) um provocador e mediador e, assim, atingindo saberes dentro da Geometria, enquanto um modelo teórico, e ascendendo a relativos patamares de pensamento geométrico.

Pode-se sugerir que para os professores participantes, foi confirmada a hipótese de que a utilização de ambientes de GD, no processo ensino-aprendizagem da Geometria, estimula a evolução dos níveis de pensamento geométrico com simultâneo desenvolvimento do raciocínio lógico-dedutivo permitindo uma melhor compreensão do significado das demonstrações, bem como desenvolvendo competências para sua elaboração.

Considerando, ainda, as propostas de alguns autores (Borba & Penteado, 2001; Garcia, 1998; Ponte, Oliveira & Varandas, 2003; Valente, 1993, 1996) acerca da formação de professores, entendendo-se que para haver mudanças é preciso que o professor queira mudar; as discussões acerca de temas relacionados às demonstrações e ao seu ensino proporcionaram a eles momentos de reflexão sobre tais conhecimentos e sobre sua própria prática pedagógica, estimulando mudanças em suas concepções sobre as demonstrações com possíveis implicações em suas atividades docentes.

Pode-se, assim, sugerir que foi verificada a segunda hipótese dessa pesquisa de que a utilização de ambientes de GD, quando num processo de formação de professores, e através de competências desenvolvidas e da prática de novas metodologias contribui para uma reflexão sobre as demonstrações e seu ensino, favorecendo uma retomada de posição favorável a sua prática pedagógica.

A Educação, a Informática e a Psicologia Cognitiva, apesar de áreas distintas, podem e devem ser trabalhadas juntas, favorecendo resultados educacionais satisfatórios, pois a intencionalidade na aquisição de novos conhecimentos é um fator comum às três. A Informática, nesse caso, estaria não só atuando sobre o conhecimento, mas oferecendo novas ferramentas que auxiliem na aprendizagem, ao estimularem a construção do conhecimento e, particularmente, o da Matemática, favorecendo o desenvolvimento do raciocínio lógico-dedutivo e provocando mudanças de visão do ensino da Matemática.

 

Referências

Alves, G. S. (2004). O uso de softwares de geometria dinâmica para o desenvolvimento de habilidades cognitivas: uma aplicação em alunos do ensino médio. Dissertação de Mestrado, Universidade Federal do Rio de Janeiro, Rio de Janeiro.        [ Links ]

Balacheff, N. (1988). Aspects of proof in pupils' practice of school mathematics. Em D. Pimm (Ed.), Mathematics, Teachers and Children (pp. 216-235). London: Hodder and Stoughton.        [ Links ]

Barra Ferreira, E., Soares, A. B., & Lima, C. A. (2005a). A contribuição dos softwares de geometria dinâmica na representação do conhecimento geométrico num curso de formação de professores. Trabalho apresentado no I Congresso Latino-Americano de Psicologia, São Paulo. São Paulo.        [ Links ]

Barra Ferreira, E., Soares, A. B., & Lima, C. A. (2005b). A representação do conhecimento geométrico e o raciocínio lógico-dedutivo de professores de Matemática num ambiente de geometria dinâmica. Trabalho apresentado no IV Congresso Norte Nordeste de Psicologia, Salvador. Bahia.        [ Links ]

Belfort, E., Guimarães, L. C., & Barbastefano, R. (1999). Geometria dinâmica e demonstrações na formação continuada de professores. Em Anais. Cabri World 1999, volume eletrônico, São Paulo. São Paulo.        [ Links ]

Borba, M. C., & Penteado, M. G. (2001). Informática e Educação Matemática. Belo Horizonte: Autêntica.        [ Links ]

Brousseau, G. (1986). Fondements et méthodes de la didactique des mathématiques. Recherches en Didactique des Mathématiques, 7(2), 33-115.        [ Links ]

Chevallard, Y. (1985). La transposition didactique. Grenoble: La Pensée Sauvage.        [ Links ]

Duval, R. (1995). Sémiosis et pensée humaine: registres sémiotiques et apprentissages intellectuels. S.A. Suisse: Peter Lang. Editions scientifiques européennes.        [ Links ]

Garcia, C. M. (1998). Formação de professores para uma mudança educativa. Portugal: Porto Editora.        [ Links ]

Gouvea, F. A. (1998). Aprendendo e ensinando geometria com a demonstração: uma contribuição para a prática pedagógica do professor de Matemática do ensino fundamental. Dissertação de Mestrado, Pontifícia Universidade Católica de São Paulo, São Paulo.        [ Links ]

Gravina, M. A. (2001). Os ambientes de geometria dinâmica e o pensamento hipotético-dedutivo. Tese de Doutorado, Universidade Federal do Rio Grande do Sul, Rio Grande do Sul.        [ Links ]

Hanna, G. (2000). Proof, explanation and exploration: an Overview. Educational Studies in Mathematics, 44(1-2), 5-23.        [ Links ]

Hoyles, C., & Jones, K. (1998). Proof in dynamic geometry contexts. Em C. Mammana & V. Villani (Eds.), Perspectives on the Teaching of Geometry for the 21st Century (vol.5, pp.121-128), London: Kluwer Academic Publishers.        [ Links ]

Laborde, C. (2000). Dynamic geometry environments as a source of rich learning contexts for the complex activity of proving. Educational Studies in Mathematics, (44), 151-161.        [ Links ]

Laborde, C., & Capponi, B. (1994). Cabri-géomètre constituant d'un milieu pour l'apprentissage de la notion de figure. Em N. Balacheff & M. Vivet (Eds), Didactique et Intelligence Artificielle (vol. 14, n. 1.2, pp. 165-210). Grenoble: Editions La Pensée Sauvage.        [ Links ]

Lorenzato, S. (1995). Por que não ensinar geometria? Educação Matemática em Revista, (4), 3-13.        [ Links ]

Pais, L. C. (2001). Didática da matemática: uma análise da influência francesa. Belo Horizonte: Autêntica.        [ Links ]

Pavanello, R. N. (1993). O abandono do ensino da Geometria no Brasil: causas e conseqüências. Revista Zetetiké, (01), 7-17.        [ Links ]

Perrenoud, P. (1999). Formar professores em contextos sociais em mudança: prática reflexiva e participação crítica. Revista Brasileira de Educação, (12), 5-21.        [ Links ]

Piaget, J. (1983). Desenvolvimento da inteligência. Rio de Janeiro: Zahar.        [ Links ]

Piaget, J. (1995). Abstração reflexionante - relações lógico-aritméticas e ordem das relações espaciais. (F. Becker & P. B. G. Silva, trads.). Porto Alegre: Artmed.        [ Links ]

Ponte, J. P. (1994). O desenvolvimento profissional do professor de Matemática. Educação e Matemática, (31), 9-12.        [ Links ]

Ponte, J. P., Oliveira, H., & Varandas, J. M. (2003). O contributo das tecnologias de informação e comunicação para o desenvolvimento do conhecimento e da identidade profissional. Em D. Fiorentini (Ed.), Formação de professores de Matemática: Explorando novos caminhos com outros olhares (pp.159-192). Campinas: Mercado de Letras.        [ Links ]

Valente, J. A. (1993). Computadores e conhecimento: repensando a educação. Campinas: NIED, Gráfica da UNICAMP.        [ Links ]

Valente, J. A. (1996). O professor no ambiente logo: formação e atuação. Campinas: Gráfica da UNICAMP/NIED.        [ Links ]

Vianna, C. S. (1988). O papel do raciocínio dedutivo no ensino da Matemática. Dissertação de Mestrado, Universidade Estadual Paulista, Rio Claro, São Paulo.        [ Links ]

 

 

Recebido em: 27/02/2008
Revisado em: 01/07/2008
Aprovado em: 27/10/2008

 

 

Sobre os autores:

^* Emilia Barra Ferreira (ebarraferreira@yahoo.com.br) - Professora da rede pública estadual do Rio de Janeiro e municipal de Angra dos Reis, Professora da rede particular de ensino em Angra dos Reis e Professora tutora da Fundação Centro de Ciências e Educação Superior à Distância do Estado do Rio de Janeiro (fundação CECIERJ/ consórcio CEDERJ).
^** Adriana Benevides Soares (absoares@posgrad.nce.ufrj.br) - Professora Titular da UNIVERSO, Universidade Salgado de Oliveira, e Professora Adjunta da UERJ, Universidade do Estado do Rio de Janeiro.
^*** Josefino Cabral Lima (clima@nce.ufrj.br) - Professor titular da UFRJ, Universidade Federal do Rio de Janeiro.
¹ Uma abordagem das demonstrações é dita tradicional quando o aluno não participa de sua elaboração; elas são apresentadas prontas, ao aluno que, por vezes, é obrigado a decorá-las, sem sequer entender seu significado.
² Num processo escolar em que se pretende uma produção semelhante ao da produção natural do saber matemático, espera-se que este conhecimento se desenvolva no aluno, através das suas ações de: observar, experimentar, conjecturar, testar, generalizar, demonstrar.
³ Objetos concreto-abstratos, concretos porque existem na tela do computador e podem ser manipulados, abstratos porque se constituem em realizações feitas a partir de construções mentais.
⁴ Numa análise das propostas das situações adidáticas, pode ser percebido um relacionamento estreito destas com as propostas de Piaget, no momento em que a ação do aluno é privilegiada numa posição de construção do seu conhecimento.
⁵ Programa desenvolvido no Instituto de Matemática da UFRJ, dentro do projeto PACE (Pesquisa em Ambientes Computacionais de Ensino), constituindo-se numa alternativa brasileira aos software de geometria dinâmica encontrados no mercado.