Psicologia Escolar e Educacional
ISSN 1413-8557
Psicol. esc. educ. v.13 n.1 Campinas jun. 2009
ARTIGOS
Modos de resolução de labirintos por alunos da escola fundamental
On solving labyrinths by students of the elementary school
Formas de resolución de laberintos por alumnos de escuelas primarias
Lino de MacedoI; Gisele Escorel de Carvalho; Ana Lúcia Sicoli PettyI
I Laboratório de Psicopedagogia (LaPp), Instituto de Psicologia, Universidade de São Paulo
RESUMO
Saber planejar expressa uma forma de antecipação com pré-correção de erros e uso de inferências. Esta questão foi aqui analisada em 60 matrizes de labirintos (20 A, 20 B e 20 C), resolvidas por 20 alunos da Escola Fundamental, entre 7 e 11 anos. Deste total, 31 matrizes foram resolvidas com um único traçado. As 29 restantes foram analisadas, considerando-se, dentre outros, procedimentos indicadores de planejamento: (1) começar do final, (2) aproveitar o traçado anterior e (3) interromper o traçado. O procedimento (1) foi utilizado pelos sujeitos em 7 matrizes; o procedimento (2) em 9; e o procedimento (3) em 5. Na discussão, apoiada em estudos comparáveis realizados por Piaget, destacaram-se três níveis de resolução das matrizes utilizadas. E, nas considerações finais, foram descritas algumas formas de intervenção, visando favorecer, em um contexto educacional, o desenvolvimento da habilidade de antecipação em crianças.
Palavras-chave: Aprendizagem, Jogos, Labirintos, Piaget.
ABSTRACT
Planning means to anticipate by pre-correcting mistakes and making use of inferences. This statement was analyzed in this study in which 60 labyrinths (20A, 20B and 20C) were solved by 20 elementary school students aged between 7 and 11 years old. From the total amount, 31 were solved with one single line. The remaining ones were closer studied and it was possible to identify three indicators of planning procedures: procedure (1) beginning from the end; procedure (2) use part of the former line; (3) stopping a wrong line before the end. Procedure (1) appeared on 7 labyrinths, (2) on 9 and (3) on 5 of them. The discussion, based on studies held by Piaget, brings up the possibility to underline three different levels of resolution. In the conclusion, possible forms of intervention are presented, aiming to suggest that, in educational contexts, labyrinths may be used to develop the anticipation skill on children who play.
Keywords: Learning, Games, Labyrinths, Piaget.
RESUMEN
El saber planificar expresa una forma de anticipación con pre-corrección de errores y uso de deducciones. Esta cuestión fue analizada aquí en 60 matrices de laberintos (20 A, 20 B y 20 C) resueltas por alumnos de escuelas primarias, entre 7 y 11 años. Del total, 31 matrices fueron resueltas con un único trazo. Las 29 restantes fueron analizadas, considerándose, entre otros, procedimientos indicadores de planificación: (1) comenzar del final, (2) aprovechar el trazo anterior y (3) interrumpir el trazo. Los sujetos utilizaron el procedimiento (1) en 7 matrices; el procedimiento (2) en 9; y el procedimiento (3) en 5. En la discusión, con base en estudios comparables efectuados por Piaget, se destacaron tres niveles de resolución de las matrices usadas. Y en las consideraciones finales fueron descritas algunas formas de intervención, con la finalidad de favorecer, en un contexto educacional, el desarrollo de la habilidad de anticipación en los niños.
Palabras clave: Aprendizaje, Juegos, Laberintos, Piaget.
Introdução
Consultando os verbetes jogo e labirinto na Biblioteca Virtual, não se verificaram registros de publicações em revistas científicas sobre este tema. No entanto, o Google Acadêmico indicou 152.000 ocorrências sobre o par jogo e labirinto, concentradas nas áreas de literatura, ambiente virtual, filosofia, clínica e arquitetura.
O presente estudo foi feito em um contexto de oficinas de jogos, visando à observação e promoção de processos de desenvolvimento e aprendizagem de crianças da Escola Fundamental. Cada oficina, em geral, divide-se em três momentos. No primeiro, são propostas atividades lúdicas ou passatempos; no segundo, realizam-se partidas de certo jogo; e, no terceiro, há uma atividade de reflexão em grupo, em que as crianças discutem um tema ou questão, elaborada pelos pesquisadores, e suas respostas são registradas em um caderno. Resolver matrizes de labirinto é uma das atividades frequentemente utilizadas na primeira parte das oficinas, tanto pelo gosto que as crianças têm por este tipo de desafio, bem como por seu valor em favorecer o desenvolvimento da habilidade de planejar e antecipar, précorrigindo erros e buscando com atenção e concentração traçar um percurso bem sucedido.
Os labirintos modernos, segundo critérios estabelecidos por Jaskolski (1997), caracterizam-se por ter uma entrada e um sistema de passagens que anunciam caminhos como possibilidades de percurso até o final. Para jogá-los, é necessário definir um trajeto que leve à saída, traçar mentalmente um plano do percurso, observar as várias possibilidades apresentadas pelas bifurcações e coordenar todas as partes.
Em Investigaciones sobre las correspondências, Piaget (1980/1982) realiza um experimento no qual propõe três labirintos, sendo os dois primeiros iguais quanto ao trajeto, porém com materiais diferentes. Os labirintos são apresentados ao sujeito, que deve descobrir o caminho que um rato percorrerá, sem retroceder, desde a entrada até a saída. Em seguida, pergunta-se o que aconteceria se um gato estivesse na saída. Nos labirintos I e II, graças a determinadas bifurcações, é possível encontrar uma solução e, no III, o rato é caçado.
Em seu estudo sobre resolução de labirintos, Piaget identificou três níveis. No Nível I, os registros indicam uma atuação por ensaio e erro, sendo casual a possibilidade de acerto. A criança resolve experimentando cada abertura (bifurcação) e percorre os caminhos até se deparar com uma impossibilidade. A relação parte-todo fica comprometida, na medida em que não atua por antecipação e só percebe os “finais mortos” mais próximos de onde está, ou seja, qualquer caminho corresponde à possibilidade de sair. Portanto, joga por afirmações e, centrada na meta a atingir, só percebe depois da ação (realizar o traçado) se a abertura escolhida leva à saída. O Nível II caracteriza-se por um conjunto de ações em que o sujeito começa a ter uma conduta de evitar os “finais mortos” quando, diante de uma abertura (bifurcação), observa se há ou não saída, o que corresponde a alguma antecipação. Já percebe que há conexão entre os percursos e amplia seu olhar para os possíveis caminhos que as bifurcações podem levar. Na maioria das vezes, consegue propor a solução sem tentar todos os caminhos. No Nível III, observa-se que o sujeito identifica que as sucessivas aberturas têm uma necessidade lógica, por isso leva em consideração todo o percurso e joga coordenando parte e todo. Para isso, antecipa suas ações e analisa as diferentes possibilidades, visando encontrar o caminho necessário.
Em síntese, Piaget (1980/1982) ressalta que a estrutura do labirinto exige a consideração do futuro para definir o presente, ou seja, o jogador deve levar em conta os elementos seguintes para tomar uma decisão. Desta forma, deverá ter em mente a necessidade de avaliar o percurso a todo instante, observando cuidadosamente as encruzilhadas. Como condição, é preciso planejar e antecipar, não esquecendo que a escolha dos meios acontecerá em função do futuro.
Além disso, o jogador deve tomar decisões apoiadas em afirmações e negações sobre os trajetos existentes. Como negar os caminhos que levam a fechamentos e escolher (afirmar) os que conduzem a aberturas? O labirinto é um sistema que abre várias possibilidades para o jogador encontrar ou não o caminho que leva à sua resolução. Então, é preciso agir coordenando os possíveis e o necessário, já que as sucessivas aberturas implicam diversos possíveis, que terão somente um necessário como resposta ao labirinto proposto. Piaget em “O possível e o necessário” (1981/1985) justifica a importância deste tipo de coordenação:
As operações exigem, com efeito, uma síntese do possível e do necessário, um exprimindo sua liberdade de procedimento, o outro, a auto-regulagem e o fechamento de suas composições. Se esse é o caso, as condições prévias de tais construções são, pois, evidentemente uma formação dos possíveis, uma elaboração do necessário e uma coordenação progressiva dessas duas modalidades. (p. 134)
Outros estudos destacam, igualmente, a importância dos labirintos. Attali (1996), por exemplo, compara o viver ao percorrer labirintos, destacando o valor de atitudes como persistir, aceitar o fracasso e não ceder à decepção. Atitudes como estas são de grande valia para que os obstáculos apresentados ao longo do “caminho da vida” possam ser ultrapassados.
Friedman e Scholnick (1997), com base em outra perspectiva teórica, concluíram que o ato de planejar, definido como formular antecipadamente um método organizado para agir, corresponde a “orquestrar” diferentes e interdependentes processos cognitivos e motivacionais, os quais são influenciados pelo contexto e agrupados a serviço de uma meta ou objetivo. Estes processos e sua “orquestração” percorrem uma complexa trajetória de desenvolvimento. Saber planejar como estratégia de resolução de problemas que envolvem desafio não é algo que ocorra de imediato. Crianças, jovens e mesmo adultos “preferem” escolher o jeito mais fácil ou rápido de fazer, quando a necessidade se impõe, a esperar e delinear um plano de ação.
Objetivo
O propósito desta pesquisa é analisar modos de planejamento na resolução de três matrizes de labirinto por crianças da Escola Fundamental. Serão analisados os seguintes aspectos: número de traçados, respeito à regra e planejamento.
Método
Sujeitos
Participaram deste estudo 20 crianças, pertencentes a duas turmas que frequentavam oficinas de jogos. Cada turma tinha dez crianças, a maioria com nove anos de idade. As oficinas ocorreram semanalmente, com duração de uma hora e vinte minutos, em período complementar ao da escola. As crianças eram alunos de escola pública e apresentavam, na visão de seus professores ou pais, dificuldades de aprendizagem.
Material
O estudo consistiu na aplicação de três matrizes propostas por Quinn, (1994) envolvendo problemas de traçar um percurso em labirintos. Foram escolhidos labirintos “modernos”, segundo Jaskolski (1997), que se caracterizam por ter uma entrada e um sistema de passagens que anunciam caminhos como possibilidades para a saída. Alguns destes caminhos dão em “finais mortos” ou em encruzilhadas sem saída.
A matriz A, apresentada na Figura 1, tem um percurso constituído por retas formando ângulos de 90°. Há até 10 bifurcações que dão em “finais mortos” e os trechos são curtos, o que favorece a visualização dos lugares sem saída.
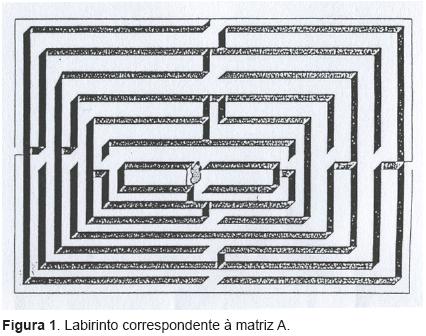
A matriz B, apresentada na Figura 2, tem seu percurso formado por um número maior de retas com ângulos de 90°. Há de 10 a 15 bifurcações que dão em “finais mortos”, sendo mais difícil ver os lugares sem saída, pois os trechos são mais longos e a quantidade é maior em relação à Matriz A.

A matriz C está apresentada na Figura 3. Ela tem um percurso que dificulta a visualização das possibilidades de resolução. A forma do percurso tem muitas pontas ou alças e as bifurcações são apresentadas por vários tipos de ângulos, resultando em um desenho complexo, o que aumenta a dificuldade de antecipação do caminho a ser seguido. São mais de quinze as bifurcações que dão em “finais mortos” e os trechos misturam-se entre curtos e longos, ficando difícil enxergar os lugares sem saída.

Procedimentos para a coleta de dados
A aplicação das matrizes foi feita no contexto das oficinas em duas sessões, sendo uma em cada oficina. Na primeira, apresentou-se a proposta da tarefa: objetivos, regras do jogo e instruções para o traçado das linhas. Para isso, utilizou-se outra matriz (não usada na análise dos resultados) para ilustrar as múltiplas possibilidades do jogo e resolver casos de dúvidas. O experimentador explicou que labirintos têm encruzilhadas sem saídas (finais mortos) e que o objetivo do jogo é procurar um caminho que as evite, fazendo-se um traçado que vá da entrada à saída. Para isso, é preciso respeitar os contornos do caminho, não os “invadindo”. Foi solicitado às crianças que deixassem sem apagar todas as tentativas para chegar à solução e que a execução fosse feita com lápis de cor. Elas deveriam registrar seus traçados usando cores na seguinte sequência: verde, castor, laranja e roxo. O objetivo desta instrução (usar cores diferentes e ordenadas) era possibilitar observar a posteriori o que as crianças tinham feito para conseguir resolver os labirintos. Concluída esta etapa, foi proposto que as crianças resolvessem, individualmente, a matriz A (ver Figura 1).
Na segunda sessão, foi proposta a resolução das matrizes B e C (ver Figuras 2 e 3). Cumpre ressaltar que, também no final desta sessão, as crianças foram entrevistadas para saber se tinham utilizado na resolução das matrizes o procedimento de percorrer, com olhos ou dedos, os caminhos a serem traçados.
Resultados e Discussão
Como mencionado, o objetivo desta pesquisa foi observar os procedimentos de resolução das 60 matrizes de labirintos quanto ao número de traçados, respeito à regra e planejamento. Foram analisadas, portanto, as três matrizes (A, B e C) de cada um dos 20 sujeitos da pesquisa.
Número de traçados
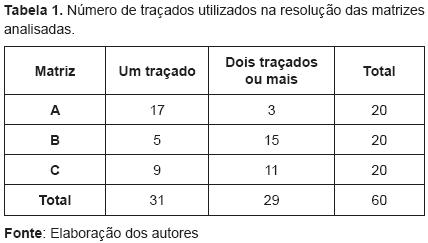
A Tabela 1 apresenta os resultados sobre o número de traçados utilizados para a resolução, identificados pela troca de cores nas matrizes. Verifica-se que, na maioria dos casos observados, a resolução da matriz A requereu apenas um traçado e que, em mais da metade das matrizes B e C, foram necessários dois traçados ou mais.
Respeito à regra
Quanto ao respeito à regra, observou-se que, em todas as matrizes, as bordas que delimitavam os trajetos não foram ultrapassadas. Ou seja, a regra foi respeitada em todos os casos.
Planejamento
Na resolução de labirintos, saber planejar consiste basicamente em antecipar os finais mortos e, portanto, evitálos. Isto implica coordenar quatro procedimentos: 1) observar as bifurcações, percorrendo o caminho com olhos ou dedos, 2) começar do final, 3) aproveitar o traçado anterior e 4) interromper o traçado, antes de chegar ao final morto.
Com relação ao primeiro procedimento &– percorrer o caminho com olhos ou dedos &–, a observação direta das matrizes, por si só, não possibilita esta verificação. Por isso, recorreu se às informações anotadas nos versos das matrizes, para saber se as crianças tinham utilizado este procedimento. Observando estes registros, verifica-se que em apenas 3 casos isto não ocorreu.
Na Tabela 2, apresentam-se os resultados sobre os outros três procedimentos analisados sobre um total de 29 matrizes (3 A + 15 B + 11 C), pois as 31 restantes (17 A + 5 B + 9 C), do total 60, foram resolvidas com apenas um traçado.
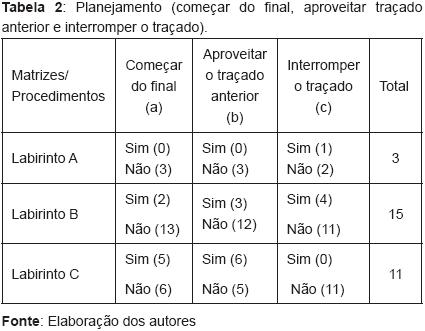
Na matriz A, não ocorreram os procedimentos: (a) começar do final e (b) aproveitar o traçado anterior. Na matriz B, nos 15 casos, em apenas cinco deles, estes dois recursos foram utilizados. Com relação à matriz C, observaram-se 11 ocorrências do uso destes dois procedimentos de planejar o caminho a ser traçado. O procedimento (c) &– interromper o traçado, evitando chegar ao final morto &– não foi verificado na maior parte dos casos. Ou seja, dentre três, apenas um caso na matriz A; dentre quinze, quatro na matriz B; e nenhum em onze, na matriz C. Estes resultados sugerem que é necessário observar as bifurcações, mas isto não é suficiente para resolver os problemas de traçar percursos em um labirinto. Em síntese, há de se coordenar pelo menos três procedimentos para que a escolha do melhor traçado seja bem sucedida.
Como foi caracterizado na Introdução, saber planejar é ação complexa que exige observação e consideração simultânea de vários aspectos. A contribuição da presente pesquisa a este respeito foi observar traçados feitos pelos sujeitos em três matrizes de labirintos. Desta observação, foram abstraídos os indicadores que caracterizam o modo de planejamento adotado por eles: começar do final, aproveitar o traçado anterior e interromper o traçado. O uso destes procedimentos, como se pôde constatar na Tabela 2, foi pequeno, o que expressa a dificuldade a ser enfrentada em situações de planejamento de coordenar realização (como fazer?) com compreensão (por que fazer?), antecipadas como conduta de projeto. Começar do final, por exemplo, implica inverter, a título de antecipação, um traçado a ser feito, considerando, de modo reversível, ponto de partida e ponto de chegada como equivalentes. Aproveitar o traçado anterior implica aproveitar a parte “certa” do percurso, corrigindo apenas o que está “errado”. Neste caso, o sujeito sabe diferenciar e integrar as partes e o todo, conservando o que está bem e corrigindo o que deve ser corrigido. Interromper traçado implica antecipar um mau resultado (atingir um final morto), sem necessidade de chegar até ele e, com isto, ser capaz de pré-corrigir erros.
Os observáveis da presente pesquisa podem ser, igualmente, analisados ao modo de Piaget, segundo pelo menos três níveis de enfrentamento ou resolução do problema proposto. No primeiro, observa-se que a criança não respeita a regra ou, se o faz, tem necessidade de percorrer todos os caminhos, recomeçando sempre do início ou chegando até um final morto, sem ser capaz de antecipar e, assim, interromper o traçado. Em outras palavras, ela entende o problema &– fazer um caminho &–, brinca com ele e, neste contexto, aprende sobre o desafio, mas não o suficiente para dominar os aspectos do planejamento que ele implica. A Figura 4 ilustra o caso de uma resolução característica deste nível.
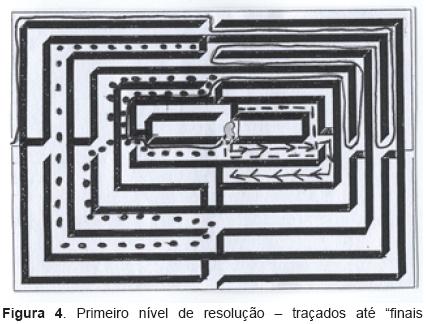
No segundo nível de resolução, a criança (a) começa a valorizar a relação entre o começo e o fim do percurso, (b) aproveita o traçado anterior e (c) sabe interrompê-lo. É o que se pode verificar na Tabela 2 em relação às matrizes B e C: 7 casos quanto ao procedimento (a), 9 casos quanto ao (b) e 4, em relação ao (c).
Na Figura 5, apresenta-se um caso em que a criança utiliza o procedimento (a), começar do final.
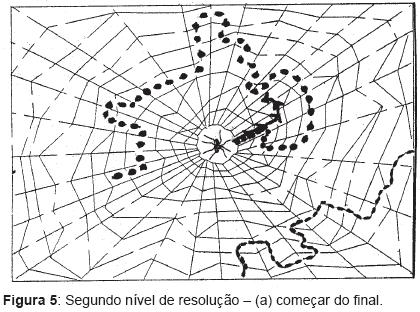
Na Figura 6, observa-se o procedimento (b), aproveitar o traçado anterior, pois a criança recomeça do momento em que considera ter ido para um caminho de “final morto”.

A Figura 7 ilustra uma resolução por interrupção do traçado (c), isto é, no qual a criança antecipa um final sem saída.

No terceiro nível, a criança já sabe coordenar as possibilidades de caminhos com a necessidade de produção de um percurso (traçado) contínuo do começo ao fim. Para isto, ela usa antecipações, ou seja, realiza “visualmente” o trajeto fazendo correções antes de riscar o percurso. É neste nível, de fato, que o problema representa um maior desafio para o sujeito, pois se trata de observar bem, fazer cálculos, evitar ciladas, fazer pré-correções de erros, ou seja, planejar bem antes de realizar a tarefa. O presente é agora regulado pelo futuro, como é próprio de toda conduta de projeto.
Considerações Finais
Como intervir, favorecendo o desenvolvimento da habilidade de planejar? Nossa prática nas oficinas é aproveitar as dificuldades apresentadas pelas crianças como um desafio de aprendizagem. Por exemplo, solicitamos que elas marquem todos os “finais mortos” que encontram na figura e, depois disso, sugerimos uma nova resolução da mesma matriz, com o desafio de as crianças chegarem em menos “finais mortos”. Outra sugestão é pedir para as crianças procurarem o número de bifurcações e identificar os destinos de cada uma delas. Além disso, se as crianças usam mais de três traçados para resolver a matriz, lançamos o desafio de, em nova oportunidade, resolver a matriz com um traçado a menos.
Em nossas oficinas, aproveitamos os procedimentos adotados pelas crianças para estimular suas reflexões sobre eles e seu valor para a resolução do problema proposto nas matrizes. Perguntamos, por exemplo, o que ela fez para acertar: começou do final?, interrompeu ou aproveitou traçados? É importante que as respostas sejam demonstradas pelas crianças destacando em sua resolução o aspecto considerado. Isto posto, solicitamos que elas resolvam novamente a mesma matriz, utilizando agora outra forma de planejamento ou, então, que busquem conseguir uma resolução melhor do que a anterior.
Nos casos em que as crianças já procedem no terceiro nível de resolução, nossa intervenção é no sentido de as crianças realizarem outras matrizes para que experimentem o fato de que se sair bem em uma matriz nem sempre é garantia de obter o mesmo resultado em outras. Ou seja, as exigências de planejamento, atenção e concentração para a realização desta tarefa continuam sendo válidas, mesmo para aqueles que são bem sucedidos.
É importante que os profissionais aprendam a observar criticamente resolução de labirintos e, igualmente, que saibam interpretar resolução de matrizes em uma perspectiva qualitativa para que suas intervenções favoreçam processos de desenvolvimento e aprendizagem. Na perspectiva das crianças, é muito bom que aprendam a construir recursos para pensar utilizando aspectos do planejamento como instrumento para resolução de desafios, o que pode ser muito valioso nas situações escolares, onde planejar é fundamental
Referências
Atalli, J. (1996). Chemins de sagesse: Traité du labyrinthe. Paris: Fayard. [ Links ]
Friedman, S. L., & Scholnick, E. K. (1997). The Developmental Psychology of Planning: Why, how and when do we plan?. London: Lawrence Erlbaum Associates. [ Links ]
Jaskolski, H. (1997). The Labyrinth. Symbol of fear rebirth and liberation. Boston & London: Shambhala. [ Links ]
Piaget, J. (1982). Investigaciones sobre las correspondencias (E. Martín & A. Moreno, Trad.). Madrid: Alianza Editorial. (Trabalho original publicado em 1980) [ Links ]
Piaget, J. (1985). O possível e o necessário: evolução dos possíveis na criança (B.M. de Albuquerque, Trad.) Porto Alegre: Artes Médicas. (Trabalho original publicado em 1981) [ Links ]
Quinn, L. D. (1994). Puzzling Mazes. New York: Dover Publications. [ Links ]
Recebido em: 02/05/2006
Reformulado em: 14/06/2009
Aprovado em: 18/06/2009
Sobre os Autores
Lino de Macedo
Professor Titular e Coordenador do Laboratório de Psicopedagogia (LaPp) do Instituto de Psicologia da Universidade de São Paulo.
Gisele Escorel de Carvalho
Especialista em atendimento de alunos com dificuldades de aprendizagem.
Ana Lúcia Sícoli Petty
Mestre em Psicologia Escolar pelo Instituto de Psicologia da USP, técnica do LaPp.
Agradecimento:
Agradecemos à Valquíria Carracedo, pela colaboração na coleta de dados.













