Estudantes com grau extremo de ansiedade à matemática: identificação de casos e implicações educacionais

 

Students with extreme degree in mathematics anxiety: identification of cases and educational implications

 

Estudiantes con grado extremo de ansiedad ante las matemáticas: identificación de casos y algunas implicaciones educativas

 

 

Alessandra Campanini Mendes^I; João dos Santos Carmo^II

^IMestre pela Universidade Federal de São Carlos. alessandra.campanini@gmail.com
^IIProfessor da Universidade Federal de São Carlos, Instituto Nacional de Ciência e Tecnologia sobre Comportamento, Cognição e Ensino

 

 

---

RESUMO

O objetivo do presente estudo foi identificar casos de extrema ansiedade à matemática em estudantes do Ensino Fundamental e Médio, e discutir implicações educacionais. Aplicou-se uma escala de ansiedade à matemática a estudantes do Ensino Fundamental e Médio, contendo 24 situações relacionadas ao estudo de Matemática. Para cada situação o participante deveria escolher uma opção: nenhuma ansiedade; baixa ansiedade; ansiedade moderada; alta ansiedade; extrema ansiedade. Dos 1106 estudantes que responderam à escala, selecionou-se 11 casos cujos escores entre 97 e 106 indicavam extrema ansiedade. Os dados são discutidos com base nas implicações educacionais que os itens da escala indicam como sendo situações ansiogênicas. Também são indicadas possíveis intervenções com o objetivo de reduzir ou reverter a ansiedade à matemática.

Palavras-chave: ansiedade à matemática; escala de ansiedade à matemática; alunos do ensino fundamental e médio.

---

ABSTRACT

The aim of this study was to identify cases of extreme math anxiety in elementary and high school students, and discuss some educational implications. A mathematics anxiety scale for elementary and high school students was applied. The scale contained 24 situations related to the study of mathematics. For each situation the respondent must select an option: no anxiety, low anxiety, moderate anxiety, high anxiety, extreme anxiety. We selected 11 cases whose scores between 97 and 106 indicated extreme anxiety out of 1106 students who responded to the scale. Data are discussed on the base of educational implications regarding to the anxiogenic situations presented in the scale. Some possible interventions aimed at reducing or reversing mathematics anxiety are indicated.

Keywords: mathematics anxiety; mathematics anxiety scale; elementary and high school students.

---

RESUMEN

El objetivo de este estudio fue identificar algunos casos de ansiedad extrema ante las matemáticas en estudiantes de la escuela primaria y secundaria, y discutir algunas implicaciones educativas. Se aplicó una escala de ansiedad ante las matemáticas para alumnos de primaria y secundaria, que contiene 24 situaciones relacionadas con el estudio de las matemáticas. Para cada situación los participantes tenían que elegir una opción: sin ansiedad, baja ansiedad, ansiedad moderada, alta ansiedad, ansiedad extrema. De los 1106 estudiantes que respondieron a la escala, se seleccionaron 11 casos cuyas puntuaciones entre 97 y 106 indica ansiedad extrema. La discusión se basa en las implicaciones educativas de los ítems de la escala que indican situaciones ansiogénicas. También se indican las posibles intervenciones dirigidas a reducir o revertir la ansiedad ante las matemáticas.

Palabras clave: ansiedad ante las matemáticas; escala de ansiedad ante las matemáticas; estudiantes de educación primaria y secundaria.

---

 

 

A instituição escolar tem sido marcada ao longo dos anos por um grande número de alunos estigmatizados como portadores de problemas de aprendizagem. No entanto, sabe-se que as dificuldades nem sempre são apenas de aprendizagem, mas, também, podem ser dificuldades de ensino por parte dos professores (Ball, Lubienski, & Mewborn, 2001; Carmo, 2003; Cunha, 2000; Oliveira & Cyrino, 2011).

Em relação à aprendizagem escolar da matemática, Skinner (1968) destaca algumas características das práticas escolares que ainda são válidas para uma análise das contingências que imperam em sala de aula. Para Skinner, o comportamento numérico (também chamado por ele de comportamento matemático) nada mais é que um repertório verbal extremamente complexo. Segundo o autor, nas escolas esse comportamento tem sido estabelecido por meio do controle aversivo explícito (utilizado em épocas passadas) ou pelo controle aversivo sutil (utilizado mais recentemente). O controle aversivo explícito compunha-se de punição física diante de "mau" desempenho em sabatinas, por exemplo.

Sobre o controle aversivo sutil, Skinner (1968) aponta várias características, como: (a) demonstração de descontentamento do professor; (b) censura e zombaria dos colegas de classe; (c) comparações vexatórias; (d) atribuição de notas baixas; (e) levar o aluno para conversar com a direção; (f) comunicar os pais acerca do baixo desempenho acadêmico do filho. Como resultado, respostas corretas tornam-se insignificantes em meio aos subprodutos do controle aversivo: ansiedade, aborrecimento, agressão.

Além dessas formas de controle aversivo, Skinner (1968) ressalta que há um intervalo de tempo considerável entre a emissão de respostas corretas e as consequências "reforçadoras" (entre aspas para ressaltar a questão de até que ponto são reforçadoras se não houver proximidade temporal entre resposta e reforço). Ou seja, a rigor a liberação atrasada de uma consequência não garante a presença de uma contingência nem estabelece um valor reforçador para o comportamento. Os reforçadores, quando ocorrem, são em pequena quantidade quando comparados à frequência da punição. Um quadro semelhante, relacionado à vida escolar como um todo, é descrito por Sidman (1989), destacando a desistência do aluno diante da impossibilidade de superar o controle coercitivo.

Nas escolas não há, ainda segundo Skinner (1968), um programa eficiente de modelagem de comportamento matemático. Ao contrário, o que se verifica é o aluno tentando realizar os exercícios como forma de esquivar-se à punição ou, em situações de testes, tentando "colar" dos colegas ou rapidamente entregando a prova a fim de fugir à estimulação aversiva.

Como resultado dessa descrição, ainda segundo Skinner,

Poucos alunos conseguem atingir o estágio no qual reforçamento automático segue-se como consequência natural do comportamento matemático. Ao contrário, os algarismos e símbolos da matemática tornaram-se estímulos emocionais típicos. Olhar de relance para uma coluna de algarismos, para não mencionar os símbolos algébricos e os sinais de integral, provavelmente origina não o comportamento matemático e sim uma reação de ansiedade, culpa ou medo. (1968, p. 18)

Além do controle aversivo em sala de aula, alguns estudos têm sugerido que regras inadequadas e autoatribuições negativas, durante o estudo da matemática, desempenham papel relevante na manutenção de respostas emocionais à matemática e no aumento significativo de erros em exercícios de matemática (Frankenstein, 1989; Hembree, 1990).

Ao conjunto de reações emocionais negativas que certos alunos apresentam durante a aprendizagem da matemática denominou-se ansiedade à matemática (Ashcraft, 2002; Dew, Galassi & Galassi, 1983; Dreger & Aiken, 1957; Geary, 1996; Hembree, 1990; Tobias, 1978).

Geary (1996) destaca que a ansiedade à matemática é "um estado de medo e apreensão que está associado a vários cometimentos em matemática, como testes, frequência a disciplinas, dever de casa, etc." (p. 274). Segundo esse autor, não há dados na literatura que indiquem qualquer relação diretamente proporcional entre ansiedade à matemática e ansiedade em outras situações. Hembree (1990) aponta que baixos níveis de desempenho em matemática estão diretamente relacionados a altos níveis de ansiedade à matemática, embora não haja qualquer comprometimento em outras áreas quando os indivíduos são submetidos a testes de inteligência.

Indivíduos com ansiedade à matemática apresentam, claramente, padrões de esquiva e fuga diante de situações que envolvem essa disciplina (Geary, 1996). Assim, por exemplo, é comum evitarem qualquer atividade que envolva o uso da matemática, inclusive escolha de profissões que exijam conhecimento e aplicação da matemática.

Além do baixo desempenho em matemática, já apontado por Hembree (1990), Geary informa que "indivíduos com altos níveis de ansiedade à matemática frequentemente resolveram problemas aritméticos, simples ou complexos, com mais rapidez e com maior número de erros quando comparados a indivíduos com níveis moderados de ansiedade" (1996, p. 275), o que tipicamente caracterizaria fuga à situação aversiva.

A identificação de ansiedade à matemática tem sido realizada por meio da aplicação de escalas tipo Likert (Brito, 1998; Hopko, Mahadevan, Bare & Hunt, 2003; Silva, Brito & Vendramini, 2002). Durante o preenchimento dessas escalas, tipicamente os respondentes declaram como se sentem diante de alguma situação relacionada à matemática e/ou se concordam acerca de uma determinada proposição relacionada à matemática em si ou ao seu desempenho em matemática. Em que pesem as limitações que declarações verbais impõem ao estudo de fenômenos comportamentais, o uso de instrumentos como escalas e inventários pode minimizar efeitos emocionais negativos e evitar expor os indivíduos a situações que poderiam gerar reações emocionais inadequadas. No caso da ansiedade à matemática, respostas verbais a itens de escalas e inventários têm se mostrado um recurso adequado de acesso indireto aos eventos privados e a contingências aversivas às quais o indivíduo esteve ou está exposto.

No Brasil ainda são raras as investigações, por meio de aplicação de escalas, acerca da ansiedade à matemática em estudantes. Além da escala traduzida, adaptada e validada por Brito (1998), alguns estudos têm sido conduzidos com a aplicação da Escala de Ansiedade à Matemática (EAM) proposta por Carmo (2008).

A Escala de Ansiedade à Matemática (Carmo, 2008) é composta por 24 itens, os quais ilustram situações tipicamente vivenciadas por estudantes de Ensino Fundamental e Médio. O aluno é convidado a responder a cada item, escolhendo uma das seguintes alternativas: nenhuma ansiedade; baixa ansiedade; ansiedade moderada; muita ansiedade; alta ansiedade; extrema ansiedade. Uma versão inicial da EAM foi aplicada por Araújo, Carmo, Costa, Figueiredo e Nogueira (2006) em estudantes do Ensino Fundamental (5ª a 8ª séries) das redes públicas e privadas de Belém e de Castanhal (Estado do Pará), num total de 477 alunos de ambos os sexos, sendo 158 de escola pública e 477 de escola privada. Os resultados indicaram que os graus predominantes de ansiedade à matemática recaíam em "ansiedade moderada" e "muita ansiedade", sendo esses graus ligeiramente mais frequentes na escola pública quando comparada à escola privada. Quando comparadas as séries, verificou-se que a 6ª série apresentava o maior índice de "muita ansiedade" independente da rede de ensino.

Outros estudos indicaram que a escala apresenta potencial para a identificação de graus diferenciados de ansiedade à matemática (Carmo et al., 2008; Carmo & Figueiredo, 2009). Como os dados disponíveis foram obtidos apenas na região Norte do país, buscou-se ampliar a amostra para estudantes de outras regiões. O presente estudo é parte integrante dessa busca de ampliação e focalizará, especificamente, a identificação de graus extremos de ansiedade à matemática. O objetivo, portanto, é identificar casos de extrema ansiedade à matemática, a partir de uma ampla amostra de estudantes que responderam à EAM, bem como discutir algumas implicações educacionais a partir dos resultados encontrados.

 

Método

Participantes

No presente estudo são analisadas as respostas de 11 alunos à EAM, cujos escores totais indicaram extrema ansiedade à matemática. Esses estudantes foram selecionados a partir de um amplo levantamento com aplicação da EAM a 1106 alunos, 770 do Ensino Fundamental Ciclo II (6º ao 9º ano) e 336 do Ensino Médio, em uma cidade do interior de São Paulo.

Todos os participantes foram previamente autorizados por seus responsáveis, por meio de assinatura do Termo de Consentimento Livre e Esclarecido (TCLE)¹ e pela direção de cada escola. Outras informações relevantes sobre os 11 participantes serão fornecidas na seção de resultados.

Local de aplicação da escala

A aplicação da escala ocorreu na própria escola dos participantes, durante o turno de aula e nas salas indicadas pelas coordenações.

Material

A Escala proposta por Carmo (2008), do tipo Likert, contém 24 situações do cotidiano escolar relacionadas à matemática, sejam em sala de aula ou fora dela. Os participantes foram convidados a escolher apenas uma opção dos cinco níveis de ansiedade para cada situação: nenhuma ansiedade;baixa ansiedade;ansiedade moderada; alta ansiedade; extrema ansiedade. Os escores da escala foram distribuídos da seguinte forma: 24 pontos indicavam nenhuma ansiedade; entre 25 e 48 pontos indicavam baixa ansiedade; escores entre 49 e 72 pontos representavam ansiedade moderada; entre 73 e 96 pontos representavam alta ansiedade; e extrema ansiedade entre 97 e 120 pontos.

Dentre as situações propostas na EAM, estão: "quando escrevo a palavra 'matemática'" (3)²; "Um dia antes da aula de matemática" (5); "Durante a aula de matemática, quando devo resolver sozinho um exercício" (8); "Quando o professor de matemática me dirige a palavra, fazendo perguntas sobre matemática" (12); "Ao fazer a tarefa de casa de matemática" (14); "Quando os colegas estão falando sobre matemática" (17); "minutos antes da prova de matemática" (20); "No dia da entrega das notas de matemática" (23)³. Os 24 itens são distribuídos aleatoriamente, de forma que não há relação entre posição da situação e maior ou menor grau de ansiedade.

Procedimentos

Ao iniciar a aplicação da escala, foram oferecidas as seguintes instruções:

A atividade faz parte de uma pesquisa acadêmica. Não possui objetivo avaliativo de desempenho, atribuição de notas às respostas ou respostas 'certas' ou 'erradas'. Não possui qualquer tipo de premiação. O preenchimento é individual. A identidade do participante e as escalas preenchidas serão mantidas em sigilo, e apenas os pesquisadores terão acesso ao material.

Os alunos responderam as questões nos mesmos períodos e nas salas de aula que frequentavam. Uma folha contendo a escala foi entregue a cada um deles para que assinalassem com a letra "X" a resposta condizente com o que sentiam diante de cada situação exposta. Para cada situação era aceita somente uma resposta.

Antes do preenchimento da escala, a seguinte questão era proposta a fim de que os participantes entendessem como deveriam se comportar diante das situações a serem lidas: "diante de uma determinada situação, como me sinto? Com nenhuma ansiedade; com baixa ansiedade; com ansiedade moderada; com alta ansiedade; com extrema ansiedade". Em seguida, um dos pesquisadores procedia à leitura das situações e níveis de ansiedade. Foi solicitada atenção dos alunos para a escolha de somente um item por questão. No momento da devolução, o participante era solicitado a aguardar alguns instantes enquanto o preenchimento da escala era conferido item a item, a fim de evitar possíveis lacunas. Caso fosse detectado algum erro no preenchimento (escolher mais de uma alternativa ou "pular" alguma situação), o participante era requisitado a proceder à correção.

 

Resultados e discussão

A Tabela 1 resume algumas informações cruciais sobre os 11 participantes. A identificação dos participantes seguirá a convenção An, sendo A a abreviação de "aluno" e n o número atribuído ao aluno seguindo um critério de valor da pontuação total obtida na escala, indo dos valores mais baixos aos mais altos. A média de pontos atingidos foi de 100,36 (com desvio padrão = 3,042), indicando que os participantes estão no nível de extrema ansiedade, conforme a escala de pontuação (intervalo de 97 a 120 pontos).

 

 

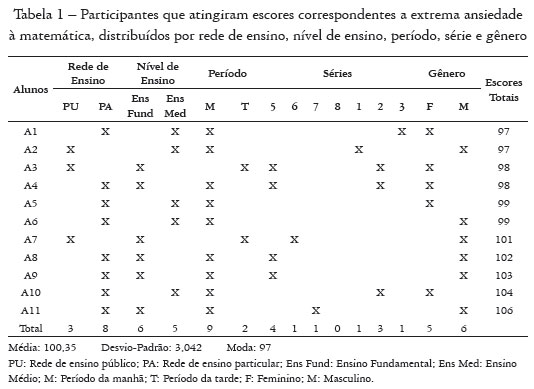
Em relação à rede de ensino, oito alunos são da rede privada (Participantes A1, A4, A5, A6, A8, A9, A10, A11) e três são da rede pública (A2, A3 e A7). Quanto ao nível de ensino, seis são do Ciclo II do Ensino Fundamental (A3, A4, A7, A8, A9, A11) e cinco são do Ensino Médio (A1, A2, A5, A6, A10). Em relação à série, quatro alunos são da 5ª série (A3, A4, A8, A9), um aluno é da 6ª série (A7), um é da 7ª série (A11) e no Ensino Médio um é do 1º ano (A2), três são do 2º ano (A3, A4, A10) e um do 3º ano (A1).

No que diz respeito ao período, nove alunos são do período da manhã (alunos A1, A2, A4, A5, A6, A8, A9, A10, A11) e apenas dois são do período da tarde (alunos A3, A7). Quanto ao gênero, cinco alunos são do gênero feminino (A3 e A4 do Ensino Fundamental do Ciclo II e A1, A5 e A10 do Ensino Médio) e seis alunos são do gênero masculino (A7, A8, A9 e A11 do Ciclo II do Ensino Fundamental e alunos A2 e A6 do Ensino Médio).

O escore mais alto na pontuação - 106 pontos - foi alcançado por A11 do gênero masculino. O aluno cursava a 7ª série do Ciclo II do Ensino Fundamental no período da manhã, em uma escola da rede privada de ensino.

Em relação às situações, os resultados apontaram que os estudantes relataram alta ansiedade e extrema ansiedade diante de situações variadas e não apenas diante de situações que poderiam tipicamente sinalizar punição. Nas situações que potencialmente sinalizariam punição, estão incluídas todas as situações da EAM que indicam uma possível consequência punitiva (nota baixa, repreensão dada pelo professor, reprovação na disciplina, produção de erro). Já nas situações que não sinalizariam uma punição, encontram-se as situações da escala que remetem a ações cotidianas e esperadas em uma aula de matemática: ouvir, ler ou escrever a palavra "matemática", folhear o caderno ou o livro de matemática.

Em relação às situações que potencialmente sinalizariam punição, em "durante a aula de matemática, quando devo mostrar os exercícios ao professor" (10), três alunos apontaram alta ansiedade (A4, A9 e A10) e sete apontaram extrema ansiedade (A1, A2, A3, A5, A6, A7 e A11). Dois alunos relataram sentir alta ansiedade (A2 e A9) e oito alunos relataram sentir extrema ansiedade (A1, A3, A4, A6, A7, A8, A10 e A11) em "durante a prova de matemática" (21). Seis alunos apontaram alta ansiedade (A4, A5, A7, A9, A10 e A11) e dois apontaram extrema ansiedade (A1 e A6) em "um dia antes de entregar uma tarefa de matemática que não consegui resolver" (15). Dois alunos apontaram alta ansiedade (A5 e A7) e nove alunos apontaram extrema ansiedade (A1, A2, A3, A4, A6, A8, A9, A10 e A11) em "no dia do resultado final, ao término do ano" (24).

Nas situações que potencialmente não sinalizariam punição, os alunos também apontaram alta e extrema ansiedade. Na situação "quando vejo escrita a palavra matemática" (1), quatro alunos apontaram alta ansiedade (A2, A7, A8 e A10) e quatro apontaram extrema ansiedade (A3, A5, A6 e A9). Em "quando ouço a palavra matemática" (2), quatro alunos apontaram alta ansiedade (A6, A8, A9 e A10) e três alunos apontaram extrema ansiedade (A2, A6 e A7). Na situação "ao folhear o livro ou o caderno de matemática" (11), três alunos apontaram alta ansiedade (A7, A10 e A11) e cinco alunos apontaram extrema ansiedade (A1, A5, A6, A8 e A9).

Embora seja arbitrária a divisão entre situações que potencialmente sinalizariam ou não sinalizariam punição, a partir das respostas à escala, pode-se inferir uma extensa história de punição dos participantes. Quando os alunos indicam sentir alta ou extrema ansiedade em situações relacionadas a ouvir a palavra "matemática" ou folhear o livro de matemática, os indícios são fortes na direção de que alguns estímulos, antes neutros, podem ter adquirido a função de pré-aversivos (Estes & Skinner, 1941), o que indica que alguns componentes envolvidos na ansiedade à matemática também estão relacionados a uma história bem estabelecida por condicionamento respondente.

Pode-se também inferir que alguns estímulos do ambiente (como o livro de matemática, o professor de matemática ou a própria palavra "matemática") podem funcionar como discriminativos para tatos extrapolados e autoclíticos (Matos, 1991). Segundo Matos, "tatos são particularmente importantes porque representam uma importante via de acesso a estados internos do emitente" (p. 337). Como no tato "os discriminativos controlados podem ser objetos, pessoas, acontecimentos, sensações, lembranças, isto é, mudanças no campo sensorial (visual, auditivo, tátil, proprioceptivo, interoceptivo, etc.) do emitente" (p. 336), com mais forte razão pode-se sugerir que contingências punitivas, presentes em vigor no passado ou presentes no ambiente atual de aprendizagem escolar, são freqüentemente verbalizadas em forma de regras acerca da matemática ou autorregras acerca do próprio desempenho (Franskenstein, 1989). Nesse último caso, pode-se sugerir que autoclíticos estão presentes e podem controlar as verbalizações internas do estudante, uma vez que, de acordo com Matos (1991), os autoclíticos mostram que o falante é ouvinte de si mesmo.

Uma informação importante a ser considerada é que, embora no presente estudo tenhamos alunos de diferentes escolas com grau extremo de ansiedade à matemática, em alguns casos o professor de matemática era o mesmo em mais de uma escola. Dentre os alunos desse professor, nove obtiveram escores de extrema ansiedade. Evidentemente essa informação não permite reduzir a questão a uma "culpa" do professor, pois diferentes fatores podem ter concorrido para a pontuação obtida pelos alunos. Esse fato, no entanto, pode sugerir que a metodologia utilizada nas aulas de matemática pelo professor, a relação professor-aluno, dentre outros fatores, são variáveis críticas na explicação dos resultados obtidos. Conforme visto anteriormente, as dificuldades de aprendizagem podem ser chamadas também de dificuldades de ensino da matemática (Ball et al. 2001; Carmo, 2003; Cunha, 2000; Oliveira & Cyrino, 2011; Skinner, 1968).

 

Considerações finais

Os objetivos do presente estudo foram (a) identificar casos de extrema ansiedade à matemática em estudantes do Ensino Fundamental, a partir das pontuações obtidas em uma escala de ansiedade à matemática, e (b) apontar algumas implicações educacionais a partir dos resultados obtidos.

Em relação ao primeiro objetivo, a escala mostrou-se eficiente na identificação de casos de extrema ansiedade à matemática e permite a inferência, com base nas respostas dos participantes, de uma história de exposição a contingências aversivas em sala de aula, particularmente no contato com a matemática.

Quanto ao segundo objetivo, os dados do presente estudo e os da literatura consultada sugerem reflexões importantes relacionadas à aquisição de respostas emocionais negativas ante a matemática, bem como padrões de interação professor-aluno e cuidados metodológicos que podem ser adotados em sala de aula de modo a reduzir ou prevenir os efeitos de práticas de ensino inadequadas.

Como exemplo ilustrativo, temos a seguinte situação. Depois de submetido ao controle aversivo em aulas de matemática, e não tendo obtido sucesso em seu aprendizado, um estudante ouve de seu colega a seguinte frase "amanhã haverá prova de matemática". A simples audição da frase passa a gerar no aluno uma série de reações emocionais negativas que podem se traduzir em esquiva a qualquer tentativa de estudo antes da prova. O estudante simplesmente evita qualquer contato com livros e anotações da matéria ou, quando diante do material de estudo, engaja-se em comportamentos incompatíveis como ouvir música, jogar vídeo game ou, simplesmente, tamborilar até que as horas passem. No dia seguinte, é possível que o aluno acorde com indisposição geral ou alguma reação orgânica desagradável. Ele vai para a escola e, no caminho, conta aos amigos que não está em condições de submeter-se à prova em função de seu estado orgânico geral. Entretanto, a prova é inevitável, ou pior, a iminência de um péssimo desempenho na prova (inclusive numa prova de segunda chamada) é esperada pelo próprio estudante. Em outra situação, a simples presença do professor de matemática ou de outros estímulos visuais ou auditivos associados à matemática (números; equações; enunciados de problemas; etc.), ou mesmo a proximidade da hora da aula, podem "paralisar" o estudante ou levá-lo a esquivar-se ou fugir dessas situações. Esse exemplo, embora fictício, não é de todo improvável no dia a dia de um estudante que apresenta ansiedade à matemática.

Como ressalta Hübner (1998), planejar o conteúdo a ser aplicado em sala de aula vai além do próprio ato de planejar apenas. Essa afirmação corrobora as de Skinner (1968), pois planejar é, a rigor, programar condições favorecedoras de aprendizagem (Kubo & Botomé, 2001). Hübner afirma que não há aluno-problema ou professor-problema e, sim, uma relação entre os dois que necessita ser revista e reestruturada quanto às contingências propostas. Para muitos estudantes, aprender ou ter êxito na escola é representado apenas pelas notas altas que têm o papel de recompensas, como afirma Sidman (1989). Isso ocorre principalmente porque significam esquivas de notas baixas.

Os dados do presente estudo sugerem que, em relação ao ensino da matemática, a escola ainda é um local no qual o aluno se sente ameaçado e recebe punições frequentes. Viecelli e Medeiros (2002) apontam que as instituições escolares, ao longo das reformas educacionais, ainda utilizam do controle aversivo cada vez mais sutil, mas não menos danoso. Notas baixas, agressões verbais, pontos negativos na média refletem tais punições e isso corrobora com as situações que mais causaram ansiedade nos alunos que responderam à escala.

Por fim, as situações que mais geraram graus extremos de ansiedade podem servir como indicativos fortes de que metodologias de ensino devem prever quais momentos são cruciais na vida escolar do aluno. Nesse sentido, alguns estudos apontam para a possibilidade de reversão de quadros de ansiedade à matemática a partir de rearranjos do ambiente escolar. Essas investigações indicam um ganho na aprendizagem e na redução de estresse em estudantes da escola elementar (Iossi, 2007; Perry, 2004; Rossnan, 2006; Toumasis, 2004; Wei, 2010), da escola secundária (Hellum-Alexander, 2010) e universitários/adultos (Iossi, 2007; Latiolais & Laurence, 2009). Os rearranjos no ambiente de estudo envolveram, principalmente, presença de monitores, trabalhos em pequenos grupos, acompanhamento individualizado, roda de conversa sobre matemática, procedimentos de ensino individualizado e ensino a distância via computador. Ainda são escassos estudos brasileiros que implementem mudanças no ambiente escolar visando auxiliar indivíduos com ansiedade à matemática, mas os indicativos do presente estudo parecem favorecer a noção de que há necessidade de tais implementações.

 

Referências

Araújo, P. V. S.; Carmo, J. S.; Costa, E. C. P; Figueiredo, R. M. E. & Nogueira, M. F. (2006). Descrição de graus de ansiedade à matemática em estudantes do ensino fundamental II. Anais do II Congresso Amazônico sobre Violência nas Escolas, [CD-Rom], 1-4.         [ Links ]

Ashcraft, M. H. (2002). Math anxiety: personal, educational, and cognitive consequences. Current Directions in Psychological Science, 11(5),181-185.         [ Links ]

Ball, D. L., Lubienski, S., & Mewborn, D. (2001). Research on teaching mathematics: The unsolved problem of teachers' mathematical knowledge. In V. Richardson (Ed.), Handbook of research on teaching (pp. 433-456). Nova York: MacMillan.         [ Links ]

Brito, M. R. F (1998). Adaptação e validação de uma escala de atitudes em relação à matemática. Zetetike, 6(9),45-63.         [ Links ]

Carmo, J. S. (2008). Escala de ansiedade à matemática. Texto não publicado. São Carlos.         [ Links ]

______. (2003). Dificuldades de aprendizagem ou dificuldades de ensino? Algumas contribuições da análise do comportamento. In M. Z. S. Brandão et al. (Orgs.), Sobre comportamento e cognição: a história e os avanços, a seleção por contingências em ação (11, pp. 396-401). Santo André, SP: ESETec.         [ Links ]

Carmo, J. S., Figueiredo, R. M. E., Nogueira, M. F., Cunha, L. O., Araujo, P. V. S. & Ferranti, M. C. (2008). Diferentes intensidades de ansiedade relatadas por estudantes do ensino fundamental II, em situações típicas de estudo da matemática. In C. M. Wander e W. C. M. P. Silva (Orgs.), Sobre comportamento e cognição: Reflexões epistemológicas e conceituais, considerações metodológicas, relatos de pesquisa (v. 22, pp. 213-221). Santo André, SP: ESETec.         [ Links ]

Carmo, J. S. & Figueiredo, R. M. E. (2009). Ansiedade à matemática em alunos do ensino fundamental: achados recentes e implicações educacionais. In R. C. Wielenska (Org.), Sobre comportamento e cognição: desafios, soluções e questionamentos (pp. 488-495). Santo André: ESETec.         [ Links ]

Cunha, M. H. (2000). Saberes profissionais de professores de matemática: Dilemas e dificuldades na realização de tarefas de investigação. Millenium, 17,1-58.         [ Links ]

Dew, K. M. H.; Galassi, J. P. & Galassi, M. D. (1983). Mathematics anxiety: some basic issues. Journal of Counseling Psychology, 30(3),443-446.         [ Links ]

Dreger, R. M.; Aiken, L. R. (1957). The identification of number anxiety in a college population. Journal of Educational Psychology, 48,344-351.         [ Links ]

Estes, W. K. & Skinner, B. F. (1941). Some quantitative properties of anxiety. Journal of Experimental Psychology, 29,390-400.         [ Links ]

Frankenstein, M. (1989). Relearning mathematics: a different third r-radical math(s) (Vol. 1). Londres: Free Association Books.         [ Links ]

Geary, D. C. (1996). Children's mathematical development: research and practical applications. Washington: American Psychological Association.         [ Links ]

Hembree, R. (1990). The nature, effect, and relief of mathematics anxiety. Journal for Research in Mathematics Education, 21,33-46.         [ Links ]

Helleum-Alexander, A. (2010). Effective teaching strategies for alleviating math anxiety and increasing self-efficacy in secondary students. Master in Teaching Thesis, The Evergreen State College.         [ Links ]

Hopko, D. R.; Mahadevan, R.; Bare, R. L.; Hunt, M. K. (2003). The abbreviated math anxiety scale (AMAS): construction, validity, and reliability. University of Tennessee at Knoxville: Medline.         [ Links ]

Hübner, M. M. C. (1998). Analisando a relação professor-aluno: Do planejamento à sala de aula. São Paulo: CLR-Balieiros.         [ Links ]

Iossi, L. (2007). Strategies for reducing math anxiety in post-secondary students. In S. M. Nielsen & M. S. Plakhotnik (Eds.), Proceedings of the Sixth Annual College of Education Research Conference: Urban and International Education Section (pp. 30-35). Miami: Florida International University.         [ Links ]

Kubo, O. & Botomé, S. P. (2001). Ensino-aprendizagem: Uma interação entre dois processos comportamentais. Interação em Psicologia, 5,133-171.         [ Links ]

Latiolais, M. P. & Laurence, W. (2009). Engaging math-avoindant college students. Numeracy, 2(1),1-10.         [ Links ]

Matos, M. A. (1991). As categorias formais de comportamento verbal em Skinner. Anais da XXI Reunião Anual da Sociedade de Psicologia de Ribeirão Preto (pp. 333-341). Ribeirão Preto, SP: SPRP.         [ Links ]

Oliveira, H. M., & Cyrino, M. C. C. T. (2011). A formação inicial de professores de matemática em Portugal e no Brasil: Narrativas de vulnerabilidade e agência. Interacções, 18,104-130.         [ Links ]

Perry, A. B. (2004). Decreasing math anxiety in college students. College Student Journal, 38(2),321-324.         [ Links ]

Rossnan, S. (2006). Overcoming math anxiety. Mathitudes, 1(1),01-04.         [ Links ]

Silva, C. B., Brito, M. R. F., & Vendramini, C. M. M. (2002). Atitudes em relação à estatística e à matemática. Psico-USF, 7(2),89-100.         [ Links ]

Skinner, B. F. (1968). The technology of teaching. Nova York: Appleton Century Crofts.         [ Links ]

Sidman, M. (1989). Coertion and its fallout. Boston: Authors Cooperative.         [ Links ]

Tobias, S. (1978). Overcoming math anxiety. Nova York: Norton.         [ Links ]

Toumasis, C. (2004). Cooperative study teams in mathematics classrooms. International Journal of Mathematical Education in Science and Technology, 35(5),669-679.         [ Links ]

Viecelli, J. & Medeiros, J. G. (2002). A coerção e suas implicações na relação professor-aluno. Psico-USF, 7(2),229-238.         [ Links ]

Wei, Q. (2010). The effects of pedagogical agents on mathematics anxiety and mathematics learning. Doctor o f Philosophy in Instructional Technology and Learning Sciences Thesis. Utah State University.         [ Links ]

 

 

1 Projeto de pesquisa aprovado pelo Comitê de Ética em Pesquisa em Seres Humanos da Universidade Federal de São Carlos / SP - Parecer Nº 349/2009.
2 Os números entre parênteses indicam em que posição a situação aparecia na escala.
3 A escala completa poderá ser fornecida aos interessados, com instruções de aplicação, a partir do contato com um dos autores.