Este trabalho trata de um problema de demarcação. Ele contém uma tese sobre o objeto primário da lógica, e sobre as relações da lógica com outras disciplinas, especialmente a epistemologia. Essa tese postula que conjuntos desestruturados de proposições são o objeto primário da Lógica, e não os argumentos, porque a consistência lógica é uma noção puramente lógica, enquanto a validade lógica é uma noção lógica epistemicamente matizada.

Essa tese não afeta as características usualmente atribuídas à lógica, a saber, formalidade, universalidade e neutralidade tópica (MacFarlane, 2002). Ela também deixa inalterada a questão sobre a relação da lógica com a filosofia: se a lógica é um mero instrumento da filosofia ou se ela, além de ser um instrumento da filosofia, também é uma parte desta. Finalmente, ela é compatível com uma concepção da filosofia como atividade racional sem, contudo, vincular a atividade filosófica a uma atividade primariamente pautada por argumentos.

No confronto entre a lógica formal clássica e as lógicas formais não-clássicas, e entre a lógica formal e a lógica informal (pensamento crítico), sustentei, em trabalhos anteriores (Sautter, 2004; 2009), que a lógica formal clássica é o único sistema puramente lógico e que todos os demais sistemas não-clássicos e a lógica informal são amálgamas de elementos lógicos com elementos extralógicos. A tese sustentada neste trabalho é uma radicalização dessa tese inicial: nem mesmo a lógica formal clássica, se entendida como um sistema inferencial, é um sistema puramente lógico.

A seção inicial fornece a motivação para a tese. Na segunda seção esclareço o que se entende por Teoria Pura da Lógica. Na terceira seção investigo as origens da concepção tradicional, rival da concepção aqui sustentada, nas obras de Aristóteles e de Frege. Na quarta seção sugiro, por intermédio do exame de jogos intelectuais conhecidos como obligationes, que a atividade filosófica pode-se dar mesmo sem a presença de argumentos. Na quinta seção avalio o principal argumento contrário à tese aqui sustentada: o argumento da interdefinibilidade. Na penúltima seção apresento o núcleo da Teoria Geral da Consistência e Inconsistência Lógicas, e na última seção apenas esboço uma extensão da tese aqui sustentada, sob a forma de uma rejeição da semântica de valores de verdade.

1. Motivação

Consideremos, a título de motivação, a seguinte forma argumentativa expressa em linguagem semiformal:

As instâncias desta forma argumentativa são válidas, ou seja, sob uma perspectiva estritamente lógica, elas são bons argumentos. Mas isso é contraintuitivo, pois as premissas ocupam-se de α, Β e ;ү, enquanto a conclusão ocupa-se de δ, que não ocorre nas premissas. Uma justificação para a validade desses argumentos é a seguinte: a conclusão parcial Se α, então ү segue-se, por silogismo hipotético, das duas primeiras premissas Se α, então β e Se β, então ү, e esta conclusão parcial é a negação da terceira premissa α e não-ү; portanto, as premissas constituem um conjunto inconsistente de proposições, ou seja, elas não podem ser simultaneamente verdadeiras; e, se elas não podem ser simultaneamente verdadeiras, o teste de validade não pode falhar, qualquer que seja a conclusão. Esse tipo de argumento é denominado argumento vacuamente válido.

A solução para esse contraste entre o intuitivo e o lógico consiste em ajustar o lógico ao intuitivo, suprimindo totalmente as consequências lógicas dos conjuntos inconsistentes de premissas. Berkeley, em O analista (1734), Kant, em Ensaio para introduzir a noção de grandezas negativas em filosofia (1763), e Strawson, em Introdução à teoria lógica (1952), são precursores dessa proposta de supressão total (Sautter, 2008).

Consideremos uma segunda forma argumentativa, também expressa em linguagem semiformal:

Não-α e não-β.

∴ Não é o caso que α ou β.

As instâncias desta forma argumentativa também são válidas, e os argumentos são, sob uma perspectiva estritamente lógica, bons argumentos. Mas isso, novamente, é contraintuitivo, pois a conclusão é, por assim dizer, uma mera variante estilística da única premissa; essas instâncias são petições de princípio.

Aqui, a solução fornecida à primeira forma argumentativa – a supressão total das consequências lógicas – não pode ser aplicada, pois é perfeitamente aceitável que, por exemplo, tanto Não-α como Não-β sejam consequências lógicas de Não-α e não-β.

Minha solução unificada às duas formas argumentativas acima apresentadas, e a muitas outras em relação às quais há um contraste entre o intuitivo e o lógico, consistirá numa reelaboração da teoria lógica: sustento que conjuntos desestruturados de proposições são o objeto primário da lógica, e não os argumentos; a lógica não visa primariamente a estabelecer a distinção entre argumentos válidos e argumentos inválidos, mas a distinção entre conjuntos consistentes de proposições e conjuntos inconsistentes de proposições.

2. A Teoria Pura do Direito e a Teoria Pura da Lógica

A tese enunciada ao término da seção anterior pode dar margem a interpretações equivocadas. Ela exige os seguintes esclarecimentos:

Não sustento que os argumentos não sejam objeto da lógica. O que sustento é que eles não são o objeto primário da lógica. As noções de argumento e, em particular, de argumento válido são noções lógicas, mas também são noções epistemicamente matizadas, porque as proposições de um argumento não são examinadas enquanto tais, mas na medida em que desempenham determinados papéis, os papéis de premissa e de conclusão.

A avaliação lógica do discurso pode dispensar a ocorrência de argumentos. A determinação da consistência do conjunto de proposições que compõem o discurso pode ser o único procedimento lógico possível em relação a determinados tipos de discurso, por exemplo, as coleções de aforismos que encontramos tanto na tradição continental, veja-se o caso de Nietzsche, como na tradição analítica, veja-se o caso de Wittgenstein. Nesse sentido, a avaliação lógica não seria muito diferente da avaliação empreendida em estudos literários, que investigam, entre outras características do discurso, sua coerência e coesão textuais. Há um livro recente de Baggini e Stangroom (2010) em que tal perspectiva é tomada a sério. Eles propõem diversos testes filosóficos cujo objetivo é identificar contradições ou tensões nas convicções dos leitores, de tal modo que a atividade propriamente filosófica consiste em desatar o nó das convicções contraditórias e das tensões entre as convicções (Baggini & Stangroom, 2010, pp. 17-18).

Uma comparação com a proposta de Hans Kelsen em sua obra maior – a Teoria pura do direito (Kelsen, 2000) – pode ajudar nesses esclarecimentos. Kelsen diagnostica um problema no terreno jurídico e propõe sua solução nos seguintes termos:

De um modo inteiramente acrítico, a jurisprudência tem-se confundido com a psicologia e a sociologia, com a ética e a teoria política. Essa confusão pode porventura explicar-se pelo fato de estas ciências se referirem a objetos que indubitavelmente têm uma estreita conexão com o Direito. Quando a Teoria Pura empreende delimitar o conhecimento do Direito em face destas disciplinas, fá-lo não por ignorar ou, muito menos, por negar essa conexão, mas porque intenta evitar um sincretismo metodológico que obscurece a essência da ciência jurídica e dilui os limites que lhe são impostos pela natureza do seu objeto (Kelsen, 2000, pp. 1-2).

Como é bem sabido, esse sincretismo metodológico traduz-se em avaliação das normas jurídicas distinta daquela que, segundo Kelsen, é própria da jurisprudência, a saber, a distinção entre normas jurídicas válidas e normas jurídicas inválidas, distinção que remete à própria existência das normas jurídicas. Esse sincretismo metodológico propõe, no lugar dessa distinção, a distinção entre normas jurídicas corretas e normas jurídicas incorretas, ou, mesmo, entre normas jurídicas eficazes e normas jurídicas ineficazes.

No caso da lógica, há uma forma mais branda de sincretismo e, exatamente por ser mais branda, mais difícil de detectar. Em relação à jurisprudência, a confusão se dá com a psicologia, a sociologia, a ética e a teoria política; em relação à lógica, tal confusão se faz com a psicologia, com a sociologia, com a epistemologia, e com a ontologia. Que uma parcela dessa confusão seja bem conhecida, o atesta o embate empreendido contra o psicologismo na segunda metade do século XIX e início do século XX.

No restante deste trabalho dirigirei meus esforços para as confusões da lógica com a epistemologia, naquilo que pode ser qualificado, por analogia com o psicologismo na lógica, de epistemicismo na lógica². Na última seção apenas apontarei o caminho para uma discussão similar a respeito da relação da lógica com a ontologia, no que pode ser denominado o problema do onticismo na lógica³

Antes de prosseguir, contudo, é preciso acrescentar que o título do trabalho não é apenas uma alusão à obra maior de Kelsen, mas também pode ser associado a Burley e a Avicena, que empregaram a expressão "pureza da arte da lógica" para intitular obras dedicadas à exposição do núcleo da lógica, sem um exame meticuloso de posições rivais (Spade & Menn, 2003).

3. Os epistemicismos de Aristóteles e de Frege

Aristóteles e Frege são, indubitavelmente, os personagens principais da história da lógica. Aristóteles reconhece a si mesmo como fundador de seu estudo sistemático, e Frege deve ser reconhecido como seu refundador. Sustentarei que ambos inserem elementos epistêmicos na apresentação da lógica, sem fazerem a devida distinção entre esta e a epistemologia. Portanto, não é inteiramente estranha a permanência até nossos dias de tais elementos, como se fizessem parte do próprio núcleo da lógica. Eles sempre estiveram presentes. Adaptando uma frase utilizada por Quine para referir-se à lógica modal, podemos dizer que a própria lógica foi concebida em pecado.

Consideremos, inicialmente, a caracterização aristotélica de dedução (Aristóteles, 1989, pp. 2, 106)⁴. Segundo Aristóteles (1989, p. 2), "uma dedução é um discurso no qual, certas coisas tendo sido supostas, algo diferente das coisas supostas resulta por necessidade porque essas coisas são assim". Sabe-se que a formulação de uma teoria geral da dedução serve, em Aristóteles, como apoio a uma teoria da ciência demonstrativa desenvolvida nos Analíticos posteriores: Aristóteles (1989, p. 1) o diz no parágrafo inicial dos Analíticos anteriores. A mera subordinação da lógica aos interesses da epistemologia, contudo, não é, por si mesma, um indício de epistemicismo. A marca da interferência indevida da epistemologia na lógica constata-se na própria caracterização de dedução; uma dedução difere de um argumento em sentido contemporâneo na medida em que: a) Uma petição de princípio não é, por definição, uma dedução; isso se depreende da exigência de que algo diferente resulte.

b) Tendo em conta que toda dedução, segundo Aristóteles, pode ser transformada em um encadeamento de silogismos em sentido estrito, o uso de premissas inúteis, premissas que não contribuem para a dedução da conclusão, é vedado na proposta aristotélica. Isto se segue do modo pelo qual a dedução em um silogismo é conduzida, por mediação de um terceiro termo.

c) O próprio modo exclusivo segundo o qual uma derivação é conduzida em um silogismo em sentido estrito – por mediação de um terceiro termo – e o status privilegiado que esse modo assume na teoria aristotélica da dedução são marcas de um epistemicismo.

Há, além disso, na identificação dos silogismos válidos, uma tensão entre a adoção de um procedimento de perfectibilização, cujo fundamento é claramente epistêmico, e um mero procedimento de redução. No primeiro caso, o procedimento de perfectibilização, há a identificação de silogismos perfeitos, ou seja, silogismos cuja validade é evidente por si mesma, quais sejam, os silogismos da primeira figura, e a validade dos demais silogismos, dos silogismos imperfeitos, é reconhecida por meio da transformação destes nos silogismos perfeitos por intermédio de inferências imediatas e por adoção de redução ao impossível. No segundo caso, o procedimento de redução, a validade de um silogismo é reconhecida por meio da transformação dele em outro silogismo válido, independentemente da autoevidência deste último. Aristóteles não distingue adequadamente esses dois procedimentos entre si.

Quanto a Frege, é preciso novamente destacar que o fato de a lógica servir, em sua obra, a um propósito epistêmico, a saber, à prova de que a Teoria dos Números está assentada sobre os fundamentos mais seguros, os fundamentos lógicos, não é, por si só, indício de epistemicismo. Há, contudo, indicações, tanto em seus primeiros escritos, como em seus escritos finais, da presença de tal tendência.

No fragmento "Lógica", escrito entre 1879 e 1891, portanto, situado entre os escritos iniciais de Frege, ele distingue entre formas de justificação da verdade de juízos: a justificação lógica, que apela a outros juízos verdadeiros previamente reconhecidos como tais, e a justificação epistêmica, que é constituída por todas as outras formas de justificação da verdade de juízos. Diz Frege (1979, p. 3):

Os fundamentos que justificam o reconhecimento de uma verdade frequentemente residem em outras verdades que já tenham sido reconhecidas. Mas, se há quaisquer verdades reconhecidas por nós enquanto tais, essa não pode ser a única forma de justificação. Deve haver juízos cuja justificação assenta-se sobre algo distinto, se eles necessitam de justificação. E, aqui, é onde entra a Epistemologia. A Lógica diz respeito somente aos fundamentos dos juízos que são verdades. Fazer um juízo porque estamos cientes de outras verdades que fornecem a justificação para ele é conhecido como inferir. Há leis governando tal tipo de justificação, e determinar tais leis da inferência válida é a meta da Lógica.

Portanto, a lógica e a epistemologia são espécies de um mesmo gênero, qual seja, o das ciências da justificação da verdade de juízos.

Dada essa caracterização de inferência, não é surpreendente que num de seus escritos finais – "Negação" –, pertencente às suas Investigações lógicas, Frege (1984, p. 375) rejeite quaisquer inferências com base em juízos falsos: "Não podemos inferir nada de um pensamento falso; mas o pensamento falso pode ser parte de um pensamento verdadeiro, do qual algo pode ser inferido". Dito de modo simples: dada essa aproximação entre lógica e epistemologia, a distinção entre argumento válido e argumento correto, esse último um argumento válido cujas premissas são verdadeiras, é dispensável e, mesmo, ininteligível na doutrina lógica de Frege. Outro sinal dessa cegueira de Frege é a polêmica dele com Hilbert sobre os fundamentos da geometria, na qual ele se põe frontalmente contra uma utilização modernizada do método axiomático, na qual a existência, e, com ela, a verdade, é relegada a um segundo plano, em prol da consistência.

4. As obligationes medievais

Logic: an introduction to elementar logic, de Wilfrid Hodges (2001, p. 1), é um raro manual de lógica em que a disciplina é apresentada sob a perspectiva da consistência lógica. A obra inicia com a seguinte caracterização, pouco usual, da lógica: "A lógica pode ser definida como o estudo de conjuntos consistentes de crenças" (Hodges, 2001, p. 1). Na sequência, Hodges (2001, p. 1) esclarece que "a lógica é sobre consistência – mas não sobre todos os tipos de consistência" e apresenta três outros tipos de consistência corriqueiros: consistência na política, consistência no direito e consistência na moral. O começo parece promissor, mas em seguida ele afirma que outros "preferem definir a lógica como o estudo de argumentos válidos" e que entre esses e ele "não há desacordo real", somente que "a consistência torna o início mais fácil" (Hodges, 2001, p. 1). A justificação para a tese de que não há real desacordo é, como mostrarei na próxima seção, a interdefinibilidade da validade e da consistência lógicas. A escolha de Hodges é, portanto, pautada por uma motivação prática, e não por uma motivação teórica. Uma segunda motivação de Hodges para a escolha da consistência diz respeito ao método de prova empregado em seu manual de lógica. Ele utiliza o método de tablôs, que é um método de prova por refutação sistemática de todo contraexemplo ao argumento. A noção de contraexemplo é facilmente caracterizável com base na noção de consistência lógica: um contraexemplo é uma circunstância que prova a consistência do conjunto formado pelas premissas e pela negação da conclusão. Não há, aqui, apesar do começo promissor, nenhuma tese substantiva sobre a precedência na lógica da noção de consistência lógica sobre a noção de validade lógica.

Talvez o mesmo não possa ser dito de um jogo intelectual popular no período medieval. Trata-se das obligationes. As principais versões desse jogo, segundo Dutilh Novaes (2007, p. 145), ocorrem nos tratados de Walter Burley e Roger Swyneshed. Dutilh Novaes apresenta e discute diversas interpretações sobre o propósito do jogo, tais como um campo para a exploração de condicionais contrafactuais, segundo P. V. Spade (citado em Dutilh Novaes, 2007, p. 147), ou como uma estrutura teórica para a análise de insolubilia e sophismata, segundo E. Stump (citado em Dutilh Novaes, 2007, p. 148), ou como uma teoria de revisão de crenças, segundo Lagerlund e Olson (citado em Dutilh Novaes, 2007, p. 148), ou como experimentos de pensamento, segundo Yrjönsuuri (citado em Dutilh Novaes, 2007, p. 149). A interpretação defendida por Dutilh Novaes (2007, p. 154) é que obligationes são jogos lógicos de manutenção da consistência, uma interpretação que combina muito bem com a tese defendida neste trabalho, e que situa as obligationes no próprio coração da lógica, o que é reforçado pelo fato de que os principais lógicos da época dedicaram tratados a elas.

Dutilh Novaes (2007, p. 155) define a seguinte estrutura conjuntista para um jogo obrigacional, na versão de Walter Burley:

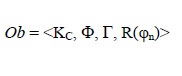
KC é conhecimento comum dos participantes da disputa, acrescido do casus, ou seja, acrescido de uma proposição cuja verdade implica a falsidade do positum; Φ é uma sequência cronológica de proposições do oponente na disputa, começando com o positum; Γ é uma sequência cronológica de proposições do proponente, fornecidas como resposta ao oponente; e R(φn) são regras procedimentais e regras lógicas das jogadas lícitas no jogo, e as regras procedimentais dizem respeito à aceitação de uma proposição, ou sua rejeição, ou dúvida a seu respeito, enquanto as regras lógicas dizem respeito precisamente à manutenção da consistência.

Essa interpretação das obligationes tem o mérito de mostrar como uma abordagem via consistência lógica pode ser factível e, até mesmo, meritória do ponto de vista prático, por desenvolver os aspectos dinâmicos do discurso, o que é completamente ignorado nos tratados atuais de lógica. Obviamente, contudo, ela não decide a questão teórica.

5. O argumento da interdefinibilidade

Provavelmente o argumento mais cogente contra minha tese seja o argumento da interdefinibilidade entre a validade lógica e a consistência lógica. Essas duas noções estão inter-relacionadas do seguinte modo: um argumento é válido se e somente se o conjunto composto pelas premissas do argumento e pela negação de sua conclusão é inconsistente, isto é, um argumento é inválido se e somente se o conjunto composto pelas premissas do argumento e pela negação de sua conclusão é consistente.

Essa interdefinibilidade sugere que nem a validade lógica de um argumento nem a consistência lógica de um conjunto de proposições são pontos de partida absolutos, mas, quando muito, pontos de partida relativos. Qualquer um deles poderia ser adotado como primitivo para fins de exposição da doutrina lógica.

Se tudo o que está em jogo é a apresentação, a mais completa possível, da doutrina lógica, não tenho objeções: a escolha de uma ou outra como noção primitiva é arbitrária do ponto de vista teórico, sendo pautada por fatores extrateóricos e de conveniência do expositor. Se o que está em jogo, entretanto, é a fundamentação da lógica, outros fatores podem fazer diferença e fazem.

No teste da consistência lógica de um conjunto de proposições, todas as proposições encontram-se no mesmo plano; elas são indiferenciadas qua proposições em relação ao teste. Já no teste da validade lógica de um argumento nem todas as proposições encontram-se no mesmo plano; elas são diferenciadas qua proposições em relação ao teste; distintas proposições podem desempenhar distintos papéis.

Esses papéis introduzem um componente epistêmico. Consistência lógica e validade lógica são ambas noções lógicas, mas a consistência lógica é uma noção lógica pura, enquanto a validade lógica é uma noção lógica epistemicamente matizada. Há muitas outras noções lógicas epistemicamente matizadas, todas relacionadas à diferenciação de papéis desempenhados pelas proposições envolvidas; por exemplo, que uma proposição seja mais forte (ou mais fraca) do que outra é uma noção epistemicamente matizada.

6. A Teoria Geral da Consistência e da Inconsistência Lógicas

Compreendida com base na perspectiva da consistência e da inconsistência de conjuntos de proposições, o núcleo da lógica clássica pode ser apresentado com base na seguinte coleção de cláusulas simples e intuitivamente corretas:

a) (Princípio da Não-Contradição) Qualquer que seja o conjunto Γ de proposições, não é o caso que Γ é consistente e Γ é inconsistente.

b) (Princípio do Terceiro Excluído) Qualquer que seja o conjunto Γ de proposições, Γ é consistente ou Γ é inconsistente.

c) (Princípio da Existência de Conjunto Maximal Consistente) Quaisquer que sejam o conjunto de proposições Γ e a proposição α, se Γ∪{α} é consistente, então Γ é consistente.

d) (Princípio da Existência de Conjunto Minimal Inconsistente) Quaisquer que sejam o conjunto de proposições Γ e a proposição α, se Γ é inconsistente, então Γ∪{α} também é inconsistente.

O Princípio da Existência de Conjunto Maximal Consistente e o Princípio da Existência de Conjunto Minimal Inconsistente fornecem duas diferentes estratégias para a totalidade de tarefas reservadas ao lógico: o Princípio da Existência de Conjunto Maximal Consistente impõe a tarefa de identificação dos conjuntos consistentes de proposições tais que o acréscimo de qualquer nova proposição resulta em um conjunto inconsistente de proposições; o Princípio da Existência de Conjunto Minimal Inconsistente impõe a tarefa de identificação dos conjuntos inconsistentes tais que a retirada de qualquer proposição resulta em um conjunto consistente de proposições. A propósito, se for exigido dos conjuntos minimais inconsistentes que sejam finitos, teremos, aqui, uma versão do Teorema da Compacidade, supostamente conhecido por Aristóteles, teorema segundo o qual, se um argumento é válido, então a conclusão é consequência lógica de um subconjunto finito de premissas (Lear, 1979).

7. O descarte da verdade

Este trabalho ocupou-se exclusivamente de elementos epistêmicos amalgamados a noções lógicas, mas pode-se também fazer a crítica a elementos ônticos indistinguidos das noções lógicas às quais eles se acoplam.

A semântica dos sistemas lógicos, e não apenas do sistema de lógica clássica, é dada, em geral, por intermédio de condições de verdade. A noção de verdade é, contudo, uma noção difusa: há muitas propostas alternativas na literatura filosófica para caracterizá-la, nenhuma das quais obteve um consenso razoável. Mesmo que uma proposta de caracterização da verdade venha, algum dia, a estabelecer-se, o problema persiste, pois a validade lógica é caracterizada como "preservação" de verdade. Mas a ideia de que a lógica lida com a "preservação" da verdade e a ideia de que a validade e a correção são assuntos distintos, embora esta dependa daquela, são difíceis de conciliar, ou seja, há uma dificuldade na conciliação da lógica como uma disciplina que visa a "preservação" da verdade e, ao mesmo tempo, a ideia de que um bom argumento, do ponto de vista lógico, não precisa ter nenhuma proposição verdadeira. Separamos, no ensino da lógica, esses dois momentos: o momento da determinação da relação entre os valores de verdade das proposições, e o momento da determinação dos valores de verdade das proposições. Somente aquele momento é próprio do avaliador qua lógico. Mas, então, por que falar da verdade em ambos os casos?

Minha proposta é reabilitar um velho discurso que, por motivos que desconheço, simplesmente foi abandonado: o discurso que confere importância à noção de informação semântica e que a utiliza para definir a noção de validade lógica com base na seguinte relação mereológica entre a informação semântica veiculada pela conclusão do argumento e a informação semântica veiculada pelas premissas deste: um argumento é logicamente válido se e somente se a informação semântica veiculada pela conclusão é uma parte, própria ou imprópria, da totalidade da informação semântica veiculada pelas premissas.

Esse tipo de abordagem foi, recentemente, reabilitado pelo trabalho de Luciano Floridi (2007)⁵.

Conta, ainda, em favor dessa abordagem, o fato de que os métodos visuais de prova e os métodos heterogêneos de prova – visuais e linguísticos ao mesmo tempo – também recentemente reabilitados pelo trabalho de Barwise e Etchemendy (1994), são muito mais propensos a um tratamento em termos de informação semântica do que em termos de verdade⁶.

Isso, contudo, é assunto para um outro trabalho.

Referências

Aristóteles (1989). Prior analytics (R. Smith, trad.). Indianapolis (IN)/Cambridge: Hackett.         [ Links ]

Baggini, J. & Stangroom, J. (2010). Você pensa o que acha que pensa? Um check-up filosófico (R. Valente, trad.). Rio de Janeiro: Zahar.         [ Links ]

Barwise, J. & Etchemendy, J. (1994). Hyperproof. Stanford (CA): CSLI Publications.         [ Links ]

Dutilh Novaes, C. (2007). Formalizing medieval logical theories: suppositio, consequentiae and obligationes. Dordrecht (PB): Springer, Col. Logic, Epistemology, and the Unity of Science, vol. 7.         [ Links ]

Floridi, L. (2011). The philosophy of information. Oxford (GB): Oxford University Press.         [ Links ]

Frege, G. (1979). Logic. In H. Hermes et al. (Orgs.), Gottlob Frege: posthumous writings (pp. 1-8). Oxford (GB): Basil Blackwell.         [ Links ]

Frege, G. (1984). Negation. In B. McGuinness (Org.), Collected papers on mathematics, logic, and philosophy (pp. 373-389). Oxford (GB): Basil Blackwell.         [ Links ]

Hodges, W. (2001). Logic: an introduction to elementar logic (2. ed.). Londres: Penguin Books.         [ Links ]

Kelsen, H. (2000). Teoria pura do direito (6. ed., 4. tir.; 2. ed. publicada em 1960). São Paulo: Martins Fontes.         [ Links ]

Lear, J. (1979). Aristotle's compactness proof. The Journal of Philosophy, 76(4), 198-215.         [ Links ]

MacFarlane, J. (2002). Frege, Kant, and the logic in logicism. The Philosophical Review, 111, 25-65.         [ Links ]

Sautter, F. T. (2004). Teoria dos estágios da argumentação. In C. Cândido & V. Carbonara (Orgs.), Filosofia e ensino: um diálogo transdisciplinar (pp. 233-244). Ijuí (RS): Unijuí         [ Links ].

Sautter, F. T. (2008). Uma expressão formal da noção kantiana pré-crítica de oposição. Filosofia UNISINOS, 9(3), 214-227.         [ Links ]

Sautter, F. T. (2009). Silogísticas paraclássicas: um estudo de caso sobre a relação entre lógica clássica e lógicas não-clássicas. Principia, 13, 185-194.         [ Links ]

Spade, P. V. & Menn, S. (2003). A note on the title of Walter Burley's On the purity of the art of logic. Recuperado em 07 de junho de 2011 de <http://pvspade.com/Logic/ docs/BurlNote.pdf>         [ Links ].

Recebido em 20/09/2011
Aprovado em 20/10/2011

¹ Este trabalho recebeu o apoio do Conselho Nacional de Desenvolvimento Científico e Tecnológico/Brasil e da Fapergs.
² A expressão "epistemicismo" não é nova. Ela é empregada, por exemplo, por Timothy Williamson em associação com a tese da vaguidade epistêmica de diversas noções de nosso cotidiano. Aqui a expressão é, evidentemente, empregada em outra acepção.
³ A expressão "onticismo" também não é nova, sendo empregada na filosofia de Heidegger como sinônima de coisismo. Aqui a expressão também é, evidentemente, empregada em outra acepção.
⁴ A tradução de sullogismos por dedução, proposta por John Corcoran e adotada por Robin Smith, visa a evitar a associação com o significado atual de silogismo. O que Aristóteles tem em vista é um argumento em geral, e não uma forma restrita de argumento como o é o silogismo em seu significado atual.
⁵ A recepção do trabalho de Floridi é bastante difícil, pois ele fornece um tratamento quantitativo tecnicamente bem sofisticado para o tema. Uma abordagem estritamente qualitativa, entretanto, parece ser suficiente
⁶ Na esteira desse trabalho de Barwise e Etchemendy tem ressurgido o interesse em métodos visuais de prova e sido reabilitado o trabalho executado por Euclides em seus Elementos.