ARTICLES EN CONTINU FLUX

 

Grammaire analytique et grammaire philosophique

 

 

Guy-Félix Duportail

Université de Paris 1, Centre de Philosophie Contemporaine de la Sorbonne
In memoriam

 

 

---

RÉSUMÉ

Dans un premier temps, je voudrais développer la thèse selon laquelle les mathèmes de Lacan peuvent être considérés comme la grammaire de l'inconscient structuré comme un langage¹. Cela Lacan ne l'a jamais dit, mais je considère que cette hypothèse éclaire considérablement le statut des mathèmes et, plus généralement, le jeu de langage de la psychanalyse. Dans un second temps, je comparerai cette grammaire de Lacan à la grammaire philosophique de Wittgenstein. J'attends de cette comparaison un surcroît de lumière quant à la compréhension de la relation entre philosophie et psychanalyse.

Mots clés: philosophie; psychanalyse; Lacan; Wittgenstein; langage.

---

 

 

1. De la grammaire analytique

Le nom de Wittgenstein apparaît à plusieurs reprises dans le séminaire de Lacan². Le sens de la relation entre les deux penseurs est loin cependant d'avoir été élucidé. Nettement moins commenté que la référence à Hegel ou à Heidegger, le rapport à Wittgenstein constitue pourtant un point crucial chez Lacan³. Comme nous voudrions le montrer, à contre-courant de la doxa sur cette question⁴, l'angle de lecture wittgensteinien éclaire puissamment la psychanalyse et son concept central: l'inconscient. Lacan lui-même nous indique le chemin. Dans l'Envers de la psychanalyse, il situe en effet «l'opération analytique» dans le champ «de ce qui se trouve incarné par Wittgenstein»:

Il n'y a pas d'autre métalangage que toutes les formes de la canaillerie, si nous désignons par là ces curieuses opérations qui se déduisent de ceci, que le désir de l'homme, c'est le désir de l'Autre. Toute canaillerie repose sur ceci, de vouloir être l'Autre, j'entends le grand Autre, de quelqu'un, là où se dessinent les figures où son désir sera capté. Aussi bien cette opération dite wittgensteinienne n'est-elle rien qu'une extraordinaire parade, qu'une détection de la canaillerie philosophique (Lacan, 1991, pp. 68-69).

L'espace commun aux deux penseurs est donc délimité par l'absence de métalangage. Dans les termes de Lacan, la critique de l'idée de métalangage s'appuie sur le fait qu'il n'y a pas d'Autre de l'Autre, de sorte que tout discours qui prétend énoncer le vrai sur le vrai est une forme d'imposture dont les philosophes ne sont pas exempts. Dans les termes de Wittgenstein, cela signifie que nous ne pouvons dire dans un (méta) langage ce qui s'exprime de soi-même dans le langage, que nous ne pouvons que le montrer à travers notre usage sensé du langage (Tractatus, 4.121). Comme on sait, dans le Tractatus logico-philosophicus, ce refus du métalangage conduit Wittgenstein à la position terminale d'un élément mystique dans l'usage du langage (le fameux «ce dont on ne peut parler, il faut le taire») (Tractatus, 4.121). Traduit au plan épistémique, la critique du métalangage correspond au rejet des «métadisciplines». Wittgenstein considérait encore qu'il s'agissait sur ce point d'un «principe directeur» de sa philosophie (Wittgenstein, 1980, I, §72-73). Dans les années trente, on retrouve l'expression de cette position dans la critique de l'idée d'un fondement des mathématiques (comme position d'une métamathématique, ce dernier terme ne s'appliquant pas seulement au programme de Hilbert mais à toute tentative de fondation des mathématiques), critique de l'attitude fondamentaliste dont le versant positif est l'assertion du caractère grammatical des propositions mathématiques (Wittgenstein, 1983).

L'idée de « grammaire » est centrale chez le second Wittgenstein (1988). Le terme y désigne à la fois les règles constitutives d'un langage et la recherche philosophique sur ces règles (Wittgenstein, 1988). Dans le contexte de la réflexion sur les mathématiques, l'important n'est pas alors de s'interroger sur l'origine transcendantale (Kant) ou sur le fondement ontologique (Platon) des propositions, mais de savoir comment elles sont utilisées. Il s'agit d'examiner le rôle de ces propositions dans une perspective foncièrement pratique (Wittgenstein, 1983). Ainsi, dans ses Remarques sur les fondements des mathématiques (1983), Wittgenstein revient inlassablement sur le fait que les propositions mathématiques sont utilisées comme des règles de grammaire, c'est-à-dire comme des normes pour la bonne formation du sens des propositions empiriques. Elles ne disent donc pas ce qui permet de représenter le monde. La grammaire du second Wittgenstein n'est donc pas davantage un métalangage que ne l'était la syntaxe logique du Tractatus.

En quoi cependant cette grammaire concerne-t-elle l'oeuvre de Lacan? Nous poserons l'implication suivante: si l'inconscient est structuré comme un langage, alors il doit avoir une grammaire. Comme on le voit, l'hypothèse est simple. Cette simplicité toutefois oblige. Pour découvrir et saisir clairement cette grammaire de l'inconscient, une confrontation plus serrée entre Lacan et le second Wittgenstein s'avère indispensable.

1.1. L'approche wittgensteinienne des mathématiques éclaire le statut des mathèmes

Nous l'avons rappelé ci-dessus, Wittgenstein, à la suite de l'échec du logicisme de Frege et de Russell, s'opposa à l'idée d'un fondement des mathématiques. Les propositions mathématiques ne répondent d'aucune réalité et sont injustifiables aux yeux de Wittgenstein. Elles sont arbitraires et dénués de sens, en ceci qu'elles appartiennent aux conditions du sens et qu'elles ne sont pas elles-mêmes représentatives de quoi que ce soit. Elles ne sont donc ni vraies ni fausses et ne peuvent a fortiori dire le vrai sur le vrai.

Positivement, les propositions mathématiques sont considérées comme appartenant à la grammaire de nos langages. En tant que règles de grammaire, elles ne parlent de rien, mais elles conditionnent la parole sensée, qui, elle, dit ou représente quelque chose et qui peut être vraie ou fausse. Comme l'écrit Wittgenstein à la fin des années trente: «La proposition démontrée par la preuve sert de règle, donc de paradigme. Car nous nous guidons d'après la règle. […] La proposition mathématique doit nous montrer ce que l'on peut dire avec SENS» (Wittgenstein, 1983, p. 153).

Il y a donc une région du langage qui montre les présupposés de tout discours signifiant. Cette région est celles des propositions qui servent de règles pour exprimer quelque chose au sens prégnant du terme. Selon Wittgenstein ce domaine est celui des propositions mathématiques démontrées. Ce qui est en position de fondement ce sont alors les propositions paradigmatiques qu'il ne viendrait à l'esprit de personne de remettre en question. Ces règles sont en effet à la base de nos pratiques et nous faisons fond sur elles⁵. Par exemple, les propositions mathématiques sont de véritables normes pour compter les objets présents dans le monde. Ainsi, la proposition 2 x 2 = 4 autorise de passer de «il y a deux paires de pommes dans le seau» à «il y a quatre pommes dans le seau» (Dictionnaire Wittgenstein, 2003, p. 359). Nous nous adossons à cette proposition mathématique (2 x 2 = 4) pour dire quelque chose de vrai à propos du monde empirique («il y a quatre pommes dans le seau»), et si d'aventure, après avoir annoncé «il y a deux paires de pommes dans le seau», nous ne trouvions que trois pommes dans le seau, nous dirions alors qu'il en manque une ou qu'il devrait y en avoir quatre, ou encore qu'il n'y a pas deux paires de pommes dans le seau, en fonction des normes de l'arithmétique. Du même coup, nous ne remettrions pas en cause la proposition mathématique, mais bien plutôt les circonstances matérielles du comptage. Du point de vue de Wittgenstein, le fondement mathématique est reconnu comme le point de départ d'une pratique et celle-ci se déploie grâce à la première (Schmitz, 1988, p. 259).

Si nous considérons maintenant les mathèmes de Lacan comme des règles grammaticales de la praxis analytique, alors nous devons en déduire que le rôle du fondement n'est pas extérieur à la psychanalyse et qu'il réside dans la position de certaines propositions dont le mode de signifiance est particulier. De ce point de vue, le philosophe n'aurait pas à fonder la psychanalyse⁶. Celle-ci serait auto-fondée. Ce qui ne veut pas dire que le discours philosophique soit inutile à l'auto-compréhension de la psychanalyse, mais qu'il sert à autre chose qu'à la justifier. Le discours philosophique procèderait plutôt à l'élucidation conceptuelle de la pratique analytique. L'avantage de la lecture wittgensteinienne sur d'autres approches philosophiques est qu'elle est immédiatement en accord avec Lacan lui-même.

Les propositions auto-fondationnelles de la psychanalyse doivent cependant être situées à un niveau logique spécifique. Les propositions mathématiques que nous dirons dorénavant grammaticales ne doivent pas en effet être situées au même niveau logique que les propositions empiriques concernant la cure analytique ou plus généralement les formations de l'inconscient (comme le Witz, l'acte manqué, le rêve, etc.). C'est d'ailleurs le niveau empirique qui nous préoccupe le plus souvent – et à juste titre – d'un point de vue existentiel. Les analysants parlent essentiellement de leur angoisse, de leur symptôme, de leur inhibition, et plus rarement de la grammaire analytique. Les propositions grammaticales sont décalées par rapport aux formations de l'inconscient, tout comme les règles d'un calcul ne sont pas explicites dans son résultat. Ainsi, je suppose que les mathèmes de Lacan sont précisément d'un autre niveau, qu'ils sont en vérité des règles grammaticales déguisées dont l'utilité est de permettre la formation d'énoncés sensés à propos de l'inconscient freudien.

Les mathèmes sont de bons candidats au rôle de règles grammaticales pour une autre raison: ils sont à la fois langagiers et non langagiers. Leur forme mathématique les distingue du langage ordinaire.

Enfin, eu égard à la communauté analytique, la fonction d'expression et de transmission du mathème est manifestement stratégique. La grammaticalité mathématique apparaît ici comme la condition du franchissement du fossé naturel entre les générations, comme la condition de l'intelligibilité et de la transmission de l'expérience freudienne.

 

2. Les mathèmes de Lacan sont-ils des paradigmes pour l'expérience analytique?

Toutefois, selon les Remarques sur les fondements des mathématiques, pour que les propositions mathématiques servent de règles dans un domaine du langage, il faut qu'elles aient été prouvées. Notre hypothèse quant à la valeur grammaticale des mathèmes n'est donc valable qui si et seulement si ceux-ci ont été prouvés. Il nous faut donc revenir sur ce point.

L'idée wittgensteinienne de la preuve est originale. Elle ne peut qu'intéresser le lecteur de Lacan en raison de la distance qu'elle prend avec l'inférence et la déduction logique⁷. On devine une affinité élective avec les formules de Lacan qui ne font pas système et qui ne se prêtent guère à la déduction. Mais, avant d'aller plus loin, essayons de cerner ce qu'il en est de la preuve chez Wittgenstein.

Nous l'avons suggéré, il ne s'agit pas d'une procédure logique dans la perspective d'établir la vérité d'une proposition à partir d'axiomes, mais d'une procédure d'un autre genre, étroitement liée à la question directrice de l'application des propositions mathématiques prises pour normes du sens à un langage constitué de propositions empiriques. Selon Wittgenstein, la preuve doit en effet nous persuader d'adopter une proposition mathématique comme règle de grammaire ; elle doit nous convaincre de donner du sens à nos expressions à partir d'elle, car la preuve mathématique n'est rien d'autre que l'exhibition du caractère légitime du sens d'une proposition au sein d'un système de règles. La proposition prouvée sert ainsi de critère du sens des autres expressions.

Ainsi, reconnaître la validité de l'identité numérique « 2 + 2 = 4 » revient selon Wittgenstein à adopter une règle qui exclut comme dénuée de sens toute assertion selon laquelle un individu X, en appliquant correctement l'algorithme de l'addition, a obtenu une expression numérique autre que « 4 ». Obtenir « 4 » assure le rôle de critère normatif de ce qu'est l'effectuation correcte de la transformation des signes numériques « 2 + 2 » en « 4 ». « 4 » est alors le paradigme du résultat correct. En présence de la preuve nous sommes à la «fin du chemin» de nos pensées:

Lorsque dans une preuve nous disons : «Cela doit être le résultat» – ce n'est pas à partir de raisons que nous ne voyons pas. Ce qui nous le fait admettre, ce n'est pas que nous obtenions ce résultat, mais que ce soit là la fin de ce chemin. Voilà la preuve qui nous convainc […]. (Idem, III §39, p. 158).

Démontrer une proposition revient donc à s'assurer que l'application des règles d'un système dont elle est issue permet bien de parvenir à telle ou telle configuration de signes (« 2 + 2 =4 ») et pas à une autre. La configuration correcte offre ainsi la fin d'un chemin balisé par des règles et dont la proposition prouvée est le terme :

Une preuve intègre la proposition à un calcul (Wittgenstein, 1980, II, §24, p. 377).

D'où encore l'importance de la visibilité de la preuve pour nous convaincre du bouclage effectif du processus de l'application des règles:

«Une preuve mathématique doit être synoptique.» Nous appelons «preuve» uniquement une structure dont la reproduction est un exercice facile à résoudre. On doit pouvoir déterminer avec certitude si nous avons ou non deux fois la même preuve sous les yeux. La preuve doit être une image pouvant être reproduite avec sûreté⁸.

2.1. Le caractère synoptique de la preuve

Insistons sur ce dernier caractère synoptique de la preuve selon Wittgenstein⁹. Qu'est-ce que cela signifie? Cette propriété nous intrigue parce qu'elle révèle qu'établir une preuve n'est pas étranger – contrairement à ce que l'on pense habituellement à propos de l'exercice de la démonstration mathématique – à la construction d'une image, en l'occurrence l'image d'une propriété essentielle¹⁰.

Par exemple, lorsque nous voyons que tout rectangle peut être décomposé en deux triangles rectangles (Schmitz, 1988, p. 204), l'image du rectangle divisé par sa diagonale est vue non pas comme un simple objet sensible, mais comme l'exhibition d'une relation interne entre un rectangle et deux triangles rectangles:

 

 

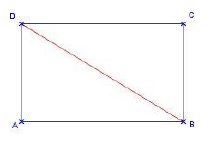
Une propriété essentielle du rectangle nous est montrée et l'image se trouve du même coup «platonisée»¹¹. Elle n'est pas exclusivement sensible, elle contient de l'intelligible. C'est la force intellectuelle de l'image que de déployer sous nos yeux le «doit» de l'implication mathématique. Elle devient selon Wittgenstein une «image marquante» (Schmitz, 1988, p. 204).

Toutefois, c'est ce que l'on va pouvoir faire avec l'image marquante (son usage) dont il est question. Comment peut-on exécuter des «coups» à partir de celle-ci ? C'est au sein d'une pratique gouvernée par des règles que l'image marquante du rectangle plaide pour que la proposition qu'elle condense devienne une règle grammaticale pour les usagers. Comprendre le sens d'une proposition paradigmatique, veut dire ici savoir ce que l'on peut en faire, quelles sont les règles qui ont été appliquées pour aboutir à elle, quel genre de calcul peut être mené à partir d'elle (Schmitz, 1988, p. 159).

Comme on s'en aperçoit, la preuve synoptique renvoie à la décision d'adopter une règle et à travers elle un système de règles solidaires, un système à l'intérieur duquel on pourra participer à un jeu, effectuer des «coups», tout comme aux échecs. Ce qui suppose un acte volontaire et une homogénéité de comportement de la part des membres de la communauté concernée par la preuve. Bref, une «forme de vie» partagée.

 

3. Retour à Lacan

Pour ce qui nous occupe, la pertinence de la notion wittgensteinienne de preuve réside en ceci qu'elle nous aide à comprendre et même à justifier le pari le plus audacieux de Jacques Lacan : celui de l'applicabilité des propositions mathématiques aux propositions empiriques de la psychanalyse freudienne. Prenons un exemple.

A partir du moment où la communauté des psychanalystes a fait sienne la proposition «3 tores + 1 quatrième = noeud du sinthome», elle a manifestement appliqué l'algorithme du nouage borroméen aux propositions issues de l'expérience clinique. Le noeud à quatre a été élu comme paradigme au sens de Wittgenstein. Grâce au mathème, suivre l'enseignement de Lacan est devenu suivre une règle. L'invention de Lacan s'est muée en image marquante pour les membres de la communauté psychanalytique qui l'ont adoptée. Or, en quoi l'image du sinthome est-elle précisément «marquante»? Le schème topologique est marquant parce qu'il montre une relation interne entre le noeud à quatre et la propriété borroméenne, dans sa manière même de faire chaîne. Il est essentiel au quatrième rond du sinthome d'effectuer un nouage borroméen ou quasi borroméen et c'est en effet cette propriété que présente aux yeux de tous la fonction réparatrice du tore supplémentaire¹². Le sinthome doit réparer un noeud mal ficelé, et le schème du noeud à quatre exhibe en toute visibilité cette nécessité:

 

 

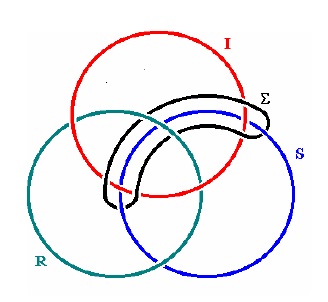
La proposition du sinthome comme noeud à quatre est en relation interne avec la prémisse selon laquelle la structure de l'esprit est borroméenne. Il s'agit là d'une propriété essentielle à l'esprit humain. Par suite, le sinthome doit être borroméen. C'est ce que montre le schème topologique. Le noeud du sinthome n'est donc pas une proposition empirique issue de l'observation des faits. Il n'est ni vrai ni faux. Il ne représente pas le monde. Il prend sens de par son appartenance au système des règles de la topologie. C'est donc une proposition proprement grammaticale et donc irréfutable par voie d'expérience. Peut-être était-ce à ce genre de mathème que pensait Lacan quand il déclara durant son séminaire, en 1978, que la psychanalyse était irréfutable. Le noeud à quatre du sinthome (noté 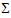sur le dessin), de par son statut grammatical, est en effet un point de certitude sur lequel la pratique des uns et des autres a pu opérer dans les cures (Wittgenstein, 1983, III, § 39, p. 157).

On nous rétorquera peut être que Lacan ne considérait pas la topologie comme un modèle. Mais encore faut-il s'entendre sur le terme de modèle. Comme Lacan ne mentionna jamais dans son Séminaire les Remarques sur les fondements des mathématiques (la traduction française est parue en 1983, deux ans après la mort de Lacan et il ne cita pas à notre connaissance l'édition anglaise de 1953; il semble que Lacan n'ait connu que le premier Wittgenstein, celui du Tractatus logico-philosophicus), de sorte qu'il ne songeait très probablement pas au sens que nous déployons dans ces lignes. Le terme de modèle renvoie plutôt chez Lacan au sens épistémologique d'une médiation nécessaire entre la théorie pure mathématisée et le domaine concret de l'expérience scientifique. Nous sommes dans ce cas bien loin de l' «image marquante» au sens de Wittgenstein.

Qu'on y songe un instant: Lacan fut – et pourrait-on dire en premier lieu – un fondateur d'école et donc un formateur éminent dans la communauté analytique et cela pendant une longue période. Grâce à sa démonstration, après sa mort, ses élèves continuèrent à parler du noeud du sinthome et ils continuent aujourd'hui encore à s'en servir. Lacan eut me semble-t-il la conviction que le noeud borroméen était pour lui «la fin du chemin» (le noeud borroméen lui allait «comme une bague au doigt» disait-il), sans doute parce qu'il tenait bien en main une preuve de son savoir faire avec (les règles de) la structure.

 

4. Les propositions normées par le mathème du noeud ne parlent pas de l'être, mais de l'Un

Avec Wittgenstein, ce que l'on gagne en grammaire, on le perd en ontologie. Il y a bien là derechef affinité manifeste avec la psychanalyse lacanienne: «La béance de l'inconscient, nous pourrions la dire pré-ontologique. J'ai insisté sur ce caractère oublié – oublié d'une façon qui n'est pas sans signification – de la première émergence de l'inconscient, qui est de ne pas prêter à l'ontologie» (Lacan, Livre XIX, déjà cité, p. 125).

En effet, s'il est acquis que le réel analytique concerne la réalité psychique telle que Freud en parlait, il ne concerne donc pas la réalité physique et les étants en général. Par suite, les propositions analytiques ne seront sensées au sens prégnant du terme, c'est-à-dire représentatives de quelque chose, que si et seulement si elles parlent de «l'autrement qu'être» propre à la psychanalyse, soit de l'Un en quoi consiste l'élémentaire de la réalité psychique: «N'est-il pas sensible à votre oreille que je parle ici de l'Un comme d'un réel – et d'un réel qui peut aussi bien n'avoir rien à faire avec aucune réalité?» (Lacan, p. 140).

La grammaire analytique se laisse donc interpréter bien plus aisément du côté d'une pensée de l'Un – du côté par conséquent d'une henologie – plutôt que du côté d'une ontologie ordonnant a priori la réalité¹³. Comme le précise Lacan sur ce point en parlant du noeud borroméen et de ses variantes: «Le dit rond est certainement la plus éminente représentation de l'Un, en ce sens qu'il n'enferme qu'un trou» (Lacan, Le Séminaire, Livre XX, Encore, déjà cité, p. 115).

Il n'y a pas d'identité de l'être et de l'Un pour Lacan, qui s'appuie ici sur les premières hypothèses du Parménide de Platon (Lacan, Le Séminaire, Livre XIX, …Ou pire, déjà cité, p. 125). Ce qui n'exclut pas une certaine pensée de l'existence comme Platon l'a montré. L'Un ek-siste de n'être pas.

«En nulle façon […]. l'Un n'a part à l'Être.» (Platon, Parménide, 142 e.)

Les mathèmes topologiques sont donc les règles que nous devons suivre pour parler de l'Un de manière sensée. Pour revenir à notre exemple, l'Un pourra être le sinthome comme Un rond en plus, ou le Un rond en plus de la nomination. D'une manière générale, il s'agira de toutes les opérations ou le Un intervient comme élément:

Qu'est-ce qu'un élément? Un élément c'est d'une part ce qui fait un, autrement dit le trait unaire, et ce qui, du fait de faire un, amorce la substitution. La caractéristique d'un élément, c'est qu'on procède à la combinatoire des éléments (Lacan, 2005, p. 146.).

Le jeu général de l'inconscient est donc analysable comme une combinatoire de Uns. Le noeud borroméen à quatre tores s'intègre alors dans le jeu général du langage de l'inconscient, déterminable, lui, comme jeu de la signifiance.

Notre hypothèse se précise: le mathème du noeud borroméen permet de spécifier la grammaire de l'inconscient structuré comme un langage. Si tel n'était pas le cas la refondation lacanienne de la psychanalyse serait d'ailleurs absurde, car si l'inconscient structuré comme un langage ignorait toute grammaire, alors il ne serait pas structuré en fonction d'un langage, mais d'autre chose. Il faut donc une grammaire au langage de l'inconscient.

Nous pensons que la grammaire borroméenne redéfinit chez le dernier Lacan les règles de la fonction signifiante. Car est signifiant non pas exclusivement un phonème selon la grille différentielle propre à une langue donnée, mais tout ce qui peut être compté pour un au sens des Uns dont on fait le noeud borroméen:

Le Un incarné dans la langue est quelque chose qui reste indécis entre le phonème, le mot, la phrase, voire toute la pensée. C'est ce dont il s'agit dans ce que j'appelle le signifiant-maître. C'est le signifiant Un, et ce n'est pas pour rien qu'à l'avant-dernière de nos rencontres, j'ai amené ici pour l'illustrer le bout de ficelle, en tant qu'il fait rond, dont j'ai commencé d'interroger le noeud possible avec un autre (Lacan, 1976, p. 131).

Le noeud borroméen donne alors la règle fondamentale de la fonction signifiante: faire chaîne. Telle est la règle à suivre pour produire une combinaison de signifiants qui se réfère à un certain réel (qui n'est pas la réalité).

 

5. Une grammaire spécifique

Toutefois, le lecteur philosophe se demandera s'il n'y a pas malgré tout une forme d'incompatibilité entre psychanalyse et philosophie. Si la grammaire analytique régit ce que l'on peut dire avec sens du réel de l'Un et non de la réalité, alors on voit mal en effet comment accorder la grammaire psychanalytique avec la grammaire philosophique du second Wittgenstein. Le propre de celle-ci est de mettre en lumière le fait que les signes ne sont pas seulement des éléments discrets et arbitraires dans une langue (Saussure), mais que leur usage les projette sur la réalité conformément aux règles d'un jeu de langage. C'est l'usage qui donne vie aux signes. Corréler les signes à la réalité est encore selon Wittgenstein l'activité qui est au coeur de la compréhension du sens d'une proposition. Comme il le dit dans sa Grammaire philosophique:

Que cette proposition d'expérience soit vraie, cette autre fausse, cela ne relève pas de la grammaire. Ce qu'on trouve en elle, ce sont toutes les conditions (la méthode) de comparaison de la proposition avec la réalité, c'est-à-dire toutes les conditions de la compréhension (du sens) (Wittgenstein, 1980, p. 121).

La grammaire philosophique au sens de Wittgenstein apparaît dès lors comme l'analogon d'une méthode géométrique de projection qui établit la correspondance entre le plan du langage et celui de la réalité au sein du milieu linguistique. Elle mesure ainsi l'espace des vérités possibles, et cela en fixant les normes de la représentation des états de choses.

En revanche, du côté de la grammaire analytique, la projection se rapporte à une réalité faussée ou déformée, puisque nous avons affaire à une réalité dégradée en réel. Qu'on y songe un instant, celui qui, à l'instar du fétichiste, juge et se déjuge en même temps quant à l'existence d'un pénis maternel, celui-là ne peut espérer rencontrer un «accord dans les jugements», comme le dit paragraphe 242 des Recherches Philosophiques. Dire d'un sexe qu'il est féminin, c'est le caractériser de telle façon qu'il ne peut pas être masculin en même temps et vice versa. Le fétichiste, lui, transgresse cet ordre syntaxico-sémantique. D'un point de vue grammatical, il en va en effet de notre façon de parler des sexes comme de notre façon de parler des couleurs, même si les conséquences ne sont pas les mêmes. On ne peut pas dire que le rouge est vert, et on ne peut pas dire non plus que les organes génitaux féminins sont phalliques. Sinon, on ne dit simplement rien du tout. Tout un faisceau de relations syntaxiques permet aux mots de renvoyer à la réalité et la désorganisation de ce faisceau ne le permet plus. Lorsque quelqu'un parle du sexe féminin nous nous attendons, selon les standards de correction de notre jeu de langage, qu'il désigne une vulve, et non pas un ersatz du sexe masculin, c'est-à-dire un fétiche. Comme de juste, le démenti pervers ou encore la forclusion du psychotique, opérations qui, chacune à sa manière, ne font pas compter la castration dans le langage, constituent des infractions aux normes grammaticales de la représentation correcte de la réalité¹⁴. L'existence d'un lien entre certaines positions subjectives négatives (refoulement, démenti, forclusion) et non-sens grammatical apparaît encore dans le fait que le démenti ou la forclusion nous font rencontrer des phénomènes erratiques, autrement dit des bouts de réel flottant en apesanteur symbolique. Rencontrer le réel dans le langage, ce n'est donc pas du tout la même chose que d'y rencontrer la réalité. La grammaire lacanienne du réel n'est pas à l'évidence la grammaire wittgensteinienne de la réalité. Le réel, lui, surgit précisément quand le sens fait défaut en raison de cette forme de non-sens qu'est le manque de sens – ou présence d'une lacune dans la symbolisation – causé par le rejet ou le déni d'une partie de la réalité. La partie (le réel non symbolisé) détachée du tout (l'ensemble de la réalité symbolisée) viole manifestement le principe de contextualité du sens¹⁵. Le fragment détaché de la réalité commune est donc le résultat d'une forme de non-sens particulière due à une attitude négative du sujet. L'exemple que nous avons choisi, à savoir le déni d'une partie de la réalité (c'est-à-dire le démenti d'une scène qui évoque la castration pour le petit enfant, comme l'occasionne la perception fortuite du sexe maternel) révèle que cette attitude négative vis-à-vis du sexe féminin peut déformer notre rapport général à la réalité¹⁶. Il en va d'ailleurs de même pour toutes les formes du réel recensées par la psychanalyse lacanienne : s'il faut en croire Lacan, rien n'ek-siste comme morceau de réel qui n'ait été auparavant déjeté du symbolique enveloppant la réalité¹⁷. Enfin, il est remarquable que Wittgenstein eût lui-même l'intuition de cette fragmentation du langage dans l'inconscient, quand il parle du récit de rêve comme d'un «fragment qui nous impressionne fortement (parfois en tout cas), de sorte que nous cherchons une explication, des connexions» (Wittgenstein, 1998, p. 78). Face à cette fragmentation du langage par le rêve, Wittgenstein préconise non pas, à la manière de Freud, une traduction du récit de rêve, puisqu'il ne s'agit pas, selon lui, d'un véritable fait de langage, mais l'élucidation de certains de ses aspects au moyen de comparaisons avec d'autres fragments (Wittgenstein, 1971, p. 95). En quoi Wittgenstein inaugure une sorte de psychanalyse du réel du rêve. En isolant le récit de rêve comme un bout de réel qui ressemble à un langage mais qui n'en est pas un, Wittgenstein cerne à la fois l'effet destructeur des opérations inconscientes sur les règles du langage ordinaire et le caractère expressif du fragment inconscient, qui «nous touche comme une idée grosse de développement» (Wittgenstein, 2002, pp. 138-139).

Or, cette tension entre rêve et langage, évidente lorsque Wittgenstein constate la non-réciprocité de la traductibilité du récit de rêve dans la langue de la vie quotidienne¹⁸, n'annule en rien, mais bien au contraire justifie, le rôle grammatical de certaines propositions freudiennes. Ce que nous voudrions souligner, c'est que, pour continuer de parler avec sens du récit de rêve, tout comme du réel, et ne pas simplement les vouer aux gémonies du non-sens, il est nécessaire de changer de grammaire ou de règles du jeu, car plus rien justement, dans ces contextes singuliers, ne se rapporte à la réalité de manière habituelle. En fait, la question revient à saisir la fonction grammaticale des propositions analytiques qui régulent le rapport du langage au réel. Autrement dit, dans quelles situations avons-nous besoin de suivre les normes de la grammaire analytique pour continuer de faire sens dans nos échanges? Quand devons-nous jouer le jeu de langage de la psychanalyse? Nous pensons que ce changement de grammaire vient de notre désir de compréhension – ou désir de sens – lorsque celui-ci est immergé dans des contextes au sein desquels le sens a pris les traits énigmatiques du symptôme ou du délire et dans lesquels la réalité est trouée ou fragmentée. L'existence même de la psychanalyse témoigne du fait que notre désir de compréhension vaut pour le non-sens aussi bien que pour le sens. C'est notre implication dans des contextes pathologiques au sein desquels le rapport du langage à la réalité et donc le langage lui-même est déformé qu'un changement de règles du jeu s'impose à nous. Par voie de conséquence, la détermination analytique de la signification d'un fragment de réel requiert de suivre des règles spécifiques, nommément celles de la grammaire analytique.

Par suite, la grammaire philosophique dont l'un des traits caractéristiques est de thématiser le rapport du langage à la réalité (Wittgenstein, 2001, §44, p. 45) ne doit pas être opposée à la grammaire analytique. Bien que la psychanalyse recycle pour ainsi dire les fragments de réel que la grammaire philosophique retire de la circulation, les deux discours demeurent complémentaires: la grammaire analytique apparaît comme la réponse rationnelle à l'altération pathologique du rapport à la réalité. La grammaire analytique prolonge ainsi la grammaire philosophique, mais par d'autres moyens, c'est-à-dire d'autres règles, afin de recontextualiser les fragments de non-sens selon un usage issu de la forme de vie analytique.

 

6. Conclusion

Certaines remarques du second Wittgenstein s'avèrent des plus utiles pour clarifier le sens et le statut du concept lacanien d'inconscient¹⁹. Celui-ci est définissable comme une structure qui ne connaît pas de méta-structure et qui se laisse analyser comme un langage obéissant à un système de règles mathématiques, même si nous ne connaissons pas ces règles. Il s'agit d'un savoir insu. Le jeu autorisé par ces règles est celui de la signifiance. L'inconscient est ce jeu de langage où se joue (sans nous) la métaphorisation du réel à l'aide d'un calcul élémentaire. Il est encore celui de nos manières de faire avec le réel, qu'on le sache ou non. Toutefois, l'erreur serait ici de croire que discourir sur le réel reviendrait à s'exempter des règles de la grammaire philosophique. Car, parler avec sens du réel de l'Un, c'est encore une façon de comprendre ce qui est dit par l'inconscient, c'est-à-dire une manière de restituer la vérité possible d'une parole qui, à première vue, paraît insensée. C'est, in fine, réintégrer le réel dans la réalité en le symbolisant pour de bon. Cela n'a pas de prix, et cela constitue selon moi l'apport de la psychanalyse à la vie des signes.

 

7. Références

Bouveresse, J. (1991). Philosophie, mythologie et pseudo-science. Wittgenstein lecteur de Freud. Paris: Éditions l'Éclat.         [ Links ]

Duportail, G.-F. (2003). A priori Littéral. Paris: Cerf.         [ Links ]

Glock, H.-J. (2003). Dictionnaire Wittgenstein. Paris: Gallimard.         [ Links ]

Lacan, J. Le Séminaire, Livre XIX, …Ou pire.

Lacan, J. (1991). L'Envers de la psychanalyse. Paris: Seuil.         [ Links ]

Lacan, J. (1966). Écrits. Paris: Seuil.         [ Links ]

Lacan, J. (1976). Encore. Paris: Seuil.         [ Links ]

Lacan, J. (2005). Sinthome. Paris: Seuil.         [ Links ]

Livet, P. (2004). Défense à la Girard. In Wittgenstein et les mathématiques. Paris: TER.         [ Links ]

Platon, Parménide, 142 e.         [ Links ]

Rigal-Granel, É. (2013). De l'« ab-sens » : Lacan et Wittgenstein. Psychanalyse, 28(3), 107-118.         [ Links ]

Schmitz, F. (1988). Wittgenstein, la philosophie et les mathématiques. Paris: PUF.         [ Links ]

Travis, C. (2003). Les liaisons ordinaires, Wittgenstein sur la pensée et le monde. Paris: Vrin.         [ Links ]

Wittigenstein, L. Tractatus logico-philosophicus.         [ Links ]

Wittgenstein, L. (1965). De la certitude. Paris, Gallimard.         [ Links ]

Wittgenstein, L. (1971). Leçons et Conversations. Paris: Gallimard.         [ Links ]

Wittgenstein, L. (1980). Grammaire philosophique. Paris, Gallimard.         [ Links ]

Wittgenstein, L. (1983). Remarques sur les fondements des mathématiques. Paris: Gallimard.         [ Links ]

Wittgenstein, L. (1988). Les cours de Cambridge, 1930-1932. Paris: TER.         [ Links ]

Wittgenstein, L. (1992). Conversations sur Freud. In L. Wittgenstein, Leçons et conversations. Paris: Gallimard.         [ Links ]

Wittgenstein, L. (1998). Culture and Value (G.-H. von Wright, éd.; P. Winch, trad.). Oxford: Blackwell.         [ Links ]

Wittgenstein, L. (2001). Grammaire philosophique. Paris, Gallimard.         [ Links ]

Wittgenstein, L. (2002). Remarques mêlées. Paris: Flammarion.         [ Links ]

 

 

¹ Le terme de grammaire désigne ici un ensemble de règles d'usage qui régissent le rapport entre le langage et la réalité, et cela en spécifiant sur un mode normatif les expressions qui ont un sens (correctes) et celles qui n'en ont pas (incorrectes). En d'autres termes, la grammaire philosophique du second Wittgenstein est à la fois syntaxique et sémantique. Elle est aussi descriptive, au sens où elle est synonyme de l'activité du philosophe analysant le langage. La philosophie est en effet selon Wittgenstein une critique du langage.
² À propos du sujet du signifiant, dans La logique du fantasme, séance du 23 novembre 1966, de l'absence de métalangage, dans l'Envers de la psychanalyse, séance du 21 janvier 1970, de la monstration du noeud borroméen, dans Ou pire… séance du 9 février 1972, pour ne citer que ces trois temps.
³ Comme l'a récemment souligné Élisabeth Rigal-Granel (2013), qui écrit: «A vrai dire, Wittgenstein occupe une place excentrique mais stratégique dans ce que l'on pourrait nommer la galerie lacanienne des philosophes».
⁴ Le plus célèbre des wittgensteiniens, en France, Jacques Bouveresse, donna le ton avec son ouvrage Philosophie, mythologie et pseudo-science. Wittgenstein lecteur de Freud (1991).
⁵ Dans De la certitude, l'avis de Wittgenstein est moins catégorique quant à la provenance des propositions normatives ou règles de grammaire. Ainsi, certains propositions empiriques peuvent devenir des normes grammaticales : « Mais ne faudrait-il pas dire alors qu'il n'y a pas de limite tranchée entre propositions de la logique et propositions empiriques ? Il se trouve que ce flou est celui que comporte la limite entre règle et proposition empirique » (Wittgenstein, 1965, p. 85).
⁶ Comme je le pensais naguère dans mon A priori Littéral (2003).
⁷ Sur ce point, on verra l'article de Pierre Livet (2004).
⁸ Idem, III §1, page 137.
⁹ La preuve synoptique de « 2+2 = 4 » est donnée au § 38 des Remarques.
¹⁰ «Mais maintenant imagine que tout ce processus, cette expérience avec les cent billes ait été filmée. [Wittgenstein imagine qu'il a sous les yeux une série de cent billes, qu'il numérote de 1 à 100 et qu'il répartit par groupes de 10, en séparant chaque série de 10 par un petit intervalle, et chaque série de 10 est elle-même séparée par un intervalle en son centre] Sur l'écran je ne vois même pas une expérience car l'image d'une expérience n'est pas elle-même une expérience – Mais ce qui «essentiellement mathématique» dans le processus, je le vois aussi dans la projection! Car apparaissent d'abord 100 taches qui ensuite sont réparties en dizaines, etc., etc. Je pourrais donc dire: la preuve ne me sert pas d'expérience, elle me sert plutôt d'image d'une expérience. […]» Et plus loin Wittgenstein de poursuivre: «Mais pourquoi ai-je le sentiment qu'une propriété de la série a été révélée, montrée? – Parce qu'alternativement, je considère ce qui est montré comme essentiel ou inessentiel à la série, ou bien parce que je pense alternativement que ces propriétés sont internes ou externes» (Wittgenstein, 1983, §36, p. 47).
¹¹ Comme le dit François Schmitz.
¹² Cela jette un jour cru sur celles et ceux qui commettent l'irréparable.
¹³ Lacan développe ici une nouvelle dialectique de l'Un et du multiple, à la fois proche et différente de celle de Platon. Nous la développons ailleurs.
¹⁴ Refuser la grammaire et refuser la castration, c'est un peu la même chose.
¹⁵ Dans les termes de Charles Travis (2003), on peut dire encore que le réel viole les standards de correction d'un jeu de langage. Le bout de réel est la partie détachée du tout qu'est le jeu de langage impliqué. Dans les contextes où un fragment de réel déjeté du symbolique est en jeu, les expressions ne se réfèrent plus aux faits qu'elles signifient au sein d'un usage modélisé par le jeu de langage de référence, elles transgressent ce que Travis désigne comme «le premier principe de Wittgenstein», à savoir que «les faits relatifs à ce qu'une expression dénomme (dénommait) ou à ce dont elle parle (parlait) ne peuvent être que ceux qui suivent des standards de correction gouvernant le tout dont il fait partie – lesquels standards suivent de ce qu'on doit attendre de sa part».
¹⁶ Tel est le fondement inconscient de la révolte féministe.
¹⁷«Rien n'existe qu'en tant qu'il n'existe pas» (Lacan, 1966, p. 392).
¹⁸«Supposez que vous considériez le rêve comme un type de langage. Une façon de dire ou de symboliser quelque chose. Ce symbolisme pourrait être régulier, sinon nécessairement alphabétique; il pourrait trouver un moyen de transposer ce symbolisme dans le langage que nous parlons ou que nous pensons communément. Mais la transposition devrait pouvoir se faire dans les deux sens. Il devrait être possible, en employant la même technique, de transposer des pensées ordinaires dans le langage du rêve. Freud le reconnaît, cela ne s'est jamais fait et ne se peut faire. De telle sorte que nous pourrions douter si le rêve est une façon de penser quelque chose, s'il est même un langage» (Wittgenstein, 1992, p. 99).
¹⁹ Ce qui n'implique pas que Wittgenstein soit avec Lacan et réciproquement. Nous nous contentons ici de la conjonction de coordination « et ».