ARTIGOS

 

Normatização da Bateria de Provas de Raciocínio (BPR-5) Usando a Teoria de Resposta ao Item

 

Standardization of the of Reasoning Tests Battery (BPR-5) using Item Response Theory

 

Estandarización de la Batería de Pruebas de Razonamiento (BPR-5) usando la teoría de respuesta al ítem

 

 

Ricardo Primi^I; Leandro S. Almeida^II; Tatiana de Cassia Nakano^III; Carolina Rosa Campos^IV

^IUniversidade São Francisco - USF. https://orcid.org/0000-0003-4227-6745
^IIUniversidade do Minho, Portugal https://orcid.org/0000-0002-0651-7014
^IIIPontifícia Universidade Católica de Campinas - PUC-Campinas https://orcid.org/0000-0002-5720-8940
^IVUniversidade Federal do Triângulo Mineiro - UFTM. https://orcid.org/0000-0002-1713-3307

Endereço para correspondência

 

 

---

RESUMO

A Bateria de Provas de Raciocínio (BPR-5) é um instrumento bastante utilizado para avaliação da inteligência no Brasil, possuindo três formas: infantil (1^o ao 6^o ano do Ensino Fundamental), Forma A (7º ao 9º ano do Ensino Fundamental) e Forma B (Ensino Médio e Superior). Visando a possibilidade de comparar os resultados entre sujeitos que respondem a formas diferentes, o presente estudo objetivou: (a) calibrar os itens das três formas pelo modelo de Rasch, realizando a equalização por itens comuns de modo a obter uma escala equiparável para as três formas, (b) atualizar as normas expandindo a representatividade das amostras e produzindo-se normas para diferentes combinações de idade, escolaridade e sexo, (c) descrever padrões de desenvolvimento da inteligência a partir da escala, comum, produzida entre 6 e 52 anos. Dois estudos foram relatados, o primeiro sobre a calibração dos parâmetros segundo o modelo de Rasch indicando um bom ajuste ao modelo. O segundo estudo exemplificou a utilização de regressão múltipla para criação de normas para testes psicológicos, considerando as variáveis idade, escolaridade e sexo como preditoras dos escores na BPR-5. Essas três variáveis tiveram efeitos significativos explicando 8% (Raciocínio Abstrato), 13% (Raciocínio Verbal), 12% (Raciocínio Espacial), 8% (Raciocínio Numérico) e 22% (Raciocínio Mecânico).

Palavras-chave: inteligência; regressão múltipla; equalização; BPR-5; normas; Teoria de Resposta ao Item; Modelo de Rasch

---

ABSTRACT

The Reasoning Tests Battery (BPR-5) is widely used in Brazil for the assessment of intelligence. It has three different forms: children (1^st to 6^th grade of elementary school), Form A (7^th to 9^th grade of elementary school) and Form B (high school and higher education). This study describes the steps followed to create a common metric across the forms. It aimed to: (a) calibrate the items of the three forms using Rasch model, link items and equate subjects' scores across forms using the anchoring of common items method, (b) update the norms by expanding the representativeness of the samples by producing norms for different combinations of age, education and sex, and (c) describe the developmental patterns of the BPR-5 subtests across a wide age range, from 6 to 52 years. We present two studies, the first reporting the calibration of item and person parameters with the Rasch model and a good fit to the model. The second illustrated the use of multiple regression analysis to create norms for the psychological tests considering the variables age, education and gender as predictors of the BPR-5 scores. These three variables had significant effects explaining 8% (Abstract Reasoning), 13% (Verbal Reasoning), 12% (Spatial Reasoning), 8% (Numerical Reasoning) and 22% (Mechanical Reasoning) of the variance.

Keywords: intelligence; multiple regression; equating; BPR-5; norms; Item Response Theory; Rasch Model

---

RESUMEN

La Batería de Pruebas de Razonamiento (BPR-5) es un instrumento muy utilizado para la evaluación de la inteligencia en Brasil, disponiendo de tres formas: infantil (1° al 6° año de la Enseñanza Fundamental), Forma A (7° al 9° año de la Enseñanza Fundamental) y Forma B (Bachillerato y Educación Superior). Teniendo como finalidad la posibilidad de comparar los resultados entre sujetos que responden a diferentes versiones, el presente estudio tuvo como objetivo: (a) calibrar los ítems de las tres formas por el modelo de Rasch, realizando la igualación por ítems comunes a fin de obtener una escala equiparable para las tres formas, (b) actualizar las normas ampliando la representatividad de las muestras y produciendo normas para diferentes combinaciones de edad, escolarización y sexo, (c) describir patrones de desarrollo de la inteligencia a partir de la escala, común, producida entre los 6 y los 52 años. Dos estudios fueron reportados, el primer sobre la calibración de los parámetros de acuerdo con el modelo de Rasch, indicando un buen ajuste al modelo. El segundo estudio ejemplificó la utilización de regresión múltiple para crear normas para tests psicológicos, considerando las variables edad, educación y sexo como predictivos de los escores en el BPR-5. Esas tres variables tuvieron efectos significativos explicando 8% (Razonamiento Abstracto), 13% (Razonamiento Verbal), 12% (Razonamiento Espacial), 8% (Razonamiento Numérico), y 22% (Razonamiento Mecánico).

Palabras clave: inteligencia; regresión múltiple; ecualización; BPR-5, normas; Teoría de Respuesta al Ítem, Modelo de Rasch.

---

 

 

Os testes de inteligência usados em processos de avaliação psicológica são parte importante da prática profissional do psicólogo em diversas áreas (educacional, clínica, organizacional, dentre outras) contribuindo com informações importantes para a tomada de decisões. Pesquisas de revisão indicam que a Bateria de Provas de Raciocínio (BPR-5) é um dos instrumentos nacionais mais frequentemente utilizados para avaliação da inteligência (Alves et al., 2016; Campos & Nakano, 2012; Primi & Almeida, 2000).

A BPR-5 (Primi & Almeida, 2000) originou-se da Bateria de Provas de Raciocínio Diferencial (BPRD) construída por Almeida (1988), sendo composta por cinco subtestes (Raciocínio Abstrato, Raciocínio Verbal, Raciocínio Numérico, Raciocínio Espacial e Raciocínio Mecânico). A bateria possui duas formas: Forma A, para alunos do 7º ao 9º ano do Ensino Fundamental, e Forma B, para alunos da 1ª à 3ª séries do Ensino Médio (podendo, sua utilização, ser ampliada para o Ensino Superior). A bateria tem como referencial a teoria Cattell-Horn-Carroll (CHC) de Inteligência (McGrew, 2009).

O modelo CHC concebe a inteligência como um construto multidimensional organizado hierarquicamente em três estratos: fator geral, capacidades amplas e habilidades específicas. O resultado geral obtido na BPR-5 pode ser compreendido como uma medida de capacidade ampla relacionada ao raciocínio fluido (Gf), sendo este o melhor indicador de inteligência geral (fator g). Isso se deve à maior correlação de Gf com o fator g e pelo fato que as tarefas requerem processo básicos mais gerais de raciocínio como, por exemplo, memória de trabalho, atenção controlada e funções executivas (Kovacs & Conway, 2016). Os subtestes da bateria associam-se também, adicionalmente, a outros fatores amplos: a prova de Raciocínio Verbal (RV) está relacionada à inteligência cristalizada (Gc); a prova de Raciocínio Espacial (RE) associada ao processamento visual (Gv); a Prova de Raciocínio Numérico (RN) está associada à habilidade quantitativa, memória de trabalho e processamento visual; a prova de Raciocínio Mecânico (RM) está associada a conhecimentos práticos mecânicos e processamento visual, e a Prova de Raciocínio Abstrato (RA) à capacidade de raciocínio fluido (Almeida & Primi, 2004; Godoy et al., 2008; Primi & Almeida, 2000; Primi, Couto et al., 2012; Primi, Nakano et al., 2012).

Métodos de Definição de Métricas por meio da Teoria de Resposta ao Item (TRI)

A BPR-5 possui três formas: Forma infantil, atualmente em desenvolvimento, para uso em crianças do 2^o ao 6^o ano do Ensino Fundamental (8 a 12 anos), Forma A para 7^o ao 9^o ano (12-13 a 14-15 anos) e Forma B para 1^o ao 3^o ano do Ensino Médio (15-16 a 17-18 anos). As formas contêm itens comuns entre si, mas, também, itens específicos. Tal fato dá origem a problemas de comparabilidade das métricas de notas obtidas em formas diferentes. Os escores brutos, calculados pela soma simples do número de acertos, não podem ser diretamente comparados visto que dependem não só do nível de habilidade do sujeito, mas, principalmente, do número de itens em cada forma e, mais importante, das dificuldades dos itens que a compõem. Considerando-se que a forma infantil tem itens mais fáceis relativamente à forma B, um escore de 10 acertos nessas duas formas não significará o mesmo nível de inteligência.

Atualmente, os escores brutos na BPR-5 são convertidos em resultados padronizados, chamados EPN (Escores Padrão Normalizados) e percentis. Nessa métrica é possível comparar estudantes com mesmo nível de escolaridade, além do desempenho do sujeito em cada tipo de raciocínio. No entanto, as comparações são sempre feitas entre resultados de uma mesma forma. A normatização original não permite comparações desenvolvimentais entre, por exemplo, crianças estudantes do 5º ano (Forma A) com estudantes do Ensino Médio (Forma B). Assim um dos objetivos deste trabalho foi construir uma escala comum entre as formas da BPR-5 permitindo esse tipo de comparação desenvolvimental, ampliando a proposta, já existente, de comparação por nível de escolaridade. Além disso buscou-se também incluir a informação referente a idade, além da escolaridade.

Para isso, empregou-se metodologias da Teoria de Resposta ao Item (TRI) chamadas "linkagem" e equalização. Esse procedimento permite estabelecer uma métrica comum entre itens de provas diferentes medindo o mesmo construto ou de habilidades entre pessoas pertencentes a diferentes grupos (De Ayala, 2009; Hambleton et al., 1991; Pasquali & Primi, 2003). Tal procedimento é chamado linkagem quando se refere à métrica comum dos parâmetros dos itens e equalização, quando se refere à métrica comum dos parâmetros das pessoas. A utilização desses recursos possibilita a elaboração de escalas de proficiências comuns a todos os anos escolares. É um procedimento comum nas avaliações educacionais, como o Sistema de Avaliação da Educação Básica (SAEB), habilitando a comparação de resultados acadêmicos em diferentes anos escolares (Klein, 2009).

A TRI modela o acerto aos itens em função da capacidade dos sujeitos e das propriedades (parâmetros) dos itens. Considere o modelo de Rasch: seguindo a notação que a habilidade da pessoa seja e a dificuldade do item j seja b_j, e a probabilidade de acertar o item 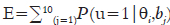seja dada por:

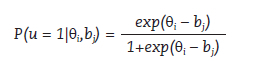
Considere dois testes, A e B, cada um com dez itens, medindo um mesmo construto. Considere que os dez itens do teste A tenham dificuldade 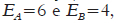e os dez itens do teste B,b_b= +.40. Suponha que um sujeito com habilidade θ=0 responda aos dois testes. Substituindo os resultados na fórmula, calcula-se o escore esperado nos dois testes que resultará em: , ou seja, seis acertos na primeira prova e quatro acertos na segunda. Assim, é possível ver que, embora o mesmo sujeito tenha respondido aos dois testes, os escores serão diferentes por causa da disparidade na dificuldade dos itens que os compõem. Na TRI, como as dificuldades dos itens estão parametrizadas pelos índices de dificuldade, ao se estimar a habilidade desse sujeito, usando esses dois testes, o modelo irá mapear escores diferentes para um mesmo nível de θ . Levando em conta a dificuldade dos testes, o modelo identificará que, apesar da diferença no número de acertos, eles refletem o mesmo nível de θ . Esse exemplo ilustra sinteticamente a base do processo de equalização.

Quando se tem parâmetros dos itens calibrados na mesma escala, isto é, linkados, é possível criar uma escala com métrica comum entre formas de testes compostos por itens diferentes que, eventualmente, tenham dificuldade média díspares. Os desenhos para esse processo são chamados estudos de ancoragem, caracterizados por dois formatos principais: via itens comuns ou via pessoas em comum (via população). Esses desenhos estão revisados detalhadamente em Andrade et al. (2000). O ponto central nesses métodos se embasa na necessidade de algum ponto de ancoragem, seja por meio de itens comuns entre as duas formas do teste que se deseja linkar ou por meio do mesmo grupo de pessoas (portanto, a mesma distribuição de habilidades) respondendo às duas formas do teste (Wolfe, 2000).

A equalização está intimamente relacionada ao problema da identificação da métrica nos modelos TRI. Para entender esse problema, considere o seguinte exemplo. Imagine que, no exemplo anterior, somassem 1,5 ao theta (resultando θ= 1, 5 ) e, o mesmo valor aos parâmetros de dificuldade dos dois testes (resultando na dificuldade média b_a=+1,10 e b_b=+1,90 dos testes A e B, respectivamente). Ao calcular os escores esperados, novamente se chegaria aos mesmos resultados. Isso ocorre porque as diferenças θi–b_j são iguais nos dois casos. Mas a métrica absoluta da escala - pessoas/itens - mudou, embora a métrica relativa permaneça inalterada. Assim, no momento de calibração dos parâmetros dos itens e estimação das habilidades - momento em que esses valores são calculados - há um problema inerente de identificação, isto é, um problema decorrente do fato de que várias soluções numéricas são possíveis. Isso é resolvido definindo-se um ponto âncora para a métrica da escala na primeira calibração. O programa Winsteps, usado neste estudo, utiliza o método de calibração por máxima verossimilhança conjunta (Joint Maximum-Likelihood Estimation JMLE). Esse método calibra, simultaneamente, as habilidades dos sujeitos e as dificuldades dos itens. A estratégia de identificação da métrica é feita: (a) fixando-se a média de dificuldade dos itens igual a zero ou (b) fixando-se a média das habilidades igual a zero (Linacre, 1999; 2017).

A equalização pode ser entendida como uma sistematização para definir a métrica da escala, ancorando-a em pontos pré-definidos escolhidos cuidadosamente pelo pesquisador, visando a obtenção de uma escala com métricas comparáveis, ainda que com provas diferentes. Este estudo utilizou o método de itens comuns - itens âncora - para linkar as escalas das três formas da BPR-5. O desenho de itens comuns com calibração conjunta produz a estimação de parâmetros dos itens e sujeitos em uma métrica comum. 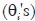Assim o primeiro objetivo do presente estudo foi realizar a estimação dos parâmetros dos itens e dos estudantes em uma métrica comum usando o procedimento de linkagem/equalização via TRI.

Métodos de Normatização via Regressão Múltipla

O procedimento de normatização consiste em transformar os resultados brutos em métricas padronizadas mais facilmente interpretáveis, adicionando sentido prático aos resultados. Há três procedimentos comumente adotados: (a) referência à norma: que transforma os resultados a partir de uma comparação com a expectativa probabilística de ocorrência de um certo resultado em um grupo normativo definido, (b) referência ao conteúdo: que transforma os resultados indicando o quanto a pessoa domina um determinado universo de tarefas/conteúdos que definem o construto avaliado pelo teste e (c) referência ao critério: que transforma os resultados indicando uma previsão dos resultados em uma medida externa chamada critério. Em cada caso, a nova escala transformada incorpora informações dessas fontes de dados adicionais, respectivamente: distribuição dos escores no grupo normativo, definição do conteúdo avaliado e variável externa, adicionando um valor interpretativo mais prático à nova métrica, além de padronizar a escala garantindo que os números da nova escala tenham sempre o mesmo sentido (Anastasi & Urbina, 1997; Nunes & Primi, 2010).

A BPR-5 (Primi & Almeida, 2000) empregou, até o momento, o procedimento de referência à norma, a partir da criação de uma escala padronizada com a métrica tradicional usada em testes de inteligência (estabelecendo a média em 100 pontos em medida de escore padrão normalizado e desvio padrão de 15 pontos), assim como em percentil. Os grupos de referência foram formados por estudantes do 7^o ao 9^o ano do Ensino Fundamental e do 1^o ao 3^o ano do Ensino Médio. Assim as notas padronizadas indicam o quanto os alunos se afastam, para cima ou para baixo, dos resultados esperados de acordo com o grupo de referência, entendido como alunos frequentando o mesmo ano escolar.

O método estatístico utilizado para transformar os escores brutos em quociente de inteligência (QI) foi o de normalização: nesse procedimento, para cada escore bruto, calcula-se a proporção de pessoas com notas iguais ou menores do que aquela em consideração. Descobre-se, então, "quais valores do escore padronizado z, em uma distribuição normal teórica, correspondiam a cada proporção. Transforma-se tais valores para a escala de QI de desvio utilizando a fórmula QI = (z .15) + 100, associando-os aos escores brutos originais" (Primi & Almeida, 2000, p. 40).

Uma potencial limitação desse procedimento é que, ao se formar os grupos e comparar os alunos dentro desses grupos, qualquer diferença devido à interação entre idade e série é eliminada. Esse procedimento compara os estudantes com colegas da mesma série, desconsiderando diferenças de idade que podem existir entre eles. Tecnicamente, o efeito das variáveis-grupo, nesse caso, a escolaridade, é eliminado no momento de interpretação dos escores dos testes.

Recentemente, Van Breukelen e Vlaeyen (2005) propuseram um método de normatização baseado na regressão múltipla. Quando se quer construir grupos normativos e, consequentemente, tabelas normativas combinando-se mais de uma variável, como sexo, idade e escolaridade, o procedimento tradicional facilmente se tornará trabalhoso, além de, muitas vezes, inviável. A inviabilidade poderá decorrer do pequeno número de pessoas nas células formadas pela combinação dessas variáveis. Os autores propõem uma solução mais eficiente usando regressão múltipla. Considere a equação de regressão como:

A variável é o escore do teste que se pretende normatizar. As variáveis X₁...X_k representam as variáveis de controle. Nesse cenário, o valor de (valor predito do escore no teste Y) será a média no teste, dados os valores das variáveis X's. Equivale a previsão da média normativa para as diversas combinações das variáveis X. Tomando o escore de uma pessoa Y_i calcula-se o resíduo obtem-se o quanto essa pessoa i se desvia do valor médio previsto para pessoas com características similares em todos os X's. Finalmente, o escore padronizado z é calculado pela fórmula: 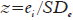. O valor de SD_e é a variância de erro da análise de regressão (MS squared error): .

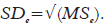Uma limitação inerente à regressão múltipla é que ela modela relações lineares entre X e Y. Se a relação entre as variáveis de controle e os escores do teste for nãolinear e/ou houver efeitos de interação entre as variáveis X, o modelo ficaria mais complicado, requerendo a inclusão de efeitos não lineares como X₂ e/ou de interação X₁ X₂.

Uma maneira mais simples para modelar relações não lineares é recodificar cada variável X_k em códigos dummy. Por exemplo, a variável ano escolar com 12 valores possíveis pode ser recodificada em 12-1 variáveis dummy s2-s12. A primeira variável, s2, terá valor 1 para os alunos do 2º ano e 0 para os alunos restantes; a variável s3 será 1 para os alunos do 3º ano e 0 para os alunos restantes, e assim sucessivamente até s12. Nesse esquema, o primeiro ano é o grupo de referência com o qual todos os outros grupos são comparados e se estimam 11 β's, um para cada ano escolar. Com isso o modelo irá incorporar eventuais padrões não lineares existentes nos dados. Essa forma de especificar as variáveis produz uma configuração similar à análise de variância (ANOVA).

Assim, diante dessa possibilidade, o segundo objetivo deste estudo foi aplicar o método de regressão múltipla na atualização das normas da BPR-5. Espera-se produzir normas atualizadas e ampliadas para a BPR-5 e, ao mesmo tempo, demonstrar uma aplicação prática do procedimento definido por Van Breukelen e Vlaeyen (2005).

Diante do exposto, a presente pesquisa objetivou: (a) calibrar os itens das três formas da BPR-5 pelo modelo de Rasch e realizar a equalização por itens comuns obtendo-se uma escala equiparável para as três formas, (b) atualizar as normas da BPR-5 expandindo a representatividade das amostras, (c) descrever os padrões de desenvolvimento da inteligência a partir da escala, comum, produzida entre as provas. Para isso, dois estudos foram conduzidos e serão apresentados, separadamente, a seguir.

 

Estudo 1: Calibração dos Parâmetros e Equalização das Notas via Modelo de Rasch

A primeira fase deste estudo objetivou realizar as calibrações dos parâmetros dos itens e estimação das habilidades das pessoas usando a TRI.

Método

Participantes

No estudo de calibração dos itens, foram usados dados de N = 4.062 crianças, adolescentes e adultos. Destes, 779 estudantes responderam à Forma i (entre 7 a 14 anos do 2^o ao 9^o ano do Ensino Fundamental), 603 estudantes responderam à Forma A (entre 11 a 19 anos no 7^o ao 9^o ano) e 2.680 estudantes responderam à Forma B, sendo 1.832 estudantes de Ensino Médio e 848 adultos universitários ou com Ensino Médio completo (entre 14 a 64 anos). Para compor tal amostra, foram combinadas bases de 14 conjuntos de dados, um dos quais é o estudo de normatização da BPR-5, e conjuntos adicionais originados de estudos que utilizaram a BPR-5 desde sua publicação, em 2000, em dissertações/teses de mestrado/doutorado orientados pelo primeiro autor e outros trabalhos de pesquisadores colaboradores na Universidade São Francisco. A amostra é balanceada em razão do sexo (50,1% do sexo feminino).

Instrumentos

A BPR-5 (Primi & Almeida, 2000), na sua versão A e B, é formada por cinco subtestes: Prova de Raciocínio Abstrato (Prova RA): composta por 25 itens envolvendo analogia com figuras geométricas ou abstratas, ou seja, A:B // C: ? (A, B, C, D, E), sendo necessário descobrir a relação existente entre os dois primeiros termos e aplicá-la ao terceiro, para se identificar a quarta figura entre cinco alternativas de resposta (tempo limite de 12 minutos); Prova de Raciocínio Verbal (Prova RV): composta por 25 itens envolvendo analogias com palavras, no mesmo formato da Prova RA (tempo limite de 10 minutos); Prova de Raciocínio Espacial (Prova RE): composta de 20 itens representando séries de cubos tridimensionais em movimento, sendo necessário identificar, entre cinco alternativas de resposta, aquela que corresponde a uma nova posição do cubo na base do seu movimento de rotação (tempo limite de 18 minutos); Prova de Raciocínio Numérico (Prova RN): composta por 20 itens representando séries de números lineares ou alternadas, em que o sujeito deve descobrir qual a relação aritmética que rege as progressões nas séries e aplicá-la escrevendo os dois últimos números que completariam a série (tempo limite de 18 minutos); Prova de Raciocínio Mecânico (Prova RM): composta por 25 itens constituídos por pequenos textos e gravuras que retratam problemas práticos, envolvendo conteúdos físico-mecânicos, cabendo ao sujeito escolher, dentre cinco alternativas de resposta, a correta (tempo limite de 15 minutos).

A versão infantil da bateria (BPR5-i, Almeida et al., 2007) foi construída para avaliar estudantes de 1^o ao 6^o ano do Ensino Fundamental, sendo composta por quatro provas: Raciocínio Abstrato (RA, 20 itens), Raciocínio Verbal (RV, 32 itens), Raciocínio Numérico (RN, 30 itens), semelhantes à versão A e B, além de Raciocínio Lógico (RL, 15 itens), composta por problemas e situações do cotidiano da criança, requerendo o raciocínio dedutivo para serem resolvidos. Essa versão da bateria ainda não é comercializada e está em desenvolvimento (Zanarella et al., 2006).

As três formas foram construídas contendo itens comuns, de modo a tornar possível a linkagem. Na Tabela 1, apresenta-se a distribuição dos itens em cada forma da BPR. A base completa contém 231 itens. As formas A e B contêm cerca de 70% de itens comuns. A forma i contém, em geral, 30% de itens comuns vindos das formas A e B. Essa forma contém um número maior de itens por estar em desenvolvimento, sendo que parte deles serão eliminados na versão final.

Procedimentos e Análise de Dados

Inicialmente as bases foram reunidas e organizadas, compatibilizando-se a codificação das variáveis adicionais dos sujeitos. Construíram-se três bases, uma para cada forma. A calibração dos parâmetros foi feita no programa Winsteps utilizando-se o modelo de Rasch apresentado na introdução (Linacre, 2017). Uma condição básica para se aplicar a TRI é a unidimensionalidade, isto é, os itens devem medir uma dimensão principal. Se houver dimensões secundárias, essas devem ter influência negligenciável. Essa análise foi objeto de um outro trabalho por meio da aplicação da análise fatorial confirmatória (bi-fatorial) dos itens (Primi et al., 2013). Esse estudo concluiu que há uma dimensão geral robusta subjacente a todas as provas, justificando o uso da TRI para se extrair uma escala comum.

Iniciou-se a calibração pela base da forma B. Para identificação da métrica da escala, ancorou-se a escala fixando a dificuldade média dos itens 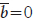. A calibração foi feita cinco vezes, uma por prova. Os parâmetros de dificuldade dos itens foram salvos e, no passo seguinte, efetuou-se a calibração da base da Forma A. Nesse caso fixou-se os parâmetros de dificuldade dos itens comuns. Com isso a métrica da Forma A ficou referenciada à métrica da Forma B. No terceiro passo, efetuou-se a calibração dos itens da Forma i (infantil) fixando-se a dificuldade dos parâmetros dos itens comuns, nos valores obtidos nas duas fases anteriores.

No processo de equalização, os itens âncora tem seu valor de dificuldade "congelados" em um valor pré-estabelecido na calibração anterior. Mas o Winsteps oferece uma opção mostrando uma estimativa do valor da dificuldade caso esses itens âncora fossem "descongelados". Esse indicador é chamado displacement e representa um indicador da qualidade dos itens âncora. Itens com valores absolutos de displacement 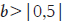indicam instabilidade no parâmetro de dificuldade devido ao potencial funcionamento diferencial do item. Assim os itens com displacement 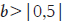foram estimados separadamente em cada forma retirando-os da lista de itens âncora.

A análise dos dados focou no ajuste ao modelo usando-se os índices infit e outfit. Esses índices são medidas globais estimadas a partir de transformações dos resíduos do modelo, isto é, diferenças entre as respostas observadas e os valores preditos pelo modelo: . O infit é mais sensível aos resíduos nos itens com dificuldade próxima à habilidade do sujeito e o outfit, sensível a padrões inesperados de respostas quando a diferença entre o theta e a dificuldade dos itens é grande - acertos inesperados em itens difíceis ou erros inesperados em itens fáceis. Valores abaixo de 1,4 são aceitáveis (Linacre, 2017). Analisou-se também o índice psicométrico clássico de correlação item-theta.

Resultados e Discussão

O primeiro objetivo deste trabalho foi calibrar os itens das três formas da BPR-5 realizando, para isso, a linkagem dos parâmetros dos itens e equalização das habilidades. Assim, começamos por apresentar os resultados da calibração. Na Tabela 2, apresentamos as estatísticas descritivas sumarizadas dos itens: o número de itens por subteste, os valores médios dos índices de dificuldade b, os valores médios e os desvios padrão das correlações item-theta r_ith e dos índices de ajuste infit e outfit.

Inicialmente os índices de ajuste estiveram próximos do valor esperado 1 com desvios padrão ao redor de 0,10, indicando que eles se agrupam ao redor do valor esperado, sendo, portanto, considerados adequados. Nenhum item teve o valor 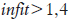. Somente oito tiveram . Esses resultados indicam um bom ajuste ao modelo e, consequentemente, a adequação das calibrações. As correlações item-theta foram altas, em média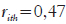 indicando uma boa consistência interna dos itens nos subtestes. Os índices de dificuldade médios dos itens variaram em função das provas e dos agrupamentos (comuns ou únicos). É importante lembrar que a métrica foi fixada na primeira calibração da Forma B, tendo o índice de dificuldade médio igual a 0 nessa forma. Nas calibrações restantes, na Forma A e i, esses valores mudam, pois estão referenciados aos valores obtidos na Forma B. Por isso, os valores para os itens únicos da Forma A e i ficaram, em média, mais difíceis.

A Figura 1 apresenta as distribuições dos parâmetros de dificuldade e dos parâmetros theta de habilidade por prova. Na metade superior da Figura 1, apresenta-se a distribuição dos itens. Cada um representado por um ponto. Tons de cinza indicam a prova. Na metade inferior, encontra-se a distribuição das habilidades (os parâmetros theta dos sujeitos na calibração). Essa Figura apresenta, ainda, uma função densidade, usando um polimento da curva de forma a apresentar um gráfico contínuo da distribuição ao invés dos histogramas. Nota-se que os itens estão bem distribuídos em relação aos valores de theta. Nota-se também que há uma quantidade alta de itens fáceis em relação à distribuição de theta. Esses itens pertencem a Forma i. Entretanto a distribuição de theta está mais deslocada à direita em função da amostra ser predominantemente de estudantes de Ensino Médio e superior, respondendo à Forma B.

A Figura 2 apresenta a Curva Característica dos Testes (CCT por forma e por subteste) fazendo a correspondência entre os valores dos escores brutos e os valores de theta equalizados. Essa função soma as equações das curvas características dos itens calculando-se o valor do escore bruto esperado, dado o valor de theta. Nota-se que, para um mesmo escore bruto, E=12, por exemplo, o em razão da composição da prova em termos da dificuldade dos itens.

 

Estudo 2: Criação de Tabelas Normativas via Regressão Múltipla

Essa fase do estudo objetivou atualizar as normas da BPR-5 empregando o método de regressão múltipla. Esse estudo usou as notas dos estudantes obtidas pela TRI calibrados em uma métrica comum entre as formas do teste.

Método

Participantes

A amostra usada para o cálculo das expectativas normativas foi composta por estudantes e adultos que apresentavam escolarização compatível com a idade. Combinou-se a amostra de calibração do Estudo 1 com dados fornecidos pela editora que comercializa o teste. Esses dados se originam do sistema online da editora para correção das provas, oferecidos aos psicólogos. Foram incluídos protocolos autorizados pelos usuários de aplicações ocorridas entre os anos de 2010 a 2015.

A amostra de normatização ficou composta por N = 30.708 estudantes e adultos. A idade variou de 11 e 59 anos. Do 6º ano até o Ensino Médio, os grupos contêm somente estudantes com idade compatível com o ano escolar. Assim as variáveis idade/escolaridade são combinadas. A correlação entre idade e escolaridade é . Depois do Ensino Médio, os grupos foram divididos por idade, de dois em dois anos. Entre 18 e 23 anos a amostra é composta por estudantes universitários. De 24 anos em diante, é composta por pessoas que tinham completado curso superior ou pós-graduação. A amostra é balanceada em termos de sexo, sendo 53% de homens.

Assim, a amostra de normatização é composta por um grupo com percurso escolar compatível com a idade - sem distorção escolaridade/idade. No caso dos adultos, incluíram-se aqueles com idade entre 18 e 23 que estavam cursando o Ensino Superior e aqueles com 24 ou mais que concluíra o Ensino Superior. Essa composição foi planejada para se ter uma estimativa do desempenho cognitivo em condições ideais de desenvolvimento intelectual. Os sujeitos selecionados para o grupo normativo tiveram um progresso de tempo de vida acompanhado de escolaridade compatível com a idade, sem interrupções. Há tabelas que não são objetos deste estudo com amostras de percursos diferentes, tais como adultos com escolaridade mais baixa do que a esperada, por exemplo, adultos com Ensino Médio somente.

Materiais, Procedimentos e Análise de Dados

No estudo de normatização, foram usados dados da Forma A e B, descritas no Estudo 1. A preparação da análise referente às expectativas normativas foi feita em seis etapas. Inicialmente as diferentes bases de dados foram compatibilizadas e agregadas em uma base comum. Após essa agregação foi feita uma análise descritiva para verificar a disponibilidade das informações sobre os sujeitos (idade, escolaridade, sexo e forma do teste). Em uma segunda etapa, selecionou-se os sujeitos que atendiam aos critérios pré-estabelecidos de compatibilidade idade/ano escolar. A compatibilidade foi assim definida: 6^o ano (11-12 anos), 7^o ano (12-13 anos), 8^o ano (13-14 anos), 9^o ano (14-15 anos), 10^o ano ou 1^o ano do Ensino Médio (15-16 anos), 11^o ou 2^o ano do Ensino Médio ano (16-17 anos), 12^o ou 3^o ano do Ensino Médio ano (17-18 anos), estudante universitário (18 a 23 anos) e adulto com Ensino Superior ou pós-graduação (24 anos ou mais).

Na terceira etapa, preparou-se uma tabela de conversão dos resultados brutos para resultados padronizados na métrica equalizada da TRI. Para isso, foram criadas treze tabelas: três para a Forma i (provas RA, RN e RV) e dez para as Formas A e B (provas RA, RV, RN, RE e RM). No cálculo das habilidades no modelo de Rasch, o escore total é suficiente para estimação do theta. Isso significa que o mesmo escore total, por exemplo E=12, está sempre associado somente a um valor de theta, independentemente de quais itens o sujeito acertou (Lord, 1980; Primi et al., 2018). Essa propriedade permite a elaboração de tabelas de conversão sem a necessidade de cálculos mais complexos, como seria o caso se tivéssemos utilizado o modelo de TRI de 2 ou 3 parâmetros. A partir dessas tabelas, transformou-se os resultados das provas nas diferentes formas para o resultado padronizado TRI. Essa conversão permitiu comparar os resultados dos diferentes grupos de sujeitos de várias idades, cujos escores foram estimados por diferentes formas do teste com itens distintos.

Na quarta etapa, foram realizadas as análises de regressão múltipla para se obter as expectativas normativas empregando o método descrito em Van Breukelen e Vlaeyen (2005). As regressões foram repetidas cinco vezes, uma por prova, assim, a variável predita era o escore padronizado TRI de cada prova e as variáveis preditoras: idade, escolaridade e sexo. A função de regressão retorna uma previsão indicando o valor médio esperado para cada grupo de idade, escolaridade e sexo, isto é, a expectativa normativa. Comparando o resultado Y_i de um indivíduo i com a expectativa normativa correspondente ao seu grupo e dividindo-se essa diferença pelo erro padrão da regressão: , o resultado padronizado zi foi obtido, indicando o quanto o indivíduo i se afasta da expectativa baseada em um grupo de pessoas com mesmo sexo, idade e escolaridade. Assim o resultado z_i é o padronizado final que se desejava calcular para construir as tabelas normativas.

Um detalhe importante nessa análise de regressão foi a maneira como as variáveis preditoras foram codificadas. Conforme discutido na introdução, usou-se a codificação dummy para acomodar eventuais padrões não lineares de associação idade/escolaridade/sexo e desempenho cognitivo. A variável idade foi transformada em 23 variáveis dummy correspondentes aos valores 13, 14, 15, 16, 17, 18, 19-20, 21-22, 23-24, 25-26, 27-28, 29-30, 31-32, 33-34, 35-36, 37-38, 39-40, 41-42, 43-44, 45-46, 47-48, 49-50, 51-52. O grupo de 12 anos foi considerado referência e é codificado quanto às 23 dummys com valor 0. A escolaridade foi codificada em três dummys: se o sujeito era estudante universitário (universt), se tinha Ensino Superior completo (sup_compl) ou se tinha pós-graduação completa (stricto ou latu sensu - pos_grad). O Ensino Fundamental e médio é representado quando essas três dummys têm valor zero. Os diferentes níveis de escolaridade no Ensino Fundamental e médio são captados pelas dummys das idades 13 a 18, já que não há distorção idade e série na amostra utilizada - idade/escolaridade são praticamente colineares. A variável sexo foi codificada por uma dummy cujo valor 1 foi atribuído às meninas. Com essa codificação, o intercepto da regressão representa a expectativa de desempenho de meninos do 6^o ano com 12 anos de idade. Os valores dos das k variáveis dummy fazem uma comparação desse grupo de referência com o subgrupo específico k indexado pela variável dummy que está sendo analisada.

Na quinta etapa, empregou-se o modelo estimado nas regressões para se construir as tabelas normativas. Criou-se uma função calcula.EPN para gerar os valores padronizados. Essa função recebe, como input, o escore bruto, a forma, o subteste e as características da pessoa (sexo, idade e escolaridade) e retorna o escore padronizado EPN com M=100 e DP=15. A função converte o escore bruto em escore padronizado TRI usando a tabela de conversão (criada na terceira etapa). Em seguida, calcula a expectativa normativa considerando, as variáveis do sujeito, usando o modelo de regressão (criado na quarta etapa). Calcula, então, o desvio padronizado z do sujeito em relação à expectativa normativa, convertendo para a escala M=100 e DP=15 e retorna o resultado.

As tabelas normativas foram criadas inicialmente produzindo-se uma tabela com todas as combinações dos valores das variáveis sexo, idade e escolaridade, o que resultou em 78 entradas, cada uma correspondente a uma tabela. Usou-se esse "grid" com a função calcula.EPN para obter os resultados padronizados para todos os escores possíveis (0 a 20 ou 0 a 25) nas cinco provas.

Na última etapa, foi criado um aplicativo shiny (https://www.rstudio.com/products/shiny/) disponibilizado na web, que implementa, automaticamente, as funções descritas anteriormente, faz a conversão dos escores brutos em padronizados e apresenta a tabela selecionada. Esse aplicativo pode ser acessado em: https://rprimi.shinyapps.io/bpr5_normas/. Ele permite automatizar a etapa de conversão, sendo que o psicólogo precisa somente selecionar a idade e escolaridade do avaliando e inserir os resultados brutos de cada subteste. O resultado padronizado será exibido sob a forma de um gráfico.

Resultados e Discussão

O segundo objetivo deste estudo foi fazer a atualização das expectativas normativas da BPR-5, para isso, empregou-se o modelo de regressão múltipla. Os parâmetros da regressão múltipla indicam a associação única encontrada entre as variáveis dummy de idade, escolaridade e sexo com as provas. Na Tabela 3, apresentamos o modelo final da regressão para as cinco provas. Para cada prova há três colunas: o coeficiente não padronizado B, o coeficiente padronizado β e a significância dos coeficientes. As linhas da Tabela apresentam todas as dummys. Nas últimas duas linhas apresentam-se o número de sujeitos por prova com as informações disponíveis e os valores da correlação múltipla ao quadrado R².

Um primeiro ponto a ser comentado é o efeito da idade. Tomando-se o coeficiente padronizado, nota-se que ele é geralmente maior nas idades de 18 a 22 anos. A partir de 22 anos, o efeito diminui. É importante lembrar que esses efeitos representam a comparação com o grupo de referência formado pelos alunos de 12 anos. Essa diminuição é mais forte nas provas de Raciocínio Mecânico, Numérico e Espacial, e menor nas provas de Raciocínio Verbal e Abstrato. Esse efeito é mais fácil de ser visualizado na Figura 3, na qual os coeficientes β's relativos às diferentes idades são apresentados como pontos.

Nessa Figura, fica mais evidente essa diferença entre as provas. Os estudos de maleabilidade mostram que: "o raciocínio fluido Gf, assim como as capacidades de processamento cognitivo crescem rapidamente desde a infância até a adolescência e passam a cair no início da idade adulta, continuando esse declínio ao longo da vida. Diferentemente, as capacidades ligadas ao conhecimento, no caso, a inteligência cristalizada Gc, crescem de maneira similar, mas com taxa de crescimento menor que o raciocínio fluido e não apresentam declínio na idade adulta" (Primi, McGrew, Schneider, Nakano, & Dias no prelo, p. 69). Assim, o achado, contrastando a prova de Raciocínio Verbal versus Mecânico/Espacial/Numérico, é condizente com esse padrão, já que o Raciocínio Verbal é a prova mais influenciada pela inteligência cristalizada. As três provas restantes são mais associadas à capacidade de processamento visual - Gv (Ackerman, 1996; Horn & Blankson, 2012).

O segundo ponto a ser notado é o efeito da escolaridade. Observou-se um efeito positivo evidente pelos β₂ encontrados (de 0,06 a 0,19). É interessante notar que o efeito é mais forte para o nível superior, isto é, comparando-se pessoas com nível superior ou pós-graduação completa com os grupos restantes, sendo também mais forte nas provas de Raciocínio Mecânico, Verbal, Numérico e Espacial (ao redor de 0,10). Por último, é possível notar o efeito do sexo. Em geral, as mulheres apresentaram desempenho ligeiramente menor que os homens. Essa diferença é mais pronunciada nas provas de Raciocínio Mecânico, Espacial e Numérico, nas quais a influência da capacidade de processamento visual é maior, sendo menos proeminente na prova de Raciocínio Verbal.

Interpretamos esse resultado como uma diferença no fator específico de processamento visual e não no fator geral ligado ao raciocínio fluido que pode ser calculado somando-se as provas. Isso foi discutido mais detalhadamente em Flores-Mendoza et al. (2013). A inclusão da variável sexo nas regressões controla a diferença no cálculo das expectativas normativas comparando mulheres e homens entre si. Dessa forma, elimina-se a diferença média entre mulheres e homens dos resultados padronizados finais. Isso é justificado pelo entendimento de que essa diferença é originada principalmente dos fatores específicos, e não do fator geral.

Em síntese, os resultados apontaram que a correlação múltipla das variáveis incluídas na regressão com o desempenho varia em função da prova. As correlações foram mais altas nas provas de Raciocínio Mecânico , Verbal e Espacial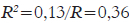 . As provas de Raciocínio Mecânico e Espacial tem uma forte influência específica do processamento visual Gv. Esse fator por sua vez é fortemente influenciado pelo sexo. De fato, se a análise sem a variável sexo no modelo for realizada, a variância explicada das notas em ambas as provas de Raciocínio Mecânico e Espacial cai para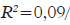 A variância explicada na prova de Raciocínio Numérico cai também para . No modelo que inclui somente idade e escolaridade, a correlação múltipla mais alta foi encontrada com a prova de Raciocínio Verbal . Isso é condizente com a ideia do crescimento maior de capacidades mais associadas à inteligência cristalizada com o aumento da escolaridade/idade.

O terceiro objetivo deste estudo foi descrever os padrões de desenvolvimento da inteligência nas diferentes provas. Isso, em parte, já foi examinado ao se comparar os efeitos relativos da idade/escolaridade nas diferentes provas, obtidos por meio da análise de regressão. Mas, para complementar essas análises, examinamos as curvas desenvolvimentais para cada prova, isto é, as médias de desempenho por prova em relação à idade nos escores TRI padronizados que permitem comparar notas em formas diferentes. Essas curvas estão apresentadas na Figura 4.

Na Figura 4, o eixo x representa os grupos de idade e o eixo y, a nota padronizada TRI que foi equalizada entre as formas do instrumento. Essa Figura apresenta a curva polida das médias de desempenho por prova e por idade. Note que foram incluídos os resultados da BPRi aplicada a crianças de 7 a 12 anos em três provas comuns com a BPR-5 (RA, RV e RN). Os sujeitos estão incluídos como pontos, cujo tamanho representa a quantidade de observações com aquela nota dentro dos grupos de idade. É importante lembrar que esses dados são transversais, isto é, compara médias de grupos de estudantes diferentes ao longo dos anos e assim não permite fazer inferência sobre como evoluem as diferenças intra-sujeitos ao longo dos anos. Dito isso é possível notar, mais uma vez, o padrão de contraste entre provas de inteligência como conhecimento versus inteligência como processamento. Assim, o desempenho na prova de Raciocínio Verbal permanece praticamente constante entre 20 a 52 anos. Nas provas de Raciocínio Numérico e Espacial os desempenhos tendem a cair a partir da idade de 28 anos.

 

Considerações Finais

Os resultados dos estudos relatados indicaram que os itens das três formas da BPR-5 apresentaram bom ajuste ao modelo predito por meio da TRI. A equalização por meio de itens comuns possibilitou o desenvolvimento de um sistema que permite a comparação do resultado de sujeitos que responderam às diferentes formas do instrumento. Desse modo, a comparação entre o desempenho de sujeitos com diferentes idades e níveis de escolaridade se tornou possível. Foram apresentados também os procedimentos para criação de tabelas normativas por meio da regressão múltipla, tomando-se as variáveis idade, escolaridade e sexo como preditoras, de modo a permitir a descrição de padrões de desenvolvimento da inteligência a partir da escala, comum, produzida entre as provas.

Como limitações do estudo convém destacar o uso somente de participantes que apresentavam idade compatível com nível esperado de escolaridade. Desse modo, outros perfis de participantes não foram considerados nas normas aqui propostas. Estudos futuros poderão envolver amostras mais diversificadas, tais como, por exemplo, adultos sem Ensino Superior, ou ainda estudantes que participam de programas de ensino de jovens e adultos (EJA), aqueles que demoraram para ingressar na universidade ou ainda analfabetos, de modo a ampliar a representatividade da amostra normativa do instrumento. Igualmente análises recorrendo a amostras que possam ser avaliadas em diferentes momentos (estudos longitudinais) também são recomendadas.

 

Agradecimentos

Não há menções.

Financiamento

Os trabalhos do primeiro autor relativos a esse artigo são financiados pela Pearson Clinical, CNPq e CAPES.

Declaração de participação da elaboração do manuscrito

Especificamente, os autores Ricardo Primi, Carolina Rosa Campos participaram da redação inicial do estudo - conceitualização, investigação, visualização, os autores Ricardo Primi participaram) da análise dos dados, e os autores Tatiana de Cassia Nakano e Leandro S. Almeida participaram da redação final do trabalho - revisão e edição. Todos os autores declaram que estão de acordo com o conteúdo do manuscrito submetido à revista Avaliação Psicológica.

Disponibilidade dos dados e materiais

Todos os dados e sintaxes gerados e analisados durante esta pesquisa serão tratados com total sigilo devido às exigências do Comitê de Ética em Pesquisa em Seres Humanos. Porém, o conjunto de dados e sintaxes que apoiam as conclusões deste artigo estão disponíveis mediante razoável solicitação ao autor principal do estudo.

Conflito de interesses

Os autores declaram que não há conflitos de interesses.

 

Referências

Ackerman, P. L. (1996). A theory of adult intellectual development: Process, personality, interests, and knowledge. Intelligence, 22(2), 227-257. http://dx.doi.org/10.1016/S0160-2896(96)90016-1        [ Links ]

Almeida S. L. (1988). O raciocínio diferencial de jovens. INIC.         [ Links ]

Almeida, L. S., & Primi, R. (2004). Perfis de capacidades cognitivas na Bateria de Provas de Raciocínio (BPR-5). Psicologia Escolar e Educacional, 8(2), 135-144.         [ Links ]

Almeida, L., Primi, R., & Cruz, M. B. Z. (2007). Bateria de Provas de Raciocínio Infantil BPR-5i. LabAPE. Universidade São Francisco.         [ Links ]

Alves, I. C. B., Rosa, H. R., Silva, M. A., & Sardinha, L. S. (2016). Avaliação da inteligência: revisão de literatura de 2005 a 2014. Avaliação Psicológica, 15, 89-97. http://dx.doi.org/10.15689/ap.2016.15ee.09.         [ Links ]

Anastasi, A., & Urbina, S. (1997). Psychological testing, 7th ed. Prentice Hall/Pearson Education.         [ Links ]

Andrade, D. F., Tavares, H. R., & C. Valle, R. da. (2000). Teoria de resposta ao item: Conceitos e aplicações. http://homes.ufam.edu.br/jcardoso/LivroTRI.pdf        [ Links ]

Campos, C. R., & Nakano, T. C. (2012). Produção científica sobre avaliação da inteligência: o estado da arte. Interação Em Psicologia, 16(2). http://doi.org/10.5380/psi.v16i2.22619        [ Links ]

De Ayala, R. J. (2009). The theory and practice of item response theory. Guilford Publications.         [ Links ]

Flores-Mendoza, C., Widaman, K. F., Rindermann, H., Primi, R., Mansur-Alves, M., & Pena, C. C. (2013). Cognitive sex differences in reasoning tasks: Evidence from Brazilian samples of educational settings. Intelligence, 41(1), 70-84. http://doi.org/10.1016/j.intell.2012.11.002        [ Links ]

Godoy, S., Noronha, A. P. P., Ambiel, R. A. M., & Nunes, M. F. O. (2008). Instrumentos de inteligência e interesses em orientação profissional. Estudos de Psicologia (Natal), 13(1), 75-81. http://doi.org/10.1590/S1413-294X2008000100009        [ Links ]

Hambleton, R. K., Swaminathan, H., & Rogers, H. J. (1991). Fundamentals of item response theory. Sage Publications Inc.         [ Links ]

Horn, J. L., & Blankson, A. N. (2012). Foundations for better understanding of cognitive abilities. In D. P. Flanagan & P. L. Harrison (Eds.), Contemporary intellectual assessment: Theories, tests, and issues, 3rd ed (pp. 73-98). The Guilford Press.         [ Links ]

Klein, R. (2009). Utilização da Teoria de Resposta ao Item no Sistema Nacional de Avaliação da Educação Básica (SAEB). Revista Meta: Avaliação, 1(2), 125-140. http://doi.org/10.22347/2175-2753v1i2.38        [ Links ]

Kovacs, K., & Conway, A. R. A. (2016). Process overlap theory: a unified account of the general factor of intelligence. Psychological Inquiry, 27(3), 151-177. http://doi.org/10.1080/1047840X.2016.1153946        [ Links ]

Linacre, J. M. (1999). Understanding Rasch measurement: Estimation methods for Rasch measures. Journal of Outcome Measurement, 3(4), 382-405.         [ Links ]

Linacre, J. M. (2017). Winsteps® (Version 3.93.0) [Computer Software] (Version 3.93.0). http://www.winsteps.com/        [ Links ]

Lord, F. M. (1980). Applications of item response theory to practical testing problems. Routledge.         [ Links ]

McGrew, K. S. (2009). CHC theory and the human cognitive abilities project: Standing on the shoulders of the giants of psychometric intelligence research. Intelligence, 37(1), 1-10. http://doi.org/10.1016/j.intell.2008.08.004        [ Links ]

Nunes, C. H. S. S., & Primi, R. (2010). Aspectos técnicos e conceituais da ficha de avaliação dos testes psicológicos. In CFP (Ed.), Avaliação Psicológica: Diretrizes na Regulamentação da Profissão (pp.101-128). Conselho Federal de Psicologia.         [ Links ]

Pasquali, L., & Primi, R. (2003). Fundamentos da teoria da resposta ao item: TRI. Avaliação Psicológica, 2(2), 99-110.         [ Links ]

Primi, R., & Almeida, L. S. (2000). BPR-5: Bateria de Provas de Raciocínio: Manual técnico. Casa do Psicólogo.         [ Links ]

Primi, R., Couto, G., Almeida, L. S., Guisande, M. A., & Miguel, F. K. (2012). Intelligence, age and schooling: Data from the Battery of Reasoning Tests (BRT-5). Psicologia: Reflexão e Crítica, 25(1), 79-88. http://dx.doi.org/10.1590/S0102-79722012000100010        [ Links ]

Primi, R., Nakano, T. C., & Wechsler, S. M. (2012). Cross-battery factor analysis of the Battery of Reasoning Abilities (BPR-5) and Woodcock-Johnson Tests of Cognitive Ability (WJ-III). Temas em Psicologia, 20(1), 121-132.         [ Links ]

Primi, R., McGrew, K. S., Schneider, W. J., Nakano, T.C., & Dias, N. M. (no prelo). Revisão de modelos de inteligência: Como a inteligência é concebida a partir de modelos baseados em evidência? In R. Primi, T. C. Nakano, K. S. McGrew, & W.J. Schneider (Eds.), Twenty-first century cognitive skills: Measures of reasoning, knowledge and creativity in large-scale assessment systems. Instituto Ayrton Senna.         [ Links ]

Primi, R., Nakano, T. C., & Wechsler, S. M. (2018). Using four-parameter item response theory to model human figure drawings. Avaliação Psicológica, 17(4), 473-483. http://dx.doi.org/10.15689/ap.2018.1704.7.07.         [ Links ]

Primi, R., Silva, M. C., Rodrigues, P., Muniz, M., & Almeida, L. S. (2013). The use of the bi-factor model to test the unidimensionality of a battery of reasoning tests. Psicothema, 25(1), 115-122. http://dx.doi.org/10.7334/psicothema2011.393.         [ Links ]

Van Breukelen, G. J. P., & Vlaeyen, J. W. S. (2005). Norming clinical questionnaires with multiple regression: The Pain Cognition List. Psychological Assessment, 17(3), 336-344. http://doi.org/10.1037/1040-3590.17.3.336        [ Links ]

Wolfe, E. W. (2000). Equating and item banking with the Rasch model. Journal of Applied Measurement, 1(4), 409-434.         [ Links ]

Zanarella, M. B., Primi, R., Almeida, L. S., & Cunha, T. F. (2006). Adaptação da BPR 5/6 para utilização em crianças brasileiras. In L. Almeida, A. Guisande, M. Gonçalves, & V. Ramalho (Orgs.), Actas da XI Conferência Internacional Avaliação Psicológica: Formas e Contextos (pp. 567-665). Psiquilíbrio.         [ Links ]

 

 

Endereço para correspondência:
Ricardo Primi
Universidade São Francisco, Programa de Pós-Graduação Stricto Sensu em Psicologia
Rua Waldemar César da Silveira, 105
Swift, Campinas/SP, CEP 13045-510
E-mail: ricardo.primi@usf.edu.br

Recebido em março de 2020
Aceito em junho de 2021

 

 

Sobre os autores
Ricardo Primi Psicólogo.Doutor em Psicologia Escolar e do Desenvolvimento Humano pela Universidade de São Paulo É Professor Associado do Programa de Pós Graduação em Psicologia da Universidade São Francisco (Mestrado e Doutorado em Avaliação Psicológica). É pesquisador membro do EduLab21 Centro de Conhecimento do Instituto Ayrton Senna.
Leandro S. Almeida Doutor em Psicologia, Psicologia da Educação, pela Universidade do Porto. Investigador do Centro de Investigação em Educação (CIEd) da Universidade do Minho. Publicações na área da inteligência, raciocínio e aprendizagem. Autor ou coautor de testes na área da inteligência.
Tatiana de Cassia Nakano Psicóloga.Mestre eDoutora em Psicologia pela PUC-Campinas. Pós-Doutorado na Universidade São Francisco (2009, bolsista Fapesp). Docente permanente do programa de pós-graduação stricto sensu em Psicologia da PUC-Campinas. Visiting scholar na University of California - Berkeley (dez/2019 a dez/2020, bolsista FAPESP.
Carolina Rosa Campos Psicóloga, Mestre e Doutora pela PUC-Campinas, com pós-doutorado pela Universidade São Francisco, na área de avaliação psicológica. Professora adjunta no Departamento de Psicologia e PPG de Psicologia e Saúde da Universidade Federal do Triângulo Mineiro.