Serviços Personalizados
Journal
artigo
Indicadores
Compartilhar
Revista Psicopedagogia
versão impressa ISSN 0103-8486
Rev. psicopedag. vol.23 no.71 São Paulo 2006
ARTIGO DE REVISÃO
Dificultades en el aprendizaje de las matemáticas: una perspectiva evolutiva
Difficulties in the mathematics learning: an evolutionary perspective
Josetxu Orrantia
Doctor em Psicológia. Profesor Titular en el Departamento de Psicologia Evolutiva y de la Educación de la Universidad de Salamanca
RESUMEN
El objetivo de este trabajo es plantear un marco teórico de carácter evolutivo que nos permita analizar y comprender las dificultades que surgen en el proceso de enseñanza y aprendizaje de las matemáticas. Para ello, comenzaremos revisando cómo se desarrolla el pensamiento matemático de los niños, ya que asumimos que las dificultades en el aprendizaje surgen en este proceso evolutivo. Posteriormente, analizaremos algunas de las dificultades, centrando nuestra atención en las dificultades relacionadas con el cálculo y la resolución de problemas.
Palabras clave: Matemática. Solución de problemas. Cognición. Niño.
SUMMARY
The aim of this paper is to describe a theoretical frame from a developmental point of view which will allow us to analyze and understand the difficulties that the teaching and learning process implies. In order to do so, we'll start reviewing how the children's mathematical thinking develops, because we assume that learning disabilities arise from this developmental process. Afterwards we analyze some of the difficulties, focusing at the difficulties related to the computation and problem solving.
Key words: Mathematics. Problem solving. Cognition. Child.
INTRODUCCIÓN
El aprendizaje de las matemáticas supone, junto a la lectura y la escritura, uno de los aprendizajes fundamentales de la educación elemental, dado el carácter instrumental de estos contenidos. De ahí que entender las dificultades en el aprendizaje de las matemáticas se haya convertido en una preocupación manifiesta de buena parte de los profesionales dedicados al mundo de la educación, especialmente si consideramos el alto porcentaje de fracaso que presentan en estos contenidos los alumnos y alumnas que terminan la escolaridad obligatoria. A esto hay que añadir que la sociedad actual, cada vez más desarrollada tecnológicamente, demanda con insistencia niveles altos de competencia en el área de matemáticas.
En este contexto, el objetivo de estas páginas es plantear un marco para analizar y entender las dificultades en el aprendizaje de las matemáticas, para que, desde este análisis, podamos imaginar la respuesta educativa que podemos ofrecer a los alumnos que presentan estas dificultades. Para ello, antes es necesario acotar lo que vamos a entender por dificultades en el aprendizaje de las matemáticas, puesto que los contenidos de matemáticas pueden ser muy diversos. Así, las dificultades pueden aparecer en contenidos como la geometría, la probabilidad, la medida, el álgebra o la aritmética. Pero muchos estamos de acuerdo en que es en la aritmética donde los alumnos encuentran más dificultades, puesto que estos son los contenidos a los que se enfrentan en primer lugar, además de que posiblemente sean la base sobre la que se asientan los demás contenidos. Por lo tanto, en las próximas páginas vamos a centrarnos en el aprendizaje de la aritmética y sus dificultades.
Ahora bien, muchos pueden estar pensando que al reducir los contenidos de las matemáticas a la aritmética nuestro interés se dirigirá fundamentalmente a los números y las operaciones básicas, dado que estos son los aspectos sobre los que tradicionalmente ha girado la enseñanza de la aritmética. Esto es parcialmente cierto. Como ya hemos expuesto en diversas ocasiones1-3 los números y especialmente las operaciones tienen sentido cuando se aprenden en el contexto de la resolución de situaciones problemáticas. Por decirlo de otra manera, las operaciones básicas deberían estar al servicio de la resolución de problemas y no al contrario, como generalmente se ha enfocado la enseñanza de la aritmética al utilizar los problemas como un mero ejercicio de las operaciones; esto es, el alumno aprendía a sumar y resolvía numerosos problemas de sumas con el fin de ejercitar la operación hasta llegar a automatizarla.
Nuestra intención es dar la vuelta a este planteamiento y considerar la resolución de problemas como eje fundamental para el proceso de enseñanza/aprendizaje de la aritmética, sin con esto despreciar las operaciones, sino entendiéndolas como un componente más de la resolución de problemas.
De esta manera, en estas páginas vamos a plantear las dificultades que pueden encontrar los alumnos en estos contenidos. Para ello, llevaremos a cabo un análisis de la aritmética, concretamente de su proceso de desarrollo, para, desde este análisis, interpretar algunas de las dificultades que pueden surgir en este proceso. Así, comenzaremos planteando cómo se adquieren y que desarrollo siguen los contenidos aritméticos básicos, distinguiendo entre aquellos que surgen desde la experiencia informal, es decir, que no implican una enseñanza explícita, y los que se adquieren a través de la enseñanza formal. En los primeros abordaremos algunos aspectos del desarrollo del número, considerando dos elementos clave: el conteo y los esquemas de razonamiento protocuantitativos. A continuación nos centraremos en el análisis de las situaciones problemáticas a las que los alumnos de enfrentan de manera informal, así como en las estrategias de conteo que utilizan para su resolución. En la aritmética más formal centraremos la atención en el análisis del proceso de resolución de problemas propiamente dicho y en las operaciones básicas. Cerraremos con la revisión de algunos de los factores que pueden explicar las dificultades que los alumnos encuentran en estos contenidos.
EL DESARROLLO DE LA ARITMÉTICA
Aritmética informal: las primeras nociones aritméticas
Hablar del desarrollo de la aritmética en particular o del desarrollo del pensamiento matemático en general supone mencionar, aunque sea brevemente, los planteamientos piagetianos sobre esta cuestión.
Para Piaget el conocimiento matemático se desarrolla como consecuencia de la evolución de estructuras más generales, de tal manera que la construcción del número es correlativa al desarrollo del pensamiento lógico. Los niños antes de los seis o siete años de edad son incapaces de entender el número y la aritmética porque carecen del razonamiento y conceptos lógicos necesarios. Y aunque aprenden a recitar la serie de números desde muy pequeños, para el psicólogo de Ginebra serían actos completamente verbales y sin significado alguno.
Desde este planteamiento, la comprensión del número se relaciona con la aparición del estadio operacional donde aparecen los requisitos lógicos del número. Antes no piensan de forma operatoria, dado que cuando han acabado de ejecutar una acción no son capaces de recordar el aspecto que tenía antes. En términos piagetianos no han conseguido la reversibilidad, dado que no pueden deshacer mentalmente sus acciones. En este sentido, su pensamiento está dominado por datos perceptuales, como se demuestra en sus famosos trabajos sobre la conservación y la clasificación. En un experimento típico de la conservación se presenta al niño por ejemplo dos filas de fichas, una con fichas azules y otra con fichas rojas, en correspondencia biunívoca, y a continuación se separan las fichas de una de las filas ante los ojos del niño. Los niños preoperatorios ya no consideran que las dos filas tengan el mismo número de fichas. Esto ocurre porque cuando se separan las fichas el niño no es capaz de imaginárselas en su posición original, guiándose a la hora de hacer juicios por variables perceptivas.
Por otro lado, en los experimentos sobre clasificación se enseña por ejemplo un conjunto con dos bolas de madera rojas y siete azules. Los niños son capaces de decir que son todas de madera y que hay más bolas azules que rojas. Sin embargo, cuando se les presenta la pregunta "¿qué hay más: bolas azules o bolas de madera?", los niños preoperatorios dicen que hay más bolas azules, dado que el dominio perceptivo de la cantidad de bolas azules interfiere con la consideración de que todas son de madera; parece incapaz de comparar un subconjunto con su propio superconjunto.
Es precisamente en el estadio de las operaciones concretas donde desaparece esta dependencia de las variables perceptivas o esta incapacidad para pensar de forma reversible. En este estadio aparece la adquisición del pensamiento lógico, la comprensión de las clases, las relaciones y las correspondencias biunívocas. En definitiva, un verdadero concepto del número y una manera significativa de contar. Desde este punto de vista, el desarrollo del número es para Piaget una cuestión de "todo o nada", puesto que, hasta que no cuente con los conceptos lógicos, el niño va a ser incapaz de comprender el número y la aritmética.
En este contexto, es fácil comprender que la enseñanza del número es inútil, puesto que antes es necesario desarrollar los requisitos lógicos. Sin embargo, están apareciendo cada vez más autores que no están de acuerdo con este enfoque del desarrollo del número, y que piensan que los niños pueden aprender mucho acerca de contar, del número y de la aritmética antes de poder conservar.
A raíz del influyente trabajo de Gelman y Gallistel4 sobre el desarrollo temprano del conteo, se empezó a demostrar que, contrario a lo que pensaba Piaget, el conteo juega un papel importante en el desarrollo del número y de las primeras nociones aritméticas, y que lo niños preescolares muestran una sorprendente competencia cognitiva en este campo.
Sin embargo, el primer conocimiento numérico es posible que se origine, como así han demostrado algunas investigaciones, antes de que los niños dispongan del conteo verbal transmitido culturalmente o de cualquier otra influencia social. O lo que es lo mismo, que puede haber un origen innato del número, similar a muchas habilidades perceptivas.
¿Cómo podemos imaginar la existencia de estas predisposiciones innatas que hacen a los niños numéricamente competentes desde que nacen? Existen una serie de investigaciones realizadas con bebés y niños preverbales que demuestran su habilidad para representar y razonar acerca de los números. Algunos de estos trabajos han utilizado el paradigma de habituación y deshabituación, que consiste en presentar a los bebés la misma estimulación repetidas veces hasta que se habitúan mostrando menos interés. Entonces se les presenta un nuevo estímulo, y si vuelve a mostrar interés podemos decir que ha percibido la diferencia entre una estimulación y otra. Esta percepción (o comprensión) suele medirse a partir de la amplitud de succión o duración de la mirada.
Desde este paradigma se ha comprobado que los bebés prestan atención a imágenes con objetos (puntos o figuras de distintas formas) a las que estaban habituados cuando estas han sido modificadas numéricamente y no cuando se modificaban otras variables como la longitud, densidad, tamaño, color o posición de los items. De estas forma, los bebés se deshabitúan cuando los cambios se producen en la numerosidad de los conjuntos, lo que implica que desechan otras características perceptivas que pueden ser interesante para ellos.
De la misma manera, se ha comprobado que los bebés pueden detectar correspondencias numéricas entre conjuntos presentados en diferentes modalidades sensoriales como visual y auditiva. En este caso se presenta al bebé dos fotografías, una con dos elementos y la otra con tres elementos y simultáneamente se presenta una secuencia de dos o tres sonidos, encontrándose que los bebés se fijan preferentemente en la fotografía cuyo número de elementos coincide con el número de sonidos. De esta forma, los bebés pueden llevar a cabo correspondencias intermodales basándose en la numerosidad de las presentaciones.
Desde estas investigaciones podemos argumentar, entonces, que los bebés son capaces de procesar datos numéricos a una edad más temprana y de un modo más complejo de lo que se consideraba. Sin embargo, y aunque estas primeras nociones del número son importantes, es a partir de los tres años de edad cuando los niños comienzan a desarrollar el primer conocimiento cuantitativo. En este desarrollo hay dos elementos que juegan un papel importante, el conteo verbal y los esquemas protocuantitativos. Concretamente, vamos a ver cómo desde la integración de estos dos aspectos los alumnos son capaces de enfrentarse a la resolución informal de las primeras situaciones problemáticas.
El conteo verbal
Si la biología nos puede proporcionar los fundamentos para el número, la cultura proporciona las oportunidades cuantitativas para construir su estructura, así como los instrumentos necesarios para conseguirlo: las palabras numéricas y el conteo. A pesar de que los contextos sociales que rodean al niño pueden variar de unas culturas a otras, lo cierto es que todas ellas ofrecen un sistema de palabras numéricas, a veces altamente elaborado como nuestro sistema de base diez, además de las oportunidades para manipular y contar pequeñas cantidades discretas de objetos. No cabe duda de que este primer conocimiento numérico aportado por la cultura juega un papel importante en el desarrollo del pensamiento matemático de los niños.
Sin embargo, y a pesar de que el conteo parezca una actividad sencilla a los ojos de un adulto, lo cierto es que en realidad necesita de la integración de una serie de técnicas que se desarrollan con el tiempo. Por ejemplo, pensemos que supondría determinar si un conjunto de nueve puntos es mayor o menor que uno de ocho. En primer lugar se necesita generar los nombres de los números en el orden adecuado. Además, se deben aplicar las etiquetas de la serie numérica una por una a cada objeto de un conjunto; para ello, es necesario coordinar la verbalización de la serie numérica con el señalamiento de cada elemento del conjunto para crear una correspondencia entre las etiquetas y los objetos. En tercer lugar hay que representar los elementos que contiene cada conjunto, para lo que se necesita la "regla del valor cardinal", por la que se establece que la última etiqueta expresada en la serie numérica representa el número total de elementos del conjunto. Por último, es preciso comprender que la posición de un número en la secuencia define la magnitud, de tal forma que se pueda establecer que el nueve viene después del ocho y por lo tanto es más grande.
Por lo tanto, desde el punto de vista cognitivo, el conteo no es una tarea sencilla, constituyendo un enorme reto para los niños de corta edad. Y su adquisición es un largo proceso que posiblemente no culmine hasta los siete u ocho años de edad.
Ahora bien, ¿qué curso sigue el desarrollo de esta habilidad?. No hay una respuesta fácil a esta cuestión. Algunos plantean la existencia de una serie de principios (conocimiento conceptual del conteo) que subyacen a la habilidad de contar. De esta forma, los niños tendrían un conocimiento implícito preexistente de estos principios, lo que les permitiría, por un lado, reconocer diferentes manifestaciones de conteo de su ambiente como conteo (una actividad significativa) que permite establecer la numerosidad de cualquier conjunto de elementos, así como identificar las palabras numéricas de la cultura como "etiquetas de conteo"; además, estos principios servirían como guía para la adquisición del conteo más temprano y para el desarrollo de esta habilidad.
En una posición distinta se encuentran los que piensan que los principios se adquieren con la experiencia. Desde este planteamiento se considera que al principio los niños aprenden a contar como una actividad rutinaria que es modelada por el entorno (padres, hermanos, profesores...), y utilizan diferentes rutinas para distintos contextos, como contar objetos distribuidos en línea o en círculo. Una vez que se han aprendido y desarrollado procedimientos para estos diferentes contextos, los niños comienzan a generalizarlos, abstrayendo lo que tienen en común, lo que tiene como resultado la adquisición de los principios del conteo.
No es este el lugar para plantear cuál de estas dos posturas es la correcta, pero independientemente de si el conteo precede o es inducido por el conocimiento de los principios, lo que sí parece claro es que una comprensión plena del número para tareas de cuantificación pasa por el desarrollo del conocimiento de los principios sobre el conocimiento conceptual del conteo.
Son los principios de correspondencia uno-a-uno, de orden estable, de cardinalidad, de abstracción y de irrelevancia, y fueron desarrollados en el trabajo pionero de Gelman y Gallistel4.
El principio de correspondencia uno-a-uno implica etiquetar cada elemento de un conjunto una vez y solo una. Conlleva, por tanto, la coordinación de dos procesos: partición y etiquetación, de tal manera que los niños mediante la partición van controlando los elementos contados y los que quedan por contar, bien separándolos o bien señalándolos, a la vez que disponen de una serie de etiquetas de modo que cada una de ellas corresponda con un objeto del conjunto contado. Es interesante hacer notar que las etiquetas utilizadas no tienen por qué seguir una secuencia correcta, incluso se pueden repetir etiquetas dentro de la secuencia; lo importante es señalar una sola vez mientras se le asigna una etiqueta.
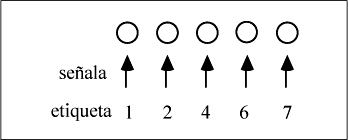
El principio de orden estable estipula que para contar es imprescindible el establecimiento de una secuencia coherente, aunque, como indican Gelman y Gallistel4, este principio se puede aplicar sin necesidad de tener que utilizar la secuencia numérica convencional, pudiéndose utilizar una secuencia propia no convencional (como puede ser la del ejemplo anterior) pero siempre de manera coherente.
El principio de cardinalidad establece que la última etiqueta de la secuencia numérica representa el cardinal del conjunto, esto es, la cantidad de elementos que contiene el conjunto. Gelman y Gallistel4 consideran que los niños comprenden este principio si repiten o ponen un énfasis especial en el último elemento de la secuencia de conteo.
El principio de abstracción determina que los principios anteriores se puedan aplicar a cualquier tipo de conjunto, tanto con elementos homogéneos como heterogéneos (objetos de distinto color o distinta entidad física).
Por último, el principio de irrelevancia indica que el orden por el que se comience a enumerar los elementos de un conjunto es irrelevante para su designación cardinal. Así, se puede contar de izquierda a derecha, de derecha a izquierda o del centro hasta los extremos sin que ello afecte al resultado del conteo.
Los principios de correspondencia, estabilidad del orden y cardinalidad establecerían las reglas procesuales sobre cómo contar un conjunto de objetos. A partir de sus experiencias con el conteo el niño va adquiriendo la secuencia numérica convencional, y esto le va a permitir establecer cuántos elementos tiene un conjunto, lo que se conoce con el nombre de enumeración.
La abstracción y la irrelevancia del orden sirven para generalizar y flexibilizar el rango de aplicación de los principios anteriores, lo que otros han llamado características no esenciales del conteo. Por ejemplo, es común que un niño considere como característica esencial el contar de izquierda a derecha, de tal forma que cuando se comienza a contar por el centro lo consideran un error. Esto significa que no ha adquirido el principio de irrelevancia.
Los esquemas protocuantitativos
Paralelamente a la habilidad de contar, los niños van desarrollando cierta experiencia con distintas formas de relaciones numéricas que son importantes para el desarrollo posterior del número y la aritmética. Estas relaciones han sido definidas por Resnick5,6 como "esquemas protocuantitativos". Esta autora hace una distinción entre dos tipos de conocimientos, lo que ella llama conocimiento representacional, que incluiría el conocimiento sobre el sistema numérico, y conocimiento relacional, caracterizado por los esquemas protocuantitativos. Desde el punto de vista de Resnick5,6, estos dos tipos de conocimientos tienen orígenes separados en el desarrollo temprano del número, y solamente a través de su integración se ejecuta el conocimiento cuantitativo.
Al igual que ocurre con el desarrollo del lenguaje, en el desarrollo del conocimiento matemático el niño va disponiendo de una variedad de términos que expresan juicios de cantidad sin precisión numérica, como mayor, menor, más o menos, lo que les permite asignar etiquetas lingüísticas a la comparación de tamaños. Estos juicios, que operan sin ningún proceso de medida, se basan en lo que Resnick5,6 llama esquema protocuantitativo de comparación. Esta autora identifica dos esquemas protocuantitativos más: uno que interpreta cambios en las cantidades como un incremento o decremento y otro que establece relaciones parte-todo.
El esquema protocuantitativo incremento-decremento permite a los niños de tres años razonar sobre cambios en las cantidades cuando se les añade o se les quita algún elemento. Por ejemplo, un niño sabe que si tiene cierta cantidad de cualquier cosa, por ejemplo dos juguetes, y consigue otro juguete tiene más que antes. De la misma manera que si le quitan tiene menos, o si no le añaden o quitan tiene la misma cantidad aún en el caso de que se modifique la distribución espacial de los objetos.
Por otro lado, y desde el esquema protocuantitativo parte-todo, los preescolares son capaces de conocer que cualquier "pieza", por ejemplo un pastel, puede ser dividida en partes más pequeñas y que volviéndolas a juntar dan lugar a la pieza original. De la misma manera, se pueden juntar dos cantidades que dan lugar a una cantidad mayor, de tal forma que, por lo menos de manera implícita, los niños empiezan a conocer la propiedad aditiva de las cantidades; pueden saber que el todo es mayor que las partes y pueden llegar a emitir este tipo de juicios sin necesidad de tener a la vista las cantidades (el pastel y sus partes). Como plantea Resnick5,6, esta comprensión de las relaciones parte-todo parece contradecir los planteamientos piagetianos de la tarea de la inclusión de clases (¿hay más pinos o más árboles en el bosque?). Sin embargo, los niños de cuatro y cinco años pueden hacer juicios correctos de inclusión de clases si las etiquetas centran la atención de los niños claramente sobre el todo más que sobre sus partes individuales (hablar de un bosque en lugar de pinos más robles).
Desde este contexto, los esquemas de razonamiento protocuantitativos constituyen un elemento básico para el desarrollo matemático posterior. Sin embargo, este conocimiento, que podemos llamar intuitivo, no es suficiente para abordar tareas cuantitativas (e.g. saber cuántos juguetes hay o saber en cuántas piezas se divide un pastel), por lo que los niños requieren hacer uso de instrumentos más precisos de cuantificación, como el conteo. De manera que cuando se integra el conocimiento relacional con el conocimiento representacional (el conteo) se desarrollan las habilidades implicadas en la resolución de distintas situaciones problemáticas, como se recoge en la Figura 1.
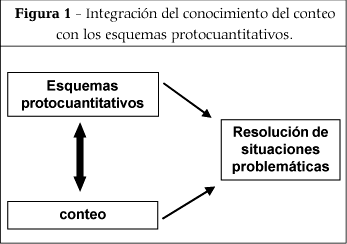
Por plantearlo de otra manera, el conteo supondría la cuantificación de los esquemas protocuantitativos a través de la resolución de situaciones problemáticas. Por lo tanto, una cuestión importante a tener en cuenta es analizar las distintas situaciones problemáticas a las que se pueden enfrentar los niños en estos primeros niveles de aprendizaje
Situaciones problemáticas
El análisis del tipo de situaciones problemáticas que existen en la vida real ha sido el foco de numerosas investigaciones en los últimos años. Se han utilizado distintas aproximaciones para clasificar estas situaciones, especialmente cuando se reflejan en un problema verbal, como el número de palabras del enunciado o el nivel de vocabulario, entre otras variables superficiales. Pero la variable considerada más relevante ha sido la estructura semántica que subyace a la situación problemática. Esto ha dado lugar a que se distingan distintos tipos básicos de situaciones de suma y resta, así como de multiplicación y división. En este trabajo vamos a centrarnos solamente en las situaciones con estructura aditiva.
En el caso de las estructuras aditivas se han distinguido tres tipos, que se corresponderían con los tres tipos problemas que los niños encuentran en las aulas: cambio (añadiendo o quitando), combinación y comparación, cuya representación gráfica se recoge en la Figura 2.
Las situaciones de cambio, tanto añadiendo como quitando, parten de una cantidad a la que se añade o quita algo para dar como resultado una cantidad mayor o menor. En este sentido se considera que estas situaciones representan operaciones unitarias. Las situaciones de combinación y comparación, por su parte, son operaciones binarias, puesto que parten de dos cantidades que se combinan o comparan para producir una tercera.
Otra distinción que se puede aplicar a estas diferentes situaciones es la posibilidad de que representen una acción, como en los problemas de cambio, o más bien representen situaciones estáticas, como en los casos de los problemas de combinación o comparación. Esto ha dado lugar, como señalan algunos autores, a que algunas clasificaciones incluyan la distinción activa/estática dentro de la distinción unitaria/binaria. Sin embargo, podemos encontrar situaciones con operaciones binarias que representen una acción, dando lugar a una nueva categoría de problemas, como son los problemas de igualación: "Juan tiene cinco juguetes y Pedro tiene tres juguetes; ¿cuántos juguetes necesita Pedro para tener los mismos que Juan?". Este tipo de situaciones se pueden considerar una mezcla de comparación y cambio, puesto que la diferencia entre dos cantidades puede ser expresada mediante la acción de añadir y no mediante la comparación estática de las dos cantidades.
Por lo tanto, contamos con cuatro tipos de situaciones que representarían los problema de suma y resta; en dos de estas hay una referencia explícita a una acción (cambio e igualación), mientras que en las otras dos se establece una relación estática entre las cantidades dadas en el problema (combinación y comparación). Como podemos apreciar, estas situaciones tienen su precursor en los esquemas protocuantitativos descritos más atrás.
Una cuestión más a la hora de analizar las diferentes situaciones problemáticas. Los problemas dentro de cada una de estas categorías reflejan el mismo tipo de acciones o relaciones, pero, dado que los problemas incluyen tres cantidades, una de las cuales es la desconocida, en cada categoría podemos identificar diferentes tipos de problemas dependiendo de qué cantidad es la desconocida. Así, en los problemas de cambio donde se produce un cambio sobre una cantidad inicial para dar un resultado, la cantidad desconocida puede ser el resultado, el cambio o la cantidad inicial; dado que el cambio puede ser añadir o quitar, encontraríamos seis tipos de problemas de esta categoría. De la misma manera, en los problemas de comparación la cantidad desconocida puede ser el conjunto de referencia, el de comparación o la diferencia, y puesto que el conjunto de referencia puede ser el mayor o el menor, también encontraríamos seis tipos de problemas de comparación. Algo similar ocurre con los de igualación. Y en las situaciones de combinación podemos desconocer una parte, otra parte o el todo; pero en este último caso, dado que no existe ninguna diferencia conceptual entre cada una de las partes se suelen considerar solamente dos tipos de situaciones de combinación: que te pregunten por el todo o por una de las partes. Por lo tanto, se identifican veinte tipos de problemas diferentes con estructura aditiva.
Es importante que tengamos en cuenta que las situaciones de suma y resta deben ser diferenciadas de las operaciones de suma y resta que se llevan a cabo para encontrar la respuesta o cantidad desconocida. En algunos casos pueden coincidir, como en las situaciones llamadas canónicas o consistentes, donde la situación de suma (o resta) se resuelve con una operación de suma (o resta); es el caso, por ejemplo, de las situaciones de cambio con el conjunto resultado desconocido. Pero en otros casos no existe esta correspondencia; son los problemas inconsistentes, en los que la situación de suma (o resta) requieren una resta (o suma) para encontrar la respuesta, como por ejemplo las situaciones de cambio que preguntan por la cantidad inicial. Evidentemente, los problemas inconsistentes son más difíciles de resolver y necesitan un conocimiento conceptual más avanzado.
En definitiva, los niños se pueden enfrentar a distintas situaciones problemáticas que corresponden con los diferentes tipos de problemas que se resuelven con las operaciones básicas de suma y resta. De cualquier forma, no es la realización de una operación la única vía con que cuentan los niños para resolver situaciones problemáticas. En un primer momento pueden modelar la situación con objetos o con los dedos para llegar a la solución. Para ello despliegan un amplio repertorio de estrategias que dependen, fundamentalmente, de la situación a la que se enfrenten; estrategias que se van haciendo más sofisticadas a medida que se desarrolla conceptualmente el conteo, hasta que, en última instancia, se resuelve el problema planteando una operación. Veamos este proceso de manera más detallada.
Estrategias de conteo
Las primeras situaciones de suma y resta a que se enfrentan los niños en la etapa infantil y primer curso de la etapa primaria pueden ser resueltas por el modelado directo, esto es, a partir de modelar directamente la situación o acción con objetos físicos, como cubos, los dedos o simplemente dibujando sobre el papel. Los objetos son utilizados para representar la situación y los números de las cantidades dadas en la misma, así como para ayudar al niños a llevar a cabo el procedimiento para llegar a la solución.
Las dos situaciones de suma más sencillas a las que los niños pueden enfrentarse en primer lugar son las de cambio añadiendo donde te preguntan por el conjunto final y combinación cuando te preguntan por el todo. Ambas se resuelven con una estrategia similar, la denominada contar todo.
En la situación de cambio las acciones consisten en representar con los objetos el conjunto inicial, e ir añadiendo a este conjunto el número de objetos indicados en el conjunto cambio (también se pueden representar ambos conjuntos por separado, sin necesidad de ir añadiendo); entonces se cuentan todos los objetos para llegar a la solución. En la situación de combinación, por su parte, se toman objetos para representar cada una de las partes y se juntan para contarlos y encontrar el resultado; en este caso también se pueden contar los objetos sin necesidad de juntarlos. La estrategia se denomina contar todo porque el resultado se determina contando todos los objetos.
La situación de resta por excelencia es la de cambio quitando en la que te preguntan por el conjunto final o resultado, que generalmente es resuelta mediante la estrategia de separación o "separar de". En este caso, se representa con objetos el conjunto inicial, y desde este se separan los objetos indicados por el conjunto cambio; el resultado es expresado por los objetos que quedan.
Los niños pueden resolver dos situaciones más en estos primeros niveles. Son las situaciones de comparación e igualación en las que se pregunta por la diferencia. En estos casos, la estrategias más habitual es el emparejamiento. Consiste en representar con objetos cada uno de los conjuntos (el mayor y el menor), los cuales son emparejados; la diferencia se establece bien contando los objetos extras del conjunto mayor (qué parte del conjunto mayor es más que el conjunto menor) para las situaciones de comparación, o bien realizando la acción de añadir al conjunto menor (o quitar al mayor) hasta que se igualan los dos conjuntos para los problemas de igualación.
Vemos, entonces, que en estos primeros niveles los niños son capaces de resolver una amplia variedad de situaciones de suma y resta sin necesidad de pasar por una enseñanza formal de estas operaciones. Y lo hacen utilizando diferentes estrategias que modelan directamente las acciones representadas en las situaciones. En la Tabla 1 aparece un resumen de estas estrategias.
Por lo tanto, con unos conocimientos mínimos sobre el número y el conteo, y con el conocimiento relacional de los esquemas protocuantitativos, los niños son capaces de resolver numerosas situaciones problemáticas. Para ello hacen uso de diferentes estrategias que modelan la situación y les permiten llegar a la solución.
Con el tiempo, y especialmente con el desarrollo conceptual del conteo, los niños van descubriendo, bien espontáneamente o bien desde la inducción, estrategias de conteo más sofisticadas, abstractas y eficientes que les permiten llegar más rápidamente a la resolución de la situación problemática. Además, hay una transición desde la utilización de materiales concretos o dedos al conteo verbal o mental, por lo que los niños comienzan también a desarrollar procedimientos que les permitan llevar la cuenta de los elementos contados. Todos estos avances en la utilización de las estrategias pueden ponerse en juego en las mismas situaciones problemáticas revisadas en el punto anterior.
Las situaciones de suma pueden resolverse utilizando la estrategia de "contar a partir del primero", que consiste en comenzar el conteo a partir del primer conjunto que aparece en la situación, sin necesidad de tener que contar todos los elementos a partir de uno, como ocurría en la estrategia de contar todo. Por ejemplo, en un problema de cambio en el que te preguntan por el conjunto final o resultado ("Alberto tiene 3 canicas y gana 5 en una partida; ¿cuántas canicas tiene después de la partida?), los niños pueden contar a partir del conjunto inicial, e ir añadiendo los elementos del conjunto cambio o transformación: "tres; cuatro (que es uno más), cinco (que es dos más), seis (que es tres más), siete (que es cuatro más), ocho (que es cinco más) -ocho". Como podemos observar, es necesario llevar la cuanta de los elementos contados, bien con los dedos, como hacen los niños al principio, o bien a partir de otros procedimientos concretos o mentales.
Una estrategia similar, aunque aparentemente algo más avanzada, es la denominada "contar a partir del mayor", en la que el inicio del conteo se lleva a cabo a partir del conjunto que incluye el sumando mayor, y no el primero como en la estrategia anterior. Siguiendo con el ejemplo anterior los niños harían lo siguiente: "cinco; seis (que es uno más), siete (que es dos más) y ocho (que es tres más) - ocho".
Es importante tener en cuenta que para utilizar una estrategia en la que el conteo comienza a partir de uno de los conjuntos es necesario contar con una serie de requisitos, los cuales están relacionados con el desarrollo del conocimiento conceptual del conteo. Así, el primer requisito y más evidente es poder comenzar el conteo a partir de cualquier punto arbitrario de la serie numérica. Otros requisitos tienen que ver con el significado de las relaciones entre conteo y cardinalidad, como se representa en la siguiente Figura 3.

Como podemos observar, es necesario que los niños vean el significado cardinal del primer conjunto o sumando (p.e. "8" en la parte superior de la figura) como el último objeto contado, lo que se denomina transición desde el cardinal al conteo; es decir, identificar el último objeto como el cardinal sin necesidad de contar los objetos. Además, es necesario extender el conteo iniciado en el cardinal del primer conjunto al segundo conjunto, de tal forma que el primer objeto de este se considere el siguiente número en la secuencia de conteo (p.e. "9" en la parte inferior de la figura). Desde estos requisitos los niños comprenden que los objetos pertenecen simultáneamente a los conjuntos o sumandos por un lado, y a la suma total por otro (el ocho no es sólo el cardinal del primer conjunto, sino también un elemento de la secuencia de conteo en la suma). Un proceso que se ha denominado "incrustación" (embedded) de los sumandos en la suma total, o "doble rol de los contadores".
Cuando los niños utilizan una estrategia de contar todo, los elementos que se cuentan del primer conjunto pertenecen primero a este conjunto y después se vuelven a contar formando parte de la suma, pero no se consideran simultáneamente miembros de un sumando y de la suma; es decir, el conteo de los conjuntos y de la suma son diferentes operaciones de conteo.
Por lo que se refiere a las situaciones de resta, también aparecen dos estrategias más abstractas y evolucionadas: el "retroconteo" y la "cuenta progresiva". El retroconteo es una estrategia inversa a contar a partir de uno de los conjuntos, dado que supone contar en orden contrario al conteo habitual o contar hacia atrás. Por ejemplo, cuando a un conjunto de nueve elementos le quitamos cuatro, caso de un problema de cambio en el que se pide el conjunto final o resultado, los niños pueden hacer lo siguiente: "nueve; ocho (que es uno menos), siete (que es dos menos), seis (que es tres menos), cinco (que es cuatro menos) -cinco", mientras van señalando los objetos del conjunto que se va quitando, o se van sacando dedos hasta formar este conjunto. A diferencia de las estrategias revisadas anteriormente para la suma, el retroconteo no es solamente un procedimiento abreviado de la estrategia menos madura de separación; además se necesita un dominio de la serie numérica en ambas direcciones, puesto que en la estrategia de separación todos los conteos son hacia adelante.
La cuenta progresiva, sin embargo, es una estrategia utilizada en la resta que utiliza el conteo hacia adelante, aunque conceptualmente se aleja de la idea de resta como quitar o separar. En este caso se parte del conjunto más pequeño y se cuenta hacia adelante hasta llegar al conjunto mayor. Si seguimos con el ejemplo anterior, los niños harían: "cuatro; cinco, seis, siete, ocho, nueve; -nueve", con algún procedimiento para llevar la cuenta de los elementos contados.
El siguiente paso en el desarrollo de las estrategias consiste en recuperar directamente desde la memoria el resultado de la operación, lo que se llama "recuperación de hechos" (p.e. siete más nueve es dieciséis) o la utilización de "hechos derivados" (p.e. siete más nueve es igual que diez más seis). En este nivel aparece la composición aditiva, que permite descomponer cualquier número en otros dos (p.e. el siete incluye el cuatro y el tres; o el dos y el cinco; o el seis y el uno; etc). Esto permite operar con el concepto parte/todo, en el que cualquier triada numérica se puede integrar dentro de un esquema sumando-sumando-suma. La suma es entonces vista como cualquier situación en la que dos sumandos son conocidos, y la resta como cualquier situación en que se conoce la suma y uno de los sumandos. Y esto permite la aparición de la reversibilidad entre la suma y la resta, lo que supone una enorme flexibilidad en la resolución de cualquier situación problemática.
Por lo tanto, podemos distinguir tres niveles en el desarrollo de las estrategias que los niños utilizan para resolver distintas situaciones problemáticas con estructura aditiva, niveles que estas mediatizados por su conocimiento conceptual del conteo. En el primer nivel los niños modelan directamente la situación utilizando su conocimiento más elemental del conteo que integran con sus esquemas protocuantitativos. En el segundo nivel, y cuando su conocimiento conceptual del conteo avanza, pueden utilizar procedimientos más abreviados en los que no hay necesidad de utilizar objetos concretos. El tercer nivel se caracteriza por la aparición de la composición aditiva y la reversibilidad, lo que permite una mayor flexibilidad en la resolución de problemas.
En resumen, en lo que hemos llamado aritmética informal, los niños desarrollan una serie de conocimientos conceptuales y procedimientos que les permiten enfrentarse a numerosas tareas aritméticas, especialmente las planteadas como resolución de situaciones problemáticas, donde el conteo juega un papel fundamental. A partir de estos conocimientos, o mejor dicho, conectando con ellos, comienza el aprendizaje de la aritmética más formal.
Aritmética formal
En este apartado vamos a centrarnos en el proceso de enseñanza/aprendizaje de la aritmética más formal, donde consideraremos el proceso de resolución de problemas propiamente dicho y el cálculo de operaciones. Aunque hagamos esta distinción no debemos olvidar, como planteábamos al principio, que el cálculo es un componente más de la resolución de problemas
Resolución de problemas
En términos globales, la resolución de un problema comienza con un texto lingüístico y termina con una operación que da lugar a una solución numérica. En este proceso podemos distinguir diferentes componentes7-15. Así, el texto verbal se traslada a una representación interna abstracta en la que se recogen las distintas proposiciones, sus relaciones, así como la situación cualitativa descrita en el enunciado. Sobre la base de esta representación se selecciona una operación aritmética o una estrategia de conteo informal para encontrar el elemento desconocido de la representación, ejecutándose posteriormente la acción u operación seleccionada. Una vez hecho esto se puede reactivar la representación inicial del problema, sustituyendo el elemento no conocido por el resultado de la acción ejecutada. A partir de aquí se llevan a cabo una serie de acciones de verificación para comprobar la exactitud de la solución encontrada.
Se han propuesto diferentes modelos para explicar este proceso de resolución de problemas16-21. Todos ellos coinciden, de una manera u otra, en que la resolución de problemas supone un elaborado proceso en el que hay que poner en marcha sofisticadas estrategias para comprender el enunciado, esto es, para trasladar el texto verbal a una representación interna abstracta en la que se recogen las distintas proposiciones, sus relaciones semánticas, así como la situación cualitativa descrita en el enunciado. Y para ello es necesario acceder a cierto conocimiento conceptual que permita establecer estas relaciones semánticas.
Así, por ejemplo, algunos modelos, como los desarrollados por Briars y Larkin16 o Riley et al.21 proponen que los problemas más difíciles necesitarían un conocimiento conceptual más avanzado, o si se quiere, los estudiantes fracasarían en la resolución de ciertos problemas porque no poseen el conocimiento conceptual necesario para resolverlos correctamente. Este conocimiento conceptual es un tipo de conocimiento esquemático, el cual implica, precisamente, operar con las relaciones semánticas descritas en el texto del problema. En el nivel más alto de competencia, el esquema del problema permite establecer relaciones semánticas que proyectan la información textual del enunciado en un esquema parte-todo. Esto significa conocer que, de los tres conjuntos que aparecen en el texto del problema de una operación, uno actúa como el "todo" y los otros dos como las "partes" dentro de una estructura parte-parte-todo (véase más adelante).
Otros autores17,18 han propuesto modelos más complejos en los que la comprensión textual interactúa con la construcción de la representación del problema en términos de conjuntos y sus interrelaciones. En este caso, el procesamiento textual y el conocimiento conceptual se integran para comprender y resolver un problema. Así, Kintsch y Greeno18 plantean que desde el texto del problema se deriva una representación textual "dual" en la que se puede distinguir, al igual que ocurre en la comprensión de textos22-24 dos componentes: una estructura proposicional de la información descrita en el enunciado o texto base, donde se representan sus aspectos superficiales y semánticos, y un modelo de la situación, que se denomina modelo del problema, en el que se incluiría la información que se infiere desde la base de conocimientos que se posee sobre el mundo y sobre los problemas aritméticos, y se excluiría, si se diera el caso, aquella información del texto base que no se necesite para resolver el problema. En este sentido, los problemas que implican algo más que la aplicación de una operación para su resolución, bien porque contienen información superflua o porque omiten información necesaria, se resolverían desde la construcción del modelo del problema.
En una extensión de estos modelos basados en la comprensión textual, Reusser19 ha propuesto un modelo que introduce un paso intermedio entre el texto base y el modelo del problema, el cual denomina modelo de la situación episódico o modelo mental de la situación denotada por el texto del problema. Este paso guiaría la comprensión de los acontecimientos específicos de la historia presentada en el problema, tales como la estructura temporal de las acciones o las intenciones de los actores implicados. En palabras del autor "los problemas situacionales se organizan en torno a algún protagonista con ciertas necesidades, motivos y propósitos, y que está implicado en ciertas interacciones con coactores, objetos e instrumentos", y que para resolver el problema "se debe convertir en transparente la estructura funcional y temporal de la acción". Supondría entonces un acceso al conocimiento del mundo real para entender el enunciado del problema.
En definitiva, para resolver un problema hay que desencadenar una serie de estrategias que permitan crear una representación del mismo; en este proceso interactúan distintos tipos de conocimientos como lingüísticos, del mundo y matemáticos.
¿Porqué algunos problemas son más difíciles de resolver?
Una vez analizados los componentes implicados en el proceso de resolución de problemas, vamos a centrarnos en los diferentes grados de dificultad de los distintos problemas. La idea fundamental que queremos plantear es que diferentes tipos de estructuras aditivas necesitan diferente conocimiento conceptual, o, para ser más precisos, el grado de dificultad de los problemas viene marcado por el tipo de conocimiento conceptual implicado en la resolución de los mismos25.
Como ya hemos apuntado, los enunciados de los problemas pueden ser considerados como verdaderos textos, esto es, como auténticas entidades discursivas. En este sentido, podemos hablar de distintos tipos de problemas en función de su estructura semántica, es decir, de las posibles relaciones que se establecen entre los conjuntos que aparecen en el enunciado. Son las cuatro categorías de estructuras semánticas básicas ya conocidas: cambio, combinación, comparación e igualación.
Es fácil imaginar que los distintos tipos de problemas ofrecen diferentes grados de dificultad en su resolución. Así, uno de los resultados más recurrentes ha sido que los problemas de comparación son los más difíciles de resolver. Sin embargo, más que la propia estructura semántica, parece jugar un papel más importante el lugar que ocupa la cantidad desconocida. Este factor hace que podamos distinguir entre problemas con un lenguaje consistente y con un lenguaje inconsistente o conflictivo, como decíamos más atrás. En los primeros los términos del enunciado (por ejemplo, "ganar" o "más que" coinciden con la operación a realizar (una suma, como en cambio 1 o comparación 3), mientras que en los segundos, los términos entran en conflicto con la operación (aparece "ganar" o "más que" y hay que hacer una resta, como en cambio 5 o comparación 5). Pero lo más importante es que lo que diferencia ambos tipos de problemas es el conocimiento conceptual implicado en cada un o de ellos.
Así, los problemas consistentes se pueden resolver a partir del modelado directo, construyendo el modelo de la situación del problema secuencialmente, proposición por proposición, tal como se presentan en el texto del problema. De esta manera, los conocimientos requeridos para este tipo de problemas no van más allá del uso de ciertas formas de relaciones numéricas de carácter protocuantitativo, que integradas con los principios básicos del conteo permiten el desarrollo de estrategias de conteo apropiadas para resolver este tipo de situaciones problemáticas. Es más, el modelo de traslación directa puede ser funcional con este tipo de problemas.
La resolución de los problemas inconsistentes, sin embargo, requieren proyectar la información textual del enunciado a un esquema parte-todo. Esto significa conocer que, de los tres conjuntos que aparecen en el texto base, uno actúa como el "todo" y los otros dos como las "partes" dentro de una estructura parte-parte-todo. Tomemos como referencia el problema de comparación que planteábamos para revisar el modelo en el punto anterior: "Juan tiene 8 canicas; él tiene 3 más que Pedro; ¿cuántas canicas tiene Pedro?". Los tres conjuntos mencionados son el conjunto referente (las canicas de Pedro), que ha sido comparado a otro, el conjunto comparado (las canicas de Juan), y la diferencia entre los dos conjuntos, el conjunto diferencia. Desde las proposiciones de la segunda frase del enunciado se infiere si el conjunto referente es el conjunto mayor y el conjunto comparado es el menor, o viceversa, de tal forma que, desde un esquema parte-todo, se conoce que "conjunto menor = conjunto mayor - conjunto diferencia" o "conjunto mayor = conjunto menor + conjunto diferencia", y así transformar la información textual en una ecuación matemática. En el problema que nos ocupa, y con la ayuda de esta transformación matemática15, se infiere que el conjunto comparado es el mayor y el conjunto referente (el desconocido) es el menor, y así decidir hacer una resta. Lógicamente, y como veíamos en el modelo propuesto de resolución de problemas, estas inferencias se llevan a cabo en el modelo de la situación del problema.
Algo similar podemos decir con los problemas de cambio más difíciles, aquellos en los que se pregunta por el conjunto inicial (cambio 5 y 6). Su resolución implica algún tipo de "reversibilidad de las operaciones mentales"16. Por ejemplo, en un problema de cambio añadiendo del tipo "conjunto inicial desconocido + conjunto cambio = conjunto final" ("Juan tenía algunas canicas; entonces ganó tres en una partida; ahora tiene ocho canicas; ¿cuántas tenía antes de la partida?"), su resolución implica identificar el conjunto inicial desconocido como más pequeño que el conjunto final; por ello, se podría resolver partiendo del conjunto final, al que se le quita las canicas ganadas para saber cuántas tenía en el conjunto inicial. Esta inversión, al igual que en los problemas de comparación, implica entender la naturaleza recíproca entre la suma y la resta, y las relaciones parte-todo que se establecen en cualquier triada numérica, base para la comprensión de la composición aditiva de los números. Es importante no confundir el conocimiento de estas relaciones parte-todo con la estructura parte-todo característica de los problemas de combinación. No se trata de convertir, en el modelo de la situación del problema, los problemas de cambio o comparación en un problema de combinación parte-parte-todo. Más bien, este tipo de conocimiento conceptual tiene que ver con el esquema parte-todo característico de relaciones numéricas avanzadas26.
Podemos concluir, entonces, que la resolución de problemas requiere poner en marcha diferentes procesos en los que la comprensión del enunciado juega un papel relevante. Pero el proceso de comprensión puede estar mediatizado por cierto tipo conocimiento conceptual, que en el caso de los problemas con estructura aditiva se relaciona con la composición aditiva (estructura parte-todo) propia de un concepto de número más avanzado.
Operaciones básicas
El proceso de resolución de problemas finaliza con la ejecución de una operación para llegar al resultado. Ya hemos visto que a este resultado se puede llegar a través de estrategias informales. Pero llega un momento en que los alumnos comienzan a dominar las combinaciones numéricas básicas, es decir, a recuperar directamente el resultado desde la memoria, lo que hemos llamado recuperación de hechos. ¿Cómo favorecer este paso? Una respuesta fácil a esta cuestión podría ser la memorización de tablas, de forma similar a como se suele hacer con las tablas de multiplicar. Un planteamiento de escasa tradición en nuestro país (por lo menos el aprendizaje directo de las tablas de sumar) pero muy extendido en otros países. Pero aunque no existe un aprendizaje explícitos de las tablas, si hay una presión por parte de los profesores para que sus alumnos pasen rápidamente del conteo a la recuperación inmediata de hechos aritméticos. En este sentido, la memorización de hechos podría ser una solución.
Sin embargo, la memorización de combinaciones numéricas resta cualquier interés a las estrategias informales que los niños utilizan cuando se enfrentan a las primeras operaciones. Y a lo largo de estas páginas hemos podido observar la importancia que tienen estas estrategias para el desarrollo de la aritmética. Es más, podríamos decir que la práctica en el cálculo informal, a través de las estrategias de conteo, es un medio para reforzar la asociación entre una operación y la respuesta generada por las estrategias de conteo.
De cualquier forma, existen otras vías por las que la experiencia informal puede contribuir a la adquisición de combinaciones numéricas básicas. Es el caso de las estrategias que permiten generar los llamados hechos derivados o las experiencias de conteo que permiten descubrir relaciones matemáticas que pueden actuar como reglas para generar combinaciones numéricas. Incluso, algunos autores, consideran que muchas combinaciones numéricas se aprenden y se representan en la memoria no como hechos separados sino como reglas que relacionan distintas combinaciones. Por ejemplo, la regla del "cero" y la regla del "más uno o número siguiente" para la suma implican no tener que aprenderse todas las combinaciones que incluyan más cero o más uno, puesto que estas combinaciones se pueden generar por reglas como "todos los números más cero son el mismo número" o "todos los números más uno son el número siguiente". Algo similar ocurre en la resta, con reglas como N - N siempre es 0, o N - 0 siempre es N, o restas con términos seguidos siempre es 1 (p.e. 7 - 6, 9 - 8, 35 - 34...).
Independientemente de que la representación de hechos en la memoria sea mediante reglas o sean hechos aislados, lo que sí parece indudable es que estas reglas pueden jugar un papel importante en el aprendizaje de las combinaciones numéricas básicas. Y también parece un hecho constatado que antes de la recuperación automática de hechos desde la memoria, las respuestas a combinaciones numéricas desconocidas se pueden generar mediante estrategias de hechos derivados.
Por estrategias de hechos derivados (también llamadas estrategias de pensamiento, estrategias heurísticas o soluciones indirectas) se entienden aquellos procedimientos en los que los números en una operación dada se redistribuyen de tal forma que se convierten en números cuyas sumas o diferencias son conocidas. Por ejemplo, la operación 6 + 7 se puede simplificar descomponiendo los números para generar hechos conocidos, como los dobles más uno ([6 + 6] + 1; "si seis más seis son doce, y siete es uno más que seis, entonces seis más siete es uno más que doce, esto es, trece"). O también utilizar la redistribución basada en el diez, muy utilizada en las combinaciones en las que uno de los sumandos sea nueve, como 9 + N o N + 9; en este caso, la combinación es descompuesta para hacer que uno de los sumandos sea diez; así, 9 + 6 se puede descomponer en 9 + [ 5 + 1] para dar 9 + 1 = 10 + 5. En el caso de la resta, cualquier combinación puede resolverse, entre otros procedimientos, recordando su combinación aditiva complementaria; por ejemplo, 8 - 5 se puede resolver pensando que se necesita añadir a cinco para hacer ocho (5 + 3 = 8); por lo tanto, las combinaciones numéricas básicas aditivas preceden en el tiempo a las de la resta.
Estas estrategias de hechos derivados también pueden utilizarse en el dominio de las combinaciones numéricas de multiplicación y división. Por ejemplo, la regla del cero en "7 X 0" se entiende como "siete grupos de nada es nada"; y la regla de multiplicar por uno como "un grupo de siete elementos es siete".
No cabe duda de que estas reglas y procedimientos pueden constituir un andamiaje para la recuperación inmediata desde la memoria de hechos numérico. Ahora bien, ¿qué papel juega la práctica en este contexto?. Pocos rechazarían la idea de que la práctica es un ingrediente importante en el dominio de las combinaciones numéricas básicas. Pero ya hemos dicho que la práctica y el ejercicio como memorización de hechos numéricos aislados no parece el camino más adecuado. Por lo tanto, no tiene sentido como proceso de aprendizaje. Pero la práctica sí puede favorecer la utilización de manera cada vez más automática de estas reglas, principio y estrategias de pensamiento
DIFICULTADES EN LA ARITMÉTICA
Una vez analizados los contenidos de la aritmética desde el punto de vista del proceso de desarrollo que siguen los niños, en este apartado vamos a analizar algunas de las dificultades que pueden surgir en este proceso. Antes, sin embargo, nos gustaría plantear una fuente de dificultades que no suele mencionarse, posiblemente por lo inespecífica que es. Nos estamos refiriendo a la desconexión que muchas veces existe en la enseñanza de la aritmética entre el conocimiento informal que los niños desarrollan espontáneamente y los conocimientos más formales que aprenden en las aulas.
Como hemos tenido oportunidad de ver a lo largo de estas páginas, los niños desarrollan, antes de la enseñanza formal de la aritmética, un amplio bagaje de conocimientos informales relacionados con el número, el dominio de combinaciones numéricas básicas, la resolución de situaciones problemáticas o incluso el dominio de los algoritmos y el valor posicional.
Sin embargo, los niños tienden a percibir la aritmética formal desconectada de sus conocimientos informales. Esto es, tienen dificultades para conectar los símbolos y reglas que aprenden de manera más o menos memorística con su conocimiento matemático. Muchos niños ven las matemáticas como algo arbitrario, como un juego con símbolos separados de la vida real y como un sistema rígido de reglas dictadas externamente y gobernadas por estándares de velocidad y exactitud. Y esto es más acuciante a medida que avanzan en niveles educativos, lo que hace que la visión de las matemáticas que tienen los alumnos cambie gradualmente desde el entusiasmo a la aprehensión, desde la confianza al miedo. No cabe duda de que este puede ser uno de los factores determinantes de las dificultades que presentan muchos alumnos en el aprendizaje de las matemáticas.
No obstante, y a pesar de que esto pueda ser así, también podemos identificar otros aspectos que generan dificultades en el aprendizaje. Concretamente nos vamos a centrar en dos. Uno de ellos, de carácter más específico, tiene que ver con las dificultades que encuentran ciertos alumnos en el dominio de las combinaciones numéricas básicas, esto es, en el cálculo. El otro, más genérico, se centra en la resolución de problemas que, como hemos argumentado, es el eje vertebrador de la aritmética. No obstante, no debemos olvidar que el cálculo es un componente más de la resolución de problemas; hacemos la distinción por motivos meramente didácticos.
Dificultades en el aprendizaje del cálculo
Cuando hablamos de dificultades en el cálculo nos referimos a un grupo no muy numeroso de alumnos que presentan déficit específicos en el dominio de las combinaciones numéricas básicas (ej. 7 + 9 = ?). De manera más concreta, diferentes trabajos han descrito dos déficit funcionales básicos: procedimentales y de recuperación de hechos. Así, tienden a presentar procedimientos aritméticos (estrategias de resolución de operaciones) evolutivamente inmaduros y una alta frecuencia de errores procedimentales de cómputo. Además, tienen dificultades en la representación y recuperación de hechos aritméticos desde la memoria a largo plazo semántica.
El trabajo de Geary es una buena muestra de lo que queremos decir27,28. Este autor comparó un grupo de niños de primer curso (con dificultades y sin dificultades) en la utilización de estrategias y tiempos de ejecución cuando resolvían problemas simples de suma (pares de números del 2 al 9, por ejemplo 3 + 4). Los resultados muestran que todos los niños utilizaron las mismas estrategias (recuperación de la memoria, conteo verbal o conteo con dedos), pero diferían en la habilidad y velocidad de ejecución de las estrategias. Así, los niños con dificultades mostraron frecuentes errores en el conteo verbal, un uso frecuente de estrategias menos maduras de conteo (por ejemplo contar todo), una alta proporción de errores de recuperación de la memoria y tiempos de respuesta en la recuperación muy variables y asistemáticos. Estos resultados sugieren que los déficit funcionales de los alumnos de primero con dificultades se caracterizan por pobres habilidades procedimentales de cómputo y una atípica representación de hechos aritméticos básicos en la memoria.
Más interesante aún son los resultados que obtuvieron diez meses después en un estudio de seguimiento. Mientras que los niños sin dificultades mostraron una mayor confianza en la recuperación de hechos de la memoria y un incremento en la velocidad de ejecución de las estrategias, el grupo de niños con dificultades no mostraron muchos cambios en su elección de estrategias. Así, y aunque hubo un abandono del procedimiento "contar todo" de conteo en favor de "contar a partir del primero", la velocidad de conteo seguía siendo más lenta que en los alumnos sin dificultades. Además, no hubo cambios en el número de hechos que podían recuperar de la memoria, ni en el tiempo de ejecución en la recuperación.
En nuestro propio trabajo29 hemos encontrado resultados similares, pero utilizando una muestra de niños con y sin dificultades en aritmética de distintos niveles educativos de educación primaria (desde segundo hasta sexto curso). Comprobamos que los niños con dificultades cometen más errores y utilizan estrategias menos avanzadas que los niños sin dificultades. Además, a medida que avanzamos en niveles educativos encontramos una tendencia evolutiva en ambos grupos. Los niños sin dificultades muestran una tendencia prototípica utilizando estrategias más desarrolladas (mayor proporción de recuperación de hechos) y de manera más eficaz. Los niños con dificultades, a pesar de mostrar una tendencia evolutiva en la utilización de estrategias, reflejado en un mayor uso de la recuperación, la eficacia contrasta con lo mostrado en el grupo sin dificultades. De manera concreta, en los niveles más bajos constatamos una representación anómala de hechos en la memoria, y en los niveles más altos (fundamentalmente sexto curso), a pesar de que pueda existir cierta representación, el acceso a la misma no esta totalmente automatizado, como ocurre con los alumnos sin dificultades.
En consecuencia, los resultados de estos estudios no sólo apoyan que los déficit de los alumnos con DM son de dos tipos: procedimental y de recuperación de hechos, sino que además, las habilidades procedimentales de estos alumnos se pueden aproximar a las de los niños sin dificultades (pueden mostrar un retraso en su desarrollo), mientras que las habilidades de recuperación de hechos no (plantean una diferencia en el desarrollo), como se recoge en la Tabla 2.
En este contexto podemos argumentar, entonces, que los mecanismos que pueden contribuir a los déficit procedimentales y de recuperación en estos niños pueden ser diferentes. Así, las estrategias menos maduras y los errores procedimentales que presenta los niños con DM se relacionan con el desarrollo del conocimiento conceptual de conteo, especialmente si consideramos la secuencia evolutiva planteada páginas atrás. Por su parte, las dificultades en la recuperación de hechos se relacionan con el decaimiento de la información de la memoria de trabajo junto con la velocidad lenta en la ejecución de estrategias de conteo así como la alta frecuencia de errores de cómputo, de tal forma que, con una velocidad de conteo lenta, hay mayor probabilidad de decaimiento de la información en la memoria de trabajo, lo que conlleva no desarrollar representaciones en la memoria; a esto se añade que los errores de cómputo llevan a asociaciones incorrectas en la memoria lo que puede conducir a errores en la recuperación.
En resumen, en las dificultades relacionadas con el cálculo se sugieren dos déficit funcionales diferentes, procedimentales y de recuperación de hechos de la memoria. Las dificultades procedimentales parecen relacionarse con un conocimiento inmaduro del conteo y es probable que en relación con los niños sin problemas, estas dificultades se consideren en ciertos casos un retraso en el desarrollo. Los déficit relacionados con la recuperación de hechos, sin embargo, parecen persistir a lo largo del desarrollo y es probable que se relacionen con la velocidad y errores en la ejecución de estrategias de cómputo así como con la disponibilidad de recursos de la memoria de trabajo.
Dificultades en el la resolución de problemas
Cuando un alumno se enfrenta a la resolución de un problema, las dificultades pueden surgir por dos factores; bien puede no comprender la situación problemática, o bien puede no contar con el conocimiento conceptual necesario para resolverla, aunque esta falta de conocimiento también puede llevar a un fracaso en la comprensión. Veamos, aún a riesgo de simplificar, cada uno de estos aspectos con dos ejemplos concretos:
(a) Juan fue a jugar a las canicas con sus amigos y ganó 27 canicas.
Al final de la partida tenía 34 canicas.
¿Cuántas canicas tenía antes de la partida?
(b) El propietario de un bar quiere saber cuánto dinero ganará con una nueva botella.
La botella tiene una capacidad de 3/4 de litro y quiere servir vasos de 1/8 de litro.
¿Cuántos vasos conseguirá?
Las dificultades que aparecen en problemas similares a estos pueden ser debidas a que los alumnos no comprenden el enunciado del problema. Por ejemplo, en el problema (a) la falta de comprensión aparece, en muchos casos, cuando el alumno se guía por una estrategia de traslación directa del texto a la operación, en vez de crear una representación coherente del enunciado. De esta manera, selecciona del texto los números (34 y 27) y la palabra clave ("gana") para llegar a una solución incorrecta del problema (34 + 27). Ahora bien, la cuestión es por qué los alumnos utilizan estrategias de este tipo. ¿Podemos decir que es una dificultad específica como veíamos en el caso del cálculo? Seguramente estaremos de acuerdo en dar una respuesta negativa. Lo más probable es que los alumnos no se enfrenten habitualmente a este tipo de situaciones problemáticas que hemos llamado no canónicas o inconsistentes. En muchos casos, como comentábamos al principio del capítulo, los problemas se utilizan para ejercitar las operaciones sin prestarle mucho interés al proceso de resolución, por lo que los problemas más utilizados (véanse, si no, los libros de texto) son los más rutinario en los que una estrategia de traslación directa es suficiente para resolverlos. En este contexto, podemos decir, entonces, que los alumnos tienen dificultades porque no utilizan las estrategias adecuadas para resolver los problemas, bien porque no se han enseñado, o bien porque no se crean las condiciones necesarias para su uso.
Algo similar podemos decir en el problema (b), salvo que en este problema la estrategia de traslación directa es más difícil, y lo más probable es que muchos alumnos ni tan siquiera sepan o intenten resolverlo. Ahora bien, si dijéramos que este problema está extraído de un libro de texto en el que se está explicando el algoritmo de la división de fracciones, muchos podrán pensar que, indudablemente, los alumnos lo resolverán dividiendo 3/4 entre 1/8. Una muestra más de la utilización de los problemas como ejercicio de las operaciones.
De cualquier forma, algunos alumnos encontrarán dificultades en estos problemas porque no cuentan con el conocimiento conceptual necesario para resolverlos. En el caso del problema (a), que podemos considerar del tipo "conjunto inicial desconocido + conjunto cambio = conjunto resultado", su resolución implica algún tipo de reversibilidad de las operaciones, esto es, implica identificar el conjunto inicial desconocido como más pequeño que el conjunto final; por ello, se podría resolver partiendo del conjunto final, al que se le quita las canicas ganadas para saber cuántas tenía en el conjunto inicial. Esta inversión supone entender la naturaleza recíproca entre la suma y la resta, y las relaciones parte-todo que se establecen en cualquier triada numérica. Sin estos conocimientos conceptuales (que páginas atrás hemos identificado en el tercer nivel de desarrollo de las estrategias de conteo) no es fácil enfrentarse a la comprensión de problemas inconsistentes de este tipo. Y a estos conocimientos hay que añadir aquellos relacionados con el concepto de valor posicional, puesto que estamos hablando de números de dos cifras.
En el problema (b) el conocimiento conceptual fundamental es, si se quiere acceder a la estructura semántica, el de división por agrupamiento, además de cierto conocimiento sobre las fracciones y sobre cómo operar con ellas (de lo que no hemos hablado en este capítulo). Recordemos que los problemas de división suponen dos tipos de situaciones dependiendo de que se pregunte por el multiplicador (número de grupos) o el multiplicando (número de elementos en cada grupo); en el primer caso hablamos de división por agrupamiento y en el segundo de división por reparto. En este sentido, el concepto de división por agrupamiento es necesario para resolver el problema (b) puesto que implica considerar cuántos "grupos" de 1/8 se pueden formar con 3/4. Por desgracia, las situaciones de división por agrupamiento son menos habituales para los alumnos, puesto que la división suele plantearse a partir del reparto, convirtiéndose, a partir de aquí, todas las situaciones como "problemas de división", sin hacer esta distinción. Sin este conocimiento es difícil resolver este problema, al menos desde un punto de vista significativo, esto es, desde la comprensión de lo que se está haciendo.
Por lo tanto, las dificultades en la resolución de problemas se producen, fundamentalmente, porque los alumnos no comprenden la situación problemática, es decir, no crean una representación adecuada de la situación denotada por el enunciado, o porque no cuentan con el conocimiento conceptual específico necesario para cada problema, aunque estos aspectos están íntimamente relacionados, puesto que el conocimiento conceptual en muchos casos es necesario para acceder a dicha representación.
Esto nos lleva a una última cuestión relacionada con las dificultades en la resolución de problemas. Si el conocimiento conceptual es necesario para llegar a una correcta representación del problema, simplificando la representación de los conceptos matemáticos se reducirá el grado de dificultad que los alumnos pueden encontrar en la resolución de problemas. Ahora bien, ¿cómo simplificar la representación de los conceptos matemáticos? En un clásico trabajo, Bruner sugirió que un concepto matemático se puede representar de tres formas distintas: enactivamente (mediante representaciones físicas), icónicamente (a través de representaciones pictóricas o gráficas) y simbólicamente (por símbolos escritos). Así, el número 45 puede ser representado de manera concreta manipulando bloques base-diez, pictóricamente dibujando los bloques base-diez y simbólicamente como "37".
En este contexto, la resolución de los dos problemas anteriores puede depender, en cierta medida, del nivel representacional en el que nos situemos. Así, un alumno con dificultades en el formato habitual de resolución, donde desde el problema se pide una operación que lleve a la respuesta, esto es, en el nivel simbólico, puede no tener tantas dificultades en otras formas de representación.
Por ejemplo, en la Figura 4 se recoge una posibilidad para representar pictórica y manipulativamente el problema (a) anterior.

Con los alumnos que no acceden al conocimiento conceptual necesario para resolver un problema de cambio cuando se pregunta por el conjunto inicial, se puede pensar en una representación pictórica para hacer ver que el conjunto desconocido es más pequeño a partir de la idea de la composición aditiva. Incluso esta idea es más sencilla si se plantea en términos manipulativos, donde con objetos concretos se puede hacer ver "a qué número se le suman 27 para conseguir 34".
De manera similar, en el problema (b) se puede plantear la idea de división por agrupamiento desde representaciones pictóricas o manipulativas, como aparece en la Figura 5.
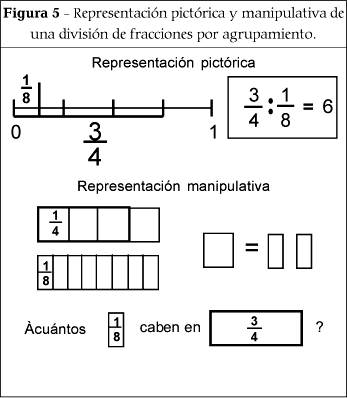
En este caso, la recta numérica es un buen ejemplo para representar pictóricamente cuántos "1/8 caben en 3/4". Y si se cuenta con los materiales adecuados no es difícil considerar la idea de división por agrupamiento desde la manipulación.
En definitiva, las dificultades en la resolución de problemas se pueden relativizar si consideramos otros formatos representacionales que permiten acceder más fácilmente al conocimiento conceptual necesario, especialmente cuando consideramos alumnos menos competentes.
CONCLUSIONES
Planteábamos al inicio del documento la necesidad de contar con un marco teórico que nos permitiera entender las dificultades que presentan los alumnos en la aritmética, uno de los contenidos fundamentales de las matemáticas y una de las fuentes principales del fracaso en este área. El marco en cuestión lo hemos planteado desde el punto de vista del desarrollo que siguen los contenidos, puesto que las dificultades solamente se pueden interpretar si situamos a los alumnos en momentos concretos de este proceso evolutivo. De ahí que hayamos dedicado una parte importante del capítulo a analizar este proceso.
La distinción entre aritmética informal y formal es importante porque nos permite analizar cómo una parte importante de las dificultades se producen por la desconexión que existe en el mundo educativo entre estos dos tipos de conocimientos. Y aunque algunas dificultades tienen que ver con los procesos más básicos implicados en la aritmética, lo que entendemos por dificultades más específicas (dominio de las combinaciones numéricas básicas), lo cierto es que estas representan un porcentaje muy pequeño del fracaso de los alumnos en la aritmética.
Si analizamos la aritmética como un todo, y consideramos la resolución de problemas como eje vertebrador, las dificultades aparecen cuando se plantea el proceso de enseñanza y aprendizaje como algo mecánico y escasamente significativo. Si entendemos la resolución de problemas como la simple aplicación de operaciones para llegar a un resultado, y no consideramos las estrategias implicadas en este proceso ni los conocimientos conceptuales necesarios para la resolución, el fracaso está servido.
Es necesario considerar la resolución como un proceso complejo que necesita de ciertas estrategias y conocimientos que se desarrollan y hacen cada ves más complejos. Aunque el acceso a estos conocimientos depende en cierta forma del nivel representacional en el que nos situemos. No en vano, las representaciones manipulativas parten del conocimiento informal que poseen los niños, por lo que este debe ser el punto de partida.
Al obrar de esta manera no significa que desaparezcan las dificultades. Solamente estamos considerando un proceso de enseñanza y aprendizaje más significativo y adaptado a las necesidades de cada alumno en función de sus conocimientos y posibilidades.
AGRADECIMIENTOS
Este trabajo ha sido financiado por el proyecto BSO2003-05075 del Ministerio de Ciencia y Tecnología español.
REFERENCIAS
1. Orrantia J. Dificultades en el aprendizaje del cálculo: una perspectiva cognitiva. Siglo Cero 1997;28:5-22. [ Links ]
2. Orrantia J. Les dificultats de l'aprenentatge de les matemàtiques. In: Sánchez E, ed. Dificultats de l'aprenentatge. Barcelona: Universitat Oberta de Catalunya;1997. [ Links ]
3. Orrantia J, Morán MC, Gracia AD, González L. ¡Tenemos un problema...! Propuesta de un programa para enseñar a resolver problemas de matemáticas. Comunicación, Lenguaje y Educación 1995;28:15-28. [ Links ]
4. Gelman R, Gallistel CR. The child's understanding of number. Cambridge:Harvard University Press;1978. [ Links ]
5. Resnick LB. Developing mathematical knowledge. Am Psychol 1989;44:162-9. [ Links ]
6. Resnick LB. From protocuantities to operators: building mathematical competence on a foundation of everyday knowledge. In: Leinhardt G, Putnam R, Hattrup RA, eds. Analysis of arithmetic for mathematics teaching. Hillsdale:LEA;1992. [ Links ]
7. Mayer RE. Mathematical ability. In: Sternberg RJ, ed. Human abilities: an information processing approach. New York:Freeman; 1985. p.127-50. [ Links ]
8. Mayer RE. Cognition and instruction in mathematics: introduction to special section. J Educ Psychol 1989;81:452-6. [ Links ]
9. Mayer RE. Thinking, problem solving, cognition. New York:Freeman;1992. [ Links ]
10. Mayer RE, Larkin JH, Kadane JB. A cognitive analysis of mathematical solving ability. In: Sternberg RJ, ed. Advances in the psychology of human intelligence vol.2. Hillsdale: Erlbaum;1984. p.231-73. [ Links ]
11. Shoenfield A. Mathematical problem solving. Orlando:Academic Press;1985. [ Links ]
12. Greeno J. Some examples of cognitive task analysis with instructional implication. In: Snow R, Federico PA, Montage WE, eds. Aptitude learning and instruction. vol. II. Cognitive process analysis of learning and problem solving. Hillsdale:Erlbaum;1980. p.1-21. [ Links ]
13. Carpenter TP, Moser JM. The development of addition and subtraction problem solving skills. In: Carpenter TP, Moser JM, Romberg YTA, eds. Addition and subtraction: a cognitive perspective. Hillsdale:Erlbaum; 1982. p.9-24. [ Links ]
14. De Corte E, Verschaffel L. The effect of semantic structure on first graders strategies for solving addition and subtraction word problem. J Res Mathematics Educ 1987;18:363-81. [ Links ]
15. Stern E. What makes certain arithmetic word problems involving the comparison of sets so difficult for children? J Educ Psychol 1993;85:7-23. [ Links ]
16. Briars DJ, Larkin JH. An integrated model of skill in solving elementary word problems. Cogn Instruc 1984;1:245-96. [ Links ]
17. Cummins DD, Kintsch W, Reusser K, Weimer R. The role of understanding in solving word problems. Cog Psychol 1988;20:405-38. [ Links ]
18. Kintsch W, Greeno J. Understanding and solving word arithmetic problem. Psychol Rev 1985;92:109-29. [ Links ]
19. Reusser K. From text to situation to equation: cognitive simulation of understanding and solving mathematical word problems. In: Mandl H, De Corte E, Bennett N, Friedrich HF, eds. Learning and instruction. vol. 2. Oxford:Pergamon;1990. p.477-98. [ Links ]
20. Riley MS, Greeno JG. Developmental analysis of understanding language about quantities and solving problems. Cogn Instruc 1988;5:49-101. [ Links ]
21. Riley NS, Greeno J, Heller JI. Development of children's problem solving ability in arithmetic. In: Ginsburg HP, ed. The development of mathematical thinking. New York:Academic Press;1983. p.153-96. [ Links ]
22. Kintsch W. The role of knowledge in discourse comprehension: a construction-integration model. Psychol Rev 1988; 95:163-82. [ Links ]
23. Kintsch W. Comprehension: a paradigm for cognition. Cambridge:Cambridge University Press;1998. [ Links ]
24. Van Dijk TA, Kitsch W. Strategies of discourse comprehension. New York:Academic Press;1983. [ Links ]
25. Orrantia J. El rol del conocimiento conceptual en la resolución de problemas aritméticos con estructura aditiva. Infanc Aprendizaje 2003;26(4):451-68. [ Links ]
26. Fuson KC, Carroll WM, Landis J. Levels in conceptualizing and solving addition and subtraction compare word problems. Cognition and Instruction 1996;14:345-71. [ Links ]
27. Geary DC, Brown SC, Samaranayake VA. Cognitive addition: a short longitudinal study of strategy choice and speed-of-processing differences in normal and mathematically disabled children. Dev Psychol 1991;27:787-97. [ Links ]
28. Geary DC, Hoard MK, Hamson CO. Numerical and arithmetical cognition: patterns of functions and deficits in children at risk for a mathematical disability. J Exp Child Psychol 1999;74:213-39. [ Links ]
29. Orrantia J, Martínez J, Morán MC, Fernández JC. Dificultades en el aprendizaje de la aritmética: un análisis desde los modelos cronométricos. Cognitiva 2002;14:183-201. [ Links ]
 Correspondência:
Correspondência:
Josetxu Orrantia
Avda. La Merced, 109 - 031
Salamanca - Espanha 37005
E-mail: orrantia @usal.es
Artigo recebido: 25/04/2006
Aprovado: 03/06/2006
Trabalho realizado na Universidad de Salamanca, Espanha.














