Serviços Personalizados
Journal
artigo
Indicadores
Compartilhar
Revista Brasileira de Psicodrama
versão On-line ISSN 2318-0498
Rev. bras. psicodrama vol.17 no.2 São Paulo 2009
SEÇÃO TEMÁTICA: Psicodrama e pesquisa: projetos, processos, resultados
A construção dos sociogramas e a teoria dos grafos
The construction of sociograms and the theory of graphs
Glauber José Vaz*
Universidade Estadual de Campinas
Universidade Paulista - UNIP
RESUMO
Os sociogramas constituem importante técnica sociométrica que permite a melhor compreensão das relações entre indivíduos de um grupo ou entre grupos. A construção de sociogramas é extremamente difícil e poucos avanços foram feitos nos últimos anos. Este trabalho propõe novos rumos para a construção de sociogramas, baseado no que se conhece sobre teoria de grafos, importante área da computação e da matemática.
Palavras chave: Sociograma, teste sociométrico, sociometria, computação.
ABSTRACT
The sociogram is an important sociometric technique that enables us to better understand relationships between individuals within a group and relationships between groups. Sociograms are extremely difficult to construct and there have been very few developments regarding this over the past years. Based on the theory of graphs, an important area of computing and mathematics, this paper offers new ways of constructing sociograms.
Keywords: Sociogram; sociometric test; sociometry; computing.
INTRODUÇÃO
Este artigo é uma versão reduzida e adaptada do trabalho de Vaz (2007), que faz um estudo detalhado da construção dos sociogramas, considerando conhecimentos extraídos da ciência da computação.
Conforme Moreno (1992a, p. 196.), o padrão do universo social é invisível, mas os gráficos podem torná-lo visível. Os sociogramas são representações gráficas das relações existentes em um grupo de indivíduos e, mais do que um método de apresentação, os sociogramas constituem um método de exploração, uma vez que possibilita a identificação de fatos sociométricos e a análise estrutural de uma comunidade.
Normalmente, os sociogramas são utilizados em conjunto com o teste sociométrico. No entanto, esta técnica não precisa ser usada somente para representar os resultados de testes sociométricos propriamente ditos. Também pode ser usada com, por exemplo, teste de familiaridade (Moreno, 1992b, p. 156), auto-avaliação sociométrica (Moreno, 1992b, p. 98), método observacional sociometricamente orientado (Moreno, 1992b, p. 118) e teste quase-sociométrico (Moreno, 1992a, pp. 202, 205).
Os sociogramas podem ser utilizados para, por exemplo, fornecer "uma visão sintética dos grupos" (Alves, 1974, p. 106), "dar indicação sobre o grau de coesão entre os membros de determinada sociedade e a afinidade ou agressividade entre duas sociedades de ordem similar" (Moreno, 1992a, p. 200), revelar "a posição que cada indivíduo ocupa no grupo, assim como as inter-relações dos diversos indivíduos" (Alves, 1974, p. 106) e permitir "a observação da estrutura dos grupos assim como a dinâmica de suas evoluções" (Alves, 1974, p. 107). Tais estruturas são enumeradas por Moreno (1992b, pp. 127-128): pares, correntes, triângulos, quadrados, círculos, estrelas.
REVISÃO DO MORENO
Moreno se orgulhava dos sociogramas (Marineau, 1992, p. 123). No entanto, ao escrever sobre esta técnica, às vezes, não deixava suas idéias muito claras. Knobel (2004, p. 123) lembra que a época em que foi publicado o livro "Quem sobreviverá", em que descreve os sociogramas, Moreno tinha pouco domínio do inglês escrito. E ainda ressalta que as traduções também podem ter comprometido a qualidade do texto. Alguns trechos em que Moreno escreve sobre sociogramas merecem uma revisão mais detalhada.
Trecho I
Moreno escreve que
"Como o padrão do universo social é invisível para nós, só os gráficos podem torná-lo visível. O gráfico sociométrico, portanto, é tanto mais útil quanto mais exata e realisticamente retratar as relações que forem descobertas. Como cada detalhe é importante, a apresentação mais exata será a mais apropriada. O problema não é apenas apresentar o conhecimento da maneira mais simples e mais rápida, porém, apresentar as relações de modo que possam ser estudadas" (Moreno, 1992a, p. 196).
É difícil entender o que Moreno quer transmitir quando afirma que o gráfico sociométrico é tanto mais útil quanto mais exata e realisticamente retratar as relações que forem descobertas, e que a apresentação mais exata será a mais apropriada.
Não fica claro o que Moreno quer dizer com relações retratadas exatamente e realisticamente. Tampouco é possível diferenciar uma apresentação mais exata, ou mais precisa, do que outra. De qualquer maneira, o que se pretende é alcançar a melhor representação possível de sociograma. Porém, é difícil determinar o que seria a melhor representação e quais os critérios para determiná-la. O estudo feito na próxima seção sobre os critérios utilizados na construção de um sociograma torna mais claro o que Moreno quis dizer com representação precisa, exata e realista das relações.
Trecho II
Moreno também escreve que:
"Um sociograma é considerado bom quando é legível. Para tal, a quantidade de linhas que se cruzam deve ser reduzida ao mínimo. Quanto menor o número destas linhas, tanto melhor será o sociograma. Após a coleta e a tabulação das escolhas, comece o sociograma pelas pessoas mais escolhidas. Coloque-as em suas formações naturais – três pessoas em um triângulo, quatro em um quadrado, cinco em um pentágono etc, bem separadas no papel. A existência de subgrupos deve ser observável no desenho" (Moreno, 1992b, p. 26).
No entanto, pode-se perceber, por exemplo, que nem sempre o sociograma que tem menor cruzamento de linhas é o mais legível. Além disso, não é simples o posicionamento das pessoas em suas formações naturais, já que cada pessoa pode fazer parte de várias formações.
Este trecho da obra de Moreno tem extrema importância, uma vez que, a partir deste, foram elaboradas as formas com que se montam os sociogramas. Então, a sentença acima é dividida em quatro partes e analisada detalhadamente:
I) Um sociograma é considerado bom quando é legível.
II) Para tal, a quantidade de linhas que se cruzam deve ser reduzida ao mínimo. Quanto menor o número destas linhas, tanto melhor será o sociograma.
III) Após a coleta e a tabulação das escolhas, comece o sociograma pelas pessoas mais escolhidas. Coloque-as em suas formações naturais – três pessoas em um triângulo, quatro em um quadrado, cinco em um pentágono etc, bem separadas no papel.
IV) A existência de subgrupos deve ser observável no desenho.
Pode-se observar, pela sentença I, que o principal objetivo dos sociogramas é tornar a leitura das relações mais fácil. O sociograma, portanto, deve permitir a visualização das relações da maneira mais clara possível.
Um dos elementos que influem nas relações entre as pessoas de um determinado grupo é a existência de subgrupos. Portanto, é fundamental que um sociograma exiba nitidamente os subgrupos existentes em um grupo. A sentença IV destaca essa característica de um bom sociograma.
Na sentença II, Moreno estabelece o que vem a ser um bom sociograma: aquele que apresenta o menor número de linhas que se cruzam com outras linhas. Já na sentença III, Moreno explica uma maneira de se conseguir o sociograma que apresenta a menor quantidade de cruzamentos.
Moreno, então, estabelece de maneira bem genérica o que é um bom sociograma na sentença I, descreve uma característica de um bom sociograma na frase IV, formaliza a noção de um bom sociograma na frase II e explica como obtê-lo na frase III.
Com as frases I e IV, não há como discordar. A principal função de um sociograma é permitir a leitura das relações em determinado grupo. Portanto, ele deve ser legível e exibir com clareza os subgrupos existentes.
Nas frases II e III, Moreno explica uma maneira simples de se construir um bom sociograma, minimizando a quantidade de cruzamentos de linhas nos sociogramas. No entanto, nem sempre este critério, tomado isoladamente, alcança o sociograma ótimo 1,. Alguns contra-exemplos são fornecidos a seguir.
Considere que os dois gráficos da Figura 1(a) são sociogramas. O primeiro apresenta um cruzamento de linhas, mas é simétrico, enquanto o segundo não apresenta cruzamento de linhas, mas não é simétrico. Um sociometrista, certamente, preferiria utilizar o primeiro sociograma a utilizar o segundo. Este é um caso em que o sociograma que apresenta menor quantidade de cruzamento de linhas não é o melhor. Isso ocorre devido a outro critério: a simetria. O mesmo ocorre quando se comparam os gráficos da Figura 1(b). Portanto, a sentença II do trecho apresentado não é verdadeira.

No entanto, a ideia de Moreno sobre o cruzamento de linhas em sociograma não é totalmente equivocada. Pelo contrário, este é um critério muito importante para a construção de sociogramas. A Figura 2(a), por exemplo, mostra muitos cruzamentos entre as linhas que interligam subgrupos, enquanto a Figura 2(b) minimiza os cruzamentos entre estas linhas. Como os sociogramas representados na Figura 02 são equivalentes, pode-se observar que a minimização dos cruzamentos de linhas que ligam subgrupos é vantajosa neste caso. Assim, foi possível verificar que o cruzamento de linhas deve ser evitado na ligação entre subgrupos, mas, dentro deles, o cruzamento de linhas, normalmente, facilita a compreensão do sociograma, uma vez que, desta forma, a figura apresenta maior simetria.

Portanto, para Moreno, o que realmente importa na construção de um sociograma é a legibilidade e a fácil observação de subgrupos. O método para alcançar este objetivo é uma questão secundária.
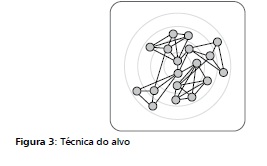
A busca por uma nova maneira de se construirem sociogramas não é inédita, já que o método de Moreno não é satisfatório em muitos casos. A própria técnica do alvo, bastante difundida entre os psicodramatistas atualmente, foi criada na década de 1940. Segundo Knobel (2004, p. 128)
"os gráficos criados por Moreno tinham uma apresentação bastante confusa. Na década de 1940, conforme Bastin (1966, p. 75), Northway reorganizou a construção dos sociogramas, tornando-os mais precisos, claros e fáceis de ler. Para isso, colocou os líderes no centro e dispôs as demais pessoas em círculos concêntricos, de dentro para as bordas, de acordo com a ordem decrescente de sua importância no grupo. Em vista de seu aspecto gráfico, formado por círculos concêntricos, essa apresentação ficou conhecida como técnica do alvo".
Porém, nada garante que, através desta técnica, alcança-se o sociograma ótimo ou mesmo um bom sociograma. Por exemplo, os sociogramas da Figura 2 são equivalentes ao da Figura 3, que utiliza a técnica do alvo. É certo que este é melhor do que aqueles nas situações em que se deseja a visualização dos indivíduos populares e excluídos e suas relações, mas não parece ser a melhor opção quando o objetivo é identificar os subgrupos existentes.
Estas não são as únicas maneiras de se obterem os sociogramas representados nestas figuras, mas tentou-se alcançar a maior simetria possível em ambos os casos.
A teoria dos grafos, área ligada à computação e à matemática, pode contribuir na obtenção de um algoritmo2 que exibe o melhor sociograma para cada caso, a partir de uma definição do que é o sociograma ótimo.
TEORIA DOS GRAFOS
Um grafo G é um conjunto não vazio de vértices (nós) V e um conjunto finito de arestas (arcos) E, tal que cada elemento do conjunto E é representado por um par de elementos de V.
V={V1, V 2,..., V n}. // V é o conjunto de vértices V 1, V 2,..., V n
E={e1, e2, ..., em}. // E é o conjunto de arestas e1, e2, ..., em
ek={Vi, V j} onde V i, V j ∈ V. // ek é a aresta que liga o vértice V i ao vérticeVj
O estudo dos grafos é conhecido como teoria de grafos.
Um sociograma é um grafo em que os vértices correspondem aos indivíduos de um grupo, e as arestas são as relações entre estes indivíduos. Por exemplo, o sociograma da Figura 4 pode ser visto como um grafo em que os vértices, representados por círculos, são indivíduos de um grupo, e as arestas, representadas por linhas, correspondem às escolhas entre eles. Neste caso,
V = {A, B, C, D, E}
E = {{A,D},{A,E},{B,C},{B,E},{C,B},{C,D},{D,A},{D,E},{E,A},{E,D}}.

O conjunto E acima identifica que existe uma aresta de A para D, uma aresta de A para E, e assim por diante. Se o grafo corresponde a um sociograma, estas arestas indicam que o indivíduo A escolhe o indivíduo D, o indivíduo A escolhe o indivíduo E, e assim por diante.
É comum que as escolhas estejam associadas a um número que determina a ordem de escolha. Por exemplo, no sociograma da Figura 4, poderia ser desejável identificar a 1ª e a 2ª escolhas de cada indivíduo do grupo. Neste caso, as arestas dos grafos poderiam ser exibidas associadas a um valor, como, por exemplo, na Figura 5, em que as primeiras escolhas são indicadas pelo número 1 na aresta e as segundas escolhas são indicadas pelo número 2. Rejeições também poderiam ser indicadas no sociograma por números negativos, por exemplo. A Figura 5 mostra as seguintes rejeições: B rejeita A, como primeira rejeição, e também rejeita D, em segundo lugar. C rejeita A.

Os grafos que apresentam valores associados às arestas, como o sociograma da Figura 5, são denominados grafos com pesos. Também existe uma diferenciação entre grafos direcionados e não direcionados. Quando as arestas, de alguma forma, representam relações simétricas, as arestas do grafo não precisam ter uma direção definida e são representadas apenas por linhas, sem setas indicando um sentido.
Grafos não direcionados são utilizados nos casos em que se deseja representar, por exemplo, mutualidades, pois, desta forma, só existe uma aresta ligando dois indivíduos (vértices) quando eles se escolhem mutuamente. A Figura 6 mostra um exemplo em que os indivíduos B e C escolhem- se mutuamente, assim como os indivíduos A, D e E.

Já nos sociogramas em que se deseja indicar cada escolha, se um indivíduo escolhe outro, não significa que, necessariamente, esta escolha seja recíproca. Portanto, o sociograma deve ser um grafo direcionado, como os grafos das Figuras 4 e 5.
O PROBLEMA DE SE DESENHAREM GRAFOS
Alves (1974, p.107) afirma que
"Moreno não se preocupou com a sistematização da técnica de feitura dos sociogramas coletivos. Isto ocasionou dois sérios inconvenientes: a) Dificuldade de representação clara da estrutura do grupo. b) A configuração do sociograma ser determinada em grande parte pelo simples acaso, ou o senso estético do sociometrista".
Porém, ele sugere que para se fazer o sociograma de relações, "é mais prático começar o sociograma pelos indivíduos mais populares e distribuir os demais em função de suas ligações com os mesmos" (Alves, 1974, p. 113.), prática que não ajuda muito na sistematização da construção de sociogramas.
Na verdade, as técnicas propostas depois de Moreno ainda não solucionam estes dois problemas. Isso é resultado da complexidade que é inerente ao problema de se construirem sociogramas, ou grafos, de uma maneira geral. A questão não é que Moreno não se preocupou com a sistematização. Ele simplesmente não conseguiu sistematizar satisfatoriamente de tal forma a abranger qualquer caso, assim como qualquer outro ser humano, porque é praticamente impossível fazer tal sistematização sem contar com ferramentas computacionais. O problema de se desenharem grafos, dependendo dos critérios utilizados, pertence à classe dos problemas NP-difíceis, que, na teoria da computação, envolvem todos aqueles problemas que são complicados de se resolverem, mesmo com a ajuda dos computadores.
Boaventura Netto (2003, pp. 279, 281) enumera os principais critérios que, normalmente, guiam a construção do traçado dos grafos:
• Simetria da figura.
• Minimização dos cruzamentos.
• Distribuição uniforme dos vértices.
• Uniformidade dos comprimentos das arestas.
• Uso de linhas retas para as arestas.
• Minimização do comprimento da maior aresta.
• Proporcionalidade entre o valor e o comprimento de suas arestas.
A importância destes critérios varia de acordo com o problema que se queira resolver. Uma análise destes critérios é feita tendo-se em mente que o objetivo é criar sociogramas.
A simetria da figura é extremamente importante na construção de sociogramas, uma vez que, quanto mais simétrico, mais legível torna-se o sociograma. Isto pôde ser observado na seção 2.2, em que alguns trechos da obra de Moreno foram revistos. O problema em relação a este critério é a dificuldade de se medir a simetria. Como é difícil quantificá-la, também é difícil sistematizar a construção de grafos que utilizam o critério da simetria. No entanto, não se pode simplesmente desconsiderar este critério no tratamento de sociogramas. Esta simetria é relacionada ao que Alves chamou de senso estético do sociometrista.
A minimização de cruzamentos também é importante e foi reconhecida por Moreno como um critério para a construção de sociogramas. No entanto, a análise de um sociograma segundo este critério não é tão simples. Moreno afirma que é necessário minimizar a quantidade de cruzamentos entre as arestas que compõem o sociograma (seção 2.2), mas não é tão simples assim, uma vez que esta minimização pode comprometer a simetria do mesmo. Portanto, em alguns casos, há a possibilidade de se construir um sociograma com menos cruzamentos e menor simetria, e um outro com mais cruzamentos, mas com maior simetria. A seção 2.2 apresentou exemplos desta situação. Nestes casos, é difícil fazer a comparação entre sociogramas, uma vez que a simetria de um grafo não pode ser facilmente quantificada e também porque é difícil fazer comparações baseadas em diferentes critérios.
A simetria da figura e a minimização de cruzamentos entre as linhas são os principais critérios para a construção de sociogramas. Considerálos já torna o problema suficientemente difícil. Mas os demais critérios também são analisados a seguir.
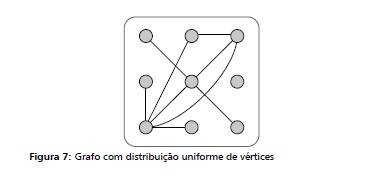
Em algumas aplicações de grafos, é importante que haja uma distribuição uniforme dos vértices. Não é o caso dos sociogramas, uma vez que os vértices representam indivíduos de um grupo e estes não formam subgrupos de maneira uniforme. Assim, normalmente, ocorre que se formam subgrupos de tamanhos diferentes, pequenos e grandes. Caso os vértices fossem distribuídos uniformemente, em uma grade (Figura 7), por exemplo, o grafo não representaria de maneira clara as estruturas do grupo.
Em relação à uniformidade do comprimento das arestas, esta característica, normalmente, ajuda na simetria do grafo. Portanto, poderia ser interessante obter sociogramas em que todas as arestas têm o mesmo comprimento ou comprimentos com diferenças as menores possíveis. No entanto, isto não deve ser uma preocupação ao se construírem sociogramas, uma vez que este critério já está, de certa forma, envolvido no critério de simetria e introduziria maior dificuldade a um problema que já é bastante difícil. Além disso, comprimentos diferentes de arestas não comprometem de maneira significativa a compreensão do sociograma. O sociograma representado à esquerda na Figura 1(a), por exemplo, apresenta arestas de tamanhos distintos – as arestas nas diagonais têm maior comprimento – e isto não compromete sua compreensão.
O uso de linhas retas para as arestas é outro critério considerado na teoria de grafos. No entanto, não deve ser motivo de preocupação na construção de sociogramas, já que o uso de linhas curvas não afeta a qualidade dos sociogramas. Portanto, a linha reta pode ser determinada como padrão, mas nos casos em que uma aresta passaria por um terceiro vértice caso ela fosse desenhada por uma linha reta, não há problema em representar a aresta por uma linha curva. Na Figura 7, por exemplo, a aresta que liga o vértice do canto superior direito ao vértice do canto inferior esquerdo deve ser curva, pois, se fosse representada por um segmento de reta, tal aresta passaria pelo vértice do centro. Deste modo, a aresta em questão seria equivocadamente interpretada como duas arestas, uma que liga o vértice do canto superior direito ao vértice do centro, e outra que liga este vértice ao vértice do canto inferior esquerdo.
O critério de minimização do comprimento da maior aresta é interessante no contexto de construção dos sociogramas, pois poderia reduzir seu tamanho global, o que poderia permitir uma melhor visualização do sociograma como um todo. No entanto, também introduziria novas dificuldades ao problema. Seria interessante considerar este critério se não fosse tornar o problema ainda mais difícil. O mesmo raciocínio vale para a proporcionalidade entre o valor ("peso") e o comprimento de suas arestas, nos casos em que os sociogramas ilustram a ordem de escolhas e rejeições entre os indivíduos do grupo.
Talvez, assim, fosse possível alcançar um grau de realismo maior, que segundo Moreno (seção 2.1) seria interessante. Este critério é levado em consideração nos sociogramas individuais de distâncias sociométricas, explicados por Alves (1974, pp. 102-103). No entanto, ter o compromisso de se manter esta proporcionalidade para todo um sociograma coletivo é um fator que dificulta muito sua construção ou, até mesmo, torna-a impossível.
Tem-se agora uma noção clara de que muitos critérios podem ser observados quando se constrói um grafo. Porém, nos casos dos sociogramas, dois critérios são mais relevantes: a simetria e a minimização dos cruzamentos entre as linhas que representam as escolhas, sendo que o primeiro merece ainda maior destaque. A simetria de uma figura, contudo, é difícil de ser mensurada, o que torna bastante complexo o problema de se desenharem sociogramas.
Quando Moreno escreveu que a representação gráfica das relações entre os indivíduos de um grupo deveria ser a mais exata, precisa e realista possível, provavelmente, ele estava se referindo, de maneira intuitiva, a critérios como estes que acabaram de ser analisados.
CONCLUSÃO
Kaufman (1993, p. 48) lembra que há uma tendência parcial no uso do teste sociométrico e que é comum vê-lo transformado num procedimento matemático, em que o que se busca é fundamentalmente a medida das interações. Com isso, perde-se a perspectiva da qualidade dos vínculos, levando a um consequente desvirtuamento da proposta original. Neste trabalho, não há intenção alguma em estimular esse uso puramente matemático. A proposta é aperfeiçoar os métodos de construção dos sociogramas para que possam auxiliar ainda mais o sociometrista que tem interesse em fazer uso desta técnica.
Mais pesquisas devem ser feitas sobre sociogramas, devido à sua grande importância e à dificuldade envolvida em sua construção. Apesar de alguns métodos de desenho de sociogramas terem sido propostos depois de Moreno, nenhum consegue obter o sociograma ideal para qualquer caso. Normalmente, propõem-se mudanças sutis nos métodos já existentes. A técnica do alvo, por exemplo, deixa a desejar em muitas situações. Na seção 2.2, foi possível perceber o quanto tal abordagem está longe do ideal quando se trata de reconhecer estruturas grupais, apesar de ser excelente para reconhecer líderes e excluídos. É necessário, portanto, criar uma nova maneira de se construirem sociogramas.
No entanto, como este é um problema extremamente complicado, não se espera que seja resolvido manualmente por homens, uma vez que envolve cálculos complexos. Uma ferramenta automática poderia fazer o trabalho de maneira simples, rápida e precisa. Já existem algumas ferramentas (Zampieri, Ledis Group) com este objetivo, que, apesar de fazer o trabalho de um sociometrista de forma muito mais simples e rápida, ainda utilizam os métodos que são utilizados pelos homens e não exploram a vantagem de que podem fazer um processamento de dados muito mais rápido e preciso do que o homem para gerar um sociograma mais próximo do ideal.
Além da necessidade de uma ferramenta automática, percebe-se também que o problema de se traçarem sociogramas não é tão isolado e tão específico quanto parece. Ele equivale ao problema do traçado em grafos, que já conta com muitos estudos realizados por pesquisadores de teoria da computação. Portanto, é fundamental um intercâmbio entre pesquisadores da computação e do psicodrama para se resolver o problema de se desenharem sociogramas da melhor maneira possível.
Este trabalho não propõe um novo método para a construção de sociogramas, mas mostra um caminho que deve ser tomado a fim de se obterem melhores sociogramas. Em vez de fechar com soluções, o presente trabalho abre novos rumos a serem seguidos. São necessárias pesquisas sobre os traçados de grafos utilizando os critérios interessantes para os sociogramas.
Referencias
ALVES, Danny José. O teste sociométrico: sociogramas. Porto Alegre: Globo, 1974. [ Links ]
BASTIN, G. As técnicas sociométricas. Lisboa: Livraria Morais, 1966. [ Links ] Apud KNOBEL, Anna Maria. Moreno em ato: a construção do psicodrama a partir das práticas. São Paulo: Ágora, 2004.
BOAVENTURA NETTO, Paulo Oswaldo. Grafos: Teoria, Modelos, Algoritmos. 3. ed. rev. amp. São Paulo: Edgard Blücher. 2003. [ Links ]
KAUFMAN, Fani Goldenstein. O teste sociométrico. In: MONTEIRO, Regina (org.). Técnicas fundamentais do psicodrama. São Paulo: Brasiliense, 1993, pp. 45-68. [ Links ]
KNOBEL, Anna Maria. Moreno em ato: a construção do psicodrama a partir das práticas. São Paulo: Ágora, 2004. [ Links ]
LEDIS GROUP. SociometryPro. Disponível em: < http://www.ledisgroup. com/eng/sociometry/sociometrypro.ph>. Acesso em: 12 fev. 2007. [ Links ]
MARINEAU, René F. Trad: José de Souza Mello Werneck. Jacob Levy Moreno, 1889-1974: pai do psicodrama, da sociometria e da psicoterapia de grupo. São Paulo: Ágora, 1992. [ Links ]
MORENO, Jacob Levy. Quem sobreviverá? Fundamentos da sociometria, psicoterapia de grupo e sociodrama. Goiânia: Dimensão, 1992 a v. 1. [ Links ]
______. Fundamentos da sociometria, psicoterapia de grupo e sociodrama. Goiânia: Dimensão, 1992 b v. 2. [ Links ]
VAZ, Glauber J. Sociogramas à luz da computação. Campinas, 2007. (Monografia apresentada para obtenção do título de sociopsicodramatista, IPPGC). [ Links ]
ZAMPIERI, Roberto. Cibertest. Disponível em: < http://www.ciclomuta. com.br/testes.htm> Acesso em: 12 fev. 2007. [ Links ]
 Endereço para correspondência
Endereço para correspondência
Rua José Bianchi, 81 - Apto. 54 Vila Conceição
Limeira - SP CEP 13480-316
e-mail: glauber.vaz@gmail.com
* Mestre em Ciência da Computação (Unicamp); professor do curso de Ciência da Computação na Unip e do curso de Tecnologia em Informática (Unicamp); sociopsicodramatista (IPPGC).
1, - O termo 'sociograma ótimo' refere-se ao melhor sociograma possível que pode ser construído.
2, - Sequência de instruções para realizar determinada tarefa.













