Serviços Personalizados
Journal
artigo
Indicadores
Compartilhar
Temas em Psicologia
versão impressa ISSN 1413-389X
Temas psicol. vol.23 no.1 Ribeirão Preto 2015
ARTICLE
Resolução de problemas aritméticos: efeitos de ensino com uma balança virtual
Arithmetic problem solving: the effects of teaching with a virtual balance
Resolución de problemas aritméticos: el efectos de la enseñanza con una balanza virtual
Ana Luisa de Freitas IégasI; Verônica Bender HayduII
IUnião das Instituições de Ensino Superior do Estado de São Paulo, Presidente Prudente, SP, Brasil
IIDepartamento de Psicologia Geral e Análise do Comportamento da Universidade Estadual de Londrina, Londrina, PR, Brasil
RESUMO
Estudos da bibliografia têm demonstrado que grande parte das dificuldades de resolução de problemas aritméticos corresponde a aspectos de natureza específica, como a posição da incógnita nos problemas e a forma de apresentação dos problemas, e que a representação gráfica dos problemas pode contribuir para reduzir esse tipo de dificuldade. O software Arit-Fácil foi usado para avaliar os efeitos de um procedimento de ensino de problemas aritméticos de adição e de subtração com balanças virtuais sobre o desempenho na resolução de problemas nas formas de operação e de sentenças-problema. Os problemas apresentavam incógnitas nas posições a, b e c. Quarenta e oito alunos de 1ª série do Ensino Fundamental foram submetidos a um pré-teste, um procedimento de ensino com problemas na forma de balança virtual e a um pós-teste. Observou-se um aumento nas porcentagens de acertos dos participantes em sentenças-problema de adição com incógnitas nas três possíveis posições e nas subtrações com incógnita na posição c; e um aumento na porcentagem de acertos nas operações com incógnitas nas três possíveis posições, exceto nas operações de adição em que o desempenho inicial foi acima de 70%. Assim, pode-se concluir, o procedimento foi apropriado para que os participantes aprendessem a solucionar problemas aritméticos.
Palavras-chave: Resolução de problemas aritméticos; adição; subtração; matemática.
ABSTRACT
Bibliography studies have shown that most of the difficulties in arithmetic problem solving correspond to aspects of a specific nature, as the position of the unknown set and the form of presentation of the problems, and that the graphic representation of the problems can contribute to reduce this difficulty. The software Arit-Fácil was used to evaluate the effects of a procedure for teaching arithmetic problems of addition and subtraction with a virtual balance on the performance in solving problems in the forms of operation and word-problems. The problems presented unknown set in positions a, b and c. Fortyeight students of the fist grade of an elementary school underwent a pretest, a teaching procedure with problems in the form of virtual balance and a post-test. It was observed an increase in the percentage of correct responses on addition word-problems with unknown set in the three possible positions, and subtractions with the unknown set at the position c; and an increase in the percentage of correct responses in the resolution of operations with the unknown set at the three possible positions, except on addition operations in which the initial performance was above 70%. Thus, it was concluded that the procedure was appropriate for participants to learn how to solve arithmetic problems.
Keywords: Arithmetic problem solving; addition; subtraction; mathematics.
RESUMEN
Los estudios de la literatura han demostrado que la mayoría de las dificultades en la resolución de problemas aritméticos corresponde a los aspectos de carácter específico, como la posición de la incógnita y la forma de presentación de los problemas, y que la representación gráfica de los problemas puede contribuir a reducir esta dificultad. El software Arit-fácil fue utilizado para evaluar los efectos de un procedimiento para la enseñanza de problemas aritméticos de suma y sustracción con una balanza virtual sobre el desempeño en la solución de problemas en las formas de operación y sentencias-problema. Los problemas presentaban incógnitas en las posiciones a, b y c. Cuarenta y ocho estudiantes del primero grado de una escuela primaria se sometió a un pre-test, un procedimiento de enseñanza con problemas en la forma de balanza virtual, y un pos-test. Se observó un aumento en el porcentaje de respuestas correctas en sentencias-problema de suma con incógnitas en las tres posiciones posibles y en sustracción con la posición de la incógnita en c; y un aumento en el porcentaje de respuestas correctas en la resolución de operaciones con incógnitas en las tres posiciones posibles, excepto en las operaciones de suma en los que el rendimiento inicial era superior al 70%. Por lo tanto, se puede concluir que el procedimiento fue apropiado para que los participantes aprendan a resolver problemas aritméticos.
Palabras clave: Solucionar problema de aritmética; suma; sustracción; matemática.
A forma mais frequente de utilização do computador na área educacional é aquela em que ele serve como apoio ao conteúdo pedagógico, enriquecendo e inovando as práticas tradicionalmente usadas. Com relação ao aspecto inovador, características importantes do computador são a interatividade e dinamismo. Esse dispositivo pode ser programado de forma a não se limitar à apresentação de informações ao aluno, mas receber, processar e liberar feedback, podendo ocorrer uma troca constante, que é realizada por meio de interfaces cada vez mais avançadas. Com o devido cuidado, podem ser programadas atividades que se caracterizam como recursos de ensino para o desenvolvimento de inúmeras habilidades e competências relativas aos mais diversos campos de atuação do ser humano. Assim, quando programado e empregado de forma apropriada, o computador pode tornar-se uma ferramenta atrativa, dinâmica e eficiente, que pode servir como apoio a alunos e professores para atingir objetivos pedagógicos.
Com vista a atingir objetivos pedagógicos, uma variedade de atividades de ensino pode ser planejada com base em princípios/conceitos de aprendizagem de Análise do Comportamento (Henklain & Carmo, 2013a), assim também aquelas realizadas por meio do uso da informática. Por exemplo, os princípios/conceitos de reforço (com a noção de liberação imediata de consequências para as respostas), de modelagem (aproximação sucessiva e reforço diferencial do comportamento alvo), de controle de estímulos (generalização e discriminação de estímulos), de operações estabelecedoras (com as noções de motivação), dentre outros, são fundamentais para arranjar as contingências para o ensino. Esses princípios/conceitos podem, portanto, contribuir para que se alcance a função primordial da Educação: "preparar a criança e o jovem para pensarem matematicamente, cientificamente, gramaticalmente" (Vademarin, 1998, p. 83).
Baseado em uma visão sobre as realidades social, cultural e econômica do brasileiro, Toro (2002) especificou sete competências a serem desenvolvidas pelos alunos: (a) domínio da linguagem e escrita, (b) resolução de problemas e realização de cálculos, (c) análise, síntese e interpretação de dados, fatos e situações, (d) compreensão do meio social e atuação sobre ele, (e) compreensão dos meios de comunicação e sua utilização com critérios, (f) localização e acesso de dados e de como utilizá-los, (g) trabalho e organização em grupo. A resolução de problemas e a realização de cálculos, foco do presente estudo, envolvem, segundo Skinner (1984), a emissão de comportamentos precorrentes, os quais podem ser públicos ou privados. Esses comportamentos consistem em manipular as variáveis relacionadas ao problema, de tal forma que o comportamento de solucionar o problema seja mais provável. Um aspecto fundamental para o ensino da resolução de problemas consiste, portanto, na identificação, pelo professor, desses comportamentos precorrentes que ele deve ensinar ao seu aluno (Levingston, Neef, & Cihon, 2009; Neef, Nelles, Iwata, & Page, 2003; ver também Strapasson & Dittrich, 2008).
Um dos comportamentos precorrentes na resolução de problemas é a discriminação das variáveis relevantes do problema. Na resolução de problemas aritméticos, por exemplo, Carpenter e Moser (1983) relataram, a partir de uma revisão da bibliografia, que as varáveis que afetam o desempenho de escolares são a posição da incógnita, os aspectos sintáticos, a estrutura semântica do problema (número de palavras no problema, a sequência das informações e a presença de palavras que sugerem uma operação particular). Dado essa diversidade, pode-se observar que na bibliografia das áreas da Psicologia e da Educação uma série de estudos foi desenvolvida para avaliar desempenho na resolução de problemas e analisar os processos envolvidos (e.g., Burg & Klein, 2001, Hiebert, 1982; Knox, Andrews, & Hood, 2010; Lemaire & Callies, 2009; Oliveira & Tourinho, 2001), bem como para testar procedimentos de ensino (Capovilla, César, Capovilla, & Haydu, 1997; Henklain & Carmo, 2013b; Schumacher & Fuchs, 2012).
O estudo desenvolvido por Hiebert (1982) visou investigar o efeito da posição da incógnita e o uso de diferentes estratégias de resolução como variáveis que afetam a solução de problemas. Participaram, em sessões individuais, 47 alunos de 1ª série do Ensino Fundamental, aos quais foram apresentados seis sentenças-problema com estrutura semântica similar, sendo três de adição e três de subtração, com variação da posição da incógnita (a, b e c). Pequenos objetos em forma de cubos podiam ser utilizados para solucionar os problemas. Cada problema era lido ao participante e relido quando necessário. Se o participante apresentasse dificuldades em resolvê-lo, era dito que ele poderia utilizar os cubos para ajudá-lo a chegar à reposta. Quando a resposta estava errada, o pesquisador pedia para o participante explicar como chegou àquele resultado. Os resultados permitem constatar que na resolução dos problemas com a incógnita na posição a, b e c, os participantes apresentaram, respectivamente, 18%, 40% e 55% de respostas corretas, demonstrando que os problemas com incógnita nas posições a e b eram mais difíceis para os participantes.
As dificuldades de resolução de problemas podem ser minimizadas, de acordo com Capovilla et al. (1997) e Neef et al. (2003), se forem apresentadas aos alunos iniciantes ou com atraso no desenvolvimento sentenças-problemas sem muitas palavras e com palavras de fácil entendimento. Além disso, as dificuldades podem ser reduzidas por meio da apresentação dos problemas aritméticos em mais de um formato, como a de uma balança, conforme sugeriram Capovilla et al. (1997) e Haydu, Costa e Pullin, (2006). No formato de balança, a posição da incógnita não está em evidência e as dificuldades relacionadas a aspectos semânticos e sintáticos não estão presentes. Esse tipo de problema requer noções de equilíbrio, o que, no entanto, crianças muito pequenas já apresentam (Halford, Andrews, Dalton, Boag, & Zielinski, 2002).
Tendo em vista os fatores que são relevantes na resolução de problemas aritméticos como o uso de objetos e representações pictóricas, a possibilidade de variar as estratégias e a condição de tornar a linguagem matemática significativa, Skemp (1971) propôs modelos de exercícios na forma de uma balança (mais especificamente uma gangorra), que permitem apresentar operações dos tipos: x+b=c; a+x=c; a+b=x; x-b=c; a-x=c; a-b=x. Capovilla et al. (1997), baseados nessa proposta, avaliaram um software, no qual o usuário equilibra os dois lados de uma gangorra para chegar ao resultado correto dos problemas de adição e subtração. Dois estudos foram desenvolvidos utilizando esse software, denominado de "Equação-Equilíbrio". Do Estudo 1, participaram um menino de 6 anos, que cursava a pré-escola e outro de 8 anos, que cursava a 1ª série pela segunda vez e apresentava dificuldades de leitura, escrita e aritmética. Foram apresentados nove problemas de adição para cada uma das três posições de incógnita. Os participantes apresentaram desempenhos equivalentes nos problemas. Para ambos participantes, em oposição aos dados de Hiebert (1982), o melhor desempenho foi obtido com a incógnita na posição a e o pior com a incógnita na posição c. Do Estudo 2, participaram sete alunos que cursavam 1ª série, do Ensino Fundamental e foram apresentados 180 problemas de adição e subtração, com números positivos e negativos, variando a posição da incógnita. Os resultados mostram que o grau de dificuldade nos problemas de subtração com incógnita na posição c foi maior do que os problemas de adição na mesma posição. Não houve diferença significativa quanto à porcentagem de erro nas sentenças-problema de adição com incógnitas nas posições a e b. A adição com incógnita na posição b foi mais fácil que subtração com incógnita nessa mesma posição. A subtração, com incógnita na posição b, foi mais difícil que adição com incógnita na posição a. Não houve diferença significativa no desempenho entre problemas de subtração com incógnitas nas posições a e c. Capovilla et al. (1997) concluíram que os processos utilizados para chegar à resposta dos problemas apresentados por meio da balança diferem daqueles envolvidos nas sentenças-problema.
Em um estudo subsequente realizado por Haydu et al. (2001), do qual participaram alunos de 2ª série do Ensino Fundamental, a resolução de problemas aritméticos apresentados sob a forma de balança, também, foi investigada. Entretanto, os problemas foram apresentados em cadernos com figuras impressas, nas formas de operação, sentenças-problema e balança (10 de cada), com a incógnita localizada nas três possíveis posições. O maior número de acertos foi apresentado nos problemas em forma de operação e sentenças-problema quando a incógnita estava na posição c e o número de acertos foi significantemente menor nas sentenças-problema com incógnita nas posições a e b. Além disso, foram apresentados mais erros nos problemas em forma de balança com a incógnita na posição c do que nas sentenças-problema com a incógnita nessa posição. Esses resultados levaram os autores a concluir que as sentenças-problema com incógnitas nas posições a e b são mais difíceis. Haydu et al. relataram ainda, que a figura de balança por eles empregada gerou certo grau de dificuldade, pois os participantes questionaram sobre como equilibrá-la, uma vez que ela foi representada com um prato e uma caixa em um dos lados da balança (a caixa representando a incógnita), e um prato do outro lado. Em razão desse aspecto e porque a software "Equação-Equilíbrio", estava desatualizado, Iégas (2003) desenvolveu o software Arit-Fácil, que foi base-ado nos desenhos das balanças de Haydu et al. Esse software permite resolver problemas aritméticos de adição e de subtração com variação da posição da incógnita, apresentados em forma de operação, sentença-problema e na forma de uma balança que se equilibra, podendo ou não ser fornecido feedback para as repostas. O presente estudo foi desenvolvido com o software Arit-Fácil, para avaliar o efeito de um procedimento de ensino de problemas aritméticos de adição e de subtração com balanças virtuais sobre o desempenho na resolução de problemas nas formas de operação e sentença-problema.
Método
Participantes
Participaram do estudo todos os 49 alunos pertencentes a duas turmas de 1ª série do Ensino Fundamental de uma instituição privada, localizada em uma cidade do interior do estado de São Paulo, com idades variando entre 6 e 8 anos, sendo eles 29 do sexo masculino e 19 do sexo feminino. Somente os resultados de 48 alunos cujos pais assinaram o Termo de Consentimento Livre e Esclarecido, autorizando o filho a participar da pesquisa, foram considerados para a análise de dados.
Cada uma das duas turmas foi distribuída em dois grupos a partir da lista de chamada. A metade de cada uma das turmas foi designada para um dos dois grupos de participantes. Nas fases do Pré-teste, Programa de Ensino e Pós-teste, dois monitores do Núcleo de Informática da escola auxiliaram a pesquisadora (primeira autora deste artigo) na aplicação do procedimento. Esses monitores foram previamente instruídos quanto à utilização do software e quanto às instruções que dariam aos participantes. Eles também auxiliaram na impressão dos relatórios com os resultados.
Materiais e Local da Coleta de Dados
As sessões aconteceram no final do 1º semestre, em uma aula no Núcleo de Informática, onde estavam instalados em mesas 36 computadores Pentium 166, sendo designado um para cada participante. A sala tinha na parede em frente os computadores, um telão onde as imagens de um dos computadores era projetada por meio de um projetor multimídia.
O software Arit-Fácil tem as funções e telas descritas a seguir. Após a abertura, o software apresenta uma tela de opções por meio da qual as tarefas a serem realizadas são programadas. As opções de tarefas incluem a forma de apresentação do problema (operação, sentença-problema ou balança); a posição da incógnita (a, b e c ou as três posições intercaladas); e para as operações e as sentenças-problema, a opção de apresentar ou não feedback. A tela seguinte tem um espaço para o usuário digitar seu nome e após clicar sobre a palavra "OK", o problema aritmético é apresentado.
Nos problemas apresentados em forma de operação e de sentença-problema, a resposta do usuário aparece em um quadrado cinza com um traço. Nas balanças, o quadrado cinza fica colocado sobre um dos braços da balança em que devem ser acrescentadas bolinhas que representam a solução do problema. Nos problemas em forma de operação e de sentença-problema, o feedback de acerto e de erro são um rosto sorridente e um rosto triste, respectivamente. Nos problemas em forma de balança, a consequência de acerto consiste de uma animação gráfica em que bolinhas, na quantidade que corresponde à resposta do usuário caem sobre o prato da balança (adição), substituindo o quadrado cinza e equilibrando a balança. Nos problemas de subtração, o número digitado como resposta para a solução do problema produz a explosão das bombas, substituindo o quadrado cinza e equilibrando a balança, se a resposta estiver correta. Respostas incorretas produzem o escurecimento da tela por 10 segundos. Após cada sequência de problemas, aparece uma tela com um link "Ver Resultado", o qual direciona o usuário para a tela do relatório em que são apresentados os seguintes dados: nome do usuário, data, número e porcentagem de respostas corretas por tipo de problema e posição da incógnita.
Problemas de adição e subtração em forma de operação, sentença-problema e balança (com animação), envolvendo valores de 0 a 10, fazem parte do conjunto de estímulos a serem escolhidos na preparação de uma sessão. Vinte e quatro problemas foram apresentados nos pré-teste e no pós-testes deste estudo, sendo 12 em forma de operação e 12 em forma se sentença-problema, os quais estão listados na Tabela 1.
Quarenta problemas diferentes quanto aos valores foram usados durante o programa de ensino. Nesses, os problemas em forma de balança e de sentença tinham as três posições da incógnita misturadas, sendo os problemas de 1 a 10 com incógnita na posição a; de 11 a 20, com posição da incógnita em b; de 21 a 30, com incógnita na posição c; e problemas com a incógnita em a, b e c apareciam misturados na sequencia de 31 a 40.
Procedimento
Os objetivos e o procedimento do estudo foram expostos à direção da escola e depois de ter sido dada a autorização para a realização do estudo, o Termo de Consentimento Livre e Esclarecido aprovado pelo Comitê de Ética em Pesquisa da instituição das autoras, foi enviado aos pais dos alunos para leitura e assinatura. A professora da sala colou o termo na agenda escolar de cada aluno, para os pais retornarem o do estudo, o Termo de Consentimento Livre e aos pais dos alunos para leitura e assinatura. A Esclarecido aprovado pelo Comitê de Ética em professora da sala colou o termo na agenda es-Pesquisa da instituição das autoras, foi enviado colar de cada aluno, para os pais retornarem o termo preenchido, autorizando ou não a participação de seus filhos na pesquisa. Antes do início da coleta de dados, telefonou-se para os pais que ainda não haviam enviado o Termo assinado. Apenas um pai não consentiu a participação do filho. Esse aluno fez parte das atividades, mas os dados referentes ao seu desempenho não foram tabulados.
Fase 1. Pré-Teste
Um procedimento de controle de ordem de aplicação da sequência dos problemas foi empregado, de tal forma que o Grupo 1 resolveu, primeiramente, os problemas apresentados em forma de operação e em seguida as sentenças-problema. O Grupo 2 resolveu os mesmos problemas, porém em ordem inversa. O pré-teste foi realizado primeiro com os participantes do Grupo 1, que foram convidados a se dirigir ao Núcleo de Informática da escola, no qual estavam os computadores com o software instalado e inicializado. Essa fase foi composta por uma sessão de aproximadamente 45 minutos. Após os alunos se acomodarem diante dos computadores, a pesquisadora disse que eles utilizariam um programa de computador desenvolvido especialmente para uma pesquisa, que envolvia problemas aritméticos. Os participantes do Grupo 2 receberam as mesmas informações, mas em uma sessão realizada a parte.
A primeira instrução dada pela pesquisadora foi:
Vocês irão resolver agora alguns problemas aritméticos, sendo 10 problemas em forma de operação, aquelas continhas que vocês já conhecem. Acabando os 10 problemas, aparecerá uma tela com a frase: VER RESULTADO. Vocês deverão erguer a mão para que um dos monitores imprima seu relatório. Daí esse monitor colocará os outros 10 problemas em forma de sentença-problema, do tipo: Maria tinha um lápis, ganhou mais um. Acabando essa sequência vocês deverão novamente erguer a mão para que um dos monitores imprima seu próximo relatório.
A primeira tela do software era apresentada simultaneamente no telão e a seguinte instrução era dada: "Clique com o mouse dentro do retângulo e digite seu nome. Depois clique no botão OK, para continuar. Após digitar o nome e clicar no botão OK, a sequência de problemas será iniciada e você poderá começar".
Para os problemas apresentados em forma de operação, a seguinte instrução era dada: "Clique no retângulo, que corresponde ao número que está faltando e digite a resposta correta para solucionar a operação. Depois clique no botão OK, para passar para a próxima operação". Enquanto a instrução era dada, foi projetado na tela o exemplo de uma operação, para que todos participantes pudessem acompanhar a explicação.
Para sentenças-problema, a seguinte instrução era dada enquanto era projetada na tela a imagem do primeiro problema desse tipo: "Leia o problema com atenção. Clique no retângulo e digite a resposta correta para o problema. Em seguida, clique no botão OK, para continuar".
Enquanto os participantes resolviam os problemas, os monitores ficavam circulando pela sala, atendendo os alunos que apresentavam dúvidas quanto ao uso do software. Durante essa fase, as respostas aos problemas não eram seguidas de feedback. Ao terminarem a sessão, os participantes eram instruídos a se dirigirem a um local específico do Núcleo de Informática e ficavam sentados brincando. Logo que todos acabavam, uma fila era formada e eles eram levados novamente para a sala de aula.
Fase 2. Programa de Ensino
Todos os alunos que participaram da fase anterior foram chamados para sessão de ensino de resolução de problemas aritméticos em forma de balança, independente do desempenho na fase anterior. Eles foram mantidos nos mesmos grupos da fase anterior. Os participantes novamente chegavam ao Núcleo de Informática e encontravam imagens do software projetadas na tela, na parte em que deve ser inserido o nome do aluno.
Essa fase foi desenvolvida em duas sessões. A primeira durou 40 min e a segunda 20 min aproximadamente. No início da primeira sessão, os participantes recebiam instruções de como os problemas em forma de balança deviam ser resolvidos, isto é, de como as balanças funcionavam. Eles resolveram primeiro 10 problemas que apresentavam a posição de incógnita a, em seguida 10 com a posição de incógnita b e, finalmente, 10 com a posição de incógnita c. Na segunda sessão, eles resolveram 10 problemas em que as três posições de incógnita estavam presentes e misturadas.
Sobre o funcionamento das balanças, foi dada a seguinte instrução diante de balanças de adição e subtração:
Nos dois lados da balança poderão aparecer tanto bolinhas quanto bombinhas. As bolinhas representam as quantidades que você acrescenta à balança e as bombinhas representam as quantidades que serão retiradas da balança. Leia com atenção a instrução que aparece em cada tela. Você terá que descobrir quantas bolinhas estão faltando ou no Prato A, que é o da esquerda, ou no Prato B, que está à direita.
Nessa fase, as respostas dos participantes eram seguidas de feedback de acerto e de erro. Logo após o feedback, o problema seguinte era apresentado.
Fase 3. Pós-Teste
Após o programa de ensino, os participantes foram submetidos ao pós-teste, em que foram apresentados problemas em forma de operação e de sentença-problema. Nesta fase, o software foi programado para não apresentar feedback. Dez problemas de cada forma de apresentação dos problemas compuseram o teste, sendo todos eles diferentes dos que foram apresentados no Pré-teste. Os participantes foram informados que eles resolveriam problemas em forma de operação e sentença-problema, da mesma forma que no pré-teste, mas que os problemas seriam diferentes e que não haveria consequências para as respostas.
Resultados
Para a análise dos resultados foi considerado, inicialmente, o efeito da ordem de resolução dos problemas (o Grupo 1 resolveu primeiro os problemas em forma de operação e depois as sentenças-problema e o Grupo 2, na ordem in-versa). A comparação foi feita por meio do Teste Mann-Whitney, o que revelou não haver efeito estatisticamente significante (p>0,05) dessa variável sobre o desempenho dos participantes, podendo-se afirmar que o grupo que iniciou pelas sentenças-problema e o grupo que iniciou pelos problemas em forma de operação não apresentam diferença na porcentagem de acertos, tanto no pré-teste (U=387,5; p=0,12) como no pós-teste (U=383; p=0,15). Por essa razão, a ordem de apresentação dos problemas foi desconsiderada nas análises subsequente dos dados, isto é, os dados dos dois grupos passaram a ser tratados como se fossem de um só grupo.
O efeito do procedimento de ensino com as balanças virtuais, considerando a forma de apresentação dos problemas e a posição da incógnita, sobre o desempenho dos participantes foi analisado, tomando-se em separado os dados dos problemas de adição e os de subtração. A porcentagem de acertos apresentada pelos participantes no pré-teste e no pós-teste, nos problemas de adição, em forma de operação e sentença-problema, em função da posição da incógnita, é exibida na Figura 1. Os dados analisados são referentes àqueles cuja participação foi autorizada pelos pais (48 dos 49 alunos). Essa análise foi realizada com o Teste de Friedman, que revelou haver efeito significativo dessas variáveis sobre o desempenho dos participantes nos problemas de adição, havendo, também, efeito produzido pela interação entre essas variáveis (x2=119,1; p=0,0001). A comparação dos pares, considerando a diferença na porcentagem de acertos em função da posição da incógnita e entre problemas em forma de operação e sentença-problema, e entre o pré-teste e o pós-testes, foi feita por meio do Student-Newman Method, tendo-se observado que houve diferença estatisticamente significativa (p<0,05) na porcentagem de acertos, em relação à posição da incógnita, somente nos problemas de adição apresentados em forma de sentença-problema. Essa diferença é verificada na comparação dos dados do pré-teste com o pós-teste, nas sentenças-problema com incógnita em a e b, revelando que houve um aumento na porcentagem de acertos no pós-teste nos problemas desse tipo, mas não quando a incógnita estava na posição c. Além disso, nos problemas de adição com incógnitas nas posições a e b, as porcentagens de acertos no pré-teste foram maiores nos problemas em forma de operações do que na forma de sentenças-problema.

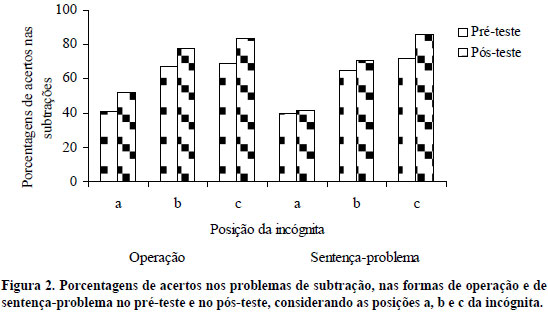
Na Figura 2 estão distribuídas as porcentagens de acertos apresentadas pelos participantes no pré-teste e no pós-teste, diante de problemas de subtração, nas formas de operação e sentença-problema. A análise de variância, realizada por meio do Teste de Friedman, demonstra que houve efeito estatisticamente significante (p<0,05) produzido pela forma de apresentação dos problemas e pela posição da incógnita sobre o desempenho dos participantes. Também, ocorreu efeito produzido pela interação entre essas variáveis (x2=115,6; p=0,0001). Na comparação dos pares feita por meio do Student-Newman Method, verificou-se que há efeito estatisticamente significante sobre o desempenho (p<0,05) tanto em relação àqueles apresentados em forma de operação quanto nas sentenças-problema. No pré-teste e no pós-teste, a porcentagem de acertos foi menor quando a incógnita estava na posição a, do que nas posições b e c, tanto nos problemas em forma de operação quanto nas sentenças-problema. A porcentagem de acertos no pré-teste é menor do que no pós-teste nas operações com incógnitas nas posições a, b e c, mas nas sentenças-problema essa diferença é significante apenas nos problemas com incógnita na posição c. A menor porcentagem de acertos ocorreu nos problemas de subtração com a posição de incógnita em a, tanto nas operações quanto nas sentenças-problema, sendo essa diferença mantida no pós-teste.
Na Figura 3 estão distribuídas as porcentagens de acertos apresentadas durante o procedimento de ensino dos problemas aritméticos em forma de balança virtual, em que foram apresentados quatro problemas de cada tipo, num total de 24 problemas aritméticos. A análise de variância (Teste de Friedman) demonstrou efeito estatisticamente significante (p<0,05), tendo se obtido efeito significante produzido pela interação entre essas variáveis (x2=65,839; p=0,0001). Na comparação dos pares feita por meio do Student-Newman Method, verificou-se que há efeito estatisticamente significante, sendo: a porcentagem de acertos nos problemas de adição com incógnita na posição a, menor que do que quando a incógnita estava na posição b e c; a porcentagem de acertos nos problemas de subtração com incógnita na posição a, menor que do que quando a incógnita estava na posição b e c; e a porcentagem de acertos nos problemas de adição e de subtração com incógnita em a, menores do que naqueles com a incógnita em b.

Na Tabela 2 estão distribuídas as porcentagens de participantes que apresentaram um aumento na porcentagem de respostas corretas nos problemas de adição e subtração ao se compara o pré-teste com o pós-teste. Para realizar essa comparação não foram considerados os dados daqueles participantes que apresentam 100% de acertos nos problemas do pré-teste. A aplicação desse critério foi feita separando-se os resultados do pré-teste de adição em forma de operação e de sentença-problema, tendo-se excluído 20 dados de operação e cinco de sentenças-problema. Dos resultados do pré-teste de subtração em forma de operação foram excluídos os dados de três participantes e de sentença-problema os de 10 participantes. O número de participantes cujos dados foram considerados para análise estão na linha abaixo dos valores referentes às porcentagens na Tabela 3, abaixo de cada porcentagem. Conforme pode ser observado nessa tabela, diante dos problemas de adição, a maior porcentagem de participantes que apresentou aumento nas porcentagens de acertos foi na resolução de problemas em forma de operação com a posição da incógnita b (70,58%) e nas sentenças-problema com a posição de incógnita c (90,9%). Nos problemas de subtração, a maior porcentagem de participantes que apresentou aumento na porcentagem de acertos no pós-teste em comparação ao pré-teste foi nos problemas com a incógnita na posição c, tanto nos problemas apresentados em forma de operação (80%) quanto nas sentenças-problema (94,11%). A menor porcentagem de participantes com aumento na porcentagem de acertos do pré-teste para o pós-teste é observada nas sentenças-problema com incógnita na posição a, no caso de subtrações e nas operações com incógnita em c nas adições. Esse é o dado obtido a partir do menor número de participantes, pois a maioria acertou 100% dos problemas no pré-teste.
Discussão
Durante a aplicação do programa de ensino, não foi feito um registro sistemático da forma como os participantes interagiram com o software, no entanto, observações não sistemáticas, permitiram verificar que esse recurso não produziu dificuldades de interação participante-computador. Nos problemas apresentados em forma de balança, alguns participantes não entenderam o funcionamento das "bombas" e perguntaram se somente a bomba explodiria e as outras bolinhas permaneceriam inteiras ou se as bolinhas também explodiam. Devido ao fato de os participantes não terem apresentado dúvidas adicionais além dessa e tendo-se constatado que ela foi solucionada, sugere-se que a forma virtual de balança que se equilibra, com a apresentação da incógnita em forma de um quadrado cinza e a colocação das bolinhas em dois pratos um de cada lado evitou dúvidas em relação à noção de equilíbrio como as relatadas pelos participantes do estudo de Haydu et al. (2001). As balanças do estudo de Haydu et al. tinham um prato de um lado e do outro um prato e uma caixa que representava a incógnita, o que gerou, de acordo com as autoras, dificuldade de compreensão de seu funcionamento.
A análise feita inicialmente, referente à ordem de aplicação dos problemas, permitiu considerar os dados dos dois grupos como se fossem de apenas um. Além disso, esse aspecto permite sugerir que efeitos de aprendizagem que pudessem ter ocorrido durante a aplicação da metade dos problemas do pré-teste foram mínimos, caso tivesse havido algum.
De acordo com os resultados do pré-teste, a menor porcentagem de acertos nos problemas de adição ocorreu nas sentenças-problema com posições de incógnitas a e b. Esses dados são semelhantes aos dos estudos de Capovilla et al. (1997), Hiebert (1982), Knox et al. (2010), indicando que a forma de apresentação dos problemas aritméticos é uma variável relevante e que ela interfere com o desempenho (Henklain & Carmo, 2013b; Namkung & Fucks, 2012). No entanto, após o procedimento de ensino, os participantes apresentaram aumento na porcentagem de acertos. Assim, pode-se afirmar que, tomando-se os dados de média dos 48 participantes, o procedimento de ensino com a balança virtual reduziu as dificuldades geradas pela posição da incógnita nas posições a e b, nos problemas de adição. Esse mesmo efeito não pode ser observado nos problemas em forma de operação, uma vez que o desempenho médio no pré-teste já era relativamente alto (acima de 74%).
Nos problemas de subtração apresentados em forma de operação, a menor porcentagem de acertos foi na posição de incógnita a, tanto no pré-teste quanto no pós-teste. Esses dados corroboram apenas parte dos que foram apresentados por Carpenter e Moser (1983), os quais relataram que problemas em forma de operação com a incógnita em a e b, produzem um número maior de erros do que com incógnita em c. Esses autores afirmaram que as estratégias utilizadas na resolução de problemas com incógnita na posição c não podem ser diretamente aplicadas à resolução de problemas com a incógnita na posição a, o que explica a diferença no grau de dificuldade dos problemas e, possivelmente, justifica os resultados no pré-teste do presente estudo. Esperava-se, no entanto que essa diferença no desempenho em relação à posição da incógnita fosse reduzida com a aplicação do procedimento de ensino, mas isso não ocorreu. Apesar de ter havido aumento nas porcentagens de acertos do pré-teste para o pós-teste nos problemas de subtração com incógnitas em a, b e c, permaneceram as diferenças entre os pós-testes, sendo menor nas operações com incógnita em a. Resultados semelhantes foram obtidos em relação às sentenças-problema, mas nesse caso, o aumento foi mais acentuado (14%) do pré-teste para o pós-teste nos problemas com a incógnita na posição c do que nos problemas com incógnita na posição b (6%) e na posição a (2%). Esses resultados possivelmente estão relacionados ao fato de que os participantes foram submetidos a um número fixo de problemas nas sessões de ensino, não se tendo programado um critério de aprendizagem para o encerramento do procedimento. O mais apropriado teria sido manter o procedimento até que o participante atingisse 100% de acertos nessa fase, para depois submetê-lo ao pós-teste, como no estudo de Henklain e Carmo (2013b).
Outro aspecto que deve ser considerado na análise do presente estudo é que as sessões foram coletivas, podendo ter havido interação entre os participantes, por exemplo, um participante pode ter solicitado ajuda a outro ou querendo comparar o resultado do problema para saber se acertou ou errou. Deve-se levar em consideração, ainda, que as fases da pesquisa (pré-teste, procedimento de ensino e pós-teste) tiveram um intervalo de uma semana e os estudantes continuaram tendo aulas regularmente. Esse aspecto pode ter contribuído para que tivesse havido al-gum tipo de influência externa no desempenho dos participantes no pós-teste. Em replicações deste estudo, sugere-se que o pré-teste, as sessões de ensino e o pós-teste sejam feitos em dias consecutivos para evitar esse tipo de variável estranha. Ademais, para estudos futuros sobre o tema permanecem as seguintes questões: (a) Qual o efeito observado se as sessões de ensino com a balança tivessem sido mantidas até que os participantes apresentem 100% de acertos, antes de serem submetidos ao pós-teste? (b) Qual o efeito da intervenção, se o procedimento fosse executado apenas com participantes que apresentassem porcentagens de acertos inferiores a 70%? (c) Qual o efeito da intervenção, se fossem submetidos ao procedimento participantes com dificuldades específicas, com delineamentos de caso único? (d) Haveria mudança no tipo de estratégia de resolução de problemas empregada pelos participantes após ter havido experiência com os problemas em forma de balança?
De forma resumida os resultados do presente estudo caracterizam-se como tendo havido um aumento na porcentagem de acertos dos participantes em sentenças-problema de adição com incógnitas nas três possíveis posições e nas subtrações com incógnita na posição c. Além disso, houve aumento na porcentagem de acertos nas operações com incógnitas nas três possíveis posições, mas não nas operações de adição diante das quais o desempenho já era relativamente alto. Assim, pode-se concluir, o procedimento contribuiu para aumentar a porcentagem de resoluções corretas de problemas de adição e de subtração, uma vez que mais de 42,85% dos participantes apresentaram aumento na porcentagem de acertos ao se comparar o pré-teste com o pós-teste. Esses resultados permitem concordar com Capovilla et al. (1997), de que o computador pode ser um recurso importante para ensinar a resolução de problemas aritméticos. Essas características advêm dos recursos gráficos e da possibilidade de se programar consequências imediatas e contingentes ao desempenho do estudante. Além disso, o computador permite incluir uma terceira forma de ensinar problemas aritméticos com incógnitas nas três possíveis posições, no caso a forma de uma balança que se equilibra. Essa tecnologia de ensino é, portanto, uma alternativa para melhorar o desempenho dos estudantes e evitar as dificuldades geradas pela posição da incógnita.
Referências
Burg, W., & Klein, A. S. (2001). Student's flexibility in solving two-digit addition and subtraction problems: Instruction effects. Journal of Education Psychology, 93,627-638. doi:10.1037//0022-0663.93.3.627 [ Links ]
Capovilla, F. C., César, O., Capovilla, A. G. S., & Haydu, V. B. (1997). Operação-equilíbrio: O modelo da balança e a análise da resolução de problemas aritméticos em escolares do Ensino Fundamental. Torre de Babel: Reflexões e Pesquisa em Psicologia, 4,189-215. [ Links ]
Carpenter, T. P., & Moser, J. M. (1983). The acquisition of addition and subtraction concepts. In R. Lesh & M. Landau (Eds.), Acquisition of mathematic concepts and processes (pp. 7-44). New York: Academic. [ Links ]
Halford, G. S., Andrews, G., Dalton, C., Boag, C., & Zielinski, T. (2002). Young Children's Performance on the Balance Scale: The influence of relational complexity. Journal of Experimental Child Psychology, 81,417-445. doi:10.1006/jecp.2002.2665 [ Links ]
Haydu, V. B., Costa, L. P. da, & Pullin, E. M. M. P. (2006). Resolução de problemas aritméticos: Efeito de classes equivalentes de diferentes formas de apresentação dos problemas. Psicologia: Reflexão e Crítica, 19,44-52. doi:10.1590/S0102-79722006000100007 [ Links ]
Haydu, V. B., Paranzini, A. C. S., Isquierdo, G. R., Ausec, H. O., Mazzo, I. M. B., Pires, I. T. M., ...Pimentel, N. S. (2001). Dificuldades e facilidades produzidas pela forma de apresentação de problemas aritméticos com a incógnita em diferentes posições. In M. C. Marquezine, M. A. Almeida, & E. D. O. Tanaka (Eds.), Perspectivas multidisciplinares em Educação Especial II (pp. 593-601). Londrina, PR: Editora da Universidade Estadual de Londrina. [ Links ]
Henklain, M. H. O., & Carmo, J. S. (2013a). Contribuições da Análise do Comportamento à Educação: Um convite ao diálogo. Cadernos de Pesquisa, 43,704-723. doi:10.1590/S0100-15742013000200016 [ Links ]
Henklain, M. H. O., & Carmo, J. S. (2013b). Equivalência de estímulos e aumento de acertos na solução de problemas de adição e subtração. Paidéia (Ribeirão Preto), 23,349-358. doi:10.1590/1982-43272356201309 [ Links ]
Hiebert, J. (1982). The position of the unknown set and children's solutions of verbal arithmetic problems. Journal for Research in Mathematics Education, 13,341-349. doi:10.2307/749008 [ Links ]
Iégas, A. F. (2003). Software para a resolução de problemas aritméticos: O modelo da balança (Dissertação de mestrado não-publicada em Educação, Universidade Estadual de Londrina, PR, Brasil). [ Links ]
Knox, K., Andrews, G., & Hood, M. (2010). Relational processing in children's arithmetic word problem solving. In W. Christensen, E. Schier, & J. Sutton (Eds.), ASCS09: Proceedings of the 9th Conference of the Australasian Society for Cognitive Science (pp. 197-203). Sydney, Australia: Macquarie Centre for Cognitive Science. Retrieved from http://www.cogsci.mq.edu.au/news/conferences/2009/ASCS2009/pdfs/Knox.pdf [ Links ]
Lemaire, P., & Callies, S. (2009). Children's strategies in complex arithmetic. Journal of Experimental Child Psychology, 103,49-65. doi:10.1016/j.jecp.2008.09.007 [ Links ]
Levingston, H. B., Neef, N. A., & Cihon, T. M. (2009). The effects of teaching precurrent behaviors on children's solution of multiplication and division word problems. Journal of Applied Behavior Analysis, 42,361-367. doi:10.1901/jaba.2009.42-361 [ Links ]
Namkung, J. M., & Fuchs L. S. (2012). Early numerical competencies of students with different forms of mathematics difficulty. Learning Disabilities Research & Practice, 27,2-11. [ Links ]
Neef, N. A., Nelles, D., Iwata, B. A., & Page, T. J. (2003). Analysis of precurrent skills in solving mathematics story problems. Journal of Applied Behavior Analysis, 36,21-33. doi:10.1901/jaba.2003.36-21 [ Links ]
Oliveira, M. S., & Tourinho, E. Z. (2001). Desempenho de crianças do ensino fundamental na solução de problemas aritméticos. Estudos de Psicologia (Natal), 6,63-74. doi:10.1590/S1413-294X2001000100007 [ Links ]
Schumacher, R. F., & Fuchs, L. S. (2012). Does understanding relational terminology mediate effects of intervention on compare word problems? Journal of Experimental Child Psychology, 111,607-628. doi:10.1016/j.jecp.2011.12.001 [ Links ]
Skemp, R. R. (1971). The psychology of learning mathematics. Middlesex, UK: Penguin. [ Links ]
Skinner, B. F. (1984). An operant analysis of problem solving. The Behavioral and Brain Science, 7,583-591. doi:10.1017/S0140525X00027412 [ Links ]
Strapasson, B. A., & Dittrich, A. (2008). O conceito de "Prestar Atenção" para Skinner. Psicologia: Teoria e Pesquisa, 24,519-526. doi:10.1590/S0102-37722008000400016 [ Links ]
Toro, B. (2002). Novos pensadores da Educação. Revista Nova Escola, 154,18-25. Recuperado em http://www.educacao.salvador.ba.gov.br/site/documentos/espaco-virtual/espaco-praxis-pedagogicas/GRANDES%20MESTRES/novospensadores.pdf [ Links ]
Vademarin, V. V. (1998). O discurso pedagógico como forma de transmissão do conhecimento. Caderno Cedes, 44,73-83. [ Links ]
 Endereço para correspondência:
Endereço para correspondência:
Verônica Bender Haydu
Rua Duque de Caxias, 1235
Rolândia, PR, Brasil 86605-180
E-mail: haydu@uel.br
Recebido: 15/12/2012
1ª revisão: 29/04/2014
Aceite final: 15/07/2014













