ARTIGOS

 

Unidimensionalidade em testes psicológicos: conceito, estratégias e dificuldades na sua avaliação

 

Psychological test´s unidimensionality: concept, procedures and difficulties in their assessment

 

Unidimensionalidad en tests psicológicos: concepto, estrategias y dificultades en su evaluación

 

 

Florbela Vitória^{I, 2}; Leandro S. Almeida^{II, 3}; Ricardo Primi^{III, 1, 4}

^I Universidade Lusíada, Portugal
^II Universidade do Minho, Portugal
^III Universidade de São Francisco, SP-Brasil

Endereço para correspondência

 

 

---

RESUMO

Os modelos mais comuns de TRI pressupõem que o conjunto de itens que compõem o teste mede apenas um fator ou construto, ou seja, que o teste em questão seja unidimensional. Dois tipos de questões, e desde logo dificuldades, se colocam neste ponto: (1) a primeira é que, por exemplo, aspectos cognitivos e de personalidade podem interferir com a resposta ao teste, em conjunto com a variável que de fato se pretendia medir, pondo assim em causa a sua unidimensionalidade; (2) outro aspecto, tem a ver o fato da determinação da unidimensionalidade não ter critérios empíricos consensuais, sendo assumida sobretudo como uma questão de grau. Pretendemos neste artigo fazer uma revisão das principais definições do conceito e métodos de avaliação.

Palavras-chave: Unidimensionalidade, Construção de testes, Psicometria, Análise factorial.

---

ABSTRACT

The most usual models of Item Response Theory (IRT) presuppose that the collection of items composing the test only measures one single factor or construct, meaning that the test is unidimensional. Two kinds of questions and difficulties arise at this point: (1) diverse factors, for instance, cognitive and personality characteristics of respondents may interfere with answers to the test, beyond the study variable, which affects unidimensionality; (2) there are no consensuses on empirical criteria for unidimensionality determination, so it is assumed in terms of degree of dimensionality. We intended, on this paper, to make a brief review of the main definitions for the concept and evaluation methods of unidimensionality.

Keywords: Unidimensionality, Psycological tests, Psychometric, Factor analisys.

---

RESUMEN

Los modelos más comunes de TRI suponen que el conjunto de ítems que componen el test miden apenas un factor o constructo, o sea, que el test por si mismo sea unidimensional. Dos tipos de cuestiones y dificultades se colocan en este punto: (1) la primera es que, por ejemplo, aspectos cognitivos y de personalidad pueden interferir con la respuesta al test en conjunto con la variable que de hecho se pretendía medir, poniendo de esa forma en duda su unidimensionalidad; (2) otro aspecto tiene que ver con el hecho de la determinación de la unidimensionalidad no tener criterios empíricos claros, siendo sobretodo tenida como una cuestión de grado. En este artículo pretendemos hacer una revisión de las principales definiciones del concepto e métodos de evaluación.

Palabras clave: Unidimensionalidad, Construcción de tests, Psicometría, Análisis factorial.

---

 

 

Introdução

A unidimensionalidade é um dos pressupostos da maioria dos modelos da Teoria de Resposta ao Item (TRI, Fernández, 1990), o que confere, à partida, atua-lidade ao seu estudo e aprofundamento. Contudo, a unidimensionalidade foi, desde sempre, considerada desejável num teste, mesmo na Teoria Clássica dos Testes (TCT), pois os conceitos de homogeneidade e dificuldade só fazem sentido quando se assume avaliar um único atributo. Por um lado, temos a identidade do próprio teste (face validity) e, por outro, quando se assume obter pontuações globais num teste, que significa medir a mesma coisa ao longo dos vários itens, assim, o teste em questão deverá ser unidimensional (Cuesta, 1996).

A avaliação da unidimensionalidade tem sido, assim, referida por vários autores como central no processo desenvolvimento de testes psicológicos (Herche & Engelland, 1996; Yuan, Fung & Reise, 2004, Hattie, 1985; Stout, 1987). Para Pasquali (2003), a unidimensionalidade deve ser considerada como uma questão de grau, uma vez que o desempenho humano é sempre multideterminado e multimotivado, logo, tendencialmente mais do que um traço latente estará presente em qualquer realização. Este autor defende, então, que para satisfazer o postulado de unidimensionalidade é suficiente admitir que haja um fator dominante. Nesta mesma linha, Hambleton e Swaminathan (1985) defendem que a unidimensionalidade não pode ser completamente conseguida e apontam alguns fatores que podem actuar concomitantemente com o traço em avaliação. Assim, o desempenho num teste pode ser influenciado por outras variáveis cognitivas, pela personalidade do sujeito ou, mesmo, por fatores inerentes à própria aplicação do teste, nomeadamente a motivação, a ansiedade, a capacidade para trabalhar em velocidade ou o uso correcto das folhas de resposta, entre outros. Portanto a questão principal não é avaliar se um teste é estritamente unidimensional mas sim em que medida as dimensões adicionais geram distorçòes na medida principal do fator dominante que os itens estão mais ou menos relacionados (Wright & Stone, 2004)

Com o objetivo de verificar se a violação da assunção de unidimensionalidade tinha repercussões importantes na TRI, Childs e Opler (2000) utilizaram duas secções do Medical College Admission Test, com uma amostra que variou, em função das análises, entre 1673 e 16157 sujeitos. Os resultados mostraram, neste caso específico, que tanto a estimação dos parâmetros como a ordenação dos resultados dos sujeitos foram relativamente pouco afectados pela multidimensionalidade. Os autores concluíram que, na prática, a unidimensionalidade é uma questão de grau, e que as implicações do grau de não unidimensionalidade dependem de como o teste é analisado e de como é que os resultados vão ser usados.

Na medida em que vários factores podem afetar a unidimensionalidade de um teste, é também possível que um teste seja unidimensional para uma população mas não para outra, caso tenha, por exemplo, uma elevada saturação cultural (Behling & Law, 2000). Outro exemplo, é a compreensão da leitura num teste de matemática: num grupo de bons leitores o teste seria unidimensional; porém, aplicado a um grupo em que estão incluídos maus leitores, surge um novo fator que influencia o resultado do teste (Hambleton & Swaminathan, 1985).

Uma segunda situação particular que dificulta a unidimensionalidade de um teste prende-se ao formato dos respectivos itens. Herch e Engelland (1996), por exemplo, chamam a atenção para o impacto na dimensionalidade do teste, do recurso à inversão da polaridade do item (itens negativos). No seu estudo, estes autores manipularam a variável teste, escala de resposta, em várias amostras de duas nacionalidades, tendo encontrado uma consistente tendência para os itens saturarem de acordo com a sua polaridade. De modo similar Wright e Stone (2004) alertam para o fato de que muitas vezes a inversão dos itens pode produzir duas dimensões relativamente independentes ao invés de dois pólos de uma mesma dimensão.

Finalmente, a presença na amostra de padrões de resposta aberrantes, devidos por exemplo a uma menor motivação ou cuidado na resposta por parte dos sujeitos, pode afetar de forma adversa as propriedades psicométricas de dimensionalidade, fidelidade e validade de construto (Yuan, Fung & Reise, 2004). Os autores propõem a medida residual-based M distance como a mais eficaz na detecção deste tipo de padrão de respostas. Nos modelos de Rasch pode-se também fazer uso dos índices de ajuste (Infit e Outfit; Ziviani, & Primi, 2002).

O conceito de unidimensionalidade

Não existe uma definição de unidimensionalidade comum a todos os autores. A dificuldade de obtenção de uma definição universal prende-se com o fato de a maioria dos autores, ou mesmo todos, definirem unidimensionalidade em função da forma como a vão avaliar (Cuesta, 1996). Outro aspecto importante é a confusão verificada entre unidimensionalidade e outros conceitos próximos. Por exemplo, a unidimensionalidade foi durante os anos 40 e 50 confundida com a homogeneidade e com a consistência interna. Porém, um teste unidimensional não é necessariamente fidedigno, homogéneo e consistente internamente (Hattie, 1984, in Cuesta, 1996). Conversamente, um teste altamente consistentente não necessáriamente será unidimensional já que a consistência interna de um teste não depende somente das corelações entre os itens mas também do número de itens na escala. De fato algumas escalas multidimensionais com um número grande de itens podem resultar coeficientes de consistência interna altos (Streiner, 2003).

O conceito de unidimensionalidade tem surgido, ainda, muito associado ao de independência local e em algumas ocasiões tomados como sinónimos (Cuesta, 1996). Na opinião de Hattie (1984, in Cuesta, 1996), apesar do conceito de independência local ser essencial para a definição de traço latente e de dimensionalidade, não podem ser tomados como sinónimos. A independência local pode ser conseguida com 1, 2, ..., k traços latentes ou dimensões.

Dada a dificuldade em encontrar uma definição comum, McDonald (1981) propõe a seguinte classificação: definições baseadas nos padrões de resposta, definições baseadas nas teorias do traço latente, e definições baseadas na consistência interna. Passamos então a especificar cada uma delas.

Definições de unidimensionalidade baseadas no padrão de respostas. Dentro desta abordagem, os testes deveriam acomodar-se ao que Guttman (1944) chamou "Escala Perfeita". Assim, os itens colocados por ordem crescente de dificuldade dariam lugar a padrões de resposta tais que, o sujeito que acertasse o item 3, acertaria também o item 1 e 2, e assim sucessivamente. Ou seja, se um sujeito possuísse uma quantidade X do traço medido então acertaria todos os itens cuja dificuldade fosse menor que X. Uma prova que se afastasse deste padrão não seria unidimensional (Cuesta, 1996).

Definições de dimensionalidade baseadas nas teorias de traço latente. Esta abordagem assume que k traços latentes explicam a realização dos sujeitos, de tal forma que, para um nível fixo de capacidade, as respostas dos sujeitos aos itens seriam estatisticamente independentes (quer dizer, cumprem a condição de independência local). Quando um único traço explica a realização dos sujeitos, então esse conjunto de itens considera-se unidimensional (Hambleton & Swaminathan, 1985).

Se num espaço de k dimensões um sujeito for representado por um ponto no espaço e se cada uma das dimensões interfere na realização dos sujeitos em, pelo menos, 2 itens do teste, então k é a dimensão desse espaço latente (Cuesta, 1996). Esta definição de dimensionalidade liga-se com a independência local através da característica de independência estatística entre as respostas dos sujeitos, que se dá quando se especificam todas as dimensões do espaço latente que explicam as respostas dos sujeitos (Cuesta, 1996). Formalmente temos que:

 

 

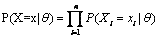
Isto significa que a distribuição conjunta das respostas a um conjunto de itens X={x1, x2,...xn}, num dado vetor de traços latentes, ={ 1, 2, .., k}, é igual ao produto das distribuições marginais dos itens dado q, ou seja, são estatisticamente independentes. Quando k=1 trata-se de um espaço unidimensional (Cuesta, 1996). Apesar de baseada na independência local, não são aqui tomadas como sinónimos, uma vez que, como afirmamos antes, a independência local pode ser conseguida com k dimensões.

Segundo Stout (1987), a noção clássica de dimensionalidade, apesar de matematicamente precisa, não faz distinção entre dimensões maiores e menores. Assim, dada a inevitabilidade da resposta aos itens de um teste ser multideterminada, havendo uma capacidade dominante principal e outras capacidades menores que exercem a sua influência num pequeno grupo de itens ou mesmo num único item, Stout (1987) defende que estas dimensões menores não deveriam ser consideradas no estudo psicométrico do teste. O autor propõe, então, o conceito de dimensionalidade essencial. Este conceito surge a partir do de independência essencial, em contraposição ao de independência local.

Para estas definições, Stout (1990, in Cuesta, 1996) propõe que um conjunto de itens diz-se essencialmente independente se, com respeito a variáveis latentes, satis faz:

 

 

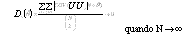
A distinção entre independência local e independência essencial é que, na primeira, se requer para todo , enquanto que a independência essencial requer apenas que o seja assintoticamente pequeno em magnitude (para todos os valores de ). Trata-se de uma assunção mais débil que a de independência local. A dimensionalidade essencial de um conjunto de itens X é a dimensionalidade mínima necessária para satisfazer a assunção de independência essencial. Quando é igual a 1 a unidimensionalidade é alcançada.

Para Cuesta (1996) a exigência de unidimensionalidade feita pela TRI não coincide com a forma como esta é, usualmente, entendida. De fato, "quando na TRI se diz que um teste é unidimensional o que se quer dizer é que todos os sujeitos que possuem a mesma capacidade estimada têm a mesma probabilidade de dar uma resposta correta a cada item" (Cuesta, 1996, 247). Esta definição não pressupõe que a capacidade seja função de um único traço, basta que a combinação de traços seja idêntica para todos os itens.

Reckase (1990, in Cuesta, 1996) distingue dois tipos de dimensionalidade: a dimensionalidade psicológica, que se refere ao número de construtos psicológicos hipotéticos, necessários para a execução com êxito de um teste; e a dimensionalidade estatística que tem a ver com o número mínimo de variáveis matemáticas que são necessárias para resumir uma matriz de respostas a itens. Na prática, os dois conceitos podem coincidir ou não. Aliás, as diferenças encontradas ao nível das variáveis matemáticas podem não traduzir diferenças ao nível dos constructos psicológicos.

Outro contributo para a compreensão da dimensionalidade é dado por Ackerman (1992). Este autor centra a dimensionalidade de um teste na interação sujeitos/itens dos testes. Esta interação pode ser unidimensional de três formas distintas: um item pode necessitar da utilização de vários traços para obter uma resposta correta, contudo os sujeitos variam apenas num desses traços ou na mesma combinação de traços; um item só mede uma dimensão e os sujeitos variam num conjunto de dimensões; e um teste formado por um único item.

Definições de unidimensionalidade baseadas na consistência interna. A conceitualização de unidimensionalidade dentro desta abordagem baseia-se na confusão entre vários termos tidos como sinónimos, tais como fidelidade, consistência interna, homogeneidade e a própria unidimensionalidade. A forma mais comum é a apresentação do coeficiente alfa como indicador de que o teste mede apenas um traço. Kumar e Dillon (1987) sublinham a necessidade de distinguir claramente a consistência e a avaliação da unidimensionalidade, afirmando a sua não equivalência. Como já foi colocado muitas vezes testes com consistência interna alta são multidimensionais.

Avaliação da unidimensionalidade: Cálculos disponíveis

Em 1984, Hattie assinalava 87 índices de avaliação ou cálculo da unidimensionalidade, tendo este número crescido desde então (Cuesta, 1996). Este número de operacionalizações reflete, naturalmente, a variedade de concepções teóricas, agrupando Cuesta (1996) estes métodos em três categorias: índices baseados nos padrões de resposta, índices baseados na fidelidade, e índices baseados no modelo fatorial e TRI.

Índices baseados nos padrões de respostas. Fundamentalmente, nesta abordagem, o que está em causa é o ajustamento (acomodação) de um teste a uma escala perfeita, ou seja, que numa pontuação obtida de n, signifique que foram acertados todos os itens mais fáceis que n e nenhum mais difícil. O teste será tido como unidimensional na medida em que se ajuste a este padrão ideal.

Outros autores propuseram índices com base nesta conceitualização (Guttman, 1944, 1955; Loevinger, 1947; Green, 1956; Wise, 1981, in Cuesta, 1996), porém, o mais conhecido é o Coeficiente de Reprodutibilidade de Guttman (1944, 1955, in Cuesta, 1996). Este índice é obtido através do número de erros cometidos ao predizer as respostas dos sujeitos em função da pontuação total:

 

 

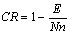
Onde E = número de erros; N = número de sujeitos; e n = número de itens, sendo 0.9 considerado um valor adequado para este coeficiente.

As críticas levantadas a este tipo de métodos prendem-se, por um lado, com a sua assunção de escalonamento implícito, que é pouco plausível com dados psicológicos; por outro lado, com este método não é possível identificar se um teste avalia um único traço ou vários traços mas igualmente ponderados; por fim, mesmo com uma escala perfeita, esta não implica a unidimensionalidade pois os itens de diferentes conteúdos podem ser escalonados em função da dificuldade.

Índices de unidimensionalidade baseados na fidelidade. Um dos indicadores de unidimensionalidade mais utilizados tem sido o coeficiente alfa de Cronbach (Green et al., 1977, in Cuesta, 1996). A sua utilização surge da confusão frequente entre dimensionalidade e os conceitos de consistência interna e de homogeneidade dos itens.

Quando Cronbach (1951) faz a demonstração de que se o alfa é elevado então o teste é homogéneo, é ele próprio que dá origem à confusão. Cronbach afirma que o coeficiente alfa é o limite inferior da proporção de variância devida aos fatores comuns entre os itens de um teste e o limite superior da variância devida ao primeiro fator comum. Daqui se deduz que valores altos do coeficiente seriam obtidos se existisse um único fator no teste. No entanto, também o coeficiente alfa pode alcançar valores altos quando a maioria da variância dos itens está determinada por vários fatores comuns (claro que se tais fatores comuns tendem a andar juntos, eles poderão entrar na definição do constructo e passam a integrar a sua unidimensionalidade). Para Green e colaboradores (1977, in Cuesta, 1996), a unidimensionalidade implica alta consistência interna, mas alta consistência interna não implica unidimensionalidade.

Índices de unidimensionalidade baseados no modelo factorial. A análise fatorial é "um método estatístico que busca analisar estruturas em matrizes de covariância ou de correlação buscando redefini-las através de um número menor de variáveis latentes" (Primi & Almeida, 1998, 226). Este é um método de aceder à dimensionalidade de um teste muito divulgado. O raciocínio de base é simples: se um teste é unidimensional, quando submetido à análise factorial ou à análise em componentes principais emergirá um único factor.

McDonald (1981) define que um conjunto de medidas é unidimensional se, e apenas se, a sua covariação é explicada por um common factor model com apenas um factor. Em termos estritamente matemáticos, um conjunto de itens é ou não unidimensional se um modelo de factor único dá a necessária e suficiente informação para determinar as correlações entre os itens no conjunto (Kumar & Dillon, 1987). As considerações feitas neste ponto englobam a análise fatorial e a análise em componentes principais (para distinção ver Stevens, 1986; Hair et al., 1995) que passamos a referir apenas como análise fatorial.

Se apenas um fator fosse responsável pelos resultados num teste, então esse fator explicaria 100% da variância comum observada. Tratando-se de variáveis psicológicas podemos considerar impossível a obtenção de um único fator nestas circunstâncias, o que remete, mais uma vez, para a questão do grau de unidimensionalidade. A alternativa é que o fator principal explique a maior quantidade de variância possível, contudo na ausência de critérios matemáticos, a decisão acaba por ter um carácter de maior ou menor subjectividade.

Alguns valores concretos de variância a serem atingidos pelo primeiro fator são sugeridos, indo desde 40% em Zeller (1979) até 20% em Reckase (1979) (in Cuesta, 1996). Outros autores defendem que não deve ser apenas tido em conta o comportamento do primeiro fator, devendo este ser comparado com os outros fatores e, em particular, com o segundo fator. Assim, Hutten (1980) e Lumsden (1957, 1960) propuseram que fosse considerado como índice o quociente entre as variâncias explicadas pelo primeiro fator e pelo segundo fator. Outra possibilidade é apontada por Lord (1980), com um procedimento a que chama grosseiro e que consiste em comprovar se o primeiro valor próprio é grande comparado com o segundo, e se o segundo não é muito maior que os seguintes (Cuesta, 1996).

Quando a análise fatorial se baseia no método de máxima verossimilhança, têm sido propostos testes estatísticos baseados principalmente no c2, mas que em amostras muito grandes é sempre significativo. A análise da matriz de covariância residual, depois de extraído o primeiro fator, é outro dos métodos propostos (Pasquali, 2003). Tal método é um dos mais frequentemente utilizados quando se implementa a análise de Rasch e chama-se Principal Components Analysis of Residuals. Uma das vantagens reivindicadas por esse procedimento é a linearização das respostas antes de submetê-las à análise fatorial (Linacre, 1998). Mais uma vez nesse tipo de análise procura-se comparar os valores dos eigenvalues do primeiro edo segundo para ver se a segunda dimensão tem relativa importância e peso na explicação da covariância das respostas. Por seu turno, Piedmont e Hyland (1993) propõem a análise da distribuição de frequências das correlações entre os itens, tomadas em valores absolutos, sendo que, se o teste for unidimensional então a distribuição será normal, com uma única moda entre 0.2 e 0.4; quando o número de dimensões aumenta, a distribuição será enviesada positivamente.

O Stout's Test of Essencial Unidimensionality mostrou ter um baixo erro tipo I e tem um bom poder estatístico (exceto para amostras pequenas ou para um número de itens pequeno) (Childs & Oppler, 2000). Este método testa a unidimensionalidade, não sendo adequado na determinação do número de fatores. Contudo, em caso de prevalência do acaso este método pode subestimar o número de dimensões.

A análise factorial não linear item-level pode ser usada para determinar a dimensionalidade de dados multidimensionais apresentando um bom poder estatístico. No entanto, não é eficaz na identificação de dimensões altamente correlacionadas (Childs & Oppler, 2000). A análise factorial confirmatória testa dimensões definidas a priori mas requer amostras grandes.

Bock e Aitkin (1981) propuseram o método full-information factor analysis (FIFA) baseado na TRI. Tem este nome por trabalhar com informações completas e não com informações sumariadas, como a matriz de correlações. Esta análise trabalha com os padrões distintos de resposta ao item em vez das intercorrelações entre itens, utilizando o modelo multifatorial de Thurstone (1947) baseado em estimativas de máxima verossimilhança marginal e no algoritmo EM de Dempster, Laird e Rubin (1977). As vantagens deste método passa por tomar em conta toda a informação empírica da aplicação do teste, conseguindo trabalhar o acerto ao acaso, os dados omissos e contorna o problema da matriz não positiva-definida, bem como casos Heywood que ocorrem frequentemente na análise fatorial.

Outro tipo de procedimento que tem se tornado comum baseado na análise fatorial chama-se parallel analisis. Embora esse procedimento apareça no âmbito mais geral ligado a decisão do número de fatores a extrair, pode ser usado na investigação da unidimensionalidade. A análise paralela busca gerar padrões de resposta aleatórios com o mesmo número de sujeitros e itens presentes na matriz real de dados. A partir disso são extraídos os fatores para os dois conjuntos de dados (real e aleatório). Os gráficos scree dessas duas análises são comparados para se verificar em que momento os eigenválues da matriz real são maiores do que os produzidos por dados aleatórios indicando, assim, o número de fatores substanciais (Reise, Waller & Comrey, 2000).

 

Conclusão

A evidente importância da determinação da unidimensionalidade de um teste, sobretudo para efeitos de clarificação dos constructos psicológicos e da investigação, contrasta com a falta de critérios consensuais e com suporte estatístico para a sua estimação. Já em 1980 Lord alertava para a grande necessidade de testes de significância estatística para a unidimensionalidade de um conjunto de itens, até porque na prática e na investigação se assume bastante indiscriminadamente a aditividade dos itens nos testes e escalas.

Reconhecida a inevitabilidade de a resposta a um teste psicológico ser determinada por mais do que um atributo, a unidimensionalidade torna-se então uma questão de grau. A resposta para a questão de qual o grau, ou qual o ponto de corte acima do qual podemos considerar a unidimensionalidade, não foi completamente respondida, deixando algum espaço à sensibilidade e bom senso. O problema complica-se quando o contributo de várias dimensões no desempenho, mesmo alguma principal e as outras secundárias, "modificam" o seu peso específico nos resultados de acordo com características das amostras ou subgrupos de sujeitos. Nesta altura um mesmo resultado, mesmo que assente na pontuação dos mesmos itens, pode significar coisas diferentes para dois sujeitos, o que não deixa de ser bastante perplexo em termos de avaliação psicológica.

Pretendemos, ao longo deste artigo, dar uma panorâmica das definições e métodos de avaliação da unidimensionalidade, ilustrando as suas dificuldades e diversidade de abordagens. Mais do que respostas últimas ao problema enunciado, foi nossa intenção deixar nos investigadores e profissionais alguma inquietação nas interpretações e conclusões que retiram ao assumirem, com relativa facilidade, a unidimensionalidade dos instrumentos de avaliação psicológica usados.

 

Referências

Behling, O. & Law, K. (2000). Translating questionnaires and other research Instruments: Problems and solutions. Sage University Papers Series on Quantitative Applications in the Social Sciencies, 07-131. Thousand Oaks, CA: Sage.        [ Links ]

Bock, R. D. & Aitkin, M. (1981). Marginal maximum likelihood estimation of item parameters: Application of an EM algorithm. Psycometrika, 46, 443-459.        [ Links ]

Chids, R. A. & Oppler, S. H. (2000). Implications of test dimensionality for unidimensional IRT scoring: an investigation of a hight-stakes testing program. Educational and Psychological Measurement, 60 (6), 939-955.        [ Links ]

Cuesta, M. (1996). Unidimensionalidade. In J. Muñiz (Ed.), Psicometría. Madrid: Editorial Universitas.        [ Links ]

Cronbah, L. J. (1951). Coeficiente alpha and the internalstruture of tests. Psychometrika, 16, 297-344.        [ Links ]

Fernández, J. M. (1990). Teoría de respuesta a los ítems: Un nuevo enfoque en la evolución psicológica y educativa. Madrid: Pirámide.        [ Links ]

Guttman, L. (1944). A basis for scaling qualitative data. American Sociological Review, 9, 139-150.        [ Links ]

Hair, J. F.; Anderson, R.; Tatham, R. & Black, W. (1995). Multivariate data: Analysis with readings. New Jersey: Prentice Hall.        [ Links ]

Hambleton, R. K. & Swaminathan, H. (1985). Item response theory: Principles and applications. Boston: Kluwer-Nijhoff.        [ Links ]

Hattie, J. (1984). An empirical study of various indices for determing unidimensionality. Multivariate Behavioral Research, 19, 49-78.        [ Links ]

Hattie, J. (1985). Methodology Review: Assessing unidimensionality of tests and items. Applied and Psychological Measurent, 9, 139-164.        [ Links ]

Herche, J. & Engelland, B. (1996). Reversed-polarity item and scale unidimensionality. Academy of Marketing Science Journal, 24, 336-374.        [ Links ]

Kumar, A.& Dillon, W. (1987). Some further remarks on measurement - Struture interaction and unidimensionality. Journal of Marketing Research, 24, 483-444.        [ Links ]

Linacre J. M. (1998). Structure in Rasch residuals: Why principal components analysis? Rasch Measurement Transactions, 12 (2), 636.        [ Links ]

McDonald, R. (1981). The dimensionality of testes and items. British Journal of Mathematical and Statistical Psychology, 34, 100-117.        [ Links ]

Muñiz, J. (1996). Psicometría. Madrid: Editorial Universitas.        [ Links ]

Pasquali, L. (2003). Psicometria: Teoria dos testes na psicologia e na educação. Petrópolis: Editora Vozes.        [ Links ]

Primi, R.& Almeida, L. S. (1998). Considerações sobre a análise factorial de itens com resposta dicotómica. Psicologia: Teoria, Investigação e Prática, 3, 225-234.        [ Links ]

Reckase, M. D. (1990). Unidimensionality data from multidimensional tests and multidimensional tests from unidimensional data. Paper presented in AERA, Boston.        [ Links ]

Reise, S. P., Waller, N. G. & Comrey, A. L. (2000). Factor analysis and scale revision. Psychological Assessment, 12(3), 287-297.        [ Links ]

Stevens, J. (1986). Applied multivariate statistics for the social sciences. New Jersey: Lawrence Erbaum.        [ Links ]

Stout, W. (1987). A nonparametric approach for assessing latent trait unidimensionality. Psychometrika, 52, 589-617.        [ Links ]

Stout, W. (1990). A new item response theory modelling approach with applications to unidimensionality assessement and ability estimation. Psychometrika, 55 (2), 293-325.        [ Links ]

Streiner, D. L. (2003). Starting at the beginning: an introduction to coefficient alpha and internal consistency. Journal of Personality Assessment, 80(1), 99-103.        [ Links ]

Wright, B. D. & Stone, M. H (2004). Making measures. Chicago: The Phaneron Press.        [ Links ]

Ziviani, C. & Primi, R. (2002). Teoria de Resposta ao Item e o modelo de Rasch de mensuração: uma análise do Provão de Psicologia. Em R. Primi (org.) Temas em Avaliação Psicológica (pp. 131-151). Campinas: IDB Digital / Instituto Brasileiro de Avaliação Psicológica.        [ Links ]

 

 

Endereço para correspondência
Largo da Feira, bl. B 1º esq. Barreira
3150-110 Condeixa - Portugal
florbela.vitoria@sapo.pt

Recebido em: fevereiro/2006
Revisado em: março/2006
Aprovado em: abril/2006

 

 

Sobre os autores:

¹ O autor agradece ao apoio financeiro do CNPQ.
² Florbela Santos da Vitória é doutoranda em Psicologia pela Universidade do Minho, bolseira da Junta Nacional de Investigação Científica e Tecnológica em 1992/93 da Fundação para a Ciência e Tecnologia de 2000 a 2005 e docente convidada da Faculdade de Psicologia e Ciências da Educação da Universidade de Coimbra.
³ Leandro Almeida é Doutor em Psicologia (Universidade do Porto). Professor no Instituto de Educação e Psicologia da Universidade do Minho. Várias publicações nacionais e estrangeiras na área do desenvolvimento cognitivo e da aprendizagem. Coordena um projecto de investigação sobre a transição e a adaptação acadêmica dos alunos ingressados no Ensino Superior, e seu impacto no desenvolvimento e rendimento acadêmico. Actualmente exerce funções de Pró-Reitor para as questões pedagógicas.
⁴ Ricardo Primi é Psicólogo, Doutor em Psicologia Escolar e do Desenvolvimento Humano pela Universidade de São Paulo com parte desenvolvida na Yale University (EUA). Coordenador do Laboratório de Avaliação Psicológica e Educacional (LabAPE). Recebe financiamento da FAPESP e do CNPq (produtividade em pesquisa nível 2C) Diretor de Pós Graduação e professor do Mestrado e Doutorado em Avaliação Psicológica da Universidade São Francisco. Presidente eleito do Instituto Brasileiro de Avaliação Psicológica (IBAP). Membro da Comissão Consultiva em Avaliação Psicológica do Conselho Federal de Psicologia.