Uso da análise fatorial exploratória em psicologia

 

Uses of exploratory factorial analysis in psychology

 

Usos de análisis factorial exploratoria en psicología

 

 

Bruno Figueiredo Damásio¹

Universidade Federal do Rio Grande do Sul

 

 

---

RESUMO

A análise fatorial exploratória (AFE) é um conjunto de técnicas estatísticas amplamente utilizadas nas pesquisas em Psicologia. Durante sua execução, diversas decisões precisam ser tomadas a fim de se obter uma estrutura fatorial adequada. O presente artigo tem por objetivo discutir alguns dos principais aspectos desta técnica, apresentando estudos atualizados sobre o tema. Diferenças entre análise fatorial exploratória e análise de componentes principais, retenção e rotação fatorial, tamanho da amostra ideal, importância da variância explicada e a confiabilidade da solução fatorial são alguns dos tópicos discutidos. Aponta-se para o fato de que todas as decisões a serem tomadas durante a execução de uma análise fatorial exploratória não podem ser arbitrárias e subjetivas, mas devem ser pautadas em critérios teóricos e metodológicos claros. Este estudo pretende auxiliar pesquisadores da área da Psicologia a realizarem AFEs com maior discernimento teórico e metodológico.

Palavras-chave: análise fatorial exploratória; rotação; retenção; tamanho amostral; análise paralela.

---

ABSTRACT

Abstract Exploratory factor analysis (EFA) is a set of widely used statistical techniques in psychological research. During its implementation, several decisions need to be taken in order to obtain a suitable factor structure. This study aims to present and discuss some of the main aspects of this technique, eliciting up-to-date studies on the topic. Differences between exploratory factor analysis and principal component analysis, factor retention and factor rotation, adequate sample size, explained variance importance, and factor solution reliability are some of the discussed topics. It is pointed out the fact that all decisions to be taken during the implementation of an exploratory factor analysis cannot be arbitrary and subjective, but must be based on clear theoretical and methodological criteria. This study intends to assist researchers in the field of Psychology to conduct EFAs with higher theoretical and methodological discernment.

Keywords:: exploratory factor analysis; rotation; retention; sample size; parallel analysis.

---

RESUMEN

El análisis factorial exploratorio (AFE) es un conjunto de técnicas estadísticas ampliamente utilizadas en la investigación en Psicología. Durante su ejecución, diversas decisiones necesitan ser tomadas con el objetivo de obtener una estructura factorial adecuada. Este artículo tiene como objetivo discutir algunos de los principales aspectos de esta técnica, presentado estudios actualizados acerca de la temática. Las diferencias entre análisis factorial exploratorio y análisis de componentes principales, retención y rotación factorial, tamaño ideal de la muestra, importancia de la variancia explicada y la confiabilidad de la solución factorial son algunos de los tópicos discutidos. Se subraya el hecho de que todas las decisiones tomadas durante la ejecución de un análisis factorial exploratorio no pueden ser arbitrarias o subjetivas, sino que deben estar basadas en criterios teóricos y metodológicos claros. Este estudio pretende ayudar los investigadores del área de Psicología a realizar AFEs con mayor discernimiento teórico y metodológico.

Palabras-clave: análisis factorial exploratorio; rotación; retención; tamaño de la muestra; análisis paralela.

---

 

 

A análise fatorial exploratória (AFE) tem sido um dos procedimentos estatísticos mais comumente utilizados no desenvolvimento, avaliação e refinamento de instrumentos psicológicos (Floyd & Widaman, 1995). Define-se AFE como um conjunto de técnicas multivariadas que tem como objetivo encontrar a estrutura subjacente em uma matriz de dados e determinar o número e a natureza das variáveis latentes (fatores) que melhor representam um conjunto de variáveis observadas (Brown, 2006). Ao analisar a estrutura das inter-relações de um determinado número de variáveis observadas, a AFE define o(s) fator(es) que melhor explica(m) a sua covariância (Hair, Anderson, Tatham & Black, 2005). As variáveis observadas “pertencem” a um mesmo fator quando, e se, elas partilham uma variância em comum (são influenciadas pelo mesmo construto subjacente) (Brown, 2006). Assim, um fator é uma variável latente (por exemplo, autoestima) que influencia mais de uma variável observada (por exemplo, ‘estou satisfeito comigo’; ‘tenho boas qualidades’; ‘sou uma pessoa de valor’), representando, assim, a covariância entre elas.

A AFE é geralmente conduzida quando: 1) o pesquisador não possui uma teoria prévia subjacente ou evidências empíricas suficientes que explicitem como os itens de determinado instrumento devem ser agrupados e avaliados; ou 2) quando o pesquisador quer confirmar ou refutar a estrutura fatorial de determinado instrumento (Brown, 2006). Durante a realização de AFEs, diversas decisões precisam ser tomadas a fim de se obter uma estrutura fatorial adequada (Costello & Osborne, 2005). Uma vez que os resultados obtidos nas AFEs dependem, em grande medida, das decisões tomadas pelo pesquisador, a técnica possui um alto potencial de produzir resultados errôneos e/ou não confiáveis (Patil, Singh, Mishra & Donavan, 2008). Assim, todas as decisões tomadas durante a realização de uma AFE devem ser pautadas em critérios teóricos e metodológicos claros, buscando a obtenção de modelos fatoriais adequados.

No que se refere à Psicologia, uma parcela significativa dos estudos que utilizam análises fatoriais exploratórias empregam métodos equivocados, desenvolvidos na metade do século passado, principalmente por estes ainda serem os métodos padrão nos principais programas estatísticos (Fabrigar, Wegener, MacCallum & Strahan, 1999; Widaman, 2007). Considerando esses aspectos, o presente artigo tem por objetivo discutir alguns dos principais pontos referentes às AFEs, trazendo informações atualizadas sobre o constante desenvolvimento desta técnica, com vistas a auxiliar os pesquisadores na sua execução.

Análises Fatoriais Exploratórias e Análise de Componentes Principais

Inicialmente, é necessário diferenciar a AFE da Análise de Componentes Principais (ACP). A AFE e a ACP são duas técnicas que têm por objetivo reduzir um determinado número de itens a um menor número de variáveis. Ainda que haja uma significativa diferença entre essas duas técnicas de redução de dados, elas são, geralmente, utilizadas indiscriminadamente na Psicologia (Widaman, 2007)

A ACP foi por muito tempo o método de redução de dados mais utilizado nas pesquisas em Psicologia. Sua popularidade se deu, em grande medida, ao fato de que seus cálculos computacionais eram mais simples, e, portanto, mais rápidos e mais baratos, quando comparados às AFEs (Costello & Osbourne, 2005; Gorsuch, 1983). Devido ao seu amplo uso e ao fato de que ACP é, ainda hoje, o método padrão de redução de dados em muitos dos principais programas estatísticos (por exemplo, SPSS e SAS), muitos pesquisadores erroneamente acreditam que ACP seja um tipo de AFE (Jollife, 2005).

As ACPs geram componentes, enquanto as AFEs geram fatores. A diferença entre componentes e fatores está relacionada à forma como os itens são retidos. Ambos os métodos de redução de dados assumem que a variância de uma variável é composta por três aspectos: variância específica; variância comum; e variância de erro. A variância específica refere-se à porção de variância do item que não é compartilhada com nenhuma outra variável. A variância comum refere-se à variância que é compartilhada entre todos os itens que compõem determinado fator ou componente. A variância de erro refere-se à parcela do item não explicada pelo componente ou fator (Ver Figura 1)

 

 

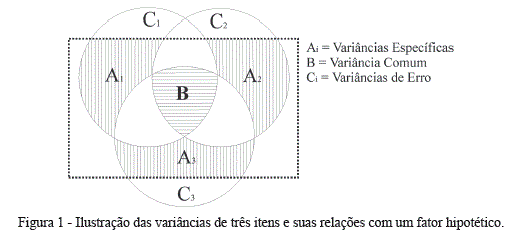
A ACP está baseada apenas na correlação linear das variáveis observadas, e não diferencia a variância comum da variância específica entre os itens. Quando os itens são retidos em um determinado componente, utilizando o método da ACP, os índices apresentados incluem tanto a variância comum quanto a variância específica (na Figura 1, A_i + B). Já nas AFEs, apenas a variância comum (a parcela de variância que os itens compartilham entre si) é considerada (na Figura 1, apenas B). Uma vez que as AFEs têm por objetivo revelar construtos latentes que explicam a covariância entre os itens, as variâncias específicas (parcelas individuais dos itens) que não covariam entre si, não são consideradas. Por exemplo, se o pesquisador está avaliando o construto depressão, apenas lhe interessará a parcela de variância dos itens que se refiram à depressão (variância comum). A parcela do item que não é influenciada pelo construto (seja ela variância específica ou variância de erro) não cabe nos objetivos da AFE, não sendo, portanto, considerada.

Ao comparar os resultados de uma ACP com os resultados de uma AFE, é possível perceber que, na ACP, os itens tendem a apresentar cargas fatoriais e comunalidades mais elevadas, e taxas de variância explicada infladas, quando comparadas a AFEs (Costello & Osbourne, 2005; Widaman, 2007). Isso ocorre porque a variância específica de cada item é considerada. Esses resultados, porém, são imprecisos quando se tem por objetivo compreender um construto latente que gera a covariância entre os itens (Costello & Osbourne, 2005; Ogasawara, 2003).

Devido ao fato de que na maioria das pesquisas em Psicologia o interesse dos pesquisadores é observar um construto latente (por exemplo, depressão; autoeficácia; satisfação no trabalho; personalidade; bem-estar psicológico, agressividade) que melhor explique a inter-relação entre um conjunto de itens, o uso da ACP é desaconselhado (Costelo & Osbourne, 2005; Floyd & Widaman, 1995; Velicer, Eaton & Fava, 2000).

Pressupostos das Análises Fatoriais Exploratórias

O primeiro passo durante a implementação de AFEs é observar se a matriz de dados é passível de fatoração, isto é, analisar se os dados podem ser submetidos ao processo de análise fatorial (Pasquali, 1999). Para isso, dois métodos de avaliação são mais comumente utilizados, a saber: o critério de Kaiser- Meyer-Olkin (KMO); e o Teste de Esfericidade de Bartlett (Dziuban & Shirkey, 1974). O índice de KMO, também conhecido como índice de adequação da amostra, é um teste estatístico que sugere a proporção de variância dos itens que pode estar sendo explicada por uma variável latente (Lorenzo-Seva, Timmerman & Kiers, 2011). Tal índice indica o quão adequada é a aplicação da AFE para o conjunto de dados (Hair e cols., 2005). O KMO é calculado por meio do quadrado das correlações totais dividido pelo quadrado das correlações parciais, das variáveis analisadas (Field, 2005). Seu valor pode variar de zero a um. Valores iguais ou próximos a zero indicam que a soma das correlações parciais dos itens avaliados é bastante alta em relação à soma das correlações totais. Nesses casos, possivelmente a análise fatorial será inapropriada (Pasquali, 1999). Como regra para interpretação dos índices de KMO, valores menores que 0,5 são considerados inaceitáveis, valores entre 0,5 e 0,7 são considerados medíocres; valores entre 0,7 e 0,8 são considerados bons; valores maiores que 0,8 e 0,9 são considerados ótimos e excelentes, respectivamente (Hutcheson & Sofroniou, 1999).

O teste de esfericidade de Bartlett, por sua vez, avalia em que medida a matriz de (co)variância é similar a uma matriz-identidade (os elementos da diagonal principal tem valor igual a um, e os demais elementos da matriz são aproximadamente zero, ou seja, não apresentam correlações entre si; Field, 2005). Segundo Hair e cols. (2005), esse teste avalia, também, a significância geral de todas as correlações em uma matriz de dados. Valores do teste de esfericidade de Bartlett com níveis de significância p < 0,05 indicam que a matriz é fatorável (Tabachnick & Fidell, 2007), rejeitando a hipótese nula de que a matriz de dados é similar a uma matriz-identidade. Em geral, os resultados dos testes de KMO e de esfericidade de Bartlett tendem a ser uniformes, aceitando ou negando a possibilidade de fatoração da matriz de dados (Dziuban & Shirkey, 1974).

Se a matriz de dados é passível de fatoração, o pesquisador deve prosseguir avaliando os índices de distribuição de normalidade multivariada da amostra, para que possa ser escolhido um método de extração apropriado (por exemplo, máxima verossimilhança; principais eixos fatoriais; mínimos quadrados generalizados; mínimos quadrados nãoponderados; fatoração alfa). Em geral, os métodos ‘máxima verossimilhança’ (maximum likelihood, ML) e ‘principais eixos fatoriais’ (principal axis factoring, PAF) fornecem os melhores resultados quando as amostras apresentam distribuição normal e não-normal, respectivamente (Costello & Osborne, 2005; Fabrigar e cols., 1999). Entretanto, se o pesquisador tem razões específicas para utilizar outros tipos de extração, estas devem ser consideradas (para maiores informações sobre os diferentes métodos de extração, sugere-se a leitura de Kim & Mueller, 1978).

Retenção de Fatores

Uma das mais importantes decisões a ser tomada durante a execução de AFEs se refere ao número de fatores a ser retido (Artes, 1998; Glorfeld, 1995). Uma extração inadequada impossibilita a interpretação dos resultados de maneira apropriada (Hayton, Allen & Scarpello, 2004). Durante o processo de retenção fatorial em uma AFE, basicamente dois problemas podem ocorrer: 1) a superestimação de fatores (reter um número de fatores maior do que o adequado); e 2) a subestimação de fatores (reter um número de fatores menor que o adequado). A superestimação de fatores retidos tende a produzir resultados não-parcimoniosos, baseados em construtos supérfluos, com reduzido ou inadequado poder explicativo (Patil e cols., 2008). Do mesmo modo, a subestimação de fatores retidos resulta em perda significativa de informação (Franklin, Gibson, Robertson, Pohlmann & Fralish, 1995).

Diversos procedimentos e critérios de retenção fatorial foram desenvolvidos. Dentre eles, o mais utilizado até então, é o critério de Kaiser-Guttman, mais conhecido como eigenvalue > 1 (Patil e cols., 2008). Tal critério propõe uma avaliação rápida e objetiva do número de fatores a ser retido. A lógica por trás do critério de Kaiser-Guttman é simples: cada fator retido apresenta um eigenvalue que se refere ao total de variância explicada por este fator. A soma total dos eigenvalues é sempre igual ao número de itens utilizados na análise (utilizando uma escala de 10 itens, a soma dos 10 eigenvalues retidos é igual a 10). Assim, um componente com eigenvalue < 1 apresenta um total de variância explicada menor do que um único item. Como o objetivo das análises fatoriais é reduzir um determinado número de variáveis observadas em um número menor de fatores, apenas fatores com eigenvalue > 1 são retidos (Floyd & Widaman, 1995).

Apesar da simplicidade, da objetividade e do amplo uso desse critério, há forte consenso na literatura de que seus resultados são imprecisos (Costello & Osbourne, 2005; Floyd & Widaman; 1995; Patil e cols., 2008; Reise, Waller &Comrey, 2000). Um estudo de simulação Monte-Carlo (Costello & Osborne, 2005) demonstrou que o critério de Kaiser-Guttman superestimou em 36% dos casos o número de fatores retidos. Fava e Velicer (1992) demonstraram que tal superestimação tende a ocorrer principalmente quando o tamanho da amostra e/ou as cargas fatoriais dos itens (saturação) são baixas.

O critério de Kaiser-Guttman foi desenvolvido com base em uma matriz de correlação populacional. Uma vez que as pesquisas em Psicologia utilizam, em geral, amostras (parcelas da população), o critério do eigenvalue > 1 tende a superestimar o número de fatores a ser retido devido ao erro amostral (Laher, 2010; Ledesma & Valero- Mora, 2007). Portanto, o critério de Kaiser-Guttman como método de retenção fatorial não é recomendado (Patil e cols., 2008; Velicer e cols., 2000).

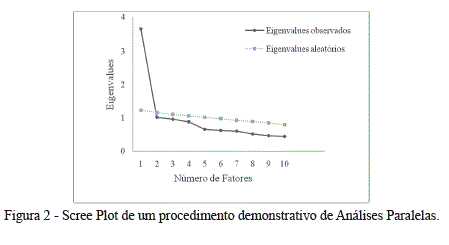
Outro método amplamente relatado, porém de pouca utilidade prática, é o teste do “scree plot” ou teste de Cattell (Cattell, 1966). Tal procedimento consiste na observação do gráfico dos eigenvalues, no qual é apresentado o número de dimensões (eixox) e seus eigenvalues correspondentes (eixo-y, ver Figura 2). Por meio da análise do gráfico, é possível observar quais fatores apresentam maiores eigenvalues, sendo, portanto, responsáveis por uma maior variância explicada. O objetivo é encontrar o ponto (comumente chamado de ‘cotovelo’) onde os eigenvalues apresentam uma tendência descente linear (Reise e cols., 2000). Muitas vezes essa identificação é confusa. Ainda que o scree plot funcione relativamente bem para fatores bem definidos, em casos mais complexos, onde não há um ponto de corte claro, a escolha do número de fatores a ser retido passa a ser subjetiva e ambígua (Fabrigar e cols., 1999; Hayton e cols., 2004).

 

 

Um terceiro critério que vem sendo cada vez mais consolidado na literatura internacional, porém ainda pouco utilizado no Brasil, é o método das análises paralelas (AP) (Horn, 1965). Inicialmente, o método da AP foi desenvolvido para ser utilizado como critério de retenção de componentes. Entretanto, tem sido adaptado para o uso no contexto das AFEs (Crawford e cols., 2010; Velicer e cols., 2000), e é considerado um procedimento adequado para determinar o número de fatores a serem retidos (Glorfeld, 1995; Lorenzo-Seva e cols., 2011; Patil e cols., 2008).

A AP é um procedimento estatístico de simulação Monte-Carlo que consiste na construção aleatória de um conjunto hipotético de matrizes de correlação de variáveis, utilizando como base a mesma dimensionalidade (o mesmo número p de variáveis e o mesmo número n de sujeitos) do conjunto de dados reais (Laros, 2004). A matriz hipotética é fatorada centenas ou milhares de vezes (dependendo da robustez adotada pelo pesquisador), e a média dos eigenvalues oriunda desta simulação é calculada. Os valores dos eigenvalues dos dados reais são comparados (pareados) com os eigenvalues aleatórios (primeiro eigenvalue real pareado com primeiro eigenvalue aleatório; segundo eigenvalue real pareado com segundo eigenvalue aleatório, e assim por diante). O número de fatores nos dados reais a ser retido refere-se àqueles que apresentam eigenvalue > 1 e que apresentam valor maior do que o respectivo eigenvalue obtido por meio dos dados aleatórios (O’Connor, 2000). Nas APs, o critério do eigenvalue > 1 também é considerado, porém, este não é o fator decisivo. Fatores com eigenvalue > 1, mas com eigenvalues menores que os obtidos nas APs são descartados. Para aumentar a acurácia do método, deve-se considerar o intervalo de confiança de 95% obtido nos valores dos eigenvalues aleatórios (Crawford e cols., 2010).

Com o objetivo de avaliar a aplicabilidade das APs e de avaliar a qualidade de estudos reportados utilizando outros critérios de retenção de fatores (eigenvalue > 1 e o scree plot), Franklin e cols. (1995) avaliaram 39 AFEs em 22 estudos aleatórios. Os autores conduziram APs utilizando as mesmas dimensionalidades (mesmo número de respondentes e mesmo número de itens) das matrizes de correlação dos artigos analisados, e concluíram que 66,7% destes estudos apresentavam superestimação do número de fatores extraídos.

A melhor acurácia das APs na determinação do número de fatores a ser retido se dá pelo fato de que a AP é uma técnica baseada em amostras, e não baseada na população, como é a técnica do eigenvalue > 1 (Franklin e cols., 1995; Zwick & Velicer, 1986). Comparando os eigenvalues dos dados reais com a média dos eigenvalues dos dados aleatórios, ao invés de fixar o valor de 1 (como no critério de Kaiser-Guttman), o erro amostral é considerado, diminuindo a probabilidade de uma retenção de fatores equivocada. Outra vantagem das APs é que este método é minimamente afetado pelo tamanho da amostra ou pelas cargas fatoriais dos itens (Velicer e cols., 2000).

A Figura 2 ilustra uma aplicação da AP, em comparação com outros métodos de retenção apresentados anteriormente (scree plot e eigenvalue > 1). O scree plot da Figura 2 foi obtido por meio de uma AFE, utilizando o método de extração Principais Eixos Fatoriais e rotação promax, em uma matriz de correlação composta por 10 variáveis (N = 500). A AP foi aplicada em uma matriz hipotética de mesma dimensionalidade (p = 10; N = 500) replicada mil vezes por meio do programa FACTOR (Lorenzo- Seva & Ferrando, 2006).

Conforme se pode observar no gráfico, a retenção de fatores utilizando o critério scree plot, proposto por Cattell (1966) é relativamente confusa. Apesar de o primeiro fator ser nitidamente preponderante, a linha onde os eigenvalues apresentam uma tendência descente linear (Reise e cols., 2000) não é totalmente clara. Já, considerando o critério de Kaiser-Guttman, se pode perceber que dois fatores deveriam ser retidos, visto que o primeiro e o segundo fator dos dados reais apresentam eigenvalue > 1. O método das análises paralelas, por sua vez, elucida esse impasse. Pode-se perceber que o segundo eigenvalue obtido por meio das APs é maior que o segundo eigenvalue obtido por meio da matriz de dados reais, demonstrando que o segundo fator não é adequado, sendo, provavelmente, oriundo de erro amostral.

Apesar de sua melhor acurácia, o método das APs ainda não é amplamente conhecido pelos pesquisadores, em parte porque não se encontra incluído nos principais programas estatísticos (Ledesma & Valero-Mora, 2007). Para sua execução, podem-se utilizar alguns programas computacionais, tais como FACTOR (Lorenzo-Seva & Ferrando, 2006); Monte- Carlo Parallel Analysis (Watkins, 2000), bem como um website desenvolvido especificamente para tal (http://ires.ku.edu/~smishra/parallelengine.htm - Patil, Singh, Mishra & Donavan, 2007).

Outro método que vem apresentando adequado desempenho na retenção de fatores é o método da média mínima parcial (Minimum Average Partial, MAP), proposto por Velicer (1976). Assim como as APs, o MAP foi inicialmente desenvolvido para ser utilizado no contexto dos componentes principais, entretando vem sendo utilizado também como critério de retenção fatorial (Lorenzo-Seva e cols., 2011).

O teste MAP de Velicer baseia-se na porção da variância sistemática e não-sistemática restante em uma matriz de correlação após uma crescente extração de fatores (Zwick & Velicer, 1986). Inicialmente, todos os itens referentes ao primeiro componente/fator são parcializados, e o coeficiente da média ao quadrado dos elementos fora da diagonal principal (off-diagonal) da matriz parcial de correlação é calculado. Num segundo momento, os dois principais componentes/fatores são parcializados na matriz de correlação, e a média ao quadrado desta segunda correlação parcial é, mais uma vez, computada. Essas análises são realizadas para um número k (referente ao número de variáveis menos um). As médias ao quadrado das correlações parciais são, posteriormente, comparadas entre si (O’Connor, 2000). No ponto em que a variância comum de todos os itens foi completamente parcializada, a média mínima generalizada atinge seu valor mínino. O momento em que esta média passa a subir, indica que a variância específica dos itens está passando a ser considerada (Velicer, 1976). Uma vez que o objetivo das AFEs é agrupar itens que compartilhem entre si apenas a variância comum, o número de fatores a ser retido refere-se ao número representado pela menor média quadrática das correlações parciais.

O processo do MAP é um critério estatístico confiável para a retenção do número de fatores, separando os fatores que consistem apenas de variância comum (Garrido, Abad & Ponsoda, 2011). De acordo com estudos de simulação Monte- Carlo (Zwick & Velicer, 1986), o teste MAP foi mais adequado na identificação do número de fatores a ser retido quando comparado aos critérios do eigenvalue > 1 e o teste de Cattell, e teve um desempenho similar ao método das APs. Recentemente, Lorenzo-Seva e cols. (2011) demonstraram que a melhor performance do MAP se deu quando a proporção do número de variáveis por fator era baixa (≤ 5) e quando a amostra era relativamente grande (> 200). Assim como o método das APs, o teste MAP de Velicer não está presente nos principais pacotes estatísticos, tais como SPSS e SAS, mas pode ser realizado por meio do programa FACTOR (para maiores informações sobre este método, sugere-se a leitura de Garrido e cols., 2011; O’Connor, 2000; Velicer, 1976; Zwick e Velicer, 1986).

Por fim, vale a pena citar um novo método de retenção fatorial, intitulado método Hull, desenvolvido por Ceulemans e Kiers (2006) e adaptado para uso na AFE por Lorenzo-Seva e cols. (2011). Tal método é baseado no conceito matemático de fecho convexo (em inglês, convex hull). O fecho convexo, na matemática, refere-se ao menor polígono que engloba todas as variáveis existentes em um eixo bidimensional. Em outras palavras, o fecho convexo de um conjunto de dados é a ligação do menor número possível dos pontos extremos de um conjunto de dados que, ao serem ligados, incluirá todos os outros dados existentes (ver Figura 3).

 

 

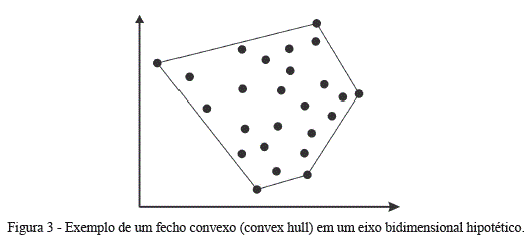
Aplicado às AFEs, o método Hull tem apresentado grande potencial enquanto método de retenção fatorial. Sua execução envolve alguns passos que serão brevemente descritos. Inicialmente, se determina a amplitude de fatores a serem avaliados. Para isso, Lorenzo-Seva e cols. (2011) sugerem utilizar o critério das APs que indicam a quantidade mínima e máxima de fatores a serem extraídos. Posteriormente, se avalia os índices de adequação de ajuste de todas as soluções fatoriais, bem como os graus de liberdade de cada um dos modelos. Os valores de adequação de ajuste podem ser obtidos por meio de diferentes índices.

Todas as soluções fatoriais são plotadas em um gráfico similar ao scree plot, no qual o eixo-y é composto pelos índices de ajuste do modelo, e o eixo-x é composto pelos seus respectivos graus de liberdade. As soluções que não estiverem no limite do fecho convexo (que não sejam os vértices do fecho) são descartadas. Assim, um número reduzido de soluções fatoriais passa a ser considerado. A solução fatorial a ser retida refere-se àquela que se encontra no cotovelo (na quebra) do gráfico plotado. Essa mesma solução apresenta o maior valor númerico scree test (st), que se refere a uma fórmula matemática que pondera a relação entre o índice de adequação de ajuste e os graus de liberdade de um modelo, em comparação com um modelo prévio (ver Ceuleman & Kiers, 2006; Ceulemans, Timmerman & Kiers, 2010; Lorenzo-Seva e cols., 2011). A denominação scree test (st) dada ao cálculo executado no método Hull advém do fato de que o método Hull é considerado como uma implementação matemática ao scree-plot (Ceulemans & Kiers, 2006; Lorenzo- Seva e cols., 2011).

Em um estudo de simulação, Lorenzo-Seva e cols. (2011) testaram a adequação do método Hull para a AFE em 114 mil matrizes de dados simuladas. Os autores manipularam cinco condições, a saber: 1) proporção de itens por fator; 2) número de fatores; 3) tamanho da amostra; 4) variância do fator; 5) grau de correlação entre os fatores. Na maioria das condições, o método Hull apresentou melhor performance quando comparado com todos os métodos anteriormente descritos (eigenvalue > 1; scree plot; AP; MAP). A adequação do método Hull foi ainda melhor quando utilizando os índices de ajuste CFI e CAF (Common part Accounted For). Esse último (CAF) se refere a um novo índice de ajuste desenvolvido pelos autores (Lorenzo-Seva e cols., 2011) e que não apresenta suposição de normalidade, podendo ser utilizado com qualquer método de extração fatorial. Diante dos resultados obtidos, os autores sugeriram utilizar o índice CFI quando os dados apresentam normalidade multivariada, e o CAF quando os dados não apresentarem distribuição normal. O método Hull de retenção fatorial pode ser conduzido por meio do programa FACTOR v8.02 (Lorenzo-Seva & Ferrando, 2006).

Rotação de Fatores

Tão importante quanto o método de retenção fatorial empregado, é o método de rotação de fatores. As rotações fatoriais têm o objetivo de facilitar a interpretação dos fatores, visto que muitas vezes as variáveis analisadas apresentam cargas fatoriais elevadas em mais de um fator. O objetivo das rotações fatoriais é, portanto, encontrar uma solução mais simples e interpretável possível, na qual cada variável apresente carga fatorial elevada em poucos fatores, ou em apenas um (Abdi, 2003). Apesar de ser um processo de manipulação de dados, as rotações fatoriais não melhoram os resultados obtidos. Ou seja, não se trata de uma técnica estatística para disfarçar resultados ruins e apresentar soluções ótimas (Costello & Osborne, 2005).

As rotações fatoriais podem ser de duas ordens: ortogonais ou oblíquas. As rotações ortogonais assumem que os fatores extraídos são independentes uns dos outros (não apresentam correlações entre si). Dentre esse tipo de rotação, vários métodos são apresentados na literatura, tais como: quartimax; equimax; e varimax. Os métodos quartimax e equimax não foram bem sucedidos, sendo raramente utilizados na literatura em Psicologia (Hair e cols., 2005). O primeiro tende a criar um grande fator geral, no qual a maioria dos itens (quando não todos) apresenta cargas fatoriais altas, ocultando possíveis fatores subsequentes (Hair e cols., 2005). O método ‘equimax’, por sua vez, também tem sido pouco utilizado por não apresentar boa estabilidade (Tabachnick & Fidell, 2007). Dentre os métodos ortogonais, o ‘varimax’ é o mais bem sucedido e o mais comumente utilizado nas pesquisas aplicadas em Psicologia (Tabachnick & Fidell, 2007; Fabrigar e cols., 1999). Entretanto, apesar da sua ampla utilização, os resultados obtidos por meio do método varimax, bem como por meio de todos os métodos ortogonais, nas pesquisas em Psicologia, tendem a ser incoerentes (Costello & Osborne, 2005).

Conforme explicitado anteriormente, as rotações ortogonais estipulam, a priori, que não há correlação entre os fatores (r = 0), gerando, portanto, fatores totalmente independentes uns dos outros. Entretanto, esse pressuposto é raramente obtido nas pesquisas das ciências humanas e da saúde. Aspectos humanos e sociais (comportamentos; sintomas; entre outros) raramente são divididos em unidades que funcionam independentes umas das outras (Schmitt & Sass, 2011). Assim, os métodos ortogonais, em geral, resultam em perda de confiabilidade se os fatores forem correlacionados, bem como tende à superestimação de variância explicada, visto que possíveis interseções entre os diferentes fatores não são consideradas.

As rotações oblíquas, por sua vez, permitem que os fatores sejam correlacionados entre si. Diferente dos métodos ortogonais, que exigem que os fatores não sejam correlacionados, os métodos oblíquos não delimitam a interação entre os fatores a priori. Logo, se os fatores não forem correlacionados os resultados obtidos mediante as rotações oblíquas serão bastante semelhantes aos que seriam obtidos por meio das rotações ortogonais (Fabrigar e cols., 1999; Sass & Schmitt, 2010). Dentre os vários métodos existentes de rotação oblíqua simples (oblimin; quartimin; promax; entre outros) parece não existir um método mais adequado que o outro. Em geral, todos eles tendem a apresentar resultados semelhantes (Costello & Osborne, 2005).

Os primeiros métodos de rotação fatorial desenvolvidos, como por exemplo, o método varimax (Kaiser, 1958) e os métodos oblíquos diretos (promax - Hendrickson & White, 1964), baseavamse nos pressupostos de Thurstone (1947), de que uma estrutura fatorial parcimoniosa seria aquela em que os itens carregassem significativamente em apenas um fator. Entretanto, diversas medidas e instrumentos utilizados na Psicologia apresentam padrões de cargas fatoriais complexas (variáveis que carregam consideravelmente em mais de um fator). Por isso, diversos métodos de extração, tanto ortogonais quanto oblíquos, continuam sendo desenvolvidos a fim de melhor avaliar essas características. Por exemplo, Lorenzo-Seva (2000) apresentou um novo tipo de rotação oblíqua, denominada weighted oblimin (em português, oblimin ponderada) que proporcionou melhores resultados do que a direct oblimin (oblimin direta) quando as matrizes de correlação apresentavam variáveis com cargas fatoriais complexas.

É importante que os pesquisadores estejam conscientes que o critério de rotação utilizado pode apresentar um impacto significativo nas correlações entre os fatores e nas cargas fatoriais dos itens. Segundo Sass e Schmitt, (2010), os pesquisadores, em geral, buscam obter estruturas fatoriais simples, por estas serem ‘limpas’ e de fácil interpretação. Entretanto, estruturas complexas (com cargas cruzadas) tendem a oferecer informações mais precisas (e muitas vezes, mais realistas) sobre a qualidade dos itens e, por conseguinte, do instrumento.

Sass e Schmitt (2010) trazem um exemplo esclarecedor sobre esse aspecto. Tomemos por base um instrumento bifatorial, no qual o primeiro fator avalia habilidades de leitura e o segundo, habilidades matemáticas. Se utilizarmos um critério de rotação que busque uma solução simples (direct oblimin, por exemplo), obteremos uma estrutura fatorial com um menor número de cargas cruzadas, e possivelmente, maior correlação entre os fatores. Entretanto, a utilização de uma rotação fatorial que permita que os itens apresentem maior complexidade fatorial poderá mostrar quais itens avaliam tanto as habilidades de leitura, quanto as habilidades matemáticas. A possibilidade de detectar e remover os itens que avaliam ambas as habilidades não só purificaria os fatores, mas aumentaria a validade discriminante destes (Sass & Schimitt, 2010). Assim, utilizar critérios de rotação que revelem a complexidade fatorial pode apresentar consideráveis benefícios durante a construção e o refinamento de instrumentos psicológicos (Sass & Schmitt, 2010).

Alguns programas computacionais, tais como o FACTOR (Lorenzo-Seva & Ferrando, 2006) e o Comprehensive Exploratory Factor Analysis (CEFA) (Browne, Cudeck, Tateneni & Mels, 2004) têm acompanhado o desenvolvimento teórico e metodológico relacionado às rotações fatoriais e oferecem diversos tipos de rotações, tanto oblíquas quanto ortogonais, desde as mais clássicas (varimax; oblimin; promax), que são mais bem utilizadas em casos de estrutura fatorial simples, até outras mais recentes, que apresentam melhor acurácia em casos de complexidade fatorial (promaj; orthosim; oblisim). Apresentar as especificidades de todas as técnicas de rotação está fora do escopo deste artigo. Entretanto, é importante considerar que as técnicas mais avançadas em análises fatoriais não fazem parte dos programas estatísticos mais populares (por exemplo, SPSS e SAS). Pesquisadores interessados devem, portanto, buscar outros e novos pacotes estatísticos para a condução dessas análises (para maiores informações, ver: Browne; 2001; Lee, 2010; Sass & Schmitt, 2010). É importante salientar que, em relação aos métodos de rotação oblíqua complexos, ainda não há na literatura estudos de simulação e diretrizes consistentes que indiquem quais são os mais adequados (Schmitt & Sass, 2011).

Tamanho da Amostra em Análises Fatoriais Exploratórias

O tamanho da amostra ideal para a execução de AFEs foi, por muito tempo, um aspecto de divergência de opiniões e controvérsias na literatura científica, principalmente no que diz respeito ao número mínimo de sujeitos necessários. Gorsuch (1983), em consonância com Hair e cols. (2005), por exemplo, recomendou que o N deveria ser de pelo menos 100 sujeitos, e um número mínimo de cinco respondentes por item. Cattell (1978) argumentou que N igual a 250 era um número minimamente recomendável, e que a razão deveria ser entre três e seis respondentes por item. Já Everitt (1975) sugeriu a presença de pelo menos 10 respostas para cada item avaliado, sendo que quanto maior o N, melhor. Apesar de haver diversas diretrizes apontando regras gerais sobre o tamanho mínimo de amostra necessário para a obtenção de uma estrutura fatorial estável, por muito tempo não houve experimentos de simulação que corroborassem ou refutassem estas informações (MacCallum, Widaman, Zhang & Hong, 1999).

Atualmente, é fortemente aceito que a utilização de amostras grandes tende a fornecer resultados mais precisos, diminuindo o efeito do erro amostral (ver MacCallum & Tucker, 1991) e fornecendo resultados mais próximos ao índice populacional, tanto no que se refere à estrutura fatorial, quanto à carga fatorial e à comunalidade dos itens (MacCallum e cols., 1999). Porém, em relação ao tamanho mínimo da amostra, os resultados ainda são imprecisos, porque a qualidade de uma solução fatorial não depende exclusivamente do número de respondentes, mas varia de acordo com a qualidade do instrumento avaliado.

Em um estudo de simulação Monte-Carlo, Barrett e Kline (1981) demonstraram que soluções fatoriais estáveis foram encontradas com um número variando de 1,2 a 3 respondentes por item. Resultados semelhantes foram encontrados por MacCallum e cols. (1999). Por meio de estudos de simulação Monte-Carlo, esses autores demonstraram que a qualidade de uma solução fatorial está amplamente relacionada com o grau de sobredeteminação (overdetermination) dos fatores obtidos. Por sobredeterminação, os autores consideraram o grau em que um fator é claramente representado por um número suficiente de itens e pela qualidade (nível) das suas cargas fatoriais e comunalidades. Se um fator é representado por um bom número de itens (tipicamente quatro ou mais), e se estes itens tendem a ser fortemente explicados pelo fator (apresentam cargas fatoriais elevadas, > 0,60), o número de respondentes tende a ser menos importante na obtenção de uma boa estrutura fatorial (MacCallum e cols., 1999). Segundo os autores, o erro amostral tende a diminuir quando os fatores são fortemente sobredeterminados, por isto, um N elevado não é tão importante (MacCallum e cols., 1999).

Tanto Barret e Kline (1981) quanto Mac- Callum e cols. (1999) concluíram que os níveis de estabilidade encontrados em seus estudos deveramse à qualidade do instrumento psicométrico, e não ao tamanho amostral. Entretanto, se o instrumento não apresenta um bom nível de sobredeterminação (apresenta poucos itens por fator, com baixas cargas fatoriais e baixas comunalidades), um N pequeno aumenta consideravelmente a probabilidade de encontrar soluções fatoriais instáveis (Hogarty, Hines, Kromey, Ferron & Mumford, 2005). Assim, ainda é sugerido um número elevado de sujeitos por item nos casos em que os instrumentos apresentem vários fatores, e com baixo nível de sobredeterminação (para maiores informações, sugere-se a leitura de Hogarty e cols., 2005; MacCallum e cols., 1999; e Velicer & Fava, 1998).

Variância Explicada

Apesar de haver uma ampla literatura sobre os principais aspectos das AFEs, há certa lacuna sobre o tópico da variância explicada (Peterson, 2000). Tal limitação deixa, por vezes, os pesquisadores no dilema de tentar compreender o valor percentual obtido em suas análises, questionando-se sobre a adequação ou inadequação da estrutura fatorial, bem como a aceitabilidade dos índices obtidos.

Na AFE, a variância explicada refere-se à porção de variância comum que um fator, ou um conjunto de fatores, consegue extrair de um determinado conjunto de dados. Segundo Tinsley e Tinsley (1987), soluções fatoriais que expliquem apenas entre 30% a 40% da variância comum entre os itens sugerem uma ampla porcentagem de variância não-explicada (resíduos). Por meio de um estudo de revisão da literatura, os autores concluíram que, em geral, as soluções fatoriais nas pesquisas em Psicologia explicavam menos de 50% da variância total.

Mais recentemente, Peterson (2000) realizou um estudo meta-analítico com o objetivo de avaliar os níveis de variância explicada nos estudos que utilizaram AFEs, bem como suas relações com aspectos referentes ao delineamento metodológico utilizado em tais estudos. De acordo com os critérios de inclusão/exclusão adotados pelo autor, foram avaliadas 803 análises fatoriais, reportadas em 568 artigos, publicados entre 1964 e 1999. Do total das AFEs executadas, 67% utilizaram o método dos componentes principais, e 82% utilizaram o método de rotação varimax. A média da variância explicada foi de 56,6%. Do total das AFEs avaliadas, 10% apresentaram variância explicada maior que 76%, e outros 10% apresentaram variância explicada menor que 34%. O nível de variância explicada apresentou correlações negativas com o número de itens dos instrumentos (r = - 0,20; valor de p não apresentado) e com o tamanho da amostra (r = - 0,12; valor de p não apresentado), de maneira que, quanto maior foi o número de itens do instrumento e a amostra, menor tendeu a ser a variância explicada.

De acordo com Peterson (2000), tais resultados fornecem certa diretriz na avaliação do que poderia ser um bom nível de variância explicada. Entretanto, o autor não sugere ‘pontos de cortes’ para o que seria um nível de variância explicada aceitável ou não aceitável. Tal cautela é pertinente. Perspectivas clássicas (Abelson, 1985; O’Grady, 1982) indicam que a porcentagem de variância explicada não deve ser considerada como um indicador de importância para a interpretação de uma AFE.

Do ponto de vista psicométrico, O’Grady (1982) argumenta que, nas pesquisas em Psicologia, nenhum comportamento será totalmente compreendido por nenhum construto hipotético, de maneira que a variância explicada nunca chegará ao seu valor total (100%). Mais que isso, a compreensão do comportamento por meio de escalas tipo likert aumentam ainda mais a imprecisão da avaliação. Nesse sentido, as limitações a priori da forma de avaliação utilizada inviabilizam a análise do nível de variância explicada como um indicador de acurácia do construto avaliado (O’Grady, 1982). O autor enfatiza, ainda, que, de um ponto de vista metodológico, o delineamento de um estudo não deve ter por objetivo a maximização do nível de variância explicada. A sua busca, em geral, tende a produzir modelos hipotéticos inválidos, com superestimação dos fatores extraídos, gerando construtos supérfluos, sem significado teórico (O’Grady, 1982).

Também é importante salientar que, na utilização de rotações fatoriais oblíquas (que permitem a correlação entre os fatores), o nível de variância explicada por cada fator pode estar sobreposto pelo outro, o que dificulta uma interpretação coerente deste índice. Assim, em consonância com Abelson (1985), sugere-se que uma avaliação adequada das medidas de variância explicada em AFEs deve ser realizada analisando a concordância entre a magnitude do delineamento teórico e metodológico, e os achados empíricos.

Avaliando a Confiabilidade da Estrutura Fatorial

A confiabilidade de uma estrutura fatorial pode ser obtida por meio de diversos critérios, dependendo tanto das escolhas do pesquisador quanto do delineamento do estudo (transversal, longitudinal, entre outros). Dentre vários critérios apresentados na literatura, o cálculo do índice de consistência interna, por meio do Alfa de Cronbach (α), é o método mais utilizado em estudos transversais - quando as medições são realizadas em apenas um único momento (Sijtsma, 2009).

O Alfa de Cronbach avalia o grau em que os itens de uma matriz de dados estão correlacionados entre si (Pasquali, 2009). Geralmente, o índice obtido varia entre 0 e 1, ainda que não haja um limite mínimo para este coeficiente (Cortina, 1993). Em geral, diretrizes para interpretação dos valores do alfa são adotadas. George e Mallery (2003) sugerem que a > 0,90 = excelente; a > 0,80 = bom; a > 0,70 = aceitável; a > 0,60 = questionável; a > 0,50 = pobre; a < 0,50 = inaceitável.

Em sua forma padronizada, o alfa de Cronbach é calculado pela seguinte fórmula:

 

 

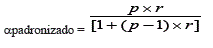
onde p é o número de itens considerados e r é a média das correlações interitens.

O valor do alfa de Cronbach é influenciado tanto pelo valor das correlações dos itens, quanto pelo número de itens avaliados. Por isso, fatores com poucos itens tendem a apresentar alfas de Cronbach menores, enquanto uma matriz com elevadas correlações interitem tende a apresentar um alfa de Cronbach elevado (Cortina, 1993).

Apesar da ampla utilização do alfa de Cronbach como um índice de confiabilidade fatorial, muitos pesquisadores desconhecem suas limitações. O alfa de Cronbach é baseado no pressuposto de ‘tau-equivalence’ (equivalência-t), o qual afirma que todos os itens retidos no fator apresentam uma correlação linear entre si, e que a covariância interitem é a mesma para todos os pares de variáveis, divergindo entre si apenas pela constante (Huysamen, 2006). Admite-se, portanto, que todos os itens retidos apresentam a mesma ‘importância’ para o fator (uma das premissas da Teoria Clássica dos Testes – TCT, amplamente criticada pela Teoria de Resposta ao Item – TRI, Pasquali & Primi, 2003). Devido, em parte, a essa limitação, cada vez mais vem sendo incentivada a utilização de outros métodos de avaliação de consistência interna, tais como o greatest lower-bound (ver Sijtsma, 2009), bem como métodos de análise fatorial confirmatória, para observar a adequação de ajuste do modelo fatorial (Brown, 2006).

Outro importante aspecto a considerar é a distinção entre confiabilidade e homogeneidade. De acordo com Cortina (1993), o alfa de Cronbach avalia a confiabilidade de uma estrutura fatorial por meio de sua consistência interna (grau de inter-relação entre as variáveis), mas não avalia a homogeneidade (que se refere à unidimensionalidade de construtos). Às vezes, os pesquisadores utilizam erroneamente o valor do alfa de Cronbach para determinar o número de fatores a ser utilizado. Por exemplo, imaginemos um instrumento de agressividade infantil, composto por dois fatores, sendo: Fator 1 - Agressividade Proativa (α = 0,75); e Fator 2 - Agressividade Reativa (α = 0,79). O pesquisador, com o intuito de avaliar um nível total de agressividade (soma da agressividade proativa e reativa) avalia os índices de consistência interna para todos os itens do instrumento em conjunto, obtendo um α = 0,85. Considerando apenas o valor do a, a conclusão poderia ser: o instrumento é mais adequado como medida unifatorial; ou ainda, o instrumento pode ser tanto bifatorial quanto unifatorial. Essa interpretação é parcialmente equivocada, se analisada, sobretudo, do ponto de vista teórico.

A literatura na área da agressividade infantil é clara em afirmar que ambos os tipos de agressividade (proativa e reativa) são fortemente correlacionados entre si, mas, devido as suas especificidades, devem ser considerados como construtos distintos (Barke e cols., 2010; Dodge & Coie, 1987). Apesar de a união dos fatores apresentar um maior alfa de Cronbach (devido à correlação entre as variáveis e a maior quantidade de itens), os aspectos teóricos que subsidiam o instrumento não podem ser negligenciados. Assim, itens podem ser altamente correlacionados, mas multidimensionais em essência (Cortina, 1993). Considerando esse aspecto, é importante que os valores estatísticos obtidos sejam sempre ponderados a partir de uma base teórica e metodológica, para que sua interpretação seja adequada.

 

Considerações Finais

O presente trabalho teve por objetivo discutir alguns dos principais aspectos da análise fatorial exploratória (AFE), apresentando estudos atualizados sobre o tema. Conforme mencionado, a AFE é uma técnica relativamente complexa que exige dos pesquisadores uma série de decisões para que possa se obter uma estrutura fatorial adequada. Tais decisões não podem ser arbitrárias e subjetivas, mas devem ser pautadas em critérios teóricos e metodológicos claros. Esses critérios, por sua vez, continuam em desenvolvimento, sendo, portanto, necessária a atualização constante por parte dos pesquisadores.

Concordando com Widaman (2007), o uso das AFEs na Psicologia ainda está longe de ser ideal. Entretanto, algumas atitudes podem ser adotadas. Sugere-se que as AFEs reportadas nos estudos sejam avaliadas com maior padrão de exigência por parte das comissões editoriais das revistas científicas. Do mesmo modo, sugere-se que os pesquisadores, ao conduzirem AFEs, apresentem detalhadamente os métodos utilizados, justificando suas escolhas. Tais preocupações podem aprimorar a utilização das AFEs na ciência psicológica.

É importante salientar que não foi possível contemplar todos os aspectos referentes à AFE, tampouco foi possível discutir em exaustão os tópicos apresentados. Entretanto, espera-se que as informações aqui presentes possam auxiliar os pesquisadores na condução de AFEs, considerando o conteúdo aqui apresentado de modo a favorecer que as decisões tomadas com base nessas análises sejam pautadas em elementos teóricos e metodológicos.

 

Referências

Abdi, H. (2003). Factor rotations in factor analyses. Em: M. Lewis-Beck, A. Bryman & T. Futing (Orgs.), Encyclopedia of social sciences research methods (pp. 1-8). Thousand Oaks, CA: Sage.         [ Links ]

Abelson, R. P. (1985). A variance explanation paradox: When a little is a lot. Psychological Bulletin, 97(1), 129-133.         [ Links ]

Artes, R. (1998). Aspectos estatísticos da análise fatorial de escalas de avaliação, Revista de Psiquiatria Clínica, 25(5), 223-228.         [ Links ]

Barke, E. D., Vitaro, F., Lacourse, E., Fontaine, N. M. G., Carbonneau, R. & Tremblay, R. E. (2010). Testing the developmental distinctiveness of male proactive and reactive aggression with a nested longitudinal experimental intervention. Aggressive Behavior, 36(2), 127–140.         [ Links ]

Barke, E. D., Vitaro, F., Lacourse, E., Fontaine, N. M. G., Carbonneau, R. & Tremblay, R. E. (2010). Testing the developmental distinctiveness of male proactive and reactive aggression with a nested longitudinal experimental intervention. Aggressive Behavior, 36(2), 127–140.

Brown, T. A. (2006). Confirmatory factor analysis for applied research. New York: The Guilford Press.         [ Links ]

Browne, M. W. (2001). An overview of analytic rotation in exploratory factor analysis. Multivariate Behavioral Research, 36(1), 111-150.         [ Links ]

Browne, M. W., Cudeck, R., Tateneni, K. & Mels, G. (2004). CEFA: Comprehensive Exploratory Factor Analysis, Version 2.00 [Computer software and manual]. Recuperado de: http://faculty. psy.ohio-state.edu/browne/software.php.         [ Links ]

Cattell, R. B. (1966). The scree test for the number of factors. Multivariate Behavioral Research, 1(1), 245-276.         [ Links ]

Cattell, R. B. (1978). The scientific use of factor analysis. New York: Plenum.         [ Links ]

Ceulemans, E. & Kiers, H. A. L. (2006). Selecting among three-mode principal component models of different types and complexities: A numerical convex hull based method. British Journal of Mathematical and Statistical Psychology, 59(1), 133–150.         [ Links ]

Ceulemans, E., Timmerman, M. E. & Kiers, H. A. L. (2010). The CHull procedure for selecting among multilevel component solutions. Chemometric and Intelligent Laboratory Systems, 106(1), 12-20.         [ Links ]

Cortina, J. M. (1993). What is coefficient alpha? An examination of theory and applications. Journal of Applied Psychology, 78(1), 98-104.         [ Links ]

Costello, A. B. & Osborne, J. W. (2005). Best practices in exploratory factor analysis: Four recommendations for getting the most from your analysis. Practical Assessment, Research & Evaluation, 10(7), 1-9.         [ Links ]

Crawford, A. V., Green, S. B., Levy, R., Lo, W., Scott, L., Svetina, D. e cols. (2010). Evaluation of parallel analysis methods for determining the number of factors. Educational and Psychological Measurement, 70(6), 885-901.         [ Links ]

Dodge, K. A. & Coie, J. D. (1987). Social-information- processing factors in reactive and proactive aggression in children’s peer groups. Journal of Personality and Social Psychology, 53(6), 1146–1158.         [ Links ]

Dziuban, C. D. & Shirkey, E. C. (1974). When is a correlation matrix appropriate for factor analysis? Some decision rules. Psychological Bulletin, 81(6), 358-361.         [ Links ]

Everitt, B. S. (1975). Multivariate analysis: The need for data, and other problems. British Journal of Psychiatry, 126(1), 237-240.         [ Links ]

Fabrigar, L. R., Wegener, D. T., MacCallum, R. C. & Strahan, E. J. (1999). Evaluating the use of exploratory factor analysis in psychological research. Psychological Methods, 4(3), 272-299.         [ Links ]

Fava, J. L. & Velicer, W. F. (1992). The effects of over extraction on factor and component analysis. Multivariate Behavioral Research, 27(3), 387-415.         [ Links ]

Field, A. (2005). Discovering Statistics Using SPSS. (2. ed.), London: Sage.         [ Links ]

Floyd, F. J. & Widaman, K. F. (1995). Factor analysis in the development and refinement of clinical assessment instruments. Psychological Assessment, 7(3), 286-299.         [ Links ]

Franklin, S. B., Gibson, D. J., Robertson, P. A., Pohlmann, J. T. & Fralish, J. S. (1995). Parallel Analysis: A method for determining significant principal components. Journal of Vegetation Science, 6(1), 99-106.         [ Links ]

Garrido, L. E., Abad, F. J. & Ponsoda, V. (2011). Performance of Velicer’s Minimum Average Partial factor retention method with categorical variables. Educational and Psychological Measurement, 71(3), 551-570.         [ Links ]

George, D. & Mallery, P. (2003). SPSS for Windows step by step: A simple guide and reference. 11.0 update (4th ed.). Boston: Allyn & Bacon.         [ Links ]

Glorfeld, L. W. (1995). An improvement on Horn’s parallel analysis methodology for selecting the correct number of factors to retain. Educational and Psychological Measurement, 55(3), 377-393.         [ Links ]

Gorsuch, R. L. (1983). Factor analysis (2nd ed.). Hillsdale, NJ: Erlbaum.         [ Links ]

Hair, J. F., Anderson, R. E., Tatham, R. L. & Black, W. C. (2005). Análise multivariada de dados. A. S. Sant’Anna & A. C. Neto (Trad.). Porto Alegre: Bookman.         [ Links ]

Hayton, J. C., Allen, D. G. & Scarpello, V. (2004). Factor retention decisions in exploratory factor analysis: A tutorial on parallel analysis. Organizational Research Methods, 7(2), 191-207.         [ Links ]

Hendrickson, A. E. & White, E. O. (1964). PROMAX: A quick method for rotation to oblique simple structure. British Journal of Statistical Psychology, 17(1), 65-70.         [ Links ]

Hogarty, K. Y., Hines, C. V., Kromey, J. D., Ferron, J. M. & Mumford, K. R. (2005). The quality of factor solution in exploratory factor analysis: The influence of sample size, communality, and over determination. Educational and Psychological Measurement, 65(2), 202-226.         [ Links ]

Horn, J. L. (1965). A rationale and technique for estimating the number of factors in factor analysis. Psychometrika, 30(1), 179-185.         [ Links ]

Hutcheson, G. D. & Sofroniou, N. (1999). The multivariate social scientist: Introductory statistics using generalized linear models. London: Sage Publications.         [ Links ]

Huysamen, G. K. (2006). Coefficient Alpha: Unnecessarily ambiguous; unduly ubiquitous. SA Journal of Industrial Pscyhology, 32(4), 34-40.         [ Links ]

Jolliffe, I. T. (2005). Principal component analysis. Em: B. S. Everitt & D. C. Howell (Orgs.), Encyclopedia of statistics in behavioral science (pp. 1580-1584). New York: John Wiley and Sons Ltd.         [ Links ]

Kim, J. & Mueller, C. W. (1978). Factor analysis: Statistical methods and practical issues. Beverly Hills, CA: Sage Publications.         [ Links ]

Laher, S. (2010). Using exploratory factor analysis in personality research: Best-practice recommendations. SA Journal of Industrial Psychology, 36(1), 1-7.         [ Links ]

Laros, J. A. (2004). O uso da análise fatorial: algumas diretrizes para pesquisadores. Em: L. Pasquali (Org.), Análise fatorial para pesquisadores. Petrópolis: Vozes.         [ Links ]

Ledesma, R. D. & Valero-Mora, P. (2007). Determining the number of factors to retain in EFA: An easy-to-use computer program for carrying out parallel analysis. Practical Assessment, Research and Evaluation, 12(1), 1–11.         [ Links ]

Lee, S. (2010). A Review of CEFA Software: Comprehensive Exploratory Factor Analysis Program. International Journal of Testing, 10(1), 95-103.         [ Links ]

Lorenzo-Seva, U. (2000). The weighted oblimin rotation. Psychometrika, 65(1), 301-318.         [ Links ]

Lorenzo-Seva, U. & Ferrando, P. J. (2006). FACTOR: A computer program to fit the exploratory factor analysis model. Behavior Research Methods, 38(1), 88-91.         [ Links ]

Lorenzo-Seva, U., Timmerman, M. E. & Kiers, H. A. (2011). The hull method for selecting the number of common factors. Multivariate Behavioral Research, 46(2), 340-364.         [ Links ]

MacCalum, R. C., Widaman, K. F., Zhang, S. & Hong, S. (1999). Sample size in factor analysis. Psychological Methods, 4(1), 84-99.         [ Links ]

MacCallum, R. C. & Tucker, L. R. (1991). Representing sources of error in the common factor model: Implications for theory and practice. Psychological Bulletin, 109(3), 502-511.         [ Links ]

O’Connor, B. P. (2000). SPSS and SAS programs for determining the number of components using Parallel Analysis and Velicer’s MAP test. Behavior Research Methods, Instruments & Computers, 32(3), 396-402.         [ Links ]

O´Grady, K. E. (1982). Measures of explained variance: Cautions and limitations. Psychological Bulletin, 92(3), 766-777.         [ Links ]

Ogasawara, H. (2003). Oblique factors and components with independent clusters. Psychometrika, 68, 299-321.         [ Links ]

Pasquali, L. (1999). Análise fatorial: um manual teórico-prático. Brasília: Editora UnB.         [ Links ]

Pasquali, L. (2009). Psicometria. Revista da Escola de Enfermagem da USP, 43(Esp.), 992-999.         [ Links ]

Pasquali, L. & Primi, R. (2003). Fundamentos da teoria da resposta ao item – TRI. Avaliação Psicológica, 2(2), 99-110.         [ Links ]

Patil, V. H., Singh, S. N., Mishra, S. & Donavan, D. T. (2007). Parallel Analysis engine to aid determining number of factors to retain [Computer software]. Retirado de: http://ires. ku.edu/~smishra/parallelengine.htm.         [ Links ]

Patil, V. H., Singh, S. N., Mishra, S. & Donavan, D. T. (2008). Efficient theory development and factor retention criteria: Abandon the ‘eigenvalue greater than one’ criterion. Journal of Business Research, 61(2), 162-170.         [ Links ]

Peterson, R. A. (2000). A meta-analysis of variance accounted for and factor loadings in exploratory factor analysis. Marketing Letters, 11(3), 261-275.         [ Links ]

Reise, S. P., Waller, N. G. & Comrey, A. L. (2000). Factor analysis and scale revision. Psychological Assessment, 12(3), 287-297.         [ Links ]

Sass, D. A. & Schmitt, T. A. (2010). A comparative investigation of rotation criteria within exploratory factor analysis. Multivariate Behavioral Research, 45(1), 73-103.         [ Links ]

Schmitt, T. A. & Sass, D. A. (2011). Rotation criteria and hypothesis testing for exploratory factor analysis: Implications for factor pattern loadings and interfactor correlations. Educational and Psychological Measurement, 71(1), 95-113.         [ Links ]

Sijtsma, K. (2009). On the use, the misuse, and the very limited usefulness of Cronbach’s alpha. Psychometrika, 74(1), 107-120.         [ Links ]

Tabachnick, B. G. & Fidell, L. S. (2007). Using Multivariate Statistics (5th. ed.). Boston: Allyn and Bacon.         [ Links ]

Thurstone, L. L. (1947). Multiple factor analysis. Chicago: University of Chicago Press.         [ Links ]

Tinsley, H. E. A. & Tinsley, D. J. (1987). Uses of factor analysis in counseling psychology research. Journal of Counseling Psychology, 34(4), 414-424.         [ Links ]

Velicer, W. F. (1976). Determining the number of components from the matrix of partial correlations. Psychometrika, 41(3), 321-327.         [ Links ]

Velicer, W. F., Eaton, C. A. & Fava, J. L. (2000). Construct explication through factor or component analysis: A review and evaluation of alternative procedures for determining the number of factors or components (pp. 41-71). Em: R. D. Goffin & E. Helmes (Orgs.), Problems and solutions in human assessment: Honoring Douglas N. Jackson at Seventy. Boston: Kluwer.         [ Links ]

Velicer, W. F. & Fava, J. L. (1998). Effects of variable and subject sampling on factor pattern recovery. Psychological Methods, 3(2), 231-251.         [ Links ]

Watkins, M. W. (2000). Monte Carlo PCA for Parallel Analysis [Computer software]. State College, PA: Ed. & Psych Associates.         [ Links ]

Widaman, K. F. (2007). Common factor versus components: Principals and principles, errors and misconceptions Em: R. Cudeck & R. C. Mac- Callum. Factor Analysis at 100: Historical Developments and Future Directions (pp. 177 - 204). London: Lawrence Erlbaum Associates.         [ Links ]

Zwick, W. R. & Velicer, W. F. (1986). Comparison of five rules for determining the number of components to retain. Psychological Bulletin, 99(3), 432-442.         [ Links ]

 

 

Recebido em julho de 2011
Reformulado em abril de 2012
Aceito em maio de 2012

 

 

Sobre o autor:

Bruno Figueiredo Damásio: Psicólogo. Doutorando em Psicologia pela Universidade Federal do Rio Grande do Sul.

¹Endereço para correspondência:
Rua Ramiro Barcelos, 2600, Sala 104. CEP 90035-003 Porto Alegre - RS Telefones: (51) 3308.5150 / (51) 9240.1055 E-mail: brunofd.psi@gmail.com