Serviços Personalizados
Journal
artigo
Indicadores
Compartilhar
Avaliação Psicológica
versão impressa ISSN 1677-0471versão On-line ISSN 2175-3431
Aval. psicol. vol.17 no.4 Itatiba out./dez. 2018
https://doi.org/10.15689/ap.2018.1704.13238.01
ARTIGOS
Técnicas de correção do teste qui-quadrado para amostras não normais
Techniques for correction the chi-square test for non-normal samples
Técnicas de corrección del test chi-cuadrado para muestras no normales
Marli Appel da SilvaI; Guilherme Welter WendtII; Irani Iracema de Lima ArgimonIII; Regina Maria Fernandes LopesIII
IPontifícia Universidade Católica do Rio Grande do Sul
IIUniversidade Federal do Rio Grande do Sul
IIIPontifícia Universidade Católica do Rio Grande do Sul
RESUMO
Este artigo tem o objetivo de avaliar técnicas de correções para o teste Qui-Quadrado (X2) aplicadas a modelos da análise fatorial confirmatória (CFA) em amostras não normais. Em uma abordagem simulada e exploratória, foram mensuradas distribuições distintas em termos de curtose multivariada. Na maioria das situações verificadas, observou-se uma tendência dos testes aferidos de realizar correções diferenciadas dos valores do X2, CFI e RMSEA em contextos similares. Como conclusão, dentre outros testes avaliados, sugere-se o uso dos seguintes: teste Elíptico com Mínimos Quadrados Reponderados (Teoria Elíptica); teste da Curtose Heterogênea com Mínimos Quadrados Reponderados (Teoria Curtose Heterogênea) e teste Escalado de Satorra-Bentler com Máxima Verossimilhança (para distribuições com excesso de assimetria e/ou curtose univariadas). Porém, devido ao fator de correção, o teste Escalado de Satorra-Bentler pode aceitar modelos moderadamente mal especificados na presença de extrema curtose.
Palavras-chave: teste qui-quadrado; distribuição não normal; análise fatorial confirmatória.
ABSTRACT
This paper aims to evaluate techniques for correcting the chi-square test (X2) as applied to Confirmatory Factor Analysis (CFA) models in non-normal data. In a simulated and exploratory approach, distinct distributions were analyzed in terms of multivariate kurtosis. In most situations, it was observed a tendency of the analyzed tests to produce differing corrections on the X2 values, as well as for the CFI and RMSEA values. Among other tests evaluated, this study suggested the use of the Elliptical Test with Least Squares (Elliptical Theory), Heterogeneous Kurtosis Test with Reweighted Least Squares (Heterogeneous Kurtosis Theory) and Satorra-Bentler Scaled Test with Maximum Likelihood estimation (for distributions with excessive univariate asymmetry and/or kurtosis). However, due to the correction factor, the Satorra-Bentler Scaled test can accept moderately poorly specified models in the presence of extreme kurtosis.
Keywords: chi-square test; non-normal distribution; confirmatory factor analysis.
RESUMEN
Este artículo tiene por objetivo evaluar las técnicas de correcciones para la prueba chi-cuadrado (X2) aplicadas a modelos del Análisis Factorial Confirmatorio (CFA) en muestras no normales. En un enfoque simulado y exploratorio, se midieron distribuciones distintas en términos de curtosis multivariada. En la mayoría de las situaciones verificadas, se observó una tendencia de las pruebas evaluadas de realizar correcciones diferenciadas de los valores del X2, CFI y RMSEA en contextos similares. En conclusión, entre otras pruebas evaluadas, se sugiere el uso de las siguientes: Prueba Elíptica con Mínimos Cuadrados Reponderados (Teoría Elíptica); Prueba de la Curtosis Heterogénea con Mínimos Cuadrados Reponderados (Teoría de la Curtosis Heterogénea) y Prueba Escalada de Satorra-Bentler con Máxima Verosimilitud (para distribuciones con exceso de asimetría y/o curtosis univariadas). No obstante, por cuenta del factor de corrección, la Prueba Escalada de Satorra-Bentler puede aceptar modelos moderadamente mal especificados en presencia de extrema curtosis.
Palabras clave: prueba chi-cuadrado; distribución no normal; análisis factorial confirmatorio.
Variados tipos de amostras podem sem obtidos na prática da pesquisa. Sobretudo em estudos das áreas das ciências sociais, as amostras nem sempre cumprem os pressupostos da normalidade (tendência de medidas centrais idênticas; Kline, 2015). Desse modo, não são incomuns as dúvidas de pesquisadores sobre quais métodos devem ser selecionados para a avaliação de modelos quando utilizadas as técnicas da análise fatorial confirmatória (Confirmatory Factor Analysis, CFA).
A CFA, usada principalmente para a verificação da validade de construtos ou da capacidade psicométrica de instrumentos, representa uma das possibilidades dentre as diversas técnicas estatísticas que integram a Modelagem de Equação Estrutural (Structural Equation Modeling, SEM). A SEM, por conseguinte, refere-se a um conjunto de métodos estatísticos voltados a modelar um padrão de hipóteses referente a relações lineares entre variáveis observadas (mensuradas) e latentes (não mensuradas diretamente) com a finalidade de estabelecer se um modelo derivado de uma determinada teoria possui um ajuste de dados aproximado do previsto por um modelo "ideal" ou hipotetizado (Green, 2016; Kline, 2015).
Na SEM, em geral, as estimações são efetuadas a partir da comparação entre a matriz de covariância do modelo estudado (S) e a matriz de covariância assintótica ou hipotetizada (∑( θ )) em referência aos graus de liberdade (degrees of freedom, df; diferença entre os parâmetros do modelo não constrito e do avaliado), gerando uma matriz residual de covariância (Fo). Mediante a hipótese nula, Fo= S - ∑( θ ) = 0. Assim, quando Fo≠ 0, os métodos de estimação ou estimadores realizam uma função de minimização (a partir de métodos estatísticos específicos a cada estimador) de Fo, ou seja, do mau ajuste ou da discrepância dos dados estudados quando cotejados com os de uma amostra hipotetizada.
Dentre os métodos de estimação, encontram-se o de Máxima Verossimilhança (Maximum Likelihood, ML), Mínimos Quadrados (Least Square, LS), Mínimos Quadrados Reponderados (Reweighted Least Squares, RLS) e Mínimos Quadrados Generalizados (Generalized Least Square, GLS). A técnica ML produz estimativas assintoticamente imparciais, mas exige o cumprimento dos pressupostos da normalidade amostral. O teste RLS possui comportamento similar à estimação ML. Já os métodos LS e GLS tendem a um desempenho insatisfatório na presença de variáveis com excesso de curtose (uma medida de dispersão da distribuição; Bentler, 2006; Green, 2016; Kline, 2015).
Assim, os estimadores ML, LS, RLS e GLS não são considerados apropriados para dados não normais. Nesse caso, existem testes que realizam a correção do qui-quadrado (X2, teste de hipótese não paramétrico; Green, 2016; Kline, 2015) estimado por tais métodos (ML, LS, RLS e GLS), propiciando com que o valor do X2 se aproxime do apresentado por uma amostra normal.
Contudo, quando ocorre a violação da normalidade amostral, há uma diversidade de testes para a correção dos valores do X2. Por exemplo, algumas distribuições atendem aos pressupostos da Teoria Elíptica, ou seja, princípio da assimetria (Sk; grau de afastamento da média amostral) igual a zero. As distribuições elípticas formam uma classe específica com a probabilidade de simetria igual a de uma distribuição normal. Porém, apresentam determinado nível de curtose homogênea (positiva ou negativa), com caudas mais leves ou pesadas que a distribuição normal clássica. Para amostras com essas características, deve ser considerado o denominado de Teste Elíptico (Elliptical Test, E). Tal teste, para a correção do X2, assume a assimetria igual a zero na presença de certo nível de curtose (Bentler, 2006; Schumacker & Cheevatanarak, 2000).
Também existem amostras em conformidade com a Teoria da Curtose Heterogênea, que diz respeito a distribuições que mantêm a característica de simetria, mas apresentam valores marginais heterogêneos de curtose (K < ±3). Nesses casos, deve ser utilizado o nominado de teste da Curtose Heterogênea (Heterogeneous Kurtosis Test, KH), que efetua correções no X2 de modo que as variáveis se aproximem do quarto momento, ou seja, do ajuste da curtose (Bentler, 2006; Kano, Berkane, & Bentler, 1990).
Se os pressupostos da Teoria da Normalidade, Elíptica e da Curtose Heterogênea não possam ser atendidos, os testes robustos podem ser considerados. Nesse âmbito, Satorra-Bentler propuseram, dentre outros, dois testes estatísticos: Teste Escalado de Satorra-Bentler (TS-B; Satorra & Bentler, 2001) e Teste Ajustado de Satorra-Bentler (TASB; Satorra & Bentler, 1994). O primeiro aplica um fator de correção de tal forma que a média do X2 se torne igual à de uma distribuição nominal do X2. O segundo utiliza um fator de correção tanto na média do X2 quanto na variância, além de ajustar os graus de liberdade (Satorra & Bentler, 1994, 2001).
Baseado nos testes TS-B e TASB, Asparouhov e Muthén (2010) propuseram o denominado de Teste com Média e Variância Corrigidas (TMVC). Esse teste efetua conjuntamente correções na média do X2 e na variância, mas opera com graus de liberdade fixos.
Os testes TS-B, TASB e TMVC são usualmente utilizados com a solução ML (Asparouhov & Muthén, 2010; Bentler, 2006). O Teste Elíptico opera com as soluções LS (TELS), RLS (TERLS) e GLS (TEGLS); e o Curtose Heterogênea, com RLS (THKRLS) e GLS (THKGLS; Bentler, 2006; Kline 2015).
Em estudo de Monte Carlo, Schumacker e Cheevatanarak (2000) verificaram que o teste TEGLS apresentou maior correção do X2 do que TERLS e TELS mediante a presença de curtose. Por sua vez, Cabrera, Olmos e Costas (1995) observaram que os testes TERLS e TEGLS melhoraram seus desempenhos em amostras com pelo menos 500 casos. Igualmente, estudos empíricos foram localizados na literatura com as soluções TERLS(e.g., Pereda, Arch, Peró, Guàrdia, & Forns, 2011) e TELS (e.g., Agus, Penna, Peró-Cebollero, & Guàrdia-Olmos, 2016).
Já o teste THKRLS apresentou bom desempenho na aceitação e rejeição de modelos em várias condições de distribuições (Hu, Bentler, & Kano, 1992). Também estudos empíricos foram encontrados com esse teste aplicado a modelos da CFA (e.g., Sullivan, Whitaker-Campbell, Bloom, & Falcão, 2014).
O desempenho dos testes TS-B, TASB e TMVC foi comparado por Foldnes e Olsson (2015); os resultados revelaram que o teste TMVC tendeu a maior correção do X2 que os testes TS-B e TASB. Além disso, o teste TS-B foi amplamente utilizado em estudos empíricos para a avaliação de modelos de CFA em áreas das ciências sociais (e.g., Couto, Bartholomeu, & Montiel, 2016). Contudo, poucos estudos empíricos com o uso do teste TMVC (e.g., Hoben, Estabrooks, Squires, & Behrens, 2016) e TASB (e.g., Silva, Wendt, & Argimon, 2017) foram encontrados na literatura, revelando a ausência de esclarecimentos sobre os seus comportamentos na prática da pesquisa (Foldnes & Olsson, 2015). Adicionalmente, embora os testes TS-B e TASB sejam promulgados como não apropriados para amostras em conformidade com os pressupostos da Teoria Elíptica e da Curtose Heterogênea - devido aos fatores de correção (Bentler, 2006; Satorra & Bentler, 1994), o desempenho do teste TMVC em amostras que cumpram os critérios dessas teorias ainda necessita de elucidação (Foldnes & Olsson, 2015).
Também não foram identificados estudos que comparassem os testes THKRLS e THKGLS. Portanto, os desempenhos desses testes, de maneira comparativa, são desconhecidos. Igualmente investigações empíricas não foram localizadas com o uso dos testes TEGLSe THKGLS, sendo escassas as informações acerca de seus comportamentos na prática da pesquisa.
Testes para a Correção do Qui-Quadrado
Quando Fo ≠ 0, os métodos de estimação ML, LS, RLS e GLS realizam uma função de minimização de Fo por meio da seguinte solução: T = F1 (N-1), sendo o F1 a função de minimização diferencialmente efetuada pelos estimadores e N igual ao número amostral. Porém, se a amostra não está em conformidade com os pressupostos da normalidade amostral, os estimadores ML, LS, GLS e RLS tendem a um desempenho pobre. Assim, uma nova função de minimização pode ser apropriada (Kline, 2015).
Quando a amostra atende os critérios da Teoria Elíptica (valores baixos de assimetria univariada [Sk < ± 1] e valores marginais homogêneos de curtose univariada [K < ± 3]; Bentler, 2006; Schumacker & Cheevatanarak, 2000), para a correção do X2, o Teste Elíptico utiliza uma nova função de minimização com base nos estimadores ML, LS ou GLS. A função efetuada por esse teste pode ser descrita como:
FELIP = 1/2(K + 1)-1 tr[(S - ∑(θ))W]2 - δ{tr[S - ∑(θ)]W}2
Nesse caso, W = S-1 para o estimador GLS; W = ∑( θ )-1 para o teste RLS; e W = 1 para a estimação com LS. Já K é o valor do coeficiente multivariado de Kappa Mardia e δ é igual a:
δ = K/[4(K + 1)2 + 2pK(K + 1)]
Se a amostra cumpre os pressupostos da Teoria da Curtose Heterogênea (valores baixos de assimetria univariada [Sk < ± 1] e valores marginais heterogêneos de curtose univariada [K< ± 3]; Bentler, 2006; Kano et al., 1990), para a estimação, uma matriz C é introduzida para a correção de cada variável observada. Assim, a função desse teste pode ser expressa por:
FHK = 1/2 tr[(S - ∑(θ))C]2
No contexto, C = A*S-1 para GLS; C = A*∑( θ )-1 para RLS. Já A é uma matriz descrita como: A = (ki+ kj)/2, onde k é a curtose univariada das variáveis observadas; e * denota os produtos da multiplicação de duas matrizes da mesma ordem, ou seja, com as mesmas quantidades de elementos.
Nos casos em que ocorra a violação dos pressupostos da Teoria da Normalidade, Elíptica e da Curtose Heterogênea, ou seja, exista excesso de curtose multivariada (índice de Mardia > 3, p ≤ 0,05; Mardia, 1970), o Teste Escalado de Satorra-Bentler (TS-B; Bentler, 2006; Satorra & Bentler, 2001) realiza a correção do X2 por meio da função: FS-B = FML/Ƶ, sendo FML a função de minimização efetuada pela estimação ML, 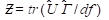 , quando
, quando 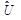 é a média da estimação da matriz de covariância assintótica e
é a média da estimação da matriz de covariância assintótica e 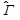 é a média da estimação da matriz de covariância do modelo estudado. Quando Ƶ = 1, o valor do X2 é o mesmo que o dos graus de liberdade (X2/df = 1). Se Ƶ > 1, a correção efetuada pelo teste TS-B será maior quanto maior for a diferença entre as estimações das médias das matrizes de covariância do modelo estudado
é a média da estimação da matriz de covariância do modelo estudado. Quando Ƶ = 1, o valor do X2 é o mesmo que o dos graus de liberdade (X2/df = 1). Se Ƶ > 1, a correção efetuada pelo teste TS-B será maior quanto maior for a diferença entre as estimações das médias das matrizes de covariância do modelo estudado 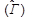 e assintótica
e assintótica 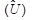 .
.
O mesmo fenômeno de correção de FML ocorre com o Teste Ajustado de Satorra-Bentler (TASB; Bentler, 2006; Satorra & Bentler, 1994). Contudo, o TASB realiza ajustes nos valores dos graus de liberdade e do X2. Assim, o teste TASB pode ser expresso pela função:
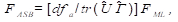
sendo dfa o maior valor inteiro aproximado de dfb:
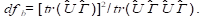
Por sua vez, o Teste com Média e Variância Corrigidas (TMVC; Asparouhov & Muthén, 2010) é, assintoticamente, a média e a variância da distribuição nominal do X2 com os graus de liberdade. Portanto, esse teste aplica um fator de correção no valor do X2 sem incorrer em ajuste nos graus de liberdade, sendo descrito pela seguinte função:
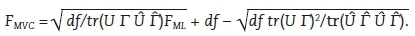
O Presente Estudo
Cada método de correção do X2 designado a amostras não normais realiza as funções de minimização de maneira diferenciada, com técnicas estatísticas específicas. Assim, os resultados apresentados podem afetar o desenvolvimento da teoria de base do modelo estudado, ou seja, este pode ser aceito ou rejeitado em razão do método selecionado (Green, 2016; Kline, 2015). Dessa forma, evidencia-se a necessidade de estudos que demonstrem, comparativamente, os comportamentos de testes para a correção do X2 em amostras não normais de forma a gerar informações destinadas à prática das investigações.
Mediante ao exposto, este estudo, de caráter simulado e exploratório, pretende averiguar o desempenho de testes de correção do X2 em modelos da CFA em delimitadas situações em que os pressupostos da normalidade são violados. Parte-se da seguinte hipótese: os testes avaliados (TELS, TERLS, TEGLS, THKRLS, THKGLS, TS-B e TASB), em condições idênticas, apresentarão correções similares do X2; e, portanto, rejeitarão modelos falsos com moderada má especificação em função de determinados índices de bondade (avaliam os ajustes dos modelos; Kline, 2015). Para a comparação dos testes, utilizaram-se amostras simuladas e retiradas da prática da pesquisa com moderado nível de má especificação. Almejou-se, dessa forma, contribuir com a tomada de decisão em relação à seleção de métodos indicados a avaliar condições amostrais específicas, bem como aprofundar o debate a cerca das técnicas utilizadas na CFA em vista da sua crescente utilização em estudos das áreas das ciências sociais aplicadas (Green, 2016; Kline, 2015).
Método
Estudos Simulados
Para as simulações, utilizou-se o programa R, versão 3.3.2, pacote SIMulated Structural Equation Modeling (Simsem; Pornprasertmanit, Miller, Schoemann, Quick, & Jorgensen, 2016). Primeiramente, estabeleceu-se o modelo da CFA (∑ = ΛΦΛ' + Ψ) a ser utilizado no estudo, com quatro fatores latentes e 12 observáveis, sem cargas cruzadas, com uma carga fatorial constrita (igual a 1) em cada fator, erros constritos (igual a 1) e parâmetros livres das covariâncias (Xia, Yung, & Zhang, 2016).
Posteriormente, uma matriz de covariância foi gerada com base na proposta de Cudeck e Browne (1992) de modo com que o índice raiz do erro quadrático médio de aproximação (RMSEA, que mensura o erro de aproximação) fosse igual a 0,07 com a estimação ML, quando Fo ≠ 0. A proposta de Cudeck e Browne (1992) insere uma matriz de erro em uma matriz com Fo = 0, gerando determinada má especificação nos parâmetros globais do modelo. Como o índice de RMSEA da população pode ser expresso como: 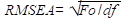 , pode explicitar o nível de má especificação de um modelo para determinados graus de liberdade (Xia et al., 2016). Valores de RMSEA entre 0,06 e 0,08 revelam moderada má especificação, sendo recomendados valores iguais ou menores que 0,05 (Browne e Cudeck, 1993; Xia et al., 2016).
, pode explicitar o nível de má especificação de um modelo para determinados graus de liberdade (Xia et al., 2016). Valores de RMSEA entre 0,06 e 0,08 revelam moderada má especificação, sendo recomendados valores iguais ou menores que 0,05 (Browne e Cudeck, 1993; Xia et al., 2016).
Essa distribuição (índice de Mardia = -0,13, p > 0,05; média [M] = 3,99; desvio padrão [DP] = 1,02) contou com o índice de ajuste comparativo (CFI, avalia a diferença do modelo estudado em relação ao independente; Kline, 2015) de 0,96 com a estimação ML (X2(48) = 164,69). Com o estimador LS (X2(48) = 186,51) e GLS (X2(48) = 143,51), os valores de RMSEA e CFI foram: 0,07 e 0,95; 0,06 e 0,89, respectivamente. Assim, os estimadores ML, LS e GLS revelaram desempenhos diferenciados em função da má especificação do modelo (Green, 2016; Kline, 2015).
Para a criação de amostras não normais, a assimetria (Sk) e curtose (K) foram manipuladas (Pornprasertmanit, Miller, Schoemann, Quick, & Jorgensen, 2016) de forma a produzir quatro tipos de distribuições: (estudo E1S) em consonância com os pressupostos da Teoria Elíptica, com variáveis (V) com valores baixos de assimetria univariada (Sk = +0,01) e marginais de curtose homogênea univariada (K = +2,90; índice de Mardia = 6,93, p > 0,05; M = 3,99; DP = 1,00); (estudo E2S) em concordância com a Teoria da Curtose Heterogênea, com variáveis com valores baixos de assimetria univariada (Sk = +0,01) e marginais de curtose heterogênea univariada (K = -1,00 [V1, V4, V7 e V10] ou +2,90; índice de Mardia = 6,76, p > 0,05; M = 3,98; DP = 1,01); (estudo E3S) com variáveis com valores altos de assimetria univariada (Sk = +1,5) e marginais de curtose univariada (K = + 2,9; índice de Mardia = 18,70; M = 3,95, p > 0,05; DP = 1,02); e (estudo E4S) com variáveis com excesso de assimetria univariada (Sk = +2 [V1, V4, V7 e V10], +4 [V2, V5, V8 e V11] e +6 [V3, V6, V9 e V12]) e curtose univariada (K = + 60 [V1, V4, V7 e V10], +70 [V2, V5, V8 e V11] ou +80 [V3, V6, V9 e V12]; índice de Mardia = 199,67, p > 0,05; M = 4,09; DP = 0,65). As amostras dos estudos E3S e E4S foram selecionas pelo fato dos testes avaliados (TS-B, TASB e TMVC) serem sensíveis ao aumento da curtose (Bentler, 2006; Foldnes & Olsson, 2015).
As quatro distribuições (E1S, E2S, E3S e E3S) foram transformadas em bancos de dados com 500 casos (Pornprasertmanit et al., 2016); amostras consideradas como grandes (N < 200), permitindo estimações mais parcimoniosas (Green, 2016; Kline, 2015). Além disso, os dados foram categorizados com cinco pontos de uma escala simétrica do tipo Likert.
Estudos Empíricos
A fim de uma aproximação com a realidade da pesquisa, de quatro investigações empíricas, foram selecionados 500 casos de maneira a atender os critérios para os tipos amostrais avaliados neste estudo em relação à assimetria e curtose univariadas, verificadas pelo programa EQS (versão 6.3; Bentler, 2006). O estudo E1E seguiu os pressupostos da Teoria Elíptica (Sk < ± 1, K < ± 3; índice de Mardia = 6,12, p ≤ 0,05; M = 3,73; DP = 1,00); e o E2E, da Curtose Heterogênea (Sk < ± 1, K < ± 3; índice de Mardia = 8,86, p ≤ 0,05; M = 3,91; DP = 0,99). Já o E3E apresentou excesso de assimetria univariada (Sk > ± 1) e curtose marginal univariada (K < ± 3; índice de Mardia = 20,26, p ≤ 0,05; M = 2,37; DP = 0,91); bem como o E4E, excesso tanto da assimetria (Sk > ± 1) como da curtose (K > ± 3; índice de Mardia = 257,91, p ≤ 0,05; M = 1,38; DP = 0,81).
Dessas pesquisas, foram eleitas variáveis para a modelagem de quatro modelos de CFA de forma com que o índice RMSEA fosse de 0,06 ou 0,07 (moderada má especificação; Xia et al., 2016) com a estimação ML. Os modelos de CFA foram modelados da seguinte forma: estudos E1E, E2E e E3E, com quatro fatores latentes e 12 observáveis; e estudo E4E, com três fatores latentes e 12 observáveis. Todas as amostras empíricas (E1E, E2E, E3E e E4E) contaram com escalas do tipo Likert.
Análise dos Dados
Os estudos E1S e E1E compararam os testes TERLS, TELS, TEGLS e TMVC; os estudos E2S e E2E, os testes THKRLS, THKGLS e TMVC; e os estudos E3S, E3E, E4S e E4E, os testes TS-B, TASB e TMVC. A Figura 1 mostra os testes avaliados neste estudo e as respectivas siglas.
Os testes TERLS, TELS, TEGLS, THKRLS, THKGLS, TS-B e TASB foram conduzidos no programa EQS (Bentler, 2006). O teste TMVC foi processado com o auxílio do programa Mplus (versão 7; Asparouhov & Muthén, 2010) nos estudos E1S, E2S, E3S, E4S, E1E, E2E e E3E. O programa R, pacote Lavaan (Rosseel, 2012), foi utilizado no estudo E4E tendo em vista que o modelo não convergiu no Mplus, possivelmente devido à matriz de correlação peculiar, fato outrora observado por Asparouhov (2005).
Foram comparadas as correções efetuadas entre os testes avaliados por meio dos seguintes índices: X2, X2/df (verifica o ajuste do X2 em relação aos graus de liberdade), CFI e RMSEA (Kline, 2015). Esses índices foram selecionados pelo motivo de serem ajustados por todos os testes avaliados neste estudo, além de frequentemente utilizados na prática da pesquisa. Torna-se necessário frisar que os testes TS-B e TASB possuem os mesmos valores dos índices CFI e RMSEA no programa EQS, diferenciando-se em função do valor do X2 e df (Bentler, 2006). Além disso, os valores do fator de correção do X2 de cada teste analisado no estudo foram avaliados por meio da seguinte razão: X2 estimador/X2 teste; em relação ao teste TASB, tal cálculo ponderou também o ajuste dos graus de liberdade. O modelo foi considerado com possibilidade de ser aceito em conformidade com os seguintes pontos de cortes: RMSEA ≤ 0,05 (Browne & Cudeck, 1993), CFI ≥ 0,95 e razão X2/df < 2 (Kline, 2015). Todos os dados foram analisados com base na correlação de Pearson, mesmo as amostras empíricas.
Resultados
Oito estudos foram conduzidos em razão das características amostrais. Os estudos E1S e E1E compararam os testes TERLS, TELS, TEGLS e TMVC em amostras em conformidade com os pressupostos da Teoria Elíptica (Sk < ± 1, K < ± 3); e os estudos E2S e E2E, os testes THKRLS, THKGLS e TMVC em amostras em consonância com os princípios da Teoria da Curtose Heterogênea (Sk < ± 1, K < ± 3). Por fim, nos estudos E3S, E3E, E4S e E4E, os testes TS-B, TASB e TMVC foram comparados em amostras que não cumpriram os pressupostos da Teoria da Normalidade, Elíptica e da Curtose Heterogênea, mas apresentaram características específicas de excesso de assimetria (Sk > ± 1) e/ou curtose (K > ± 3) univariadas.
Estudos E1S e E1E
Nos modelos que seguiram os princípios da Teoria Elíptica, o teste TELS apresentou o maior fator de correção do X2 no estudo E1S em comparação com outros testes avaliados; tal como o teste TMVC no estudo E1E (Tabela 1). O teste TEGLS revelou um desempenho pobre, tendo em vista que o índice CFI se mostrou subcorrigido em ambos os estudos (E1S e E1E). Além disso, os testes TERLS e TELS apresentaram os maiores valores de CFI em comparação com o teste TMVC; bem como os valores de RMSEA foram idênticos entre os testes TMVC, TERLS e TELS em ambos os estudos (E1S e E1E); mas menor para o teste TEGLS no estudo E1S.
Estudos E2S e E2E
Nos estudos E2S e E2E, em amostras que atenderam os pressupostos da Teoria da Curtose Heterogênea (Tabela 2), os fatores de correção do X2 foram maiores para o teste TMVC que para THKRLS. Porém, o teste THKRLS demonstrou o maior valor de CFI; assim como o TMVC, o menor valor de RMSEA. Por seu turno, o teste THKGLS apresentou um desempenho pobre (valores do X2 maiores que a solução GLS, o modelo independente não convergiu no estudo E2S, subcorreção do índice CFI no estudo E2E).
Os modelos foram aceitos pelo teste TMVC com base nos índices RMSEA (≤ 0,05; Browne & Cudeck, 1993) e CFI (≤ 0,95; Kline, 2015); além de rejeitados pelo teste THKRLS em função do índice RMSEA. A razão X2/df (< 2; Kline, 2015) proporcionou a rejeição de todos os modelos (E2S e E2E).
Estudos E3S, E4S, E3E e E4E
Os estudos E3S, E4S, E3E e E4E (Tabela 3), com amostras que apresentaram características específicas de excesso de curtose multivariada (índice de Mardia > 15, p ≤ 0,05; Mardia, 1970), o teste TMVC apresentou os maiores valores do fator de correção do X2, seguido dos testes TS-B e TASB. Ao se comparar o estudo E3S com o E4S e o estudo E3E com o E4E, verificou-se valores superiores do fator de correção do X2 nas amostras com maior curtose multivariada (E4S e E4E).
Em referência aos índices RMSEA e CFI, os testes TS-B, TMVC e TASB revelaram valores similares (considerando o arredondamento para duas casas decimais) em todos os estudos (E3S, E4S, E3E e E4E). Além disso, os modelos foram aceitos pelos três testes (TS-B, TMVC e TASB) em relação ao índice RMSEA (≤ 0,05; Browne & Cudeck, 1993) e CFI (≤ 0,95; Kline, 2015) nos estudos E4S, E3E e E4E, bem como rejeitados pelo índice RMSEA no estudo E3S. Também, no estudo E4E, o p-valor (≥ 0,05) gerou a aceitação dos modelos por parte dos testes TMVC e TASB, tal como rejeição pelo teste TS-B. Levando em conta a razão X2/df (< 2; Kline, 2015), o modelo do estudo E4S foi aceito pelo teste TMVC e por todos os testes (TS-B, TMVC e TASB) no estudo E4E.
Discussão
A hipótese deste estudo foi rejeitada. Na maioria dos casos, observou-se uma tendência dos testes avaliados (TERLS, TELS, TEGLS, THKRLS, THKGLS, TS-B, TASB e TMVC) de realizar correções diferenciadas dos valores do X2 mediante amostras não normais. Para a pesquisa aplicada, esses achados representam que a estimação do X2 poderá depender do teste selecionado, impactando na possibilidade de aceitação ou rejeição de um modelo (Foldnes & Olsson, 2015; Green, 2016; Kline, 2015).
Por exemplo, no estudo E1S, em comparação com a solução ML, o teste TELS tendeu a supercorreção da inflação do X2 apresentada por LS, gerando um maior valor do fator de correção do que outros testes (TERLS, TEGLS e TEGLS). Já, no estudo E4S, a razão X2/df (< 2; Kline, 2015) permitiu a aceitação do modelo estimado pelo teste TMVC, enquanto foi rejeitado pelos testes TS-B e TASB; tais achados confirmaram o estudo de Foldnes e Olsson (2015). Por sua vez, os testes TS-B, TASB e TMVC revelaram uma tendência de maior correção do X2 mediante ao aumento de curtose (Asparouhov & Muthén, 2010; Bentler, 2006). Assim, modelos falsos (estimados por ML com moderada má especificação; RMSEA = 0,06 e 0,07) podem ser aceitos pelos testes TS-B, TASB e TMVC em decorrência de extrema curtose.
Em relação aos testes que utilizaram a solução GLS (TEGLS e THKGLS), identificou-se uma determinada problemática referente à estimação do modelo independente, consequentemente, do índice CFI. O mesmo fenômeno pôde ser verificado em relação ao teste TMVC em amostras que seguiram os pressupostos da Teoria Elíptica (estudos E1S e E1E) e da Curtose Heterogênea (estudos E2E e E2S); considerando que o teste TMVC supercorrigiu os valores do X2 em relação aos testes TERLS e THKRLS, mas apresentou os menores valores do índice CFI. Contudo, no estudo E4E, o índice CFI necessitou de correção para os testes TMVC, TS-B e TASB (Brosseau-Liard & Savalei, 2014).
Pontua-se que os testes TS-B e TASB estão presentes em vários programas informatizados de SEM (e.g., EQS, R, Mplus, Lisrel). Os testes TERLS, TELS e THKRLS estão disponíveis apenas no programa EQS; tal como o TMVC, unicamente no Mplus e R (Lavaan).
Nesse aspecto, vale destacar que o modelo não convergiu com amostra com substancial excesso de curtose multivariada no programa Mplus (estudo E4E). O mesmo fenômeno foi citado no estudo de Asparouhov (2005) mediante à determinada matriz de correlação peculiar. Sendo assim, para tal condição amostral, apenas foi possível processar o teste TMVC com o pacote Lavaan (programa R), que não apresenta o índice CFI corrigido para esse teste na saída de dados (output). Como não foram localizados estudos sobre a correção do índice CFI para o teste TMVC, aplicou-se a este teste o ajuste proposto para o TS-B por Brosseau-Liard e Savalei (2014), cujos autores ressaltaram: "os índices de ajuste incremental baseados na estimação ML são afetados negativamente pela presença da não normalidade dos dados" (p. 469). Portanto, considerando as disponibilidades dos programas informatizados, em determinadas condições, os testes TS-B e TASB podem ter vantagens sobre o TMVC, já que estão disponíveis no pacote Lavaan R, que é de distribuição livre, com o índice CFI robusto corrigido.
Ademais, este estudo seguiu a proposta de Cudeck e Browne (1992) para a geração dos dados simulados. Tal proposta foi promulgada por Xia et al. (2016) como possibilitando maior controle das variáveis que "os métodos ingênuos, com a remoção e a adição de cargas ou a alteração do número de fatores" (p. 3).
Porém, níveis diferenciados de má especificação de modelos não foram testados e comparados neste estudo, contextos que podem alterar o comportamento dos testes avaliados (Xia et al., 2016). Igualmente, o tamanho amostral não foi manipulado nesta investigação. Destaca-se que o X2 e o índice RMSEA tendem a ser sensíveis ao tamanho amostral (Kline, 2015). Além disso, os estudos empíricos foram estimados através da correlação de Pearson, pertinente apenas para dados contínuos. Porém, as escalas do tipo Likert utilizadas na prática da pesquisa possuem distâncias entre os "thresholds" (pontos da escala) desconhecidas. Assim, tais escalas devem ser consideradas como dados categóricos. Nesse contexto, a correlação policórica pode ser mais apropriada (Holgado-Tello, Chacón-Moscoso, Barbero-García, & Vila-Abad, 2010). Contudo, os testes TERLS, TELS, TEGLS, THKRLS, THKGLS e TMVC aceitam somente dados contínuos (Asparouhov & Muthén, 2010; Bentler, 2006), sendo limitação desses testes. Além disso, existem outras opções de técnicas que não foram abordadas neste estudo, bem como outras variedades de amostras podem ser encontradas na realidade da pesquisa empírica. Tais aspectos podem ser apontados como as principais limitações deste estudo.
Todavia, diante do crescente uso e interesse pelas técnicas de SEM, faz-se necessário ampliar os conhecimentos sobre as vantagens e limitações de testes específicos para dados não normais, já que nem sempre a normalidade amostral pode ser alcançada na área das ciências sociais (Kline, 2015). Desse modo, o presente estudo visou expandir o conhecimento prévio sobre a temática, ressaltando as alternativas para que os pesquisadores possam tomar decisões acerca de seus conjuntos de dados de modo mais correto ou coerente.
Considerações Finais
A partir deste estudo, na maioria dos casos, observou-se uma tendência dos testes analisados (TERLS, TELS, TEGLS, THKRLS, THKGLS, TS-B, TASB e TMVC) de realizar correções diferenciadas dos valores do X2 em contextos similares. Houve também variações, mesmo que pequenas (considerando o arredondamento das casas decimais), nos valores dos índices CFI e RMSEA (excetuando os testes TS-B e TASB que possuem os mesmos valores na saída de dados do programa EQS).
Nos contextos analisados, como recomendações, sugere-se a adoção do teste TERLS (Teoria Elíptica); THKRLS (Teoria da Curtose Heterogênea) e TS-B (amostras com excesso de assimetria e/ou de curtose univariadas). Os testes TERLS e THKRLS utilizam a solução RLS, que possui o mesmo comportamento que a estimação ML (Bentler, 2006), conhecida por produzir estimativas assintoticamente imparciais, além de possuir uma vasta literatura a respeito. O teste TS-B pode ser considerado como consagrado na literatura e seu desempenho em relação à correção do X2 parece melhor retratar o nível de má especificação do modelo que o teste TMVC. Porém, pelo fato do teste TS-B aumentar a correção do X2 mediante à elevação da curtose, pode gerar a aceitação de modelos falsos moderadamente mal especificados na presença de extrema curtose. Tal fenômeno também pode ser descrito para os testes TASB e TMVC.
Seguindo a alegação de Foldnes e Olsson (2015), o teste TASB pode ser contraintuitivo aos pesquisadores por corrigir também os graus de liberdade. Contudo, o seu uso pode ser aconselhado caso a questão do ajuste dos graus de liberdade fique explicitada na investigação, tendo em vista que esse teste pode apresentar uma menor correção do X2 do que o teste TS-B; portanto, sendo mais preciso na estimação de modelos com má especificação. Já o teste TMVC pode tender a supercorreção do X2 em variadas situações amostrais, o que pode gerar maior aceitabilidade de modelos falsos com moderada má especificação que outros testes avaliados (TERLS, THKRLS, TS-B e TASB).
Por conseguinte, o teste TELS parece ter um comportamento variável; por exemplo, efetuando maior correção do X2 quando a solução LS se apresenta mais inflada em comparação com a estimação ML. Ademais, não se recomenda o uso dos testes com base no estimador GLS (TEGLS e THKGLS) em amostras que não cumpram os pressupostos da normalidade amostral em virtude da estimação do modelo independente, consequentemente, do índice CFI.
Haja vista a ausência de investigações que comparem os testes avaliados neste estudo, sugere-se a efetuação de outras pesquisas com as mesmas ou outras tipologias de amostras em modelos da CFA, levando em conta níveis diferenciados de má especificação de modelos e tamanho amostral. Também se recomenda mais esforços para a melhoria dos programas informatizados em SEM, considerando as limitações encontradas com esses programas para a realização deste estudo.
Referências
Agus, M., Penna, M, P., Peró-Cebollero, M., & Guàrdia-Olmos, J. (2016). Assessing probabilistic reasoning in Verbal-Numerical and Graphical-Pictorial Formats: An evaluation of the psychometric properties of an instrument. Eurasia Journal of Mathematics, Science & Technology Education, 12(8), 2013-2038. doi: 10.12973/eurasia.2016.1265 [ Links ]
Asparouhov, T. (2005). Sampling weights in latent variable modeling. Structural Equation Modeling: A Multidisciplinary Journal, 12(3), 411-434. doi: 10.1207/s15328007sem1203_4 [ Links ]
Asparouhov, T., & Muthén, B. (2010). Simple second order chi-square correction. Mplus technical appendix, pp. 1-8. Recuperado de https://www.statmodel.com/download/WLSMV_new_chi21.pdf [ Links ]
Bentler, P. M. (2006). EQS 6 Structural Equations program manual. Encino, CA: Multivariate Software. [ Links ]
Brosseau-Liard, P. E., & Savalei, V. (2014). Adjusting incremental fit indices for nonnormality. Multivariate Behavioral Research, 49(5), 460-470. doi: 10.1080/00273171.2014.933697 [ Links ]
Browne, M. W., & Cudeck, R. (1993). Alternative ways of assessing model fit. In K. A. Bollen & J. S. Long (Eds.), Testing structural equation models (pp. 136-162). Newbury Park, CA: Sage. [ Links ]
Cabrera, J. A. H., Olmos, J. G., & Costas, C. S. L. (1995). Acerca de la robustez de los estimadores multinormales y elípticos bajo ciertas condiciones de asimetría, tamaño muestral y complejidad de los modelos de estructuras de covarianza. Anales de Psicología, 11(2), 203-217. [ Links ]
Couto, G., Bartholomeu, D., & Montiel, J. M. (2016). Estrutura interna do Myers Briggs Type Indicator (MBTI): evidência de validade. Avaliação Psicológica, 15(1), 41-48. Recuperado de http://pepsic.bvsalud.org/scielo.php?script=sci_arttext&pid=S1677-04712016000100006&lng=pt&tlng=pt [ Links ]
Cudeck, R., & Browne, M. W. (1992). Constructing a covariance matrix that yields a specified minimizer and a specified minimum discrepancy function value. Psychometrika, 57, 357-369. doi:10.1007/BF02295424 [ Links ]
Foldnes, N., & Olsson, U. H. (2015). Correcting too much or too little? The performance of three chi-square corrections. Multivariate Behavioral Research, 50(5), 533-543. doi: 10.1080/00273171.2015.1036964 [ Links ]
Green, T. (2016). A methodological review of structural equation modeling in higher education research. Studies in Higher Education, 41(12), 2125-2155. doi: 10.1080/03075079.2015.1021670 [ Links ]
Hoben, M., Estabrooks, C. A., Squires, J. E., & Behrens, J. (2016). Factor structure, reliability and measurement invariance of the Alberta Context Tool and the Conceptual Research Utilization Scale, for German Residential long term care. Frontiers in Psychology, 7, 1339. doi: 10.3389/fpsyg.2016.01339 [ Links ]
Holgado-Tello, F. C., Chacón-Moscoso, S., Barbero-García, I., & Vila-Abad, E. (2010). Polychoric versus Pearson correlations in exploratory and confirmatory factor analysis of ordinal variables. Quality and Quantity, 44(1), 153-166. doi: 10.1007/s11135-008-9190-y [ Links ]
Hu, L., Bentler, P. M., & Kano, Y. (1992). Can test statistics in covariance structure analysis be trusted? Psychological Bulletin, 112(2), 351-362. doi: 10.1037/0033-2909.112.2.351 [ Links ]
Kano, Y., Berkane, M., & Bentler, P. M. (1990). Covariance structure analysis with heterogeneous kurtosis parameters. Biometrika, 77(3), 575-585. doi: 10.1093/biomet/77.3.575 [ Links ]
Kline, R. (2015). Principles and practice of Structural Equation Modeling. 4th ed. New York: Guilford Press. [ Links ]
Mardia, K. V. (1970). Measures of multivariate skewness and kurtosis with applications. Biometrika, 57(3), 519-530. doi: 10.1093/biomet/57.3.519 [ Links ]
Pereda, N., Arch, M., Peró, M., Guàrdia, J., & Forns, M. (2011). Assessing guilt after traumatic events. The Spanish adaptation of the Trauma-Related Guilt Inventory. European Journal of Psychological Assessment, 27(4), 251-257. doi: 10.1027/1015-5759/a000071 [ Links ]
Pornprasertmanit, S., Miller, P., Schoemann, A., Quick, C., & Jorgensen, T. (2016). Package 'simsem'. Recuperado de https://cran.r-project.org/web/packages/simsem/simsem.pdf [ Links ]
Rosseel, Y. (2012). Lavaan: An R Package for Structural Equation Modeling. Journal of Statistical Software, 48(2), 1-36. Recuperado de http://www.jstatsoft.org/v48/i02/ [ Links ]
Satorra, A., & Bentler, P. M. (1994). Corrections to test statistics and standard errors in covariance structure analysis. Em A. V. Eye & C. Clogg (Eds.), Latent variable analysis: Applications for developmental research (pp. 399-419). Newbury Park, CA: Sage. [ Links ]
Satorra, A., & Bentler, P. M. (2001). A scaled difference chi-square test statistic for moment structure analysis. Psychometrika, 66(4), 507-514. doi:10.1007/BF02296192 [ Links ]
Schumacker, R. E., & Cheevatanarak, S. A. (2000). Comparison of normal and elliptical estimation methods in Structural Equation Models. Trabalho apresentado no "Annual Meeting of the American Educational Research Association". New Orleans, LA. Recuperado de http://files.eric.ed.gov/fulltext/ED441872.pdf [ Links ]
Silva, M. A., Wendt, G. W., Argimon, I. I. L. (2017). Propriedades psicométricas das medidas do Questionário Psicossocial de Copenhague I (COPSOQ I), versão curta. Revista de Gestão da Universidade de São Paulo, 24(1), 348-359. doi: 10.1016/j.rege.2017.05.007 [ Links ]
Sullivan, P. J., Whitaker-Campbell, T., Bloom, G. A., & Falcão, W. R. (2014). A Confirmatory Factor Analysis of the Coach Behavior Scale for sport. Journal of Sport Behavior, 37(2), 190-202. [ Links ]
Xia, Y., Yung, Y., & Zhang, W. (2016). Evaluating the selection of Normal-Theory weight matrices in the Satorra-Bentler Correction of chi-square and standard errors. Structural Equation Modeling: A Multidisciplinary Journal, 23(4), 585-584. doi: 10.1080/10705511.2016.1141354 [ Links ]
 Endereço para correspondência:
Endereço para correspondência:
Rua Dr. Flores, 163, cj. 1101, 90020-120
Porto Alegre, RS
Tels.: (51) 99844-2041 / 3894-2142
E-mail: mappel@uol.com.br
Recebido em dezembro de 2016
Aceito em março de 2018
Sobre os autores
Marli Appel da Silva é psicóloga (PUCSP), Mestre e Doutora em Psicologia pela Pontifícia Universidade Católica do Rio Grande do Sul (PUCRS). Colaboradora do Grupo de Pesquisa Avaliação e Intervenção no Ciclo Vital.
Guilherme Welter Wendt é psicólogo (PUCRS), Mestre em Psicologia pela Unisinos e Doutor em Psicologia pela Universidade de Londres. Atualmente, é bolsista PDJ/CNPq na Universidade Federal do Rio Grande do Sul.
Irani Iracema de Lima Argimon é psicóloga, Mestre em Educação e Doutora em Psicologia pela Pontifícia Universidade Católica do Rio Grande do Sul (PUCRS). Coordenadora do Grupo de Pesquisa Avaliação e Intervenção no Ciclo Vital e Pesquisadora do CNPq.
Regina Maria Fernandes Lopes é psicóloga, Mestre e Doutora em Psicologia pela Pontifícia Universidade Católica do Rio Grande do Sul (PUCRS). Pós-Doutorado no Grupo de Pesquisa Avaliação e Intervenção no Ciclo Vital. Coordenadora dos Cursos de Especialização e extensão do Núcleo Médico Psicológico( PortoAlegre/RS).














