Serviços Personalizados
Journal
artigo
Indicadores
Compartilhar
Escritos sobre Educação
versão impressa ISSN 1677-9843
Escritos educ. v.5 n.1 Ibirité jun. 2006
ARTIGOS
Atividade investigativa na formação de professores das séries iniciais do ensino fundamental
Investigation tasks in an undergraduate course for teachers in the initial cycles of education
Gilmer Jacinto Peres1
Instituto Superior de Educação Anísio Teixeira
RESUMO
Este trabalho analisa as possibilidades de utilização de tarefas investigativas em um curso de formação de professores que irão atuar nos ciclos iniciais de ensino. A atividade buscava recuperar os conhecimentos acerca de seqüências numéricas dentro da perspectiva de uma atividade de investigação e foi aplicada pelo professor regente em uma turma do curso Normal Superior. Essa turma, inexperiente nos processos de realização de uma Atividade Investigativa, apresentou dificuldades iniciais, sobretudo quanto ao registro escrito das idéias. Diversas vantagens foram comprovadas, reafirmando as tarefas investigativas como um processo privilegiado na construção do conhecimento matemático.
Palavras-chave: Atividades investigativas, Seqüências numéricas, Estratégia de ensino, Formação de professores.
ABSTRACT
This work analyzes the possibilities of use investigative tasks in an undergraduate course for teachers who will work in the initial cycles of education. The activity performed aimed at recovering the knowledge concerning numerical sequences in an investigation exercise. It was applied in a specific class of Normal Undergraduate course. This group, inexperienced in the processes of accomplishment of an investigative task, presented initial difficulties mainly about written registering of the ideas. Many advantages had been proved, reaffirming the investigative tasks as a privilege process in the construction of mathematical knowledge.
Keywords: Investigation tasks, Numeric sequence, Learning strategy, Formation of teachers.
Introdução
O presente trabalho apresenta os resultados e as reflexões feitas no desenvolvimento de uma atividade investigativa que abordou o conteúdo de Progressão Aritmética aplicado em uma turma de graduação.
Dos objetivos indicados para o Ensino Fundamental, presentes nos Parâmetros Curriculares Nacionais (PCNs), destacamos a necessidade de o aluno ser motivado a:
questionar a realidade formulando-se problemas e tratando de resolvê-los, utilizando para isso o pensamento lógico , a criatividade, a intuição, a capacidade de análise crítica, selecionando procedimentos e verificando sua adequação 2.
Nesse sentido, a realização de uma atividade investigativa pode contribuir para a efetivação desse objetivo, pois investigar é descobrir relações entre objetos matemáticos conhecidos ou desconhecidos (PONTE; BROCARDO & OLIVEIRA, 2003, p.13).
Já a discussão e reflexão das potencialidades educacionais, existentes na realização de uma atividade investigativa, contribuem na formação de professores, uma vez que:
a idéia de reflexão surge associada ao modo como se lida com problemas da prática profissional, à possibilidade da pessoa aceitar um estado de incerteza e estar aberta a novas hipóteses dando, assim, forma a esses problemas, descobrindo novos caminhos, construindo e concretizando soluções. (OLIVEIRA & SERRAZINA, 2002).
Em vista disso, e com o objetivo de explorar as potencialidades das atividades investigativas na formação de professores, foi pesquisado o perfil de entendimento dos alunos acerca de seqüências numéricas. O trabalho tinha ainda como objetivo propiciar que os alunos recuperassem os conceitos acerca dessas seqüências, assim como permitir que eles vivenciassem uma nova estratégia de ensino para que pudessem, enquanto futuros profissionais, trabalhar atividades investigativas com seus alunos.
Os resultados evidenciaram similaridades dos processos de investigação entre os grupos e, no momento de socialização, a discussão de como uma atividade de investigação pode ser desenvolvida com alunos das séries iniciais trouxe uma nova forma de pensar para esses alunos. As atividades investigativas em matemática se destacam como um instrumento que pode privilegiar a construção do conhecimento matemático e, sobretudo, a formação de professores.
A investigação como ferramenta para o ensino de Matemática
A atividade de investigação propicia aos alunos momentos de pesquisa, pois eles irão descobrir padrões existentes em uma atividade proposta, o que contribui para o desenvolvimento do espírito crítico dos alunos e, consequentemente, sua auto-estima, pois leva os alunos a acreditarem em suas potencialidades. (FERREIRA, PERES & VAZ, 2006).
Nesse sentido, trabalhar a investigação na formação de professores abre para eles um novo campo que propicia um ensino mais participativo, por parte dos alunos.
A atividade de investigação tem três momentos importantes:
(i)introdução da tarefa, em que o professor faz a proposta à turma, oralmente ou por escrito, (ii) realização da investigação, individualmente, aos pares, em pequenos grupos ou com toda a turma, e (iii) discussão dos resultados, em que os alunos relatam aos colegas o trabalho realizado. (PONTE, BROCARDO, OLIVEIRA, 2003, p.25)
Trabalhar a investigação na formação de professores pode fornecer, a esses profissionais, uma nova linha de trabalho, mostrando novas estratégias de atuação que permitam um ensino mais participativo e criativo.
E, por isso, proporcionar experiências em matemática deve ser uma tarefa constante do professor. Isso adquire importância à medida que uma experiência matemática é coletiva, cultural e política, uma vez que é vivenciada por pessoas com uma história, inseridas numa cultura, parte de uma comunidade (FROTA, 2004). Portanto, uma prática que aborde investigações na formação de professores pode adquirir diferentes significados e interpretações, de acordo com o contexto no qual será realizada. Logo, atividades investigativas podem ser utilizadas em qualquer nível de ensino, conforme afirma Ferreira (2006).
Como papel do professor em uma aula de investigação, destacamos ações que ele deve desenvolver: desafiar os alunos; avaliar o desempenho; incentivar o raciocínio matemático e apoiar o trabalho 3. Em cada uma dessas ações, o professor deve acompanhar a turma sem, no entanto, fazer interferências que possam induzir ao desenvolvimento do trabalho pelos alunos. Por isso, o papel do professor, na condução de uma aula investigativa, assume várias faces. Ele deve se assegurar de que todos os alunos compreendam bem as formas de desenvolvimento e execução da atividade.
Descrição da atividade desenvolvida com o aluno
A tarefa investigativa foi elaborada por professores participantes do grupo PINEM 4, e tinha como objetivo revisitar, de modo significativo, o entendimento dos alunos acerca das Progressões Aritméticas. Essa atividade foi desenvolvida no primeiro semestre de 2006 e aplicada em uma turma de 8º período do curso Normal Superior, na disciplina Conteúdos Metodológicos do Conhecimento – Matemática VI, em uma instituição particular de Ibirité 5.
A atividade, cujos resultados são aqui analisados, consistia na apresentação de uma seqüência: [8, 11, 14, 17, 20, 23, 26, 29, 32,....], solicitando-se aos alunos que observassem os dados e registrassem as informações que pudessem obter na sua observação. Além disso, pedia-se que encontrassem, a partir dessa seqüência, o décimo termo, o vigésimo termo e o centésimo termo. Indagava-se, ainda, se os alunos seriam capazes de nomear este tipo de seqüência em matemática. Não foi entregue aos alunos nenhuma fórmula; eles deveriam, por si mesmos, encontrar os caminhos que julgassem necessários para a obtenção da resposta.
Os instrumentos utilizados na coleta dos dados foram: o registro escrito dos alunos; gravação em áudio dos momentos de socialização e os protocolos de observação do professor.
Já no momento de socialização, a forma de condução respeitou as especificidades do contexto. O momento de socialização foi utilizado, sobretudo, como um espaço de formação para a docência em que os alunos deveriam socializar o que construíram.
Na análise dos dados, optou-se por enfatizar os raciocínios dos alunos, evidenciados ao longo do processo, na tentativa de evidenciar similaridades e diferenças.
Os resultados apresentados procuram destacar o desenvolvimento dos alunos, do ponto de vista de produção de conhecimento matemático, e o engajamento nas tarefas em grupo.
Socialização e análise das estratégias utilizadas
Para a realização do trabalho, e para propiciar a discussão entre os alunos, a turma foi dividida em grupos com quatro alunos em cada um, totalizando onze grupos. Foram estabelecidas duas etapas para a realização da atividade: a primeira, para a realização da tarefa, com duração aproximada de quarenta minutos; a segunda, foi destinada à apresentação dos grupos e discussão das estratégias utilizadas na realização da tarefa; com duração aproximada de 60 minutos.
Com o intuito de verificar quais grupos já possuíam componentes que lecionam na educação infantil e nas séries iniciais do ensino fundamental, verificando se isso influenciaria na realização da tarefa, o professor constatou que nos onze grupos, praticamente todos os componentes já atuam como professores.
Como essa turma ainda não havia vivenciado um momento de investigação, após a entrega da atividade, alguns grupos solicitaram a presença do professor para mostrar se o caminho que eles estavam seguindo estava correto, conforme a fala da aluna Luciana: Professor, olhe aqui! Nós fizemos a primeira atividade dessa maneira, está correto? Ao contrário de certificar as respostas dos alunos, o professor procurou incentivá-los a buscar, por eles mesmos, as respostas.
Alguns grupos começaram a distribuir as questões entre seus componentes com o objetivo de terminar em menor tempo a atividade. Entretanto, eles perceberam, pela fala do professor, que essa atitude prejudicaria o desempenho do grupo, pois uma atividade investigativa em grupo requer que todos os componentes discutam sobre a mesma questão. O professor aproveitou esse momento para enfatizar que os grupos deveriam explorar ao máximo as observações encontradas em cada uma das questões e que, para isso, seria necessária uma maior discussão entre os componentes do grupo.
Por ser a primeira vez que essa turma participou de uma experiência com atividade investigativa, foi possível perceber certa resistência, por parte deles, em aceitar os resultados que conseguiram com a atividade. Mesmo tendo o professor ressaltado que: Essa atividade não tem uma única estratégia de desenvolvimento podendo cada grupo chegar a diferentes propostas.
Antes da apresentação, o professor conversou com a turma sobre a importância do momento de socialização, pois nele cada grupo iria relatar as estratégias realizadas na observação, construção e execução da tarefa, bem como os resultados alcançados.
O grupo liderado pela aluna Luzia destacou que a seqüência era uma série em seqüência que varia de três em três unidades. Eles utilizaram os mesmos procedimentos para resolver as letras b e c. Já na letra d ela relatou que o grupo multiplicou o décimo termo (35) por nove e disse que o centésimo termo era o número 315. Como outros grupos chegaram a resultados diferentes, perguntaram por que razão eles escolheram o número nove para multiplicar pelo último termo. Luzia respondeu:
Como nessa seqüência os números mudam de três em três, multiplicamos 3 vezes 3, chegando a nove, portanto, o número nove deve multiplicar o décimo termo para encontrarmos o centésimo. Nosso raciocínio está correto! 6
O grupo liderado pela aluna Élida se manifestou pedindo que Luzia encontrasse, com esse mesmo raciocínio, o vigésimo termo. Imediatamente, a aluna Maria Lúcia, pertencente ao grupo da aluna Luzia, foi ao quadro auxiliar sua colega pegando o segundo termo (11) e multiplicando-o por nove. Ela relatou que eles haviam completado a seqüência até o centésimo termo e, por isso, já sabiam que ele era o número sessenta e cinco. Ao reproduzir o método que eles desenvolveram, ela percebeu que não chegou ao valor desejado, virando-se para o seu grupo com um olhar frustrante: Meninas, acho que erramos!. O professor incentivou esse grupo a reavaliar suas estratégias, de modo a localizar o momento em que erraram. A aluna Eusimar gritou: Já sei! Erramos ao efetuar a conta! Eu refiz os cálculos e encontrei o erro!. A postura desses dois grupos demonstra uma maturidade das alunas na capacidade de fazer e receber críticas mediante um trabalho realizado, pois a conjectura proposta pelo grupo liderado pela aluna Luzia foi posta à prova e refutada, mediante um raciocínio indutivo.
Ao falar sobre a segunda questão, Luzia fez um questionamento, achando que toda seqüência deveria começar do número zero (0), e que o assunto que envolvia essa atividade era o de Probabilidade, Seqüência Lógica e de uma Progressão Aritmética. Terminada essa apresentação, o professor perguntou se algum aluno da turma tinha alguma consideração a ser feita. Como ninguém se manifestou, ele chamou a atenção sobre a fala desse grupo para que todos aprendessem sobre a diferença entre seqüência e série 7, e que uma seqüência não precisa, necessariamente, começar pelo número zero. O outro conceito utilizado de forma equivocada, apresentado por esse grupo, foi o de probabilidade. Para um maior esclarecimento, o professor fez uma exposição para a turma, explicando as definições e a aplicabilidade do conteúdo probabilidade. O espaço foi ainda utilizado pelo professor para destacar o papel da observação e da experimentação na construção do conhecimento matemático; problemas podem ser equacionados e desenvolvidos de maneiras variadas e com significado para o aluno.
Essa situação destaca o valor educativo que tem uma atividade de investigação, pois é um momento em que o aluno expõe o seu olhar sobre um tema proposto, permitindo ao professor lapidar esse olhar. É através de actividades matemáticas intencionais, das experiências que vive, que um indivíduo consolida, descobre ou inventa conhecimento. (SILVA, Albano et al., 1999).
As alunas Elaine e Fabiana, de grupos distintos, destacaram um mesmo raciocínio, relatando que a variação, a cada dez termos da seqüência, era sempre de trinta unidades. Fabiana disse ainda que o grupo montou uma tabela com dez colunas e percebeu essa regularidade, conforme apresentado na tabela abaixo:

Indagadas sobre os motivos que levaram à criação da tabela, esse grupo destacou que a escolha de dez colunas não foi feita de forma intencional, e que a tabela foi montada para vermos os números de forma mais organizada. (Fabiana).
Outra estratégia foi apresentada pelo grupo liderado pela aluna Lília que fez uma regra de três simples, da seguinte maneira:
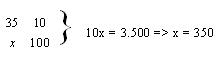
Nesse momento, o professor-pesquisador interrompeu novamente a apresentação, solicitando que toda a turma refletisse sobre a construção, tentando destacar o erro cometido pelo grupo. Houve um período de conversa entre os alunos e, como ninguém conseguiu chegar a uma resposta, o professor foi à frente da turma e explicou que a regra de três trabalha a idéia de proporção entre grandezas e que, neste caso, não existia uma proporção entre um termo da seqüência e a sua ordem.
O grupo liderado pela aluna Élida foi o único que conseguiu chegar à elaboração de uma fórmula matemática. Inicialmente, eles utilizaram a fórmula: Pn= Pn-1 + 3. Entretanto, eles relataram que, nela, seria necessário o termo P99 para determinar o termo P100. Esse grupo, então, começou a discutir e a lembrar qual seria a fórmula. Rosângela lembrou que o primeiro termo deveria estar presente. A partir daí, eles foram experimentando e verificando diferentes variações de uma fórmula até conseguir chegar a Pn= P1 + (n – 1)r 8.
Considerações para a sala de aula
No desenvolvimento da atividade pode-se perceber, por parte dos alunos, uma grande resistência à realização da atividade investigativa. Muitos alunos não se conformavam em realizar uma atividade em que o uso de estratégias pré-estabelecidas não se fazia necessário. A postura do professor, na condução desse impasse, foi de primordial importância no sucesso obtido nesse trabalho. Após ter esclarecido para toda a turma que a atividade investigativa tem uma nova característica, e essa vai além da resolução de um simples problema mediante a utilização de uma fórmula matemática, os alunos foram entendendo o sentido da tarefa e desenvolvendo o trabalho, se engajando na atividade. Essa postura dos alunos pode ser explicada pelo fato de eles nunca terem vivenciado uma atividade investigativa.
Apesar disso, em todos os grupos foi observada certa dificuldade em registrar o que pensavam, confirmando os resultados de Ferreira (2006), segundo os quais os alunos apresentaram dificuldades em registrar, comunicar, formalizar idéias e conclusões .
Em alguns grupos, chama a atenção o fato de alguns alunos completarem a seqüência até o centésimo termo, sem utilizar nenhuma outra estratégia. Tal fato pode nos levar a refletir acerca da importância de uma formação matemática em que as fórmulas se apresentem como resultados de sistematização e mais ainda que os alunos sejam conduzidos de forma a atribuir significado a essas fórmulas.
A grande maioria dos grupos mergulhou mais no desenvolvimento da atividade, envolvendo-se na busca de estratégias próprias de solução.
Os resultados encontrados nos levam a pensar que uma atividade de investigação, elaborada e desenvolvida junto a alunos que futuramente irão atuar em sala de aula, precisa incorporar características que levem em conta esse interesse. O envolvimento em um processo de investigação e descoberta requer tempo. Entender que a construção do conhecimento matemático, através de experiências que permitem o desenvolvimento de diversas situações, leva-nos a perceber que a matemática se aprende fazendo e, não, apenas memorizando fórmulas.
Nesse sentido, o papel exercido pelo professor parece ser imprescindível.
Referências
FERREIRA, A. R. Atividades investigativas em EJA: um estudo sobre potências e funções exponenciais. SIPEMAT, 2006. [ Links ]
FERREIRA, A. R.; PERES, G. J.; VAZ, I. C. Construindo significados para o conhecimento matemático através de atividades investigativas em diferentes modalidades de ensino. In: IV Encontro Mineiro de Educação Matemática, Diamantina, 2006, Anais no prelo. [ Links ]
FROTA, M.C.R. Experiência matemática e investigação matemática. V CIBEM, Porto, Portugal, jul. 2005. Disponível em: http://www.matematica.pucminas.br/ Grupos de Trabalho/Grupo PINEM.
OLIVEIRA, Isolina; SERRAZINA, Lurdes. A reflexão e o professor como investigador. In: GTI – Grupo de Trabalho de Investigação (org.). Reflectir e investigar sobre a prática profissional. Portugal: APM, 2002, p.29-42. [ Links ]
PONTE, J. P. Investigar, ensinar e aprender. Actas do ProfMat, Lisboa, 2003b Disponível em: http://www.educ.fc.ul.pt/docentes/jponte/ docs-pt/03-Ponte(Profmat).pdf.
et BROCARDO, J.; OLIVEIRA, H. Investigações matemáticas na sala de aula. Belo Horizonte: Autêntica, 2003. [ Links ]
SILVA, A. et al. O currículo de matemática e as actividades de investigação. In: P. Abrantes, et al. (Eds.), Investigações matemáticas na aula e no currículo. Lisboa: Projecto MPT e APM, 1999. p. 69-85. [ Links ]
Recebido em: 29/03/2006
Aceito em: 16/04/2006
1 Mestrando em Ensino de Matemática - PUC Minas. Professor do Instituto Superior de Educação Anísio Teixeira. E-mail: professorgilmer@terra.com.br
2 BRASIL – MEC/SEF. Parâmetros Curriculares Nacionais: matemática – Secretaria de Educação Fundamental. 2.ed.; Rio: DP&A, 2000.
3 Ver (PONTE, BROCARDO, OLIVEIRA, 2003, p.47 - 53).
4 GRUPO PINEM – Práticas Investigativas em Ensino de Matemática da PUC Minas.
5 Instituto Superior de Educação Anísio Teixeira – ISEAT.
6 Esse grupo entendeu que, como para números de 0 à 99 a variação era de 3 unidades, nos números entre 100 e 999 a variação deveria ser de 9 unidades (3 x 3).
7 Seqüência numérica: sucessão numérica que obedece a uma fórmula de recorrência; Série: soma dos n termos de uma seqüência.
8 Termo Geral de uma Progressão Aritmética.














