Serviços Personalizados
Journal
artigo
Indicadores
Compartilhar
Ciências & Cognição
versão On-line ISSN 1806-5821
Ciênc. cogn. v.14 n.3 Rio de Janeiro nov. 2009
ARTIGO CIENTÍFICO
A modelagem matemática através de conceitos científicos
The mathematical modeling through scientific concepts
Helisângela Ramos da Costa
Departamento de Matemática, Universidade do Estado do Amazonas (UEA), Manaus, Amazonas, Brasil
RESUMO
Este artigo tem como objetivo apresentar uma proposta que utiliza a modelagem matemática para promover uma aprendizagem significativa dos conceitos matemáticos de limite e continuidade a partir de conceitos científicos. Para isso, a proposta apóia-se nos princípios defendidos pela Educação Matemática, pelos Parâmetros Curriculares Nacionais e pela abordagem construtivista de Ausubel. O tema científico escolhido para elaborar as situaçõesproblema, e assim, explorar os conceitos matemáticos, foi a Lei de Transformação dos Gases de Charles-Gay Lussac. As situações-problema elaboradas propiciam o desenvolvimento de capacidades como observação, análise, interpretação e validação de dados. Além disso, é capaz de promover um ambiente estimulante de educação científica e tecnológica mobilizando o potencial criativo dos estudantes. Dessa forma, acredita-se que a proposta permite ao estudante utilizar a modelagem matemática como uma ferramenta para compreender os conceitos matemáticos e para resolver problemas de diversas áreas do conhecimento.
Palavras-chave: modelagem matemática; aprendizagem significativa; conceitos científicos.
ABSTRACT
This article aims to present a proposal that uses mathematical modeling to promote a meaningful learning of mathematical concepts of limits and continuity from scientific concepts. For this reason, the proposal is based on the principles defended by the Mathematics Education by the National Curriculum Parameters and the constructivist approach to Ausubel. The scientific theme chosen to develop the problem situations, and thus explore the mathematical concepts, it was the Law of Transformation of gases Charles Gay-Lussac. The situations problem developed provide building capacity as observation, analysis, interpretation and validation of data. Moreover, it is able to promote a stimulating environment for scientific and technological education mobilizing the creative potential of students. Thus, it is believed that the proposal allows the student to use mathematical modeling as a tool to understand the mathematical concepts and solving problem in various fields.
Keywords: mathematical modeling; meaningful learning; scientific concepts.
1. Introdução
A modelagem matemática está presente na vida do homem desde os tempos remotos, ao utilizar conhecimentos matemáticos para modelar e resolver situações problemáticas com as quais se deparava. Quando esses conhecimentos se mostravam insuficientes, a busca de novos objetos e/ou relações matemáticas fazia-se necessário (Costa e Ghedin, 2007). Eis alguns modelos importantes criados pelo homem: a roda inventada pelos sumérios no ano 3000 a.C.; o modelo criado por Eratóstenes (276-196 a.C) para calcular a circunferência da Terra e os modelos criados por Galileu Galilei (1564-1642) para a queda dos corpos e para o movimento parabólico dos projéteis.
Mas, apesar das evidências de que a Matemática foi e ainda é desenvolvida a partir das necessidades humanas, no processo educativo predomina uma postura formal assumida por grande parte dos educadores, onde o conhecimento matemático é aceito somente dentro do terreno da Matemática, não interessando questões como "para que serve isso?". Mas, essa orientação formalista vem sendo questionada.
A falta de integração entre as posturas formal e aplicada frente à Matemática é ressaltada por D'Ambrósio (1999a: 01) ao considerar que "o problema maior do ensino de ciências e matemática é o fato das mesmas serem apresentadas de forma Desinteressante, Obsoleta e Inútil, e isso DÓI para o jovem". Uma discussão a ser levantada aqui é que a postura epistemológica do professor que apresenta algumas visões distorcidas da ciência pode influenciar na carência de propostas metodológicas que privilegiem o desenvolvimento da criatividade e das capacidades cognitivas.
Dentre as visões deformadas da ciência, Cachapuz (2005) destaca: a descontextualização; a concepção individualista e elitista; a concepção empiro-indutivista e ateórica (considera que a essência do trabalho científico está na experimentação, deixando em segundo plano a concepção teórica); a visão rígida, algorítimica e infalível; a visão aproblemática e ahistórica (considera que os conhecimentos são apresentados sem preocupação com os problemas que lhe deram origem e quem contribuiu para solucioná-los); visão exclusivamente analítica (considera que não é necessário estabelecer relações dos problemas abordados com outros campos da ciência) e visão acumulativa (considera que não é necessário privilegiar os processos de mudança de paradigmas científicos).
A fim de romper com essas barreiras epistemológicas, a modelagem matemática surge para desenvolver ambientes de investigação em sala de aula que privilegiem a construção e aplicação dos conceitos, respeitando os aspectos históricos, teóricos e de relacionamento com outras ciências. Por isso, o artigo apresenta uma proposta baseada na modelagem matemática, com o objetivo de promover uma aprendizagem significativa dos conceitos matemáticos de limite e continuidade a partir do tema científico: A Lei de Transformação dos Gases de Charles-Gay Lussac. Mas, para elaborar a proposta foi necessário conhecer as características, potencialidades, limitações e etapas da modelagem matemática quando aplicada em cursos regulares.
2. Modelagem matemática: características, potencialidades, limitações e etapas metodológicas
Como método científico a modelagem apresenta algumas características de investigação que também se fazem presentes quando aplicada no ensino. Conforme Ponte e colaboradores (2005: 13), investigar em Matemática "é descobrir relações entre objetos matemáticos conhecidos ou desconhecidos, procurando identificar as respectivas propriedades". Envolve quatro momentos: exploração e formulação de questões, organização de dados e formulação de conjecturas, realização de testes e reformulação das conjecturas, justificação e avaliação.
Diante dessas características investigativas apresenta algumas potencialidades que permite aos alunos desenvolver uma aprendizagem significativa. Dentre os argumentos favoráveis a sua utilização no ensino, Barbosa (2004a, 2004b), Bassanezi (2004) e Monteiro e Junior (2001) destacam:
• A motivação, uma vez que os estudantes são convidados a participar de um ambiente de investigação por meio da Matemática, situações oriundas de outras áreas da realidade. Conforme (Barbosa, 2001: 06-07). "A investigação é o caminho pelo qual a indagação se faz. É a busca, seleção, organização e manipulação de informações." Envolve quatro momentos: exploração e formulação de questões, organização de dados e formulação de conjecturas, realização de testes e reformulação das conjecturas, justificação e avaliação. (Ponte et al., 2005). É neste sentido que este ambiente se aproxima daquele proposto para o ensino de Ciências.
• A facilitação da aprendizagem, pois, na concepção vygotskyana, o individuo só se desenvolve plenamente como suporte de outros indivíduos da sua cultura, ocupando uma posição de destaque a troca de experiências entre alunos e, também, entre alunos e professores (Vygotsky, 1991).
• O desenvolvimento da competência crítica e de habilidades gerais de exploração, preparando o estudante para a vida como cidadãos atuantes na sociedade, competentes para construir juízos próprios, reconhecer problemas e buscar soluções, utilizando os conceitos matemáticos em diferentes áreas.
Embora sejam vários os argumentos favoráveis ao uso da modelagem, Bassanezi (2004) e Monteiro e Junior (2001) destacam algumas dificuldades a serem enfrentadas para que ela possa ser utilizada em cursos regulares, tais como:
• A necessidade de tempo para planejar as atividades de modelagem, preferindo, assim, restringir suas aulas ao conteúdo do livro didático, que geralmente apresenta a seqüência: teoria, exemplos, exercícios de fixação e problemas de aplicação.
• A mudança de postura dos estudantes exigida pelo ambiente de modelagem, de passiva para ativa, pois acostumados a ver o professor como transmissor de conhecimentos, quando colocados no centro do processo ensino-aprendizagem, muitas vezes oferece resistência ao uso da modelagem. Acostumados a aplicarem algoritmos e fórmulas, conseguem atingir o seu objetivo (na maioria das vezes, é obter boa nota) com problemas mais simples (estritamente matemáticos).
• A falta de conhecimento pelos professores para desenvolver atividades de modelagem, seja por falta de conhecimento do processo ou por medo de se depararem em situações embaraçosas devido desconhecerem as áreas onde as aplicações matemáticas foram abordadas. Esse último fator reflete mais uma vez a necessidade de uma reorientação epistemológica dos professores no que diz respeito à visão descontextualizada, algorítmica, infalível e analítica da ciência.
Mas, alguns dos obstáculos citados podem ser minimizados na medida em que os temas e situação-problema escolhidos sejam motivadores; não apresentem, a princípio, grande grau de dificuldade tanto para o aluno quanto para o professor, especialmente se este não tiver experiência em atividades de modelagem matemática; o professor esteja atento e auxilie os alunos na condução das atividades e esteja disposto a pesquisar temas de outras áreas e de relevância social que possam ser fontes de investigação matemática (Monteiro e Junior, 2001).
Além disso, é importante que o professor conheça as etapas da modelagem para que possa definir os responsáveis (aluno e/ou professor) pelas atividades de cada etapa e adequar sua aplicação à realidade da turma, considerando aspectos como: os conceitos prévios estudados pelos alunos; o conteúdo programático a ser desenvolvido; os objetivos conceituais, de atitudes e habilidades; o tempo para sua aplicação e a experiência do professor com atividades de modelagem.
As etapas para aplicação da modelagem matemática em cursos regulares são apresentadas por autores como Biembengut e Hein (2003), Bassanezi (2004) e Rosa (20001 apudRosa 2005) com características comuns, exceto o diagnóstico, encontrado apenas em Biembengut e Hein (2003). Estas etapas são sugeridas como uma forma de minimizar as dificuldades para sua aplicação. Um esquema das principais etapas é apresentado na figura 1.
No diagnóstico o professor deve fazer um levantamento sobre a realidade sócio-econômica, os interesses e metas dos alunos, o conhecimento matemático que possuem; considerar o tempo disponível para realização de trabalho extraclasse e destinar um número de horas-aula para orientação do trabalho.
1) Escolha do tema:com base no diagnóstico, o(s) tema(s) pode(m) ser escolhido(s) pelo professor, pelos alunos ou em conjunto. Biembengut e Hein (2003) sugere que o professor selecione possíveis temas para que os alunos não escolham um tema inadequado ao desenvolvimento do conteúdo desejado ou um tema complexo em relação ao conhecimento matemático que possuem. Caso sejam escolhidos vários temas, os estudantes devem ser distribuídos em grupos que possuem o mesmo interesse de pesquisa.
2) Interação com o tema:faz-se um estudo (coleta de informações) sobre o tema escolhido através de visitas técnicas a órgãos e profissionais, pesquisa na internet, livros, revistas, entrevistas, reportagens de jornais ou experimentos. Caso os alunos não tenham acesso à internet, ou para otimizar o tempo, o professor pode fornecer os dados (Rosa, 2005; Barbosa, 2001, 2004a).
Os estudantes devem propor questões que de uma maneira geral, inicialmente são bastante simples, podendo ser solucionadas utilizando conceitos matemáticos que já conhecem. O professor pode, então, ajudá-los a formular questões mais complexas que permitam desenvolver o novo conteúdo programático e possibilite fazer generalizações com a utilização de analogias com situações correlatas (Rosa, 2005).
3) Formulação do problema:o professor deve auxiliar os estudantes na formulação do(s) problema(s) matemático(s) relacionado(s) ao tema, das hipóteses utilizando a simbologia adequada e descrevendo as relações em termos matemáticos, uma vez que a transferência da linguagem verbal para linguagem matemática é na maioria das vezes uma tarefa que exige esforço dos alunos. Na medida em que se está formulando ou resolvendo o problema, o conteúdo programático vai sendo desenvolvido. Deste modo, a matemática vai sendo desenvolvida à medida que se faz necessária (Rosa, 2005).
4) Elaboração dos modelos matemáticos:o professor deve orientar os estudantes na construção do modelo devido sua natureza conceitual e abstrata. Deve-se indicar porque algumas características do modelo foram consideradas e outras rejeitadas. A partir do modelo obtido, os estudantes podem elaborar estratégias que os auxiliam na explicação, análise e resolução do problema.
5) Resolução dos problemas matemáticos:nesta etapa, os conceitos matemáticos que foram identificados na elaboração dos modelos matemáticos devem ser sistematizados. (Rosa, 2005). O professor deve mostrar outros exemplos e propor exercícios para que o conteúdo não se restrinja ao modelo obtido, permitindo assim, que o aluno aprimore a apreensão dos conceitos (Biembengut e Hein, 2003).
6) Interpretação da solução:cada grupo/estudante deve avaliar e interpretar a solução, verificando a adequação da solução obtida ao modelo utilizado. A interpretação da solução envolve uma retomada dos conceitos matemáticos que estão relacionados ao problema. Por isso, recomenda-se que a interpretação do resultado obtido com a resolução do modelo matemático seja realizada de diferentes maneiras: analítica, gráfica, geométrica ou algébrica (Rosa, 2005).
7) Validação da solução:o resultado obtido pelo modelo matemático é comparado com o sistema "real".
8) Exposição escrita e oral do trabalho:esta etapa é importante, pois muitas vezes, os alunos não possuem um registro escrito organizado daquilo que fizeram e têm muitas limitações na comunicação matemática oral (Ponte et al., 2005). Cada grupo deve elaborar um relatório contendo o objetivo do trabalho, a justificativa e referencial teórico do tema escolhido; a definição do problema, das hipóteses e questões levantadas; os procedimentos utilizados para organizar os dados, validar as conjecturas, obter o modelo e solucionar o problema; as tentativas realizadas e dificuldades encontradas; as conclusões do trabalho e a bibliografia (Biembengut e Hein, 2003; Ponte et al., 2005). Após elaboração do relatório, os grupos devem expor os resultados da pesquisa para os demais, pois eles podem colaborar com sugestões para a modificação ou aperfeiçoamento dos modelos obtidos.
9) Avaliação:devem ser avaliados critérios como organização, clareza e criatividade (Ponte et al.2005). Uma sugestão dada por (Rosa, 2005), é que cada grupo seja avaliado pelo desempenho global e cada aluno seja avaliado pelos elementos de cada grupo e pelos elementos do próprio grupo. O professor avalia as apresentações e os relatórios apresentados pelos grupos.
Ao conhecer as etapas da modelagem matemática e os princípios epistemológicos de sua área de conhecimento, o professor de Matemática pode propor atividades de modelagem que incorporem conceitos científicos. Na seção a seguir serão apresentadas algumas contribuições de trabalhos realizados por outros autores nesse sentido.
3. Algumas contribuições da modelagem matemática na abordagem de conceitos científicos
Embora nos últimos anos, há indicação de avanços na busca de superação do reducionismo conceitual, tem se buscado novos paradigmas para a melhoria do ensino e aprendizagem das Ciências da Natureza e Matemática que possam favorecer a efetividade das propostas voltadas à construção do conhecimento em torno do modelo de aprendizagem como investigação (Gurgel, 2002).
Vasconcelos e colaboradores (2005) considera que muitos dos estudantes do ensino médio no Brasil, que possuem dificuldades em compreender conteúdos que envolvam Física e Matemática, não desenvolveram atividades de modelagem no ensino fundamental enquanto resolução de problemas.
Conforme Fernandes e Matos (2004), a Matemática, muitas vezes, surge incorporada nas ferramentas e nas práticas, mas não é visível a quem utiliza. Os alunos sabem, por exemplo, resolver equações na aula de Matemática e não as sabem resolver na aula de Física.
Estudos feitos por pesquisadores como Cachapuz e colaboradores (2005) demonstram que a ciência é ensinada, basicamente, por transmissão dos conhecimentos científicos já elaborados, sem permitir aos estudantes a aproximação com a forma como esses conhecimentos são construídos, levando a visões distorcidas da ciência, que criam desinteresse e constituem-se em obstáculos para o aprendizado dos estudantes.
Essas visões distorcidas ou deformadas foram ao longo do tempo se consolidando socialmente pela própria educação científica através da visão descontextualizada, da concepção individualista e elitista, da concepção empiro-indutivista e ateórica, da visão rígida, algorítimica, infalível, da visão aproblemática e ahistórica, da visão exclusivamente analítica e da visão acumulativa da ciência. Mas, os autores ressaltam que estas visões, socialmente aceitas, não se constituem características da ciência, mas visões deformadas da ciência e da tecnologia.
D'Ambrósio (1999b, 1999c) um dos principais defensores da Educação Matemática, onde está inserida a modelagem matemática, sugere trazer mais Ciências para a educação dos matemáticos e mais Matemática para os futuros cientistas e engenheiros, o que requer novos currículos e maior acesso às técnicas e idéias matemáticas.
Assim, a modelagem insere-se na política de educação científica defendida pela UNESCO (2005:06):
"O desenvolvimento de uma política de educação cientifica visa a promover a inclusão social e a melhoria da qualidade da educação, de modo a contribuir para que crianças e jovens desenvolvam as competências, habilidades, atitudes e valores que lhes permitam aprender e continuar aprendendo, compreender, questionar, interagir, tomar decisões e transformar o mundo em que vivem, promovendo valores sociais e culturais de uma sociedade solidária pacifica, participativa e democrática."
Mas, para que essa política de educação científica se desenvolva, é necessário assumir uma mudança na perspectiva metodológica, em que a escola deva propor atividades que envolvam seus estudantes na aprendizagem, a partir de situações-problema com temas de seu interesse e que tenham relevância social.
As características desta proposta também são defendidas por Cachapuz e colaboradores (2005), sendo denominada de investigação orientada. Tanto a investigação orientada como a modelagem permite estabelecer 'pontes' com outros campos da ciência, modificar crenças e atitudes (pessoais ou sociais), concepções sobre a ciência além de construir novos conhecimentos. Em ambas as propostas, o professor tem o papel de orientador do processo.
Hurd (20002 apudKfouri, 2006: 02) também chama a atenção para a necessidade de uma nova postura em relação ao Ensino de Ciências.
"O ensino de ciências do século 21 deve ser organizado em termos de problemas, projetos, investigações e experimentos relativos aos assuntos de sua própria cultura, de forma que os estudantes participem da tomada de decisão, formando julgamentos, e escolhendo ações que envolvem elementos de risco, incerteza, valores e ética; fazendo uso de conhecimentos científicos e tecnológicos."
Ao ressaltar que grande parte dos modelos utilizados em Física, Química e Biologia são modelos dinâmicos2, Vasconcelos e colaboradores (2005), destaca que a modelagem matemática propicia a construção e manipulação destes modelos de forma clara e concisa.
"O uso da modelagem matemática no ensino de ciências, em qualquer nível, pode ser uma forma de trazer questionamentos a alunos e professores, despertando a reflexão e o espírito crítico tão necessários para ter educaçãocientífica ao invés de treinamento para resolução de problemas padronizados." (Cury, 2003: 15)
A modelagem matemática, na perspectiva da interdisciplinaridade, também contempla as competências sugeridas pelos Parâmetros Curriculares Nacionais do Ensino Médio (PCNEM) na medida em que permite:
• Identificar e relacionar os dados, interpretar informações relevantes em uma dada situação-problema, sendo apresentados em diferentes linguagens e representações;
• Reconhecer a natureza e situar o objeto de estudo dentro dos diferentes campos da Matemática e das demais ciências;
• Utilizar, elaborar e interpretar modelos e representações matemáticas para análise de situações-problema;
• Identificar regularidades para estabelecer regras, algoritmos e propriedades;
• Analisar os noticiários e artigos relativos à ciência e tecnologia, identificando o tema em questão e interpretando, com objetividade, seus significados;
• Expressar as idéias com clareza, utilizando a linguagem matemática;
• Reconhecer a contribuição do conhecimento matemático, físico, químico e biológico no desenvolvimento da tecnologia, nas relações sociais de cada época, nas transformações e na criação de novas necessidades, nas condições de vida e suas implicações no mundo cotidiano;
• Compreender a responsabilidade social associada à aquisição e uso do conhecimento matemático, fazendo-o sentir-se mobilizado para diferentes ações (Brasil, 1999a).
Autores como Veit e Teodoro (2002); Araújo e colaboradores (2004) defendem o uso da modelagem para melhor compreender o conteúdo de Física principalmente quando aliada ao uso de tecnologias. Defendem o uso do software Modellusdesenvolvido para realização de atividades de modelagem no ensino de Ciências e Matemática. Esses autores apresentam como maior vantagem do software além da gratuidade a linguagem utilizada ser bastante semelhante àquela usada para descrever um modelo no papel, tanto para funções quanto para equações diferenciais ordinárias, conforme mostra a figura 2.
A equação utilizada no software 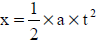 é utilizada para que o aluno observe o comportamento de um objeto, representado por um carro, ao deslocar-se no decorrer do tempo segundo a equação dada. Como a equação fornecida depende do parâmetro aceleração "a", seu valor foi fixado em 10m/s2. O software apresenta duas formas simultâneas de visualização: tabular e gráfica. Assim, o aluno pode observar através da variação dos valores na tabela (parte inferior esquerda da Figura 02) e através do gráfico representado pela parábola com cavidade para cima. Para compreender o comportamento da velocidade, o aluno deve relacionar o conceito de velocidade com a derivada da função posição em relação ao tempo, que pode ser visualizado através do gráfico representado pela reta que passa pela origem. O professor deve chamar a atenção do aluno para o fato de que essa característica gráfica da velocidade sempre irá ocorrer independente do valor dado para o parâmetro "a", uma vez que ao derivar x(t) terá sempre uma função linear dada por v(t)=axt. Ou seja, "v" e "t" são grandezas diretamente proporcionais sendo a constante de proporcionalidade dada por "a".
é utilizada para que o aluno observe o comportamento de um objeto, representado por um carro, ao deslocar-se no decorrer do tempo segundo a equação dada. Como a equação fornecida depende do parâmetro aceleração "a", seu valor foi fixado em 10m/s2. O software apresenta duas formas simultâneas de visualização: tabular e gráfica. Assim, o aluno pode observar através da variação dos valores na tabela (parte inferior esquerda da Figura 02) e através do gráfico representado pela parábola com cavidade para cima. Para compreender o comportamento da velocidade, o aluno deve relacionar o conceito de velocidade com a derivada da função posição em relação ao tempo, que pode ser visualizado através do gráfico representado pela reta que passa pela origem. O professor deve chamar a atenção do aluno para o fato de que essa característica gráfica da velocidade sempre irá ocorrer independente do valor dado para o parâmetro "a", uma vez que ao derivar x(t) terá sempre uma função linear dada por v(t)=axt. Ou seja, "v" e "t" são grandezas diretamente proporcionais sendo a constante de proporcionalidade dada por "a".
Uma outra experiência com modelagem matemática no ensino de Ciências é relatada por Cury (2003) onde as atividades propostas incluíam conceitos de Física, Química, Biologia e Matemática. Dentre os modelos desenvolvidos destacam-se: o número provável de filhotes, nascidos ao final de duas gestações, em uma criação de chinchilas; as relações entre valor nutricional e despesas com a merenda em uma escola de ensino básico da rede pública; o tempo mínimo para estacionar um carro em uma garagem de um prédio e a massa atingida por uma determinada espécie de peixes em uma indústria pesqueira de um município de Santa Catarina para verificar o tempo ótimo para a captura.
Questões ambientais também tem sido frequentemente abordadas em atividades de modelagem matemática no ensino de Matemática por autores como Caldeira (1998), Ferreira (2003) e Chaves (2005). Através da análise de questões ambientais utilizando a matemática os autores mostraram que é possível fazer com que os estudantes compreendam a utilidade da Matemática e a partir do contato com a natureza, divulgação dos conhecimentos ecológicos e interpretação dos fenômenos naturais os alunos sentirão naturalmente a necessidade de sua conservação.
Por exemplo, a partir do tema água, Ferreira propôs uma atividade onde os estudantes analisassem o comportamento populacional em relação ao consumo de água no período de 1995 a 2000 a partir de dados obtidos junto à Companhia responsável pelo abastecimento de água de Rio Claro conforme mostram a tabela 1 e a figura 3.
Observa-se que foram exploradas as representações através de tabela e de gráfico do conceito de função, onde se verifica que o consumo de água aumentou até 1999, superando o crescimento populacional entre 1997 e 1999. A partir de 1999 apesar de a população ter continuado seu crescimento, o consumo tendeu a diminuir. O professor pode levantar uma discussão sobre possíveis motivos que justifiquem essa diminuição do consumo de água, como a conscientização da comunidade para não desperdiçar água, aumento da taxa de contribuição pelo seu consumo, etc.
Um outro exemplo é encontrado no trabalho proposto por Stieler e Bisognin (2006) intitulado "Radiação Solar e Ultravioleta e a Modelagem Matemática". Em uma das situações-problema apresentadas, o autor encontra uma função para modelar a variação da radiação solar durante o dia. Para isso, foram obtidos dados no laboratório do Instituto nacional de (INPE) sobre o índice de raio ultravioleta (IUV) em um determinado dia sem interferências de nuvens da cidade de Santa Maria, no Rio Grande do Sul. Através do Excel foi obtida a função quadrática dada por: I(t)= -0,5211t2 + 13,192 t - 71,809, onde I(t) representa a variação do IUV do dia em função do tempo t, em horas. O valor máximo obtido para a função mostrou que a máxima radiação solar foi atingida às 12 horas e 39 minutos. Deste modo, chamou atenção para a importância de se verificar o tempo que cada pessoa pode ficar exposta ao sol de acordo com o horário. Outras variáveis também foram consideradas como o tipo de pele.
Com a breve descrição dessas atividades, verifica-se que o foco de seus trabalhos foi aplicar os conceitos relacionados à função em diversas situações-problema com contextos científicos e não construí-los junto com os alunos, diferente do que pretende a proposta apresentada na próxima seção.
4. Uma proposta para o ensino e a aprendizagem do conceito de limite e continuidade
A proposta apóia-se em abordagens construtivistas do conhecimento como a Teoria de Aprendizagem Significativa de Ausubel, onde os conceitos relacionados ao limite e à continuidade serão construídos a partir dos conceitos prévios de duas áreas do conhecimento: Matemática e Ciências. Apresenta-se como uma proposta possível de ser aplicada em cursos regulares respeitando o currículo de matemática escolar e algumas limitações como o tempo disponível para aplicação de atividades de modelagem matemática. A relevância da proposta está na construção dos conceitos matemáticos de limite e continuidade a partir da necessidade apontada pelas situações-problema contextualizadas, o que não ocorre em várias pesquisas, como de Ferreira (2003) e Chaves (2005), onde apenas aplicam os conceitos matemáticos em situações-problema contextualizadas ou a partir de temas de outras áreas do conhecimento.
Na Matemática são utilizados os conceitos prévios de funções e em Ciências são utilizados conceitos relacionados às transformações gasosas, que são pressão, temperatura e volume através de uma das leis de transformação dos gases, a de Charles-Gay Lussac.
Conforme Moreira (1999) a aprendizagem significativa ocorre quando uma nova informação é assimilada através da interação com conceitos relevantes preexistentes na estrutura cognitiva do aprendiz. E para que isso ocorra, são necessárias duas condições básicas: a) as informações a serem assimiladas devem ser potencialmente significativas para o aprendiz, ou seja, ele deve ter em sua estrutura cognitiva conceitos relacionáveis, de forma substantiva e não-arbitrária vinculados diretamente com o conhecimento a ser aprendido, o qual, por sua vez, deve ter significado lógico. b) o aprendiz deve manifestar uma disposição para relacionar o novo material, de forma substantiva e não arbitrária, à sua estrutura cognitiva.
A proposta foi elaborada para ser aplicada por professores de Matemática, que lecionam tanto no 3º ano do ensino médio ou em cursos de nível superior e que possuem a disciplina Cálculo Diferencial e Integral ou outra equivalente onde o conteúdo limite se faça presente na ementa.
A utilização da informática também é um recurso que foi utilizado para modelar e interpretar as situações-problema de modo mais dinâmico.
De acordo com Scucuglia (2006: 04) "As tecnologias informáticas possibilitam novas abordagens [...] que não refutam o aspecto dedutivo, mas buscam privilegiar as inferências informais, como a visualização e a experimentação".
O software escolhido para ser utilizado no desenvolvimento da atividade de ensino foi o Winplot, devido respeitar algumas características defendidas pelo Programa Nacional de Informática na Educação (PROINFO) que promoveu, em maio de 1999, o IV Encontro Nacional do PROINFO. Nesse documento constam alguns requisitos que, de maneira geral, um softwareeducacional deve atender. Dentre eles destacam-se (Brasil, 1999b):
a) Favorecer a construção do conhecimento a partir da ação-reflexão-ação;
b) Possibilitar o registro e consulta das ações desenvolvidas, permitindo o processo de depuração;
c) Desafiar o usuário através de atividades que incentivem o estabelecimento de hipóteses, a interação, a reflexão, a troca e a construção do seu conhecimento;
d) Apresentar atividades variadas, contemplando diversos níveis de complexidade.
Além desses requisitos, é um software freeware(gratuito), que faz parte da Peanut Softwares(uma coleção de softwaresmatemáticos freewares),o que permite ser utilizado em qualquer instituição de ensino que tenha laboratório de informática ou que tenha projetor multimídia e uma CPU disponível para a sala de aula além de permitir que os alunos utilizem em suas próprias casas. O softwarepossui uma versão no idioma português. Trata-se de um programa gráfico de propósito geral, que permite o traçado e animação de gráficos em 2D e em 3D, através de diversos tipos de equações (explícitas, implícitas, paramétricas e outras). Permite, assim, explorar as múltiplas representações de funções (algébrica, tabular e gráfica), realizar simulações (através do traçado simultâneo de gráficos de uma família de equações de curvas, considerando determinados parâmetros), dentre outros.
O professor pode iniciar a abordagem do conteúdo através de uma contextualização histórica, destacando matemáticos que contribuíram para o desenvolvimento do conceito de limite. Dessa forma, permite que o aluno compreenda a evolução dos conhecimentos de acordo com a contribuição de vários estudiosos. Dentre eles, destaca-se Augustin Louis Cauchy (1789-1857) que, embora tenha ressaltado o conceito de limite de outro matemático D'Alembert, deu-lhe um caráter aritmético mais preciso "Quando valores sucessivos atribuídos a uma variável se aproximam indefinidamente de um valor fixo de modo a acabar diferindo dele por tão pouco quanto se queira, este último chama-se o limite de todos". (Boyer, 1999: 355).
A seguir são apresentadas 6 situações-problema para abordar o conceito de limite.
Questão 1:Considerando a função 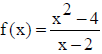 qual o valor de f(2)?
qual o valor de f(2)?
Para responder a pergunta, o aluno terá que reconhecer que o conceito prévio a ser utilizado para resolver a questão é o domínio de uma função, pois antes de saber se existe a sua imagem, deve saber se o valor especificado para sua variável dependente pertence ao seu domínio. Neste caso, a função não está definida para x≠2. Logo, deve concluir que não existe f(2). O professor pode solicitar que verifiquem o comportamento da função para x ≠2, porém próximo de 2.
Questão 2:Como se comporta a função para valores muito próximos de 2?
Para isso, os alunos devem aplicar na função valores próximos de 2. O professor pode sugerir que construam uma tabela relacionando x e f(x). Como cada aluno deve construir sua tabela, o intervalo escolhido por eles pode ser diferente. Mas, independente do intervalo definido para x, desde que sejam escolhidos valores próximos de 2, o resultado da imagem da função aproxima-se de 4 (tabela 2).
Questão 3:Utilizando o Winplotexibir o gráfico da função dada na questão 1.
Quando o aluno visualizar a reta (Figura 04), como aparentemente passa pelo ponto (2,4) deverá questionar: "Como a função não está definida em 2, se reta passa por este ponto?" Então, o professor pode pedir que utilize a opção "Plotar lista" em x=2. O softwarenão irá plotar nenhum ponto, pois não está definida nele. Para representar a falta de definição neste ponto, pode utilizar o recurso "Ponto (x, y)" e definir através de "círculo" a chamada bola aberta.
Com esta atividade, o aluno poderá perceber que mesmo utilizando modelos distintos (tabular e gráfico), quando x se aproximam de 2, os valores da função se aproximam de 4.
A partir daí, o professor pode apresentar a notação matemática para a solução do problema. Ou seja,
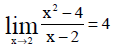
Depois é que o professor deve apresentar a notação matemática de limite para qualquer função.
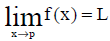
Para definir limite sugere-se que o professor construa a definição com os alunos mostrando graficamente (Figura 05), tomando dois números positivos δ e ε suficientemente pequenos (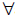 ε > 0,
ε > 0, 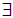 δ > 0 ) de modo que a distância entre o valor de "x" pertencente ao domínio da função ( x
δ > 0 ) de modo que a distância entre o valor de "x" pertencente ao domínio da função ( x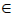 A ) e o ponto p seja menor que o valor de δ (0<|x - p|<δ) tem-se que a distância entre o valor de f(x) e o valor de L seja menor que o valor de ε (|f(x) - L|<ε).
A ) e o ponto p seja menor que o valor de δ (0<|x - p|<δ) tem-se que a distância entre o valor de f(x) e o valor de L seja menor que o valor de ε (|f(x) - L|<ε).
Vale destacar que como o modelo matemático que representa a distância entre um valor e outro é dado pelo módulo da diferença dos valores, e constitui-se em um conceito prévio para o aluno. Portanto, o professor pode apresentar a definição utilizando a notação matemática de módulo. Tem-se, então, a definição de limite:
Dizemos que o número real L é o limite de f(x) quando x tende para p se,
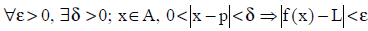
A partir da compreensão do conceito de limite de uma função, o professor pode mostrar aplicações a partir da lei de transformações dos gases para abordar os conceitos científicos de pressão, temperatura e volume, que também representam conceitos prévios para alunos do 3º ano do ensino médio ou ensino superior.
Conforme a lei de Charles-Gay Lussac um gás que apresenta pressão constante, seu volume e sua temperatura absoluta são diretamente proporcionais. Ou seja, se a temperatura aumenta o volume aumenta. As transformações em que isso ocorre são chamadas isobáricas. Por exemplo, para a pressão atmosférica, qualquer transformação realizada em ambiente aberto é isobárica, com exceção de transformações explosivas ou extremamente rápidas.
Questão 4:Determinar através de uma expressão matemática a Lei de Charles-Gay Lussac para transformações isobáricas chamando V de volume e T de temperatura.
Como o conceito de duas grandezas diretamente proporcionais é um conceito prévio dos estudantes devem encontrar a expressão:
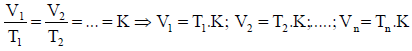
K é a constante de proporcionalidade.
Questão 5:Se a função que relaciona o volume e a temperatura de um gás com pressão p1 e temperatura inferior a 200º K é dada por V=2,5*T e se a função de volume deste gás com pressão p2 e temperatura superior a 200 º K é dada por V=3,5*T, o que acontece com o limite da função de volume do gás quando T tende a 200 º K?
Para determinar o limite da função volume, o professor deverá mostrar ao aluno a necessidade de se calcular os chamados limites laterais, pois de acordo com o intervalo de T, muda a definição da função volume. Por isso, terão que calcular 2 limites: para valores um pouco maiores que 200 º K (limite pela direita do ponto) e para valores menores que 200 º K (limite pela esquerda do ponto). Por exemplo, ao substituírem T=190ºK na função V=2,5*T devem obter 500 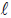 e ao substituírem T=210ºK na função V=3,5*T devem obter 700
e ao substituírem T=210ºK na função V=3,5*T devem obter 700 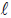 . Se analisarem graficamente no Winplot(Figura 06) será identificado um salto da função volume exatamente no ponto T=200 º K. Ou seja, o volume do gás para temperaturas próximas de 200 ºK não se aproxima de um único valor.
. Se analisarem graficamente no Winplot(Figura 06) será identificado um salto da função volume exatamente no ponto T=200 º K. Ou seja, o volume do gás para temperaturas próximas de 200 ºK não se aproxima de um único valor.
Ou seja, os limites laterais são diferentes. Portanto, não existe o limite da função volume quando T tende a 200 º K. Utilizando a notação matemática tem-se:
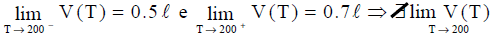
Questão 6:O que deve ocorrer com a definição da função volume do gás para que exista o valor do limite em T= 200 º K?

Os alunos deverão perceber que um das possibilidades é quando a função tem uma única definição independente do intervalo da variável (neste caso T). Por exemplo, para V=2,5*T tem-se que:
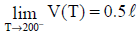 e
e 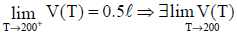
Analisando o gráfico obtido na Figura 07 os alunos irão observar que a função não apresentou mais o salto em T= 200 º K. Ou seja, além de existir o limite da função ele coincide com o valor do volume do gás nesta temperatura.
Neste momento, os alunos estarão diante de uma função contínua e o professor poderá construir com eles a notação matemática que representa a continuidade da função volume do gás em T=200 º K, obtendo, assim, a expressão:
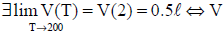 é contínuo em T = 200 º K
é contínuo em T = 200 º K
Ao generalizar a continuidade de qualquer função f(x) em xo tem-se:
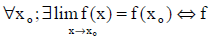 é contínua em xo
é contínua em xo
Dessa forma, em todas as atividades desenvolvidas o professor pode construir os conceitos de limite e continuidade com os alunos a partir de casos particulares, porém contextualizados, o que dificilmente ocorre no ensino tradicional, onde os conceitos e as definições surgem prontos, de modo abstrato e quando aplicados, muitas vezes, restringem-se apenas ao plano matemático, dificultando assim, a aprendizagem significativa dos alunos.
5. Considerações finais
Cada vez mais fica evidente a necessidade de integração entre as questões científicas das diversas áreas do conhecimento nos sistemas educacionais. Deve-se reconhecer que as atividades didáticas devem favorecer a construção do conhecimento mediada pela utilização de ferramentas que auxiliem o estudante a observar, interpretar e discutir a realidade.
A utilização da modelagem matemática no ensino de Matemática a partir de conceitos científicos exige que os educadores revejam suas concepções epistemológicas da ciência, procurando conhecer suas características, do que é ou não específico da cientificidade, refletindo sobre sua evolução histórica, seus fundamentos, suas implicações no ensino e na aprendizagem, a fim de que possam optar por posturas condizentes com uma perspectiva construtiva do conhecimento, respeitado as relações entre os atos de ensinar e aprender.
Desta forma, o educador através da modelagem estará dando oportunidade ao aluno de vivenciar um ambiente investigativo baseado no processo de "reflexão-na-ação." Esse processo quando incorporado ao currículo merece alguns cuidados para que os resultados desejados sejam alcançados, como a prática com atividades investigativas; o domínio das suas etapas metodológicas; o conteúdo programático a ser desenvolvido; a aprendizagem dos alunos; os objetivos a serem atingidos e o tempo para sua aplicação. Vale destacar que o domínio das etapas metodológicas passa fundamentalmente pela formação do professor, que muitas vezes, não teve a oportunidade de vivenciar experiências com a modelagem matemática. Oliveira e Barbosa (2007) chamam a atenção para a necessidade de o professor experimentar a modelagem matemática primeiramente como aluno para que possa compreender as dificuldades por ele sentidas e buscar alternativas para minimizá-las.
As atividades investigativas, características da modelagem matemática, exigem o exercício constante tanto do professor quanto dos alunos de habilidades como a busca, a seleção, a organização, o levantamento de hipóteses, a manipulação, análise, interpretação e validação de informações. Os professores em sua formação inicial, e mesmo na sua prática profissional, estão acostumados a utilizar os exemplos e exercícios já formulados pelos livros didáticos. Por isso, quando apresentados à proposta da modelagem, onde praticamente não há nada pronto, sentem um impacto muito grande e dificuldades em colocá-la em pratica.
Percebe-se que a partir das situações-problema apresentadas na proposta, os conceitos de limite e continuidade surgem de forma natural, onde cada nova informação interage com algum aspecto relevante da estrutura cognitiva do indivíduo. Dessa forma, as atividades respeitam os princípios defendidos pela Teoria da Aprendizagem Significativa de Ausubel.
Nesse sentido, a proposta busca contribuir com a prática dos professores de Matemática interessados em utilizar a modelagem matemática a partir de conceitos científicos, que permitam aos alunos aprenderem de modo significativo, relacionando a Matemática com a realidade que está em sua volta e com outras áreas, a partir da oportunidade que lhe são dadas atuando na construção do seu próprio conhecimento. Assim, os alunos realmente compreendem o que estão fazendo e são capazes de aplicar os conhecimentos matemáticos adquiridos em outras situações-problema contextualizadas.
Diante dessas possibilidades, é preciso que a modelagem, na perspectiva da Educação Matemática, seja utilizada como ferramenta para compreensão das ciências e para a atividade humana, como instrumento da vida cotidiana, como instrumento do exercício dos direitos democráticos. É importante que pesquisas científicas se ocupem em investigar de que forma o aprendiz relaciona e compreende os conceitos matemáticos trabalhados com o uso da modelagem na perspectiva construtivista.
6. Referências bibliográficas
Araujo, I.S.; Veit, E.A. e Moreira, M. A. (2004). Atividades de modelagem computacional no auxílio à interpretação de gráficos na Cinemática. Revista Brasileira de Ensino de Física, 26 (02), 179-184. Retirado em: 06/12/06 no World Wide Web: http://www.sbfisica.org.br. [ Links ]
Barbosa, J.C. (2001, outubro). Modelagem na Educação Matemática: Contribuições para o debate teórico. Anais, 24ªReunião Anual da ANPED (pp. 01-15). Caxambu. Retirado em: 12/062008, no World Wide Web: http://www8.pr.gov.br/portals/portal/institucional/def/areas/matematica/modelagem.pdf. [ Links ]
Barbosa, J.C. (2004a). Modelagem Matemática: O que é? Por que? Como? Veritati, 4, 73-80. Retirado em: 25/032007, no World Wide Web: http://www.uefs.br/nupemm/publicacoes.html. [ Links ]
Barbosa, J.C. (2004b). A "contextualização" e a Modelagem na educação matemática do ensino médio. Recife. Anais, 8º Encontro Nacional de Educação Matemática. Retirado em: 08/092007, no World Wide Web: http://www.uefs.br/nupemm/publicacoes.html. [ Links ]
Bassanezi, R.C. (2004). Ensino-aprendizagem com modelagem matemática. 2ª ed. São Paulo: Contexto. [ Links ]
Biembengut, M.S. e Hein, N. (2003). Modelagem matemática no ensino. 3ª ed. São Paulo: Contexto. [ Links ]
Boyer, C. História da Matemática. (Gomide, E. Trad.) São Paulo: Edgard Blücher Ltda. 1999. (Original publicado em 1976). [ Links ]
Brasil (1999a). Secretaria de Educação Média e Tecnológica. Parâmetros Curriculares Nacionais parao Ensino Médio. Parte III -Ciências da Natureza, Matemática e suas Tecnologias. Brasília: Ministério da Educação, Secretaria de Educação Média e Tecnológica. Retirado em: 13/09/2007, no World Wide Web: http://portal.mec.gov.br/seb/arquivos/pdf/ciencian.pdf. [ Links ]
Brasil (1999b). Secretaria de Educação a Distância. Documento Norteador de Desenvolvimento, Uso e Avaliação de SoftwareEducacional. Brasília: Ministério de Educação, Secretaria de Educação a Distância. Programa Nacional de Informática na Educação. (Documento Aprovado no IV Encontro Nacional do PROINFO). [ Links ]
Cachapuz, A.; Perez, G.D.; Carvalho, A.M.P.; Praia, J. e Vilches, A. (Orgs) (2005). A necessária renovação do ensino das ciências.São Paulo: Cortez. [ Links ]
Caldeira, A.D. (1998). Educação Ambiental: um contexto de mudança. Tese de Doutorado. Programa de Pós-Graduação em Educação, Universidade Estadual de Campinas, Campinas. Retirado em: 03/03/07 no World Wide Web: htttp://libdigi.unicamp.br/document/. [ Links ]
Chaves, M.I.A. (2005). Modelando matematicamente questões ambientais relacionadas com a água a propósito do ensino-aprendizagem de funções na 1ª série do ensino médio.Dissertação de Mestrado. Programa de Pós-Graduação em Educação em Ciências e Matemáticas, Universidade Federal do Pará, Belém. Retirado em 09/09/07 no World Wide Web: http://www.ufpa.br/npadc/index.htm. [ Links ]
Costa, H.R. e Ghedin, E. (2007). Epistemologia do Ensino de Matemática. Em: Universidade Luterana do Brasil (Org.), Anais, 4º Congresso Internacional de Ensino de Matemática (pp.01-08), Rio Grande do Sul: Universidade Luterana do Brasil de Canoas (RS). [ Links ]
Cury, H.N. (2003). Modelagem matemática e problemas em ciências: uma experiência em um curso de mestrado. Revista Perspectiva, 27 (98), 75-86. Retirado em: 05/08/2007 no World Wide Web: http://www.pucrs.br/famat/helena/pages/Perspectiva_Cury.pdf. [ Links ]
D' Ambrósio, U. (1999a). Informática, ciências e matemática. Retirado em: 20/01/2007 no World Wide Web: http://vello.sites.uol.com.br/tve.htm. [ Links ]
D' Ambrósio, U. (1999b). Matemática para uma sociedade em transição. Retirado em: 05/12/2006 no World Wide Web: http://vello.sites.uol.com.br/eprem.htm. [ Links ]
D' Ambrósio, U. (1999c). Do saber matemático ao fazer pedagógico: o desafio da educação.Conferência de abertura do 2º Encontro de Educação Matemática do Rio de Janeiro, Rio de Janeiro. Retirado em: 20/01/2007 no World Wide Web: http://vello.sites.uol.com.br/macae.htm. [ Links ]
Fernandes, E. e Matos, J.F. (2004). Aprender Matemática na escola versusser matematicamente competente - que relação? Em: Universidade da Madeira de Lisboa (Org.), Anais, 15º Seminário de Investigação em Educação Matemática, Lisboa: Associação de Professores de Matemática (APM), Retirado em: 05/10/2007 no World Wide Web: http://dme.uma.pt/people/faculty/elsa.fernandes/artigos/SIEMl.pdf. [ Links ]
Ferreira, D.H.L. (2003). O tratamento de questões ambientais através da modelagem matemática: um trabalho com alunos do ensino fundamental e médio. Tese de Doutorado, Programa de Pós-Graduação em Educação Matemática, Universidade Estadual Paulista, Rio Claro, São Paulo. Retirado em 03/03/07 no World Wide Web: http://www.biblioteca.unesp.br/bibliotecadigital/. [ Links ]
Guidorizzi, H.L. (2001). Um Curso de Cálculo (v.01). 5ª ed. Rio de janeiro; São Paulo: LTC Livros Técnicos e Científicos. [ Links ]
Gurgel, C.M.A. (2002). Educação para as ciências da natureza e matemáticas no Brasil: um estudo sobre os indicadores de qualidade do SPEC (1983-1997). Ciência & Educação,8 (2), 263-276. Retirado em: 12/12/2007 no World Wide Web: http://www2.fc.unesp.br/cienciaeeducacao/include/getdoc.php?id=573&article=202&mode=pdf. [ Links ]
Kfouri, W. (2006). Explorar e Investigar para Aprender Matemática Através da Modelagem Matemática. Em: Universidade Federal de Minas Gerais (Org.). Anais, Encontro Brasileiro dos Estudantes de Pós-Graduação em Educação Matemática(pp. 1-14), Minas Gerais: Universidade Federal de Minas Gerais. Retirado em: 05/01/2007 no World Wide Web: http://www.fae.ufmg.br:8080/ebrapem/completos/09-02.pdf. [ Links ]
Monteiro, A. e Junior, G. P. (2001). A matemática e os temas transversais. São Paulo: Moderna. (Educação em pauta: temas transversais). [ Links ]
Moreira, M.A. (1999). Teorias de Aprendizagem. São Paulo: EPU. [ Links ]
Oliveira, A.M.P. e Barbosa, J.C. (2007). A primeira experiência de modelagem matemática e a tensão do "próximo passo". Recife. Anais, 9º Encontro Nacional de Educação Matemática. Retirado em: 12/10/2008, no World Wide Web: http://uefs.br/nupemm/CC74390627520.pdf. [ Links ]
Ponte, J.P.; Brocardo, J. e Oliveira, H. (2005). Investigações Matemáticas na Sala de Aula.Belo Horizonte: Autêntica (Coleção Tendências em Educação Matemática, v. 7). [ Links ]
Rosa, M. (2005). Currículo e matemática: algumas considerações na perspectiva etnomatemática. Plures -Humanidades, Ribeirão Preto, 6, 81-96. Retirado em: 30/06/2007 no World Wide Web: http://mestrado.mouralacerda.edu.br/plures/Plures2005internet.pdf. [ Links ]
Sampaio, F.F. (1998, dezembro). Modelagem Dinâmica Computacional e o Processo de Ensino-Aprendizagem: Algumas Questões Para Reflexão...Trabalho apresentado no Taller Internacional de Software Educativo, Santiago, Chile. Retirado em: 20/08/2007 no World Wide Web: http://www.c5.cl/tise98/html/trabajos/modelag/index.htm. [ Links ]
Stieler, M.C. e Bisognin, V. (2006). Radiação Solar Ultravioleta e a Modelagem Matemática. Em: Universidade de Caxias do Sul (Org.), IX Encontro Gaúcho de Educação Matemática(pp. 01-08). Rio Grande do Sul: UCS. [ Links ]
Scucuglia, R. (2006). Investigando o Teorema Fundamental do Cálculo com Calculadoras Gráficas. Universidade Federal de Minas Gerais (Org), Anais. Minas Gerais: 10º Encontro Brasileiro de Estudantes de Pós-Graduação em Educação Matemática(pp.1-15). Retirado em: 12/10/2008 no World Wide Web: http://www.c5.cl/tise98/html/trabajos/modelag/index.htm. [ Links ]
Unesco (2005). A ciência na escola: um direito para todos. Brasília. Retirado em: 02/07/2007 no World Wide Web: http://unesdoc.unesco.org/images/0014/001400/140099porb.pdf. [ Links ]
Vasconcelos, F.H.L.; Carvalho, R.E.; Romeu, M.C.; Santana, J.R. e Neto, H.B. (2005). A utilização de softwareeducativo aplicado ao ensino de física com o uso da modelagem. Anais, XVI Simpósio Nacional de Ensino de Física, (pp.01-04). Rio de Janeiro. Retirado em: 20/08/2007 no World Wide Web: http://www.sbf1.sbfisica.org.br/eventos/snef/xvi/cd/resumos/T0164-2.pdf. [ Links ]
Veit, E.A. e Teodoro, V.D. (2002). Modelagem no ensino-aprendizagem de Física e os novos parâmetros curriculares nacionais para o ensino médio. Revista Brasileira de Ensino de Física, 24 (02), 87-95. Retirado em: 06/12/06 no World Wide Web: http://www.sbfisica.org.br. [ Links ]
Vygotsky, L.S. (1991). A formação social da mente. (Neto, J. C., Trad.). 4ª ed. São Paulo: Martins Fontes. [ Links ]
Submetido em 16/06/2009
Revisado em 08/07/2009
Aceito em 24/09/2009
Notas
(1) Rosa, M. (2000). From reality to mathematical modeling: A proposal for using ethnomathematical knowledge. 2000. 205 f. Dissertação de Mestrado em Artes. Department of Teacher Education. California: State University, Sacramento, 2000.
(2) Hurd, P.H. (2000). Science education for the 21st Century. School Science and Mathematics, 100 (6), 282-287.
(3) Modelos dinâmicos são modelos que se modificam (evoluem) com o tempo (Sampaio, 1998: 03).
H.R. da Costaé Bacharel em Processamento de Dados (Universidade Federal do Amazonas, UFAM), Graduada em Licenciatura e Bacharel em Matemática (UFAM), Especialista em Instrumentação para o Ensino de Matemática (Universidade Federal Fluminense) e Mestre em Educação e Ensino de Ciências na Amazônia (UEA). Atua como Professora do Departamento de Matemática (UEA) e participa de projetos educacionais de Matemática na modalidade presencial mediado com uso de tecnologias. Endereço para correspondência: Rua J, casa 55, conj. Eldorado, parque-Dez, Manaus, AM 69.050-200. Telefone: +55-21-32361562. E-mailpara correspondência: helisangelar@gmail.com.














