Serviços Personalizados
artigo
Indicadores
Compartilhar
Revista Latinoamericana de Psicología
versão impressa ISSN 0120-0534
Rev. Latinoam. Psicol. v.38 n.3 Bogotá dez. 2006
ARTÍCULOS
Procedimientos estadísticos alternativos para evaluar la robustez mediante diseños de medidas repetidas1
Alternative satatistical procedures to assess the robustness using repeated measures designs
Pablo Livacic-RojasI, 2; Guillermo VallejoII; Paula FernándezII
IUniversidad de Santiago de Chile, Universidad Mayor, Chile
IIUniversidad de Oviedo, España
ABSTRACT
The purpose of this investigation was assessing the robustness of a series of new procedures under the traditional ANOVA approach to analyze some data corresponding to repeated measures by means of Monte Carlo simulation. In order to study the efficacy of these procedures for the control of Type I rate of errors, four variables were handled: sample size; structure of dispersion matrixes; relationship between the group sizes and the dispersion matrices, and population distribution pattern. Results suggest that the Improved General Approach, Proc Mixed program with the Kenward-Roger solution, Brown-Forsythe and Welch James procedures offer a very good behavior to control the Type I rate of errors both for the main effect of the measurement opportunities as well as the effect of interaction, under all the assessed conditions.
Keywords: Robustness, ANOVA, Type I Rate of Error, Alternative Procedures, SAS Proc Mixed, Monte Carlo Simulation.
RESUMEN
El propósito de la presente investigación radica en evaluar la robustez de una serie de nuevos procedimientos alternativos al tradicional enfoque ANOVA para analizar datos de medidas repetidas mediante el método de simulación Monte Carlo. Para estudiar la eficacia de estos procedimientos en el control de las tasas de error de Tipo I se manipularon cuatro variables: tamaño de la muestra, estructura de las matrices de dispersión, relación entre el tamaño de los grupos y el de las matrices de dispersión y forma de distribución de la población. Los resultados obtenidos sugieren que los procedimientos Aproximación General Mejorada, Proc Mixed con la solución Kenward-Roger, Brown-Forsythe y Welch James ofrecen un muy buen comportamiento para controlar las tasas de error de Tipo I, tanto para el efecto principal de las ocasiones de medida como para el efecto de la interacción, bajo todas las condiciones evaluadas.
Palabras clave: Robustez, ANOVA, Tasa de Error de Tipo I, Procedimientos Alternativos, SAS Proc Mixed, Simulación Monte Carlo.
INTRODUCCIÓN
Los diseños de medidas repetidas se caracterizan por evaluar el patrón de cambio de los sujetos a través del tiempo en función de los tratamientos u otras variables de tipo biológicas, psicológicas o sociales. Los diseños de medidas repetidas se diferencian de los diseños experimentales más clásicos (inter-sujetos) en que en ellos (a diferencia de los segundos) la unidad experimental recibe todos los niveles de la variable independiente. Un tipo particular de estos diseños es el de medidas parcialmente repetidas, el cual implica una estructura con un factor inter entre-sujetos y otro factor intra-sujetos. Este puede representarse esquemáticamente como la toma de q medidas (k=1,...,q), de las n (i=1,...,n), unidades experimentales independientes que se han agrupado en los p (j=1,...,p) niveles de la variable de clasificación. Permite, entre otras características, estudiar el paso del tiempo (efectos de arrastre o práctica) en cada grupo de la variable inter sujetos y en cada sujeto dentro de cada grupo (Vallejo, Fernández, Herrero & Conejo, 2004a).
Dadas las condiciones bajo las cuales un investigador realiza su labor, resulta de importancia implementar un diseño ajustado a los objetivos y complejidad del tema en estudio en términos del análisis de los datos como la implicación práctica de los resultados. De este modo, en los contextos aplicados tanto los diseños de medidas repetidas como de medidas parcialmente repetidas han mostrado ser una solución en ámbitos experimentales y empíricos para evaluar programas de intervención en Psicología, Educación y Ciencias de la Salud, así como también, por su pertinencia en el tratamiento de diferentes problemas sociales de corta y de larga escala (implementación de programas educativos, laborales y comunitarios, entre otros, Vallejo, Fernández & Secades, 2004).
Por otra parte, en el contexto analítico, tradicionalmente se han utilizado metodologías clásicas (Modelo Lineal Clásico) para evaluar los efectos fijos del diseño, las cuales se basan preferentemente en modelos univariados de medidas repetidas o en modelos de normalidad conjunta multivariada con una estructura de covarianza general, en la cual se cumplen los supuestos paramétricos con algunas restricciones. Dado que es común que los datos en Psicología no se ajusten a los supuestos para aplicar el ANOVA (no existe igualdad en las matrices de dispersión y los diseños no se encuentran convenientemente equilibrados), el investigador quecontrasta hipótesis referidas a los efectos de los tratamientos mediante este procedimiento debe estar atento a la evaluación previa de los supuestos a fin de no cometer errores en las inferencias y extracción de conclusiones. En tal sentido, en caso de que situaciones como estas pasen desapercibidas en el campo aplicado para el psicólogo, se aumenta la probabilidad de implementar programas o terapias de bajo o inexistente impacto para la mejoría de los pacientes. Asociado al intento de solventar algunos de estos problemas, no es casualidad que durante los últimos treinta años se hayan desarrollado método alternativos a la prueba ANOVA, los cuales han centrado su interés en el estudio de la violación de los supuestos de la independencia de las puntuaciones (Judd & Kenny, 1981), la falta de normalidad de las mismas (Micceri, 1989; 2003) y la ausencia de esfericidad de las matrices de dispersión (Huynh & Feldt, 1970; Rouanet & Lepine, 1970).
Uno de los supuestos de importancia en los diseños de medidas repetidas es el la esfericidad. Cuando éste se incumple, se han usado pruebas univariadas con los grados de libertad corregidos mediante procedimientos tipo Box (Bellavance, Tardif & Stephen, 1996; Lecoutre, 1991; Quintana & Maxwell, 1994), pruebas multivariadas que asumen la igualdad de las matrices de dispersión y una combinación de ambas, como sucede con el procedimiento Empírico Bayesiano (EB) desarrollado por Boik (1997). Sin embargo, cuando las matrices de dispersión difieren entre sí (existe alta heterogeneidad entre los sujetos de los grupos), la literatura empírica cuestiona la pertinencia para utilizar dichos enfoques con el objeto de controlar las tasas de error de Tipo I, debido a que aumenta el riesgo de declarar que un tratamiento es eficaz en circunstancias de que no lo es (ver Keselman, Algina y Kowalchuk, 2002). Para tal efecto, se han desarrollado diversas pruebas orientadas a solventar las dificultades surgidas con el control de las tasas de error, dentro de las cuales cabe destacar: la de Aproximación General Mejorada (AGM) desarrollada por Huynh (1978); la prueba Welch-James (WJ) desarrollada originalmente por Johansen (1980) e implementada por Keselman, Carriere y Lix (1993) en el ámbito de los diseños de medidas repetidas; la versión multivariada de la prueba Brown-Forsythe de 1974, propuesta por Vallejo, Fidalgo y Fernández (2001; BF); la técnica de remuestreo bootstrap (BOOT) creada por Efron y colaboradores (Efron & Tibshiriani, 1993) y el modelo mixto lineal general (MLM).
En el contexto de los procedimientos disponibles, el MLM es un modelo estadístico que se ha desarrollado como una alternativa de solución para el análisis de los datos. Este modelo presenta diferencias respecto de los otros procedimientos, y es de gran utilidad en Psicología debido a que permite analizar los datos en diseños de medidas repetidas o de otro tipo cuando existen observaciones perdidas (solución práctica y muy versátil), determinar a priori la estructura de covarianza de los datos utilizando criterios de búsqueda semiautomáticos (p.e., AIC de Akaike o BIC de Schwarz), manejar covariadas cambiantes a lo largo del tiempo, ser aplicado independientemente de que el número de mediciones exceda al número de unidades de observación, obtener de una forma más eficiente los estimadores de los parámetros usados en el modelado de la estructura de medias y también errores estándar más adecuados de estos estimadores (Núñez-Antón & Zimmerman, 2001), permitir que el modelo contenga tanto variables de efectos fijos como de efectos aleatorios (Raudenbush & Bryk, 2002), extender su uso para el manejo de medidas repetidas de naturaleza categórica (Davis, 2002), ajustarse a condiciones donde los sujetos tengan diferente número de observaciones y que los intervalos de tiempo puedan ser específicos para cada sujeto, lo cual posibilita modelar las variaciones entre e intra sujetos tanto para datos completos como incompletos (Vallejo, Fernández & Secades 2004).
No obstante, las ventajas señaladas, este modelo presenta el inconveniente de que los estimadores de precisión e inferencia para los efectos fijos (estructura de medias del modelo) se basan en su distribución asintótica, lo cual puede ocasionar serios problemas cuando setrabaja con muestras reducidas (Chen & Wei, 2003; Wolfinger, 1996). Por lo tanto, cuando los tamaños de los grupos son pequeños, las inferencias que el investigador realice pueden ser incorrectas. Para solventar esta dificultad, Elston (1998), Fai y Cornelius (1996) y Kenward y Roger (1997) han desarrollado tres soluciones diferentes con grados de libertad corregidos. Además, y como señalan Kowalchuk, Keselman, Algina y Wolfinger (2004), el investigador no debe perder de vista que con mucha frecuencia surgen dificultades con la identificación correcta de las estructuras de covarianza. La aplicación de criterios de selección de modelos resulta, así, muy importante para detectar la estructura de covarianza más parsimoniosa y favorece la precisión y eficiencia del análisis a la hora de detectar el patrón de cambio operado en los participantes en el estudio (ver también Keselman, Algina, Kowalchuk & Wolfinger, 1999).
Por otra parte, la técnica bootstrap se ha aplicado escasamente en los diseños de medidas repetidas, aunque se ha implementado en otros ámbitos desde la década de los ochenta (ver Lunnerborg, 2000). Según Vallejo, Cuesta, Fernández y Herrero (2006), la técnica en cuestión constituye una alternativa viable a las pruebas tradicionales (t, F) basadas en el muestreo de poblaciones. Estos autores evaluaron la robustez de la técnica bootstrap-F junto con los enfoques BF y AGM en diseños transversales de series temporales cortas, encontrando que la técnica bootstrap controla adecuadamente el error de Tipo I cuando los datos se desvían de la normalidad al contrastar hipótesis referidas a los efectos principales y que, cuando las matrices de dispersión múltiplos entre sí no contienen a otras el mismo número de veces, la técnica es superada por el test BF.
Como se ha visto, la versatilidad que ofrecen estos procedimientos se basa, en parte, en que han sido elaborados bajo modelos estadísticos diferentes, que respetan la estructura de los datos propia de las investigaciones en Psicología y Educación, razón por la cual permiten realizar inferencias más rigurosas y, con ello, optimizar la toma de decisiones, fortaleciendo a su vez la importancia práctica de los estudios. A su vez, conviene señalar que su desarrollo, vigencia y extensión ha sido posible gracias al uso intensivo de programas estadísticos tales como el SAS, SPSS, o S-PLUS entre otros, los cuales permiten procesar un importante volumen de datos con alta precisión y en corto tiempo. En tal sentido, nos atrevemos a decir que el reemplazo de los procedimientos tradicionales se impondrá en breve plazo.
El presente trabajo pretende evaluar comparativamente mediante métodos de simulación la robustez de varios procedimientos alternativos de análisis en diseños de medidas parcialmente repetidas cuando se incumplen los supuestos de normalidad y homogeneidad, tanto conjuntamente como por separado. Los procedimientos utilizados son el de Aproximación General Mejorada (AGM), la versión multivariada del procedimiento modificado de Brown-Forsythe (BF), la extensión multivariada de Welch y James (WJ), el procedimiento de Welch-James con medias recortadas (MR), la técnica bootstrap no paramétrica (BOOT), el modelo mixto sin ajustar los grados de libertad (F), el modelo mixto con grados de libertad ajustados mediante la solución de Kenward y Roger (1997, KR) y la solución tipo Satterthwaite desarrollada por Fai y Cornelius (S). Hasta la fecha, no se ha realizado un trabajo de investigación en el que se comparen simultáneamente todas las técnicas analíticas alternativas reseñadas.
PROCEDIMIENTOS ESTADÍSTICOS USADOS EN LA INVESTIGACIÓN
Cuando se incumpla el supuesto de homogeneidad de las matrices de dispersión, se pueden ajustar y evaluar modelos lineales univariados y multivariados utilizando pruebas basadas en dos principios de estimación general. Esencialmente, métodos de estimación basados en el principio de los mínimos cuadrados ordinarios (enfoques AGM, BF y WJ) versus métodos de estimaciónbasados en el principio de máxima verosimilitud (enfoque del modelo mixto lineal general).
El enfoque del modelo mixto
El modelo mixto lineal general usa el enfoque de los mínimos cuadrados generalizados para estimar la estructura de medias y el enfoque de la máxima verosimilitud para estimar los componentes de varianza. Este procedimiento permite a los investigadores seleccionar el patrón de covarianza que en teoría mejor describe sus datos, y con ello les da la oportunidad de encontrar un equilibrio entre los criterios de flexibilidad y parsimonia. Un modelo excesivamente flexible (p.e. el clásico enfoque MANOVA, el enfoque multivariado de Brown-Forsythe o el enfoque multivariado de Welch-James) puede producir estimaciones ineficientes, mientras un modelo excesivamente parsimonioso (p.e., el tradicional enfoque ANOVA propuesto por Scheffé.) puede producir pruebas sesgadas. Cabe esperar, al menos en teoría, que en aquellas situaciones donde los diversos procedimientos controlen adecuadamente las tasas de error, el enfoque del modelo mixto resulte más potente que el resto de los enfoques referidos, sobremanera si la estructura de covarianzas juega un papel importante en la estimación. En estos casos, los errores estándar de los estimadores del modelo lineal de coeficientes mixtos son más pequeños que los de los enfoques multivariados, lo cual no es extrañar, ya que estos enfoques pierden muchos grados de libertad en la estimación de la matriz de dispersión no estructurada. El procedimiento PROC MIXED del SAS (SAS Institute, 2002) ofrece varias estructuras de covarianza para ajustar, entre ellas, estructura de simetría combinada, de Huynh-Feldt, no estructurada y autorregresiva de primer orden utilizando los criterios de información de Akaike y de Schwarz (ver Littell, Milliken, Stroup & Wolfinger, 2006) y, también, permite ajustar los grados de libertad mediante las soluciones KR y S. La elección del procedimiento de estimación para el análisis del modelo mixto y los estadísticos de prueba están convenientemente descritos en Littell et. al. (2006).
Enfoque Multivariado de Brown-Forsythe
A partir del trabajo de Nel y van der Merwe (1986), Vallejo et al. (2001) abordan el problema de encontrar una aproximación a la distribución de las matrices sumas de cuadrados y productos cruzados (SS&CP) debidas a la hipótesis y al error, respectivamente, cuando las covarianzas son heterogéneas. Básicamente, el denominado enfoque MBF utiliza el criterio de los mínimos cuadrados ordinarios y se basa en un modelo en el cual los efectos aleatorios son tratados como fijos y los parámetros de la matriz de dispersión como arbitrarios. Además, la matriz SS&CP correspondiente al error se estima usando un enfoque similar al denominado estimador Sandwich, utilizado comúnmente con el método de ecuaciones de estimación generalizada propuesto por Liang y Zeger (1986), para acomodar la dependencia serial propia de los estudios longitudinales. Esta forma de construir la matriz SS&CP debida al error, asegura que bajo hipótesis nula su valor esperado coincida con el de la matriz SS&CP referida a hipótesis. Esta solución es sustancialmente menos vulnerable a la violación de los supuestos distribucionales de homogeneidad y normalidad multivariada que el tradicional enfoque MANOVA, y actualmente también puede ser utilizada dentro de un programa informático SAS (para detalles ver Vallejo, Moris & Conejo, 2006).
Aunque el enfoque BF solventa alguno de los problemas que plantea el enfoque MANOVA cuando las matrices de dispersión son heterogéneas, sin embargo, otros permanecen. Básicamente, existen cuatro inconvenientes a la hora de implementar el enfoque BF en contextos donde el control experimental sea limitado. En primer lugar, el enfoque BF puede ser difícil de implementar en situaciones donde exista desgaste de muestra, bien sea por la pérdida de participantes, de ocasiones de medida o de valores en alguna de las ocasiones de medida. En este caso el analista puede confinar su atención en los vectores de datos completos. También cabe la posibilidad de generar los datos faltantes mediante imputación múltiple. Este método se encuentra disponible en varios paquetes estadísticos (p.e., SAS, SOLAS, AMELIA) y se pueden utilizar con cualquier tipo de datos y con cualquier tipo de técnica analítica. En segundo lugar, el enfoque BF sólo puede utilizarse en aquellas situaciones en las cuales el número de ocasiones en que se realizan las mediciones sea menor que el número de participantes. En tercer lugar, el enfoque BF no permite manejar covariadas cambiantes. En cuarto lugar, el enfoque BF puede resultar ineficiente cuando la estructura de la matriz de dispersión requiera estimar un número reducido de parámetros. Una descripción detallada de los aspectos formales requeridos para implementar el enfoque BF en el contexto de los diseños de medidas repetidas univariados se encuentra en el trabajo de Vallejo y Livacic (2005).
Enfoque de la Aproximación General Mejorada
Hay tres hipótesis globales de interés acerca de los efectos de tratamientos que usan el diseño de medidas parcialmente repetidas más simple: (a) la hipótesis nula de ausencia de interacción entre grupos y las ocasiones de medida (ensayos), (b) la hipótesis nula de ningún efecto de las ocasiones de medida, y (c) la hipótesis nula de ningún efecto de los grupos. La hipótesis nula referida a la interacción grupos × ensayos se prueba comparando el cuadrado medio de la interacción con el cuadrado medio del error intragrupo del usual ANOVA [Fp×q =MSp×q / MSq×s(p)]. Si el supuesto de esfericidad multimuestral se mantiene, ya hemos dicho que Fp×q~F[(p-1)(q-1), (n-p)(q-1)]. Cuando la suposición de esfericidad es falsa, Huynh (1978) recomendó modificar la prueba F asumiendo que Fp×q≈aF[α; h'*, h*]. Los estimadores referentes a la falta de esfericidad (a), a los grados de libertad (hI*,h*) y la corrección debida a Lecoutre (1991) son presentados en Algina (1994) y Algina y Oshima (1995).
El estadístico F para comprobar la hipótesis nula referida a la igualdad de los ensayos (medias no ponderadas) es Fq=MSq / MSq×s(p). Si el supuesto esfericidad multimuestral es satisfecho, el valor de la F empírica es comparado con el de la distribución de F con los grados de libertad sin ajustar. Si se incumple el supuesto de esfericidad multimuestral la razón Fq es aproximada por bF[α;h'#, h#], donde los estimadores de b, h'# y h# y la corrección debida a Lecoutre (1991) son presentados en Algina (1994) y Algina y Oshima (1995).
Finalmente, la hipótesis nula referida a la igualdad de los grupos, promediando a través de los ensayos, es probada comparando el cuadrado medio de los grupos con el cuadrado medio residual de los sujetos anidados dentro de los grupos [Fp= MSp / MSs(p)]. Si las matrices de covarianza son homogéneas, es bien conocido que Fp~F[(p-1), (n-p)] bajo la correspondiente hipótesis nula. Para conducirse con la heterogeneidad de covarianza a través de los grupos, la razón Fp es aproximada por cF[α; h'•, h•] , donde los estimadores debidos al sesgo por la falta de homogeneidad y los estimadores de los grados de libertad coinciden con los valores críticos de Box (1954). Además del trabajo seminal de Huynh (1978), los trabajos de Algina (1994) y Algina y Oshima (1995) son especialmente recomendables para una descripción más detallada del procedimiento.
Enfoque multivariado de Welch-James
Este procedimiento multivariado fue desarrollado por Keselman et al. (1993) y, se aplica para contrastar las hipótesis referidas a los efectos principales y de la interacción cuando el diseño está desequilibrado y no existe homogeneidad en las matrices de covarianza, las cuales, no requieren ser esféricas. El estadístico obtenido se aproxima a la distribución F a través de los grados de libertad del error provenientes de los datos de la muestra, considerando las matrices de covarianza y el tamaño de los grupos (Blanca, 2004).
La prueba estadística de Welch-James puede expresarse como

donde 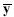 es un vector de orden (p q×1) obtenido tras concatenar verticalmente las medias de
es un vector de orden (p q×1) obtenido tras concatenar verticalmente las medias de  es una matriz de contrastes cuyo orden depende de la hipótesis que se esté interesado en probar y P es una matriz diagonal de bloques de orden (p q×p q) con el j-ésimo bloque igual a
es una matriz de contrastes cuyo orden depende de la hipótesis que se esté interesado en probar y P es una matriz diagonal de bloques de orden (p q×p q) con el j-ésimo bloque igual a  . El estadístico TWJ dividido por una constante, c, se distribuye aproximadamente como el estadístico F con grados de libertad v1(rango de la matriz R) y v2=v1(v1+2)/3A. Las constantes c y A valen, respectivamente, c=v1+2A-(6A/v1+2) y
. El estadístico TWJ dividido por una constante, c, se distribuye aproximadamente como el estadístico F con grados de libertad v1(rango de la matriz R) y v2=v1(v1+2)/3A. Las constantes c y A valen, respectivamente, c=v1+2A-(6A/v1+2) y

donde tr denota el operador traza y Qj es una matriz diagonal de bloques de orden (p q×p q) con el jésimo bloque Iq y el resto ceros.
Prueba multivariada de Welch-James con estimadores robustos
Cuando el tamaño de muestra sea reducido y los datos hayan sido extraídos desde distribuciones sesgadas, Keselman, Kowalchuk, Lix, Wilcox y Algina (2000) sugieren que la robustez del procedimiento WJ se puede incrementar sustancialmente reemplazando las usuales medias y matrices de covarianza con medias recortadas y matrices de covarianza winsorizadas.
El primer paso para aplicar estimadores robustos al procedimiento WJ es winsorizar las observaciones. En un diseño como el que venimos considerando, la winsorización se debe efectuar para cada uno de los niveles de los factores entre sujetos e intra sujetos. En concreto, tras ordenar los valores del j-ésimo grupo para la k-ésima ocasión de medida, los valores winsorizados son dados por

donde gj=[γnj] indica la cantidad de datos a recortar en cada extremo de la distribución, siendo γ la proporción de recorte y [nj] la parte entera del valor entre corchetes.
El segundo paso consiste en calcular las medias recortadas y las matrices de covarianza winsorizadas. Para cada j y k, la media recortada se obtiene como

donde hj=nj - 2gj y Y(1)jk ≤ Y(2)jk ≤...≤ Y(nj)jk y son los del jk-ésimo grupo de tratamiento escritos en orden ascendente. Basados en los trabajos de Yuen (1974), para cada nivel de la variable entre grupos la matriz de covarianza muestral winsorizada, 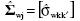 , viene dada por
, viene dada por

para k,kI = q. Donde 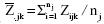 , es la media muestral winsorizada para el j-ésimo nivel de la variable entre grupos para la k-ésima ocasión o ensayo.
, es la media muestral winsorizada para el j-ésimo nivel de la variable entre grupos para la k-ésima ocasión o ensayo.
El estadístico WJ para probar la hipótesis lineal general para las medias recortadas, H0: Rμt = 0, donde μt es un vector poblacional de medias recortadas, viene dado por  , donde
, donde 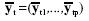 , con
, con  , Pw es una matriz diagonal de bloques de orden (p q×p q) con el j-ésimo bloque igual a
, Pw es una matriz diagonal de bloques de orden (p q×p q) con el j-ésimo bloque igual a  y A definida como en (2), pero con Pwy (hj-1) en lugar de P y (nj-1).
y A definida como en (2), pero con Pwy (hj-1) en lugar de P y (nj-1).
El enfoque bootstrap-F
De acuerdo con Vallejo, et al. (2006b), aplicar la metodología bootstrap para contrastar las hipótesis del diseño multigrupo de medidas repetidas p×q requiere efectuar cuatro operaciones sumamente sencillas. La primera consiste en definir la unidad de muestreo a utilizar y en desplazar las distribuciones empíricas de manera que la hipótesis nula sea verdadera. Lo común es que dicha unidad sean los vectores de errores asociados con los valores observados para cadauna de las poblaciones de muestreo existentes. Esto supone que los datos obtenidos por esta vía mantienen las mismas propiedades distribucionales que los datos originales y también las mismas matrices de varianzas y covarianzas. La operación de centrado garantiza que en cada uno de los p niveles de la variable entre grupos, las medias de los q niveles de la variable ocasiones de medida no difieran entre sí. El uso de la distribución empírica desplazada constituye la piedra angular en la que se basa la técnica bootstrap para estimar los valores críticos apropiados (Westfall & Young, 1993).
A continuación, desde la muestra nula de observaciones originales, se extraen muestras bootstrap efectuando un muestreo aleatorio con reposición de nj vectores de observaciones centradas. Debido a la existencia de matrices de dispersión heterogéneas y a la falta de equilibrio que presentan los diferentes grupos que configuran el diseño, el procedimiento de remuestreo se efectúa para cada j-ésimo nivel del factor entre grupos. De este modo, cada muestra bootstrap se obtiene desde una distribución para la cual las hipótesis de nulidad son verdaderas. Posteriormente se calcula F* el valor del estadístico F basado en la muestra bootstrap, y se genera la distribución muestral empírica del estadístico (F* b) repitiendo el proceso b veces, siendo b = 1,...,B. De acuerdo con Wilcox (2001; 2003), el valor de B puede ser convenientemente fijado en 599. Hall (1986) proporciona la justificación teórica para dicha elección. La distribución muestral bootstrap de F*b se utiliza para determinar la excepcionalidad del valor obtenido tras aplicar la prueba estadística F a la muestra de datos originales.
Finalmente, la significación de las razones F se estima directamente mediante el nivel de significación alcanzado (NSA) por el procedimiento de remuestreo bootstrap. En concreto, siguiendo el trabajo de Efron y Tibshiriani (1993), definimos NSA por
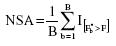
donde  , la usual función indicador, es igual a 1 si F*b>F y a 0 si es menor. La proporción de valores F*b que supera al valor F observado representa el valor p bootstrap. Por tanto, bajo este método, a diferencia de lo que sucedía con los enfoques anteriores, los valores críticos derivados desde la teoría normal son innecesarios.
, la usual función indicador, es igual a 1 si F*b>F y a 0 si es menor. La proporción de valores F*b que supera al valor F observado representa el valor p bootstrap. Por tanto, bajo este método, a diferencia de lo que sucedía con los enfoques anteriores, los valores críticos derivados desde la teoría normal son innecesarios.
MÉTODO
En orden a evaluar la robustez de los enfoques descritos arriba, se llevó a cabo un estudio de simulación usando un diseño de medidas repetidas que tenía un factor entre sujetos (p=3) y un factor intra sujetos (k=4). En él se comparó la robustez de los enfoques propuestos cuando se incumplían los supuestos de esfericidad multimuestral y normalidad, tanto conjuntamente como por separado. Para tal fin se manipularon cuatro variables: (a) el tamaño de muestra total, (b) la relación entre el tamaño de los grupos y el de las matrices de dispersión, (c) el tipo de matrices de dispersión y (d) la forma de la distribución de la población. Estas variables fueron seleccionadas por ser de uso habitual en otras investigaciones similares a la nuestra.
El comportamiento de estos estadísticos fue investigado usando tres tamaños de muestras totales distintos: n = 30, n = 45 y n = 60 Estos tamaños grupales fueron seleccionados por ser representativos de los encontrados en la práctica, particularmente, en áreas tales como la Psicología Animal, la Psicología Clínica y la Psicología Educativa. Dentro de cada condición, el coeficiente de variación muestral (Δ) se fijó en 0,33, donde  , siendo n el tamaño promedio de los grupos. Para n = 30, los tamaños grupales fueron: 6, 10 y 14; para n = 45, los tamaños grupales fueron: 9, 15 y 21. Mientras que para n = 60, los tamaños grupales fueron: 12, 20 y 28.
, siendo n el tamaño promedio de los grupos. Para n = 30, los tamaños grupales fueron: 6, 10 y 14; para n = 45, los tamaños grupales fueron: 9, 15 y 21. Mientras que para n = 60, los tamaños grupales fueron: 12, 20 y 28.
Las relaciones entre las matrices de dispersión y el tamaño de los grupos pueden tener diferentes efectos en las pruebas estadísticas. Por esto, se investigó el comportamiento de los tres enfoques referidos utilizando diseños equilibrados y no equilibrados. Cuando los diseños estaban equilibrados, la relación entre las matrices de dispersión y el tamaño de los grupos era nula. Cuando los diseños carecían de equilibrio, la relación podía ser tanto positiva como negativa. Una relación positiva implica que el grupo de menor tamaño se asocia con la matriz de dispersión menor, mientras que una relación negativa implica que el grupo de menor tamaño se asocia con la matriz de dispersión mayor. Cuando los tamaños de muestra son iguales, (Δ) vale 0, mientras que el valor del coeficiente se incrementa cuanto más difiere el tamaño de los grupos entre sí. En nuestro caso, el grado de desequilibrio existente entre los grupos se puede tildar de moderado tendiendo a severo. El grado de heterogeneidad de las matrices de dispersión incluido en el presente trabajo fue  .
.
El patrón de matrices de dispersión tenía cuatro niveles; en los tres primeros las matrices son múltiplos unas de otras, mientras que en el cuarto no lo son. Las estructuras de covarianza por manipular para generar los datos simulados en el caso proporcional serán las tres que siguen: coeficientes aleatorios (CA), autorregresiva de primer orden heterogénea (ARH(1)) y no estructurada (NE). Los tres patrones representan estructuras de covarianza heterogéneas. En concreto, el primer patrón es un ejemplo de modelo jerárquico que permite modelar un interceptor y una tendencia (véase Khattree & Naik, 1995). El segundo patrón es típico de los diseños de series temporales cortas (véase Bono & Arnau, 1997), y no es más que la generalización de la matriz autorregresiva de primer orden. Como se puede apreciar, este patrón pone de manifiesto que las varianzas de las medidas próximas en el tiempo mantienen entre sí una correlación superior a la de las varianzas que están más alejadas. Por su parte, el tercer patrón representa la estructura de covarianza más general y, por ende, la menos parca de las tres estructuras expuestas. No obstante, a costa de estimar muchos parámetros, es la que mejor se ajusta a los datos.
Para el trabajo que nos ocupa, la primera requiere estimar cuatro parámetros, la segunda cinco y la tercera diez. Las matrices de covarianza utilizadas bajo la presente condición, esto es, matrices de dispersión heterogéneas, pero múltiplos unas de otras, fueron idénticas a las del estudio de Keselman et al. (1999). En nuestra investigación el valor del parámetro de esfericidad se mantuvo constante en .75.
Por lo que se refiere al caso en que no sean múltiplos unas de otras, las matrices de los diferentes grupos diferirán entre sí. El índice de esfericidad de las matrices de covarianza correspondiente a cada uno de los grupos se fijará igual a 1,00, 0,75 y 0,50, respectivamente. De este modo, aunque las matrices sean distintas, mantienen entre sí la relación siguiente:  . Al igual que en el caso anterior, también se manipulará el grado de heterogeneidad de las matrices mediante la relación
. Al igual que en el caso anterior, también se manipulará el grado de heterogeneidad de las matrices mediante la relación  . Por consiguiente, se cumplirá que
. Por consiguiente, se cumplirá que  y tr
y tr  .
.

La última variable investigada fue la forma de la distribución de la variable de medida. Este factor tenía cuatro niveles: normal, ligeramente sesgado, moderadamente sesgado y severamente sesgado. Al igual que en el estudio de Berkovits, Hancock y Nevitt (2000), los valores de los índices de asimetría (γ1) y apuntamiento (γ2) 2 g seleccionados para generar las distribuciones no normales multivariadas fueron: ligeramente sesgada (γ1 = 1, γ2= 0.75), moderadamente sesgada (γ1 = 1.75, γ2 = 3.00) y fuertemente sesgada (γ1 = 3.00, γ2 = 21.00). Una de las razones de haber utilizado distribuciones sesgadas se debe a que éstas son representativas de la mayor parte de las investigaciones realizadas con datos aplicados (véase, por ejemplo, Micceri, 1989).
Para cada una de las condiciones del diseño, se crearon, con el lenguaje matricial IML del SAS (SAS Institute, 2002), 10.000 conjuntos de datos replicados, utilizando la extensión multivariada que Vale y Maurelli (1983) desarrollaron del método de la potencia propuesto por Fleishman (1978). Para cada replicación se ejecutaron los enfoques bootstrap-F, BF, AGM, MLM y WJ usando un nivel de significación del 5%. Las comparaciones se efectuaron examinando las tasas de error de Tipo I. Los valores críticos de los enfoques BF, AGM, MLM y WJ se obtuvieron mediante la función FINV del SAS. Por su parte, los valores críticos del enfoque bootstrap se determinaron mediante el procedimiento descrito por Vallejo et al. (2006a) a partir de 599 remuestreos de tamaño obtenidos del conjunto de datos simulados. Dichos valores, además de haber sido utilizados en otras investigaciones similares a la nuestra (p.e., Keselman et al., 2000), cumplen con la recomendación efectuada por Hall (1986) acerca de la conveniencia de elegir B tal que (1- ) sea múltiplo de 1/(B+1). Todos los cálculos se realizaron mediante un programa de simulación escrito por el profesor Dr. Guillermo Vallejo en lenguaje de programación SAS/IML. Bajo la hipótesis nula la proporción empírica de errores de Tipo I se obtuvo dividiendo el número de veces que cada estadístico excedía su valor crítico por las 10.000 réplicas efectuadas.
RESULTADOS
Tasas de error de Tipo I para efectos principales.
Según los resultados de la Tabla 1, se observa que los procedimientos KR, BF, WJ, AGM y MR satisfacen el criterio de robustez bajo todas las condiciones investigadas. A su vez, los procedimientos S, BOOT y F (basado en el modelo mixto sin ajustar grados de libertad) no satisfacen el criterio de robustez en 1, 2 y 8 condiciones experimentales, respectivamente. En el caso del procedimiento S, la ausencia de robustez se encuentra asociada a la matriz NE bajo condiciones de apareamiento negativo (3,7%). Para la técnica BOOT, la ausencia de robustez se encuentra asociada a la matriz CA bajo condiciones de apareamiento positivo y negativo (7,41%). En cuanto a la prueba F, la ausencia de robustez se encuentra asociada a la matriz ARH y NE bajo condiciones de apareamiento nulo, positivo y negativo (29,63%).
En la distribución levemente desviada de la normalidad, los procedimientos KR, BF y AGM satisfacen el criterio de robustez bajo todas las condiciones investigadas, esto es, tipo de matrices de dispersión y proporcionalidad. Los procedimientos S, WJ, MR, F y BOOT no satisfacen el criterio de robustez en 1, 1, 2, 7 y 8 condiciones experimentales, respectivamente. Para el procedimiento S, la ausencia de robustez se encuentra asociada a la matriz NE bajo condiciones de apareamiento negativo (3,70%). El procedimiento WJ, se encuentra asociada a la matriz CA bajo condiciones de apareamiento negativo (3,70%). En cuanto a la prueba MR, se encuentra asociada a la matriz CA bajo condiciones de apareamiento nulo y negativo (7,41%). La prueba F se encuentra asociada a las matrices CA y NE bajo condiciones de apareamiento nulo, positivo y negativo (25,93%). La técnica BOOT se encuentra asociada a las matrices CA, ARH y NE bajo condiciones de apareamiento nulo, positivo y negativo (29,63%). Conviene señalar que una de las causas de que esta prueba presente este grado de liberalidad se debe a que en la gran mayoría de las veces exhibe una tasa de error inferior al a = 0,025.




En la distribución moderadamente desviada de la normalidad (ver Tabla 2), los procedimientos S, KR y AGM son los únicos que satisfacen el criterio de robustez bajo todas las condiciones. Los procedimientos BF, WJ, F, MR y BOOT no satisfacen el criterio de robustez en 1, 4, 6, 12 y 13 condiciones, respectivamente. Para el procedimiento BF, la ausencia de robustez se encuentra asociada a la matriz NE bajo condiciones de apareamiento negativo (3,70%). En cuanto al procedimiento WJ, la ausencia de robustez se encuentra asociada a la matriz CA bajo condiciones de apareamiento nulo, positivo y negativo (14,81%). La prueba F presenta ausencia de robustez cuando se encuentra asociada a las matrices CA y NE bajo condiciones de apareamiento nulo, positivo y negativo (22,22%). Respecto a la prueba MR, la ausencia de robustez se encuentra asociada a las matrices CA, ARH y NE bajo condiciones de apareamiento nulo, positivo y negativo (44,44%). Por su parte, la técnica BOOT exhibe ausencia de robustez cuando se encuentra asociada a las matrices CA, ARH y NE bajo condiciones de apareamiento nulo, positivo y negativo (48,15%). Conviene señalar que en estas condiciones la prueba exhibe un grado de liberalidad relacionado con una tasa de error igual o inferior 0,025 en menos del 50% de las veces.
Cuando la distribución es severamente desviada de la normalidad, sólo los procedimientos S y AGM satisfacen el criterio de robustez bajo todas las condiciones. Los procedimientos KR, BF, WJ, F, BOOT y MR no satisfacen el criterio de robustez en 2, 3, 7, 7, 12 y 15 condiciones, respectivamente. Para el procedimiento KR, la ausencia de robustez se encuentra asociada a la matriz ARH bajo condiciones de apareamiento positivo y negativo (7,41%). El enfoque BF presenta ausencia de robustez asociada a la matriz NE, ARH y CA bajo condiciones de apareamiento nulo y negativo (11,11%). A su vez, el enfoque WJ exhibe ausencia de robustez asociada a la matriz CA bajo condiciones de apareamiento nulo, positivo y negativo (25,93%). La prueba F presenta la ausencia de robustez cuando se encuentra asociada a la matriz CA y NE bajo condiciones de apareamiento nulo, positivo y negativo (25,93%). Finalmente, la técnica BOOT presenta la ausencia de robustez cuando se encuentra asociada a la matriz CA, ARH y NE bajo condiciones de apareamiento nulo, positivo y negativo (44,44%). En cuanto a la prueba MR, la ausencia de robustez se encuentra asociada a la matriz CA, ARH y CA bajo condiciones de apareamiento nulo, positivo y negativo (55,56%).
Tasas de error de Tipo I para efectos de la interacción.
Bajo distribución normal, los procedimientos AGM, WJ, KR, BF, MR, F y BOOT satisfacen en orden decreciente el criterio de robustez para todas las condiciones (ver tabla 3). De este conjunto, KR, BF y AGM satisfacen el criterio de robustez en todas las condiciones investigadas. Por su parte, los procedimientos WJ, MR, S, BOOT y F no satisfacen el criterio de robustez en 3, 3, 9, 21 y 21 condiciones experimentales respectivamente. En el caso del procedimiento WJ, la ausencia de robustez se encuentra asociada a las matrices CA, ARH y NE bajo condiciones de apareamiento negativo (11,11%). El procedimiento MR se encuentra asociado a las matrices CA, ARH y NE bajo condiciones de apareamiento negativo (11,11%). El procedimiento S se encuentra asociado a las matrices ARH y NE bajo condiciones de apareamiento nulo, positivo y negativo (33,33%). La técnica BOOT se asocia a las matrices CA, ARH y NE bajo condiciones de apareamiento nulo, positivo y negativo (77,78%). Finalmente, la prueba F se encuentra asociada a las matrices CA, ARH y NE bajo condiciones de apareamiento nulo, positivo y negativo (77,78%).
Cuando la distribución se desvía levemente de la normalidad, AGM y BF satisfacen el criterio de robustez bajo todas las condiciones sometidas a investigación. Los enfoques KR, WJ, MR, S, F y BOOT no satisfacen el criterio de robustez en 1, 3, 3, 7, 12 y 22 condiciones experimentales, respectivamente. Para el enfoque KR, la ausencia de robustez se encuentra asociada a la matriz ARH bajo condiciones deapareamiento negativo (3,70%). Para el enfoque WJ, se encuentra asociada a las matrices CA, ARH y NE bajo condiciones de apareamiento negativo (11,11%). En cuanto a la prueba MR, se encuentra asociada a las matrices CA, ARH y NE bajo condiciones de apareamiento nulo y negativo (11,11%). El enfoque S se encuentra asociado a la matriz NE bajo condiciones de apareamiento nulo, positivo y negativo (25,93%). La prueba F se encuentra asociada a las matrices CA, ARH y NE bajo condiciones de apareamiento nulo, positivo y negativo (44,44%). La técnica BOOT se encuentra asociada a las matrices CA, ARH y NE bajo condiciones de apareamiento nulo, positivo y negativo (81,48%). Conviene señalar que, al igual que para los efectos principales, la tasa de error inferior es al a = 0,025; por lo tanto, resulta un enfoque muy conservador.
Cuando la distribución se desvía moderadamente de la normalidad (ver Tabla 4), sólo el procedimiento AGM satisface el criterio de robustez bajo todas las condiciones investigadas. Los procedimientos BF, WJ, KR, S, F, MR y BOOT no satisfacen el criterio de robustez en 2, 3, 5, 8, 11, 14 y 26 condiciones respectivamente. Para el procedimiento BF, la ausencia de robustez se encuentra asociada a las matrices ARH y NE bajo condiciones de apareamiento negativo (7,41%). A su vez, el procedimiento WJ se encuentra asociada a la matriz CA bajo condiciones de apareamiento negativo (11,11%). Respecto al procedimiento KR, se encuentra asociada a la matriz ARH bajo condiciones de apareamiento nulo, positivo y negativo (18,52%). En cuanto al procedimiento S, se encuentra asociada a la matriz NE bajo condiciones de apareamiento nulo, positivo y negativo (29,63%). En la prueba F se encuentra asociada a las matrices CA y NE bajo condiciones de apareamiento nulo, positivo y negativo (44,44%). En el procedimiento MR, se encuentra asociada a las matrices CA, ARH y NE bajo condiciones de apareamiento nulo, positivo y negativo (51,85%). La técnica BOOT se encuentra asociada a las matrices CA, ARH y NE bajo condiciones de apareamiento nulo, positivo y negativo (96,30%). Conviene señalar que, en todos los casos, hubo una tasa de error inferior al a= 0,025, lo cual convierte a esta técnica en conservadora.
Cuando la distribución se desvía fuertemente de la normalidad (ver Tabla 4), ninguno de los procedimientos satisface el criterio de robustez bajo todas las condiciones manipuladas. Los procedimientos WJ, S, AGM, F, KR, MR, BF y BOOT no satisfacen el criterio de robustez en 1, 4, 7, 8, 11, 17, 18 y 25 condiciones respectivamente. Para el procedimiento WJ, la ausencia de robustez se encuentra asociada a la matriz CA bajo condiciones de apareamiento negativo (3,7%). Para el procedimiento S, se encuentra asociada a la matriz ARH bajo condiciones de apareamiento nulo y negativo (14,81%). Respecto al procedimiento AGM, se encuentra asociada a las matrices ARH y NE bajo condiciones de apareamiento nulo, positivo y negativo (25,93%). En cuanto a la prueba F, se encuentra asociada a las matrices ARH y NE bajo condiciones de apareamiento nulo, positivo y negativo (29,63%). En el procedimiento KR, se encuentra asociada a la matriz ARH bajo condiciones de apareamiento nulo, positivo y negativo (40,74%). A su vez, el procedimiento MR se encuentra asociado a la matrices CA, ARH y NE bajo condiciones de apareamiento nulo, positivo y negativo (62,93%). La técnica BOOT se encuentra asociada a las matrices CA, ARH y NE bajo condiciones de apareamiento nulo, positivo y negativo (95,59%). En este contexto, tanto el procedimiento MR como la técnica BOOT exhiben en la mayoría de los casos una tasa de error inferior al a = 0,025, convirtiéndose en pruebas conservadoras.
DISCUSIÓN
El propósito de esta investigación mediante métodos de simulación de datos ha sido evaluar la robustez de ocho procedimientos para analizar diseños de medidas repetidas en ausencia de esfericidad multimuestral. Específicamente, se ha examinado el grado de control que sobre las tasas de error de Tipo I ejercen los procedimientos multivariado de Brown Forsythe (modificado por Vallejo et al., 2001), la técnica Bootstrap, el modelo mixto con los grados de libertad sin ajustar (prueba F), el procedimiento de Aproximación General Mejorada (AGM), el modelo mixto con los grados de libertad ajustados mediante el procedimiento desarrollado por Kenward-Roger (1997) (KR), el procedimiento de Welch-James con Medias Recortadas, el modelo mixto con los grados de libertad ajustados al procedimiento propuesto por Fai y Cornelius (S) y el procedimiento de Welch-James cuando los supuestos de normalidad multivariada y homogeneidad de las matrices de dispersión eran violados independiente y simultáneamente. Este objetivo se llevó a cabo manipulando diversos tamaños de muestra generados desde distribuciones sesgadas y con diferentes estructuras de covarianza propias de las investigaciones en Psicología.
En términos generales, si el investigador detecta en su análisis que los datos presentan el cumplimiento insuficiente de los supuestos, se sugiere que utilice los procedimientos AGM, KR, BF y WJ dado que ofrecen un muy buen comportamiento para controlar las tasas de error de Tipo I, tanto para el efecto principal como de la interacción, para todas las condiciones evaluadas. De igual modo, se observa que los procedimientos S, MR, F y BOOT presentan un rendimiento menos efectivo que los anteriores, dado que las tasas de error aumentan para ambas fuentes de variación, excepto en el método S para los efectos principales.
En términos prácticos, el investigador puede optar por cualesquiera de los cuatro primeros procedimientos, aunque el mejor control de las tasas de error para el efecto principal y de la interacción bajo diferentes condiciones de apareamiento de tamaños de matrices y tamaños de grupo, tipo de matrices e índices de asimetría y apuntamiento lo ofrece el enfoque AGM (2,78% de ausencia de robustez en promedio).
A su vez, los procedimientos KR, BF y WJ representan alternativas útiles. El procedimiento KR exhibe dificultades sólo cuando las distribuciones se encuentran severamente sesgadas, con mayor tendencia en el apareamiento negativo (50%) y para efectos de la interacción preferentemente. Sin embargo, en la totalidad de las ocasiones la desviación no sobrepasa el a = 0,025 de la tasa de error; por lo tanto, se puede considerar como una prueba conservadora, y con otros criterios puede ser evaluada con mayor robustez aun.
El procedimiento BF exhibe un comportamiento muy similar al de KR. Las dificultades se presentan sólo cuando las distribuciones se encuentran severamente sesgadas, con mayor tendencia en apareamiento negativo (61,54%) y para efectos de la interacción. De igual modo, en la totalidad de las ocasiones sus desvíos no sobrepasan el a = 0,025 de las tasas de error; por lo tanto, es una prueba conservadora, y con otros criterios puede ser evaluada con mayor robustez.
El procedimiento WJ exhibe dificultades sólo cuando las distribuciones se encuentran leve y severamente sesgadas para el efecto principal, con mayor tendencia en el apareamiento negativo (66,67%). Para el efecto de la interacción, la falta de robustez es similar cuando las matrices son múltiplos unas de otras. No obstante, en la totalidad de las ocasiones sus desvíos sobrepasan el a=0,075 de las tasas de error; por lo tanto, es un enfoque que, con otro criterio de robustez, sería evaluado como liberal.
Por otro lado, los procedimientos menos recomendables son los MR, F y BOOT, dado que exhiben un comportamiento más deficiente bajo condiciones de desvíos de la normalidad y cuando se evalúan los efectos de la interacción en una mayor medida que los efectos principales. Es oportuno mencionar que, al igual que en la sección de resultados, la técnica BOOT exhibe ausencia de robustez en un 83,44% del total de ocasiones. Los resultados muestran que se encuentran en un punto igual o inferior a a = 0,025, lo cual la convertiría en un procedimiento con tendencia a ser conservador. Es probable que esta evaluación ocurra porque las tasas de error caen por debajo del criterio establecido. Por lotanto, es probable que, con otros criterios de robustez, sea considerada en una medida muy diferente como un procedimiento recomendable. Cabe señalar que esta técnica, aplicada con otros estadísticos como el F, ha mostrado ser eficiente (ver en Berkovits et al., 2000; Vallejo et. al, 2006).
Respecto al procedimiento MR, se reproduce la situación referida a la prueba BOOT. En un 40% de las ocasiones exhibe tasas de error inferiores al a = 0,025. Por tanto, sería esperable que el investigador desprendiera sugerencias similares.
La prueba F es la que presentaría, en términos comparativos y rescatando las advertencias hechas, un desempeño más deficiente que los demás procedimientos, bajo las diferentes condiciones evaluadas. En términos de efectos principales y de la interacción, exhibe altos niveles de ausencia de robustez.
En resumen, es posible concluir que el procedimiento AGM es el más recomendable para utilizar por el investigador tanto si se cumplen o no los diferentes supuestos. De igual modo, los procedimientos KR y BF son recomendables en una proporción similar a AGM, con la advertencia de que exhiben mayores tasas de error cuando la distribución se encuentra severamente sesgada. Por lo tanto, estas leves diferencias no restan su valor como enfoques robustos a la hora de seleccionar alguno. No obstante lo anterior, estimamos oportuno subrayar que el procedimiento AGM no presenta garantías suficientes para estimar errores cuando existen observaciones perdidas; por lo tanto, el investigador debe ser cauteloso a la hora de considerar el análisis de los datos en series temporales, dado que en ellas es frecuente su ocurrencia. En tal sentido, los procedimientos recomendables de aplicar serían KR y S (modelo mixto con grados de libertad corregidos), así como BF.
REFERENCIAS
Algina, J. (1994). Some alternative approximate tests for a split-plot design. Multivariate Behavioral Research, 29, 365-384. [ Links ]
Algina, J. & Oshima, T. C. (1995). An improved general approximation test for the main effect in a split-plot design. British Journal of Mathematical and Statistical Psychology, 48, 149-160. [ Links ]
Bellavance, F, Tardif, S. & Stephen, M. A. (1996). Test for the analysis of variance of cross-over designs with correlated errors. Biometrics, 52, 607-612. [ Links ]
Berkovits I., Hancock G. & Nevitt J. (2000). Bootstrap resampling approaches for repeated measure designs: relative robustness to sphericity and normality violations. Educational and Psychological Measurement, 60, 877-892. [ Links ]
Blanca, M. J. (2004). Alternativas de análisis estadístico en los diseños de medidas repetidas. Psicothema, 16, 509-518. [ Links ]
Boik, R.J. (1997). Analysis of repeated measures under second-stage sphericity: An empirical Bayes approach. Journal of Educational and Behavioral Statistics, 22 (2), 155-192. [ Links ]
Bono, R. & Arnau, J. (1997). El estadístico C: Aplicación a diseños conductuales. Revista Latinoamericana de Psicología, 29, 49- 63. [ Links ]
Box, G. E. P. (1954). Some theorems on quadratic forms applied in the study of analysis of variance problems, I. Effects of inequality of variance in the one-way classification. Annals of Mathematical Statistics, 25, 290-303. [ Links ]
Chen, X. & Wei, L. (2003). A comparison of recent methods for the analysis of small-sample cross-over studies. Statistics in Medicine, 22, 2821-2833. [ Links ]
Davis, Ch. (2002). Statistical Methods for the Analysis of repeated measurements. New York: Springer-Verlag. [ Links ]
Efron, B. & Tibshiriani, R. (1993). An introduction to the Bootstrap. New York: Chapman & Hall. [ Links ]
Elston, D. A. (1998). Estimation of denominator degrees of freedom of F-distributions for assessing Wald statistics for fixed-effect factors in unbalanced mixed models. Biometrics, 54. 1085-1096. [ Links ]
Fai, A. & Cornelius, P. (1996). Approximate F-test of multiple degree of freedom hypotheses in generalized least squares analysis of unbalanced split-plot experiments. Journal of Statistical Computation and Simulation, 54, 363-378. [ Links ]
Hall, P. (1986). On the number of bootstrap simulations required to construct a confidence interval. Annals of Statistics, 14, 1431- 1452. [ Links ]
Huynh, H. (1978). Some approximate tests for repeated measurement designs. Psychometrika, 43, 161-165. [ Links ]
Huynh, H. & Feldt, L. S. (1970). Conditions under which mean square ratios in repeated measurements design have exact Fdistributions. Journal of the American Statistical Association, 65, 1582-1585. [ Links ]
Johansen, S. (1980). The Welch-James approximation to the distribution of the residual sum of squares in a weighted linear regression. Biometrika, 67, 85-92. [ Links ]
Judd, C. M. & Kenny, D. A. (1981). Estimating effects of social interventionism. Cambridge, MA: Cambridge University Press. [ Links ]
Kenward, M. G. & Roger, H. J. (1997). Small sample inference for fixed effects from restricted maximum likelihood. Biometrics, 53, 983-997. [ Links ]
Keselman, H. J., Carriere, M. C. & Lix, L. M. (1993). Testing repeated measures hypotheses when covariance matrices are heterogeneous. Journal of Educational Statistics, 18, 305-319. [ Links ]
Keselman H.J., Algina J., Kowalchuck R. & Wolfinger, R. D. (1999). A comparison of two approaches for selecting covariance structures in the analysis of repeated measurements. Communications in Statistics-Simulation and computation, 28 (12), 2967- 2999. [ Links ]
Keselman, H. J., Algina, J. & Kowalchuck, R. K (2002). A comparison of data analysis strategies for testing omnibus effects in higher-order repeated measures designs. Multivariate Behavioral Research, 37 (3), 331-357. [ Links ]
Keselman, H. J., Kowalchuk, R. K., Algina, J., Lix, L. M. & Wilcox, R. R. (2000). Testing treatment effects in repeated measures designs: Trimmed means and bootstrapping. British Journal of Mathematical and Statistical Psychology, 53, 175-191. [ Links ]
Khattree, R. & Naik, D.N. (1995). Applied Multivariate Statistics with SAS Software. Cary, NC: SAS Institute. [ Links ]
Kowalchuck, R. K., Keselman, H. J., Algina, J. & Wolfinger, R. D. (2004). The analysis of repeated measurements with mixedmodel adjusted F test. Educational and Psichological Measurements, 64, 224-242. [ Links ]
Lecoutre, B. (1991). A correction for the approximate test in repeated measures designs with two or more independent groups. Journal of Educational Statistics, 16, 371-372. [ Links ]
Liang, K. R. & Zeger, S. (1986). Longitudinal data analysis using generalized linear models. Biometrika, 73, 13-22. [ Links ]
Littell, R. C. (2002). Analysis of unbalanced mixed model data: A case study comparison of ANOVA versus REML/GLS. Journal of Agricultural, Biological, and Environmental Statistics, 7, 472-490. [ Links ]
Littell, R. C., Milliken, G. A., Stroup, W. W. & Wolnger, R. D. (2006). SAS System for Mixed Models. (2nd. Edition). Cary, NC: SAS Institute Inc. [ Links ]
Lunneborg, C. E. (2000). Data Analysis by Resampling: Concepts and Applications. Pacific Grove, CA: Duxbury Press. [ Links ]
Micceri, T. (1989). The unicorn, the normal curve, and other improbable creatures. Psychological Bulletin, 92, 778-785. [ Links ]
Nel, D. G. & Van der Merwe, C. A. (1986). A solution to the multivariate Behrens-Fisher problem. Communications in Statistics- Theory and Methods, 15, 3719-3735. [ Links ]
Núñez-Antón, V. & Zimmerman, D. L. (2001). Modelización de datos longitudinales con estructuras de covarianza no estacionarias: Modelos de coeficientes aleatorios frente a modelos alternativos. Qüestiió, 25, 225-262. [ Links ]
Quintana, S. & Maxwell, S. E. (1994). A Monte Carlo comparison of seven adjustment procedures in repeated measures designs with sample sizes. Journal of Educational Statistics, 19, 57-71. [ Links ]
Raudenbush, S. W. & Bryk, A. S. (2002). Hierarchical Linear Models: Applications and Data Analysis Methods (2nd ed.). Thousand Oaks, CA: SAGE Publications, Inc. [ Links ]
Rouanet, H. & Lepine, D. (1970). Comparison between treatments in a repeated-measures design: ANOVA and multivariate methods. British Journal of Mathematical and Statistical Psychology, 23, 147-163. [ Links ]
SAS Institute (2002). SAS/STAT software: Version 9.0 (TS M0).Cary, NC: SAS Institute Inc. [ Links ]
Vale, C. D. & Maurelli, V. A. (1983). Simulating multivariate nonnormal distributions. Psychometrika, 48, 465-471. [ Links ]
Vallejo, G., Cuesta, M, Fernández, P. & Herrero, J. (2006). A comparison of the bootstrap-F, improved general approximation and Brown-Forsythe multivariate approaches in a mixed repeated measures design. Educational and Psychological Measurement, 66, 35-62. [ Links ]
Vallejo, G. Fernández, P., Herrero, J, & Conejo, N. (2004). A Comparison of the Kenward-Roger's Mixed Model and Modified Multivariate Brown-Forsythe Tests for Testing Fixed Effects in Repeated Measures Designs. Psicothema, 16, 498-508. [ Links ]
Vallejo, G., Fernández, J. R. & Secades, R. (2004). Application of a mixed model approach for assessment of interventions and evaluation of programs. Psychological Reports, 95, 1095-1118. [ Links ]
Vallejo, G., Fidalgo, A. M. & Fernández, P. (2001). Effects of covariance heterogeneity on three procedures for analysing multivariate repeated measures designs. Multivariate Behavioral Research, 36, 1-27. [ Links ]
Vallejo, G. & Livacic-Rojas, P. (2005). A comparison of two procedures for analyzing small sets of repeated measures data. Multivariate Behavioral Research, 40, 179-2005. [ Links ]
Vallejo, G., Moris, J. & Conejo, N (2006). A SAS/IML program for implementing the modified Brown-Forsythe procedure in repeated measures designs. Computer Methods and Program in Biomedicine, 83, 169-177. [ Links ]
Westfall, P. H. & Young, S. S. (1993). Resampling-based multiple testing. New York: John Wiley. [ Links ]
Wilcox, R. R. (2001). Fundamentals of modern statistical methods: Substantially improving power and accuracy. New York: Springer. [ Links ]
Wilcox, R. (2003): Applying contemporary statistics techniques. San Diego, CA: Academic Press. [ Links ]
Wolfinger, R. D. (1996). Heterogeneous variance-covariance structures for repeated measures. Journal of Agricultural, Biological, and Environmental Statistics, 1, 205-230. [ Links ]
Yuen, K. K. (1974). The two sample trimmed t for unequal population variances. Biometrika, 61, 165-170. [ Links ]
Zimmerman, D. L. & Núñez-Antón, V. (2001). Parametric modeling of growth curve data: An overview. Test, 10, 1-73. [ Links ]
Recepción: noviembre de 2005
Aceptación final: agosto de 2006
1Este trabajo ha sido financiado mediante los proyectos DICYT 030593LR de la Universidad de Santiago de Chile y SEJ-2005-01883 del Ministerio de Educación y Ciencia de España. Los autores de este trabajo agradecen a los revisores anónimos y al editor por sus comentarios y sugerencias.
2Correspondencia: PABLO LIVACIC-ROJAS, Universidad de Santiago de Chile. E-mail: plivacic@usach.cl













