Serviços Personalizados
Journal
artigo
Indicadores
Compartilhar
Actualidades en psicología
versão On-line ISSN 0258-6444
Actual. psicol. v.19 n.106 San José 2003
Uso del modelo de Rasch para poner en la misma escala las puntuaciones de distintos tests
Gerardo Prieto AdánezI; Angela Dias VelascoII; *
IUniversidad de Salamanca, España
IIUniversidad Estadual Paulista, São Paulo, Brasil
RESUMEN
Los usuarios de los tests tienen que poner en una escala común las puntuaciones de distintos instrumentos en varias situaciones prácticas, tales como la evaluación académica, la selección de personal, los estudios acerca del cambio de un atributo psicológico o educativo, la construcción de bancos de ítems, la validación intercultural de tests y los estudios sobre el funcionamiento diferencial de los ítems. Situar en una escala común las puntuaciones de diferentes tests es una de las principales aplicaciones del modelo de Rasch. En este artículo, mostramos el proceso de equiparación de dos tests (diseño, análisis de datos e interpretación) usando como anclaje un conjunto de ítems comunes.
Palabras clave: Anclaje de tests, Equiparación de puntuaciones, Modelo de Rasch.
ABSTRACT
Test users have to link scores of different instruments in several practical situations, such as academic assessment, personnel selection, change studies, item banking, cross-cultural validity studies, and differential item functioning analyses. Test linking is one of the main utilities of the Rasch model. In this paper, we show the process of linking two tests (design, data analysis and interpretation) using as anchor a commom set of items.
Keywords: Test anchoring, Test linking, Test equating, Rasch model.
Introducción
Poner en la misma escala las puntuaciones obtenidas con distintos tests que miden el mismo atributo psicológico o educativo es un procedimiento imprescindible en varias situaciones prácticas, entre las que cabe destacar:
1. El uso de distintas pruebas para el ingreso en la universidad, la selección de personal, la evaluación académica o la certificación profesional. En este tipo de aplicaciones se suelen emplear varias versiones de un mismo test con el fin de evitar el fraude e incrementar la seguridad. Aunque los redactores de las pruebas intenten construir versiones con la misma dificultad, no es posible garantizar que las puntuaciones de los distintos tests (en el modelo más usual el número de respuestas correctas) sean equivalentes: ¿10 respuestas correctas en el test A indican la misma competencia que 10 respuestas correctas en el test B?. Si el éxito en la selección se basa en superar un punto de corte o en lograr situarse en un grupo de excelencia (por ejemplo, el 10% superior), será necesario situar en una escala común las puntuaciones de las distintas pruebas.
2. Medición del cambio producido en un atributo (aptitudes, actitudes, disfunciones psicológicas, progreso educativo) por la maduración o la intervención psicológica y educativa. Por ejemplo, para estudiar cómo cambia una aptitud a lo largo del ciclo vital (crecimiento, estabilización, decremento) se recurre a pruebas psicométricas para evaluar el nivel cuantitativo en poblaciones de distinta edad. Obviamente, se han de usar diferentes tests que sean apropiados para cada edad. Para determinar la curva de cambio es necesario que las puntuaciones de los distintos tests se sitúen en la misma escala. Sin esa operación no es posible analizar el cambio: ¿cómo equiparar 10 respuestas correctas en el test para 8 años con 10 respuestas correctas en el test para 16 años?. Una situación similar se produce cuando se desea analizar el cambio cuantitativo producido por una intervención psicoterapéutica o educativa. En estos casos, es frecuente emplear un diseño en el que se mide el nivel del atributo antes y después de la intervención mediante dos versiones (pre y post) del mismo test. Para obtener las puntuaciones de cambio (post-pre), es imprescindible que las puntuaciones de ambas versiones estén en una escala común.
3. Construcción de bancos de ítems. Esta tecnología es uno de los recursos fundamentados en los nuevos modelos psicométricos derivados de la Teoría de Respuesta a los Ítems (en adelante, TRI). Las instituciones encargadas de llevar a cabo periódicamente evaluaciones psicométricas para el ingreso en la universidad, la selección de personal, la evaluación académica, la certificación profesional, etc, suelen recurrir a este procedimiento como una fuente para seleccionar las pruebas a emplear en cada caso. Un banco de ítems, calibrado con el modelo de Rasch, está integrado por un amplio conjunto de cuestiones de las que se han estimado empíricamente sus características psicométricas (dificultad, ajuste, etc). Periódicamente es necesario añadir nuevos ítems al banco y es imprescindible equiparar sus parámetros con la escala del banco para que las puntuaciones de los subtests sean comparables.
4. Validación intercultural de tests. En las últimas décadas está creciendo extraordinariamente el interés por la investigación intercultural. Por un lado, los psicólogos interesados en el ámbito teórico necesitan llevar a cabo comparaciones entre culturas para destacar los aspectos comunes, las leyes generales explicativas de la conducta. Por otro lado, la expansión mundial de la psicología aplicada demanda la adaptación intercultural rápida y eficaz de los recursos técnicos generados en los países con mayor potencial científico. Este interés por la investigación intercultural tiene importantes repercusiones en la construcción y adaptación de los instrumentos de evaluación psicológica que, como es obvio, constituyen una de las vías regias para la obtención de los datos empleados en las investigaciones. Los constructores de tests aptos para la comparación de culturas se enfrentan con frecuencia al dilema etic-emic (Prieto y Almeida, 1997). Esta terminología procede de las investigaciones en el campo de la Antropología Cultural (Spindler, 1975). El enfoque emic parte de la suposición de que las culturas han de ser comprendidas a partir de sus peculiaridades y de su especificidad. El énfasis en esta perspectiva dificulta establecer comparaciones interculturales. El enfoque etic, por el contrario, se refiere a las leyes universales de la conducta humana que operan en todas las culturas. Se ocupa de los conceptos que no son específicos de las culturas o, al menos, de los que son conceptualmente equivalentes y posibilitan establecer comparaciones significativas. El dilema emic-etic (especificidad-generalidad) plantea al investigador interrogantes difíciles de resolver. Si se pone el acento en la explicación profunda y exhaustiva de las leyes que rigen el comportamiento en una cultura determinada, el investigador no podrá obviar sus manifestaciones conductuales peculiares, dificultando establecer comparaciones con otras culturas en las que dichas manifestaciones apenas estan presentes. Si, por el contrario, el objetivo es establecer comparaciones interculturales, los datos relevantes son los relativos a manifestaciones comunes que, en ocasiones, pueden aportar sólo una descripción poco nítida de la cultura a analizar. El dilema especificidad-generalidad es especialmente arduo en el campo de la medición psicológica. Spindler (1975), y Hui y Triandis (1985) propusieron como solución desarrollar métodos emic para medir constructos etic. Se trata de medir un constructo psicológico universal a partir de indicadores conductuales que incluyan los específicos de cada cultura. En este caso, la comparación requiere poner en la misma escala los tests desarrollados específicamente para cada cultura.
5. Análisis del funcionamiento diferencial de los ítems (FDI). La exclusión de los ítems con FDI es una práctica habitual en la construcción de tests libres de sesgo cultural o social. El término funcionamiento diferencial de los ítems se refiere a diferencias en los estadísticos de los ítems de los tests entre grupos sociales o culturales que tienen el mismo nivel en el atributo medido. La inclusión de este tipo de ítems en pruebas empleadas para la evaluación académica, la acreditación profesional, la admisión en la universidad, etc., puede favorecer injustamente a alguno de los grupos. La detección del FDI desde los modelos de la TRI requiere situar en la misma escala las estimaciones de los parámetros de los ítems correspondientes a los distintos grupos.
La metodología para poner en la misma métrica las puntuaciones de distintos tests fue denominada equiparación de puntuaciones en la literatura psicométrica clásica. En la actualidad, el término equiparación se reserva para el proceso de derivar puntuaciones estrictamente intercambiables entre formas paralelas o equivalentes del mismo test (AERA, APA y NCME, 1999; Navas, 2000). Se denomina escalamiento en la misma métrica al proceso de situar en una escala común las puntuaciones de tests que miden el mismo constructo, pero que pueden tener distintas características (formato de los ítems, dificultad, etc). En este último término, se inscribe la metodología descrita en este trabajo.
El número de publicaciones aparecido sobre este tema en la literatura psicométrica especializada ha sido ingente. Para el lector interesado, recomendaríamos la monografía de Kolen y Brennan (1995). En castellano se han publicado asimismo excelentes trabajos (Navas, 1996 y 2000). La metodología para establecer una equiparación de las puntuaciones de distintos tests no es un campo específico del modelo de Rasch o de otros modelos de la TRI. Como señala Muñiz (1997), éste es un tema que no recibió mucha atención por parte de la Psicometría Clásica, como se manifiesta en el nulo o escaso tratamiento en textos clásicos como los de Gulliksen (1950), Lord y Novick (1968) y los Standards de la APA de 1974. No obstante, algunos autores como Angoff (1984) desarrollaron técnicas de equiparación desde la Teoría Clásica de los Tests (en adelante, TCT). Ciertamente estos procedimientos clásicos son eficientes cuando las puntuaciones a equiparar son altamente fiables y se distribuyen de forma similar (Embretson y Reise, 2000). Cuando estas condiciones no se cumplen, aparecen errores en la equiparación, especialmente cuando los tests tienen distinta dificultad (Peterson, Marco y Stewart, 1982). Este es el caso de los tests que hemos utilizado en este trabajo, en el que se pretende escalar en la misma métrica dos tests de distinta dificultad. Para solventar estos problemas, es preferible recurrir a la metodología de equiparación desarrollada en el marco de la TRI, dado que esta teoría tiene indudables ventajas respecto de la TCT. Como se señala más adelante, estas ventajas son especialmente relevantes en el caso de los modelos tipo Rasch, tanto en el modelo inicial de Rasch para ítems dicotómicos como en sus extensiones para ítems politómicos (Masters y Wright, 1982 y 1996).
El objetivo general de este trabajo es ilustrar el procedimiento de escalamiento común mediante un modelo TRI con óptimas características métricas formulado por Rasch en 1960.
El modelo de Rasch
Desde comienzos del siglo XX, la construcción y el uso de tests psicométricos se ha basado principalmente en la TCT, un modelo simple, flexible y muy conocido (Gulliksen, 1950), pero que no está exento de limitaciones (Embretson y Hershberger, 1999).
En 1960 el matemático danés Georg Rasch propuso un modelo de medida que permite solventar muchas de las deficiencias de la TCT y construir pruebas más adecuadas y eficientes, por lo que está creciendo su aplicación en el ámbito de la evaluación psicológica y educativa. La formulación más conocida del modelo de Rasch, por su difusión en los textos de TRI (Embretson y Reise, 2000; Hambleton, Swaminathan y Rogers, 1991; Muñiz, 1997), se deriva de la predicción de la probabilidad de una respuesta al ítem (resolverlo correctamente, estar de acuerdo, etc.) a partir de la diferencia en el atributo entre el nivel de la persona (?s) y el nivel del ítem (ßi). En este caso,
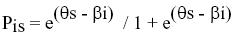
Donde e es la base de los logaritmos naturales (2,7183).
Como en el resto de los modelos TRI y a diferencia de la TCT, los valores escalares de las personas y los ítems se sitúan en la misma escala (por esta razón la medición TRI es denominada medición conjunta o escalamiento simultáneo, de acuerdo con la clásica taxonomía formulada por Torgerson en 1958). Estos valores pueden expresarse en distintas métricas (Embretson y Reise, 2000). La más utilizada es la escala logit, que es el logaritmo natural de (Pis /1 - Pis,) es decir, ?s - ßi. Aunque la escala logit puede adoptar valores entre más y menos infinito, la gran mayoría de los casos se sitúa en el rango ± 5. La localización del punto 0 de la escala es arbitraria. En la tradición de Rasch, se suele situar dicho punto en la dificultad media de los ítems. Por ello, cuando se estiman los parámetros de los ítems y de las personas de distintos tests, los valores están en escalas con un origen diferente: el punto 0 de cada test se sitúa en la dificultad media de los ítems que lo integran. En consecuencia, es necesario efectuar un escalamiento común con el mismo origen y la misma unidad de medida.
Las ventajas del modelo de Rasch respecto a la TCT y a otros modelos TRI han sido ampliamente difundidas (Andrich, 1988; Bond y Fox, 2001; Embretson y Hershberger, 1999; Embretson y Reise, 2000; Hambleton, Swaminathan y Rogers, 1991; Prieto y Delgado, 2003; Wright y Stone, 1979). Destacaremos aquí las características que, a nuestro juicio, son más relevantes: medición conjunta, estadísticos suficientes, objetividad específica, propiedades de intervalo, especificidad del error típico de medida y ajuste de los patrones de respuesta de los sujetos al modelo.
Medición conjunta. Significa que los parámetros de las personas y de los ítems se expresan en las mismas unidades y se localizan en el mismo continuo. En primer lugar, esta propiedad confiere al modelo de Rasch un carácter más realista que el de la TCT, puesto que no es razonable mantener el supuesto de la invarianza de los ítems: es obvio que no todos los ítems miden la misma cantidad del constructo. En segundo lugar, esta característica permite analizar las interacciones entre las personas y los ítems. En consecuencia, la interpretación de las puntuaciones no se fundamenta necesariamente en normas de grupo, sino en la identificación de los ítems que la persona tiene una alta o baja probabilidad de resolver correctamente. Esta característica dota al modelo de Rasch de una gran riqueza diagnóstica.
Estadísticos suficientes. La estimación de los parámetros de las personas depende únicamente de las puntuaciones en el test, no de la expresión concreta del vector de respuestas ni de suposiciones adicionales, puesto que la probabilidad de un vector de respuestas para un nivel de aptitud determinado, depende únicamente del número de aciertos. Esta propiedad sólo la tienen los modelos tipo-Rasch (Santisteban y Alvarado, 2001).
Objetividad específica. Una medida sólo puede ser considerada válida y generalizable si no depende de las condiciones específicas con que ha sido obtenida. Es decir, la diferencia entre dos personas en un atributo no debe depender de los ítems específicos con los que sea estimada. Igualmente, la diferencia entre dos ítems no debe depender de las personas específicas que se utilicen para cuantificarla. Esta propiedad fue denominada objetividad específica por Rasch (1977).
Supóngase que dos personas de distinto nivel contestan al mismo ítem. De acuerdo con la ecuación (1):
ln (Pi1 / 1 – Pi1 ) = ?1 -ß i , y ln (Pi2 / 1 - Pi2 ) = ?2 - ßi .
La diferencia entre ambas personas será igual a:
ln (Pi1 / 1 - Pi1 ) - ln (Pi2 / 1 - Pi2 ) = (θ1 - βi ) - (θ2 - βi ) = θ1- β2.
De forma similar, si la misma persona contesta a dos ítems de diferente dificultad:
ln (P1s / 1 - P1s ) = θs - β1, y ln (P2s / 1 - P2s ) = θs - β2 .
La diferencia en dificultad entre ambos ítems será igual a:
ln (P1s / 1 - P1s ) - ln (P2s / 1 - P2s ) = (θs - β1 ) - (θs - β2 ) = β1- β2.
En consecuencia, si los datos se ajustan al modelo, las comparaciones entre personas son independientes de los ítems administrados y las estimaciones de los parámetros de los ítems no estarán influenciadas por la distribución de la muestra que se usa para la calibración. Nótese que en la TCT las puntuaciones de las personas dependen de los ítems administrados y la dificultad de los ítems puede variar entre grupos de personas. En la propiedad de objetividad específica se fundamentan aplicaciones psicométricas muy importantes como la equiparación de puntuaciones obtenidas con distintos tests (el objetivo principal de este trabajo), la construcción de bancos de ítems y los tests adaptados al sujeto.
Propiedades de intervalo
Es importante notar que la interpretación de las diferencias en la escala es la misma a lo largo del atributo medido. Es decir, a diferencias iguales entre un sujeto y un ítem le corresponden probabilidades idénticas de una respuesta correcta. Por ello, la escala logit tiene propiedades de intervalo. Por el contrario, en la TCT las puntuaciones son casi siempre ordinales. Para los partidarios de la medición dirigida (Burke, 1963), la métrica intervalar tiene gran importancia, puesto que es una condición necesaria para usar con rigor los análisis paramétricos más frecuentemente empleados en las ciencias sociales (análisis de varianza, regresión, etc) y, además, garantiza la invarianza de las puntuaciones diferenciales a lo largo del continuo (un requisito imprescindible en el análisis del cambio).
Especificidad del error estándar
Como han subrayado Embretson y Reise (2000), la objetividad específica no implica que la precisión de las estimaciones de los parámetros sea similar en distintos conjuntos de ítems y de personas. Si los ítems son fáciles, se estimarán con más precisión los parámetros de los sujetos de bajo nivel. De forma similar, si los sujetos son de alto nivel, se estimarán con mayor precisión los parámetros de los ítems difíciles. En la TCT, se supone que los tests miden con la misma fiabilidad en todas las regiones de la variable. El modelo de Rasch no asume este supuesto tan poco verosímil. Permite, por el contrario: (i) cuantificar el error estándar con el que se mide en cada punto de la dimensión y (ii) seleccionar los ítems que permiten decrementar el error en regiones del atributo previamente especificadas. Este último aspecto es de sumo interés en los tests referidos al criterio, en los que interesa maximizar la fiabilidad en torno a los puntos de corte.
Ajuste de los datos al modelo
Las ventajas del modelo de Rasch sólo pueden ser obtenidas si los datos empíricos se ajustan al modelo. De acuerdo con la ecuación (1), la probabilidad de respuesta a un ítem depende sólo de los niveles de la persona y el ítem en el atributo medido. La presencia de respuestas aberrantes tales como que personas poco competentes resuelvan correctamente ítems difíciles, indicarían que los parámetros de sujetos e ítems son meros numerales carentes de significado teórico. La falta de ajuste podría deberse a diversos factores: multidimensionalidad o sesgo de los ítems, falta de precisión en el enunciado o en las opciones, respuestas al azar, falta de motivación o cooperación, errores al anotar la respuesta, copiado de la solución correcta, etc (Karabatsos, 2000a). Los procedimientos de análisis permiten detectar los ítems y las personas que no se ajustan al modelo. Este segundo aspecto (el ajuste de las personas al modelo) ha recibido más atención en los modelos tipo Rasch que en el resto de los modelos TRI. Se han propuesto diversos estadísticos para evaluar el ajuste de los datos (Karabatsos, 2000a, 2000b; Masters y Wright , 1996; Meijer y Sijtsma, 2001; Smith, 2000). Aquí mencionaremos los estadísticos basados en residuos (diferencias entre las respuestas observadas y las esperadas), debido a que están implementados en los programas de ordenador más usados. La fórmula de un residuo es:

Donde xis es la respuesta observada y Pis la probabilidad de una respuesta correcta de la persona s al ítem i.
Se suelen estandarizar los residuos dividiéndolos por su desviación típica:

Para cuantificar el ajuste al modelo, se emplea preferentemente el estadístico Infit que es la media de los residuos cuadráticos ponderados con su varianza (Wis).

Se puede calcular Infit para un ítem o una persona promediando los valores correspondientes. El valor esperado de este estadístico es 1. Por convención se considera que los valores superiores a 1,3 indican desajuste en muestras con menos de 500 casos, 1,2 en muestras de tamaño medio (entre 500 y 1000 casos) y 1,1 en muestras con más de 1000 casos (Smith, Schumaker y Bush, 1995). Los programas de ordenador aportan representaciones gráficas que facilitan la interpretación de los estadísticos de ajuste.
Procedimiento básico para establecer el escalamiento común
Supongamos que se desea escalar en la misma métrica dos tests (A y B) que miden el mismo atributo pero que tienen ítems diferentes (contenido, formato, dificultad, etc). El procedimiento consiste en incluir en ambos tests un número de ítems comunes (K) que se denomina test de anclaje. Cada test se administra a una muestra de personas (incluyendo el test de anclaje) y se estiman los parámetros de dificultad de los ítems (β) separadamente en cada muestra. Para cada ítem de anclaje, se dispone de un par de valores de dificultad procedentes de la aplicación del test A (βiA) y del test B (βiB). A partir de los pares de valores de los ítems de anclaje, se determina la constante (GAB) que permitirá situar los parámetros de los ítems del test B a la métrica del test A. De acuerdo con Wright y Stone (1979), la constante será:

La calidad del procedimiento de escalamiento depende de la existencia de una serie de características (Navas, 1996):
1. Una relación lineal entre los parámetros de dificultad de los ítems de anclaje en ambos tests.
2. Un número suficiente de ítems de anclaje (en torno al 20% de los ítems del test).
3. Muestras suficientemente grandes para estimar adecuadamente los parámetros de los ítems (en torno a 200 casos).
4. Los ítems de anclaje deben de aplicarse en el mismo orden en ambas pruebas y deben de tener características similares al del resto de los ítems del test (rango de dificultad, contenido, etc).
Procedimientos informáticos
Afortunadamente equiparar o poner en la misma métrica distintos tests es un proceso sencillo y poco laborioso cuando se recurre a alguno de los programas informáticos al alcance de los usuarios. A nuestro juicio, cualquiera de los programas más empleados dedicados al modelo de Rasch, tales como Quest (Adams y Khoo, 1996), Conquest (Wu, Adams y Wilson, 1998), Winsteps (Wright y Linacre, 1998) o RUMM (Sheridan, Andrich y Luo,1996) permiten efectuar el proceso de equiparación de forma muy simple.
Objetivos
El diseño de los items desde la perspectiva de la psicología cognitiva es una de las corrientes actuales más importantes en la construcción de tests de aptitudes (Embretson, 1996; Irvine y Kyllonen, 2002). La utilización de principios cognitivos en la planificación de un test requiere partir de hipótesis en las que se especifique la influencia de las características de los ítems en la complejidad cognitiva de la tarea (los procesos cognitivos, las estrategias y las estructuras de conocimiento implicadas en la resolución). En consecuencia, la generación de los ítems parte de un diseño experimental en el que, por un lado, se seleccionan las características de los estímulos que inducen el uso de los procesos relevantes para medir el constructo y, por otro, permiten controlar las características asociadas a los procesos irrelevantes.
Los análisis empíricos permiten contrastar si los ítems representan la peculiaridad cognitiva que se supone y, en consecuencia, representan adecuadamente el constructo. Uno de los procedimientos heurísticos más utilizados en este enfoque es el análisis de la influencia en la dificultad de los ítems de las condiciones experimentales de la tarea (Lohman, 2000).
El objetivo primario de este trabajo es ilustrar el procedimiento de escalamiento común de dos tests de visualización espacial, construidos a partir de los nuevos enfoques de la psicología cognitiva e integrados por ítems de diversa complejidad y, en consecuencia, de distinta dificultad teórica.
Un segundo objetivo consiste en analizar la influencia de las condiciones de la tarea en la dificultad empírica de los ítems. Para lograr este objetivo, es imprescindible situar en la misma métrica los parámetros de dificultad de los ítems de ambos tests.
Método
Participantes
En este estudio participaron 397 alumnos brasileños del primer curso de los estudios de Ingeniería, procedentes de la Universidad Estadual Paulista (Campus de Guaratingueta, São Paulo), de la Escuela Politécnica de la Universidad de São Paulo y de la Facultad de Ingeniería Química de Lorena. La edad media de los participantes era 19 años y la desviación típica de 3 años y 6 meses. La mayor parte de los encuestados eran varones (66,50%).
Instrumento
Se administraron las formas A y B de un test de visualización espacial, denominado TVZ-2002, que es una versión actualizada del TVZ-2001 (Prieto y Delgado, 2002; Prieto y Velasco, 2002).
La visualización es una de las aptitudes más importantes de la aptitud espacial general. Ha sido definida como la habilidad para generar una imagen mental, llevar a cabo diversas transformaciones sobre la misma y retener los cambios producidos en la representación (Lohman, 1979). Desde una perspectiva cognitiva, Lohman (1988) propuso que las transformaciones mentales de la figura son los procesos más característicos de la visualización. La complejidad de la tarea vendría determinada por el número de transformaciones mentales requerido para solucionar un problema.
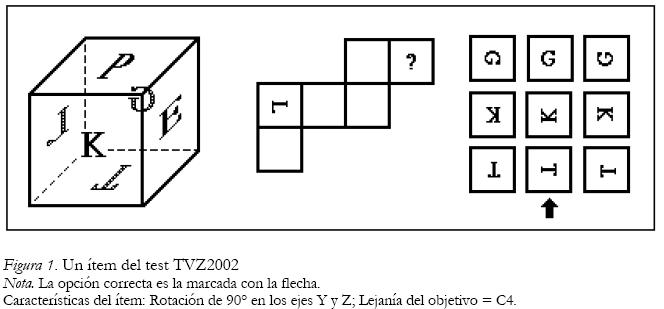
Con el objetivo de minimizar las estrategias de resolución analítico-verbales, hemos optado en el diseño del TVZ-2002 por usar en todos los ítems una figura regular. Cuando se emplean figuras irregulares, se facilita el etiquetado verbal de características distintivas de la figura (ángulos, tamaño, etc) que permite el empleo de procesos que no son de carácter espacial. En consecuencia, la tarea consiste en un cubo en el que todas sus caras están identificadas con letras. A la derecha del cubo, aparece éste desplegado en el plano con una de sus caras identificada y otra marcada con una interrogación (?). Se pide al sujeto que identifique la letra de la cara marcada con la interrogación y su apariencia. El observador debe elegir la respuesta correcta entre las 9 opciones que se le facilitan (véase la Figura 1).
Los ítems se diseñaron con las siguientes condiciones:
1. Disparidad angular. El cubo y la figura desplegada pueden aparecer con disparidades angulares (rotaciones) de 0º y 90º.
2. Rotación en los siguientes ejes: Y (horizontal) y Z (profundidad). La finalidad de las condiciones 1 y 2 es inducir rotaciones mentales de toda la figura en uno o dos ejes.
3. Lejanía del objetivo (cara marcada con la interrogación) respecto de la cara identificada.Para operacionalizar la condición 3, se designan las caras del cubo de la siguiente forma:
C0: Cara identificada con una letra en el cubo desplegado.
C1: Cara adyacente a C0.
C2: Cara adyacente a C1.
C3: Cara adyacente a C2.
C4: Cara adyacente a C3.
C5: Cara adyacente a C4.
En el TVZ-2002 se han incluido ítems con la interrogación en las caras C2, C3, C4 y C5. Finalidad: inducir el número de transformaciones mentales de la figura, tales como plegamientos, torsiones, etc. Se asume que el número de transformaciones mentales se incrementará de acuerdo con el siguiente orden de las condiciones: C5>C4>C3>C2.
Las versiones A y B del test tenían 20 y 19 ítems respectivamente. Desde un punto de vista teórico, los ítems de la versión A eran más fáciles que los de la versión B, dado que en la primera se incluyeron fundamentalmente ítems con disparidad angular de 0º, rotación en un sólo eje y las condiciones C2 y C3 de la lejanía del objetivo. Por el contrario, en la versión B se incluyeron fundamentalmente ítems con disparidad angular de 90º, rotaciones en uno o dos ejes y las condiciones C4 y C5 de la lejanía del objetivo.
Ambas formas tenían, como anclaje, cuatro ítems comunes: ítems 1 (disparidad=0º, rotación en el eje Y y C2), 5 (disparidad=90º, rotación en el eje Y y C3), 9 (disparidad=0º, rotación en el eje Y y C4) y 16 (disparidad=90º, rotación en el eje Y y C5).
En la Figura 1 se muestra un ítem con las siguientes condiciones: disparidad angular 180º, rotación en el eje Z y lejanía del objetivo C4.
Procedimiento
Cada versión del test (A y B) fue administrada en una única sesión en las aulas habituales de los alumnos y por la misma aplicadora. La forma A fue administrada a 238 alumnos y la forma B a 159 alumnos. Las características de ambas muestras fueron equivalentes, por lo que no era esperable que presentasen diferencias en el constructo de visualización. Se siguieron las mismas instrucciones y los alumnos hicieron los mismos ejemplos para aprender y para practicar con la tarea. En ambas formas se empleó el mismo tiempo de ejecución (20 minutos).
Resultados
Para analizar los datos, se empleó el programa Quest (Adams y Khoo, 1996).
Calibración de ambas formas por separado
En primer lugar, se llevó a cabo, tanto la estimación de los parámetros de los ítems de cada forma por separado, como el análisis del ajuste de sus ítems al modelo de Rasch. Las ventajas del modelo de Rasch sólo pueden ser obtenidas si los datos empíricos se ajustan al modelo. Aquí hemos empleado el estadístico denominado Infit, debido a que es muy usual y está implementado en los programas de ordenador más usados.
Aunque sea conveniente para el usuario estudiar a fondo el manual del programa Quest, vamos a mostrar que los procedimientos básicos de análisis son muy sencillos.
En primer lugar, es necesario escribir los ficheros de datos y guardarlos en la modalidad de sólo texto. En la tabla 1 se muestra parte del fichero de datos de la Forma A.

En segundo lugar, se han de escribir los ficheros de comandos y guardarlos en la modalidad de sólo texto. En la tabla 2 se muestra el fichero de comandos de la Forma A.

Una vez preparados estos ficheros, han de ser almacenados en la carpeta del disco duro en la que está incluido el programa Quest.
Para ejecutar el análisis, se abre el programa Quest y se escribe el comando submit y el nombre del fichero de comandos. Tras pulsar la tecla intro, comienza a ejecutarse el análisis. Esta forma de proceder ha de ser similar en el resto de los análisis que describiremos en adelante.
Los resultados aparecen en la tabla 3.
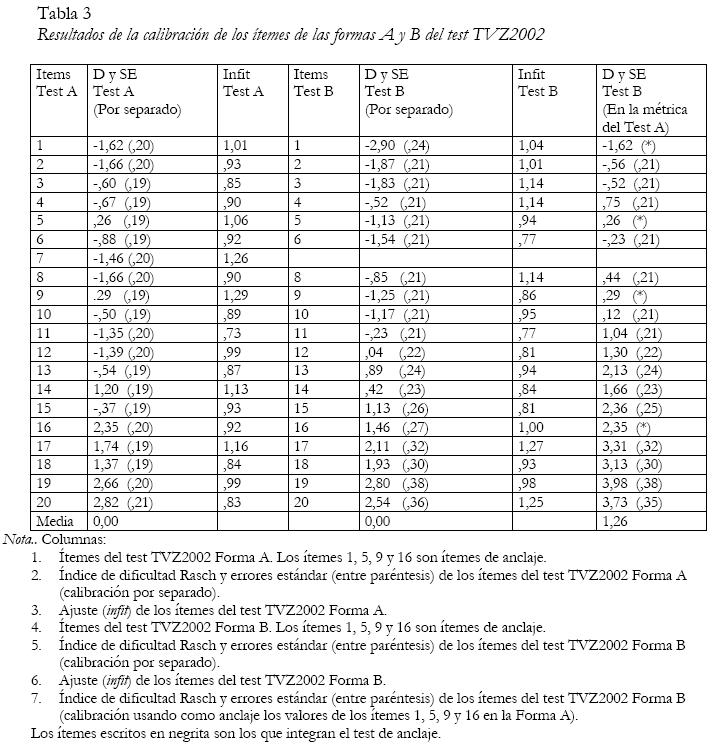
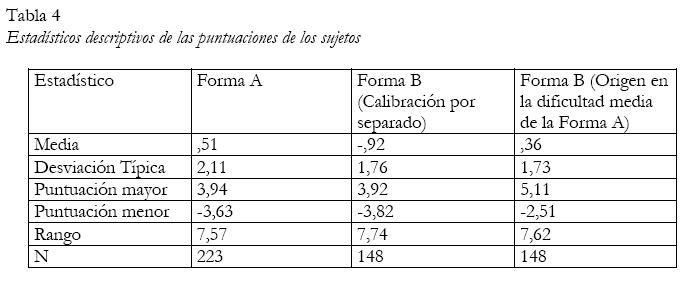
En las columnas segunda y quinta de la tabla 3 aparecen los parámetros de dificultad de los ítems y sus errores estándar en las formas A y B del test TVZ-2002, después de efectuar una calibración por separado de ambas pruebas. Obsérvese que en ambas formas la media de la dificultad de los ítems es igual a 0. Esta circunstancia ocurre siempre puesto que, como hemos indicado con anterioridad, el origen de la escala se suele situar convencionalmente en la dificultad media de los ítems. Por tanto, los parámetros de dificultad de los ítems de las dos formas no son directamente comparables cuando los tests han sido calibrados separadamente. Por ejemplo, observe, en la tabla 3 que los parámetros de dificultad de los ítems de anclaje (1, 5, 9 y 16) no son iguales en las calibraciones por separado de la forma A y la forma B. Esta cuestión suele desconcertar a los principiantes en el uso de los modelos TRI, dado que una de las propiedades más publicitadas es la independencia entre los parámetros de los ítems y la muestra de sujetos. La divergencia se debe a que las escalas de ambos tests no tienen un origen común. Sin embargo, los datos muestran que los parámetros de los ítems de anclaje están relacionados linealmente. En este caso, la correlación producto-momento de Pearson es de 0,99. Dado que las escalas tienen distinto origen, tampoco es posible comparar las puntuaciones de las personas que han realizado distintos tests. En la tabla 4 aparecen los estadísticos descriptivos de las muestras de sujetos que realizaron ambas formas. Como se ha indicado con anterioridad, las características de las muestras de alumnos que realizaron ambas formas del test fueron equivalentes, por lo que no era esperable que presentasen diferencias en el constructo de visualización. Sin embargo, las medias de ambas muestras difieren notablemente en los datos procedentes de la calibración por separado. De nuevo, se ha de tener en cuenta que la comparación de los sujetos que han hecho distintos tests requiere establecer una métrica común.
Establecimiento de una métrica común
Para establecer una métrica común, se ha de tomar la decisión del lugar en el que se quiere situar el origen de la escala general (el punto cero). En este estudio, hemos optado por situar el origen en la dificultad promedio de los ítems del test más fácil (forma A) y escalar la forma B en base a esta convención (escalamiento de la forma B en la métrica de la forma A). Para efectuar el escalamiento común se toma como referencia los parámetros de dificultad de los ítems de anclaje procedentes de la calibración por separado de la forma A. Observe en la tabla 3 que dichos parámetros son: ítem 1= -1,62; ítem 5= ,26=; ítem 9= ,29 e ítem 16= 2,35. Con dichos parámetros se construye el fichero de anclaje (tabla 5) que es el criterio para el escalamiento en la misma métrica, y que hemos denominado convencionalmente ancla par.

El fichero de anclaje se ha de guardar en la carpeta del disco duro en la que está incluido el programa Quest, junto con el de datos de la forma B y con el fichero de comandos escrito para realizar el anclaje (tabla 6). Todos estos ficheros deben de estar en la modalidad de sólo texto.

Los resultados del anclaje aparecen en las tablas 3 y 4.
En la última columna de la derecha de la tabla 3 se han incluido los parámetros de dificultad de los ítems de la forma B (en la misma métrica de la forma A). Como se esperaba, de acuerdo con el diseño de ambos tests, la dificultad media de la forma B (1,29) es superior a la de la forma A (0,00). Puede observarse que con ambos tests se cubre un amplio rango de competencia: desde –1,66 (dificultad del ítem más fácil) hasta 3,98 (dificultad del ítem más difícil).
En la última columna de la derecha de la tabla 4 aparecen los datos descriptivos de la muestra de alumnos que cumplimentó la forma B (en la misma métrica de la forma A). En base a estos datos es posible comparar la ejecución de las dos muestras de alumnos, aunque hayan efectuado distintos tests. Como se esperaba, las medias de ambas muestras (Muestra B = ,36; Muestra A= ,51) no difieren significativamente (t de Student = ,75; gl= 369).
Interpretación de la dificultad de los ítems
Este apartado se refiere al objetivo secundario de este trabajo: ¿cómo influyen las condiciones experimentales que han guiado el diseño de la tarea (disparidad angular, rotación en unos o dos ejes, lejanía del objetivo) en su dificultad empírica?.
Para obtener datos que permitan contestar a la pregunta anterior, se ha llevado a cabo un análisis de regresión múltiple paso a paso, en el que se predijo la dificultad de los ítems de ambas formas a partir de las tres variables predictoras antes mencionadas. Como es obvio, es necesario utilizar los parámetros de dificultad en la métrica común.
La correlación múltiple (R = 0,95) indica que las condiciones experimentales de la tarea explican el 90% de la varianza de la dificultad de los ítems. El predictor más eficiente de la dificultad de la tarea es la lejanía del objetivo (R = 0,88; 77% de la varianza), el número de ejes de la rotación permite incrementar la explicación un 11% y la disparidad angular (grados de rotación) un 7% adicional.
Estos datos concuerdan con estudios similares (Embretson, 1996; Prieto y Delgado, 2002) y refuerzan la conclusión de que los altos niveles de visualización están asociados a la capacidad para llevar a cabo transformaciones mentales de figuras tridimensionales: plegamientos y traslaciones de partes de la figura, giros, etc (Lohman, 1988). En los últimos años, se ha asociado la habilidad para manipular mentalmente la figura con la memoria de trabajo visual. Desde este punto de vista, el almacenamiento temporal, el mantenimiento activo y el control de las transformaciones jugarían un papel relevante en las tareas de visualización (Logie, 1995; Miyake y Shah, 1999).
Esta interpretación se ve facilitada visualizando las características de los ítems extremos en el rango de dificultad (Figura 2).
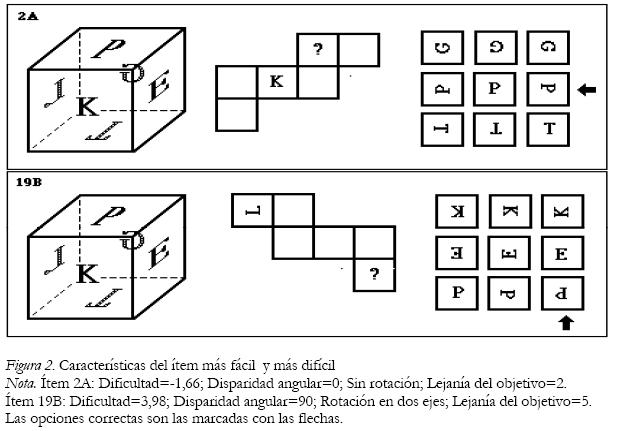
Conclusión
El objetivo básico de este trabajo es de carácter tutorial. Hemos tratado de exponer diversas circunstancias de la práctica psicoeducativa en las que es imprescindible usar distintas pruebas y poner sus resultados en una métrica común. Esta metodología está muy facilitada por los nuevos modelos psicométricos derivados de la teoría de respuesta al ítem, entre los que el modelo de Rasch ocupa un lugar preferente, dadas sus óptimas propiedades métricas. Hemos tratado de ilustrar de manera práctica el procedimiento, mediante un ejemplo empírico en el que se escalan conjuntamente dos tests de visualización de distinta dificultad hipotética. Finalmente, aunque se trataba de un objetivo secundario, hemos analizado empíricamente de forma sucinta la influencia de las condiciones de la tarea en la variable medida, a fin de inferir qué procesos cognitivos podrían ser la fuente de la dificultad.
Desde nuestro punto de vista, el software psicométrico permite simplificar extraordinariamente los procedimientos, por lo que se puede aventurar que el escalamiento común de distintas pruebas será una práctica extendida en los próximos años.
Referencias
Adams, R.J. & Khoo, S. (1996). Quest: The interactive test analysis system. Victoria: ACER. [ Links ]
American Educational Research Association (AERA), American Psychological Association (APA) & National Council on Measurement in Education (NCME). (1999). Standards for educational and psychological testing. Washington, DC: AERA. [ Links ]
American Psychological Association (1979). Standards for educational and psychological tests and manuals. Wahshington, DC: Autor. [ Links ]
Andrich, D. (1988). Rasch models for measurement. Newbury Park: Sage. [ Links ]
Angoff, W. H. (1984). Scales, Norms and Equivalent Scores. Princeton, NJ: Educational Testing Service. [ Links ]
Assessment Systems Corporation (1995). The Rasch model item calibration program. User´s manual for the MicroCAT testing system. St. Paul, Minnesota. [ Links ]
Bond, T.G. & Fox, C.M. (2001). Applying the Rasch model: fundamental measurement in the human sciences. Mahwah, NJ: LEA. [ Links ]
Burke, C.J. (1963). Measurement scale and statistical models. En M.H. Marx (Ed.). Theories in contemporary psychology. New York: Macmillan. [ Links ]
Embretson, S.E. (1996). Cognitive Design Principles and the Successful Performer: A Study on Spatial Ability. Journal of Educational Measurement, 33, 29-39. [ Links ]
Embretson, S.E. & Hershberger, S.L. (1999). The new rules of measurement. Mahwah, NJ: LEA. [ Links ]
Embretson, S.E. & Reise, S.P. (2000) Item response theory for psychologists. Mahwah, NJ: LEA. [ Links ]
Gulliksen, H. (1950). Theory of mental tests. New York: Wiley. [ Links ]
Hambleton, R. K., Swaminathan, H. & Rogers, H. J. (1991). Fundamentals of item response theory. Beverly Hills, CA: Sage. [ Links ]
Hui, C. H. & Triandis, H. C. (1985). Measurement in cross-cultural psychology: a review and comparison of strategies. Journal of Cross-Cultural Psychology, 16, 131-152. [ Links ]
Irvine, S.H. & Kyllonen, P. (2002). Item generation for test development. Mahwah, NJ: LEA. [ Links ]
Karabatsos, G. (2000a). A critique of Rasch residual fit statistics. Journal of Applied Measurement, 1, 152-176. [ Links ]
Karabatsos, G. (2000b). Using Rasch measures for Rasch model fit analysis. Popular Measurement, 3, 70-71. [ Links ]
Logie, R.H. (1995). Visuo-Spatial Working Memory. Hove: LEA. [ Links ]
Lohman, D.F. (1979). Spatial ability: A review and reanalysis of the correlational literature (Tech. Rep. No. 8). Stanford, CA: Stanford University Press. [ Links ]
Lohman, D.F. (1988). Spatial abilities as traits, processes and knowledge. En R.J. Sternberg (Ed.), Advances in the psychology of human intelligence, Vol. 4. Hillsdale, NJ: Lawrence Erlbaum Associates. [ Links ]
Lohman, D.F. (2000). Complex information processing and intelligence. En R.J.Sternberg (Ed.) Handbook of Intelligence. (pp. 285-340). Cambridge, UK: Cambridge University Press. [ Links ]
Lord, F.M. & Novick, M.R. (1968). Statistical theories of mental tests scores, Reading, Mass.: Addison-Wesley. [ Links ]
Masters, G.N. & Wright, B.D. (1982). Rating scale analysis. Chicago: MESA Press. [ Links ]
Masters, G.N. & Wright, B.D. (1996). The partial credit model. En W.J. van der Linden y R.K. Hambleton (Eds.). Handbook of modern item response theory. New York: Springer. [ Links ]
Meijer, R.R. & Sijtsma, K. (2001). Methodology review: Evaluating person fit. Applied Psychological Measurement, 25, 107-135. [ Links ]
Miyake, A. & Shah, P. (1999). Toward unified theories of working memory. Emerging general consensus, unresolved theoretical issues, and future research directions. En A. Miyake & P. Shah (Eds.), Models of working memory. Mechanisms of active mainenance and executive control. Cambridge, UK: Cambridge University Press. [ Links ]
Muñiz, J. (1997). Introducción a la teoría de respuesta a los ítems. Madrid: Pirámide. [ Links ]
Navas, M.J. (1996). Equiparación de puntuaciones. En J. Muñiz (Coord.) Psicometria. Madrid: Universitas. [ Links ]
Navas, M.J. (2000). Equiparación de puntuaciones: exigencias actuales y retos de cara al futuro. Metodología de las Ciencias del Comportamiento, 2, 151-165. [ Links ]
Peterson, N., Marco, G. & Steward, E. (1982). A test of the adecuacy of linear score equating models. En P. Holland & D. Rubin (Eds.), Tests equating. New York: Academic Press. [ Links ]
Prieto, G. & Almeida, L.S. (1997). Equivalência de puntuaçoes nos testes: Uma solução psicométrica para o dilema émic-étic na avalição psicológica. Psicologia. Teoria, investigaçao e práctica, 2, 19-29. [ Links ]
Prieto, G. & Delgado, A.R. (2002). Diseño cognitivo de un banco de ítems de visualización espacial. Metodología de las Ciencias del Comportamiento, volumen especial, 452-455. [ Links ]
Prieto, G. & Delgado, A.R. (2003). Análisis de un test mediante el modelo de Rasch. Psicothema, 15, 94-100. [ Links ]
Prieto, G. & Velasco, A. D. (2002). Construção de um teste de visualização a partir da psicologia cognitiva. Avaliação Psicologica,1, 39-47. [ Links ]
Rasch, G. (1960). Probabilistic models for some intelligence and attainment tests. Copenhagen: Danish Institute for Educational Research. [ Links ]
Rasch, G. (1977). On specific objectivity: An attempt at formalizing the request for generality and validity of scientific statements. En M. Glegvad (Ed.). The Danish Yearbook of Philosophy. Copenhagen: Munksgarrd. [ Links ]
Santisteban, C. & Alvarado, J.M. (2001). Modelos psicométricos. Madrid: UNED. [ Links ]
Sheridan, B., Andrich, D. & Luo, G. (1996). Welcome to RUMM: A windows-based item analysis program employing Rasch unidimensional measurement models. User´s Guide. [ Links ]
Smith, R.M. (2000). Fit analysis in latent trait measurement models. Journal of Applied Measurement, 1, 199-218. [ Links ]
Smith, R.M., Schumaker, R.E. & Bush, M.J. (1998). Using item mean squares to evaluate fit to the Rasch model. Journal of Outcome Measurement, 2, 66-78. [ Links ]
Spindler, L.G. (1975). Researching the psychology of cultural-change. En T. R.Williams (Ed.). Psychological Anthropology. The Hague: Mouton. [ Links ]
Torgerson, W.S. (1958). Theory and methods of scaling. New York: Wiley. [ Links ]
Wright, B.D. & Linacre, J.M. (1998). WINSTEPS : A Rasch computer program. Chicago: MESA Press. [ Links ]
Wright, B.D. & Stone, M.H. (1979). Best test design. Rasch measurement. Chicago: MESA Press. [ Links ]
Wu, M.L., Adams, R.J. & Wilson, M.R. (1998). ConQuest: Generalised Item Response Modelling Software. Victoria: ACER. [ Links ]
Artículo recibido: 30-5-2003
aceptado: 8-3-2004
*Dirección postal: Gerardo Prieto Adánez, Facultad de Psicología, Universidad de Salamanca, avenida de La Merced, 109-131. 37001 Salamanca, España. Ce: gprieto@usal.es














