Serviços Personalizados
artigo
Indicadores
Compartilhar
Psicologia: ciência e profissão
versão impressa ISSN 1414-9893
Psicol. cienc. prof. v.3 n.2 Brasília 1983
Evolução da noção de conservação de quantidade e desempenho em matemática*
Nelson RosamilhaI; Anália Rodrigues de FariaII
IInstituto de Psicologia da Universidade de São Paulo
IIFaculdade de Educação, Filosofia, Ciências Sociais e da Documentação. UNESP, Marília
RESUMO
Foram confrontadas nesta pesquisa a afirmação piagetiana de que o ensino da matemática deve basear-se no desenvolvimento das estruturas mentais da criança e a realidade do ensino dessa matéria na 1.ª série do primeiro grau. Estudou-se a relação existente entre a noção de conservação e o grau de desempenho em matemática. Constituíram a amostra 47 sujeitos da 1.ª série do 1.° grau (17 do sexo masc. e 30 do fem.), nível sócio-econômico médio-inferior para baixo-superior, idade de 6 anos e meio a 11 anos, sem escolarização anterior. A avaliação do desempenho relativo ao domínio da noção de conservação foi feita através do teste de conservação de quantidades descontínuas, e a do desempenho em matemática, através da observação sistemática e de uma prova. O coeficiente de correlação de postos de Good man e Kruskal (1945 e 1963] mostrou relação significante a um nível de 1% para conservação e porcentagem de acertos na prova (g = 0,7) e a um nível de 5% para a conservação e conceitos atribuídos pelo professor (G = 0,44). A análise dos dados categorizados pela técnica de Grizzle, Starmer e Koch (1969) a um nível de 5% indicou apenas efeito do fator sexo sobre a noção de conservação. Os resultados obtidos estão de acordo com a teoria piagetiana que indica ser a noção de conservação uma condição necessária para a aprendizagem da matemática, embora não suficiente.
A evasão e a repetência na primeira série do primeiro grau alcançam no Brasil índices muitos altos, ao redor de 50%. Isto é bastante grave quanto se consideram os problemas de escolarização e financiamento do ensino, sem falar nas conseqüências a médio e a longo prazo na atitude geral das crianças em relação à escola e à cultura (RosamiIha, 1979).
Um dos fatores que se supõe responsável pela configuração desse quadro é a falta de adequação dos programas de ensino às necessidades e possibilidades de cada fase de desenvolvimento infantil. Bruner (1975, p. 16) a esse respeito, assim se expressa: "O primeiro problema, e o mais óbvio, é como preparar currículos que possam ser aplicados por professores comuns a alunos comuns e, ao mesmo tempo, reflitam claramente os princípios básicos ou fundamentais dos vários campos da investigação. Este é um duplo problema: primeiro, de que modo reescrever as matérias básicas e refazer seus recursos de ensino, de forma a atribuir-se papel central às idéias e atitudes penetrantes e poderosas com eles relacionadas; segundo, como combinar os níveis desses recursos de ensino com as potencialidades de estudantes de diferentes capacidades, em diferentes níveis escolares". Rosamilha (1979), por exemplo, mostrou o papel das atividades lúdicas e jogos no desenvolvimento cognitivo, psicomotor e afetivo de crianças de primeira série, mesmo quando se tratavam de crianças repetentes, e que era possível aumentar significantemente o índice de aprovação na primeira série.
Piaget (1975, p. 17 e seg.) fala da necessidade do mestre não se limitar ao conhecimento de sua ciência, mas seja informado a respeito das peculiaridades do desenvolvimento psicogenético da inteligência da criança e do adolescente. Isto só se toma possível mediante um trabalho conjunto de vários especialistas, onde a figura do psicólogo escolar se torna indispensável para a prática dos métodos ativos nas escolas.
Em várias obras, Piaget e seus colaboradores têm sugerido que o ensino da matemática deva basear-se no desenvolvimento das estruturas mentais. Admitem que existe uma convergência entre as principais operações usadas espontaneamente pela criança e as noções aritméticas que a escola tenta inculcar abstratamente: "Na realidade, se o edifício da matemática repousa sobre estruturas que correspondem, por um lado, às estruturas da inteligência, é necessário basear a didática da matemática na organização progressiva destas estruturas". (Piaget et alii, 1963, p. 27). Piaget (1970, p. 46) mostra a tendência que existe desde o trabalho da Escola de Bourbaki para o ensino da matemática estar de acordo com uma seqüência de estruturas mentais. Entre elas destaca-se a noção de conservação de substância (processo de quantificação) que aparece depois de um longo período de construções mentais que se sucedem à construção da invariante do objeto sólido, na fase do pensamento sensório-motor. O aparecimento dessa noção se justifica por elaborações mentais sucessivas, das quais cada uma realiza um equilíbrio superior ao das precedentes e garante, ao mesmo tempo, equilibrações futuras.
Trata-se de um conhecimento lógico-matemático que surge no estágio operacional concreto, aproximadamente aos 7 anos de idade, sendo considerado por Piaget e Szeminska (1971) um pré-requisito para a aprendizagem da matemática. Como é empregada por Piaget, tal noção refere-se à compreensão de que certas propriedades (quantidade, número, comprimento, etc.) permanecem invariantes a despeito da ocorrência de mudanças perceptuais dessas mesmas propriedades.
Quando a criança entra na escola de primeiro grau, espera-se que já tenha adquirido a noção de conservação de quantidade ou se encontre numa fase de transição de um equilíbrio instável para um equilíbrio móvel, que só será alcançado mediante a descentração completa que caracteriza o agrupamento. O número tem sua base no agrupamento, pois extrai das classes a sua estrutura de inclusão (1 incluído em 2; 2 em 3; 3 em 4, etc.); e da ordem serial a propriedade de distinguir uma unidade da seguinte (1 depois de 1, depois de 2, etc). De acordo com Piaget (1961, p. 189): "O agrupamento realiza, assim, pela primeira vez, o equilíbrio entre a assimilação das coisas em face à ação do sujeito e à acomodação dos esquemas subjetivos às modificações das coisas", e isso ocorre quando as cinco transformações dos agrupamentos são produzidas. Essas transformações são as seguintes:
Composição: a composição de dois elementos quaisquer de um agrupamento, origina um novo elemento do mesmo agrupamento. Assim, dentro do pensamento lógico, duas classes distintas podem ser reunidas numa classe de conjunto que as engloba: duas relações A<B e B<C podem ser reunidas numa relação A<C que as contém etc.; ou do pensamento matemático: 2 + 3 = 5, 2 + 2 = 4, etc.
Reversibilidade: o que caracteriza qualquer transformação é a reversibilidade que permite que duas classes ou duas relações, quando unidas num primeiro momento, possam dissociar-se num segundo momento ou que a cada operação direta do pensamento matemático corresponda uma operação inversa (subtração implica na adição, a divisão comporta a multiplicação, etc.).
Associatividade: um mesmo resultado ou ponto de vista pode ser atingido por dois caminhos diferentes. A criança não duvida do ponto de vista lógico, que (A + A') + B = A + (A' + B), ou, do ponto de vista numérico, que se juntar à soma de dois números (2 + 1) um terceiro número (3) obtem-se o mesmo que se juntar um dos números considerados (2) à soma de outros dois (1 + 3).
Identidade: uma operação combinada com seu inverso é anulada, ou ainda, o retorno ao ponto de partida leva a encontrá-lo idêntico às suas partes diante da possibilidade dessas mesmas partes voltarem a compor o todo.
Identidades especiais ou tautologia: enquanto um elemento qualitativo repetido não acrescenta nada de novo a si mesmo, como no caso de A + A = A (tautologia), um elemento numérico, ou seja, uma unidade acrescentada a ela mesma leva a um número novo pela aplicação da composição; 1 + 1=2 (iteração). O número desencaixa-se em unidades para dar-lhe uma mobilidade operatória completa, enquanto a lógica as mantém encaixadas em totalidades de classes sem que elas percam seu significado.
Estas transformações próprias do agrupamento estão presentes quando a criança domina a noção de conservação que é concomitante ao domínio da noção de quantidade: "... a criança não chega de início à noção de quantidade, para atribuir-lhe em seguida a constância, mas ela só descobre a quantidade real no momento em que se torna capaz de construir totalidades que se conservam" (Piaget, 1971, p. 26). Estas transformações próprias do agrupamento parecem ser essenciais para a aprendizagem da matemática.
Apesar da importância do problema, os estudos que relacionam o desenvolvimento cognitivo com aprendizagem e, especialmente com a aprendizagem da matemática, não têm sido numerosos. As pesquisas nesta área têm enfocado mais a noção de igualdade numérica (quantidade) do que a noção de conservação de quantidade, que é uma aquisição posterior (Greco e Morf, 1962).
Elkind (1961) fez uma réplica do estudo de Piaget (1952) sobre o desenvolvimento do pensamento quantitativo e verificou que a noção de quantidade desenvolve-se em estádios ordenados hierarquicamente, resultado esse que estava de acordo com as descobertas de Piaget. No estádio III, quando a criança dominava a quantidade extensiva, era capaz de relacionar o todo com suas partes (Ex.: X é metade de Y, X é duas vezes Y). Cathcart (1971), partiu da hipótese de que raciocínios de identidade, reversibilidade e de compensação representavam um papel importante na aquisição da noção de conservação, a qual, por sua vez, afeta o nível de desempenho dos estudantes em matemática. Os resultados indicaram uma predominância do grupo de raciocínio reversível (7,44), seguido pelo grupo de raciocínio identidade operacional (6,71), depois pelo grupo de identidade real (5,79) e finalmente pelo grupo de raciocínio por compensação (5,20). O desempenho mais elevado, em matemática foi observado nos sujeitos que usavam vários tipos de raciocínio. Os resultados mostraram, ainda, uma relação significante entre tipos de raciocínio e inteligência, nível sócio-econômico e compreensão da linguagem e, também, relação significante entre tipos de raciocínio com idade e sexo. Omotoso (1975) verificou que existia relação entre as habilidades de conservação (comprimento, volume, número), classificação e, principalmente, seriação e desempenho em matemática. Verificou, ainda, que os meninos de 8 anos de idade tiveram um desempenho significativamente melhor que as meninas da mesma idade nas provas de conservação de comprimento e de volume. Também Rohr (1973) encontrou relações entre habilidade de conservação (número, massa, área e volume) e desempenho em matemática. Rowland (1973), por sua vez, verificou que no nível do estágio operacional concreto avançado, as crianças tinham um bom desempenho na medida de ângulos.
Entre as investigações que procuraram mostrar a influência dos fatores idade cronológica, sexo e nível sócio-econômico sobre a aquisição da noção de conservação encontramos os trabalhos de Goldschmid (1967), Bat-Haee (1971), Brekke e Willians (1973), Schorr (1975), além de muitos outros, embora os resultados das pesquisas nestes campos sejam, muitas vezes, conflitantes.
Partindo da aceitação da proposição de Piaget e Szeminska (1971, p. 24) de que "... trate-se de quantidades contínuas e descontínuas, de aspectos quantitativos percebidos no universo sensível ou de conjuntos e números percebidos pelo pensamento, trate-se de contatos mais primitivos da atividade numerativa, em qualquer lugar e sempre a conservação de alguma coisa é postulada pelo espírito a título de condição necessária de qualquer inteligência matemática", o objetivo principal deste trabalho é verificar se existe relação positiva entre o desempenho no teste de conservação de quantidades descontínuas e desempenho escolar em matemática, na fase inicial da escolarização do primeiro grau.
MÉTODO
Sujeitos:
A escola, sorteada para o estudo, estava situada numa zona periférica da cidade de Presidente Prudente, São Paulo, cuja população estudantil incluía o nível sócio-econômico médio-inferior e o baixo-superior. O levantamento dos dados que permitiram a classificação do nível sócio-econômico foi feito através da adaptação do questionário utilizado pela Equipe do Grupo Escola-Ginásio Experimental "Dr. Edmundo de Carvalho" de São Paulo (1972). Os 47 sujeitos da primeira série do primeiro grau (17 do sexo masculino e 30 do sexo feminino) apresentavam idades cronológicas que varia, dos 6 anos e meio aos 11 anos, sem apresentar nenhuma escolarização anterior.
Material e procedimentos para avaliação da noção de conservação:
O desempenho operatório foi avaliado através de uma prova piagetiana que avalia a conservação de quantidades descontínuas.
O teste foi construído a partir da análise de vários protocolos utilizados por Piaget e colaboradores (Piaget e Inhelder, 1971; Piaget e Szeminska, 1971; Inhelder, Sinclair e Bovet, 1974) que ilustram tipos de questões propostas para avaliar a noção de conservação. Essas questões enquadraram-se, na presente pesquisa, no modelo padronizado com base na forma sugerida por Goldschmid e Bentler (1968). Tal esquema foi adotado em função da necessidade de se dar um tratamento estatístico aos dados obtidos.
O material utilizado na prova incluía:
a) 2 copos idênticos;
b) 1 copo baixo e longo;
c) 4 frascos pequenos "beaker" de 50 ml;
d) 32 bolinhas de gude, de duas cores diferentes (16 brancas e 16 azuis).
O procedimento básico consistiu em sugerir à criança uma brincadeira: cada vez que colocávamos uma bolinha no copo A a criança colocava uma bolinha no copo A1. Terminada a operação de correspondência termo a termo concluía-se ou não se houvera apreensão da igualdade pela criança. A pergunta feita era se havia a mesma quantidade (ou o mesmo tanto) nos copos A e A1. Estabelecida a igualdade, procedia-se aos transvasamentos das bolinhas para os copos de tamanhos e formatos diferentes. Às respostas de julgamento (igual ou diferente) e de explicação (porque) seguia-se a pergunta relativa à possibilidade de se fazer dois colares com as bolinhas dos dois copos e se estes colares seriam iguais ou diferentes quanto ao tamanho e não quanto à cor (pergunta de previsão).
Procedimento para avaliação do desempenho em matemática:
O desempenho em matemática foi avaliado em função dos objetivos propostos no planejamento escolar semestral, através da observação sistemática da professora e através de uma prova de 25 questões, sendo obtida para cada aluno uma percentagem de acertos nesta prova.
A observação foi feita com base em uma ficha, previamente elaborada para esse fim, precedida do conhecimento de um rol de indicadores de rendimento em matemática, adaptado de um roteiro elaborado pela Equipe Técnica de Estudos de Rendimento Escolar, da Secretaria da Educação de São Paulo (1973, p. 71). A síntese das observações resultou em conceitos atribuídos a cada aluno: Desempenho Bom (DB), Desempenho Mediano (DM), Desempenho Fraco (DF).
RESULTADOS
Para testar a hipótese de que existe relação positiva entre o desempenho no teste de conservação de quantidades descontínuas e desempenho escolar em matemática, foram realizadas duas análises.
Na primeira análise foram estabelecidas classes de porcentagem de acertos para os resultados da prova de matemática, a fim de se colocar as freqüências relativas à classificação dos alunos de acordo com porcentagem de acertos e estádios mentais. Para isso especificou-se, a priori, uma divisão em três grupos: 1.° grupo, de 0 &— 50%, 2°, de 51% &— 75% e 3.° grupo, de 76% a 100%. Quanto aos estádios de desenvolvimento da noção de conservação, os alunos foram classificados em três: estádio I (não conservação), estádio II (conservação parcial), estádio III (conservação). Os dados aparecem na Tabela I.

O objetivo principal foi estudar, através de uma metodologia estatística apropriada**, se há uma equivalência entre categoria I de estádio mental e 1.° grupo de porcentagem de acertos na prova de matemática; categoria II de estádio mental e 2° grupo de porcentagem de acertos; categoria III de estádio mental e 3.° grupo de porcentagem de acertos. Para isso utilizamo-nos do teste de associação sobre a diagonal principal (Wada, 1977, p. 63), numa tabela de contingência 3 x 3, cuja hipótese formulada foi:
Ho: H .i = H i. H i i = 1, 2, 3
isto é, considerando-se a hipótese de não associação sobre a diagonal principal.
A soma dos quadrados para testar a hipótese é um X2 (qui quadrado) com 3 graus de liberdade.
Obteve-se, através dos cálculos estatísticos, o valor X2 = 8,00 e como o X2 crítico é de 7,81, rejeitou-se a hipótese de não associação ao nível de 5%. Existe, portanto, uma associação entre estádios da noção de conservação e porcentagem de acertos em uma prova de matemática.
Para verificar a associação não apenas sobre a diagonal principal, vista acima, utilizou-se o teste de independência X2 de Pearson. O resultado foi X2 = 20,56 que, para 4 graus de liberdade, é significante ao nível de 5%. As variáveis são, portanto, dependentes.
O grau de associação foi estimado através do coeficiente de correlação de postos de Goodman e Kruskal (1954 e 1963), nos níveis de significância de 5% e de 1%. O resultado foi G = 0,7. Isto revela a existência de forte relação, em concordância crescente, entre estádios da noção de conservação e desempenho escolar em matemática, medido através de uma prova.
Para a segunda análise, utilizou-se o mesmo procedimento apresentado acima. Para verificar a associação existente entre conceitos atribuídos em três níveis DF, DM e DB e estádios da noção de conservação I, II e III, construiu-se uma tabela de contingência 3 x 3, que aparece a seguir:
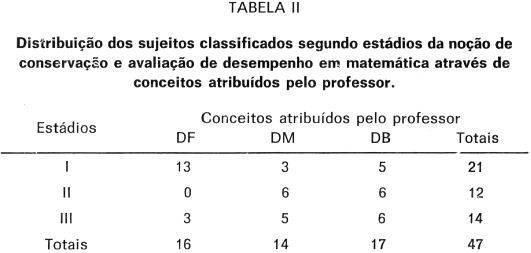
O teste de independência do X2 de Pearson resultou no X2 = 11,15. Para 4 graus de liberdade, ele é significante ao nível de 5%. As variáveis estádios da noção de conservação e conceitos do professor são, portanto, dependentes. O grau dessa associação, verificado através do coeficiente de correlação de postos de Goodman e Kruskal (1954 e 1963) é significante ao nível de 5%. Obteve-se um G = 0,4.
Uma terceira análise foi realizada com o objetivo de obter outras informações sobre os sujeitos, relativas a idade cronológica, sexo e nível-sócio-econômico. Duas tabelas de classificação cruzada foram elaboradas: na primeira foram considerados os fatores sexo, idade e os estádios de desenvolvimento da noção de conservação; na segunda, os fatores nível sócio-econômico, idade e estádios de desenvolvimento da noção de conservação. A Tabela III refere-se às variáveis sexo, idade e estádios da noção de conservação.
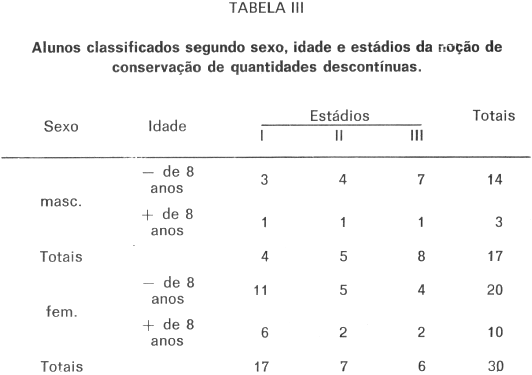
A análise dos dados da Tabela III foi feita através da formulação de logits (Williams e Grizzle, 1972). A análise de variância resultante pode ser vista na Tabela IV.

Esses resultados revelam que para:
a) X2 = 4,8703, há interação entre fatores sexo e estádios da noção de conservação, ao nível de significância de 5%;
b) X2 = 0,0665, existe homogeneidade na associação do fator sexo e categorias de estádios I, II e III, ao nível de 5% de significância;
c) X2 = 0,1923, existe interação entre os fatores idade e estádios da noção de conservação ao nível de 5%;
d) X2 = 0,1777, há ajuste do modelo aos dados e também, em outras palavras, a não interação entre sexo e idade;
A Tabela V refere-se ao nível sócio-econômico, idade e estádios, constituindo-se numa tabela de classificação cruzada, na qual o fator nível sócio-econômico é representado pelos níveis BI/BS (baixo inferior e baixo superior) e MI/MS (médio inferior e médio superior), o fator idade pelos grupos de menos de 8 anos e de mais de 8 anos e o fator estádios pelos algarismos romanos I, II e III.
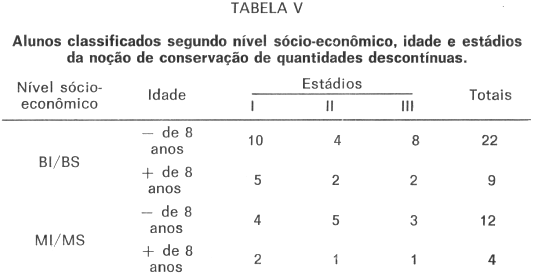
Os resultados da análise de variância encontram-se na Tabela VI.
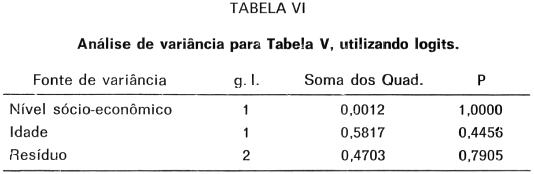
Esses resultados revelam que:
a) X2 = 0,0012 não é significante ao nível de 5% (X2 = 3,84), isto é, não existe relação entre os fatores nível sócio-econômico e estádios da noção de conservação;
b) X2 = 0,5817 não é significante ao nível de 5%, ou seja, não existe associação entre os fatores idade e estádios;
c) X2 = 0,4703 não é significante, isto é, o modelo se ajusta aos dados e é considerado também como indicação de não existência da interação entre nível sócio-econômico e idade.
DISCUSSÃO E CONCLUSÕES
A hipótese proposta para este trabalho foi confirmada, uma vez que ao nível de 5% e 1% foi significante (G1 = 0,7) o coeficiente de correlação de postos de Goodman e Krusikal (1954 e 1963), entre os dados resultantes do desempenho no teste de conservação de quantidades descontínuas e os dados resultantes da prova de matemática. Isso revela que existe uma forte associação, em concordância crescente, entre o desempenho nos testes de conservação e o desempenho escolar em matemática. O mesmo tipo de coeficiente foi calculado para os dados relativos ao desempenho no teste de conservação de quantidades descontínuas e ao desempenho escolar em matemática expresso através de conceitos, e obteve-se G2 = 0,44, significante a um nível de 5%.
Convém salientar que para ambos os tipos de verificação da escolaridade foi comum uma dificuldade: discernir entre uma aquisição mecânica do conteúdo matemático (hábito), de uma aquisição operatória. Aebli (1974, p. 67) demonstra que alguns conteúdos matemáticos podem ser adquiridos tanto através de uma coleção de hábitos, como através de um grupo de operações (tabuada, por exemplo) e chama atenção para o fato de a aprendizagem realizada pelo primeiro sistema ser rapidamente esquecida.
A despeito das limitações apontadas, os resultados estão de acordo com os estudos realizados por Piaget (1952) e replicados por Elkind (1961) revelando que a noção de quantidade desenvolve-se em estádios ordenados hierarquicamente. Isto parece exolicar a diferença de desempenho em matemática encontrada na presente pesquisa entre crianças de diferentes estádios (I, II e III).
Os dados confirmam as conclusões de Cathcart (1971), Rohr (1973), Rowland (1973), Omotoso (1975), segundo as quais o domínio da noção de conservação é fator importante para a aprendizagem da matemática, ficando evidente que o desempenho mais elevado em matemática está relacionado a estádios mais avançados da aquisição da noção de conservação.
A diferença de desempenho escolar em matemática a favor das crianças dos estádios mais avançados em relação aos menos avançados, constatada nesta pesquisa, sugere que o desenvolvimento das operações favorece a aprendizagem. Esta hipótese é apoiada pelo conceito de equilibração. O equilíbrio, como proposto pelos adeptos da escola de Genebra, ocorre em função de uma adaptação do pensamento a uma realidade particular, quando tal pensamento conseguir assimilar seus próprios quadros, às novas circunstâncias apresentadas por esta realidade. O aperfeiçoamento das regulações compensadoras (retroações e antecipações) constitui a base da equilibração entre a assimilação e a acomodação. Estas regulações estão ausentes no estádio I do processo de aquisição da noção de conservação (equilíbrio instável), daí a falta de coordenação das relações (igual e diferente). Elas começam a aparecer no estádio II e se completam no estádio III (equilíbrio estável ou móvel). Quando a criança atinge este último estádio, pode ter um maior controle sobre seu pensamento, uma vez que as regulações compensadoras lhe possibilitarão combinar uma sua ação com a outra, anular ou compensar ações anteriores, etc.
Verificando-se a existência de sujeitos que dominavam a noção de conservação e que tiveram baixo desempenho, tanto na avaliação expressa por um conceito, como através da prova, tentou-se identificar outros fatores, que pudessem influenciar o processo de aprendizagem. Para isso, procurou-se estudar dois sujeitos. Um desses sujeitos apresentava problema de deficiência visual (5,75 de miopia e 0,50 de astigmatismo no olho direito e 5,0 de miopia e 1,75 de astigmatismo no olho esquerdo); no outro sujeito o exame médico (eletroencefalograma) e o teste para avaliar o aspecto psicomotor, mostraram resultados dentro da normalidade. O teste da árvore revelou uma personalidade com agressividade reprimida, dificuldade de objetivação e de conhecimento das relações entre as coisas, que parecem constituir obstáculo para um natural desenvolvimento das potencialidades. Esta criança, de nível sócio-econômico baixo, mostrou na entrevista um nível motivacional também baixo em relação à escola e à sua futura vida profissional: "Não gosto da escola. Ela não serve para nada. Quando crescer serei empregada doméstica". Isso indica que tanto para a aprendizagem de leitura e de escrita, como na da matemática, há problemas de prontidão nas dimensões afetiva e psicomotora a serem considerados (cf. Rosamilha, 1979).
Estes dados ajudam a esclarecer a posição assumida por Piaget (1971, p. 23) ao tratar da conservação como pré-requisito da aprendizagem: "... dizemos simplesmente que a conservação constitui uma condição necessária de toda atividade racional, sem preocupar-nos em saber se essa condição é suficiente para explicar essa atividade ou exprimir a natureza da realidade". Aebli (1975) reforça esta posição afirmando que o educador, ao propor tarefas para determinada idade, não pode se apoiar num fator isolado mas deve considerar um conjunto de fatores nem sempre observados com facilidade.
Quanto ao efeito de outros fatores como idade cronológica, sexo e nível sócio-econômico no processo de aquisição da noção de conservação de quantidade descontínuas, a análise de variância indicou que existe efeito do fator sexo na resposta estádios de conservação. Estes resultados estão de acordo com os encontrados por Omotoso (1975), Goldschmid (1967), Palmer (1966), Faria e Teixeira (1977) que revelaram a superioridade de um sexo sobre o outro; neste caso, o exame da Tabela III mostra o sexo masculino como ligeiramente superior ao feminino. Por outro lado os dados mostraram que não existe efeito do nível sócio-econômico na resposta estádios da noção de conservação de quantidades descontínuas.
Convém considerar que os sujeitos pertenciam a duas faixas contíguas, ou seja, nível sócio-econômico baixo inferior e baixo superior (BI/BS) e médio inferior e médio superior (MI/MS) e de certa forma pouco diferenciadas entre si. Se a amostra contivesse também alunos de nível sócio-econômico elevado, talvez os resultados fossem diversos. Estudos de Schorr (1975) revelam que crianças de nível sócio-econômico médio mostraram maior aquisição da noção de conservação do que as crianças de nível sócio-econômico baixo. Além disso não se verificou interação do fator idade e estádios a um nível de 5%. Esse resultado concorda com os que foram encontrados por Cathcart (1971) e Goldschmid (1967), embora se deva admitir ressalvas no cotejo desses dados devido à divisão, nesta pesquisa, das idades dos sujeitos em dois níveis (mais de 8 anos e menos de 8 anos).
As explicações dadas por Piaget referem-se aos vários fatores responsáveis pelo desenvolvimento cognitivo e apoiam os resultados encontrados: "A prova deste caráter limitado do papel da maturação está em que, se os graus de desenvolvimento que acabamos de descrever se sucedem sempre na mesma ordem, do mesmo modo que os seus subgraus, o que bem demonstra o caráter "natural" e espontâneo de seu desenvolvimento seqüencial (cada um deles sendo necessário à preparação do seguinte e à conclusão do precedente), eles não correspondem, por sua vez, a idades absolutas, observando-se, pelo contrário, acelerações ou retardamentos segundo os diversos meios sociais e a experiência adquirida. Os psicólogos canadenses têm constatado, por exemplo, retardamento de até 4 anos, do ponto de vista de nossas provas operatórias..." (Piaget, 1970, p. 38).
Considerando-se que o domínio da noção de conservação de quantidades descontínuas é importante para a aprendizagem de conteúdos matemáticos, alguns estudiosos acham mais importante favorecer o desenvolvimento mental no pré-primário e mesmo no curso primário antes de introduzir os conhecimentos do currículo escolar. Furth (1972, p. 20) admite que, embora o desenvolvimento do pensamento seja espontâneo e independa da escola, esta pode ser organizada no sentido de facilitar a aprendizagem de conceitos permanentes de tempo, espaço, relações, classes, combinações, etc, que constituem a matéria-prima da inteligência. Alguns tipos de atividades, como as lúdicas empregadas por Rosamilha (1979), parecem atuar sobre o desenvolvimento das crianças. Elkind (1972, p. 124), por sua vez, levanta a hipótese seguinte: "... por mais tempo que retardarmos a instrução formal, até certos limites, maior é o período de plasticidade e mais alto o nível último de realização".
A preocupação dos psicólogos e educadores com a adequação da escola ao desenvolvimento mental da criança, já se reflete nos objetivos e programas de ensino do primeiro grau de nossas escolas (cf. Dib, Pfromm Netto e Rosamilha, 1979). Estes objetivos são estruturados visando não apenas à aprendizagem de conteúdos matemáticos, mas a aprendizagem do pensamento matemático que supõe técnicas específicas. Compete ao professor, ao ministrar o seu ensino, usar uma metodologia que explore os exercícios operatórios (coordenação de ações) presentes na construção da noção de conservação, bem como de outras estruturas mentais. Dienes (1970; 1975) sugere que se proporcione à criança manipulação de materiais concretos e semi-abstratos favorecendo uma rica variedade de experiências matemáticas, a partir das quais a criança pode construir conceitos matemáticos... A favor desse ponto de vista é pertinente a afirmação de Aebli (1974, p. 87): "Dizer que o aluno deve conhecer certas matérias, significa que deve aprender a executar certas operações. Sempre são as operações que definem as noções, e é sua execução que deve o ensino provocar, primeiro efetivamente e depois sob a forma "interiorizada" ou "representativa".
Em nosso meio tem havido esforços no sentido de planejar materiais instrucionais, como livros por exemplo, obedecendo a esses requisitos, lembrados por Bruner (1975). É o caso de Dib, Pfromm Netto e Rosamilha (1979) que prepararam uma série incluindo textos para alunos e para orientação do professor da primeira à quarta série, na área da matemática.
Ponto que devemos destacar, ainda, é que numa classe de 47 alunos de uma escola pública, verifica-se que apenas 14 deles atingiram o estádio III da noção de conservação (30%), que outros 12 (25%) estão na fase de alcançá-la e que 21 (45%) ainda não apresentam essas condições. Como agir em relação a essa realidade? Temos o direito de reprovar tais crianças? Obrigá-las a seguir o ritmo das mais avançadas? São questões importantes a considerar, principalmente se lembrarmos novamente do problema da repetência e evasão na primeira série.
As investigações feitas, nesta pesquisa, no campo cognitivo, bem como as proposições de numerosos estudiosos do assunto, fortalecem a idéia de que aprender e ensinar são tarefas complexas. Esta complexidade está a merecer aprofundamento de estudos que resultem em novas alternativas para uma metodologia e programas mais voltados para o desenvolvimento mental da criança. Caso contrário assistiremos fracassos escolares contínuos, com outras conseqüências, notadamente na matemática, com possíveis efeitos emocionais, como ansiedade e atitudes negativas (Rosamilha, 1971; Rosamilha e Cariola, 1980).
REFERÊNCIAS
AEBLI, H. — A Evolução Mental da Criança. Trad. do origina! alemão de 1963 por C. Benemann. Rio de Janeiro, Vozes, 1975. [ Links ]
AEBLI, H. — Didática Psicológica. Trad. do original francês de 1966 por J. T. D'Olim Marote. São Paulo, Nacional, 1974, 2ª ed. [ Links ]
BAT-HAEE, M. A. — Conservation of mass, weigt and volume in intermediate grades. Psychological Reports, 1971, 28 (1), 163-168. [ Links ]
BREKKE, L. e WILLIAMS, J. D. — Conservation and sex. Perceptual & Motor Skills, 1973, 37 (1), 14. [ Links ]
BRUNER, J. S. — O Processo da Educação. São Paulo, Companhia Editora Nacional, 1975. Quinta edição. [ Links ]
CATHCART, W. G. — The relationship between primary students rationalization of conservation and their mathematical achievement. Child Development. 1971, 42, 755-765. [ Links ]
DIB, C. Z., PFROMM NETTO, S. e ROSAMILHA, N. — Atividades em Matemática, primeira a quarta série do primeiro grau (Guia do Professor) Rio, Primor, 1979, 2ª edição revista. [ Links ]
DIENES, Z. P. — Aprendizado Moderno da Matemática. Trad. do original inglês de 1967 por José Enéas Fortes. Rio de Janeiro, Zahar, 1970. [ Links ]
DIENES, Z. P. — As Seis Etapas do Processo de Aprendizagem em Matemática. Trad. do original francês de 1967 por Maria Pia B. de M. Charlier e René François J. Charnier. São Paulo, E.P.U., 1975, primeira reimpressão. [ Links ]
ELKIND, D. — Crianças e Adolescentes. Ensaios interpretativos sobre Jean Piaget. Trad. do original americano de 1970 por N. de Almeida. Rio de Janeiro, Zahar, 1972. [ Links ]
ELKIND, D. — The development of quantitative thinking; a systematic replication of Piaget's studies. The Journal of Genetic Psychology. 1961, 98, 27-46. [ Links ]
FARIA, A. R. e TEIXEIRA, L. R. M. — Questões de contra-argumentação: efeito da apreensão de avaliação nos contra-argumentos, numa prova de conservação de quantidade. Trabalho apresentado ao curso de Pós-Graduação, USP, área de Psicologia do Escolar, 1977 (mim.) [ Links ]
FURTH, H. G. — Piaget na Sala de Aula. Trad, do original americano de 1970 por D. M. Garschagen. Rio de Janeiro, Forense, 1972, quarta edição. [ Links ]
GOLDSCHMID, M. L. — Different types of conservation and non-conservation and their relation to age, sex, IQ, MA, and vocabulary. Child Development. 1967, 38(4), 1230-1246. [ Links ]
GOLDSCHMID, M. L. e BENTLER, P. M. — Concept Assesment Kit-Conservation. San Diego, California, Educational and Industrial Testing Service, 1968. [ Links ]
GOODMAN, L. A. e KRUSKAL, W. K. — Measures of association for cross classifications. JASA, 49, 1954, 734-764. [ Links ]
GOODMAN, L. A. e KRUSKAL, W. K. — Measures of association for cross classifications. III: approximate sampling theory. JASA, 58, 1963, 310-364. [ Links ]
GRÉCO, P. e MORF, A. — Structures Numériques Élémentaires. Paris, Presses Universitaires de France, 1962. [ Links ]
INHELDER, B., SINCLAIR, M. e BOVET, M. — Apprentissage et Structures de la Connaissance. Paris, Presses Universitaires de France, 1974. [ Links ]
OMOTOSO, H. M. — Conservation, seriation and classification as factors in the acquisition of mathematics in nigerian children. Dissertation Abstracts International, 1975, 36 (3), 1398-A. [ Links ]
PALMER, E. L. — How Elementary School Children Resolve Experimentally Produced Conflicts in Ihinking. Tallahasse, Florida State University, 1966. [ Links ]
PIAGET, J. — Las estruturas matemáticas y las estruturas operatórias de la inteligência. Em Piaget, J. e col. — La Ensenanza de las Matemáticas. Madrid, Aguilar, 1963. [ Links ]
PIAGET, J. — Psicologia e Pedagogia. Trad. do original francês de 1969 por D. A. Lindoso. Rio de Janeiro, Forense, 1970. [ Links ]
PIAGET, J. e SZEMINSKA, A. — A Gênese do Número na Criança. Trad. do original francês de 1964 por C. M. Oiticica. Rio de Janeiro, Zahar, 1971. [ Links ]
PIAGET, J. e INHELDER, B. — O Desenvolvimento das Quantidades Físicas nas Crianças. Trad. do original francês de 1962, por C. M. Oiticica. Rio de Janeiro, Zahar, 1971a. [ Links ]
PIAGET, J. — Psicologia da Inteligência. Trad. do original francês de 1956 por E. de Alencar. Rio de Janeiro, Fundo de Cultura, 1961. [ Links ]
PIAGET, J. — Para Onde Vai a Educação? Trad. do original francês de 1948 por Ivette Braga. Rio de Janeiro, José Olympio, 1975. [ Links ]
ROHR, J. A. G. — The relationship of the ability to conserve on piagetian tasks to achievement in mathematics. Dissertation Abstracts International. 1973, 34 (5), 2398-A. [ Links ]
ROSAMILHA, N. e CARIOLA, T. — Ansiedade e atitudes em relação à matemática. Arquivos Brasileiros de Psicologia, 1980 (no prelo). [ Links ]
ROSAMILHA, N. — Psicologia da Ansiedade Infantil. São Paulo, Pioneira/Editora da USP, 1971. [ Links ]
ROSAMILHA, N. — Psicologia do Jogo e Aprendizagem Infantil. São Paulo, Pioneira, 1979. [ Links ]
ROWLAND, J. M. — Relations between children's developmental in learning angle measure, in upper elementary grades. Dissertation Abstracts International. 1973, 34 (1), 125-A. [ Links ]
SCHORR, M. — A study of the relationship between school experience, socio-economic status, and conservation attainment in first grade boys and girls. Dissertation Abstracts International, 1975, 36 (4), 2111-2112-A. [ Links ]
WADA, C. Y. — Análise de Dados Categóricos por Modelos Lineares. Tese de Mestrado. Instituto de Matemática e Estatística da Universidade de São Paulo, São Paulo, SP, 1977. [ Links ]
WILLIAMS, O. D. e GRIZZLE, J. E. — "Analyses of contingency tables having ordered response categories". JASA, 67, 1972, 55-63. [ Links ]
* Este trabalho é resultado parcial da pesquisa para dissertação de mestrado defendida por A. R. Faria na Universidade de São Paulo, sob orientação de N. Rosamilha.
** O tratamento estatístico dos dados desta pesquisa, bem como a análise dos resultados relativos aos fatores idade, sexo e nível sócio-econômico utilizando o programa Gencat (Landis e Stanish, Departamento of Biostatistic, School of Public Health, University of North Carolina, Chapel Hil, North Carolina), foram realizados no Centro de Computação Eletrônica da Universidade de São Paulo, com a colaboração da professora C. Wada da Faculdade de Educação, Filosofia, Ciências Sociais e da Documentação de Marília, UNESP, à qual os autores agradecem.













