Servicios Personalizados
Articulo
Indicadores
Compartir
Psicologia: teoria e prática
versión impresa ISSN 1516-3687
Psicol. teor. prat. vol.23 no.1 São Paulo ene./abr. 2021
http://dx.doi.org/10.5935/1980-6906/ePTPPA12625
ARTICLES
PSYCHOLOGICAL ASSESSMENT
Creating an objective measurement for the Enem: an analysis using the Rasch Model
Creando una verdadera medida para Enem: un análisis por el modelo rasch
Hudson F. GolinoI ; Cristiano Mauro A. GomesII
; Cristiano Mauro A. GomesII ; Alexandre José de S. PeresIII
; Alexandre José de S. PeresIII
IUniversity of Virginia (UVA), Charlottesville, VA, United States
IIFederal University of Minas Gerais (UFMG), Belo Horizonte, MG, Brazil
IIIFederal University of Mato Grosso do Sul (UFMS), Paranaíba, MS, Brazil
ABSTRACT
In the 1930s, a group of scientists argued that the empirical concatenation of observable elements was not possible in the human and social sciences and was, thus, not feasible to obtain objective measurements similar to those found in physics. To address this issue, mathematical theories that do not require concatenation were proposed in the 1960s, including the Additive Conjoint Measurement Theory (ACMT). In the same decade, George Rasch developed the simple logistic model for dichotomous data as a probabilistic operationalization of the ACMT. This study investigates the possibility of developing a fundamental measure for the National Exam of Upper Secondary Education (ENEM) that applies Rasch's model to students' performance on the 2011 ENEM exam. The results indicate an adequate model fit, demonstrating the viability of a fundamental measure using ENEM data. Implications are discussed.
Keywords: National Exam of Upper Secondary Education (ENEM); Theory of Additive Conjoint Measurement; Rasch model; Item Response Theory; educational assessment.
RESUMEN
En los años 1930, un grupo de científicos argumentó que la concatenación empírica de elementos observables no sería posible en Ciencias Humanas y Sociales y por consiguiente sería inviable obtener medidas verdaderas similares a las de Física. Para abordar este problema, a partir de los años 1960 se proponían teorías en las cuales la concatenación empírica no es necesaria, como la Teoría de Medidas Aditivas Conjuntas (TMAC). Al mismo período, George Rasch desarrolló el modelo logístico simple para datos dicotómicos, una operacionalización probabilista de la TMAC. Este estudio investigó la posibilidad de desarrollar una medida verdadera para el Examen Nacional de la Secundaria Superior (ENEM), aplicando el modelo logístico simple en los datos referentes a la performance de los participantes en la prueba de 2011 del ENEM. Los resultados indicaron adecuado ajuste del modelo, asi como la viabilidad de una medida verdadera para el ENEM. Implicaciones son discutidas.
Palabras clave: Examen Nacional de la Secundaria Superior (ENEM); Teoría de Medidas Aditivas Conjuntas; modelo de Rasch; Teoría de Respuesta al Ítem; evaluación educativa.
1. Introduction
In the 1930s, a group of physics and psychology researchers met at the British Association for the Advancement of Science to discuss the feasibility of measurement in psychology, education, and related fields (Borsboom, 2005). No consensus was drawn, but most followed notes made by Campbell (1920) would be impossible to develop any type of measure in the social sciences and humanities in general because the study objects of these areas did not allow concatenating objects to create systems for the comparison of quantities. At this time, measurement was defined and operationalized through classical representationalism (Borsboom, 2005). Concatenation was, in turn, considered fundamental and mandatory for the generation of a measurement because, through it, the empirical system (of relationships observed in nature) could be mapped into a representational system (of numbers and mathematical operations of comparison; see Golino & Gomes, 2015) that generated a measurement that represented characteristics of the object correctly or truly.
After a long period, the seminal work by Krantz, Suppes, Luce, and Tversky (1971) showed that concatenation is a mandatory condition for an adequate mapping between the empirical (i.e., objects) and representational systems (i.e., numbers) and, consequently, for the generation of an objective or fundamental measurement. These authors founded a new area called contemporary representationalism, from which they axiomatized the theory of measurement and mathematically defined a series of fundamental properties that result in adequate numerical measurements for physics, geometry, and other areas of the exact sciences and for education, psychology, and related areas. The authors contrast this with classical representationalism and state that it is wrong to think that only a single formal system of relations leads to objective measurement. They show that physics itself works with the measurement of attributes not subject to empirical concatenation operations such as temperature, for example.
To obtain an objective measurement without the need for concatenation, Krantz et al. (1971) proposed the Additive Conjoint Measurement Theory (ACMT). According to this theory, rules to be followed in mapping the relational system into the numerical system are strict and must satisfy four axioms (Borsboom, 2005; Golino & Gomes, 2015). To facilitate their understanding, let us describe the axioms by means of an example. Suppose that one is interested in measuring an object or attribute such as an ability in mathematics and that this attribute is studied through two conjoint dimensions (i.e., independent variables): people's mathematical ability and difficulty of the items used to evaluate mathematical ability. The conjoint realization of these dimensions (i.e., the encounter of people with items) generates a third variable, which is a dependent variable - people's responses. When an adequate mapping of the system of qualitative relationships is verified by the dependent variable of a numerical system that represents these relationships, four outcomes representing the ACMT axioms should result.
The first consequence (Axiom 1 of ACMT) is that the value of one of the dimensions, the ability, can be chosen without affecting the value of the other dimension, the difficulty of the items, which indicates a separation between what is being measured and the measurement object - a necessary condition for the measurement of attributes (Thurstone, 1931). In this sense, a person's abilities do not affect an item's estimated difficulty, nor does the difficulty of an item affect the estimation of a person's abilities.
The second consequence (Axiom 2), which comes directly from the first, is the independent ordering of ability and difficulty along the constructed measurement (i.e., of mathematical ability). In other words, people of a higher ability will assume a higher position on the measurement scale than those of a lesser ability, regardless of the items that are used to measure such ability. Similarly, more difficult items will assume a higher position on the measurement scale than easier items, regardless of who answers those items.
As the third consequence (Axiom 3), a quantitative increase in the produced measurement has specific effects on ability and difficulty, but in an independent way. Finally, the fourth consequence (Axiom 4) implies that people's abilities are comparable, such that differences between people's scores reflect real differences in their abilities. Likewise, item difficulty levels are comparable, such that differences in item scores reflect real differences in their difficulty levels.
While the axioms developed by Krantz et al. (1971) serve as an alternative to the classical test theory, they would not be effective without a statistical analysis capable of verifying whether the quantifications produced in the human and social sciences meet these axioms and can be evaluated as objective measurements (see Bond & Fox, 2015; Golino & Gomes, 2015). George Rasch's (1960) psychometric models eliminated this problem by defining functions that allow for the mapping of qualitative relationships in a numerical representational system that obeys axioms of Krantz et al.'s (1971) measures. In their rationality, the Rasch models statistically verify whether the structure of the data from quantifications derived from measurement instruments (e.g., educational tests, psychological tests, among others) fit the additive conjoint relationships that satisfy the four measurement axioms pointed above.
When the data do not fit the Rasch models, the quantification does not reflect an additive conjoint structure and, consequently, it does not reflect an objective measurement. From a methodological point of view, what the Rasch models do is to search for anomalies in quantifications that distance them from a mathematically well-defined operational criterion, to which the quantifications should fit to support an objective measurement. It is not coincidental that Andrich (2004, p. 12) states that "identifying substantive anomalies from statistical misfit, resisting modification of the model, collecting new data guided by the model, is consistent with the role of measurement in the physical science enunciated by Kuhn".
Considering that the Rasch models are crucial for the effectiveness of the ACMT axioms, their rationality will be demonstrated. However, we only present the dichotomous model because it is the simplest and may be sufficient for this demonstration. This model, also called the simple logistic model (SLM), states that response X pi, which arises from person p encountering item i, depends on a person's ability β and an item's difficulty δ expressed in probabilistic terms. The probability of a person correctly answering a particular item depends on his ability β. Thus, if βp is equal to δi, it is estimated that a person has a 50% chance of correctly answering an item. If βp is lower than δi, a person can be expected to have less than a 50% chance of success. On the other hand, if βp is greater than δi, a person should have more than a 50% chance of responding correctly. The relationship between ability and difficulty is represented by the following generic mathematical relationship for dichotomous responses:
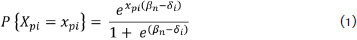
Among the various properties of the Rasch model for dichotomous data, invariance can be identified as one of the most important. This property ensures that parameters of the measured object and of the measuring instrument are separable, i.e., comparisons of people's abilities are independent of item difficulty and vice versa. This is a mathematical model property and not of the empirical data themselves (Wright & Stone, 1999). For a pair of items, the probability of a person correctly answering the first item and not the second, given that he/she correctly answers only one of the two, depends exclusively on the difficulty of these items. This property can be verified below (see Andrich, 1988). Suppose a person (p) answers two dichotomous items: item 1 and item 2. The following results are possible: 1) he incorrectly answers both items; 2) he incorrectly answers the first and correctly answers the second; 3) he correctly answers the first and incorrectly answers the second; or 4) he correctly answers both items. Consider, now, that person p correctly answers the first item and incorrectly answers the second item. This probability is calculated as:
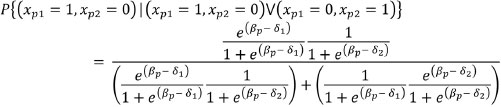
Although the expression of probability above is large and seems very difficult to understand, it is relatively simple. The numerator is the person's conjoint probability of correctly answering the first item and incorrectly answering the second. The denominator is the person's conjoint probability correctly answering the first item and incorrectly answering the second or incorrectly answering the first item and correctly answering the second. This probability equation is developed further below:
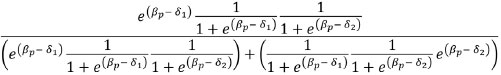
Now, we isolate the product of the probability of incorrectly answering each item in the denominator of the equation (Andrich, 1988):
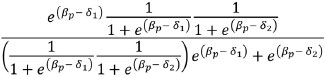
Now, we can eliminate the product of the probability of incorrectly answering each item by canceling this probability of the numerator with the probability of the denominator:
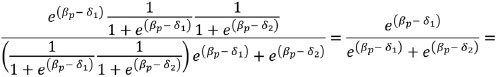
We then isolate in the numerator and denominator:
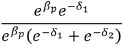
Finally, we cancel ebpof the numerator with the denominator:
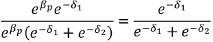
Thus, we eliminate the person parameter from the equation (Andrich, 1988). In other words, the probability of person p answering item 1 correctly and item 2 incorrectly, given that he only correctly answers one of the items, is given by a relationship exclusively based on the difficulty of both items (sufficiency equation of the items). That is:
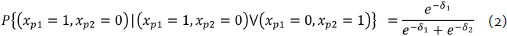
Similarly, assuming that two people respond to item i, the probability of the first person correctly answering this item and the second person incorrectly answering it, given that only one of the two correctly answers the item, depends exclusively on these people's abilities. This property is expressed as follows:
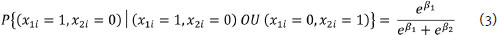
The invariance expression of the dichotomous parameters of the Rasch model parameters satisfies one of the main axioms of the ACMT: the doubly independent relationship between the factors (in this case, ability, and difficulty). It is a mathematical verification in which the model assumes two conditions. The first one states that the value of β can be chosen without affecting the value of δ (independence of the realization of the components). The second states that the components β and δ have independent effects on the attribute to be measured (in this case, a latent variable). Thus, the dichotomous Rasch model mathematically supports the independent ordering of β and δ along with the latent variable, satisfying ACMT Axiom 2.
In addition to satisfying the two conditions of Axiom 2, the expression of parameter invariance also causes the increase in the latent variable to increase ability β and difficulty δ, but independent of each other. Consequently, Axiom 3 of the ACMT is satisfied (double cancellation). Finally, as the comparison of the abilities of people β1 and β depends on the relationship between their abilities, the β values are comparable. Similarly, as the comparison of the difficulty of items δ1 and δ depends on the relationship between these items' difficulties, the δ values are also comparable. Thus, axiom 4 of the ACMT (Archimedes Axiom) is satisfied. Finally, if the data of a quantification fit the dichotomous Rasch model, the order between the relationships is of the weak type and Axiom 1 of the ACMT is satisfied (Borsboom, 2005). If the order of the relationships is not weak, the data do not fit the model, and the quantification does not support an objective measurement.
We add that the dichotomous Rasch model (1960) and the models derived from it are the only existing probabilistic functions that map the qualitative relationships found in additive conjoint structures in a numerical representational system such that all four ACMT axioms are satisfied. Therefore, we emphasize that, in addition to the Rasch models, no other Item Response Theory (IRT) model or any model derived from other methodologies allows for this type of analysis. Some proponents of two- and three-parameter IRT models argue that the Rasch models are only simplified versions of these models with more parameters, which is an epistemological position that goes against arguments presented in the international measurement literature, as explored in detail by Andrich (2004). When adding parameters, a fundamental element, the sufficiency of the total score for estimating people's ability parameters, is lost. This is the central point that causes the Rasch models to generate a sufficiency equation of items without the ability parameter, enabling the comparison of invariant items in relation to people's locations. This mathematical property is exclusive to Rasch models.
As Andrich (2004) points out, in the Rasch models, no additional information is provided in the response pattern because different response patterns have different probabilities and can be used for model misfit verification. In turn, in the two - and three - parameter IRT models, different response patterns lead to different ability estimates (Andrich, 2004). Consequently, in the Rasch models, the items' characteristic curves are parallel, denoting an invariance in the ordering of the difficulty of the items along with the latent trait (or along with abilities). Therefore, easier items for people of lesser ability are also easier for those of moderate or high ability. In the two- and three-parameter models, the items' characteristic curves are not parallel, meaning that there is no invariance in the ordering of the difficulty of the items. Therefore, items that are easier for people of lesser ability may become more difficult for those of higher ability (see Andrich, 2004).
While initial evidence showing that the Rasch model is a special case of the ACMT was provided by Perline, Wright, and Wainer (1979), the definitive mathematical proof was presented by Newby, Conner, Grant, and Bunderson (2009).
In summary, we highlight that if significant advances made in the twentieth century enabled the production of objective measurements in the area of human sciences, it is extremely relevant that this area uses these advances. If the production of a true measurement can only be an option in some cases, in high stake evaluations, it should be indispensable. Certainly, this is the case of the National Exam of Upper Secondary Education (ENEM) because the quantifications obtained from its exams have direct and impacting social consequences for millions of Brazilian students and for secondary schools, which are often evaluated by means of their students' scores on this exam (Travitzki, 2013).
Currently, the National Institute for Educational Studies and Research Anísio Teixeira (Inep, 2012), an autarchy of the Brazilian Ministry of Education responsible for the ENEM, adopts the three-parameter logistic model (3PL) of the IRT to model the measurement of latent domains of the ENEM. Epistemologically, the Rasch models and the model adopted by the ENEM are very different. While the Rasch model follows ACMT assumptions and aims to test how well empirical data fit the requirements of an objective measurement, the IRT model adopted by the ENEM seeks to create a model capable of explaining the properties present in the data by adding model parameters that maximize their fit and that closely represent the data structure (e.g., discrimination and random correct answers). Bond and Fox (2015) summarize this epistemological difference by classifying the Rasch model as confirmatory and predictive, while the IRT model adopted by the ENEM is considered an exploratory and descriptive model.
Despite not using Rasch models to analyze the items, the ENEM states that its scores are measures of the domains of languages, mathematics, natural sciences and human sciences. As we have argued throughout this text, an objective measurement is supported in human sciences from the conceptual framework of the ACMT and its testing via Rasch models. In this sense, to date, we do not know whether the ENEM actually measures the domains as proposed or only produces mere quantifications. The implications of this are extremely relevant. Without a true measurement, it is not possible to assume that the generated quantifications are independent of the items used in the exam or of individuals who have taken it. As we have explained, an objective measure must demonstrate this independence. Moreover, this condition has long been recognized in the field of psychometrics, and Thurstone (1931) has extensively discussed this need since the beginning of the twentieth century.
Considering the above, in this article, we aim to verify whether the ENEM actually generates objective measurements. For this purpose, we applied the Rasch model for dichotomous data on data of the students' binary (correct/incorrect) responses to the 180 items of the 2011 edition of the exam. This model is correctly used only when the data analyzed are one-dimensional: in the case, of an exam, its items must be mostly explained by a single ability. This seems to be the case for the ENEM, as previous studies have shown that the general factor of student performance on the ENEM explains the most significant and relevant portion of the variance of items of the exam and is more reliable (Gomes, Golino, & Peres, 2016, 2018). It is important to note that most previous studies show that, when controlling for the effect of the overall performance factor on the ENEM (through a bi-factor model), not only is the fit to the data more appropriate, but the composite reliability of the overall factor remains high while that of specific educational factors remains very low (Gomes, Golino, & Peres, 2016, 2018), rendering the separate analysis of educational exams by content problematic. Furthermore, in practical terms, this overall score determines students' admission to Brazilian public universities and, therefore, what actually causes a greater social impact. This is the case because universities usually adopt average scores in the four domains evaluated (i.e., mathematics, languages, natural sciences, and human sciences) as one of the most important criteria for the selection of candidates. That is, while Inep does not calculate any measure referring to a general score, this information seems to be most commonly used in selection systems for admission to higher education in Brazilian public universities.
2. Method
2.1 Participants
The scores of 66,880 students who participated in the 2011 ENEM exams and completed notebooks 120, 124, 125, and 129 were analyzed. The data were obtained from microdata made publicly available by Inep (2012).
2. 2 Instrument
The 2011 ENEM exam is composed of 180 items separated into four groups of 45 items referring to the four domains (i.e., constructs or latent traits) evaluated by the Exam: Languages, Codes and its Technologies (LC); Mathematics and its Technologies (MT); Natural Sciences and its Technologies (NS); and Human Sciences and its Technologies (HS). All items are multiple-choice, producing dichotomous data (i.e., correct or incorrect answers). The database used in this study is the same as that used in previous studies verifying the existence of a general factor (Gomes, Golino, & Peres, 2016, 2018).
2. 3 Procedures
The data were downloaded, extracted, imported, and initially processed using the ENEM package (Golino, 2014). Participants absent from the exams were excluded from the analyses. Then, the dichotomous score for each item of each exam was calculated by correcting responses from the template. The missing data were transformed to zero for our analyses.
2. 4 Data Analysis
The Rasch model for dichotomous data was applied by using the R (R Core Team, 2014) eRm package (Mair, Hatzinger, & Maier, 2015). To verify the fit of the items to the dichotomous Rasch model, the outfit mean square and infit mean square indices (hereinafter called outfit and infit, respectively) were used, and the Andersen likelihood ratio test (1973) was applied.
The outfit is a fit index calculated from the mean square of the standardized residuals of an item. The infit is a fit index that balances the standardized residual by the variance of this residual and then divides this result by the average residual variance (Marais, 2015). Thus, the infit does not penalize items located far from people on the latent variable continuum. The interpretation of (and predilection for) the use of the infit mean square is that, if an item difficulty is located far from people's abilities on the latent trait continuum, this problem is not due to the quality of the item in the measurement of the construct, but to characteristics of the sample used. Thus, if an item is too difficult for those in the study sample, the outfit will penalize the fit of the item, but the infit will not. In this case, the outfit points to the need to find new participants with greater ability to answer the item. Similarly, if the item is too easy for those in the sample, the outfit will penalize the fit of the item, indicating that it is necessary to find participants with lesser ability to answer the item.
Values of outfit and infit between 0.7 and 1.3 represent items with an adequate fit to the data, but the range of 0.8 to 1.2 indicates a good fit (Marais, 2015). Both the outfit and the infit have an expected value of 1.0. Values lower than 1.0 indicate that people's responses to an item fit better than expected by the model. Similarly, values higher than 1.0 indicate that people's responses to an item fit worse than expected. Infit and outfit indices also indicate item discrimination. Items that discriminate less than the average level of item discrimination have infit and outfit values greater than 1.0 (Marais, 2015). Items that discriminate more than the average level of item discrimination will have infit and outfit values of less than 1.0.
Conversely, the Andersen likelihood ratio test (1973) assesses the underlying principle that, in arbitrarily disjointed subgroups of people, the item parameter estimate is the same (null hypothesis) across groups. Thus, if the null hypothesis that the item parameter is the same for k subgroups is refuted, this is evidence of a misfit of the items to the dichotomous Rasch model. To apply the Andersen likelihood ratio test, we separated our sample into four random subsamples.
In addition to the outfit, infit, and Andersen test, another quality indicator is the separation reliability of people and items. Both are calculated from the relationship between the variance of the standard error of the parameter and the mean square error (MSE) of the parameter:
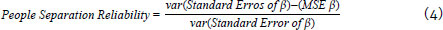
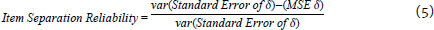
The values of the separation reliability of people and item are interpreted as the reliability value indicated by Cronbach's alpha. Values closer to 1.0 denote a more reliable measurement. However, these coefficients are interpreted as how well people's responses or item correctness levels fit the measurement structure. In other words, people separation reliability indicates the likelihood of a person with estimated ability β2 having more ability than another person of estimated ability β1, in which β2 > β1. Similarly, item separation reliability indicates one's level of confidence that item of estimated difficulty is more difficult δ2 than the item of estimated difficulty δ1, in which δ2 > δ1.
3. Results
The infit of the 180 items analyzed ranges from 0.81 to 1.21 with a mean of 0.99 and standard deviation of 0.09. The outfit ranges from 0.71 to 1.65, with a mean of 1.02 and a standard deviation of 0.15. Regarding the infit of the items, all 180 items have values within the reference range from 0.70 to 1.30 (Marais, 2015). However, some items have an outfit value falling outside the reference range (letters represent theoretical domains, numbers denote item numbers, and outfit values are shown in parentheses): NS25 (1.66), MT20 (1.54), NS39 (1.46), NS33 (1.36), NS14 (1.34), NS8 (1.33), LC33 (1.33), NS3 (1.33), HS22 (1.33), MT33 (1.32), and NS19 (1.31). These outfit values indicate that the items discriminate less than the average discrimination of all the analyzed ENEM exam items. Responses to these items by the Rasch model are less predictable than expected. Despite falling outside the reference range from 0.70 to 1.30, the items show adequate infit values.
The Andersen likelihood ratio (LR) test indicates that it is not possible to refute the null hypothesis that the item parameter is the same for four random subsets of the sample (LR = 513.022; Degrees of Freedom = 537; p = 0.76). People separation reliability is 0.95, while the item separation reliability is 0.99.
The items' difficulties vary from -2.91 to 2.39 logits (M = 0; SD = 0.92). While we use the unidimensional Rasch model for dichotomous data, thus, verifying the latent variable of general school performance, it is interesting to verify the difficulty of the ENEM items according to the school domain, as the items are constructed based on a theoretical orientation that covers the four domains (NS, HS, LC, and MT). The items constructed within the NS domain present difficulties from -2.75 to 2.39 logits (M = 0.42; SD = 0.96), the HS domain ranges from -2.91 to 1.43 logits (M = -0.29; SD = 0.89), the LC domain ranges from -1.91 to 1.24 logits (M = -0.445; SD = 0.75) and the MT domain ranges from -1.32 to 1.64 logits (M = 0.30 SD = 0.75). The estimated difficulty of the items per school domain is shown in Figure 3.1 and their 95% confidence intervals. Figure 3.2, in turn, shows the distribution of people's abilities and the difficulty of the items of the 2011 ENEM exams.
4. Discussion
The results indicate that the items adequately fit the Rasch model, considering the very high infit index with people and item separation reliability (0.95 and 0.99, respectively). In addition to the fit index and separation reliability, the fit of the data to the Rasch model was verified using the Andersen likelihood ratio test, which reveals that the item parameters are equal in different sampling subgroups. Regarding the estimated difficulty of the items, we found that the items comprise almost the entire spectrum of the exam subjects' abilities. However, the abilities of a small group of people (more than 2.5 logits) were not reliably estimated, as there are no items of sufficiently high difficulty to estimate them. In summary, the 180 items of the 2011 ENEM exam are of sufficient quality to obtain an objective measure of overall student performance.
We present some implications of these results. From the epistemological point of view of psychometrics, the 2011 edition of the ENEM meets the axioms of the ACMT, which consists of an objective or fundamental measurement. This finding gives this exam greater certainty regarding its measurement model, which is crucial, given that the ENEM is a high stake exam, i.e., it affects the lives of millions of Brazilians and policies of basic and higher education.
However, it is necessary to relativize this result to the following point. In this study, we analyzed a general performance factor of a level higher than that of the four theoretical domains (i.e., NS, HS, MT, and LC) comprising the exam. Previous studies have shown that the bi-factor model better fits the data than the model of noncorrelated factors currently adopted by the ENEM (Gomes et al., 2016, 2018). This general factor is the only factor with reliability greater than 0.95 (Gomes et al., 2016, 2018). Thus, the present study corroborates that the addition of a general factor to the ENEM theoretical model, in addition to further explaining result variance, contributes to the quality of the measurement instrument. This study also supports the practice of many higher education institutions of using the mean of the four domains as a criterion for student selection.
It is important to remember that the mathematical characteristics of the ACMT apply only to Rasch's models. Nevertheless, Inep, the institution responsible for developing, applying, and calculating ENEM scores, uses the three-parameter IRT model. Both the two- and three-parameter models do not allow one to obtain an objective or fundamental measurement because they are not additive (Borsboom, 2005). That is, these models cannot meet the assumptions of the ACMT. What these models do is model or explain the dataset (Andrich, 2004).
As we have argued, there is a considerable difference between modeling and measuring. The former attempts to verify how the data behave by adopting the model that best fits the data - the one that best describes it. Therefore, it is a data-dependent procedure (Andrich, 2004). In turn, measurement seeks to identify anomalies in the data that make them move away from a mathematically well-defined operational criterion to which the data should fit. If the data do not fit the measurement operational criterion, new data are obtained, and this procedure is repeated until the data fit the model. As Andrich (2004) argues, "identifying substantial anomalies based on misalignment analysis, by resisting modification of the model [and] collecting new data guided by the model is consistent with the role of measurement in the physical sciences, as stated by Kuhn..." (P. 12). Readers interested in this discussion can consult Andrich (2004), which lists what differentiates Rasch models from the two- and three-parameter IRT models from a measurement point of view.
Obtaining objective measures in education and psychology is relevant when drawing comparisons between individuals to make decisions related to the selection of people based on their performance. For this process to be technically fair, it is necessary to use models that include a mathematical criterion that supports the separation of people's abilities from items that make up the evaluation, and the only models that have this property are the Rasch models.
In other words, the comparison of two people in terms of their abilities should not be affected by items that make up the evaluative instrument. This invariance can be checked by comparing the parameters of different groups of a sample, as is usually done in the two- and three-parameter IRT models (Andrich, 2004). However, in these IRT models, invariance is not a mathematical characteristic, but an empirical verification. For this reason, this strategy leads to situations in data analysis that contradict the very definition of invariance, as items easier for people of low ability can be estimated as more difficult for people of high ability, which collapses the measurement system since the order of item difficulty can be inverted into different subgroups (see Andrich, 2004). This situation generates incongruity and an unfair measurement process in the context of high-stake assessments.
5. Conclusion
As we report, our results indicate that the ENEM meets the assumptions of the ACMT when considering overall performance. This result serves as favorable evidence for the use of mean scores of the four specific domains by higher education institutions in selecting students. It should also be treated as an indication of relevance from a psychometric and pedagogical point of view, such that Inep can start to consider the general factor when disclosing ENEM results.
Finally, we hope that this study serves to disseminate the epistemological debate presented to other researchers in the areas of psychometry and educational and psychological assessment. We seek to show that, when constructing measurement instruments in psychology, education, and related fields, it is necessary not only to identify a psychometric model that best describes responses to the items, but also to go beyond data modeling and investigate whether the epistemological assumptions of the objective or fundamental measurement are met. Exams as important as the ENEM must be systematically subjected to scrutiny with models testing the quality of quantifications and their feasibility for the generation of objective measures to ensure the quality, significance, and fairness of the measurements produced by them.
References
Andersen, E. B. (1973). A goodness of fit test for the Rasch model. Psychometrika, 38,123-140. doi:10.1007/BF02291180 [ Links ]
Andrich, D. (1988). Quantitative Applications in the Social Sciences: Rasch models for measurement. Thousand Oaks, CA: SAGE Publications, Inc. doi:10.4135/9781412985598 [ Links ]
Andrich, D. (2004). Controversy and the Rasch model: A characteristic of incompatible paradigms? Medical Care, 42(1),7-16. doi:10.1097/01.mlr.0000103528.48582.7c [ Links ]
Bond, T. G., & Fox, C. M. (2015). Applying the Rasch Model. Fundamental Measurement in the Human Sciences (3rd ed.). London: Routledge. [ Links ]
Borsboom, D. (2005). Measuring the mind: Conceptual issues in contemporary psychometrics. New York: Cambridge University Press. doi:10.1017/CBO9780511490026 [ Links ]
Campbell, N. R. (1920). Physics, the elements. Cambridge, UK: Cambridge University Press. [ Links ]
Golino, H. F. (2014). ENEM: An implementation of functions to help automatic downloading, importing, cleaning and scoring of the Brazilian's National High School Exam (ENEM). Unpublished Software. [ Links ]
Golino, H. F., & Gomes, C. M. (2015). Teoria da Medida e o Modelo Rasch. In H. F. Golino, C. M. Gomes, A. Amantes, & G. Coelho. (Eds.), Psicometria contemporânea: Compreendendo os Modelos Rasch (pp. 13-41). São Paulo, SP: Casa do Psicólogo/ Pearson. [ Links ]
Gomes, C. M. A., Golino, H. F., & Peres, A. J. S. (2016). Investigando a validade estrutural das competências do ENEM: Quatro domínios correlacionados ou um modelo bifatorial. Boletim Na Medida, 5(10),33-38. Retrieved from http://download.inep.gov.br/publicacoes/boletim_na_medida/2016/Boletim_Na_Medida_10.pdf [ Links ]
Gomes, C. M. A., Golino, H. F., & Peres, A. J. S. (2018). Análise da fidedignidade composta dos escores do ENEM por meio da análise fatorial de itens. European Journal of Education Studies, 5(8),331-344. doi:10.5281/zenodo.2527904 [ Links ]
Instituto Nacional de Estudos e Pesquisas Educacionais Anísio Teixeira - Inep. (2012). Microdados do ENEM - 2011. Exame Nacional do Ensino Médio: Manual do Usuário. Retrieved from http://portal.inep.gov.br/web/guest/microdados [ Links ]
Krantz, D. H., Luce, R. D., Suppes, P., & Tversky, A. (1971). Foundations of measurement (Vol. I). New York: Academic Press. [ Links ]
Mair, P., Hatzinger, R., & Maier M. J. (2015). eRm: Extended Rasch Modeling (Version 0.15-5) [Software]. Retrieved from https://cran.r-project.org/web/packages/eRm/ [ Links ]
Marais, I. (2015). Implications of removing random guessing from Rasch item estimates in vertical scaling. Journal of Applied Measurement, 16(2),113-28. [ Links ]
Newby, V. A., Conner, G. R., Grant, C. P., & Bunderson, C. (2009). The Rasch model and additive conjoint measurement. Journal of Applied Measurement, 10(4),348-354. [ Links ]
Perline, R., Wright, B. D., & Wainer, H. (1979). The Rasch model as additive conjoint measurement. Applied Psychological Measurement, 3(2),237-255. doi:10.1177/ 014662167900300213 [ Links ]
R Core Team. (2014). R: A language and environment for statistical computing. Vienna, Austria: R Foundation for Statistical Computing. Retrieved from http://www.R-project.org/ [ Links ]
Rasch, G. (1960). Probabilistic models for some intelligence and attainment tests. Copenhagen, Denmark: Paedagogiske Institut. [ Links ]
Thurstone, L. L. (1931). The measurement of social attitudes. The Journal of Abnormal and Social Psychology, 26(3),249-269. doi:10.1037/h0070363 [ Links ]
Travitzki, R. (2013). ENEM: Limites e possibilidades do Exame Nacional do Ensino Médio enquanto indicador de qualidade escolar (Tese de Doutorado não publicada). Faculdade de Educação, Universidade de São Paulo, São Paulo, Brasil. [ Links ]
Wright, B., & Stone, M. (1999). Measurement essentials. Wilmington, United States: Wide Range, Inc. [ Links ]
 Correspondence:
Correspondence:
Cristiano Mauro Assis Gomes
Universidade Federal de Minas Gerais, Departamento de Psicologia, gabinete 4036, Campus Pampulha
Av. Antônio Carlos, 6627, Pampulha
Belo Horizonte, Minas Gerais. Brazil. CEP 31270-901
E-mail: cristianomaurogomes@gmail.com
Submission: 02/07/2019
Acceptance: 23/06/2020
This article stems from a project funded by the National Institute for Educational Studies and Research "Anísio Teixeira" (INEP) through Public Call Inep/Dired N. 05/2012. Cristiano Mauro Assis Gomes received a productivity scholarship from CNPq, level 2.
Authors' notes:
Hudson F. Golino, Department of Psychology, University of Virginia (UVA); Cristiano Mauro A. Gomes, Postgraduate Program in Neuroscience (PPG Neurociências) and Postgraduate Program in Psychology, Cognition and Behavior (PPGPsiCogCom), Federal University of Minas Gerais (UFMG); Alexandre José de S. Peres, Postgraduate Program in Psychology (PPGPSICO), Federal University of Mato Grosso do Sul (UFMS).










 texto en
texto en