Serviços Personalizados
Journal
artigo
Indicadores
Compartilhar
Revista Brasileira de Terapia Comportamental e Cognitiva
versão impressa ISSN 1517-5545
Rev. bras. ter. comport. cogn. vol.3 no.1 São Paulo abr. 2001
ARTIGOS
Steven M. Kemp; David A. Eckerman1
University of North Carolina at Chapel Hill
ABSTRACT
Recently, some behavior analysts have recommended the use of computer simulations to augment, or even replace, verbal and mathematical interpretations of behavior. This report raises the question as to what computer simulation adds to other analyses of behavior. We present examples of the human behavior of arithmetic calculation in order to illustrate the benefits of computation even where the results are known. The claim is made that mechanical computation (computer simulation) can have the same sorts of benefits, magnified by the power and speed of the electronic computer.
Key words: Computer simulation, verbal behavior, neural process.
RESUMO
Ultimamente, alguns analistas do comportamento têm recomendado o uso de simulações de com putador para aumentar, ou mesmo substituir, as interpretações verbais e matemáticas do comporta mento. Este estudo investiga a questão sobre o que a simulação de computador acrescenta a outras análises de comportamento. Apresentamos exemplos do comportamento humano de fazer cálculos aritméticos para ilustrar os benefícios da computação, mesmo quando os resultados são conheci dos. Propõe-se que a computação mecânica (simulação de computador) pode ter os mesmos tipos de benefícios, ampliados pelo poder e velocidade do computador eletrônico.
Palavras-chave: Simulação de computador, comportamento verbal, processo neural.
To the complaint 'There are no people in these photographs,' I respond, 'There are always two people; the photographer and the viewer.'
Ansel Adams
The recent interest in computer simulation with in behavior analysis (Hutchison Sc Stephens, 1987; Kehoe, 1989; Staddon & Zhang, 1991; Donahoe, Burgos & Palmer, 1993; Donahoe & Palmer, 1994; Tryon, 1995a, 1995b; Donahoe, Palmer, & Burgos, 1997; Burgos, 2000; Kemp & Eckerman, 2000) has led some behavior analysts to ask what computer simulation adds, if anydiing, to the analysis of behavior. For instance, if we know the contingencies (i.e., the inputs in computer terms) for our experimental design, the functional relations (the algorithm) from our analysis (either qualitative or quantitative), and the behavior (the outputs) from our data, what more will computer simulations teach us?
Donahoe and Palmer (1994), argue that computer simulations provide a formal mode of interpretation that offers specific advantages over more traditional verbal interpretations (where implications of a behavioral analysis are expressed in words). The use of formal modes of interpretation is called the quantitative analysis of behavior (QAB). Many such analyses do not require computers. Some quantitative analyses that do require computers, use them for a slightly different purpose than the simulations used by modelers such as neural network researchers. (We will describe this difference later.)
We begin with Donahoe and Palmer's (1994) description of scientific analysis and interpretation to set our question for describing what computer simulation adds beyond other types of QAB.
1. Experiments tell us about the actual behavior of actual animals.
2. Verbal interpretations show us how the principles discovered by the experimental analysis of behavior explicate behavior we see in the world around us.
3. A quantitative analysis formalizes this interpretation. Our question is: What can a computer simulation add to this?
The answer is twofold. First, the use of computers in general provides a particular form of stimulus control that resembles tacting (i.e., verbal behavior under control of discriminative stimuli, Skinner, 1957, p.81 ff.). Second, the use of computers for simulation makes this form of tacting available for the purpose of expanding verbal as well as formal interpretations of behavior. The remainder of the present paper elaborates on these two issues.
What computers do
Computers were originally designed as scientific instruments. Despite their use in many other forms of human endeavor, they retain the basic functional character of any scientific instrument. As Skinner puts it in his book, Verbal Behavior (1957, p. 428), a scientific instrument "extends our responses to nature by... clarifying events which can serve as stimuli." In the case of the computer, the events are the settings of millions of electrical switches. (Ordinarily, these settings are mechanical translations of human readable text constituting the computer program and operating system.) These settings specify manipulations according to a logical system known as the propositional calculus. The clarification is due to a mechanical process that mimics a form of response manipulation called the substitution of terms (Skinner, 1957, pp. 423-424).
Substitution of terms occurs, for example, when humans edit text, crossing out one word and replacing it with another. Substitution of terms can be governed by highly restrictive systems of rules such that the substitutions can be carried out by mechanical means. Algebra is a good example, where sequences of letters and symbols can be exchanged only for certain others and individual letters can be exchanged for certain others. In computers, substitution allows us to see the implication of the programmed settings for the switches.
In English, prior to the 1940s, the word "computer" was defined in the dictionary as the profession of persons who calculated numerical results for mathematical tables. As such, computing specifies a type of behavior. Scientific, mathematical, and logical behavior are elaborate forms of behavior that have evolved due to their reliability in contributing to successful action on the part of listeners. According to Skinner (1957, p. 418), the rules of logic and the rules of mathematics effectively govern certain types of verbal behavior on the part of the speaker that are especially effective in governing behavior on the part of the listener. So, for example, we can use numbers to obtain more precise control over the listener's behavior by saying, "Please bring me five apples," than by saying, "Please bring me some apples." A surprisingly large proportion of the speaker's precurrent responses used in editing logical and mathematical verbal behavior consists in the substitution of terms. For instance, "some" can be replaced by "five," but "three" cannot be. Within limits, these precurrent responses can be implemented by mechanical means and this is what a computer does.
The logico-mathematical manipulations of the computer program transform a text authored by the computer programmer (the input) into another text (the output) by means of a long and complex series of substitutions (and other related transformations). These manipulations are governed by two separate sets of rules:
1. The computer itself, together with its operating system and application software, contains preset rules that insure that the transformations conform to the rules of logic and arithmetic.
2. And the computer program, provided by the programmer, contains specific rules to govern the computer's operations so that the overall transformation clarifies events in the manner desired.
Clarification as the revelation of subtle properties
According to Skinner (1957, p. 428), an important characteristic of many experimental methods is to "bring responses under stricter stimulus control by manipulating states of affairs so that relevant properties are emphasized." This is also a benefit of much scientific instrumentation. A good example is the cumulative recorder, which transforms switch closures into changes in the motion of a pen on paper so as to emphasize the temporal patterning of responding. We propose tiiat the transformations of text effected by the computer do something very similar to what is accomplished by a cumulative recorder. Computer operations also bring the reader's behavior under stricter stimulus control by emphasizing relevant numerical properties of either the theoretical assertions, the data, or the relation between them.
Numbers. Since the properties of interest are for the most part numerical, we need to consider just what sort of properties numbers are from a behavioral perspective. (In our presentation here, we focus on the numerical rather than the other uses of computers.) In tacting, numbers are controlled by quantitative properties of the stimulus. As such, the numerical tacts of counting and measuring, etc., are instances of generic extension (Skinner, 1957, p. 91-92). One type of generic extension is where a single (abstract) property controls responding, as when a red chair and a red ball both evoke the word, "red." Numbers clearly are generic extensions in this sense. The abstract property of having a count of 4 is shared by the cardinal points of the compass and the Gospels. The abstract property of having a measure of 4.3 is shared by my cat's weight measured in kilograms and the length of my study measured in meters.
Numbers specify properties that have properties. (This is not unusual. Red is a property that has the property of being the color with the lowest frequency in the spectrum.) Numbers are unusual in that they have a very large number of properties (such as being even or odd, being prime, being the square of one number and the square root of another, etc.). These properties are related to one another in a large and elaborate hierarchical system of relations.
Revelation of numerical properties. Due to the large quantity of complex properties for any one number, not to mention a data set full of numbers, the computer is particularly useful for specifying and emphasizing those few properties relevant to an analysis. The computer accomplishes tins change in emphasis by substitution of terms. The large quantity of properties for each number make for a large quantity of terms equivalent to (and thus substitutable for) each number. The number 6, for instance, is the successor of 5, the product of 2 and 3, the sum of 1 and 5 (as well as the sum of 5678 and -5672), the arithmetic inverse of -6, the multiplicative inverse of 1/6, the square root of 36 and the lowest perfect number, etc. By substituting any one of these terms for 6, different properties are revealed.
Logico-mathematical transformations of the type able to be performed mechanically by a computer can manipulate complex arrays of numbers in such a way as to emphasize properties deemed relevant by the computer programmer. Borrowing an example from Donahoe & Palmer (1994, p. 271), a very simple computer program could be constructed that would take 67 as input and give , "the smallest prime number greater than 61" as output or vice versa. More complex programs can take larger arrays of numbers (coded as switch closures) and manipulate them so as to emphasize even more obscure properties.
Epistemic uses of computations in simulation
We have seen how computers can reveal things about numbers that are not obvious from simple observation or even graphing. And when those numbers are experimental data, the advantages of using a computer seem clear. But computer simulations are more than just data transformations. Simulations are special types of computation where the time course of the computation is intended to parallel the time course of some real world events. The inputs to a computer simulation are models of antecedent events. The algorithm is a model of causal relations. The computation is a model of temporal-causal processes. The outputs are models of consequences. In the computer simulation of behavior, the causal relations and processes are behavioral. We seek to show that when numbers are involved in such calculations, the revelation of their occult properties can be useful to the analysis of behavior.
Arithmetic examples The uses of clarification in computations where inputs, processes and outputs are all known can be illustrated by examples drawn from simple arithmetic problems. Consider the following problem:
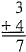
The inputs are 3 and 4. The process is addition. The output is 7. Both the inputs and the output are different texts specifying the same number, seven, but emphasizing different properties of that number. The text above the line specifies seven as the sum of three and four. The text below the line specifies seven as the number standardly designated by the numeral "7". The computation involved transforms the text specifying the sum into the text specifying the numeral.
For most adults, the use of a computer to perform the calculations specified in the above example would be superfluous. Not only can most adults rapidly perform this calculation "in their heads," but the text reading, "3+4" is most likely a stimulus that readily evokes most of the same responses as does the numeral, "7". These two texts are homonyms (Skinner, 1957, p. 118).
A slightly more complex problem:
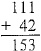
illustrates a case where the calculation can still be performed rapidly, with very high probability of giving the correct response (i.e., the response most reliably reinforced by the mathematical community). Here, the text specifying the sum is most likely a novel stimulus to which the reader has never been conditioned. The sum evokes no responding. In cases such as this, the symbol, "+",' which mands the type of computation required, will most likely control responding. The reader will compute the result.
It is also possible that the reader will simply look beneath the horizontal line to the text specifying the output, "153", and trust the authors to have calculated correctly. In the present context, the more complex the calculation, the more likely this is to occur, as the next example illustrates:
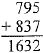
But what of other contexts? Suppose you are giving an important exam to your students. The problem is provided in a handbook, complete with the answer. You use the problem in the exam, leaving the answer for grading purposes. If the exam is important enough and the problem counts for enough points, you are more likely to perform the calculation (or have it performed) in order to check to make sure that there is no error in the handbook. Problems and solutions given in teaching materials do have errors on occasion.
When the calculation is even more complex, readers may no longer even trust their own computational skills and choose to rely on mechanical means:
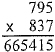
(as did we).
In the foregoing examples, the text above the line is always a homonym for text below the line, at least for a mathematical audience. But the degree to which the relational property of homonymy controls the reader's responding varies from strong to weak. In the final example above, homonymy exerts such weak control that, in the appropriate context, the reader is likely to take steps to clarify whether or not the property is present at all. And the computer is the perfect instrument for such clarification. When the text above the line is entered into a calculator (a simplified form of computer to be sure), and the numeral-homonym operator ("=") button is pressed, the text below the line appears in the display. This is what Skinner (1957, p. 425-428) calls confirmation.
In the first example above, homonymy exists for the mathematical audience and also for the general reader. In the later examples, homonymy in Skinner's behavioral sense does not exist for the general reader first approaching the text. It is only after the confirmatory calculations are performed that the text above the line may come to exert the right sort of stimulus control so that the two texts exhibit homonymy. And tire ability of the text above the line to exert such stimulus control may not perdure. As Skinner notes, any statement asserting the homonymy of the two texts may be a tact or an intraverbal depending upon the intervening behavior. (Clearly, there is a difference between the presence of homonymy in the form of having each of the two stimuli control the same responding and the obvious presence of homonymy in the form of the two stimuli together controlling such utterances as, "These two are equal.")
In conclusion, the first use of a computer in simulation is confirmation. This can be done when all of the relevant components are known from prior analyses. It remains to consider what other uses there may be for computer simulation when different elements of the analyses inputs, processes, or outputs - are wholly or partially missing.
Marshalling stimuli. Skinner (1969, p. 136-138) speaks of constructing discriminative stimuli as central to the process of problem solving. Donahoe & Palmer (1994) speak of marshalling stimuli, generating stimuli in conjunction with other stimuli that increase the probability of responding that generate further stimuli that eventually produce a response that is the solution to the problem. If any of the three elements of the analyses are absent, then the situation can be thought of as a problem to be solved by filling in the missing pieces. When useful stimuli are generic extensions of occult numerical properties of any of these elements, computers may come in handy by assisting in the process of constructing stimuli for the user to marshall.
The most straightforward case is when the inputs and process are known and the outputs are not known. The standard programming solution is to encode the inputs and apply the process in the form of a computer program. The computer then generates outputs which can be interpreted as predictions of the outcome of the real world events. The problem is that it is very rare that processes complex enough or important enough are sufficiently well understood to write a computer program that encodes the process precisely. Even in physics, only the simplest problems can be managed in this way. And the simplest problems are laboratory phenomena. The simplest physical circumstances of everyday life are far too complex to be adequately simulated at the present time (Hobbs, Blenko, Croft, Hager, Kautz, Kube & Shoham, 1985; Donahoe & Palmer, 1994, p. 127). One need only look at the cartoonish quality of Virtual Reality games on the computer to verify this fact.
The most common approach to handling prediction when the processes are only partially understood is statistical estimation. A good example of this in the case of a physical system is weather forecasting. Understanding of the physical processes is limited. Knowledge of the antecedent conditions is limited. The outcomes are unknown. Using highly sophisticated statistical models and the largest and fastest super-computers in the world, moderately acceptable predictions are made on a just-in-time basis from day to day for some parts of our world. Even under the best circumstances, this, the easiest form of computer simulation is terribly difficult.
The next most straightforward case is computing the inputs when the process and the outputs are known. The very first use of computers, calculating tables for artillery, involved this problem. Newton's Laws of Motion are known. The direction and distance of the target is known. What is needed is the angle of elevation for firing. There are three basic techniques: function inversion, "brute force," and search, hi function inversion, the mathematical inverse of the function characterizing the process is calculated and encoded as a program. The outputs are input into the inverted process and the inputs appear as output. The main problem is that not all mathematical functions are invertible; it is not always possible to determine if a function is invertible or not; and the inverse of some invertible functions cannot be calculated.
For very small problems, the brute force method involves calculating outputs for all possible inputs over a given range. This provides a table relating all inputs and outputs over that range. The firing tables calculated for artillery were such tables. Inputs are calculated by reading the table backwards, looking up the outputs and reading off the matching inputs. Most problems are too large for the brute force method. Instead, for a given set of outputs, the space of all possible inputs is systematically searched to locate a set of inputs that will produce the given outputs. There is a tremendous variety of search methods, including gradient descent (Rumelhart, McClelland & The PDP Research Group, 1986), simulated annealing (Press, Flannery, Teukolsky & Vetterling, 1986), genetic algorithm (Holland, 1975), and tuning (Cox, Park, Sacks & Singer, 1992).
The final case, and by far the most difficult, is when the inputs and outputs are known, but the process is unknown. There are no general solutions. The usual approach is to assume that the process is one of a specific set of algorithms and to search the space of such algorithms. Traditional statistical regression does this for various sets of polynomial functions. The most general technique searches the space of Turing functions (Biermann, 1972). The most important problem is that, if the actual process is not in the target set, these technique give wrong answers.
Consider a variant on the last example given above:
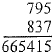
The problem is to find out what operation on the first two numbers will give the third as a result. If we know that the operation is one of addition, subtraction, multiplication, or division, then the problem is easy. But if the operation might be any mathematical function, the problem could be impossibly difficult.
The best known problems of inferring processes are number series problems. Borrowing a set of examples from Donahoe & Palmer (1994, p. 282):

The problem is to find out what single operation on each number in the sequence will give the next number. This operation is then applied to the last number in order to fill in the blank at the end. Even when the problems are restricted to sequences of monotonically increasing integers, these problems are by no means trivial.
The role of computers in scientific interpretation
What role can the elucidation of obscure numerical (and related) properties have in the scientific interpretation of behavior? One role has already been suggested, the transformation of actual experimental data. Computers can and do take the place of cumulative recorders, translating behavioral data from time.event format (tables listing events with each row labeled in order with the time of occurrence, Church, 1997) into cumulative records. Further, in QAB, when a functional analysis is expressed in terms of general relations, these relations can be taken as premises and predictions of more specific relations can be inferred as conclusions. For instance, in research on the Matching Law, the slope and intercept of the prediction line are calculated from the data together with the law itself. When the inference is too complex, a computer can be helpful. However, neither of these uses of the computer is ordinarily considered a computer simulation.
Like quantitative analyses, simulations generally involve interpretation of functional relations that themselves are derived from experimental analyses. Like data transformation, the output of simulations is often expressed as a time course of hypothetical behavioral events, rather than as a specification of predicted relations. In combining these two features, computer simulations offer unique contributions to scientific interpretation.
Interpretation without Simulation
In order to illustrate the unique benefits of computer simulation, it will be useful to briefly mention the benefits of other sorts of computer calculations to scientific interpretation. In the case of the computer control of animal experiments and computer transformation of animal data, the benefits are straightforward. In the case of computer control, the reinforcement schedule is specified in a parametric form, as a set of premises. At each point in time, the computer infers the appropriate settings for the operanda, discriminative stimuli, feeder, etc. In the case of data transformation, numerical properties of the behavioral data stream, the best example being response rate, are emphasized. This purpose is served identically whether the mechanism is a cumulative recorder or a computer.
In the case of quantitative analysis, the role of the computer is somewhat different. The model of the functional relations is encoded into the computer's program as a set of general premises. The computer then infers specific behavioral predictions. The only difference between this and computer simulation is that, in computer simulation, specific predictions as to the next behavioral event are made in sequence, on a moment-to-moment basis. Any other sorts of predictions are still quantitative analyses, but not computer simulations. Quantitative analyses include the inference of functional relations that will appear in specific circumstances. For instance, a computer can be used to predict relative proportions of responding for other dian VI-VI concurrent schedules from the Matching Law (Herrnstein & Hey man, 1979). These sorts of inferences predict synchonic (time independent) features of the data based upon synchronic principles.
Simulation for Interpretation
The uses of simulation include cases of confirmation where inputs, processes and outputs are known, as well as cases of using the computer to infer or estimate values for unknown components.
Confirmation. Psychological experiments derive real outputs from real inputs. Behavioral theories postulate accounts as to how those outputs have been derived. Verbal interpretations are most often used to confirm that, in the case of die particular experiment, the behavioral theory in question predicts the results actually obtained in the experiment. As Donahoe & Palmer (1994, p. 128-129) note, computer simulations, properly done, are less subject to the type of miscalculations made by humans than humans are. As Skinner (1957, pp. 425-426) suggests, confirmation is best obtained by using a variety of means subject to different sorts of errors. Using the independent variables of the experiment as inputs and die behavioral theory as the program, the outputs of die computer simulation are compared to the experimental results, confirming (or disconfrrming) the verbal interpretation to the effect that the theory predicts the results obtained (Church, 1997; Kemp & Eckerman, 2001).
Missing outputs. The most difficult and challenging use of computer simulation is when the inputs and processes are known, but the outputs are unknown. The paradigm case is when a theory has been confirmed against many previously completed experiments and then a simulation is run to make a prediction for an experiment not yet performed. This sort of thing only happens for the best of theories predicting the simplest of experiments. As noted earlier, event the best of theories cannot be used to predict simple real world events.
The more intricate the prediction, the more difficult the requisite computation. Synchronic properties are inherently less intricate than (diachronic) moment-to-moment sequences of events. Quantitative analyses focussed on the prediction of specific properties of the data can be computed much more easily than tiie simulation of behavioral sequences. Conversely, the most simple predictions do not require use of the computer at all. In sum, the tremendous difficulties in prediction due both to the inadequacy of current theory and to the ineliminable complexities of the world (Donalioe & Palmer, 1994, p.127) render the marginal utility of automatic computation very small. The fantasy that computer simulation can be used to replace animal experimentation will remain unfulfilled for many, many decades, if not forever.
Missing inputs. After confirmation, the second most important use of simulation is the estimation of unknown input values. This process is referred to as setting free parameters. It is both technical and subsidiary to the process of confirmation. In psychology, a common variant is when the model requires more types of input than are available from the experimental design. In mentalistic models, there may be two sets of input parameters. One set, called fixed parameters, are assigned values based on the experimental design (stimuli, contingencies, etc.). The other set, whose values correspond to no aspect of the observable features of the experiment, may be assumed in some scientific traditions to correspond to internal unobservable aspects of the behaving organism. When free parameters are included in behavioristic models, they are usually not given any such surplus meaning.
In order to estimate values for free parameters, all of the various search techniques can be and are used. (The presence of the fixed parameters does not affect use of these techniques.) Non-search techniques are generally inapplicable. There are important psychometric issues surrounding the use of free parameters that are beyond the scope of the present paper.
Unknown processes. The greatest challenge in psychology, and the thing that most prominently divides one approach to research from another, is coping with the study of behavior with so little knowledge of die neural processes involved. Were there effective computational techniques for calculating unknown processes given known inputs and outputs, this would provide an important technique for resolving this age-old dilemma of psychological inquiry. But, as we noted above, there are no such techniques. The unknown process can only be hypothesized.
After that hypothesis is made, the computer may come into play as a confirmatory tool, but the computer has little to offer by way of its own hypotheses. Ultimately, human effort in biobehavioral research will be the solution to improving our hypotheses about intervening events.
Discussion
When the core of a verbal interpretation of behavioral principles is encoded into a computer simulation program, we are able to check the reasoning underlying that interpretation in three ways. First, because the encoded version is not only formal, but also designed to be sufficient to infer moment-to-moment activity, we find gaps in the original logic that need to be filled in. One of the most important benefits of logic is the ability govern the listeners' behavior more strictly than ordinary language. Part of that strictness is enabling the listener to discriminate lacunae in the speaker's reasoning (and, in principle, to punish contingent on such lacunae).
Implementation of moment-to-moment streams of output on the computer also provides strict punishment, because any computer program designed to provide streams of real-time data is extraordinarily sensitive to programming error. If the behavior analyst performing verbal interpretation makes a slight error, neither pen nor paper complains, and the reader may fail to detect the error. If the behavior analyst programming a computer simulation makes an error, the computer either produces wildly nonsensical results, or, more likely, just stops dead in its tracks.
Second, once the computer program is up and running, the reader gets to confirm the author's reasoning, just like the reader does when she reads a verbal interpretation. The only difference is that as a scientific instrument, the computer simulation has clarified matters by emphasizing the most important results for the reader.
Third, the power and speed of the electronic computer make it possible to make inferences from the data (or from the initial verbal interpretations) quite impossible in the lifetime of one or even several inquirers. Additional inferences mean additional opportunities to confirm or disconfirm. When there is no opportunity for any confirmation of the initial verbal interpretation, computer simulation may be the only opportunity.
References
Biermann, A.W. (1972). On the inference of Turing machines from sample computations. Artificial Intelligence, 3,181-198. [ Links ]
Burgos, J. E. (2000). Editorial: Neural Networks in Behavior Analysis: Models, Results, and issues. Revista Mexicana de Análisis de la Conducta. (The Mexican Journal of Behavior Analysis), 26,129-134. [ Links ]
Church, R. M, (1997). Quantitative models of animal learning and cognition. Journal of Experimental Psychology: Animal Behavior Processes, 23,379-389. [ Links ]
Cox, D., Park, J. S., Sacks, J., & Singer, C. (1992). Tuning complex codes to data. Proceedings of the 23rd Symposium of the Interface of Computing Science and Statistics, 226-271. Fairfax Station, VA: Interface Foundation. [ Links ]
Donahoe, J. W., Burgos, I. E. & Palmer, D. C. (1993). A selectionist approach to reinforcement. Journal of the Experimental Analysis of Behavior, 60,17-40. [ Links ]
Donahoe, J. W. & Palmer, D. C. (1994). Learning and complex behavior. Boston: Allyn & Bacon. [ Links ]
Donahoe, J. W., Palmer, D. C. & Burgos, J. E. (1997). The S-R issue: Its status in behavior analysis and in Donahoe & Palmer's Learning and Complex Behavior. Journal of the Experimental Analysis of Behavior, 67,193-211. [ Links ]
Herrnstem, R. J., & Heyman, G. M. (1979). Is matching compatible with reinforcement maximization on concurrent variable interval, variable ratio? Journal of the Experimental Analysis of Behavior, 31,209-223. [ Links ]
Hobbs, J. R., Blenko, T., Croft, B., Hager, G., Kautz, H. A., Kube, P., & Shoham, Y. (1985). Commonsense Summer: Final Report (Report No. CSLI-85-35). Stanford, CA: Stanford University. Center forthe Study of Language and Information. [ Links ]
Holland, J. H. (1975). Adaptation in Natural and Artificial Systems. Ann Arbor, MI: University of Michigan Press. [ Links ]
Hutchison, W. R. & Stephens, K. R. (1987). Integration of distributed and symbolic knowledge representations. Proceedings of the First International Conference on Neural Networks, 2,395-398. IEEE Press. [ Links ]
Kehoe, J. E. (1989). Connectionist models of conditioning; A tutorial. Journal of the Experimental Analysis of Behavior, 52,427-440. [ Links ]
Kemp, S. M. & Eckerman, D. A. (2000). Behavioral patterning by neural networks lacking sensory innervation. Revista Mexicana de Anaiisis de la Conducta. (The Mexican Journal of Behavior Analysis), 26,229-249. [ Links ]
Kemp, S. M., & Eckerman, D. A. (2001). Situational descriptions of behavioral procedures: The In Situ testbed. Journal of the Experimental Analysis of Behavior, 75,135-164. [ Links ]
Press, W. H., Fiannery, B. P., Teukolsky, S. A., & Vetterling, W. T. (1986). Numerical recipies: The art of scientific computing. Cambridge: Cambridge University Press. [ Links ]
Rumelhart D. E., McClelland, J. L., & The PDP Research Group. (1986). Parallel Distributed Processing: Explorations in the microstructitre of cognition, Volume I: Foundations. Cambridge, MA: Bradford Books/MIT Press. [ Links ]
Skinner, B. F. (1957). Verbal behavior. New York: Appleton-Century-Crofts. [ Links ]
Skinner, B. F. (1969). Contingencies of reinforcement: A theoretical analysis. New York: Appleton-Century-Crofts. [ Links ]
Staddon , J. E. R. & Zhang, Y. (1991). On the assigmnent-of-credit problem in operant learning. In M. L. Commons, S. Grossberg, & J. E. R. Staddon (Eds.), Neural network models of conditioning and action: A volume in the Quantitative Analyses of Behavior series (ch. 11, pp. 279-293). Hillsdale, NJ: Lawrence Erlbaum. [ Links ]
Tryon, W. W. (1995a). Neural networks for behavior therapists: What they are and why they are important. Behavior Therapy, 26,295-318. [ Links ]
Tryon, W. W. (1995b). Synthesizing animal and human behavior research via neural network learning theory. Journal of Behavior Therapy and ExperimentalPsychiatiy, 26,303-312. [ Links ]
1. Special thanks go to two valued participants in a recent seminar given at the University of São Paulo for asking the question that suggested the topic of the present paper. For additional information and reprints of prior research, etc., please contact: Steven M. Kemp, Psychology Dept., Davie Hall, CB#3270, University of North Carolina, Chapel Hill, NC 27599-3270. e-mail: steve_kemp@unc.edu - URL: http://www.unc.edu/~skemp/