Serviços Personalizados
artigo
Indicadores
Compartilhar
Avaliação Psicológica
versão impressa ISSN 1677-0471versão On-line ISSN 2175-3431
Aval. psicol. v.4 n.2 Porto Alegre nov. 2005
ARTIGOS
Impacto do tamanho da amostra na calibração de itens e estimativa de escores por teoria de resposta ao item
Impact of the sample size in the item and subject's parameters estimates under item response theory
Carlos Henrique Sancineto da Silva Nunes I, 1 , 2; Ricardo PrimiII, 3
I Universidade Federal do Rio Grande do Sul - Instituto de Psicologia / Laboratório de Mensuração
II Programa de Pós Graduação Stricto Sensu em Psicologia, Universidade São Francisco
RESUMO
A teoria da resposta ao item (TRI) tem sido considerada um grande marco para a psicometria moderna, pois apresenta importantes vantagens em relação à TCT, como a virtual invariância dos parâmetros dos itens em relação à amostra, estimação mais precisa e interpretável do nível de habilidade dos indivíduos e procedimentos de equalização de testes mais eficientes. Contudo, tem sido discutido o tamanho mínimo da amostra para a utilização da TRI. O objetivo do presente estudo foi verificar o impacto do tamanho da amostra sobre a calibração de itens por TRI, bem como na estimativa da habilidade dos testandos. Para tanto, 9 amostras de diferentes tamanhos foram montadas a partir de um banco de dados com as respostas de 44 mil estudantes do Estado da Bahia a um exame educacional de matemática. Os resultados indicaram que os parâmetros dos itens e a habilidade dos avaliados podem ser estimados adequadamente para amostras a partir de 200 participantes, sendo que amostras menores geram estimativas instáveis.
Palavras-chave: Teoria de resposta ao item, Tamanho da amostra, Estatística e Metodologia.
ABSTRACT
Item Response Theory (IRT) has been considered an important development for the modern psychometrics because of its several advantages compared to Classic Test Theory (CTT), such as: the virtual invariance of item parameters in respect to the sample used in their estimation, more reliable and interpretable identification of person`s ability and more efficient procedures for test equating. Nevertheless, there are discussions in respect to the minimal number of subjects in studies using IRT. The aim of the study was to investigate the effect of sample size in the fluctuations of item and person parameters. Nine samples with different sizes were assembled from a database of 44.000 answers from students of Bahia State to an educational exam in mathematics. Results indicated that item and person parameters can be adequately estimated from samples starting form 200 subjects. Smaller sample size produces greater instability with the three-parameter model.
Keywords: Item Response Theory, Sample Size, Statistics and Methodology.
Introdução
Freqüentemente os profissionais e/ou organizações precisam tomar decisões importantes baseadas na mensuração de variáveis mais subjetivas. Por exemplo, na seleção de pessoal é preciso decidir quais candidatos possuem um perfil pré-definido de características pessoais, com base no resultado de testes medindo tais construtos. Na certificação ocupacional é preciso decidir se um candidato apresenta as competências mínimas necessárias para desempenhar as tarefas centrais da sua ocupação. Para isso, avalia-se um conjunto de competências definidas como fundamentais para uma determinada área profissional e verifica-se se o candidato apresenta um desempenho maior do que um padrão de mérito previamente definido (Carter, 2005; Naquin, & Wilson, 2002). No contexto da educação, é essencial identificar o impacto de programas e variáveis contextuais sobre o desempenho dos alunos, promovendo, com base nessas informações, capacitações em áreas estratégicas para professores e diretores escolares, bem como dar condições às escolas a auto-gestão da qualidade do ensino oferecido aos alunos.
Situações desse tipo nos levam ao problema da precisão das medidas, isto é, quão estável ou livre de erros uma determinada medida é. Erros nessa situação podem produzir uma instabilidade ou incertezas no processo de tomada de decisão e, portanto, precisam ser previamente estimados para que possam ser considerados nesse processo. Geralmente antes de efetivamente se utilizar os testes nas situações de decisão, eles são pré testados para se investigar os parâmetros psicométricos de precisão e validade (AERA, NCME & APA, 1999). Os resultados dessa fase são fundamentais para garantir a legitimidade das decisões ulteriores que serão tomadas com base nos testes.
Uma questão muito freqüente que os psicometristas se defrontam quando delineiam os estudos de pré-teste de instrumentos que serão usados em avaliação de larga escala é: Qual o tamanho da amostra, no pré-teste, para garantir a estabilidade mínima das estimativas dos parâmetros psicométricos? Os estudos de pré-teste trabalham com uma pequena amostra do grupo de pessoas que potencialmente serão objeto de avaliação e que serão afetadas pela decisão tomada com base no teste. Por razões evidentes não é possível realizar o pré-teste com todos esses sujeitos. O custo financeiro de um estudo desse tipo inviabilizaria a criação do instrumento e, além disso, há o problema do sigilo das questões, já que as pessoas passariam a conhecer os itens antes de se submeterem efetivamente à prova. Então quanto menor a amostra de pré-testagem menor é o custo e o risco. Por outro lado quanto menor é a amostra, maior é a chance de que ela seja menos representativa e, por conseguinte, maior a incerteza em relação aos valores dos parâmetros psicométricos estimados. Assim incorre-se em uma questão ética de incerteza quanto à generalidade dos argumentos favoráveis à validade da prova que são baseados nos parâmetros estimados na pré testagem. Portanto a questão nesses casos passa a ser, quão pequena a amostra de pré teste pode ser sem comprometer as estimativas dos parâmetros, isto é, sem que eles passem de um limite tolerável de incerteza?
Na construção de instrumentos para avaliação em larga escala geralmente são empregados os métodos da psicometria moderna chamada Teoria de Resposta ao Item (TRI). Tal método passou a ser conhecido, principalmente, a partir do ano de 1968 com o trabalho de Lord e Novick intitulado "Statistical Theories of Mental Tests Scores" (Muñiz, 1994). Na literatura especializada esta nova abordagem aparece intitulada como: modelos de traços latentes [em inglês: Latent Trait Models, LTM] ou modelos de curvas características dos itens [em inglês: Item Characteristic Curve Model, ICC], e mais recentemente teoria de resposta ao item [em inglês: Item Response Theory, IRT] (Hambleton & Swaminatham 1985; Muñiz (1990).
Inúmeras aplicações da TRI têm sido exploradas nas últimas três décadas tais como: criação de bancos de itens, avaliação adaptativa computadorizada, equalização de provas, avaliação de mudança cognitiva. Um detalhamento das principais aplicações é encontrado, por exemplo, em Lord (1980); Whiely (1980) e Wainer (1989). Alguns exemplos de avaliação em larga escala que utilizam a TRI são o teste TOEFL [em inglês Test of English as a Foreign Language]; o teste GRE [em inglês: Graduate Record Examinations], que vem sendo aplicado oficialmente via microcomputador usando avaliação adaptativa baseada na TRI (Educational Testing Service, 1995, 1996).
Embora a TRI não entre em contradição com os princípios da psicometria clássica, traz uma nova proposta de análise centrada nos itens que supera as limitações principais da teoria clássica (Muniz, 1994, Hambleton, Swaminatham, Cook, Eignor & Gifford 1978), além de apresentar novos recursos tecnológicos para a avaliação. A TRI tem como unidade de análise o item e formaliza a relação que existe entre a probabilidade de acertar o item e a capacidade latente requerida na sua resolução. Quanto maior a capacidade de um sujeito, chamado de traço latente, maior será a probabilidade de que este sujeito acerte um determinado item que meça este construto. Portanto é possível construir uma função que expresse a relação entre a probabilidade de acerto, dados os valores do traço latente.
Na literatura dois tipos de funções matemáticas têm sido utilizadas para modelar esta relação: funções de distribuição normal acumulada (ogivas normais) e funções de distribuição logística acumulada. Estas funções tomam a forma geral exemplificada na Figura 1. Como se pode observar, o valor de theta, ou da variável latente, é dado em escore padrão z. Observa-se que na medida em que o escore na variável latente aumenta, aumenta também a probabilidade de se acertar o item. Um segundo fato importante é que a relação pode tomar diferentes formas, dependendo das propriedades dos itens, nomeadamente: (a) a dificuldade, (b) o poder discriminativo, e (c) a probabilidade de acertar o item ao acaso. Essas informações podem estar presentes nas equações, possibilitando uma maior caracterização do item.
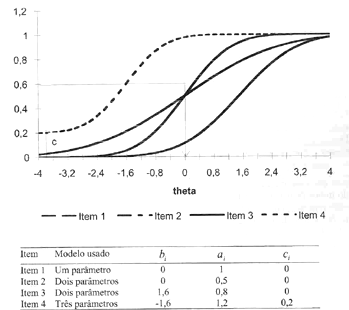
Figura 1. Exemplo de quatro curvas características de itens com parâmetros distintos.
São chamados modelos de um parâmetro aqueles que incluem na função somente a informação sobre a dificuldade dos itens; modelos de dois parâmetros aqueles que incluem, além da dificuldade, o poder discriminativo, e modelos de três parâmetros os que incluem além da dificuldade, o poder discriminativo e a probabilidade de acertar o item por acaso. Portanto podem existir funções baseadas nos modelos normais de um, dois e três parâmetros e modelos logísticos de um, dois ou três parâmetros. Atualmente as funções logísticas são as mais utilizadas, dado que as funções normais envolvem cálculos mais complexos (Baker, 1992). Na Figura 2 são apresentadas as funções logísticas para os modelos de um, dois e três parâmetros.
Como pode ser notado nas equações, a probabilidade de acertar um item está em função do valor da variável latente. Como o resultado é dado em probabilidades, pode assumir valores de 0 a 1. O caso mais geral é o modelo de três parâmetros, o que foi usado nesse estudo. Na Figura 1 as curvas de quatro itens diferentes foram apresentadas. O modelo utilizado e os valores dos parâmetros foram apresentados em seguida. Nota-se que para os quatro itens o aumento do valor de theta corresponde a um aumento na probabilidade de acerto. Contudo essas curvas têm formas diferentes dependendo da característica do item.
Índice de dificuldade (b)
Este índice, que usualmente tem a notação b, é um parâmetro do item que diz respeito ao valor de theta (variável latente) em que a probabilidade de acerto é 0,50. Portanto nos Itens 1 e 2, b = 0, já que este valor da variável latente corresponde a probabilidade de 0,50. No Item 3, b = 1,6 e no Item 4, b = -1,6. Observa-se que a única exceção a essa regra é o Item 4. Nesse caso o índice de dificuldade corresponde ao valor da variável latente em que a probabilidade de acerto for igual a (1 + c)/2, portanto 0,50 se c1 =0.

Figura 2. Funções logísticas de um, dois e três parâmetros da curva característica do item.
Nota-se que esse índice não tem o mesmo significado do índice de dificuldade na psicometria clássica. Ele não representa uma estimativa geral da probabilidade de acerto de um determinado item (ou seja, o ID da psicometria clássica). Aqui a probabilidade de acerto é fixada em 0,50, e é avaliado o valor de theta relacionado a esta probabilidade. Avalia-se para cada item qual o valor de theta exigido para a obtenção de 50% de acertos. Dentre os quatro itens apresentados na Figura 1 o Item 3 é o mais difícil, já que o valor de theta para uma probabilidade de acerto 0,50 é 1,6, maior do que todos os outros. Já o Item 4 é o mais fácil. Pode ser demonstrado matematicamente que o valor de b é o ponto onde a curva característica do item tem sua maior inclinação, a partir do qual há inflexão, ou seja, onde a curva passa a diminuir sua inclinação. Por isso este é o ponto onde há discriminação máxima.
Índice de discriminação (a)
O valor do índice de discriminação que usualmente tem a notação a refere-se a inclinação da curva. Quanto maior for a inclinação da curva maior será o valor deste índice. Pode-se demonstrar que ele é proporcional ao coeficiente angular da reta tangente ao ponto de máxima inclinação (ou seja onde P = 0,50). Nota-se que quanto maior a inclinação da curva maior é a possibilidade de discriminação da escala de habilidade, ou seja, para uma mesma variação do theta, quanto maior for a variação de P, mais intensa é a discriminação entre estes níveis de theta, porque mais diferentes são as probabilidades. Dentre os itens da Figura 7 o Item 4 é o mais discriminativo e o Item 2 o menos discriminativo. No Item 1 o valor de a = 1 assim como todas as curvas dadas pelo modelo de um parâmetro. Nota-se que o item não discrimina igualmente em toda a escala de theta. Isto é um ponto importante a ser ressaltado e é tratado em mais detalhes quando se criam as funções de informação do item que informam qual a precisão do item para os diferentes níveis de theta. Em termos psicológicos, se uma escala avalia, por exemplo, raciocínio verbal, um item com maior valor de "a" é capaz de diferenciar pessoas com níveis distintos nesse construto das demais. No entanto, vale salientar que a capacidade de discriminação dos itens varia de acordo com o nível de habilidade avaliado (ou theta).
Probabilidade de acertar o item ao acaso (c)
Esse parâmetro corresponde a probabilidade de acertar o item quando a habilidade tende a . Assim este valor representa a probabilidade de acerto quando a habilidade é muito baixa, ou seja, a probabilidade de acerto não dependente da habilidade; relacionando-se portanto aos acertos ao acaso. Na Figura 1 o valor deste parâmetro é 0,20 para o Item 4 e 0 para os itens restantes.
A aplicação da TRI envolve inicialmente a estimação dos parâmetros para os itens. Uma vez calibrados pode-se usar o instrumento para se obter medidas dos sujeitos que respondem aos itens. Mais uma vez as medidas para os sujeitos são estimadas a partir dos padrões de resposta aos itens considerando os parâmetros desses itens. Com base nessas informações os procedimentos de cálculo elaboram uma função que relacionam os valores possíveis da medida com a probabilidade de terem produzido aquele padrão específico de respostas para aquele dado conjunto de itens. Há diferentes métodos em função da informação disponível. Geralmente nas estimações iniciais é preciso estimar as medidas dos sujeitos e os parâmetros dos itens simultaneamente. Portanto os métodos têm que lidar com o problema de não ter informações nem dos parâmetros dos itens e nem dos sujeitos. Já quando se tem os parâmetros dos itens estimados os cálculos das capacidades dos sujeitos é mais facil. Uma discussão mais detalhada desses métodos pode ser encontrada em Embretson & Reise (2000).
Como qualquer estimativa estatística estas produzem um valor mais próximo possível do valor verdadeiro juntamente com um erro de amostragem. Assim a quantidade de sujeitos na amostra utilizada na estimação, isto é, sua representatividade, influencia diretamente a magnitude da confiabilidade das estimativas (ou o erro amostral). A questão que nos propomos estudar nesse artigo refere-se ao impacto que diferentes amostras com números cada vez mais reduzidos de sujeitos teriam na estimação dos parâmetros dos itens e dos sujeitos. Esse estudo é muito útil para se perceber qual o tamanho mínimo da amostra sem que haja perdas muito grandes em termos de aumento do erro das estimativas.
Embretson e Reise (2000) indicam que é possível a estimação dos parâmetros dos itens por TRI com amostras de 250 participantes, em dados gerados por simulação Monte Carlo. No entanto, os autores indicam a necessidade de realização de estudos com dados reais, a partir de instrumentos que efetivamente avaliam construtos psicológicos. De uma forma geral, os autores indicam que a avaliação de amostras pequenas deve ser cuidadosa e é essencial a heterogeneidade dos mesmos para o construto avaliado. Justificam que, principalmente em escalas politônicas são prejudicadas caso algumas categorias apresentem poucos casos.
Sendo assim, o objetivo desse estudo foi verificar o efeito do tamanho da amostra na confiabilidade das estimativas dos parâmetros dos itens e das habilidades dos avaliados. Foi empregado o modelo de três parâmetros, frequentemente utilizado na avaliação psicológica, educacional, certificação ocupacional, entre outros.
Método
Participantes
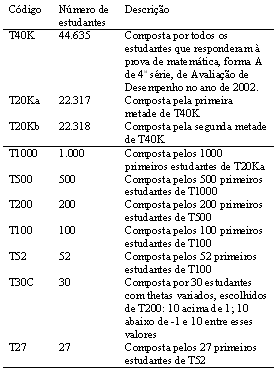
Para a realização do estudo, foi utilizada uma base de dados cedida pelo Projeto de Avaliação Externa - ISP / UFBA - FAPEX, contendo as respostas obtidas em uma prova de Avaliação de Desempenho aplicada no ano de 2002. A base de dados inclui respostas de 44.636 estudantes de 4ª série do ensino básico na disciplina de matemática. Foram criadas, a partir da base de dados original, 9 bases parciais, com códigos e características descritas na Tabela 1.
Tabela 1. Descrição das amostras utilizadas no presente estudo.
Instrumentos
O instrumento utilizado foi a prova de matemática para Avaliação de Desempenho, composto por 25 itens de múltiplas escolhas, com quatro alternativas. A prova foi elaborada pelo núcleo de conteúdo do Projeto de Avaliação Externa, a partir de matrizes de conteúdos que foram validadas por especialistas em educação, diretores e professores do Estado da Bahia, bem como pela comunidade geral. A prova era composta por itens que nos estudos de pré-testagem haviam atendido às especificações mínimas indicadas pelo setor de psicometria do Projeto de Avaliação Externa.
Procedimentos
Os dados foram analisados com a utilização do Software XCalibre, específico para a estimação dos parâmetros psicométricos de itens dicotômicos, por TRI, nos modelos de dois e três parâmetros. O programa também permite a equalização de teste a partir da fixação dos parâmetros de itens comuns entre eles.
Inicialmente, os parâmetros dos itens foram estimados em todas as amostras, exceto para T30C. Em seguida, foi feito o cálculo de theta dos participantes para as amostras estudadas e foram escolhidos, da amostra composta por 200 pessoas, 10 estudantes para cada faixa de desempenho: 10 com thetas acima de 1; 10 com thetas abaixo de -1 e 10 com escores intermediários (entre -1 e 1).
Com o auxílio de um software para montagem de bases de dados, os thetas estimados para os estudantes em todas as amostras foram agrupados considerando-se o seu código individual. Também foram montadas planilhas com os resultados das análises dos parâmetros "a" (discriminação dos itens) e "b" (nível de dificuldade) para os itens da prova.
Resultados e Discussão
Para verificar o impacto do tamanho da amostra na estimativa do nível de dificuldade dos itens, foi calculada a dificuldade da prova a partir da média dos "b" de todos os seus itens. Em seguida, foi calculada a diferença dos valores encontrados nas amostras parciais em relação à amostra completa (com 44 mil estudantes). Também foram calculadas as correlações dos "b" dos itens entre as amostras parciais e a amostra completa. A Tabela 2 apresenta as informações citadas e a Figura 3 (anexo 1) apresenta os níveis de dificuldade (parâmetro b) para os 5 primeiros itens da prova, na parte A, e nas partes B e C os diagramas de dispersão dos b's sempre em comparação com a amostra completa.
Tabela 2. Dificuldade dos itens nas amostras utilizadas.
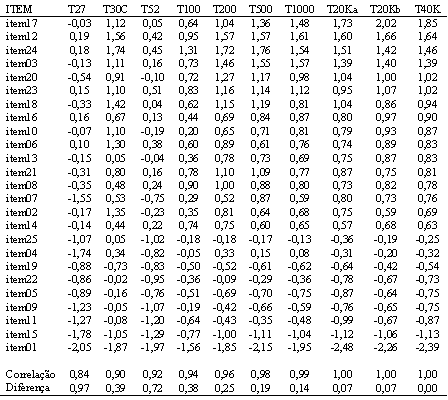
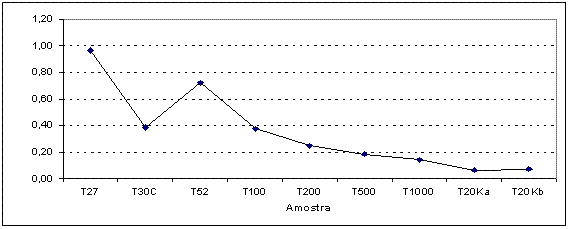
Figura 4. Diferença entre a média de dificuldade da prova nas amostras.
A Figura 4 apresenta graficamente os dados das diferenças em relação à amostra completa entre as médias dos b's para as diferentes amostras.
É possível verificar-se que os valores variam muito nas amostras com até 100 pessoas, tornando-se razoavelmente estáveis com as amostras compostas por 200 estudantes. Vale notar que esse perfil tende a repetir-se com todos os itens da prova. Se considerarmos a relação custo benefício, é possível verificar que os parâmetros de dificuldade são praticamente os mesmos se usarmos amostras com 200 sujeitos ao invés de 44 mil.
Para verificar o impacto do tamanho da amostra na estimativa da capacidade de discriminação dos itens (parâmetro "a" na TRI), este parâmetro foi calculado em todas as amostras estudadas, bem como a diferença entre a média de discriminação para cada amostra parcial e a amostra completa e a sua correlação. A Tabela 3 apresenta o resultado dessa análise, que pode ser visualizada para 5 itens na parte A da Figura 5 (anexo 2). Nas partes B e C são apresentados os diagramas de dispersão dos valores dos índices de discriminação estimados pelas amostras parciais e completa.
Essa análise tráz alguns pontos bem interessantes. Em primeiro lugar os resultados das amostras com até 100 estudantes indicaram parâmetros virtualmente iguais para todos os itens avaliados próximos a 0,80. Também é importante notar que esse valor é exatamente o valor do parâmetro "a" definido a priori no processo de calibração dos itens. Portanto em amostras pequenas o valor de discriminação varia muito pouco. Em segundo lugar, verificando-se a correlação entre os índices de discriminação dos itens das amostras parciais em comparação com a amostra completa, nota-se que a mesma é moderada para os grupos pequenos e é considerada alta com grupos a partir de 200 pessoas (nessa amostra a correlação atinge 0,87). A partir desse tamanho os parâmetros mantêm a posição relativa. Entretanto a dispersão dos valores da discriminação é baixa.
A Figura 6 apresenta a diferença entre a média da discriminação dos itens das amostras parciais em relação à amostra total. É possível verificar-se que essas diferenças não são muito acentuadas, mesmo para as amostras pequenas. A partir de 500 sujeitos as estimativas são bem mais próximas e com a amostra de 20.000 sujeitos, praticamente idênticas às estimativas derivadas da amostra completa.
Em síntese a dispersão dos índices de discriminação aumenta com o aumento da amostra. Isso pode ser decorrência de uma maior quantidade de sujeitos nos vários segmentos da escala de theta criados para estimação dos parâmetros o que faz com que as estimativas das probabilidades de acerto sejam mais estáveis sendo possível revelar com mais clareza a os casos de maior ou menor inclinação da curva característica do item.
Tabela 3. Discriminação dos itens nas amostras estudadas.
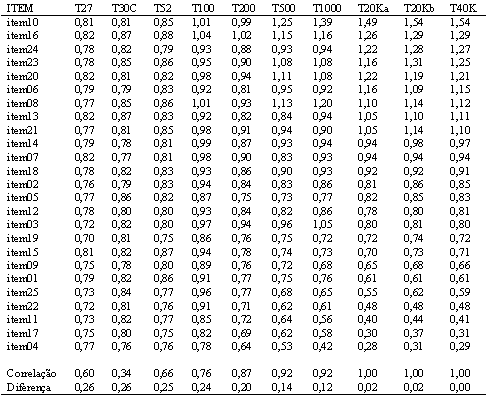
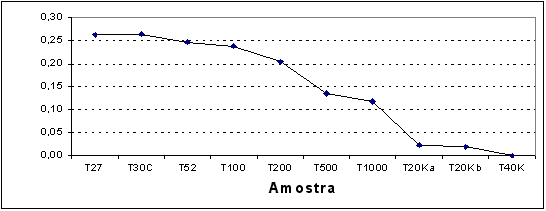
Figura 6. Diferenças entre o índice de discriminação médio das provas nas amostras.
Para verificar-se o impacto do tamanho da amostra na estimativa de habilidade dos participantes (Theta), estes foram calculados a partir do método da Máxima Verossimilhança (Maximum Likelihood) em todas as amostras. Como cada estudante avaliado apresentava um código específico, foi possível realizar a comparação dos thetas dos mesmos gerados nas amostras com diferentes tamanhos. Para verificar-se a eficácia da equalização por parâmetros fixados, foram calculados os escores dos estudantes na amostra de 50 pessoas com os parâmetros estimados na amostra completa (com 44 mil estudantes). Os resultados são descritos na variável theta50E.
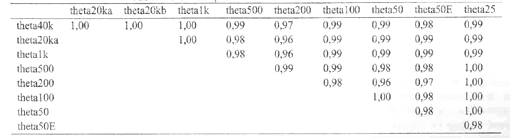
A Tabela 4 apresenta a correlação entre os thetas dos participantes em todas as amostras estudadas. É possível verificar-se que os escores estimados, independentemente do tamanho da amostra, apresentam uma associação extremamente forte.
No entanto, observando-se os valores absolutos dos escores dos participantes, foi possível verificar-se que estes apresentavam algumas discrepâncias significativas, principalmente entre a amostra completa (com 44 mil participantes) e as menores amostras. Para verificar-se a magnitude dessas diferenças, foram realizadas regressões lineares nas quais o theta da amostra completa foi considerado como variável dependente e o theta das amostras parciais como independentes. É importante salientar que as regressões foram realizadas independentemente para cada amostra parcial. A idéia básica na realização dessa análise é que se não houvesse diferenças significativas entre os escores estimados nas amostras, o valor da constante estimada pela regressão linear deveria estar próximo de zero enquanto que o valor de B deveria ficar próximo de 1.
Tabela 4. Correlação entre os Thetas estimados nas amostras.
A tabela 5 apresenta o valor da constante e de B nas regressões calculadas. É possível notar que o valor da constante é relativamente pequeno com amostras a partir de 200 pessoas, sendo que o valor de B nesta amostra está bem próximo ao esperado (1). Pode-se também verificar que o valore encontrado na amostra de 50 pessoas após a sua equalização (theta50E) apresenta-se muito mais próximo do esperado do que quando não é feita a equalização (theta 50).
Tabela 5. Regressão entre o theta das amostras parciais comparados à amostra completa.

Esse resultado indica que o principal erro ao estimar o theta de pessoas em grupos pequenos a partir da TRI encontra-se na perda de referência da habilidade média (estimada como 0 na TRI). No entanto, a partir do procedimento de equalização, esse efeito pode ser minimizado e, mesmo quando são avaliados pequenos grupos, a TRI pode ser utilizada desde que os parâmetros dos itens sejam antecipadamente estimados em amostras maiores.
Considerações Finais
Esse estudo objetivou verificar o efeito do tamanho da amostra na confiabilidade das estimativas dos parâmetros dos itens e das
capacidades dos sujeitos. De forma geral pode-se concluir que amostras com 500 sujeitos trazem resultados muito próximos aos estimados com amostras maiores. Amostras com 200 sujeitos também geram resultados bastante aproximados principalmente quanto aos parâmetros de dificuldade e de capacidade dos sujeitos. Essa aproximação não é tão eficaz quando se considera os parâmetros de discriminação. Vale salientar, no entanto, que mesmo para o parâmetro "a", a posição relativa dos itens foi estimada, ou seja, os itens que apresentaram maior capacidade de discriminação na amostra com 200 participantes foram os mesmos em amostras maiores.
Tais resultados corroboram os dados apresentados na literatura especializada gerados, na sua maioria, a partir de dados simulados (Embretson & Reise, 2000; Hambleton & Swaminatham, 1985 e Muñiz 1990). Tal informação pode ser útil nas decisões sobre a definição da amostra em estudos de pré-testagem uma vez que demonstra que com amostras muito mais reduzidas (200 ou 500 em relação a 40000) podemos obter praticamente os mesmos resultados que obteríamos se analisássemos amostras muito maiores.
Algumas limitações precisam ser consideradas quanto a generalização das recomendações sugeridas nesse estudo. Os dados podem variar se estivéssemos analisando dados de outro construto (conhecimento em geografia, por exemplo) ou de outras amostras com distribuições mais assimétricas ou, por outro lado, até mesmo próximas das condições ideais. Em tais casos o número mínimo de sujeitos recomendado para se recuperar os valores "verdadeiros" dos parâmetros pode variar. Mas considerando a concordância com os dados da literatura as sugestões sugeridas aqui são seguras para uma grande variedade de situações.
Referências
American Educational Research Association, American Psychological Association, Nacional Concil on Measurement in Education (1999). Standards for Educational and Psychological Testing. Washington, DC: American Educational Research Association [ Links ]
Baker, F. B. (1992). Item response theory parameter estimation techniques. New York: Marcel Dekker Inc. [ Links ]
Carter, S. D. (2005). The Growth of Supply and Demand of Occupational-Based Training and Certification in the United States, 1990-2003. Human Resource Development Quarterly, 16, 33-54. [ Links ]
Educational Testing Service (1996). GRE 1996/97 Information & Registration Bulletin. Princeton: Educational Testing Service. [ Links ]
Educational Testing Service (1995) TOEFL Practice Tests. Princeton: Educational Testing Service. [ Links ]
Embretson, S., & Reise, S. (2000). Item Response Theory for Psychologists. Mahwah, New Jersey: Lawrence Erlbaum Associates. [ Links ]
Hambleton, H. K., Swaminatham, H. & Rogers, H. J. (1991). Fundamentals of item response theory. Newbury park, CA: Sage Publications. [ Links ]
Hambleton, R. K. & Rovinelli R. J. (1986). Assessing the dimensionality of a set of test items. Applied Psychological Measurement, 10(3), pag. 287-302. [ Links ]
Hambleton, H. K. & Swaminatham, H. (1985). Item response theory: principles and applications. Boston: Kluwer. [ Links ]
Hambleton, H. K., Swaminatham, H., Cook, L. L., Eignor, D. R. & Gifford, J. A. (1978). Developments in latent trait theory: models, technical issues, and applications. Review of Educational Research, 48(4), 467-510. [ Links ]
Hutchinson, L.; Aitken, P.; Hayes, T. (2002). Are medical postgraduate certification processes valid? A systematic review of the published evidence. Medical Education, 36, 73-91. [ Links ]
Lord, F. M. (1980). Aplications of item response theory to practical testing problems. New Jersey: Lawrence Erlbaum Associates. [ Links ]
Lord, F. M. & Novick, N. R. (1968). Statistical Theories of mental test scores. Reading Mass: Addison - Weslley. [ Links ]
Muñiz, J. (1994). Teoría clásica de los tests. Madrid: Ediciones Pirámide, S.A. [ Links ]
Muñiz, J. (1990). Teoría de respuesta a los ítems: un nuevo enfoque en la evolución psicológica y educativa. Madrid: Ediciones Pirámide, S.A. [ Links ]
Naquin, S. S.; Wilson, J. (2002). Creating competency standards, assessments, and certification. Advances in Developing Human Resources, 4, 180-187. [ Links ]
Wainer, H. (1989). The future of item analysis. Journal of Educational Measurement, 26(2), 191-208. [ Links ]
Recebido em Fevereiro de 2006
Aprovado em Março de 2006
1 Ricardo Primi, Universidade São Francisco, Laboratório de Avaliação Psicológica e Educacional (LabAPE), Mestrado em Psicologia
Rua Alexandre Rodrigues Barbosa, 45, CEP 13251-900, Itatiba, São Paulo, Fone (0XX11) 45348118
Correio eletrônico:ricardo.primi@saofrancisco.edu.br ou rprimi@uol.com.br
Sobre os autores:
2 Carlos Henrique Sancineto da Silva Nunes: Psicólogo, Doutor em Psicologia do Desenvolvimento pela Universidade Federal do Rio Grande do Sul e pesquisador do Laboratório de Mensuração da UFRGS.
3 Ricardo Primi: Psicólogo, Doutor em Psicologia Escolar e do Desenvolvimento Humano pela Universidade de São Paulo e docente na graduação e Pós Graduação Stricto Sensu em Psicologia da Universidade São Francisco.
As atividades de pesquisa do primeiro autor que deram origem a esse artigo foram financiadas pelo Governo do Estado da Bahia. O segundo autor recebe financiamento do CNPq e FAPESP
ANEXO 1

Figura 3. Comparação dos Índices de dificuldade dos itens nas amostras estudadas.
ANEXO 2
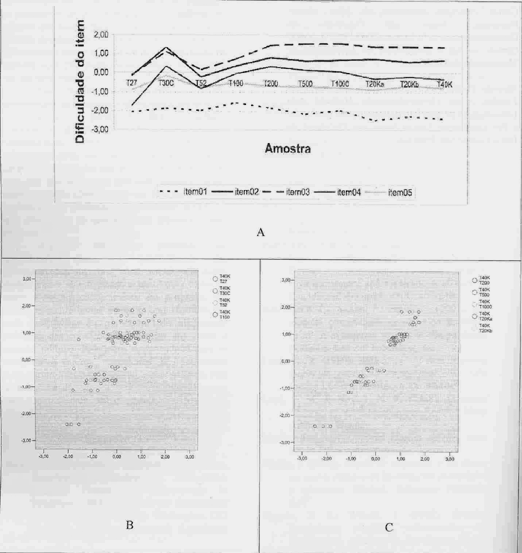
Figura 5. Índice de discriminação dos itens nas amostras estudadas.














