Serviços Personalizados
artigo
Indicadores
Compartilhar
Avaliação Psicológica
versão impressa ISSN 1677-0471versão On-line ISSN 2175-3431
Aval. psicol. vol.14 no.3 Itatiba dez. 2015
Measuring self-esteem in Spanish adolescents: Equivalence across gender and educational levels
Medindo a autoestima dos adolescentes espanhóis: equivalência através de gênero e níveis educativos
Midiendo la autoestima de los adolescentes Españoles: equivalencia a través de género y niveles educativos
José M. Tomas1,I; Patrícia SanchoII; Laura GalianaI; Amparo OliverI; Pedro HontangasI
IUniversitat de València
IIUniversidad de Zaragoza
ABSTRACT
Rosenberg's self-esteem scale (RSES) has been applied in many areas of psychology, highlighting the interest in the study of gender differences and educational level. At the same time, there was a methodological debate on its psychometric properties. Evidence points at a scale measuring a single trait confounded by a method factor associated to negatively worded items. The aim of the study is to examine RSES differences due to gender and educational level at the factor level, while controlling for the presence of method effects, in Spanish students. A completely a priori model was separately tested in four subsamples: college men and women, and high school men and women, and an invariance routine implemented for them. The primary conclusions are that the scale measures equally well in the four samples, and there were no latent mean differences due to gender or educational level.
Keywords: invariance routine; Rosenberg self-esteem scale; gender and educational level differences.
RESUMO
A escala de autoestima de Rosenberg (RSES) já foi aplicada em muitas áreas da Psicología, destacando o interesse pelo estudo das diferenças de gênero e nível educativo. Paralelamente, houve um debate metodológico sobre suas propiedades psicométricas: a evidência assinala que mede apenas um fator de autoestima, mas confundido com um efeito de método associado a itens invertidos. O objetivo deste estudo é examinar as diferenças em gênero e nível educativo da RSES, controlando pela presença de efeitos de métodos em estudantes espanhóis. Foi estimado um modelo completamente a priori em quatro amostras: estudantes homens e mulheres de institutos e de universidades, e se implementou uma rotina completa de equivalência fatorial. As conclusões são que a escala mede de forma adequada nas quatros amostras e que não houve diferenças nas médias latentes em função do gênero ou nível educativo.
Palavras-chave: rotina de equivalencia; escala de autoestima de Rosenberg; diferenças de gênero e nível educativo.
RESUMEN
La escala de autoestima de Rosenberg (RSES) se ha empleado en muchas áreas de la psicología, destacando el interés por el estudio de las diferencias de género y de nivel educativo. Paralelamente, ha habido un debate metodológico sobre sus propiedades psicométricas: la evidencia señala que mide un solo rasgo de autoestima, pero confundido con un efecto de método asociado a los ítems invertidos. El objetivo de este estudio es examinar las diferencias en género y nivel educativo de la RSES, controlando por la presencia de efectos de método en estudiantes españoles. Se estimó un modelo completamente a priori en cuatro muestras: estudiantes hombres y mujeres de instituto y de universidad, y se implementó una rutina completa de invarianza factorial. Los principales resultados son que la escala mide de forma adecuada a las cuatro muestras y no hubo diferencias en las medias latentes en función del género o el nivel educativo.
Palabras-clave: rutina de invarianza; escala de autoestima de Rosenberg; diferencias de género y nivel educativo.
Self-concept refers to an individual's perceptions of the self that are formed through experiences and evaluative feedback received from significant others (Shavelson, Hubner, & Stanton, 1976), or at all thoughts and feelings relating to oneself (Rosenberg, 1979). It is a central psychological construct, being essential in the individual understanding, and being related or explaining many variables in almost every psychological domain (for example, organizational or educational psychology, Gergen, 1984; Stevens, 1996).
Self-esteem is closely related to self-concept, and it can be defined as a positive or negative attitude towards a particular object, the self (Rosenberg, 1965). Therefore, self-esteem involves an evaluative component of self-concept. The difference between both concepts is disputed, with some authors differentiating the two terms (Watkins & Dhawan, 1989), while others supporting their narrow theoretical and empirical relationship (Shavelson et al., 1976). Distinguishing between both concepts is even more difficult when operationalizing the concepts into specific measuring instruments is our target (Romero, Luengo, & Otero-López, 1994), and sometimes self-esteem and self-concept terms are interchangeably used in the scales validated for their measurement.
There are indeed a large number of instruments available to measure either self-esteem or self-concept from very diverse nature: projective techniques, observational measures and, the most commonly used selfreport measures. Among the self-report scales, some of the most employed are: Janis and Fields (1959), Self- Esteem Scale, Rosenbergs Self-Esteem Scale (RSES; Rosenberg, 1965), the Self-Description Questionnaire I and later versions (Marsh, 1988, 1989, 1990), the Multidimensional Self Concept Scale (Bracken, 1992), the AF5 scale (Bustos, Oliver, & Galiana, 2015), and the State Self Esteem Scale (Bagozzi & Heatherton, 1994; Heatherton & Polivy 1991).
Of those, Rosenberg's (1965) scale is clearly the most widely used self-report instrument for assessing global self-esteem (Marsh, 1996). The scale is thought to measure the self-acceptance aspect of self-esteem (Crandall, 1973). Originally developed as a Guttman scale scored dichotomously (Fleming & Courtney, 1984; Rosenberg, 1965), it has been used intensively as a Lykert-type scale, usually with four or five points. It consists of ten items, five positively worded and five negatively worded. A positively worded item is, for example "I feel good about myself", whereas a negatively worded item is, for example, "I certainly feel useless at times". Rosenberg developed this scale to measure a global self-esteem factor.
Since its development the scale has been massively used in all areas of psychology. For the purposes of current study, two areas of interest stand up from others: the study of gender differences on self-esteem and its potential change across educational levels. Most studies conducted on self-esteem have highlighted the presence of sex differences, both in global and domain-specific instruments (e.g., Gentile et al., 2009; Kling, Hyde, Showers, & Buswell, 1999). However, some literature reviews have pointed no gender differences (Maccoby & Jacklin, 1974; Wylie, 1979).
In any case, meta-analytic research provides the strongest evidence on self-esteem gender differences. In a recent meta-analysis dealing with gender differences in domain specific self-esteem, which included 428 effect sizes from 115 scientific papers, men rated significantly higher than women in physical appearance, athletic, personal and self-satisfaction self-esteem, whereas women rated higher than men in behavior and moral-ethical self-esteem. And finally, no statistically significant gender differences were found for academic, social, familiar, and affective self-esteems (Gentile et al., 2009). When it comes to gender differences in global self-esteem, as measured by the RSES, a meta-analysis by Kling et al. (1999) showed a small but statistically significant difference between men and women in self-esteem, a difference favoring men (d=0.22). Kling et al. (1999) meta-analytical evidence came from 218 studies, of which 62% (135) employed the RSES.
Regarding self-esteem differences across educational level, Gentile, Twenge, and Campbell (2008) reviewed three meta-analyses on this issue and concluded that there is an increase in RSES scores among American middle school, high school, and college students. Interestingly, they also found that college students' scores change only when the RSES is administered with a 4-point Likert scale with no midpoint. In a different meta-analysis, Twenge and Campbell (2001) analyzed RSES data across 199 studies (a meta-analysis) and found a significant effect of age on RSES: self-esteem increased with age (particularly between the high school and college years). In a wider age range, Sinclair, Blais, Gansler, and Sandberg (2010) provided important evidence of an increase in self-esteem across the life span as measured by the RSES.
All the aforementioned evidence on differences across groups by gender and educational level (or age) in the RSES is based on observed mean differences. In parallel to this substantive literature, there has been a methodological debate on the measurement of selfesteem by means of the RSES. The methodological literature has tried to verify the factorial structure of the RSES and the cumulated evidence points out that it measures a single trait (self-esteem) but confounded, at least, by a method factor associated to negatively worded items (see for example, Bachman & OMalley, 1986; Bagozzi, 1993; Carmines & Zeller, 1974, 1979; Corwyn, 2000; Goldsmith, 1986; Hensley & Roberts, 1976; Kaufman, Rasinski, Lee, & West, 1991; Kohn, 1977; Marsh, 1996; Marsh & Grayson, 1995; Salgado & Iglesias, 1995; Supple, Plunkett, Peterson, Kevin, & Bush, 2013; Tomás & Oliver, 1999, 2004; Tomás, Galiana, Hontangas, Oliver & Sancho, 2013; Tomás, Oliver, Galiana, Sancho, & Lila, 2013; Wang, Siegal, Falck, & Carlson, 2001). Wording items positively and negatively has been an attempt to avoid acquiescence, agreement or affirmation bias (DeVellis, 1991; Nunnally, 1978). However, it has been proved that this strategy interferes with examinations of the latent structure of the self-report instrument (e.g. Carmines & Zeller, 1979; Marsh, 1996; Tomás & Oliver, 1999) and as seen before, this interference is apparently ubiquitous in the particular case of the RSES across populations and versions of the scale. At this point, it should be borne in mind that the reviewed meta-analytical evidence on RSES differences has not controlled for these method effects associated with negatively worded items, and therefore it could be misleading evidence. There is no clear evidence that self-esteem differences still hold when these well-known method effects are controlled for. As an example, a recent study by Supple et al. (2013) evaluated factor structure and method effects associated to negatively worded items of the RSES with samples of European, Latino, Armenian, and Iranian- American adolescents. Their findings suggested that method effects in the RSES were more pronounced among ethnic minority adolescents, and they pointed out that accounting for method effects is necessary to avoid biased conclusions regarding cultural differences in self-esteem.
According to the reviewed literature, the aim of the study is to examine RSES differences due to gender and/or educational level at the factor level (mean factor differences) while controlling for the presence of method effects. The population under study was formed by students from the city of Valencia, either high school or college ones, which answered the Spanish version of the scale.
Método
Participantes
A total of 525 high school and first year college students from the city of Valencia (Spain) were convenience sampled for the purposes of the study. 268 (51%) were high school students from two public schools, while the remaining 257 (49%) were college students at the University of Valencia. The college students were freshmen either at the Psychology or Physiotherapy degrees, 76.7 and 23.3%, respectively. In the overall sample, 38.7% were men and 61.3% women with mean age of 17.8 (SD=3.69). Their mean age was 22.42 (SD=6.20) for college men, 20.98 (SD=3.33) for college women, 15.16 (SD=.69) for high school men, and 15.09 (SD=1.55) for high school women. In order to test for the invariance across subsamples, the total sample was divided in four groups according to educational level and gender: college men (n=82), college women (n=175), high school men (n=120) and high school women (n=144).
Instruments and Procedure
The survey included several scales, but the Spanish version of the RSES (Rosenberg, 1965, 1979) was the only scale of interest. This scale is a 10-item self-report questionnaire assessing global self-esteem (Rosenberg, 1965). Items were scored as Likert–type ordinal measures ranging from 1 (strongly disagree) to 4 (strongly agree). This scale was developed to represent a single trait factor of global self-esteem. Five items were negatively worded (numbers 3, 5, 8, 9, and 10). The sociodemographic information recovered was only sex, age and grade due to confidentiality reasons. With respect to ethic principles, the education authorities gave all permits for the research, the ethics committee of the university favorably reported, and the participation of the students was completely voluntary. Before proceeding to survey, students were informed of the research scope and the treatment of their responses. Absolute anonymity was assured. Standard survey application lasted for about 30 minutes and it was self-administered during the school/college classroom time. Trained interviewers were present at the time of the survey in order to overcome any difficulties.
Data Analyses
A CFA model based on previous research on method effects for the RSES was specified with a trait selfesteem factor underlying at the ten items and an uncorrelated method factor underlying the negatively worded items (Tomás et al., 2013). The model is presented in Figure 1, and it was separately tested in the four subsamples: college men, college women, high school men, and high school women. These models were prior to testing the invariance routine and the mean differences in the latent factors. All models were estimated with EQS 6.1 software. The scale is ordinal with four points, and observed data were not normally distributed neither at the unidimensional level (high kurtosis and negative asymmetry) nor at the multivariate one: Multivariate kurtosis for college men was 51.22 (normalized estimate = 14.87), college women was 63.83 (normalized estimate = 26.38), high school men was 35.21 (normalized estimate = 11.07), and high school women 26.99 for women (normalized estimate = 9.62). Given these distributional conditions and according to recommendations by several authors (Finney & Di Stefano, 2006) Maximum Likelihood estimation was used with Satorra- Bentler corrections (Bentler, 1995).
The equivalence or invariance routine applied is the standard procedure (Thompson & Green, 2006). This routine comprises a hierarchical set of steps. First, the model in Figure 1 was separately tested on the four groups. After the determination of good fit for each group, a configural model was tested simultaneously for the groups and established as the baseline model. This model tested the so-called weak factorial invariance or configural equivalence. Then, an equality constraint was specified for trait factor loading scores across groups, testing metric invariance at the trait level. Then, an equality constraint was specified for all (trait and method) factor loadings across groups, testing metric invariance for both trait and method factors. Finally, a model with constrained item means tested for scalar invariance or strong factorial invariance. No constraints for invariance of errors or factor variances were imposed (strict factorial invariance) as most researches omit these constraints as not really needed for mean comparisons (Millsap & Olivera-Aguilar, 2012). Byrne (2006) presents the EQS syntax for the complete invariance routine.

The plausibility of the models was assessed using several fit criteria (Hu & Bentler, 1999; Tanaka, 1993): (a) chi-square statistic (Kline, 1998); (b) the comparative fit index (CFI; Bentler, 1990) of more than .90 (and, ideally, greater than .95; Hu, & Bentler, 1999); and the (c) the root mean squared error of approximation (RMSEA) of .08 or less (and, ideally less, than .05); Hu and Bentlers (1999) suggested that a CFI of at least .90, and a RMSEA less than .06 together, would indicate a very good fit between the hypothesized model and the data. The models in the invariance routine are nested. When nested models are compared there are two rationales (Little, 1997), the statistical and the modeling one. The statistical approach employs ?2 differences (??2) to compare constrained to unconstrained models, with non-significant values suggesting multigroup equivalence or invariance. This statistical approach has been criticized (Cheung & Rensvold, 2002; Little, 1997), recommending the modeling approach that uses practical fit indices to determine the overall adequacy of a fitted model. From this point of view, if a parsimonious model (such as the ones that posit invariance) evinces adequate levels of practical fit, then the sets of equivalences are considered a reasonable approximation to the data. Usually, CFI differences (?CFI) are used to evaluate measurement invariance. CFI differences lower than .01 (Cheung & Rensvold, 2002) or 0.05 (Little, 1997) are usually employed as cut-off criteria.
Resultados
As a previous step in the equivalence routine, the CFA model in Figure 1 was separately tested in the four subsamples. This a priori model adequately fitted the data in the four samples (see Table 1), and therefore to test for factorial and mean invariance across sample seems sensible.

Next, the invariance routine was implemented for the four subsamples of this study. The goodness-of-fit indices for the hierarchy of models are presented in Table 2. Although one chi-square statistic was statistically significant (p<.05), the practical fit indices showed very good model fit for every case. With respect to the invariance routine, the comparison of models yielded quite clear results. Metric invariance for trait factor loadings was clear, as both statistical and practical approaches to model comparison agreed that there were no statistically significant differences between baseline and metric (trait) invariance models, and therefore the more parsimonious (invariant) model could be retained. Exactly the same result was found when metric invariance of method factor loadings were added to the second model, the chi-square difference was not statistically significant (p>.05) and practical fit indices remained extremely similar or even slightly improved (the RMSEA). Therefore, according to these results, Rosenbergs self-esteem scale could be considered metrically invariant for the four subsamples. When intercepts were included in the model and made invariant across samples, the chi-square difference was statistically significant (p=.001), but differences in practical fit were minimum and the most parsimonious model (scalar invariance) showed adequate levels of practical fit, and consequently the sets of equivalences were considered tenable. In other words, strong factorial invariance was considered tenable for both educational levels and gender.

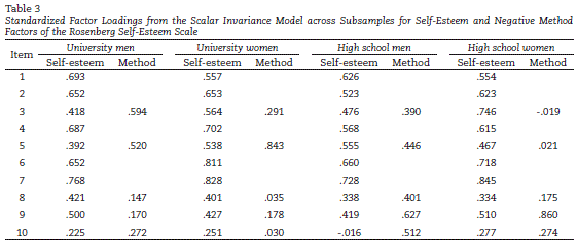
The standardized factor loadings in the retained model are presented in Table 3. Once the strong invariance was established, the latent means differences were investigated. The latent mean values for the trait and method factors (see Figure 1) were fixed to zero in the first group, men in high school, and freely estimated in the other three groups. Estimated latent mean values showed no statistically significant difference for all the groups in self-esteem. The mean differences were calculated considering a value of zero for the latent mean of the reference group and then estimating the points that the other groups differed from this fixed value. Therefore the mean differences are given in an unstandardized value. These estimates and their standard errors can be used to develop z-statistics which test for the statistical significance of these differences (Tomás, Gutiérrez, Sancho, & Romero, 2015). The comparisons with the reference group (high school males) were: (a) Mean difference = 2.91, z=1.31, p>.05, with college males; (b) Mean difference = -3.443, z=-1.69, p>.05, with high school females; and (c) Mean difference = -0.354, z=-0.188, p>.05, with college females. With respect to latent mean differences in method effects, again they were all statistically non-significant: (a) Mean difference = -.609, z=-1.06, p>.05, with college males; (b) Mean difference = -0.632, z=-1.14, p>.05, with high school females; and (c) Mean difference = -0.745, z=-1.22, p>.05, with college females.
Discussão
There is a large amount of evidence that self-esteem varies across both gender and educational levels. Moreover, most of the cumulated evidence comes from meta-analyses, a methodologically sound way to summarize research results (Gentile et al., 2008; Gentile et al., 2009; Kling et al., 1999; Sinclair et al., 2010; Twenge & Campbell, 2001). Parallel to these substantive research, a line of research has centered on how item wording may confuse the measurement of self-esteem (specifically the RSES), and it has also accumulated a lot of evidence concluding that the RSES measures a single trait (self- -esteem) but confounded, at least, by a method factor associated to negatively worded items (see among others, Bagozzi, 1993; Corwyn, 2000; Marsh, 1996; Marsh & Grayson, 1995; Tomás & Oliver, 1999, 2004; Tomás et al., 2013; Wang et al., 2001).
These two lines of research, self-esteem differences and self-esteem measurement, have not frequently got in touch and affected each other, and indeed they should have dialogued to each other. It must be borne in mind that the reviewed meta-analytical research on RSES differences has not controlled for these method effects, and therefore it could well be misleading evidence. Up to this point, there is not much research that test for gender and/or educational level self-esteem differences that also controls for the method effects repeatedly found in the psychometric literature. To our knowledge, there is a single study that used mean and covariance structure analysis to test for gender invariance in self-esteem including (and thus controlling for) method effects associated to negatively worded items. This article found no gender differences in the method factor associated to negatively worded items (DiStefano & Motl, 2009). However, in a recent study, Tomas et al. (2013) estimated and tested several multiple indicators and multiple causes models that found an inconsistent effect of gender on method effects, with both positive and negative small effects depending on the scale tested.
The conclusions of this research are, therefore, twofold. There are substantive conclusions and implications, as well as methodological ones. On one hand, the substantive conclusions are related to the mean differences in self-esteem across gender and educational level. On the other hand, the methodological conclusions are related to the measurement invariance, gender and educational level differences in the presence of method effects, and how these differential method effects could confound the assessment of mean differences in the trait factor.
With respect to substantive results, current research has found neither statistically significant latent mean difference due to gender nor to educational level. Most studies have found gender differences in global self-esteem. Of particular interest is the meta-analysis by Kling et al. (1999), which showed a small but statistically significant difference between men and women in self-esteem favoring men (d=0.22). However, the only study that tested for latent mean differences by gender in a MACS framework was in line with our results, finding few differences in the measurement of self-esteem, and non-significant latent mean differences in the trait factor (DiStefano & Motl, 2009). As regards educational level (or one of his proxies age), a meta-analysis by Twenge and Campbell (2001) found a significant effect of age on RSES: self-esteem increased with age. This result was particularly true between high school and college years, the same educational levels considered in this research. In a wider age range, Sinclair et al. (2010) provided important evidence of an increase in self-esteem across the life span by RSES. These results are not coincident with those found in this research. But again, a MACS analysis by Whiteside- Mansell and Corwyn (2003) that studied measurement invariance and self-esteem mean differences across age groups demonstrated a strong invariance of RSES among adolescents (12-17) and adults (18-82), and no mean differences due to age. It is important to note that, although the latent mean comparisons for self-esteem in this study were not statistically significant, the effects were always in the hypothesized direction. That is, in the comparisons, women always had less self-esteem than men and college students had, in general, higher levels of self-esteem than high school students.
With respect to methodological conclusions, the results point out that data support the scalar and metric invariance of the RSES both at the trait and method levels. This result is in line with most of the available literature on RSESs invariance. For example, Lindwall, et al. (2012) found invariance of method effects for men and women in a sample of elderly Europeans. DiStefano and Motl (2009) also found an almost perfect equivalence across gender in the RSES. Mullen, Gothe, and McAuley (2013) analyzed the invariance across gender, educational level (without and with a college degree) and age (60-70 vs. 71-95) among older adults. There was no gender, educational level or age differences. With respect to the invariance across educational level, the evidence is sometimes confounded with age differences, but nevertheless, some of the accumulated evidence suggests that the RSES is basically invariant across educational levels. Halama (2008) and Corwyn (2000) compared adolescents and adults, and found no differences. Vasconcelos-Raposo, Fernandes, Teixeira, and Bertelli (2012) analyzed method effects between youngster of 15-17 years and those of 18-20 years old, and again found no differences. And finally, another study showed invariance across various age groups of adolescents (Bagley, Bolitho, & Bertrand, 1997). However, some other works have reported structural differences due to age and/or educational level. Owens (1993) found that self-esteem was not structurally equivalent across late adolescence and early adulthood, while a second study concluded that the RSES is not equivalent between college students and older adults (Goldsmith, 1986). Therefore, not all the existing literature, but most of it, has shown measurement invariance for the RSES. Current research provides new evidence supporting this equivalence.
This research has both strengths and limitations. The main strength is that, to our knowledge, it is the first time that gender and educational level measurement invariance and latent means differences has been tested in the Spanish version of the RSES, while considering the effects associated with negatively worded items. The main limitations have to do with the sample and subsamples. With respect to the sample, its main problem is the sampling scheme, a convenience one. Additionally, and given that an invariance routine has been applied, there is also an issue of subsamples sizes that may affect the statistical power to detect differences. The subsample of college men was probably too small, and it could prevent some differences to be statistically significant. The research should be replicated in larger samples from the same population in order to understand if some of the invariances found in this research could be a consequence of low statistical power. Further research on sex invariance of self-esteem instruments for different populations and languages is still needed, as most of the studies on self-esteems gender have not considered the presence of these method effects.
Referências
Bachman, J. G., & OMalley, P. M. (1986). Self-concept, self-esteem, and educational experiences: The frog pond revisited (again). Journal of Personality and Social Psychology, 50(1), 35-46. [ Links ]
Bagley, C., Bolitho, F., & Bertrand, L. (1997). Norms and construct validity of the Rosenberg Self-Esteem Scale in Canadian high school populations: Implications for counseling. Canadian Journal of Counseling, 31, 82-92. [ Links ]
Bagozzi, R. P. (1993). Assessing construct validity in personality research: Applications to measures of self-esteem. Journal of Research in Personality, 27, 49-87. [ Links ]
Bagozzi, R. P., & Heatherton, T. F. (1994). A general approach to representing multifaceted personality constructs: Application to state selfesteem. Structural equation modeling, 1(1), 35-67. [ Links ]
Bentler, P. M. (1990). Comparative fit indices in structural models. Psychological Bulletin, 107, 238-246. [ Links ]
Bentler, P. M. (1995). EQS program manual. Encino, CA: Multivariate Software. [ Links ]
Bracken, B. A. (1992). Multidimensional self-concept scale. Austin, USA: PRO-ED. [ Links ]
Bustos, V., Oliver, A., & Galiana, L. (2015). Validación del autoconcepto forma 5 en universitarios de Perú: Una herramienta para la psicología positiva. Psicologia Reflexão e Crítica, 28(4), 690-697. [ Links ]
Byrne, B. M. (2006). Structural equation modeling with EQS: Basic concepts, applications, and programming (2 Ed.). Mahwah, NJ: Erlbaum. [ Links ]
Carmines, E. G., & Zeller, R. A. (1974). On establishing the empirical dimensionality of theoretical terms: An analytical example. Political Methodology, 1(4), 75-96. [ Links ]
Carmines, E. G., & Zeller, R. A. (1979). Reliability and validity assessment. Beverly Hills, CA: Sage. [ Links ]
Cheung, G. W., & Rensvold, R. B. (2002). Evaluating goodness-of-fit indexes for testing MI. Structural Equation Modeling, 9, 235-55. [ Links ]
Corwyn, R. F. (2000). The factor structure of global self-esteem among adolescents and adults. Journal of Research in Personality, 34(4), 357-379. [ Links ]
Crandall, R. (1973). The measurement of self-esteem and related constructs. Em J. P. Robinson, & P. R. Shaver (Eds.), Measures of social psychological attitudes (2 Ed., pp. 45-167). Ann Arbor, MI: Institute for Social Research. [ Links ]
DeVellis, R. F. (1991). Scale development: Theory and applications. Newbury Park, CA: Sage. [ Links ]
DiStefano, C., & Motl, R. W. (2009). Self-esteem and method effects associated with negatively worded items: Investigating factorial invariance by sex. Structural Equation Modeling, 16(1), 134-146. [ Links ]
Finney, S. J., & DiStefano, C. (2006). Non-normal and categorical data in SEM. Em G. R. Hancock, & R.O. Mueller (Eds.), Structural equation modeling: A second course. Greenwich, CO: Information Age Publishing. [ Links ]
Fleming, J. S., & Courtney, B. E. (1984). The dimensionality of self-esteem: II. Hierarchical facet model for revised measurement scales. Journal of Personality and Social Psychology, 46(2), 404-421. [ Links ]
Gentile, B., Dolan-Pascoe, B., Twenge, J. M., Grabe, S., Wells, B. E., & Maitino, A. (2009). Gender differences in domain-specific selfesteem: A meta-analysis. Review of General Psychology, 13(1), 34-45. [ Links ]
Gentile, B., Twenge, J. M., & Campbell, W. K. (2008). Birth cohort differences in self-esteem, 1988-2008: A cross-temporal meta-analysis. Review of General Psychology, 14(3), 261-268. [ Links ]
Gergen, K. J. (1984). Theory of the self: Impasse and evolution. Em L. Berkowitz (Ed.), Advances in experimental social psychology. Theorizing in social psychology: Special topics (Vol. 17, pp.49-115). London, UK: Harcourt Brace Jovanovich/Academic Press. [ Links ]
Goldsmith, R. E. (1986). Dimensionality of the Rosenberg self-esteem scale. Journal of Behavior and Personality, 1(2), 253-264. [ Links ]
Halama, P. (2008). Confirmatory factor analysiss of Rosenberg self-esteem scale in a sample of Slovak high school and university students. Studia Psychologica, 50(3), 255-266. [ Links ]
Heatherton, T. F., & Polivy, J. (1991). Development and validation of scale for measuring state self-esteem. Journal of Personality and Social Psychology, 60(6), 895-910. [ Links ]
Hensley, W. E., & Roberts, M. K. (1976). Dimensions of Rosenbergs self-esteem scale. Psychological Reports, 38(2), 583-584. [ Links ]
Hu, L., & Bentler, P. M. (1999). Cut-off criteria for fit indexes in covariance structure analysis: Conventional criteria versus new alternatives. Structural Equation Modeling, 6(1), 1-55. [ Links ]
Janis, I. L., & Field, P. B. (1959). A behavioral assessment of persuasibility: Consistence of individual differences. Em C. I. Hovland & I. L. Janis (Eds.), Personality and persuasibility (pp. 259-268). New Haven, USA: Yale University Press. [ Links ]
Kaufman, P., Rasinski, K. A., Lee, R., & West, J. (1991). National education longitudinal study of 1988. Quality of the responses of eight-grade students in NELS88. Washington, DC: U.S. Department of Education. [ Links ]
Kline, R. B. (1998). Principles and practice of structural equation modeling. New York: Guilford. [ Links ]
Kling, K. C., Hyde, J. S., Showers, C. J., & Buswell, B. N. (1999). Gender differences in self-esteem: A meta-analysis. Psychological Bulletin, 125(4), 470-500. [ Links ]
Kohn, M. L. (1977). Class and conformity: A study of values (2nd Ed.). Chicago: University of Chicago Press. [ Links ]
Lindwall, M., Barkoukis, V., Grano, C., Lucidi, F., Raudsepp, L., Liukkonen, J., & Thøgersen-Ntoumani, C. (2012). Method effects: The problem with negatively versus positively keyed items. Journal of Personality Assessment, 94(2), 196-204. [ Links ]
Little, T. D. (1997). Mean and covariance structures (MACS) analyses of cross-cultural data: Practical and theoretical issues. Multivariate Behavioral Research, 32(2), 53-76. [ Links ]
Maccoby, E. E., & Jacklin, C. N. (1974). The psychology of sex differences. Stanford, CA: Stanford University Press. [ Links ]
Marsh, H. W. (1988). Self-description questionnarie-I. San Antonio, USA: The Psychological Corporation. [ Links ]
Marsh, H. W. (1989). Age and sex effects in multiple dimensions of self-concept: Preadolescence to early adulthood. Journal of Educational Psychology, 81(3), 417-430. [ Links ]
Marsh, H. W. (1990). Self-description Questionnarie-II. San Antonio, USA: The Psychological Corporation. [ Links ]
Marsh, H. W. (1996). Positive and negative global self-esteem: A substantively meaningful distinction or artifactors? Journal of Personality and Social Psychology, 70(4), 810-819. [ Links ]
Marsh, H. W., & Grayson, D. (1995). Latent variable models of multitrait-multimethod data. Em R. H. Hoyle (Ed.), Structural equation modeling: Concept, issues, and applications (pp. 177-198). Thousand Oaks, CA: Sage. [ Links ]
Millsap, R. E., & Olivera-Aguilar, M. (2012). Investigating measurement invariance using confirmatory factor analysis. Em R. H. Hoyle (Ed.), Handbook of structural equation modeling. New York: The Guilford Press. [ Links ]
Mullen, S. P., Gothe, N. P., & McAuley, E. (2013). Evaluation of the factor structure of the Rosenberg self-esteem scale in older adults. Personality and Individual Differences, 54(2), 153-157. [ Links ]
Nunnally, J. C. (1978). Psychometric theory (2nd Ed.). New York: McGraw-Hill. [ Links ]
Owens, T. J. (1993). Accentuating the positive and the negative: Rethinking the use of self-esteem, self-deprecation, and self-confidence. Social Psychological Quarterly, 56(4), 288-299. [ Links ]
Romero, E., Luengo, M. A., & Otero-López, J. M. (1994). La medición de la autoestima: Una revisión. Psicologemas, 8(15), 41-60. [ Links ]
Rosenberg, M. (1965). Society and the adolescent self-image. Princeton, NJ: Princeton University Press. [ Links ]
Rosenberg, M. (1979). Conceiving the self. New York: Basic Books. [ Links ]
Salgado, J. F., & Iglesias, M. (1995). Estructura factorial de la escala de autoestima de Rosenberg: Un análisis factorial confirmatorio. Psicológica, 16, 441-454. [ Links ]
Shavelson, J., Hubner, J. J., & Stanton, G. C. (1976). Self-concept: Validation of construct interpetactions. Review of Educational Research, 46(3), 407-442. [ Links ]
Sinclair, S. J., Blais, M. A., Gansler, D. A., & Sandberg, E. (2010). Psychometric properties of the Rosenberg self- esteem scale: Overall and across demographic groups living within the United States. Evaluation & the Health Professions, 33(1), 56-80. [ Links ]
Stevens, R. (1996). Understanding the self. London, UK: Sage. [ Links ]
Supple, A. J., Su, J., Plunkett, S. W., Peterson, G. W. & Kevin R., & Bush, K. R. (2013) Factor structure of the Rosenberg self-esteem scale. Journal of Cross-Cultural Psychology, 44(5), 748-764. [ Links ]
Tanaka, J. S. (1993). Multifaceted conceptions of fit in structural equation models. Em K. A. Bollen (Ed.), Testing structural equation models (pp. 10-39). Newbury Park, CA: Sage. [ Links ]
Thompson, M. S., & Green, S. B. (2006). Evaluating between-group differences in latent means. Em G. R. Hancock & R. O. Mueller (Eds.), Structural equation modeling: A second course. Greenwich, Connecticut: Information Age Publishing. [ Links ]
Tomás, J. M., & Oliver, A. (1999). Rosenbergs self-steem scale: Two factors or method effects. Structural Equation Modeling, 6(1), 84-98. [ Links ]
Tomás, J. M., & Oliver, A. (2004). Análisis psicométrico confirmatorio de una medida multidimensional del autoconcepto en español. Interamerican Journal of Psychology, 38(2), 285-293. [ Links ]
Tomás, J. M., Galiana, L., Hontangas, P., Oliver, A., & Sancho, P. (2013). Evidencia acumulada sobre los efectos de método asociados a ítems invertidos. Psicológica, 34(2), 365-381. [ Links ]
Tomás, J. M., Gutiérrez, M., Sancho, P., & Romero, I. (2015). Measurement invariance of the satisfaction with life scale (SWLS) by gender and age in Angola. Personality and Individual Differences, 85, 182-186. [ Links ]
Tomás, J. M., Oliver, A., Galiana, L., Sancho, P., & Lila, M. (2013). Explaining method effects associated to negatively worded items in trait and state global and domain-specific self-esteem scales. Structural Equation Modeling Multidisciplinary Journal, 20(2), 299-313. [ Links ]
Twenge, J. M., & Campbell, W. K. (2001). Age and birth cohort differences in self-esteem: A cross-temporal meta-analysis. Personality and Social Psychology Review, 5(4), 321-344. [ Links ]
Vasconcelos-Raposo, J. Fernandes, H. M., Teixeira, C. M., & Bertelli, R. (2012). Factorial validity and invariance of the Rosenberg selfesteem scale among portuguese youngsters. Social Indicators Research, 105(3), 483-498. [ Links ]
Wang, J., Siegal, H. A., Falck, R. S., & Carlson, R. G. (2001). Factorial structure of Rosenbergs self-esteem scale among crack-cocaine drug users. Structural Equation Modeling, 8(2), 275-286. [ Links ]
Watkins, D., & Dhawan, N. (1989). Do we need to distinguish the constructs of self-concept and self-esteem? Journal of Social Behavior and Personality, 4(5), 555-562. [ Links ]
Whiteside-Mansell, L., & Corwyn, R. F. (2003). Mean and covariance structures analyses: An examination of the Rosenberg Self-Esteem Scale among adolescents and adults. Educational and Psychological Measurement, 63(1), 163-173. [ Links ]
Wylie, R. C. (1979). The self-concept: Theory and research on selected topics. Lincoln: University of Nebraska Press. [ Links ]
recebido em dezembro de 2014
reformulado em outubro de 2015
aprovado em outubro de 2015
Sobre os autores
José M. Tomás: es profesor doctor del Departamento de Metodología de las Ciencias del Comportamiento de la Universitat de València.
Patricia Sancho: es profesora doctora de la Universidad de Zaragoza.
Laura Galiana: es profesora doctora del Departamento de Metodología de las Ciencias del Comportamiento de la Universitat de València.
Amparo Oliver: es profesora doctora del Departamento de Metodología de las Ciencias del Comportamiento de la Universitat de València.
Pedro Hontangas: es profesor doctor del Departamento de Metodología de las Ciencias del Comportamiento de la Universitat de València.
1Endereço para correspondência: Facultad de Psicología, Universitat de València, Av. Blasco Ibañez, 21, 46010, Valencia, España. E-mail: tomasjm@uv.es