Servicios Personalizados
Articulo
Indicadores
Compartir
Ciências & Cognição
versión On-line ISSN 1806-5821
Ciênc. cogn. vol.17 no.1 Rio de Janeiro abr. 2012
Artigo Científico
Habilidades de cálculo em jovens e adultos integrados em classes de alfabetização tardia
Calculation skills in young people and adult classes who are integrated to late literacy
Elias José Mengarda
Departamento de Ciências da Comunicação (DECOM), Universidade Federal de Santa Maria (UFSM), Frederico Westphalen, RS, Brasil
Resumo
O objetivo desse estudo é avaliar a habilidade de cálculo e as estratégias que os jovens e adultos integrados em classes de alfabetização tardia utilizam para a resolução de problemas. Os três grupos (2 experimentais e 1 controle) foram testados uma vez no início da alfabetização e a segunda vez, seis meses depois. A metodologia consistiu na aplicação de uma bateria de testes para avaliar as habilidades de cálculo e que estratégias utilizam para a resolução de problemas. Foram testadas três hipóteses: a) hipótese da independência cognitiva; b) influência da alfabetização; c) influência da escolarização formal. Ao compararmos os sujeitos que leem com os que não leem, verificou-se que as hipóteses que se destacam são a da alfabetização e a da escolarização, visto que os sujeitos que leem são melhores nas habilidades linguísticas e cognitivas. Contudo, há um grupo minoritário de sujeitos, que não lê nem escreve e que se destaca em algumas habilidades cognitivas, concluindo-se que nem a hipótese da alfabetização, nem a da escolarização são suficientes para explicar o desenvolvimento das habilidades de cálculo, embora a escolarização formal e, possivelmente, a alfabetização tenham contribuído para uma pequena melhora, conforme indicam a análise estatística dos dados. © Cien. Cogn. 2012; Vol. 17 (1): 016-036.
Palavras-chave: habilidades de Cálculo; estratégias de solução; jovens e adultos; alfabetização tardia.
Abstract
The aim of this study is to evaluate the ability of calculation and the strategies that young people and adults embedded in late literacy classes, use to solve problems. The three groups (2 experimental and 1 control) were tested once in the beginning of the literacy and the second time, six months later. The methodology consisted of several tests to evaluate calculation skills and what strategies were used to solve problems. We tested three hypotheses: a) cognitive independence hypothesis, b) literacy influence, c) formal schooling influence. When comparing those who read with those who don't read, it was found that the chances that stand out are the literacy and schooling, are the ones who read have better language and cognitive skills. However, there is a small group of citizens that don't read or write and is prominent in some cognitive abilities, concluding that neither the hypothesis of literacy, schooling nor sufficient to explain the development of calculation skills, although formal schooling and, possibly, literacy may have contributed to a slight improvement, as indicated by the statistical analysis. © Cien. Cogn. 2012; Vol. 17 (1): 016-036.
Keywords: calculation skills; solution strategies; youth and adults; late literacy.
Introdução
O objetivo deste estudo é avaliar a capacidade de cálculo e os tipos de estratégias que os jovens e adultos integrados em classes de alfabetização tardia utilizam para a resolução de problemas de cálculo oral (mental) e escrito. Além disso, procurou-se verificar em que medida os escores dos sujeitos testados evoluíram do primeiro para o segundo teste, levando-se em conta a frequência às aulas durante um período de 3 a 4 meses. É de se esperar que esse tempo de instrução formal produza algum tipo de efeito em suas performances em cálculo. Para efeitos de comparação testamos também um grupo controle composto por sujeitos adultos que não frequentavam as classes de alfabetização inicial.
Entendemos por alfabetização tardia o processo educacional que envolve as pessoas que buscam aprender a ler na idade adulta, portanto, fora do padrão que conhecemos, ou seja, a partir de 6 ou 7 anos, quando as crianças frequentam a escola e iniciam o processo de alfabetização. As motivações que levam cada vez mais adultos a buscar as classes de alfabetização de adultos são múltiplas e vão desde desafios de ordem pessoal ou por exigência profissional. Nessa perspectiva, aprender a ler e a escrever torna-se condição obrigatória para a realização efetiva da cidadania e da integração social visto que a escrita sempre foi compreendida como uma ferramenta social básica da sociedade moderna. Por isso nos interessa investigar a relação entre alfabetização e desenvolvimento das habilidades de cálculo nessa categoria de sujeitos.
Há estudos como os realizados por Scribner e cole (1981), que indicam que a linguagem escrita promove conceitos abstratos, raciocínio analítico e novos modos de categorização, embora os efeitos específicos do letramento sejam muito pequenos, conforme destaca morais (2002, p. 2). Em relação às funções cognitivas mais gerais como raciocínio analógico, memória de curto prazo, memória de trabalho, procura na memória de longo prazo e aprendizagem há evidências para crer que a escolarização influencia o indivíduo a pensar logicamente.
Outras pesquisas sugerem que o "uso da escrita facilita, ou até provoca formas de pensamento superiores" como podemos conferir em (Vygotsky, 1962; Olson, 1977, 1997; Bruner & Olson, 1977; Luria, 1992).
Sabe-se que o desenvolvimento cognitivo não cessa em algum ponto da existência humana e que devido ao progresso rápido e às transformações culturais que vivemos é necessário que o indivíduo se adapte aos desafios da sociedade da informação para poder dar respostas novas e eficazes. Esse contexto de contínua inovação tecnológica suscita uma questão importante, que é saber "se existem períodos sensíveis para sistemas de conhecimento culturalmente transmissíveis, tais como os que são responsáveis pela leitura" e o cálculo (acréscimo meu), conforme questionam Blakemore e Frith (2000). Para essas autoras, a resposta ainda é desconhecida. Por outro lado, Morais (2002) afirma que há indivíduos que se tornam letrados só na idade adulta e que atingem um alto nível de habilidade em relação à leitura e à escrita. De todo o modo, é certo que o sistema cognitivo das pessoas, independente da idade, está apto a absorver novas aprendizagens sejam estas de cunho escolar ou do cotidiano. No caso da nossa investigação, trata-se de sujeitos adultos que pretendem aprender a ler, escrever e calcular em programas especiais de alfabetização. O fato de estarem inseridos num contexto de evolução e expansão das tecnologias da informação exige-lhes, independente de nível de escolaridade e de idade, aprendizagens contínuas, tanto explícitas quanto implícitas para poderem sobreviver de forma autônoma e independente.
Portanto, uma questão crucial é saber se o desenvolvimento cognitivo tem um limite com a aproximação da velhice e, depois disso, passe a sofrer algum tipo de declínio ou até mesmo um término das possibilidades de desenvolvimento e de que forma este processo ocorre. Há possibilidade de que os escores em testes de capacidade cognitiva continuem aumentando indefinidamente? Em que medida a habilidade em leitura pode estar relacionada à habilidade de cálculo?
De acordo com Polya (1945/1983), resolver um problema significa achar um caminho para sair de uma dificuldade, um caminho para contornar um obstáculo, para alcançar um propósito que não é imediatamente alcançável. Resolver um problema é uma tarefa específica da inteligência e é um dom específico do ser humano: pode-se considerar a resolução de problemas como uma atividade que é característica do gênero humano.
A resolução de qualquer problema de aritmética simples ou cálculos matemáticos complexos implica a capacidade de leitura, a habilidade de compreensão e de interpretação dos enunciados. Portanto, a resolução de problemas depende da capacidade interpretativa das proposições expressas por meio de signos linguísticos e/ou numéricos. Ou seja, há uma dimensão simbólica que precisa ser apreendida para poder obter-se sucesso na resolução de problemas que demandam algum nível de abstração.
Morais (1986) e Morais e Kolinsky (2004) explicam que a leitura é uma habilidade cognitiva porque se caracteriza como processamento de informação. É uma habilidade que deve ser aprendida a partir de instrução explícita. Além disso, é importante compreender em que medida as habilidades de leitura têm implicação nas habilidades de cálculo. Portanto, considerando que a aprendizagem da leitura exige complexas operações cognitivas, propomos três hipóteses para explicar o comportamento cognitivo dos jovens e adultos integrados em classes de alfabetização tardia mediante a resolução de problemas, tais como o cálculo mental e escrito.
Estabelecemos que de acordo com a hipótese da independência cognitiva, o desenvolvimento das funções cognitivas superiores envolvidas na resolução de problemas, depende apenas da maturação cognitiva e não das aprendizagens escolares. Uma segunda hipótese, que pode ser classificada de influência da alfabetização, a aprendizagem da leitura (e talvez de outras habilidades também), haja vista que ela exige o conhecimento de correspondências grafofonêmicas e a aplicação constante dessas correspondências, algumas vezes não biunívocas (por exemplo, o grafema "ss" lê-se /s/, mas o fonema /s/ só em certos casos se escreve "ss", pode influenciar o próprio desenvolvimento das capacidades cognitivas necessárias à resolução deste tipo de problemas.
Postulamos também uma terceira hipótese que pode ser chamada de influência da escolarização, tendo em vista que as atividades escolares incluem a formulação de problemas abstratos, a aplicação e a verificação de certos princípios lógicos e a procura de estratégias e heurísticas para a resolução desses problemas, poderiam influenciar o desenvolvimento da capacidade para resolver problemas do tipo indicado. O exame de indivíduos diferindo pela escolarização e a alfabetização deveria permitir distinguir entre as hipóteses propostas para essa investigação.
A avaliação das capacidades de cálculo em populações adultas integradas em classes de alfabetização tardia constitui-se num fato de pesquisa a ser continuamente aprofundado a fim de podermos criar metodologias e materiais sempre mais adequados para este público. Além disso, não se encontra uma definição padronizada das capacidades de cálculo comparável às que foram estabelecidas em leitura e escrita, considerando-se, por isso, oportunas e importantes as pesquisas nesta área de conhecimento.
A emergência das capacidades de cálculo numérico
Morais (2011) destaca que as habilidades de leitura, escrita e cáculo operam com sistemas simbólicos, isto é, com sistemas que representam convencionalmente realidades abstratas por meio de signos concretos, permitindo combinações e transformações geradoras de novos sentidos ou novos fatos. As palavras, incluindo as palavras de algarismos, são símbolos culturais arbitrários. Cada uma reúne e condensa, num pequeno objeto mental, diferentes informações e, sobretudo, segmenta a continuidade inerente às representações analógicas pré-verbais. Aquilo a que se chama habitualmente de aprendizagem da leitura e da matemática, ou mais restritamente da aritmética, é, respectivamente, a aprendizagem de sistemas de representação simbólica de fonemas e de quantidades numéricas.
Wagner (2000) reitera que nos países em desenvolvimento, só muito raramente foram realizados levantamentos em que foram coletados dados sobre as capacidades em matemática, e as raras avaliações da alfabetização que incluíam análises separadas das capacidades de cálculo não proporcionaram informação suficiente para julgar os níveis de domínio específicos.
O conhecimento de cálculo parece emergir de uma combinação de fatores inatos e experienciais, possuindo, portanto, bases biológicas, conforme sugerem os pesquisadores Briars e Siegler (1984), Geary (1995) e Gelman e Gallistel (1978). Estes autores mencionam cinco princípios de contagem implícita, os quais incluem correspondências "uma a uma" (uma e somente uma palavra reunida, tal como "um" e "dois" é assinalado para cada objeto contado), o princípio de ordem estável, o princípio de cardinalidade, o princípio da abstração (objetos de qualquer tipo podem ser reunidos e contados), e o princípio da irrelevância da ordem (itens de uma dada série podem ser reunidos em qualquer sequência).
Os estudos de Reis, Guerreiro, Garcia e Castro-Caldas (1995) e Carraher, Carraher e Schliemann (1982) mostraram que as habilidades envolvidas em operações matemáticas e de raciocínio podem se desenvolver a partir de situações da vida diária, e não necessariamente a partir da educação formal ou como um resultado do uso de números. Esta dissociação mostra que a escolarização pode facilitar o desenvolvimento de uma variedade de operações aritméticas, enquanto para indivíduos não escolarizados, o componente lexical dos números pode ter maior relação com o conceito de quantidade. Esta diferença pode novamente ser interpretada como um nível mais concreto do processamento matemático.
De todo o modo, a questão fundamental é compreender como se desenvolvem os conceitos matemáticos. Para Sternberg (1992), entender as razões do estudo desta capacidade matemática tem importância tanto prática quanto teórica. A dimensão prática apresenta implicações diretas para o ensino e a dimensão teórica ajuda a compreender a solução de problemas em um domínio que tem implicações para a questão da cognição humana em geral.
Sabe-se que a compreensão e a produção de números requer a habilidade de processar verbalmente o número, por exemplo, "quarenta e dois" e representar o número arábico "42", bem como a compreensão do significado dos números processados. Por exemplo, 4 em 42 representa quatro séries de 10. O processamento do número é também a habilidade de codificar ou traduzir números de uma representação para outra, como, por exemplo, quarenta e dois para 42 (Seron & Fayol, 1994).
Morais (2011) explica que a aprendizagem dos sistemas de escrita, leitura e cálculo envolve, inicialmente, processos conscientes, intencionais e controlados, os quais, pela prática, conduzem ao estabelecimento de habilidades que permitem um tratamento rápido e automático da informação correspondente; e que estas habilidades são cruciais para a eficácia tanto da compreensão em leitura como da resolução de problemas matemáticos. Além disso, ambas as aprendizagens dependem fortemente de fatores culturais e socioeconômicos, assim como do desenvolvimento das regiões cerebrais subjacentes às capacidades correspondentes.
Existem duas abordagens básicas para entender as capacidades matemáticas. A primeira é chamada de abordagem psicométrica e a segunda, de abordagem do processamento de informação. A abordagem psicométrica define a capacidade para a matemática a partir do que os testes medem. Assim, a capacidade matemática é a habilidade para um bom desempenho nos testes. Esta abordagem oferece um meio excelente para a medição da capacidade matemática, mas não consegue proporcionar uma descrição independente do que está sendo medido (Sternberg, 1992).
Por sua vez, a abordagem do processamento de informação é baseada na análise da tarefa. Qualquer problema matemático pode ser dividido em componentes de informação, isto é, em operações mentais simples, habilidades e conhecimento necessário para a solução de um determinado problema. Vejamos o exemplo de um tipo de problema à luz desta abordagem: "João tem um níquel. Pedro tem 3 centavos a mais que João. Quantos centavos Pedro têm?" Que espécie de operação mental e que tipo de conhecimento são necessários para a solução deste problema? A solução deste problema deve ser dividida em duas partes principais:
a) Representação do problema: conversão de um problema de matemática para uma representação interna;
b) Solução do problema: aplicar as operações legais da matemática à representação interna, a fim de chegar a uma resposta final.
A representação de quantos "centavos" envolve uma tradução de cada sentença para uma equação e a integração das informações relevantes em uma representação coerente do problema. Já a solução do problema envolve o desenvolvimento e o monitoramento de um plano de solução, bem como a execução deste plano. Para solucionar esta tarefa o indivíduo precisa ter um certo conhecimento específico deste domínio.
Existem outros tipos de conhecimento que podem ser relevantes para a representação e solução de problemas, tais como:
a) Conhecimento linguístico;
b) Conhecimento factual (conhecimento de mundo e das medidas);
c) Conhecimento do esquema, isto é, conhecer tipos de problemas tais como problemas de força e problemas de movimento.
Lembramos que no caso da matemática, os símbolos representam grandezas, mais precisamente quantidades, as quais podem ser exprimidas diretamente em números. No exemplo "João tem 2 moedas de 10 centavos a mais do que Pedro", o conhecimento linguístico é necessário para a análise da sentença em suas variáveis, isto é, "João e Pedro" e uma relação quantitativa entre eles, isto é, 2 moedas de 10 centavos a mais do que; além disso, o conhecimento factual é necessário para a representação de "2 moedas de 10 centavos" como 20 centavos.
A seguir, são relacionados alguns fatores importantes para alcançar a solução de um problema:
a) Integração do problema: o componente seguinte para a solução do problema matemático é reunir as proposições de um problema em formato de "estória" em uma representação coerente. A fim de integrar ou compreender o problema, o indivíduo que o soluciona precisa ter algum conhecimento sobre os tipos de problemas (conhecimento esquemático). No caso dos centavos, o solucionador precisa perceber que se trata de um problema de comparação no qual dois conjuntos são comparados um com o outro.
b) Planejamento da solução: O próximo passo é organizar um plano de solução, pois, a pessoa que vai tentar solucionar o problema precisa ter algum conhecimento de heurística da solução de problemas (conhecimento estratégico). As pessoas podem usar uma estratégia de contagem progressiva para calcular sua resposta. Elas também podem diferir em sua capacidade para construir corretamente planos de solução e tais diferenças podem estar relacionadas ao conhecimento estratégico.
c) Execução da solução: a execução da solução exige que a pessoa que vai resolver o problema seja capaz de realizar operações tais como o cálculo computacional. A execução de soluções para os problemas exige algum tipo de conhecimento sobre os procedimentos para a solução, ou seja, de um conhecimento algorítmico, como, por exemplo, saber que a soma de 3 + 5 é igual a 8. As pessoas podem diferir em sua capacidade para realizar operações e as diferenças podem estar relacionadas ao conhecimento algorítmico.
A seguir, apresentamos alguns modelos de contagem para algoritmos de adição das crianças:
a) Contagem total: para 3 + 5, a criança recita "1, 2, 3, 4, 5, 6, 7, 8".
b) Modelo de contagem progressiva: para 3 + 5, a criança declara "4, 5, 6, 7, 8".
c) Modelo mínimo: para contagem progressiva, 3 - 5, a criança declara "6, 7, 8".
Os alunos de primeira série comportam-se como o previsto pelo modelo mínimo de Groen e Parkman (1972). Por exemplo, de acordo com o modelo mínimo, nenhum incremento é necessário em "0 + 2, 2 + 0, 8 + 0", e assim por diante; um incremento é exigido em "4 + 1, 1+ 4, 8 + 1" e dois incrementos são exigidos em "2 + 7, 7 + 2, 5 + 2".
Parece que na primeira série, o algoritmo dominante para a soma simples é usar um procedimento de contagem progressiva tal como no modelo mínimo. As crianças pré-escolares usam procedimentos de contagem total, desenvolvendo procedimentos mais sofisticados como a contagem progressiva à medida que adquirem experiência com problemas de adição.
Há pesquisas como as realizadas por Baroody (1987), Fuson (1982) e Carpenter e Mosner (1982) que mostram que antes da instrução formal do primeiro grau, as crianças internalizam princípios e procedimentos básicos de contagem tais como a adição e a subtração em uma variedade de contextos. Além disso, podem resolver problemas de história simples e usam uma ampla quantidade de estratégias para resolver fatos numéricos básicos.
Em recente investigação, Ostad (1998) comparou a performance de crianças com deficiência de cálculo na segunda, quarta e sexta séries com crianças que realizavam estas tarefas normalmente, mas introduziu variações em termos de complexidade verbal. Foram apresentados às crianças quatro tipos de problemas:
a) Problemas de troca: ex. Peter tem 7 bolinhas de gude. Então, Sam deu a ele mais 5 bolinhas de gude. Quantas bolinhas de gude Peter têm agora?
b) Problemas de igualdade: ex. Rose tem 7 bolinhas de vidro. Dora tem 10 bolinhas de vidro. Quantas bolinhas de vidro Rose pode obter para ter tantas bolinhas de vidro quanto Dora?
c) Problemas de combinação: ex. Fred tem 7 bolinhas de gude. John tem 5 bolinhas de vidro. Quantas bolinhas de vidro eles têm juntos?
d) Problemas de comparação: ex. Jane tem 12 bolinhas de vidro. Mary tem 7 bolinhas de vidro. Quantas bolinhas de vidro Jane tem a mais do que Mary?
Os problemas de troca e igualdade envolvem ações que aumentam ou decrescem as quantidades de uma série. Em um problema de troca a quantidade inicial é aumentada ou diminuída por uma ação específica; problemas de igualdade envolvem duas quantidades separadas, uma das quais é trocada para ser a mesma quanto a outra quantidade. Problemas de combinação e de comparação envolvem relações estáticas ao invés de ações.
Outros estudos mostraram que a habilidade em resolver problemas de história aumenta gradualmente, durante o ensino fundamental, com problemas de troca e combinação sendo os mais fáceis, e os problemas de comparação os mais difíceis.
À medida que as crianças adquirem mais experiência com problemas de soma simples, desenvolve-se um novo procedimento, chamado por Fuson (1982) de "fatos conhecidos". O novo procedimento é a memorização das respostas para problemas de soma simples. Os alunos de primeira série parecem ser muito rápidos em "dobros", tais como "2 + 2, 3 + 3, etc". Parecem memorizar as respostas para alguns fatos, mas não para todos os fatos da soma. Assim, um procedimento de "fatos conhecidos" é usado para alguns problemas, mas um procedimento de contagem progressiva é usado para outros.
Concluímos esse item, enfatizando que há uma diferença essencial entre os sistemas de representação escrita da fala, em especial o alfabeto, e o sistema numérico. É que os primeiros utilizam combinações de unidades elementares para formarem compostos, as palavras, segundo regras fonotáticas, isto é regras que definem as combinações e, portanto, as sequências possíveis; ao passo que o sistema numérico é utilizado para calcular novas quantidades a partir de combinações específicas (as operações) de outras quantidades. Nas palavras escritas, a combinação é invariavelmente do mesmo tipo (sequencial) e a identidade das unidades é preservada no resultado das combinações, ao passo que no cálculo aritmético as combinações são de diferentes tipos e os operandos (as quantidades que entram na operação) desaparecem no resultado (Morais, 2011).
Ainda, segundo o mesmo autor, no que se refere à leitura, quase todos os psicolinguistas estão hoje convencidos de que existe uma interação recíproca entre a aprendizagem da leitura e a consciência dos fonemas, isto é a aprendizagem da leitura impulsiona a tomada de consciência dos fonemas e esta desempenha um papel importante no desenvolvimento do processo de descodificação grafofonológica. Uma relação do mesmo tipo tem lugar entre a aprendizagem da aritmética e o estabelecimento de uma representação linear das quantidades numéricas.
Habilidade de cálculo em adultos
A cognição na vida adulta parece estar muito mais ligada a questões pragmáticas da vida real, ao constatarmos que os adultos geralmente procuram aprender a resolver problemas da sua vida quotidiana (Knowles, 1986), (Smith, 1988), (Knapper & Cropley, 1985) por conta de sucessivas experiências práticas proporcionadas pelo tipo de atividade que exercem. Assim, é necessário considerar que a cognição na vida adulta produz outros tipos de operações que vão além das operações formais, ou seja, requer operações pós-formais. Considera-se que na idade adulta, os fatos numéricos estão bem memorizados e a contagem de algoritmos pode não ser mais necessária. Além disso, à medida que os alunos adquirem mais fatos conhecidos, podem usá-los para extrair respostas para problemas relacionados (ou de fatos conhecidos). Por exemplo, 5 + 7 = ___, podemos tirar 1 do 7 e dá-lo ao 5, portanto, 6 + 6 = 12. A decomposição envolve a reconstrução da reposta baseada sobre a recuperação de uma soma parcial.
As investigações empíricas recentes sobre a cognição numérica demonstram que os adultos com boa performance em aritmética básica, como, por exemplo, 3 x 6 = ___? refletem tipicamente a recuperação de fatos discretos da memória ao invés de execução de algoritmos genéricos de cálculo. Fuson (1982) sugere uma progressão da contagem total para a contagem progressiva. Woods, Resnick e Groen (1975) dão exemplos de algoritmos para problemas simples de subtração. São apresentados três modelos na forma "m - n = ___" como veremos a seguir:
a) Modelo de incrementação (aumento): "5 - 3", inicia com 3 enquanto recita "4, 5", estende-se 1 e depois dois dedos.
b) Modelo de decrementação (decréscimo): exige contar para trás "n" vezes. Exemplo: "5 - 3", exige iniciar com "5" e, enquanto verbaliza ou recita "4, 3, 2" estende "1, 2 e depois 3 dedos".
c) Modelo de escolha: usa-se o modelo de incrementação (aumento) ou decrementação (decréscimo), dependendo de qual exige a mínima quantidade de contagem. Exemplo: "5 - 3" exige 3 decrementos usando-se o modelo de decrementação, mas apenas dois incrementos usando-se o modelo de incrementação. Em contraste, "5 - 1" exige um passo de contagem usando-se o modelo de decrementação, e quatro passos usando-se o modelo de incrementação.
As sutis diferenças na apresentação do problema tais como: o formato visual horizontal vs. vertical ou variações do símbolo usado para denotar uma operação aritmética pode afetar o processamento? Embora todos estes questionamentos enfoquem a aritmética, há claramente analogias em outros domínios.
Portanto, considera-se que qualquer problema que difira somente com relação ao formato de apresentação ou às características relacionais entre os elementos, como, por exemplo, a ordem dos operadores, horizontal vs. apresentação vertical, ou variações nos símbolos aritméticos usados, acessará o mesmo (chunk) de memória.
O desenvolvimento de competências procedurais reflete uma força gradual do uso frequente da soma e procedimentos máximos para o uso frequente de contagem mínima. O uso de procedimentos também parece resultar no desenvolvimento da representação de memória de fatos básicos, conforme descrevem Siegler e Shrager (1984), que, por seu turno, sustentam o uso da memória baseada em processos de resolução de problemas. Com a recuperação direta, as crianças recuperam um fato aritmético da memória de longo termo (Ashcraft & Battaglia, 1978).
Uma vez que os alunos tenham adquirido alguma proficiência na adição ou subtração simples, o cálculo simples pode tornar-se um componente nos algoritmos maiores. Por exemplo, os algoritmos para a soma em duas ou três colunas (com transporte) ou subtração (com empréstimo) incorporam cálculos simples como uma única operação.
Quando se aprende a resolver problemas de aritmética simples, como, por exemplo, (5 + 3), as crianças confiam tipicamente sobre o seu conhecimento de contagem e os procedimentos associados (Siegler & Shrager, 1984). Estes procedimentos são às vezes executados com a ajuda dos dedos e às vezes sem eles (contagem verbal). Os dois procedimentos comumente mais usados em contagem são cunhados como contagem mínima, soma ou contagem geral (Fuson, 1982; Groen & Parkman, 1972).
Estes achados levantam algumas questões fundamentais sobre a estrutura e a organização deste conhecimento na memória. Por exemplo, os problemas aritméticos que são apresentados em diferentes modalidades ou formatos (por exemplo, 4 x 7 e quatro vezes sete) acessam uma única estrutura de memória semântica, ou estruturas de modalidade de memória específica ou separada? A ordem complementar dos operadores de um problema (por exemplo, 6 x 8 e 8 x 6), ou duas operações diferentes envolvendo problemas complementares (por exemplo, 3 x 9 = ... e 3 x ... = 27), ou problemas relacionados dentro de uma operação não comutativa (7 x ... = 35 e 5 x ... = 35), acessa as mesmas e/ou as diferentes estruturas de memória?
Em contraste, problemas que difiram com relação a um ou mais elementos acessará pedaços (chunks) de memória completamente diferente. Então, 4 x 7 e 7 x 6 acessará pedaços (chunks) de memória totalmente diferente. Uma predição um tanto menos intuitiva é que os problemas complementares de duas operações (por exemplo, 4 x 7 = ... e 4 x ... = 28) e problemas relacionados dentro de uma operação não comutativa (por exemplo, 28 = ... x 4 e 28 = ... x 7) acessa "chunks" de memória completamente diferentes.
O que os estudiosos afirmam é que esta área relacionada ao cálculo ainda necessita de estudos mais detalhados. Reis, Guerreiro, Garcia e Castro-Caldas (1995) mostraram em suas pesquisas que há sujeitos iletrados que demonstram notável conhecimento em cálculo mental, embora isso não seja a regra. A necessidade de tratar com números e tarefas de cálculo na vida diária requer que estes sujeitos gerem estratégias muito próprias. Os autores relatam em suas pesquisas como a mulher era capaz de fazer uma lista dos números de telefone usando desenhos para identificar a pessoa ou o local e um sistema de representação da quantidade para cada dígito.
Materiais e método
Foram testados 3 grupos de sujeitos. Dois em uma condição experimental, no início e fim de semestre letivo e um controle, também em duas oportunidades. O 1º grupo era formado por 6 mulheres e 6 homens com idades que variavam de 21 a 57 anos matriculados em uma classe de alfabetização (total 12). A média de idade era de 32,8 anos. Deste grupo, terminaram o 2º teste 5 mulheres e 1 homem totalizando seis sujeitos. O segundo grupo de sujeitos era formado por 6 mulheres e 5 homens (total 11). Suas idades variavam de 17 a 52 anos, correspondendo à média de 33,63 anos e também estavam matriculados numa classe de alfabetização. Deste grupo, terminaram o 2º teste 2 mulheres e 4 homens totalizando 6 sujeitos. O grupo controle era formado por 1 homem e 5 mulheres e não estavam matriculados em nenhum programa de alfabetização ou similar e residiam no mesmo bairro (total 6). As idades variavam entre 17 e 65 anos. A média de idade era de 45,2 anos.
Os 2 grupos experimentais tinham 23 sujeitos no total, quando realizam os testes pela primeira vez, no início do 1º semestre. Na aplicação do reteste, pela segunda vez, ambos ficaram reduzidos a 6 sujeitos cada, devido às desistências ou faltas sistemáticas às aulas inviabilizando sua inclusão nos resultados finais. No grupo controle, todos os sujeitos realizaram os testes a segunda vez sem ter havido nenhuma desistência.
Os sujeitos dos 3 grupos testados resolveram tarefas constituídas de operações de adição, subtração, multiplicação, divisão, problemas do cotidiano e contagem de figuras. Além disso, solicitou-se a oralização dos números de 1 a vinte e escrita de números de uma, duas ou mais casas decimais, contagem de figuras, realização de operações aritméticas mentalmente e por escrito a fim de verificar a capacidade e o grau de conhecimento em operações básicas de cálculo seja mental ou por escrito.
Resultados e discussão
As tarefas de cálculo consistiam em fazer uma série de operações aritméticas mentalmente e por escrito a fim de verificar a capacidade e o grau de conhecimento em operações básicas de cálculo em nível mental ou escrito. Foram apresentadas aos sujeitos problemas de aritmética básica tais como contagem de figuras, operações de adição, subtração, multiplicação, divisão e problemas do cotidiano.
Contagem em voz alta
Todos os sujeitos, dos três grupos, foram capazes de contar corretamente de 1 a 20 quer no 1º teste quer no 2º teste.
Contagem de figuras
Os grupos 1º, 2º e controle obtiveram, respectivamente, em média (sobre 10 ensaios), 8.09 respostas corretas, 8.75 e 8.83 (desvios-padrão: 2.34, 1.60 e 1.47). Observou-se que a performance de contagem diminuiu com o aumento do número de figuras. A tabela 1 apresenta a percentagem, em média, de sujeitos, sem distinção de grupo, que responderam corretamente para diferentes números de figuras.
| Número de figuras | 4-5-6 | 8-9-10 | 11-12 | 13-14 |
| % de sujeitos | 96.6 | 85.1 | 50.6 | 51.7 |
Tabela 1 - Apresenta o percentual, em média dos sujeitos, sem distinção de grupo que responderam corretamente para diferentes números de figuras.
A comparação entre o 1º e 2º testes fez-se sem distinção de grupo, porque o número de sujeitos, depois de retirados os sujeitos que já tinham alcançado a performance máxima no 1º teste, foi de apenas 10. O fator teste revelou-se não significativo (F(1,9) = 1.82).
Esta prova é aparentemente simples, cabendo ao sujeito conferir a figura que apresenta a quantidade de objetos solicitada pelo investigador. O S2 obteve dois acertos (20%) sobre um total de 10 respostas corretas. Dos 12 sujeitos quatro conseguiram acertar todas as provas. Os demais erraram até três respostas.
A atitude de alguns sujeitos era simplesmente contar uma vez e indicar sem conferir novamente se realmente aquela era a resposta correta. Este tipo de erro indica a ausência de comportamento metacognitivo, uma vez que alguns sujeitos não se preocupavam em revisar se a resposta dada estava realmente correta. Quando o investigador questionava se realmente aquela era a resposta, alguns sujeitos limitavam-se a dizer - "acho que é, professor" - ao invés de conferir novamente as figuras como ocorreu, por exemplo, com outros sujeitos que contavam e recontavam até chegar a uma resposta definitiva em que eles próprios confirmavam suas respostas pela revisão de contagem.
Escrita de números
Os grupos 1º, 2º e controle obtiveram, respectivamente, em média (sobre 10 ensaios), 4.27 respostas corretas, 2.50 e 2.33 (desvios-padrão: 3.82, 3.94 e 3.62).
É de notar que a performance de escrita de números diminuiu com o aumento da quantidade exprimida.
| Números | 1 | 4 | 7 | 9 | 12 | 18 | 25 | 53 | 136 | 1402 |
| Sujeitos | 12 | 10 | 13 | 11 | 12 | 10 | 7 | 6 | 5 | 4 |
Tabela 2 - Apresenta o número total de sujeitos (em 29), sem distinção de grupo, que escreveram corretamente os diferentes números.
A tabela 2 indica que 12 sujeitos escreveram corretamente o número "1", 10 o número "4" e assim sucessivamente. A comparação entre 1º e 2º teste fez-se sem distinção de grupo, porque o número de sujeitos retestados, depois de retirados aqueles que já tinham alcançado a performance máxima no 1º teste, foi de apenas 14. O fator teste revelou-se não significativo (F<1).
Na escrita de números os sujeitos que tinham alguma noção de leitura e escrita conseguiram escrever os números mais simples, como, por exemplo, "1, 4, 7 ou 9" mas a grande maioria falhou na escrita dos números "136 ou 1402". No 1º teste, 1º grupo, apenas dois sujeitos conseguiram escrever todos os números (S10 e S11). O S9 conseguiu escrever os números até o item (18) depois desistiu. No 2º teste o S1 do 1º grupo obteve 7 respostas corretas e o S9 melhorou seu índice não conseguindo desta vez escrever apenas o último item da lista. Mas o que é mais surpreendente é o fato de o S2 do 1º grupo, 2º teste, ainda não conseguir escrever absolutamente nada.
No 2º grupo, 1º teste, temos 3 sujeitos que não conseguiram escrever absolutamente nada. Curiosamente, o S10 escreveu apenas o número "12", mas não soube escrever, por exemplo, o número "1" ou o "7". O número "12" é o quinto item da lista, precedido pelos itens "1, 4, 7, 9, 12...". Ao ser questionado a respeito dessa particularidade, não soube justificar exatamente, porque sabia escrever apenas o número "12". Neste grupo houve apenas 2 sujeitos que conseguiram escrever a totalidade dos itens - (S6 e S9) com 100% de acerto. No 2º grupo, 2º teste, apenas o S10 acertou a escrita de todos os itens. Os S8 e S10 não acertaram nenhum item. No grupo controle, 1º teste, o S3 conseguiu escrever 9 dos 10 itens de modo correto. No 2º teste, curiosamente, o S3 acertou apenas 6 dos 10 itens. Além disso, 4 sujeitos não escreveram absolutamente nada. O S2 conseguiu escrever apenas o número "1". Os demais sujeitos não escreveram absolutamente nada.
Cálculo mental (adição, subtração e multiplicação)
A tabela 3 apresenta o número de respostas corretas em média (sobre 5 cálculos) e os respectivos desvios-padrão, separadamente para adição, subtração e multiplicação e para cada grupo.
| Grupos | |||||||
| 1º grupo | 2º grupo | Controle | |||||
| Adição | 2.82 | 3.17 | 1.33 | ||||
| (2.27) | (1.99) | (2.16) | |||||
| Subtração | 2.36 | 3.33 | 0.50 | ||||
| (2.20) | (1.78) | (1.23) | |||||
| Multiplicação | 1.18 | 1.42 | 0.67 | ||||
| (2.09) | (1.62) | (1.63) | |||||
Tabela 3 - Relação de respostas corretas em média sobre cinco cálculos e os respectivos desvios-padrão.
Apesar da inferioridade aparente do grupo controle, a análise estatística não mostrou um efeito significativo devido em parte ao fraco efetivo deste grupo (6 sujeitos) e em parte à grande variabilidade inter-individual. De fato, em adição, por exemplo, 5 sujeitos do 1º grupo e 5 sujeitos do 2º grupo fizeram os cálculos corretamente, mas 3 sujeitos do 1º grupo, e 2 do 2º grupo todos erraram. No grupo controle, enquanto 4 sujeitos falharam nesses mesmos cálculos, 1 sujeito acertou 3 e o restante acertou todos os cálculos.
Esta análise de variância também não revelou interação grupo x operação (F(4,52) = 1.44). Houve, sim, um efeito significativo da operação (F(2,52) = 8.25, p<0.0008), tendo os testes Scheffé revelado diferenças significativas entre a adição e a multiplicação (p<0.0002) e entre a subtração e a multiplicação (p<0.007), mas não entre a subtração e a adição.
| Adição | 5+1 | 3+4 | 8+7 | 19+6 | 42+23 |
| Número de sujeitos | 19 | 17 | 15 | 14 | 12 |
| Subtração | 4-2 | 7-5 | 9-4 | 17-8 | 57-23 |
| Número de sujeitos | 17 | 18 | 18 | 11 | 9 |
| Multiplicação | 2x3 | 4x5 | 5x7 | 10x6 | 14x8 |
| Número de sujeitos | 11 | 9 | 5 | 6 | 3 |
Tabela 4 - Apresenta o número total de sujeitos (em 29), sem distinção de grupo, que acertaram os diferentes cálculos.
A comparação entre 1º e 2º testes foi realizada sem ter em conta os sujeitos do grupo controle, devido ao fato de que 4 dos 6 sujeitos do grupo controle tiveram zero (0) tanto no 1º como no 2º teste para as três operações. Além disto, só incluímos os sujeitos que não alcançaram 5 em nenhuma das operações durante o 1º teste. Assim, apenas nos foi possível incluir a subtração e a multiplicação e 8 sujeitos (3 do 1º grupo e 5 do 2º grupo).
Esta análise indicou que o efeito de teste é não significativo (F(1,7) = 2.77, p<0.14) e a tendência aponta no sentido de uma diminuição (1.81 em média no 1º teste e 1.50 no 2º teste). O teste não interage com a operação (F<1). Quanto à operação, ela é de novo significativa (F(1,7) = 17.78, p<0.004), tendo a subtração conduzido, como esperado, a uma performance (2.50) mais elevada do que a multiplicação (0.98).
Nos problemas de adição e subtração alguns sujeitos fizeram uso dos dedos a fim de representar as quantidades. Mesmo com quantidades pequenas a grande maioria dos sujeitos adotou esta estratégia. As maiores dificuldades que os sujeitos enfrentaram relacionavam-se às operações de multiplicação e divisão. O maior número de erros ou de omissão de resposta são encontrados nas contas de multiplicação em provas como 2 x 3 =; 4 x 5 =; 5 x 7 =; 10 x 6 =; 14 x 8 =; ou 16 x 7 =; 212 x 8 =; 534 x 39 =.
Cálculo escrito (adição, subtração, multiplicação e divisão)
Como era esperado, a performance do grupo controle foi quase nula. Em adição, 2 sujeitos conseguiram realizar apenas um cálculo cada um. Nas outras operações não houve nenhuma resposta correta. Assim, este grupo não interveio nas análises estatísticas. A multiplicação e a adição colocaram também dificuldades gravíssimas aos outros grupos. Na multiplicação, um sujeito 1º grupo e um sujeito 2º grupo conseguiram respectivamente resolver 2 e 1 problemas. Na divisão, um sujeito 1º grupo e um sujeito 2º grupo resolveram cada um 2 problemas; outro sujeito 2º grupo resolveu um cálculo de divisão, tudo o resto sendo performances nulas. Nestas condições, limitamo-nos a comparar em análise de variância os grupos 1º e 2º grupos na adição e na subtração. Nem o grupo nem o teste são significativos (F<1 nos dois casos); a sua interação também não é significativa (F(1,21) = 1.57).
A tabela 6 apresenta o número de sujeitos (em 29) que resolveram corretamente os diferentes cálculos, sem distinção de grupo.
A comparação 1º teste vs. 2º teste dispensa análise estatística para a multiplicação e a divisão. De fato, na multiplicação, apenas 2 dos 6 sujeitos do 1º grupo e 1 dos 6 sujeitos do 2º grupo resolveram um cálculo a mais no 2º teste do que no 1º teste; e na divisão não houve qualquer diferença entre os dois testes. A análise de variância mostrou que o efeito de teste é não significativo (F<1; em média, 1.42, com desvio-padrão de 1.02, para o 1º teste e 1.33 (1.24) para o 2º teste). Nenhum outro efeito ou interação é significativo, com F<1 ou ligeiramente acima de 1, com exceção do efeito de operação que mostrou uma tendência à significação (F(1,10) = 4.09, p<0.071).
| 1º grupo | 2º grupo | |
| Adição | 1.27 | 1.25 |
| (1.19) | (0.97) | |
| Subtração | 1.09 | 1.42 |
| (1.14) | (1.31) |
Tabela 5 - Relação das performances médias (em 5) e os respectivos desvios-padrão para os dois grupos e as duas operações por escrito.
| Adição | 361+54 | 42+24+11 | 581+439+80 |
| Número de sujeitos | 9 | 18 | 4 |
| Subtração | 276-31 | 157-44 | 582-413 |
| Número de sujeitos | 13 | 11 | 5 |
| Multiplicação | 16x7 | 212x8 | 534x39 |
| Número de sujeitos | 1 | 2 | 0 |
| Divisão | 15:5 | 180:3 | 572:11 |
| Número de sujeitos | 3 | 2 | 0 |
Tabela 6 - Performance dos sujeitos em adição, subtração, multiplicação e divisão.
Repete-se neste tipo de problema a estratégia do uso dos dedos para fazer as operações de adição e subtração. Os sujeitos (1, 2, 5, 8, 10) do 1º grupo, 1º teste (adição), desenharam bolinhas ou traços em uma folha e a partir disso, fizeram as operações contando e recontando as bolinhas ou os traços para obter os resultados desejados. A demanda de tempo para solucionar o problema foi bastante grande.
As operações que envolviam números baixos possibilitavam para alguns sujeitos a realização satisfatória dessas operações. Todavia, quando os números eram altos e envolviam operações de adição e subtração com dezenas e centenas ou milhar o processamento das operações não era realizado e os sujeitos desistiam de realizar a tarefa. Os sujeitos que manifestavam essa dificuldade afirmavam que implicava escrever traços ou bolinhas em grande quantidade para chegar à solução adequada e isso demoraria muito tempo. A seguir, alguns exemplos de como os sujeitos tentaram resolver os problemas propostos.
Os problemas que envolviam "multiplicação para a resposta escrita" eram abandonados pela grande maioria dos sujeitos, visto que tinham enormes dificuldades em operar com multiplicação por escrito. Apenas o S6 obteve 2 acertos (66%) para multiplicação para resposta escrita.
Em contas que implicavam a habilidade de "divisão" para resposta escrita, novamente, a grande maioria dos sujeitos encontrou dificuldades nos mesmos patamares da multiplicação. Apenas o S6, 2º grupo, obteve 2 acertos sobre as três operações enquanto os demais não obtiveram nenhum acerto em divisão por escrito.

Figura 1 - S5, 1º grupo, 1º teste, cálculo 7.10, divisão por escrito.
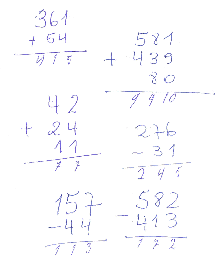
Figura 2 - S1, 1º grupo, 1º teste, adição e subtração por escrito.
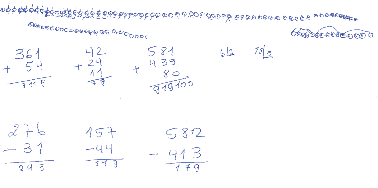
Figura 3 - S9, 1º grupo, 1º teste, cálculo adição e subtração.
O S9 utiliza a estratégia das bolinhas para a obter a resolução das operações de divisão, conforme se observa na figura. No canto supeiror à direita da figura 3, há diversos agrupamentos de símbolos não numéricos como tentativa de solução. Na Figura 4, observamos a estratégia para a solução de uma operação de adição. O S10 apresentou três séries de riscos (símbolos não numéricos) para indicar as quantidades de cada numerador obtendo o resultado correto. Ou seja, parte da representação de um saber cotidiano concreto para tentar atigir o conceito de cientificidade. Nos lembra a criança que conta nos dedos para atingir a solução. Aqui, nesse caso, o sujeito adulto usa riscos ou sinais gráficos para tentar representar uma possível solução. O tempo dispendido é enorme, e nem sempre a solução é atingida com sucesso.

Figura 4 - S10, 1º grupo, 1º teste, cálculo de adição por escrito.
Morais (2011) explica que essas demonstrações são situações em que os indivíduos não escolarizados, que não dispõem de representações numéricas verbais, são forçados a recorrer às representações aproximativas. A capacidade para representar sequências numa linha mental, em todo o caso de maneira espacial, é provavelmente uma capacidade biológica universal.

Figura 5 - S10, 1º grupo, 1º teste, conta de divisão por escrito.
Na Figura 5 observamos a forma como o S10 tenta obter a solução de uma operação de divisão, desenhando 5 blocos de 3 riscos de modo que unindo cada bloco de três riscos tenta conseguir visualizar a quantidade na conta de divisão por escrito.
Como vermos, os sujeitos usam símbolos não numéricos para tentar a solução dos problemas. Se deve notar também que a solução inicia da esquerda para a direita, o que demonstra que isso advém da influência cultural, embora se saiba que essa capacidade não seja uma pura construção cultural.
Segundo Morais (2011), a direção da linha mental numérica tem sua origem na ligação forte que existe, na organização funcional do cérebro, entre as representações numéricas e espaciais. A espacialização dos números resulta da existência de circuitos cerebrais comuns que por um lado suportam a representação mental dos números e por outro garantem a atenção ao espaço exterior. Muitos estudos têm mostrado que as tarefas numéricas implicam áreas parietais posteriores envolvidas na percepção do espaço e na atenção espacial.
Problemas da vida cotidiana
O grupo controle resolveu, em média, ligeiramente mais problemas (2.67) do que o 1º grupo (2.09) e o 2º grupo (2.27) (desvios-padrão de 1.52, 1.58 e 1.10, respectivamente).
| 1º grupo | 2º grupo | Controle | |
| 1 | 8/11 | 12/12 | 6/6 |
| 2 | 8/11 | 9/12 | 5/6 |
| 3 | 4/11 | 5/12 | 4/6 |
| 4 | 3/11 | 2/12 | 1/6 |
Tabela 7 - Resolução de problemas e quantidade de sujeitos que obtiveram sucesso na resolução.
A comparação entre 1º e 2º testes, pela análise de variância, tendo-se excluído dois sujeitos do 1º grupo que tinham resolvido os 4 problemas no 1º teste, não revelou efeito significativo do teste embora houvesse uma tendência à melhoria (2.00 em média no 1º teste, com desvio-padrão de 0.88, e 2.36 no 2º teste, com desvio-padrão de 1.01; f(1.11) = 3.3, p<0.1).
A grande maioria dos sujeitos não conseguiu converter a quantia de 20 dólares em reais, conforme solicita o problema (4) em problemas da vida cotidiana. Houve apenas 3 sujeitos que conseguiram resolver este problema. Os demais não conseguiram representar mentalmente esta operação de conversão por implicar um tipo de cálculo bem mais sofisticado do que as operações aritméticas básicas como as solicitadas em adição para cálculo mental. Além disso, o problema coloca uma dificuldade a mais, ao apresentar aos sujeitos, números fracionados.
Os erros mais comuns praticados pelos sujeitos que se encorajavam em resolver os problemas de adição ou de subtração relacionavam-se às noções de transporte ou empréstimo. As operações que configuravam dezenas ou centenas criavam enormes dificuldades para a sua solução.
Considerações finais
Os resultados monstram que os sujeitos que conseguem ler apresentam um domínio mais amplo de habilidades em cálculo. À medida que o domínio em leitura decai, observa-se que o domínio em cálculo também diminui. O que é curioso é que aqueles sujeitos que não leem, ou leem muito rudimentarmente, às vezes, apresentam habilidades em resolução de problemas cotidianos. Ainda com relação aos problemas cotidianos, ou seja, a habilidade em resolver problemas, mentalmente, é demonstrada por 3 sujeitos (1, 2, 9). O que chama atenção é que em cada nível de leitura há 1 sujeito com performance no nível mais alto, outro no nível intermédio e outro no nível mais baixo de leitura.
Ocorreram algumas situações que chamam atenção no 2º grupo, em que os sujeitos que leem continuam a apresentar um leque de habilidades mais desenvolvidas, porém, em nível de habilidades de cálculo se constatou que o S11 não as expressou nesta área de conhecimento. O S4, de nível intermediário de leitura, manifestou habilidades em cálculo um pouco abaixo do S5 que não lê ou lê muito rudimentarmente.
Ao compararmos os sujeitos que conseguem ler e escrever ao final de um determinado período de alfabetização com aqueles que não leem nem escrevem observa-se que o leque de habilidades que estes desenvolvem são bem maiores do que aqueles que não leem e nem escrevem.
Os resultados revelam que os sujeitos que dominam a leitura e a escrita se distinguem nas habilidades linguísticas e cognitivas em relação àqueles que não apresentam este domínio. Contudo, encontramos uma minoria de sujeitos que consegue se destacar nalguma habilidade cognitiva independente de saber ler ou escrever.
Quando analisamos os escores dos sujeitos que frequentam o curso de alfabetização de adultos fica bastante evidente que não há praticamente diferença entre os sujeitos que são testados no princípio do ano e aqueles que são retestados ao final de 3 ou 4 meses de atividades escolares. Os resultados demonstram objetivamente o grau de evolução num determinado percentual de testes de cálculo. Se os resultados indicam algum progresso numa ou noutra modalidade de cálculo, por outro lado, a aprendizagem destes sujeitos não atingiu o que se esperava após um determinado tempo de frequência às aulas de alfabetização específicas para adultos "analfabetos".
Estes resultados permitem que se considerem alguns fatores que podem contribuir para entender as performances obtidas pelos sujeitos. A primeira observação que deve ser levada em conta é proceder a uma análise criteriosoa em relação ao tipo de método utilizado na educação de Jovens e Adultos. É pertinente pensar que todo o esforço empreendido em busca de uma prática pedagógica, embasada na propalada eficácia da perspectiva filosófico-pedagógica construtivista, pareceu não gerar os resultados esperados. Está ainda para ser feita uma revisão profunda dos efeitos desta perspectiva pedagógica em termos da aprendizagem na educação de jovens e adultos em nível das classes de alfabetização.
Também se deve considerar que o aluno para apropriar-se do conhecimento formal demanda de sua parte uma determinação particular para desenvolver as habilidades de leitura e escrita. Alguns sujeitos estão frequentando as aulas porque necessitam solucionar o problema de não ter, por exemplo, a carteira de motorista sem a qual enfrentam problemas com a polícia de trânsito. Algumas vezes, observamos que determinados sujeitos não têm uma motivação mais profunda quanto à busca da formação científica e cultural, tendo em vista que seus objetivos são de alcance imediato e, uma vez atingidos, retiram-se da escola. O objetivo não é a busca da formação científica ou a busca de aprimoramento cultural, mas a solução de seus problemas imediatos de sobrevivência.
Ficou evidente ao longo das testagens que o efeito do programa de educação de jovens e adultos, em termos de formação e de aprendizagem não apresentou os resultados esperados. Os sujeitos testados demonstraram em suas performances que os resultados (aproveitamento) estão aquém do que deveriam ou poderiam ter atingido num período de quatro meses de escolarização (um semestre). As habilidades de cálculo apresentaram situações interessantes, sobretudo aquelas relacionadas às estratégias que os sujeitos criaram para solucionar problemas. Nesse ponto mencionamos os exemplos de estratégias que alguns sujeitos utilizaram para resolver determinados problemas, baseando-se em representações gráficas como desenhos, círculos e traços. Embora denote uma habilidade rudimentar de solução do problema aritmético proposto, significa que os sujeitos ainda não interiorizaram e/ou não captaram o sistema numérico como representação simbólica de quantidades numéricas que representam realidades abstratas por meio de signos concretos, permitindo combinações e transformações geradoras de novos sentidos ou novos fatos.
Ao fazermos a comparação entre os sujeitos que leem com aqueles que leem ou leem de modo rudimentar e outros que não leem nada, observamos que o leque de habilidades cognitivas que se evidenciam nos sujeitos que leem são bem mais amplas ou desenvolvidas do que aqueles que leem rudimentarmene ou nada. Contudo, afirmar que estes sujeitos conseguiram aumentar ou se distinguir nas habilidades cognitivas, devido ao efeito da alfabetização ou da escolarização, também é crucial porque há uma minoria de sujeitos que não leem e que evidenciam habilidades cognitivas desenvolvidas.
Isso nos leva a pensar que apesar de não serem condições necessárias, verifica-se que a escolarização e talvez também a alfabetização contribuam para uma melhoria da performance em termos dos escores alcançados em algumas habilidades cognitivas e linguísticas em nível individual e de grupo. Como já foi mencionado, os sujeitos que leem apresentaram um número maior de habilidades, tanto em nível linguístico quanto cognitivo.
Via de regra, se deve destacar que as operações pós-formais na vida adulta acentuam o pragmatismo na resolução de problemas da vida real, a possibilidade de múltiplas soluções, a coexistência entre a relatividade do pensamento (contextualidade) e a universalidade (regras gerais). O raciocínio do adulto não segue a lógica formal, sendo, por isso, contextualizado, apresentando, consequentemente, alguma flexibilidade cognitiva. Desta forma, o raciocínio dialético (raciocínio que tem em conta a contextualidade e as regras gerais) é fundamental na interpretação das experiências do indivíduo adulto que está se alfabetizando.
Portanto, pode-se presumir que há uma minoria de sujeitos iletrados ou recém-alfabetizados que consegue distinguir-se em algumas habilidades cognitivas, independentemente de saberem ler ou escrever. O fato de encontrarmos sujeitos iletrados capazes de resolverem bem certos problemas pode advir de sua habilidade em encontrar certas estratégias particulares para aquele determinado problema. Essa capacidade pode advir de suas experiências de vida bastante particulares.
Salientamos que a hipótese da "alfabetização" é considerada um pré-requisito para desenvolver o pensamento lógico e abstrato. Observamos que existem sujeitos que criam estratégias próprias e conseguem resolver problemas que exigem certo nível de abstração. É o caso de crianças e adolescentes brasileiros que trabalham como vendedores ambulantes e que conseguem fazer cálculos mentais rápidos naquele contexto, porém, quando são solicitados a fazer a demonstração num contexto escolar não o conseguem.
Na nossa pesquisa, citamos o exemplo típico do S5, 2º grupo, que trabalha como cobrador de uma empresa de ônibus na cidade de Florianópolis. A atividade exige operações mentais rápidas para poder devolver o troco aos passageiros para cédulas de 5, 10 ou 20 reais, no entanto, se examinarmos os seus resultados em cálculo escrito, que são operações de multiplicação e divisão, não conseguiu resolver nenhuma das operações propostas. No entanto, destacamos que ele apresenta bons resultados nos testes de cálculo mental e em problemas da vida cotidiana. Este foi um dos sujeitos que conseguiu resolver todas as operações mentalmente com rapidez. Como vemos, apresenta bom desempenho em algumas operações, mas não em outras que são fundamentais no conjunto das operações de cálculo.
Em síntese, os efeitos das hipóteses de que a alfabetização e por extensão a escolarização têm repercussões ao nível da linguagem e da cognição, ainda exigem maior aprofundamento. Ao compararmos, porém, os sujeitos que leem e escrevem com os que não leem nem escrevem observa-se que o leque de habilidades que estes desenvolvem são bem maiores do que aqueles que não leem e nem escrevem.
Os resultados revelam que os sujeitos que têm domínio em leitura e escrita se distinguem nas habilidades linguísticas e cognitivas em relação àqueles que não apresentam este domínio, embora possamos encontrar uma minoria de sujeitos que se destaca nalguma habilidade cognitiva independente de saber ler ou escrever.
Para finalizar, ressaltamos que após essa minuciosa análise dos dados, o processo de aprendizagem do adulto que quer alfabetizar-se necessita de professores preparados, de programas e de metodologias adequados ao seu contexto sociocultural. Constatamos que existem desafios imensos que devem ser enfrentados, pois, assim como os jovens e adultos procuram cada vez mais os núcleos de alfabetização, há também muita evasão, por se sentirem incapazes de realizar as aprendizagens propostas.
Referências bibliográficas
Ashcraft, M.H.; Battaglia, J. (1978). Cognitive arithmetic: evidence for retrieval and decision process in mental addition. Journal of Experimental Psychology: human learning and memory, 4, 527-538. [ Links ]
Blakemore, S.J.; Frith, U. (2000). The implications of recent development in neuroscience. London: Institute of Cognitive Neuroscience, 17. [ Links ]
Baroody, A.J. (1987). The development of counting strategies for single-digit addition. Journal for Research in Mathematics Education, 18, 141-157. [ Links ]
Briars, D.; Siegler, R.S. (1984). A featural analysis of preschoolers' counting knowledge. Developmental Psychology, 20, 607-618. [ Links ]
Bruner, J.S.; Olson, D.R. (1977). Symbols and texts as tools of intelect. Interchange, 8, 1-13. [ Links ]
Carpenter, T.P.; Mosner, J.M. (1982). The development of addition and subtraction problem-solving skills. Em: Carpenter, T.P.; Moser, L.; Romberg, T.A. (Ed.). Addition and subtraction: a cognitive perspective. Hillsdale: Erlbaum, 9-24. [ Links ]
Carraher, T.N.; Carraher, D.; Schliemann, A.D. (1982). Na vida dez; Na escola zero. Os contextos culturais da aprendizagem da matemática. Cadernos de Pesquisa, 42, 79-86. [ Links ]
Carraher, T.N.; Carraher, D.; Schliemann, A.D. (1985). Mathematics in the streets and in the schools. British Journal of Developmental Psychological, 3, 21-22. [ Links ]
Fuson, K.C. (1982). An analysis of the counting-on solution procedure in addition. Em: Carpenter, T.P.; Moser, J.M.; Romberg, T.A. (Ed.). Addition and subtraction: a cognitive perspective. Hillsdale: Erlbaum. 67-82. [ Links ]
Geary, D.C. (1995). Reflections of evolution and culture in children's cognition. Implications for mathematical development and instruction. American Psychologist, 50, 24-37. [ Links ]
Gelman, R.; Gallistel, C.R. (1978). The child's understanding of number. Cambridge: Harward University Press. [ Links ]
Groen, G.J.; Parkman, J.M. (1972). A chronometric analysis of simple addition. Psychological Rev., 79, 329-343. [ Links ]
Knapper, C.K.; Cropley, A.J. (1985). Lifelong learning and higher education. London: Kogan Page. [ Links ]
Knowles, M. (1986). The adult learner: a neglected species. 3º ed. Houston: Gulf Publishing Company. [ Links ]
Luria, A.R. (1992). Desenvolvimento cognitivo. São Paulo: Ícone. [ Links ]
Morais, J. (1986). A arte de ler. São Paulo: Editora da Universidade Estadual Paulista. [ Links ]
Morais, J. (2002). Influência da literacia e da escolaridade sobre a linguagem e a cognição. III Encontro Nacional (I Internacional) de Investigadores em Leitura, Literatura Infantil e Ilustração. Viana, F.L.; Martins, M.; Coquet, E. (2002). Leitura, Literatura Infantil e Ilustração. Investigação e Prática Docente, 3º ed. Braga: Centro de Estudos da Criança da Universidade do Minho, 45-62. [ Links ]
Morais, J. (2011). A aprendizagem dos sistemas simbólicos dos fonemas e das quantidades numéricas: semelhanças, diferenças e relações. Crato, N. et. al.(Org.). Matemática e ensino: questões e soluções. Lisboa: Fundação Calouste Gulbenkian. [ Links ]
Morais, J.; Kolinsky, R. (2004). A Ciência cognitiva da leitura e a alfabetização. Revista Pátio, 13-17. [ Links ]
Olson, D.R. (1977). From utterance to text: the bias of language in speech and writing. Harward Educational Review, 47. [ Links ]
Olson, D.R. (1997). O mundo no papel - as implicações conceituais e cognitivas da leitura e da escrita. São Paulo: Editora Ática. [ Links ]
Ostad, S.A. (1998). Developmental differences in solving simple arithmetic word problems and simple number-fact problems: a comparison of mathematically normal and mathematically disabled children. Mathematical Cognition, 4, 1-20. [ Links ]
Polya, G. (1983). Come risolvere i problemi di matematica. Feltrinelli: Milano. (Edição original, 1945). [ Links ]
Reis, A.I.; Guerreiro, M.; Garcia, C.; Castro-Caldas, A. (1995). How does an illiterate subject process the lexical component of arithmetics? Journal of the International New Psychology Society, 1, 206. [ Links ]
Scribner, S.; Cole, M. (1981). The psychology of literacy. Cambridge, MA: Harvard University Press. [ Links ]
Seron, X.; Fayol, M. (1994). Number transcoding in children: a funtional analysis. British Journal of Development Psychology, 12, 281-300. [ Links ]
Siegler, R.S.; Shrager, J. (1984). Strategy choices in addition and subtraction: How do children know what to do? Em: Sophian, C. (Ed.), The origins of cognitive skills. Hillsdale, NJ: Erlbaum, 229-293. [ Links ]
Smith, R.M. (1988). Learning how to learn: applied theory for adults. Milton Keynes: Open University Press. [ Links ]
Sternberg, R. (1992). Human abilities - an information-processing approach. W. H. Freeman and Company. [ Links ]
Vigotsky, L.S. (1962). Thought and language. MIT Press: Cambridge. [ Links ]
Wagner, D. (2000). Alfabetização: construir o futuro. Brasília: SESI-DN. [ Links ]
Woods, S.S.; Resnick, L.B.; Groen, G.J. (1975). An experimental test of five process models for subtraction. Journal of Educational Psychological, 67, 17-21. [ Links ]
Notas
E.J. Mengarda
Endereço para correspondência: Departamento de Ciências da Comunicação (DECOM), Universidade Federal de Santa Maria (UFSM), Centro de Educação Superior Norte (RS), Cesnors, Linha Sete de Setembro s/n - BR386 Km 40, Frederico Westphalen, RS 98.400-000, Brasil.
E-mail para correspondência: mengarda@smail.ufsm.br.