Serviços Personalizados
artigo
Indicadores
Compartilhar
Psicologia em Pesquisa
versão On-line ISSN 1982-1247
Psicol. pesq. vol.14 no.3 Juiz de Fora dez. 2020
http://dx.doi.org/10.34019/1982-1247.2020.v14.29542
Modelagem multinomial aplicada à pesquisa em psicologia
Multinomial modeling applied to psychological research
Modelo multinomial aplicado a la investigación psicológica
Carlos F. A. GomesI; Luciano G. BurattoII
IUniversidade Federal de Juiz de Fora - UFJF. E-mail: carlos.fagomes@gmail.com ORCID: https://orcid.org/0000-0001-8383-7807
IIUniversidade de Brasília - UnB. E-mail: lburatto@unb.br ORCID: https://orcid.org/0000-0002-7003-7824
RESUMO
Teorias sobre fenômenos psicológicos frequentemente fazem referência a processos que não são diretamente observáveis (processos latentes). Tradicionalmente, no entanto, a investigação desses fenômenos é feita de forma indireta aos processos latentes. O objetivo deste artigo é introduzir os conceitos fundamentais de modelagem multinomial. Aqui mostramos como modelos de processos latentes são derivados de modelos puramente descritivos através da redução do espaço de parâmetros motivada por uma ou mais teorias psicológicas. Os resultados são os modelos multinomiais que fornecem medidas simples de processos psicológicos (probabilidades) e que podem ser quantitativamente testados com dados reais. O uso de modelagem multinomial permite a análise direta dos efeitos de variáveis independentes nos próprios processos latentes que controlam o desempenho em uma ou mais tarefas experimentais, assim, facilitando o teste de predições e explicações teóricas sobre fenômenos psicológicos.
Palavras-chave: Modelagem matemática; Processos latentes; Distribuição multinomial; Processos estocásticos; Estados mentais.
ABSTRACT
Theories about psychological phenomena often refer to unobservable processes (latent processes). Traditionally, however, the psychological investigation of these phenomena is done indirectly to the latent processes themselves. The objective of this article is to introduce fundamental concepts about multinomial modeling. Here we show that latent processes models are derived from purely descriptive models by reducing the parameter space according to one or more psychological theories. The result is multinomial models that deliver simple measures of psychological processes (probabilities) and that can be tested quantitatively with real data. The use of multinomial modeling allows direct analysis of the effects of independent variables on the latent processes that control performance on one or more experimental tasks, thus making it easier to test theoretical predictions and explanations about psychological phenomena.
Keywords: Mathematical modeling; Latent processes; Multinomial distribution; Stochastic processes; Mental states.
RESUMEN
Teorías sobre fenómenos psicológicos a menudo se refieren a procesos que no son directamente observables (procesos latentes). Sin embargo, la investigación de estos fenómenos se realiza tradicionalmente de manera indirecta con respecto a los procesos latentes. El propósito de este artículo es presentar los conceptos fundamentales del modelado multinomial. Aquí mostramos cómo los modelos de procesos latentes se derivan de modelos puramente descriptivos al reducir el espacio de parámetros motivado por una o más teorías psicológicas. El resultado son modelos multinomiales que proporcionan medidas simples de procesos psicológicos (probabilidades) y que pueden probarse cuantitativamente con datos reales. El uso de modelos multinomiales permite el análisis directo de los efectos de variables independientes en los procesos latentes que controlan el rendimiento en una o más tareas experimentales, lo que facilita la prueba de predicciones y explicaciones teóricas sobre fenómenos psicológicos.
Palabras clave: Modelo matemático; Processos latentes; Distribución multinomial; Processos estocásticos; Estados mentales.
Teorias sobre fenômenos psicológicos frequentemente fazem referência a processos que não são diretamente observáveis (processos latentes), tais como a contribuição de diferentes tipos de representações mentais durante a lembrança de um evento do passado (e.g., Brainerd, Gomes, & Moran, 2014) ou o nível de ativação lexical durante a leitura de uma narrativa (e.g., Walker & Hickok, 2016) ou lista de palavras associadas (e.g., Buratto, Gomes, Prusokowski, & Stein, 2013). Tradicionalmente, a investigação científica de fenômenos psicológicos é feita de forma indireta aos processos latentes, como através da manipulação de uma variável independente e subsequente análise do seu efeito em uma ou mais variáveis que são facilmente observáveis e medidas - por exemplo, o tempo de reação médio de cada resposta, a proporção de acerto, ou o nível de oxigenação sanguínea em determinadas regiões do cérebro -, ao invés da análise do efeito da variável independente nos próprios processos latentes que controlam o desempenho na tarefa experimental.
Um dos fatores complicadores da análise de processos latentes é que, ao contrário do procedimento tradicional, o mesmo exige a definição precisa de conjuntos de operações e relações entre variáveis observáveis e latentes que frequentemente vai além de um simples mapeamento de um para um - isto é, desempenho em uma condição experimental pode refletir a contribuição de múltiplos processos latentes que são relevantes para o desenvolvimento e teste de uma ou mais teorias psicológicas. Além disso, o desenvolvimento e o uso de sofisticados modelos psicológicos exigem uma bagagem de conhecimento técnico que é de difícil acesso em uma área ainda sem tradição de treinamento em exatas, como é o caso da Psicologia nas instituições de ensino do Brasil. Felizmente, uma ferramenta analítica, chamada modelagem multinomial - ou em inglês, modelos multinomial processing tree - MPT (Batchelder & Riefer, 1986; Hu & Batchelder, 1994; Riefer & Batchelder, 1988) - tem sido desenvolvida ao longo das últimas quatro décadas como alternativa de meio-termo entre métodos de análise de dados tradicionais (e.g., análise de variância, regressão logística) e complexos modelos matemáticos psicológicos (e.g., Anderson, Betts, Bothell, Hope, & Lebiere, 2019; Lehman & Malmberg, 2013; Ratcliff, Gomez, & McKoon, 2004).
O apelo de modelos MPT é que os mesmos possibilitam obter medidas quantitativas simples de processos latentes, utilizam um formalismo acessível e possuem procedimentos e programas bem estabelecidos para realização de teste estatístico de ajuste do modelo e de invariância de parâmetros intra- e entrecondições experimentais (Hu & Phillips, 1999; Singmann & Kellen, 2013; Stahl & Klauer, 2007). Além disso, MPT é uma área que continua em constante aprimoramento, destacando o surgimento de generalizações para análise multinível/hierárquica (Klauer, 2010; Smith & Batchelder, 2010), análise via métodos Bayesianos (Matzke, Dolan, Batchelder, & Wagenmakers, 2015), discretização de variáveis contínuas no estudo de modelos MPT tradicionais (Heck & Erdfelder, 2016; Klauer & Kellen, 2018) e medidas de complexidade para seleção de modelos (Kellen & Klauer, 2020; Wu, Myung, & Batchelder, 2010).
No Brasil, no entanto, o uso de MPT aplicada à pesquisa em psicologia é virtualmente inexistente. Por esse motivo, o objetivo deste artigo é introduzir MPT ao público de língua portuguesa, particularmente estudantes e pesquisadores brasileiros, como uma ferramenta de aprimoramento na investigação de fenômenos psicológicos. O artigo está organizado em três partes principais, divididas ao longo de cinco seções. Na primeira parte, são abordadas as ideias por trás da MPT que dizem respeito à origem em modelos puramente descritivos. Na segunda parte, são apresentados os conceitos de estado mental e como ele serve de guia para elaboração de modelos multinomiais baseados em teorias psicológicas. Já na terceira e última parte, são abordadas as questões técnicas diretamente pertinentes à MPT aplicada à pesquisa em Psicologia. Leitores interessados em um tratamento mais aprofundado dos conceitos centrais em MPT podem consultar Riefer e Batchelder (1988) e Hu e Batchelder (1994). Para tratamentos mais avançados e recentes, ver Smith e Batchelder (2010), Heck, Arnold e Arnold (2018) e Klauer e Kellen (2018).
Fundamentos de modelagem multinomial
Na aplicação de qualquer formalismo, primeiro é preciso considerar o tipo de representação dos dados a serem modelados. De forma breve, a MPT se aplica a (a) dados de natureza discreta, (b) que possuem um número finito de categorias mutuamente excludentes e (c) cujas observações são independentes e distribuídas de forma idêntica (IDI). Assim, um paradigma experimental adequado para o uso da MPT precisa gerar dados que possam ser classificados em categorias observáveis de um conjunto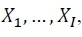 , no qual Ké um número inteiro positivo igual a cardinalidade (ou tamanho) do conjunto de categorias. Essas categorias, por sua vez, são mutuamente excludentes, como cinco cores distintas (e.g., amarelo, roxo, preto, azul, verde) ou diferentes localizações de um estímulo alvo na tela de um computador (e.g., meio, acima, abaixo, direita, esquerda), por exemplo. Entretanto, isso não implica que dados de outra natureza não possam ser estudados através de MPT. De fato, dados como tempo de reação ou grau de inclinação de um objeto podem ser modelados através da discretização dos dados de natureza contínua em múltiplos intervalos (e.g., classificação do tempo de reação em rápido, médio ou lento). De forma similar, técnicas de análise qualitativa de dados (Miles, Huberman, & Saldaña, 2014) podem ser utilizadas como pré-tratamento para gerar um número finito de classificações a serem estudadas com modelos multinomiais, constituindo um exemplo da complementaridade entre técnicas qualitativas e quantitativas.
, no qual Ké um número inteiro positivo igual a cardinalidade (ou tamanho) do conjunto de categorias. Essas categorias, por sua vez, são mutuamente excludentes, como cinco cores distintas (e.g., amarelo, roxo, preto, azul, verde) ou diferentes localizações de um estímulo alvo na tela de um computador (e.g., meio, acima, abaixo, direita, esquerda), por exemplo. Entretanto, isso não implica que dados de outra natureza não possam ser estudados através de MPT. De fato, dados como tempo de reação ou grau de inclinação de um objeto podem ser modelados através da discretização dos dados de natureza contínua em múltiplos intervalos (e.g., classificação do tempo de reação em rápido, médio ou lento). De forma similar, técnicas de análise qualitativa de dados (Miles, Huberman, & Saldaña, 2014) podem ser utilizadas como pré-tratamento para gerar um número finito de classificações a serem estudadas com modelos multinomiais, constituindo um exemplo da complementaridade entre técnicas qualitativas e quantitativas.
Já o pressuposto de IDI implica que, ao longo de múltiplas observações, a observação de uma determinada categoria (e.g., o número 4 em um jogo de dado) não dependa das observações anteriores e, de forma similar, as probabilidades de cada categoria são sempre iguais ao longo de múltiplas observações. Uma violação do pressuposto de IDI ocorreria, por exemplo, em um jogo de roleta modificado no qual, para se observar o #13, primeiro é preciso se observar um número par - isto é, neste caso, as categorias não são independentes. Outro exemplo de violação do pressuposto de IDI ocorreria em um jogo de cartas, no qual a chance de revelar o dois de copas do topo de um baralho aleatorizado muda conforme o número de cartas reveladas - isto é, a probabilidade de revelar um dois de copas não é constante ao longo de múltiplas observações, pois o tamanho da amostra diminui conforme o número de cartas reveladas do topo do baralho; neste último caso, a probabilidade seria adequadamente descrita por uma distribuição hipergeométrica multivariada.
Um modelo multinomial é uma generalização de um modelo binomial, no qual o número de possíveis resultados de um experimento é maior do que dois. Em um jogo de moeda, por exemplo, existem apenas dois resultados possíveis - cara ou coroa - e, portanto, ao longo de 𝑛 jogos de moeda, a probabilidade de se obter exatamente 𝑥 caras é descrita pela função massa de probabilidade binomial. Mais formalmente, se uma variável aleatória 𝑋 ~ 𝐵(𝑛,𝑝), no qual 𝐵(𝑛,𝑝) é a função binomial com probabilidade 𝑝 de sucesso ao longo de 𝑛 ensaios independentes (em inglês, Bernoulli trials), então a probabilidade de se observar exatamente 𝑥 sucessos é definida pela função massa de probabilidade binomial
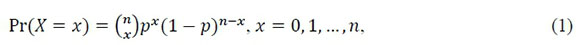
no qual 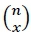 é o coeficiente binomial das possíveis formas de se distribuir x sucessos ao longo de n ensaios, calculado por
é o coeficiente binomial das possíveis formas de se distribuir x sucessos ao longo de n ensaios, calculado por  por exemplo, para
por exemplo, para 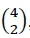 , existem seis formas de se distribuir dois sucessos ao longo de quatro ensaios, especificamente, 1100, 1010, 1001, 0110, 0101, e 0011. Para ilustrar, considere uma moeda enviesada na direção de coroa
, existem seis formas de se distribuir dois sucessos ao longo de quatro ensaios, especificamente, 1100, 1010, 1001, 0110, 0101, e 0011. Para ilustrar, considere uma moeda enviesada na direção de coroa  , a probabilidade de se observar exatamente 15 coroas ao longo de 20 jogos de moeda é
, a probabilidade de se observar exatamente 15 coroas ao longo de 20 jogos de moeda é  = .20, enquanto que com uma moeda justa
= .20, enquanto que com uma moeda justa  , a probabilidade do mesmo cenário é
, a probabilidade do mesmo cenário é
No entanto, se fosse utilizado um dado de seis lados ao invés de uma moeda, a função binomial seria inadequada para descrever por completo os resultados do experimento hipotético. Neste caso, existem seis resultados possíveis de um jogo de dado - face #1, #2, #3, #4, #5, e #6 - e portanto, ao longo de n jogos com um dado de seis lados, a probabilidade de se obter exatamente descrita pela função massa de probabilidade multinomial. Formalmente, se um vetor
descrita pela função massa de probabilidade multinomial. Formalmente, se um vetor 
 , no qual
, no qual 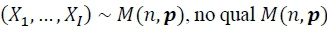 é a função multinomial com vetor de probabilidade
é a função multinomial com vetor de probabilidade  das
das  categorias ao longo de
categorias ao longo de  ensaios, então a probabilidade de se observar exatamente 𝑥1,𝑥2,𝑥3,𝑥4,𝑥5 e 𝑥6 é definida pela função massa de probabilidade multinomial
ensaios, então a probabilidade de se observar exatamente 𝑥1,𝑥2,𝑥3,𝑥4,𝑥5 e 𝑥6 é definida pela função massa de probabilidade multinomial

no qual  e com 𝑝𝑖definido no espaço de parâmetros
e com 𝑝𝑖definido no espaço de parâmetros 
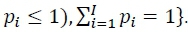 . Por exemplo, com um dado enviesado na direção do lado #6 (p6 = .20, p1 = p2 = p3 = p4 = p5 = .16), a probabilidade de se observar exatamente 5 #6 e 3 de cada um dos demais lados ao longo de 20 jogos de dado é
. Por exemplo, com um dado enviesado na direção do lado #6 (p6 = .20, p1 = p2 = p3 = p4 = p5 = .16), a probabilidade de se observar exatamente 5 #6 e 3 de cada um dos demais lados ao longo de 20 jogos de dado é  = .001, ou a chance de 1 observação a cada 1000 jogos. Em contrapartida, quando é utilizado um dado justo (p1 = p2 = p3 = p4 = p5 = p6 = 1/6), a probabilidade do mesmo cenário é menor,
= .001, ou a chance de 1 observação a cada 1000 jogos. Em contrapartida, quando é utilizado um dado justo (p1 = p2 = p3 = p4 = p5 = p6 = 1/6), a probabilidade do mesmo cenário é menor, 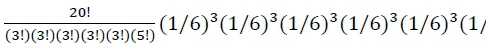
 = .0007, ou a chance aproximada de 1 observação a cada 1.429 jogos.
= .0007, ou a chance aproximada de 1 observação a cada 1.429 jogos.
Modelagem multinomial aplicada ao estudo de estados mentais
Na aplicação de MPT à psicologia, uma das ideias centrais é a de que em uma tarefa experimental composta por um conjunto finito de categorias mutuamente excludentes de resposta 𝑋1,…,𝑋𝐼 existe um conjunto finito de estados mentais 𝑇1,…,𝑇𝐽 que geram a categoria 𝑋𝑖, no qual 𝐽 é um número inteiro positivo igual à cardinalidade do conjunto de estados mentais. Considere, por exemplo, os diagramas apresentados na Figura 1, que ilustram o cenário hipotético de uma tarefa composta por cinco categorias de resposta, 𝑋1,…,𝑋5, e de acordo com uma teoria qualquer, as categorias são geradas por um total de três estados mentais, 𝑇1,𝑇2,𝑇3. Na Figura 1A, temos o espaço de respostas, segmentado de acordo com as categorias mutuamente excludentes do experimento e cuja área é proporcional à probabilidade marginal de cada categoria. De forma similar, na Figura 1B, temos o espaço de respostas, agora segmentado de acordo com os estados mentais postulados por uma teoria psicológica e como antes, cuja área é proporcional à probabilidade marginal de cada estado mental. Ao interpolar as Figuras 1A e 1B (ver Figura 1C), é possível visualizar graficamente as intersecções entre categorias de resposta e estados mentais para este experimento hipotético (Na Figura 1D, para a condição 𝑋1, as intersecções com os estados mentais foram indicadas por diferentes tonalidades de cinza). Em termos estocásticos, a noção de que estados mentais produzem categorias de resposta de um experimento pode ser reformulada pelas probabilidades implicadas na Figura 1. Mais especificamente, a probabilidade de se observar a categoria 𝑋𝑖, definida pelo termo Pr(𝑋i), pode ser calculada através da soma das probabilidades das intersecções entre 𝑋𝑖 e os estados mentais que geram o mesmo, ou seja

no qual Pr(𝑋𝑖|𝑇𝑗) é a probabilidade condicional da categoria 𝑖, dado o estado mental 𝑗, e Pr(𝑇𝑗) é a probabilidade marginal do estado mental 𝑗. Portanto, na Figura 1C, as probabilidades das condições 𝑋1,…,𝑋5 são dadas pelas respectivas equações

Na prática, estimar o valor de Pr(𝑋𝑖) é algo trivial, pois ele é obtido diretamente das respostas que os participantes da tarefa experimental fornecem, por exemplo, ao longo de um ou mais itens. O desafio, portanto, é estimar os valores desconhecidos das probabilidades condicionais das categorias, Pr(𝑋𝑖|𝑇𝑗), e marginais dos estados mentais, Pr(𝑇𝑗), utilizando os valores conhecidos das probabilidades marginais das categorias, Pr(𝑋𝑖). Um dos complicadores, no entanto, é que na Eq. 3 existem 𝐼-1 graus de liberdade (df) para estimar 𝐽𝐼-1 parâmetros desconhecidos e, portanto, se torna necessária a introdução de uma forma de reduzir a quantidade de parâmetros desconhecidos para estimá-los através de métodos tradicionais, como máxima verossimilhança. Em MPT, isso é usualmente feito através do pressuposto de que Pr(𝑋𝑖|𝑇𝑗) e Pr(𝑇𝑗) são definidos por um conjunto de parâmetros de processos latentes funcionalmente independentes 𝜃1,…,𝜃𝐾, no qual 𝐾 é igual ou menor do que 𝐼-1, ou seja, 𝐾≤𝑑𝑓<𝐼. Os parâmetros θk são probabilidades de processos mentais definidos no espaço de parâmetros 𝒬={𝜽=(𝜃1,…,𝜃𝑘,…,𝜃𝐾) | (𝜃𝑘∈ℝ | 0≤𝜃𝑘≤1),𝑘=1,…,𝐾}. Ao longo de 𝐼 categorias que compõem uma tarefa experimental, o desenvolvimento de um modelo multinomial psicológico é então feito através do mapeamento entre as probabilidades das categorias de respostas explicitadas na Eq. 2, 𝒑=(𝑝1,…,𝑝𝐼), e o conjunto de parâmetros de processos latentes, 𝜽=(𝜃1,…,𝜃𝐾), tal que se uma função contínua 𝒑 tem intervalo definido por 𝒬′={𝒑(𝜃) | 𝜃∈𝒬}, então 𝒬′ é um subconjunto 𝐾 dimensional de 𝒫. Felizmente, em MPT, existem múltiplas maneiras de se desenvolver tal mapeamento de forma intuitiva, sendo o uso de diagramas em forma de árvore a técnica mais frequentemente utilizada e descrita na literatura (e.g., Knapp & Batchelder, 2004). Essa técnica e sua relação com o formalismo apresentado anteriormente são descritas em seguida.
Diagramas em forma de árvore
Um diagrama em forma de árvore é um dígrafo (Gross, Yellenm, & Zhang, 2003), usualmente orientado da esquerda para direita (ou de cima para baixo), composto por quatro componentes estruturais principais, conforme ilustrado na Figura 2A: (a) a raiz de uma árvore, também chamada de nó de decisão inicial do diagrama; (b) múltiplos nós de decisão de processos latentes; (c) múltiplos galhos; e (d) terminações em categorias de resposta. Ao longo de cada galho de um diagrama, existem um ou mais parâmetros de processos latentes e ao término de cada galho, existe uma categoria de resposta da tarefa experimental que é gerada pela intersecção dos processos latentes ao longo do respectivo galho. Na Figura 2B, por exemplo, a categoria de resposta 𝑋2 é gerada pelo processo latente 𝜃1, enquanto na Figura 2C, a categoria de resposta 𝑋1 é gerada pelos processos latentes (1 - 𝜃1) e 𝜃2. Além disso, um modelo multinomial pode ser representado por uma ou mais árvores, a depender das diferentes condições experimentais que compõem a tarefa. Por exemplo, no modelo de memória de reconhecimento chamado two-high threshold (Bröder & Schütz, 2009), existe um total de duas árvores, uma para cada tipo de item (alvo, distrator não relacionado). Já no modelo de falsas memórias, chamado conjoint recognition (Brainerd, Reyna, & Mojardin, 1999), existe um total de nove árvores, uma para cada combinação fatorial entre 3 (tipo de item: alvo, distrator relacionado, distrator não relacionado) x 3 (instrução do teste: literal, essência, literal ou essência).
Diagramas como o apresentado na Figura 2 são membros de uma subclasse de modelos multinomiais chamados de modelo multinomial binário (em inglês, binary multinomial processing tree - BMPT), em função de existir apenas duas alternativas em cada nó de decisão de processos latentes. Cada nó de um BMPT é representado por duas junções direcionais, sendo um quando um processo latente ocorre com probabilidade 𝜃𝑘 e o outro, quando ele não ocorre com probabilidade complementar, 1 - 𝜃𝑘. Na Figura 2, quando o processo latente 𝜃1 ocorre com sucesso, o participante produz a resposta 𝑋2 (galho realçado na Figura 2B); quando o processo latente 𝜃1 não ocorre e o processo latente 𝜃2 ocorre com sucesso, o participante produz a resposta 𝑋1 (Figura 2C); e quando ambos os processos latente 𝜃1 e 𝜃2 não ocorrem, o participante produz a resposta 𝑋3 (Figura 2D). A representação em formato de BMPT é a mais comum na literatura, sendo um dos motivos principais a propriedade de que qualquer modelo multinomial é estatisticamente equivalente a uma representação BMPT (Hu & Batchelder, 1994).
Com um diagrama em forma de árvore desenvolvido numa representação BMPT, a probabilidade de cada categoria de resposta pode ser calculada através da soma das probabilidades de todos os galhos que terminam na respectiva categoria, sendo a probabilidade de cada galho igual ao produto de todos os processos latentes ao longo do mesmo. Mais formalmente, uma árvore no formato BMPT define um conjunto de processos latentes 𝜽∈𝒬 ao longo de 𝐽𝑖 caminhos de um conjunto de galhos 𝐺𝑖1,…,𝐺𝑖𝑗,…,𝐺𝑖𝐽, cuja terminação é uma categoria de resposta 𝑋𝑖, tal que a probabilidade de um galho tem forma

na qual 𝑎𝑖𝑗𝑘 e 𝑏𝑖𝑗𝑘 são números inteiros positivos (𝑎𝑖𝑗𝑘,𝑏𝑖𝑗𝑘≥0) que definem o número de nós no galho 𝐺𝑖𝑗 associados com os processos latentes 𝜃𝑘 e 1−𝜃𝑘, respectivamente. No modelo hipotético ilustrado na Figura 2, por exemplo, as probabilidades dos três galhos são dadas por

A probabilidade da categoria de resposta 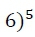 é então calculada como a soma dos galhos com terminação
é então calculada como a soma dos galhos com terminação 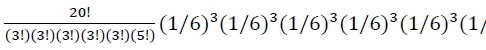 e, portanto, tem forma
e, portanto, tem forma

sendo que  =1. No exemplo da Figura 2, essas probabilidades são idênticas às Eq. 10-12, pois, para cada condição experimental, existe apenas um galho associado (𝐽1=𝐽2=𝐽3=1).
=1. No exemplo da Figura 2, essas probabilidades são idênticas às Eq. 10-12, pois, para cada condição experimental, existe apenas um galho associado (𝐽1=𝐽2=𝐽3=1).
Observe a relação entre Eq. 3 e Eq. 13. Na primeira, a probabilidade de uma categoria de resposta é definida em função da união dos estados mentais que a produzem, enquanto, na segunda, a probabilidade de uma categoria de resposta é definida em função da união de galhos cujos processos latentes produzem a respectiva categoria de resposta. De fato, em MPT, o galho de um diagrama em forma de árvore corresponde a um estado mental que, ao longo de múltiplos galhos, descreve o espaço de resposta por completo em termos de processos latentes. Dessa forma, a função de probabilidade de um modelo multinomial, 𝐿(𝜽|𝑿), é apenas uma extensão da função massa de probabilidade multinomial (Eq. 2), especificamente,
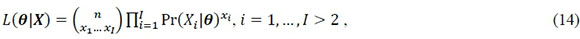
na qual  é a frequência observada da categoria ,
é a frequência observada da categoria , 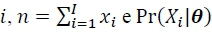 e é definido conforme a Eq. 13. Como o coeficiente binomial não varia em função das estimativas dos processos latentes, ele é frequentemente omitido no uso prático da Eq. 14 (e.g., Gomes, Brainerd, & Stein, 2013), assim como também é computacionalmente mais eficiente utilizar o logaritmo da função de probabilidade, já que ele reduz a Eq. 14 a uma série de somas, ao invés de uma série de produtos.
e é definido conforme a Eq. 13. Como o coeficiente binomial não varia em função das estimativas dos processos latentes, ele é frequentemente omitido no uso prático da Eq. 14 (e.g., Gomes, Brainerd, & Stein, 2013), assim como também é computacionalmente mais eficiente utilizar o logaritmo da função de probabilidade, já que ele reduz a Eq. 14 a uma série de somas, ao invés de uma série de produtos.
Identificabilidade
O conceito de identificabilidade é central na aplicação de modelos matemáticos a conjunto de dados, pois se refere à capacidade de estimar variáveis desconhecidas - neste caso, parâmetros livres de processos latentes - utilizando variáveis cujos valores são conhecidos - frequências observadas de um conjunto de categorias de resposta. A identificabilidade global de um modelo é obtida quando existe um único mapeamento direto (um a um) entre um local qualquer no espaço de parâmetros e um conjunto de probabilidades das categorias de resposta. Identificabilidade local, em contrapartida, se refere a um mapeamento na vizinhança do valor verdadeiro de um conjunto de parâmetros e é requerido para existência de estimativas únicas. Se os parâmetros de modelo multinomial não são sequer localmente identificáveis, então existem múltiplos conjuntos de estimativas de processos latentes para o mesmo conjunto de probabilidades de categorias e o modelo não pode ser testado quantitativamente.
Soluções analíticas para o problema de identificabilidade não são sempre possíveis, instrutivas ou eficientes, em função do elevado número de parâmetros livres que um MPT possa ter e o nível de complexidade de suas equações. Um critério de identificabilidade simples, chamado de regra da contagem, é o de que os parâmetros de um modelo multinomial não são localmente identificáveis se o número de categorias independentes geradas pela tarefa experimental for menor do que o número de parâmetros a serem estimados. Na Figura 1, por exemplo, existem quatro categorias independentes, então, se um MPT com cinco ou mais parâmetros livres fosse utilizado, de acordo com a regra da contagem, existiriam um ou mais parâmetros não identificáveis e, portanto, o modelo não poderia ser testado quantitativamente para aquele conjunto de dados. Apesar de simples, a regra da contagem é excessivamente rigorosa na definição de identificabilidade e, consequentemente, por vezes classifica um modelo multinomial como não testável quando os parâmetros do mesmo são de fato localmente identificáveis (Bamber & van Santen, 2000). Em função disso, uma prática comum é adotar outros dois critérios alternativos à regra da contagem. O primeiro deles, chamado de regra Jacobiana, é o de comparação do ranking da matriz Jacobiana com o número de parâmetros livres. A matriz Jacobiana de um modelo multinomial com múltiplos parâmetros é a matriz de derivadas parciais da função de probabilidade do modelo em todos os pontos deriváveis da função no espaço de parâmetros e respostas. Em álgebra linear, o cálculo do ranking de uma matriz mostra o maior número de linhas (ou de forma equivalente, colunas) linearmente independentes umas das outras. Dessa forma, se o ranking da matriz Jacobiana for menor do que o número de parâmetros livres do modelo multinomial, então existe um ou mais parâmetros do modelo que não são identificáveis. Uma propriedade de modelos multinomiais é que os mesmos atingem o ranking máximo da matriz Jacobiana em praticamente qualquer ponto do espaço de respostas admissível (Bamber & van Santen, 1985), o que permite realizar o cálculo usando um vetor de dados qualquer - por exemplo, como o conjunto de dados obtido após a realização de um experimento ou através de simulação. O cálculo do ranking da matriz Jacobiana é fornecido automaticamente por diversos programas de análise de modelos multinominais, como o pacote MPTinR para R (Singmann & Kellen, 2013) e o programa multiTree (Moshagen, 2010).
O segundo critério alternativo se chama identificabilidade simulada (Rouder & Batchelder, 1998). De forma breve, este critério diz respeito à capacidade do modelo em gerar estimativas dos parâmetros, dentro de um intervalo de tolerância, ao longo de múltiplos pontos aleatórios do espaço de parâmetros. Mais especificamente, um algoritmo define uma localização aleatória no espaço de parâmetros e, com base nesses valores, gera estimativas das categorias de resposta, que por sua vez são utilizadas para re-estimar os parâmetros do modelo. Esse procedimento é repetido múltiplas vezes (e.g., 10.000 iterações) e a diferença entre valores iniciais (verdadeiros) e preditos são verificadas, de forma que se um ou mais parâmetros do modelo não são identificáveis, então será observado um desvio entre valores iniciais e preditos maior do que o valor de tolerância1. De conhecimento dos autores, apenas o programa multiTree possui opção para realizar identificação simulada de modelos multinomiais.
Estimação de parâmetros e ajuste do modelo
Com um MPT cujos parâmetros são identificáveis, é então possível estimar a probabilidade de ocorrência dos seus processos latentes para um conjunto de frequências das categorias de resposta. Uma forma tradicional de se obter estimativas de parâmetros livres é através da maximização da função de probabilidade do modelo (Myung, 2003) e, consequentemente, as estimativas obtidas com esse método são frequentemente referidas como estimativa de máxima verossimilhança (em inglês, maximum likelihood estimate - MLE). Esse procedimento é ilustrado na Figura 3 e, de forma breve, consiste em achar um conjunto de estimativas de parâmetros que está associado com o ponto mais "elevado" da função de probabilidade do modelo. Mais especificamente, para um MPT com  múltiplos parâmetros livres, a máxima local da função de probabilidade satisfaz as condições
múltiplos parâmetros livres, a máxima local da função de probabilidade satisfaz as condições  em um ou mais locais no espaço de parâmetros
em um ou mais locais no espaço de parâmetros  , sendo a máxima global a máxima local de maior valor da função de probabilidade do modelo. É a máxima global que usualmente é reportada, seguida pelo conjunto de MLE dos parâmetros de processos latentes,
, sendo a máxima global a máxima local de maior valor da função de probabilidade do modelo. É a máxima global que usualmente é reportada, seguida pelo conjunto de MLE dos parâmetros de processos latentes, 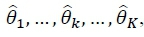 , associado à mesma.
, associado à mesma.
Existem múltiplos algoritmos capazes de maximizar a função de probabilidade de um modelo multinomial, como gradiente descendente, simplex e maximização da expectativa. Para MPT simples e processadores modernos, a diferença em desempenho entre grande parte dos algoritmos é imperceptível, pois ocorre em uma janela de milissegundos ou menos. Conforme o nível de complexidade de um modelo aumenta, as limitações e ineficiências de alguns algoritmos (e.g., gradiente descendente) se mostram mais problemáticas (e.g., maior tempo de execução; chance de ficar preso em uma máxima não global, a depender dos valores iniciais utilizados). No entanto, esses algoritmos têm em comum o objetivo de diminuir a distância entre valores observados das categorias de resposta e valores preditos pelo modelo. Essa medida de distância é um membro da família de divergência de potência (em inglês, power divergence) (Cressie & Read, 1984; Read & Cressie, 2012), definida pela equação

na qual 𝜆 é um parâmetro da família de divergência, 𝑥𝑖 é a frequência observada da categoria 𝑖, 𝑛 é a frequência total e Pr(𝑋𝑖|𝜽) é a probabilidade predita da categoria 𝑖. Alguns membros conhecidos da família de divergência de potência - como 𝜒2 de Pearson - podem ser derivados da Eq. 15 no limite do valor apropriado do parâmetro 𝜆 (e.g., 𝜆=−1). Em MPT, a medida de distância da família de divergência de potência mais frequentemente utilizada é a medida 𝐺2 do log da razão de verossimilhança. Essa estatística é derivada do lim𝜆 →0𝐷𝜆 e definida pela equação
→0𝐷𝜆 e definida pela equação

Assim, quanto menor for o valor de 𝐺2, menor será a discrepância entre valores observados e preditos e, de forma inversa, quanto maior for o valor de 𝐺2, maior será a discrepância entre valores observados e preditos (Note na Eq. 16 que quando a frequência predita é igual à observada, 𝑛×Pr(𝑋𝑖|𝜽)=𝑥𝑖, o valor de 𝐺2 será igual a zero). Por exemplo, se o conjunto de MLE de parâmetros de processos latentes de um MPT fornece uma boa descrição dos dados observados, espera-se que o valor de 𝐺2 obtido com o mesmo seja pequeno.
Para estabelecer um critério de "ajuste bom o suficiente", pesquisadores frequentemente se valem da propriedade de que a medida de 𝐺2 é assintoticamente distribuída como 𝜒2. Isso significa que, quando a quantidade de dados observados tende ao infinito, a medida de 𝐺2 se aproxima à medida de 𝜒2 e, portanto, inferências estatísticas sobre a qualidade de ajuste do modelo aos dados podem ser baseadas em tradicionais tabelas de distribuição de 𝜒2. Por definição, o ajuste de um modelo saturado não pode ser testado, em função de não existirem graus de liberdade (df) para realizar testes. Apenas o ajuste de modelos não saturados e cujos parâmetros são identificáveis pode ser avaliado através da medida de 𝐺2. Nesse último caso, o grau de liberdade do teste de ajuste é igual à diferença entre o número de categorias de respostas independentes e o número de parâmetros de processos latentes estimados. Em geral, isso se resume à fórmula 𝑑𝑓= 𝐼−𝐽−1, no qual 𝐼 é o número de categorias de respostas e 𝐽 é o número de parâmetros livres do modelo (a subtração por um implica que existe apenas uma única categoria de resposta dependente - isto é, apenas uma categoria de reposta que pode ser definida como sendo o complemento de outras - conforme apresentado na Eq. 8. Entretanto, em modelos multinomiais com múltiplas árvores, é possível que existam mais de uma categoria de reposta dependente, de forma que, ao invés da subtração por um na fórmula do df, o correto seria subtrair pelo número de categorias de resposta dependentes). Por exemplo, para um modelo com quatro parâmetros (𝐽=4) definidos ao longo de oito categorias de resposta (𝐼=8), a medida de 𝐺2 é avaliada com três graus de liberdade (𝑑𝑓= 8−4−1), de forma que o valor crítico de 𝜒2 para rejeitar a hipótese nula de ajuste do modelo é igual a 𝜒2(𝑑𝑓=3)=7.81 no nível convencional de 𝛼=0.05.
Em função da medida de 𝐺2 ser um teste de razão de verossimilhança, o mesmo princípio adotado para testes de ajuste de modelo também é adotado para testes de invariância de estimativas de parâmetros intra- e entrecondição experimental. Neste último caso, no entanto, os graus de liberdade do valor crítico serão iguais ao número de restrições (e.g., 𝜃1=𝜃2) entre os modelos comparados - isto é, modelo sem restrição vs. modelo com restrição - e o valor do teste de razão de verossimilhança será igual à diferença entre 𝐺2 dos modelos comparados.
Distribuição da função de probabilidade do modelo multinomial descrito nas Eq. 10-12 para um experimento hipotético em que a frequência observada das categorias de resposta foi X1 = 10, X2 = 20 e X3 = 15. Os parâmetros θ1 e θ2 são probabilidades de processos latentes. A seta max{L(θ|X)} aponta para a máxima global da função de probabilidade do modelo multinomial, que está associada com as estimativas de máxima verossimilhança dos parâmetros 𝜃̂1 = .45 e 𝜃̂2 = .40.
Considerações finais
O objetivo deste artigo foi introduzir os conceitos básicos em MPT de forma a facilitar o seu uso na pesquisa psicológica sobre processos latentes. De forma breve, foi mostrado como modelos de processos latentes são derivados de modelos puramente descritivos através da redução do espaço de parâmetros motivada por uma ou mais teorias psicológicas. O resultado é MPT que fornecem medidas simples de processos psicológicos (probabilidades) e que podem ser quantitativamente testados com dados reais. A existência de sofisticados programas de análise de MPT, como os pacotes MPTinR (Singmann & Kellen, 2013) e treeBUGS (Heck, Arnold, & Arnold, 2018) para o programa de análise estatística R (R Core Team, 2020), torna o uso desse formalismo algo quase trivial. Além disso, a área de MPT continua ativa e em expansão. Numa revisão publicada em 1999, Batchelder e Riefer (1999) reportaram 30 modelos multinomiais na área de cognição humana, enquanto numa revisão publicada em 2009, Erdfelder et al. (2009) reportaram mais de 70 modelos multinomiais espalhados em mais de 20 áreas de investigação psicológica. Espera-se que, com este artigo, estudantes e pesquisadores de língua portuguesa da área de Psicologia tenham maior exposição aos conceitos da MPT e possam inovar através da aplicação dessa ferramenta em pesquisas de interesse.
Agradecimentos
O conteúdo deste artigo foi baseado na oficina de trabalho ministrada pelo primeiro autor e organizada pelo segundo autor na Universidade de Brasília, bem como na apresentação realizada pelo primeiro autor durante o II Simpósio Internacional Mente-Cérebro. A preparação deste artigo foi financiada por uma bolsa do Programa Nacional de Pós-Doutorado (PNPD) da Fundação CAPES (PNPD/CAPES) ao primeiro autor.
Referências
Anderson, J. R., Betts, S., Bothell, D., Hope, R., & Lebiere, C. (2019). Learning rapid and precise skills. Psychological Review, 126(5), 727-760. https://doi.org/10.1037/rev0000152 [ Links ]
Bamber, D., & van Santen, J. P. (1985). How many parameters can a model have and still be testable? Journal of Mathematical Psychology, 29(4), 443-473. https://doi.org/10.1016/0022-2496(85)90005-7 [ Links ]
Bamber, D., & van Santen, J. P. (2000). How to assess a model's testability and identifiability. Journal of Mathematical Psychology, 44(1), 20-40. https://doi.org/10.1006/jmps.1999.1275 [ Links ]
Batchelder, W. H., & Riefer, D. M. (1986). The statistical analysis of a model for storage and retrieval processes in human memory. British Journal of Mathematical and Statistical Psychology, 39(2), 129-149. https://doi.org/10.1111/j.2044-8317.1986.tb00852.x [ Links ]
Batchelder, W. H., & Riefer, D. M. (1999). Theoretical and empirical review of multinomial process tree modeling. Psychonomic Bulletin & Review, 6(1), 57-86. https://doi.org/10.3758/BF03210812 [ Links ]
Brainerd, C. J., Gomes, C. F. A., & Moran, R. (2014). The two recollections. Psychological Review, 121(4), 563-599. https://doi.org/10.1037/a0037668 [ Links ]
Brainerd, C. J., Reyna, V. F., & Mojardin, A. H. (1999). Conjoint recognition. Psychological Review, 106(1), 160-179. https://doi.org/10.1037/0033-295X.106.1.160 [ Links ]
Bröder, A., & Schütz, J. (2009). Recognition ROCs are curvilinear-or are they? On premature arguments against the two-high-threshold model of recognition. Journal of Experimental Psychology: Learning, Memory, and Cognition, 35(3), 587-606. https://doi.org/10.1037/a0015279 [ Links ]
Buratto, L. G., Gomes, C. F. D. A., Prusokowski, T. D. S., & Stein, L. M. (2013). Inter-item associations for the Brazilian version of the Deese/Roediger-McDermott paradigm. Psicologia: Reflexão e Crítica, 26(2), 367-375. https://doi.org/10.1590/S0102-79722013000200017 [ Links ]
Cressie, N., & Read, T. R. (1984). Multinomial goodness‐of‐fit tests. Journal of the Royal Statistical Society: Series B (Methodological), 46(3), 440-464. https://doi.org/10.1111/j.2517-6161.1984.tb01318.x [ Links ]
Erdfelder, E., Auer, T. S., Hilbig, B. E., Aßfalg, A., Moshagen, M., & Nadarevic, L. (2009). Multinomial processing tree models: A review of the literature. Zeitschrift für Psychologie/Journal of Psychology, 217(3), 108-124. https://doi.org/10.1027/0044-3409.217.3.108 [ Links ]
Gomes, C. F., Brainerd, C. J., & Stein, L. M. (2013). Effects of emotional valence and arousal on recollective and nonrecollective recall. Journal of Experimental Psychology: Learning, Memory, and Cognition, 39, 663-677. [ Links ]
Gross, J. L., Yellen, J., & Zhang, P. (Eds.). (2003). Handbook of graph theory. Boca Raton, FL: CRC press. [ Links ]
Heck, D. W., Arnold, N. R., & Arnold, D. (2018). TreeBUGS: An R package for hierarchical multinomial-processing-tree modeling. Behavior Research Methods, 50(1), 264-284. https://doi.org/10.3758/s13428-017-0869-7 [ Links ]
Heck, D. W., & Erdfelder, E. (2016). Extending multinomial processing tree models to measure the relative speed of cognitive processes. Psychonomic Bulletin & Review, 23, 1440-1465. https://doi.org/10.3758/s13423-016-1025-6 [ Links ]
Hu, X., & Batchelder, W. H. (1994). The statistical analysis of general processing tree models with the EM algorithm. Psychometrika, 59(1), 21-47. https://doi.org/10.1007/BF02294263 [ Links ]
Hu, X., & Phillips, G. A. (1999). GPT. EXE: A powerful tool for the visualization and analysis of general processing tree models. Behavior Research Methods, Instruments, & Computers, 31(2), 220-234. https://doi.org/10.3758/BF03207714 [ Links ]
Kellen, D., & Klauer, K. C. (2020). Selecting amongst multinomial models: An apologia for normalized maximum likelihood. Journal of Mathematical Psychology, 97, 102367. https://doi.org/10.1016/j.jmp.2020.102367 [ Links ]
Klauer, K. C. (2010). Hierarchical multinomial processing tree models: A latent-trait approach. Psychometrika, 75(1), 70-98. https://doi.org/10.1007/s11336-009-9141-0 [ Links ]
Klauer, K. C., & Kellen, D. (2018). RT-MPTs: Process models for response-time distributions based on multinomial processing trees with applications to recognition memory. Journal of Mathematical Psychology, 82, 111-130. https://doi.org/10.1016/j.jmp.2017.12.003 [ Links ]
Knapp, B. R., & Batchelder, W. H. (2004). Representing parametric order constraints in multi-trial applications of multinomial processing tree models. Journal of Mathematical Psychology, 48, 215-229. https://doi.org/10.1016/j.jmp.2014.11.001 [ Links ]
Lehman, M., & Malmberg, K. J. (2013). A buffer model of memory encoding and temporal correlations in retrieval. Psychological Review, 120(1), 155-189. https://doi.org/10.1037/a0030851 [ Links ]
Matzke, D., Dolan, C. V., Batchelder, W. H., & Wagenmakers, E. J. (2015). Bayesian estimation of multinomial processing tree models with heterogeneity in participants and items. Psychometrika, 80, 205-235. https://doi.org/10.1007/s11336-013-9374-9 [ Links ]
Miles, M. B., Huberman, A. M., & Saldaña, J. (2014). Qualitative data analysis: A methods sourcebook. Thousand Oaks, CA: Sage. [ Links ]
Moshagen, M. (2010). multiTree: A computer program for the analysis of multinomial processing tree models. Behavior Research Methods, 42(1), 42-54. https://doi.org/10.3758/BRM.42.1.42 [ Links ]
Myung, I. J. (2003). Tutorial on maximum likelihood estimation. Journal of Mathematical Psychology, 47(1), 90-100. https://doi.org/10.1016/S0022-2496(02)00028-7 [ Links ]
R Core Team (2020). R: A Language and environment for statistical computing. R Foundation for statistical computing, Vienna, Austria. Recuperado de https://www.R-project.org/.
Ratcliff, R., Gomez, P., & McKoon, G. (2004). A diffusion model account of the lexical decision task. Psychological Review, 111(1), 159-182. https://doi.org/10.1037/0033-295X.111.1.159 [ Links ]
Read, T. R. C., & Cressie, N. A. C. (2012). Goodness-of-fit statistics for discrete multivariate data. New York, NY: Springer Science & Business Media. [ Links ]
Riefer, D. M., & Batchelder, W. H. (1988). Multinomial modeling and the measurement of cognitive processes. Psychological Review, 95(3), 318-339. https://doi.org/10.1037/0033-295X.95.3.318 [ Links ]
Rouder, J. N., & Batchelder, W. H. (1998). Multinomial models for measuring storage and retrieval processes in paired associate learning. In C. E. Dowling, F. S. Roberts, & P. Theuns (Eds.), Recent progress in mathematical psychology: Psychophysics, knowledge, representation, cognition, and measurement (pp. 195-225). New Jersey, NJ: Lawrence Erlbaum Associates Publishers. [ Links ]
Singmann, H., & Kellen, D. (2013). MPTinR: Analysis of multinomial processing tree models in R. Behavior Research Methods, 45, 560-575. https://doi.org/10.3758/s13428-012-0259-0 [ Links ]
Smith, J. B., & Batchelder, W. H. (2010). Beta-MPT: Multinomial processing tree models for addressing individual differences. Journal of Mathematical Psychology, 54(1), 167-183. https://doi.org/10.1016/j.jmp.2009.06.007 [ Links ]
Stahl, C., & Klauer, K. C. (2007). HMMTree: A computer program for latent-class hierarchical multinomial processing tree models. Behavior Research Methods, 39(2), 267-273. https://doi.org/10.3758/BF03193157 [ Links ]
Walker, G. M., & Hickok, G. (2016). Bridging computational approaches to speech production: The semantic-lexical-auditory-motor model (SLAM). Psychonomic Bulletin & Review, 23(2), 339-352. https://doi.org/10.3758/s13423-015-0903-7 [ Links ]
Wu, H., Myung, J. I., & Batchelder, W. H. (2010). Minimum description length model selection of multinomial processing tree models. Psychonomic Bulletin & Review, 17(3), 275-286. https://doi.org/10.3758/PBR.17.3.275 [ Links ]
 Endereço para correspondência:
Endereço para correspondência:
Carlos F. A. Gomes
carlos.fagomes@gmail.com
Recebido em: 03/02/2020
Aceito em: 17/07/2020
1 Ao estimar os parâmetros de um MPT com base em um conjunto de dados, o algoritmo de estimação necessita de um ponto em que as estimativas são consideradas boas o suficiente - chamado de critério de convergência. Por exemplo, em algoritmos de maximização da função de probabilidade, esse critério é de que novas mudanças nas estimativas resultam em uma mudança maior do que zero, porém desprezável, no valor da função de probabilidade do modelo. Neste exemplo, o algoritmo de maximização deve parar quando atinge o critério de convergência, já que novas iterações não resultarão em estimativas drasticamente diferentes das atuais se o algoritmo estiver de fato numa máxima global da função. Por esse motivo, o processo de estimação de parâmetros de um modelo não saturado sempre criará resíduo e, portanto, é necessário estabelecer um valor de tolerância para concluir que as estimativas sejam próximas o suficiente aos valores aleatórios iniciais (valores verdadeiros) da simulação.














